Modelación por el Método de Elementos Finitos (MEF), mediante el Software ANSYS del elemento placa

(1)

1 MODELACIÓN POR EL MÉTODO DE ELEMENTOS FINITOS (MEF), MEDIANTE EL

SOFTWARE ANSYS DEL ELEMENTO PLACA

EDWARD ESTID RUIZ GALEANO

CHRISTIAN CAMILO ARIAS GIRÓN

UNIVERSIDAD DISTRITAL FRANCISCO JOSÉ DE CALDAS

FACULTAD TECNOLÓGICA

INGENIERÍA CIVIL

BOGOTÁ D.C

(2)

2 MODELACIÓN POR EL MÉTODO DE ELEMENTOS FINITOS (MEF), MEDIANTE EL

SOFTWARE ANSYS DEL ELEMENTO PLACA

EDWARD ESTID RUIZ GALEANO

CHRISTIAN CAMILO ARIAS GIRÓN

MONOGRAFÍA PARA OPTAR POR EL TITULO DE INGENIERO CIVIL

DIRECTOR DEL PROYECTO DE GRADO

PAULO MARCELO LÓPEZ PALOMINO

INGENIERO CIVIL- MAGISTER EN INGENIERÍA CIVIL ÉNFASIS ESTRUCTURAS DOCENTE DE TIEMPO COMPLETO OCASIONAL

UNIVERSIDAD DISTRITAL FRANCISCO JOSÉ DE CALDAS

FACULTAD TECNOLÓGICA

INGENIERÍA CIVIL

BOGOTÁ D.C

(3)

3 Nota de aceptación

Firma del Jurado

(4)

4 DEDICATORIA

(5)

5 AGRADECIMIENTOS

Un proyecto sin importar su finalidad u orientación es un conjunto de conocimientos compartidos por distintas partes, donde se requiere acompañamiento, constancia, y un gran desempeño de los involucrados; para así generar un producto educativo de excelente calidad con miras al fortalecimiento de los saberes de la humanidad.

Agradecemos la colaboración de familiares y amigos que nos brindan su cariño e incondicional compañía durante no solo el camino académico sino también de la vida misma. De la misma manera a la Universidad Distrital por los años que nos otorgaron en nuestra formación profesional y personal.

Agradecemos la revisión, seguimiento y conocimiento continúo entregado por nuestro tutor, El Ingeniero Paulo Marcelo López Palomino, Docente de tiempo completo ocasional del área de estructuras de la Universidad Distrital Francisco José de Caldas – Facultad Tecnológica del Proyecto Curricular de Ingeniería Civil.

(6)

6 TABLA DE CONTENIDO

Pág.

RESUMEN

INTRODUCCIÓN

1 OBJETIVOS ... 18

1.1 OBJETIVO GENERAL ... 18

1.2 OBJETIVOS ESPECÍFICOS ... 18

2 MARCO TEÓRICO ... 19

2.1 DESCRIPCIÓN GENERAL ... 19

2.2 HISTORIA ... 19

2.3 CONCEPTOS GENERALES DEL MÉTODO ... 22

2.3.1 Tipos de Elementos de modelación ... 23

3 DESARROLLO DEL ELEMENTO VIGA ... 27

3.1 RIGIDEZ DE LA VIGA ... 27

3.1.1 Ejemplo comparativo ... 30

4 DESARROLLO DEL ELEMENTO PLACA ... 34

4.1 CONCEPTOS BÁSICOS DE LA PLACA A FLEXIÓN ... 35

4.1.1 Suposiciones básicas de geometría y deformación ... 35

4.1.2 Suposiciones de Kirchhoff ... 36

4.1.3 Rotaciones Esfuerzos/Deformaciones ... 38

4.2 DEDUCCIÓN DE LA MATRIZ DE RIGIDEZ Y ECUACIONES DEL ELEMENTO PLACA A FLEXIÓN ... 39

4.3 ALGUNAS COMPARACIONES NUMÉRICAS DEL ELEMENTO PLACA ... 44

4.4 SOLUCIÓN POR COMPUTADORA A UN PROBLEMA DE PLACA A FLEXIÓN ... 46

4.4.1 Ejemplo ... 47

5 DESARROLLO DE ESFUERZOS PLANOS Y DEFORMACIÓN PLANA (ECUACIÓN DE RIGIDEZ) ... 50

5.1 EJEMPLO DE ESFUERZOS PLANOS Y DEFORMACIONES PLANAS ... 51

(7)

7

6.1 OBTENCIÓN DE LA MALLA. ... 59

7 MODELACIÓN DEL ELEMENTO PLACA ... 61

7.1 MODELO A ... 64

7.1.1 CARGA PUNTUAL, MODELACIÓN EN SAP 2000 (MANUAL DE USO) 64 7.1.2 CARGA PUNTUAL, MODELACIÓN EN ANSYS (MANUAL DE USO) .... 77

Introducción. ... 77

Consideraciones: ... 77

7.2 MODELO B ... 99

7.2.1 CARGA DISTRIBUIDA, MODELACIÓN EN SAP 2000 ... 99

7.3 CARGA DISTRIBUIDA, MODELACIÓN EN ANSYS ... 103

8 ANÁLISIS DE RESULTADOS ... 109

9 CONCLUSIONES ... 112

10 RECOMENDACIONES ... 114

(8)

8 LISTA DE FIGURAS

Pág.

Figura 1.Cigüeñal montado en el bloque motor ... 21

Figura 2. Modelación del cigüeñal ... 22

Figura 3. Discretización del cigüeñal ... 22

Figura 4. Elemento tipo barra ... 23

Figura 5. Forma alternativa del elemento viga. Orientación del Nodo K ... 24

Figura 6. Elementos Membrana. Triangulares ... 25

Figura 7. Elementos Membrana. Cuadrados ... 25

Figura 8. Elementos tipo ladrillo o bloque... 26

Figura 9. Elemento viga con desplazamientos nodales positivos, rotaciones, fuerzas y momentos ... 28

Figura 10.Sentido de orientación de los momentos flectores y fuerzas cortantes . 28 Figura 11.Curva flexionada de la viga ... 29

Figura 12. Sección de una chimenea modelada como Elemento Finito (Vista rotada de 45º) (584 vigas y 252 placas planas son los elementos) ... 35

Figura 13.Placa delgada básica que muestra carga transversal y dimensiones ... 36

Figura 14.Corte diferencial de placa de espesor t (a) Antes de ser cargada y (b) Desplazamientos del punto P después de ser cargada, basada en la teoría de Kirchhoff ... 37

Figura 15.Elemento diferencial de una placa con (a) Esfuerzos mostrados en los bordes de una placa y (b) Diferenciales de momentos y fuerzas ... 39

Figura 16.Elemento rectangular placa básico con nodos y grados de libertad... 40

Figura 17. Comparaciones Numéricas: Formulaciones del Elemento placa cuadrada ... 45

Figura 18.Comparaciones numéricas para una placa cuadrada simplemente soportada sujeta a la carga central. Formulaciones de elementos triangulares .... 46

Figura 19. Placa de evaluación ... 47

Figura 20.Desplazamientos de la placa de ejemplo ... 48

Figura 21. Modelo de elementos viga y placa combinados en el centro de línea de los elementos ... 49

Figura 22. Deflexión vertical para una parte del modelo ... 49

Figura 23. Modelo que muestra elementos de viga desplazada para el elemento placa ... 50

(9)

9 Figura 25.Plano de esfuerzos (a) carga horizontal en una presa (b) carga vertical en

un tubo ... 51

Figura 26. Elemento placa, sujeta a esfuerzos de tensión ... 52

Figura 27. Discretización de la placa ... 52

Figura 28. Elemento 1 de la placa discretizada ... 53

Figura 29. Elemento 2 de la placa discretizada ... 55

Figura 30. Elemento área tipo Shell ... 64

Figura 31. Selección del Elemento y sistema de unidades ... 65

Figura 32. Asignación de propiedades geométricas ... 66

Figura 33. Definición del material ... 67

Figura 34. Definición del material, Concreto 3000Psi ... 67

Figura 35. Definición de las áreas ... 68

Figura 36. Elemento área Tipo Shell Thin ... 68

Figura 37. Elemento área Tipo Shell Thin, característica ... 69

Figura 38. Elemento placa, SAP 2000... 70

Figura 39. Selección de tipos de apoyos ... 70

Figura 40. Apoyos Empotrados ... 71

Figura 41. Patrón de carga ... 72

Figura 42. Carga Puntual (Dirección eje Z, negativo) ... 73

Figura 43. Carga Puntual (Dirección eje Z, negativo) ... 74

Figura 44. División de la placa en elementos finitos ... 74

Figura 45.Analisis de carga ... 75

Figura 46. Deformación en función del número de elementos finitos ... 75

Figura 47. Deformación de una placa de 400 elementos finitos ... 76

Figura 48. Análisis de resultados, tabulación de SAP 2000 ... 76

Figura 49. Interfase de modelación de ANSYS ... 78

Figura 50. Interfase Estructural de ANSYS ... 79

Figura 51. Interfase de requerimientos generales de ANSYS ... 80

Figura 52. Interfase de geometría de ANSYS ... 80

Figura 53.Contorno del elemento ... 81

Figura 54.Dimensionamiento del elemento ... 82

Figura 55.Atributos geométricos ... 82

Figura 56.Generación del solido ... 83

Figura 57.Evaluación de la geometría ... 83

Figura 58.Aceptación de la geometría ... 84

Figura 59.Interfase del mallado ... 84

Figura 60.Resolución del mallado ... 85

Figura 61.Controles de tamaño ... 85

Figura 62.Tamaño del elemento ... 86

Figura 63.Verificación del mallado ... 87

(10)

10

Figura 65.Visualización del mallado ... 88

Figura 66.Verificación del mallado ... 88

Figura 67.Interfase de parámetros físicos ... 89

Figura 68.Vinculación de atributos ... 89

Figura 69.Asignación y creación de materiales ... 90

Figura 70.Validación de materiales ... 90

Figura 71.Condiciones de borde o de contorno ... 91

Figura 72.Designación de apoyos ... 91

Figura 73.Asignación de la carga ... 92

Figura 74.Punto de origen de la carga ... 92

Figura 75.Aceptación de la carga ... 93

Figura 76.Fijación de los apoyos ... 93

Figura 77.Apoyos de tercer grado; empotrados ... 94

Figura 78.Visualización de los apoyos ... 95

Figura 79.Opciones de solución ... 95

Figura 80.Resolver Física... 96

Figura 81.Verificación de los parámetros físicas ... 96

Figura 82.Evaluación estructural ... 97

Figura 83.Evaluación estructural ... 98

Figura 84.Esfuerzos equivalentes ... 98

Figura 85.Esfuerzos equivalentes ... 99

Figura 86. Patrón de carga distribuida, SAP 2000 ... 100

Figura 87. Carga de área, uniforme Shell, SAP 2000 ... 100

Figura 88. Configuración de la carga por área, SAP 2000 ... 101

Figura 89. Elementos finitos, carga distribuida, SAP 2000 ... 101

Figura 90.Deformaciones debido a la carga distribuida, SAP 2000 ... 102

Figura 91.Esfuerzos debido a la carga distribuida, SAP 2000... 102

Figura 92.Definición de carga Distribuida, ANSYS ... 103

Figura 93.Condiciones de borde, carga Distribuida, ANSYS... 103

Figura 94.Opciones de solución, ANSYS ... 104

Figura 95 .Atributos físicos, ANSYS ... 105

Figura 96 .Fuerzas de reacción, ANSYS ... 105

Figura 97 .Reacción en los apoyos, ANSYS ... 106

Figura 98 .Esfuerzos equivalentes, ANSYS ... 107

Figura 99 .Esfuerzos en los apoyos, ANSYS ... 107

(11)

11 LISTA DE ILUSTRACIONES

Pág.

Ilustración 1.Esquema general del Elemento Finito ... 23

Ilustración 2. Viga de ejemplo comparativo ... 30

Ilustración 3. Viga compuesta de un solo elemento ... 31

Ilustración 4. Reacciones de la viga, método matricial ... 32

Ilustración 5. Elementos de la viga, Método MEF ... 32

Ilustración 6. Convergencia de los desplazamientos ... 34

Ilustración 7.Discretización adecuada ... 59

Ilustración 8.Triangulación del dominio de una superficie ... 60

Ilustración 9.Mallado de elemento solido (3D) ... 60

Ilustración 10.Placa bajo carga Puntual, Modelo A ... 62

Ilustración 11.Placa bajo carga Distribuida, Modelo B... 63

Ilustración 12. Convergencia de la carga Puntual ... 111

(12)

12 LISTA DE TABLAS

Pág.

(13)

13 GLOSARIO

ANSYS: (Swanson Analysis System) Es utilizada en la experiencia de elemento finito y dinámica de fluido computacional. El software se enfoca en la simulación, bajo la teoría de elemento finito para estructuras y volúmenes para fluidos. (Cubo Perez, 2010)

ASIMETRÍA: Es la carencia de simetría de un elemento u objeto. No existe correspondencia en cuanto a las dimensiones, las formas y las ubicaciones de diversos componentes que conforman un todo. (Beltrán, 1998-99)

CONTORNO - CONDICIONES DE FRONTERA: También denominadas en matemáticas como problemas de valor o condición, de borde o contorno, indican las soluciones de una ecuación diferencial. Son los parámetros mínimos que se deben cumplir describir y obtener las soluciones deseadas a un comportamiento. (Logan, 2007)

DEFORMACIÓN: Indica la inconsistenciade un material, objeto o elemento frente a la imposición de cargas externas, donde dejan su forma natural o habitual. En resistencia de materiales las deformaciones son desviaciones de un punto con respecto a su posición original, indicando trasformaciones permanentes o reversibles en cuanto a su forma. (Vargaz Felix, 2010)

DOMINIO: Es el conjunto de existencia de la función, en términos generales son los valores para los cuales la función está definida. Además, considera el conjunto de todos los objetos que puede transformar. (Logan, 2007)

(14)

14 ENERGÍA POTENCIAL: Es la energía mecánica asociada a la localización de un cuerpo dentro de un campo de fuerzas o a la existencia de un campo de fuerzas en el interior de un cuerpo. Esta es una consecuencia de que el sistema de fuerzas que actúa sobre el mismo sea conservativo. (Periago Esparza, 2011)

ESFUERZO: Aplicación de una fuerza por unidad de área. En análisis estructural nos referimos a las deformaciones unitarias debido a las cargas que actúan sobre ellos, los esfuerzos normales son perpendiculares a la cara de análisis. (Periago Esparza, 2011)

GRADO DE LIBERTAD: Número mínimo de coordenadas independientes necesarias para definir completamente el estado deformado de la estructura en cualquier instante. (Otero Pereiro, Novo Soto, & Fernandez Salgado, Junio 1997)

MALLA: Se define como la unión de elementos y nodos que se convierte en la estructura central para el Análisis por Elementos Finitos. (Frias Valero, 2004)

MATRIZ DE RIGIDEZ: El significado físico de la matriz de rigidez indica las fuerzas unitarias necesarias para producir un desplazamiento unitario. Desde el punto de vista operativo relaciona los desplazamientos incógnita de una estructura con las fuerzas conocidas, lo cual permite encontrar las reacciones, esfuerzos internos y tensiones en cualquier punto de la estructura. (Logan, 2007)

MEF: Acrónimo del término Método de Elementos Finitos, método numérico ampliamente utilizado para la solución de problemas de Ingeniería y física, dado que permite resolver sistemas de ecuaciones diferenciales parciales, las cuales se dificultan analíticamente o con modelos matemáticos simples. (Beltrán, 1998-99)

(15)

15 MODULO DE ELASTICIDAD: También conocido como módulo de Young es un parámetroque caracteriza el comportamiento de un material elástico, según la dirección en la que se aplica la fuerza axial. Para un material elástico lineal e isotrópico, el módulo tiene el mismo valor para una tracción que para una compresión. (Beltrán, 1998-99)

NODO: Es un punto determinado del dominio, posee características de lo localización, dentro de un plano cartesiano, a menudo, el vértice de muchos elementos, llamado también como punto nodal. (Beltrán, 1998-99)

TRABAJO VIRTUAL: Es un método utilizado en resistencia de materiales para el cálculo de desplazamientos reales en estructuras isostáticas e hiperestáticas, y para el cálculo de incógnitas que no podemos abordar con el equilibrio en estructuras hiperestáticas. Es un método energético, que indica el trabajo realizado por todas las fuerzas externas en trabajo interno o energía de deformación. (Logan, 2007)

(16)

16 RESUMEN

El Método de Elementos Finitos (MEF) es un método numérico ampliamente utilizado para la solución de problemas de Ingeniería y física, dado que permite resolver sistemas de ecuaciones diferenciales parciales, las cuales se dificultan analíticamente o con modelos matemáticos simples. Este método se fundamenta en la discretización de un medio continuo, es decir dividir la estructura de estudio en una serie de subdominios “Elementos Finitos” con determinadas condiciones de vínculo entre los mismos, con el fin de generar sistemas lineales, que permitan la evaluación del medio, con la ayuda de herramientas computacionales, debido a que el número de incógnitas es directamente proporcional al número de nodos generados en la discretizacion.

En el campo de la Ingeniería Civil es indispensable la determinación de desplazamientos, deformaciones y esfuerzos que se generan en los distintos elementos estructurales cuando interactúan con cualquier tipo de excitación externa. Métodos de análisis como el matricial poseen limitaciones de solución debida a su naturaleza puramente discreta.

(17)

17 INTRODUCCIÓN

La determinación de las características de resistencia frente a solicitaciones externas de una estructura es de suma importancia, en campos como la Ingeniería Civil, la Aeronáutica, la Mecánica de sólidos, la Mecánica de fluidos y los relacionados con la transferencia de calor entre otros.

Mediante las simulaciones se logra una agilización continua en el proceso de ingeniería básica de un proyecto, al reducir la cantidad de prototipos, permitiendo la predicción de las concentraciones de esfuerzos, deformaciones, frecuencias naturales y modos de vibración de las partes específicas de la estructura analizada. La articulación del MEF y del software de modelación permitirá realizar un análisis estructural del Elemento Placa, determinando las características anteriormente mencionadas, teniendo en cuenta que los programas de modelación estructural actuales concentran su desarrollo en los conceptos del MEF es de gran relevancia desarrollar el concepto, su justificación y su adecuada utilización en el campo de estudio para posteriores proyecciones. Debido a que gran parte de los métodos clásicos de análisis estructural se basan en el estudio de elementos propiamente discretos como el caso del análisis matricial, dejando a un lado estructuras de carácter continúo es necesario hondar en las bases teóricas del Método de Elementos Finitos, empleando los conceptos de elasticidad bidimensional desarrollo para tal fin en la primera mitad del siglo XX.

Para el desarrollo de la simulación de elemento de estudio es imperante abordar los conceptos fundamentales del MEF, dada la naturaleza del mismo se estimará los errores asociados a los resultados obtenidos en el estudio. Esta modelación y sus fundamentos teóricos brindarán soporte a construcciones futuras en el mismo campo de ejecución estructural, además de ser una guía de conocimiento para aquellos interesados en el área de estructuras en la UD.

(18)

18 1 OBJETIVOS

1.1 OBJETIVO GENERAL

 Simular el comportamiento del Elemento Placa en el software ANSYS bajo el fundamento del Método de Elementos Finitos (MEF)

1.2 OBJETIVOS ESPECÍFICOS

 Establecer el tipo de mallado a utilizar en la modelación en ANSYS 17.0  Modelar el elemento placa en SAP 2000

 Determinar las deformaciones y esfuerzos que sufre la placa bajo las cargas impuesta en ambos modeladores

 Generar un manual de uso e instrucciones para modelación de futuros elementos estructurales en el ambiente de ANSYS 17.0

(19)

19 2 MARCO TEÓRICO

2.1 DESCRIPCIÓN GENERAL

El método de Elementos Finitos (MEF) o por sus siglas en ingles FEM, es un método de carácter numérico para la resolución de ecuaciones diferenciales e integrales, utilizados en diversos problemas de Ingeniería y física. Se basa en la división de un cuerpo, estructura u objeto en una serie de subdominios (Elementos Finitos); donde se cuenta con ecuaciones integrales de cada uno. El conjunto de estos elementos se llama discretización. Dicha discretización genera (n) elementos; los cuales adquieren nodos o puntos de interés de adyacencia con los otros elementos, las agrupaciones de nodos forman elementos, y estos a su vez adquieren un subdominio del campo original. Finalmente se genera un proceso de mallado para la unión de los elementos generados. (Vargaz Felix, 2010)

Los cálculos se realizan sobre el mallado; involucrando relaciones de adyacencia entre los nodos, siendo estos últimos puntos representativos que conforman cada elemento. Cada nodo cuenta con grados de libertad “Conjunto de Variables o incógnitas definidas “Dada la complejidad de solución analítica de las ecuaciones generadas es indispensable del uso de ordenadores para calcular inicialmente los desplazamientos, luego las deformaciones y tensiones mediante relaciones cinemáticas o constitutivas de cada elemento y globalmente. El error asociado a este método difiere de la convergencia generada, es decir; entre mayor sea el número de elementos finitos generados, mayor será el número de incógnitas desarrolladas pero mayor proximidad para la solución numérica.

En conclusión, el MEF se basa en la discretización de un continuo con infinitos grados de libertad transformándolo en un problema discreto con un número de grados de libertad finitos. Las ventajas de este método con respecto a otros “Diferencias Finitas”, radica en el tratamiento de geométricas de alta complejidad, la generación de condiciones generales de borde o contorno, fundamentos teóricos sólidos y la posibilidad de estimación del error; lo cual genera alta confiabilidad en el mismo.

2.2 HISTORIA

(20)

20 desplazamientos virtuales para tales sistemas, uno de los principales problemas radicaba en el cálculo de los puentes sometidos a cargas en movimiento “Líneas de influencia”, dado el efecto del movimiento de la carga sobre los esfuerzos. En el diseño de estructuras es necesario conocer las deflexiones o los desplazamientos en solo algunas uniones de tal manera se desarrolló el “Teorema de Castigliano”, u otros métodos para la solución de armaduras o estructuras estáticamente indeterminadas. De lo anterior se deduce que el MEF no constituye un descubrimiento dentro del campo de Resistencia de materiales y de la teoría de la elasticidad, si no que sienta sus bases sobre estos.

Arquímedes utilizo un método similar para determinar el área y volumen de algunos sólidos, por ejemplo, dividió los objetos en elementos geométricos más sencillos. Esta fue un aproximación vana al concepto actual del método donde se premisa que “la energía del sistema, es igual a la suma de la energía de cada elemento”, y para tal afirmación él necesitaba la definición de derivadas, no concebidas en ese entonces, sino siglos después (Gallagher, 1975, pág. 78). La primera aparición del método o concepto del mismo en la Ingeniería Estructural data entre los años 50 al 60; para la solución de ecuaciones diferenciales en derivadas parciales en el campo elástico; durante el año de 1941 se desarrollaron las bases del método con la solución de problemas bajo el método de trabajo del marco [Hrenikoff], años más tarde Courant contribuyó con la interpolación polinomial por partes, para subregiones de carácter triangular en problemas de torsión.

Las ideas básicas del MEF se originaron en el análisis estructural de las Aeronaves. Para la primera mitad del siglo XX se involucra el método por rigidez directo formulado y perfeccionado por Turner, dichas matrices aplicadas para armaduras, vigas y otros elementos. No fue sino hasta 1960 que el término de Elemento Finito fue incorporado por Clough, utilizado en ese entonces para el análisis de esfuerzos, flujo de fluidos y transferencia de calor. El primer libro de elementos finitos fue publicado por Zienkiewicz y Cheng en 1967, donde se abordan temas del campo elástico, plástico y elásto-plástico en solidos continuos, homogéneos, isotrópicos y aniso trópicos.

(21)

21 como “Cosmos” para el análisis de las estructuras de los trasbordadores. (Vargaz Felix, 2010)

En la actualidad existen métodos más avanzados que el MEF como lo es el Método de Elementos de Contorno (MEC) desarrollado en la década de los 60 con la misma finalidad, pero cuya principal ventaja radica en la reducción de la magnitud de los datos a manipular, lo que ocasiona una reducción en la capacidad de almacenamiento y operación de los ordenadores. La solución por este método se realiza a partir de una ecuación integral que relacione las variables del contorno.

Un ejemplo claro de la importancia del MEF y su relación con la simulación de un medio continuo se puede evidenciar en la Ingeniería Naval. Consideremos el estudio y diseño del cigüeñal (Figura 1), donde se aprecia la complejidad y robustez de la estructura, casi imposible de solucionar analíticamente. El estudio sobre este elemento permite predecir las concentraciones de tensiones, deformaciones, frecuencias y los modos de vibración en puntos específicos de la estructura, además de lograr una agilización en el proceso de ingeniería básica del proyecto.

Figura 1.Cigüeñal montado en el bloque motor

Fuente: UCA, Universidad de Cádiz

(22)

22 Figura 2. Modelación del cigüeñal

Figura 3. Discretización del cigüeñal

Fuente: (Cubo Perez, 2010)

La figura 2 muestra el proceso de modelamiento que se debe realizar en cual sea el tipo de software empleado, en este caso se uso el CATIA , para posteriormente discretizar dicho elemento continuo como se representa en la figura 3. Lo anterior expuesto es una idea basica del estudio a realizar del Elemento Placa mediante el sftware ANSYS.

2.3 CONCEPTOS GENERALES DEL MÉTODO

(23)

23 el elemento, por ende, generar grados de libertad finitos a partir de infinitos; en cualquier elemento que se desee analizar por este método podemos distinguir lo siguiente (Ilustración 1)

Ilustración 1.Esquema general del Elemento Finito

Fuente: (Logan, 2007) 2.3.1 Tipos de Elementos de modelación

Los elementos dependen de las restricciones de frontera, tipo de carga y de la geometría del elemento original.

2.3.1.1 Barra tipo armazón: Se utilizan para modelar torres, puentes y edificios. Generan tres grados de libertad (𝑢, 𝑣, 𝑤) con respecto a los desplazamientos, y poseen dos nodos. Pueden emplearse en las siguientes situaciones:

 La longitud del elemento con respecto a su ancho esta entre 8 y 10 veces  Las uniones del elemento no transmiten momentos

 Las fuerzas externas son aplicadas únicamente en los nodos o en las articulaciones.

Figura 4. Elemento tipo barra

(24)

24 2.3.1.2 Elementos de Viga: Este tipo de elemento ofrece resistencia a fuerzas y momentos, usados para modelar torres de transmisión, puentes y pórticos. Además, soportan momentos flectores y de torsión.

Los elementos básicos de las vigas son las fuerzas de inercia, los empotramientos y las cargas intermedia o en los vanos. Poseen 3 nodos

(𝑥, 𝑦, 𝑧) en el campo tridimensional, el nodo con respecto al eje “z” específica los ejes fuertes o débiles (inercia); la implementación de vigas se hace cuando:

 La longitud del elemento es mayor a su ancho.

 La sección transversal y sus propiedades son constantes  Poseen la capacidad de transferir momentos

 Tiene la capacidad de distribuir de cargas en su longitud

Figura 5. Forma alternativa del elemento viga. Orientación del Nodo K

Fuente: (Olmedo Salazar, 2015)

2.3.1.3 Elemento de membrana: Simulan solidos de poco grosor que no tiene afectación de esfuerzos normales. Las membranas no tienen grados de libertad de rotación, pero si los necesarios de traslación. Formado por tres o cuatro nodos, permitiendo la modelación de redes y tejidos; y son empleados cuando:

 El espesor del elemento es muy pequeño comparado con la longitud o su ancho.

(25)

25 Figura 6. Elementos Membrana. Triangulares

Fuente: (Olmedo Salazar, 2015)

Figura 7. Elementos Membrana. Cuadrados

(26)

26 2.3.1.4 Elementos elásticos de dos dimensiones: Se utilizan para analizar objetos como rodamientos y empaques o estructuras como presas. Poseen grados de libertad en traslación, mas no en rotación; además de estar formados por tres o cuatro nodos paralelos al eje YZ. Se emplean cuando. (Se utilizan los mismos elementos de la figura 6 y 7)

 Para modelar la sección transversal de un componente  Dibujar el modelo en el plano YZ

 Cuando no existe deformación en el sentido del eje X, pero pueden existir esfuerzos en dicha dirección, por ejemplo, en el caso de las presas.

2.3.1.5 Elementos tipo ladrillo o bloque: Empleados para modelar ruedas y aspas de turbinas (en el caso de los bloques básicos), poseen seis u ocho nodos para formar caras en 3D. Dichos bloques generan tres grados de libertad de traslación, pero ninguno de rotación, y se emplean cuando:

 Se desea conocer el resultado de esfuerzos alineados al grosor del elemento

 Solo hay fuerzas aplicadas y no momentos  El modelo tiene una fuerza hidrostática aplicada

(27)

27 Fuente: (Olmedo Salazar, 2015)

2.3.1.6 Elemento tipo placa: Permiten modelar placas automotrices y contenedores de pared delgada, poseen tres o cuatro nodos. Se pueden emplear grados de libertad de rotación, desplazamiento, fuerzas nodales, momentos, presión normal, gravedad, fuerzas centrifugas entre otros, y se emplean cuando:

 Relación entre ancho y largo es de 1 a 10  Desplazamientos relativamente pequeños  El elemento permanece plano

 Distribución de esfuerzos es lineal

 No hay rotación en la dirección normal del elemento

La selección adecuada del tipo de elemento y el método empleado de resolución incrementan o simplifican generación de resultados claros y confiables.

3 DESARROLLO DEL ELEMENTO VIGA

Se ejemplifica el elemento viga debido a que el comportamiento a nivel estructural, en comparación con un elemento placa, difiere en sus principios en el análisis bidimensional que se desarrolla, para ser más claros; un elemento viga se analiza estructuralmente desde una dimensión, generando reacciones, giros y momentos torsores, por el contrario una placa se analiza en toda su extensión de área, por lo tanto el número de fuerzas resultantes será mayor al del análisis de la viga pero con condiciones estructurales similares. Es por esta razón que se desarrolla inicialmente el análisis MEF de la viga, para posteriormente extrapolar el mencionado análisis al elemento placa.

En este capítulo se desarrolla la matriz de rigidez para el elemento viga, esta es la más común de todos los elementos estructurales como se evidencia en las edificaciones, puentes, torres, y en muchas otras estructuras. El elemento viga se considera recto y con una sección transversal constante. Primero deduciremos la matriz de rigidez usando los principios para la teoría de la una viga simple bajo la determinación de las funciones de forma y los coeficientes asociados.

Se presenta un ejemplo simple que ilustra el ensamblaje de la matriz de rigidez del elemento viga con la deducción de la ecuación de la curvatura.

3.1 RIGIDEZ DE LA VIGA

(28)

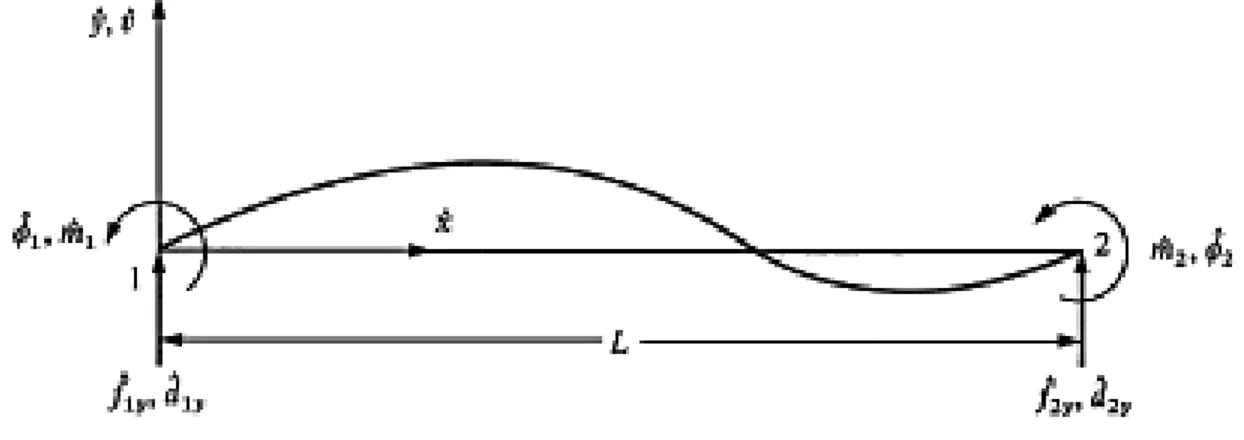
28 transversales a los nodos locales están dados por 𝑑̂1𝑦 y las rotaciones por ∅̂1. Las fuerzas del nudo local están dadas por 𝑓̂_1𝑦 y los momentos flectores por 𝑚̂₁ como se muestra. Inicialmente despreciamos todos los efectos axiales.

Para todos los nodos se debe seguir la siguiente convención de signos:

1. Los momentos son positivos en sentido opuesto a las manecillas del reloj 2. Las rotaciones son positivas en el sentido opuesto de las manecillas del reloj 3. Las fuerzas son positivas en la dirección positiva de 𝑦

4. Los desplazamientos son positivos en el sentido positivo de 𝑦

Figura 9. Elemento viga con desplazamientos nodales positivos, rotaciones, fuerzas y momentos

Fuente: The First Course in the Finite Element-Logan

La figura 10 indica la convención de los signos usada en la teoría simple de una viga para las fuerzas cortantes positivas 𝑣̂ y los momentos flectores 𝑚̂.

Figura 10.Sentido de orientación de los momentos flectores y fuerzas cortantes

(29)

29 Cuando la viga se deforma a causa de una carga, dicha deformación puede ser descrita de forma analítica, como se muestra en la siguiente figura

Figura 11.Curva flexionada de la viga

La ecuación de la curvatura permite relacionar el momento con el radio de curvatura mediante:

𝑑2_𝑣 𝑑𝑥2 =

𝑀 𝐸𝐼

Resolviendo la ecuación para 𝑀 y sustituyendo el resultado se obtiene

𝑑2 𝑑𝑥2(𝐸𝐼

𝑑2_𝑣

𝑑𝑥2) = −𝑤(𝑥)

Para la constante 𝐸𝐼 y solo una fuerza nodal y momentos, llegamos a

(𝐸𝐼𝑑_𝑑𝑥4𝑣₄) = 0

A continuación, se presenta la matriz de rigidez general del elemento viga (sin deformación debida al corte transversal)

{ 𝑓_1𝑦 𝑚1 𝑓2𝑦 𝑚2

} =𝐸𝐼_𝐿₃[

12 6𝐿

6𝐿 4𝐿2 −12

6𝐿 −6𝐿2𝐿2

−12 6𝐿

−6𝐿 2𝐿2 12

−6𝐿 −6𝐿4𝐿2 ]

{ 𝑑1𝑦

∅1 𝑑2𝑦

∅₂}

(30)

30 𝑘 = | | | 12𝐸𝐼 𝐿3 6𝐸𝐼 𝐿2 6𝐸𝐼 𝐿2 4𝐸𝐼 𝐿 −12𝐸𝐼 𝐿3 6𝐸𝐼 𝐿2 −6𝐸𝐼 𝐿2 2𝐸𝐼 𝐿 −12𝐸𝐼 𝐿3 6𝐸𝐼 𝐿2 −6𝐸𝐼 𝐿2 2𝐸𝐼 𝐿 12𝐸𝐼 𝐿3 −6𝐸𝐼 𝐿2 −6𝐸𝐼 𝐿2 4𝐸𝐼 𝐿 | | |

La forma matricial indica que 𝑘 relaciona las fuerzas transversales y los momentos flectores con los desplazamientos transversales y rotaciones, sin embrago los efectos axiales son despreciables.

3.1.1 Ejemplo comparativo

El siguiente ejemplo busca comparar el método matricial, tradicionalmente utilizado para el cálculo estructural y el MEF, para la solución de la viga en voladizo propuesta, para denotar además la convergencia entre ambos en cuanto a la estimación de las reacciones.

Ilustración 2. Viga de ejemplo comparativo

Fuente: Propia

(31)

31 Ilustración 3. Viga compuesta de un solo elemento

Fuente: Propia

Se evidencia que existe dos grados de libertad, y se debe al desplazamiento y a la rotación en el nudo 2 por consiguiente, puesto que el nodo 1 está totalmente restringido,

𝑣₁ = ∅₁ = 0

Además 𝐸𝐼 es

𝐸𝐼 = 20 ∗ 106_∗0.3 ∗ 0.43

12 = 32000𝑘𝑁 ∗ 𝑚2

El elemento 1-2 matricialmente estaría dado por

{ 𝑓12 𝑚₁₂

𝑓₂₁ 𝑚₂₁

} =𝐸𝐼_𝐿₃[ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮⋮

−12 6𝐿

−6𝐿 2𝐿2 12

−6𝐿 −6𝐿4𝐿2 ] { 𝑣1 ∅₁ 𝑣₂ ∅₂ }

Reorganizando la matriz ensamblada se tiene

{ −30 0 𝑦1 𝑀₁ } = [ 6000 −12000 −12000 32000 6000

−12000 1200016000 ] {

𝑣₂ ∅₂ 𝑣₁ = 0 ∅1 = 0

}

La rotación en el nudo 2 es

[_∅𝑣2

2] = [ −6000

−12000 −12000 32000 ]

−1 [−30

0 ] = [ −0.02−7.5 ∗ 10−3] 𝑚_𝑟𝑎𝑑

Finalmente, el vector de fuerzas está dado por

[_𝑀𝑦1

1] = [ −6000

12000

−12000 16000] [−7.5 ∗ 10−0.02−3] = [ 30₁₂₀] 𝑘𝑁_{𝑘𝑁 ∗ 𝑚}

(32)

32 Ilustración 4. Reacciones de la viga, método matricial

Fuente: Propia

Ahora analizaremos la misma viga, pero desde el punto de vista del Método de Elemento Finitos. En la ilustración 5 se evidencia la cantidad de elementos que dispondremos para analizar en comparación con el método anterior, entonces la gran diferencia entre los mismos, dado que a mayor cantidad de elementos en que se descomponga la estructura la convergencia del análisis es mayor. En el ejemplo actual mediante el método directo solo analizamos un elemento, mientras que por MEF analizamos 4, cabe aclarar que podemos generar muchos más elementos con el fin de establecer una mayor proximidad a datos más idóneos frente a las solicitaciones, pero se hace con base a una simple comparación de los métodos.

Ilustración 5. Elementos de la viga, Método MEF

Fuente: Propia

Suponemos inicialmente un elemento finito de un solo elemento, es decir nodo 1 y nodo 5. Partiendo de la afirmación que 𝑑1𝑦 = ∅1 = 0, determinamos los desplazamientos y rotaciones en el nodo 5, mediante el uso de la función cubica de desplazamiento que se ha asumido

𝑣 = [2

𝐿3(𝑑1𝑦− 𝑑2𝑦) + 1

𝐿2(∅1− ∅2)] 𝑥3+ [− 3

𝐿2(𝑑1𝑦− 𝑑2𝑦) + 1

(33)

33

𝑣(𝑥) = 1

𝐿3(−2𝑥3+ 3𝑥2𝐿)𝑑2𝑦+ 1

𝐿3(𝑥3𝐿 − 𝑥2𝐿2)∅2

Evaluando en 𝑥 = 1𝑚 obtenemos una función de desplazamientos y rotaciones en el nodo 2, resaltando que los valores de 𝑑5𝑦 y ∅5 , son los obtenidos por el método matricial por que suponen una solución exacta en el extremo libre de la viga, de igual manera se alcanza dichos valores por el método de doble integración.

𝑣(1𝑚) = 1

43(−2(1)3 + 3(1)2(4))(−0.02) + 1

43((1)3(4) − (1)2(4)2)(−7.5 ∗ 10−3)

𝑣(1𝑚) = 1.718 × 10−3_𝑚

De la misma manera se determina los desplazamientos para los nodos restantes. La siguiente tabla

Tabla 1. Desplazamientos nodales de la viga

Fuente: Propia

El método de elementos finitos permite establecer los momentos en los puntos nodales a partir de los desplazamientos de dicho elemento.

𝑀 = 𝐸𝐼𝑣𝑛 _{= 𝐸𝐼}𝑑

2_{(𝑁 𝑑)}

𝑑𝑥2 = 𝐸𝐼

𝑑2_(𝑁) 𝑑𝑥2 𝑑

Donde 𝑑 nos es una función de 𝑥. En términos de la matriz gradiente 𝑩 tenemos

𝑀 = 𝐸𝐼𝐵𝑑

Donde

𝐵 =𝑑2𝑁 𝑑𝑥2 = [(

−6 𝐿2 +

12𝑥 𝐿3 ) (

−4 𝐿 +

6𝑥 𝐿2) (

6 𝐿2−

12𝑥 𝐿3 ) (

−2 𝐿 +

6𝑥 𝐿2)]

Para una solución simple de un elemento, el momento flector está dado por

𝑀(𝑥) = 𝐸𝐼 [(−6 𝐿2 +

12𝑥

𝐿3 ) 𝑑1𝑦+ ( −4

𝐿 + 6𝑥

𝐿2) ∅1+ ( 6 𝐿2−

12𝑥

𝐿3 ) 𝑑5𝑦 + ( −2

𝐿 + 6𝑥

𝐿2) ∅5]

(34)

34

𝑀(0) = 32000 [(6 42 −

12(0)

43 ) (−0.02) + ( −2

4 + 6(0)

42 ) (−7.5 × 10−3)]

𝑀(0) = −120 𝑘𝑁 ∗ 𝑚

La siguiente tabla muestra los momentos en función de 𝑥 = 0, para cada nodo Tabla 2. Momentos flectores de la viga en los nodos

Fuente: Propia

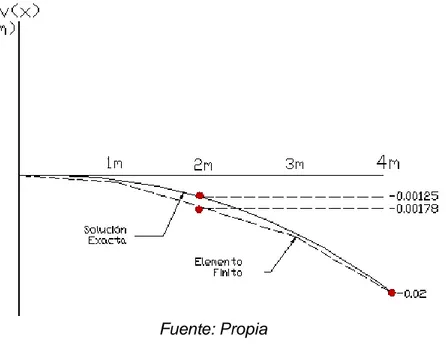
La siguiente ilustración muestra la convergencia en la curvatura del elemento, se evidencia que a mayor número de elementos finitos se disponga la proximidad de los valores de los desplazamientos será mayor entre los métodos utilizados.

Ilustración 6. Convergencia de los desplazamientos

Fuente: Propia

4 DESARROLLO DEL ELEMENTO PLACA

El elemento placa es uno de los elementos estructurales más importantes y es usado para modelar y analizar estructuras como entrepisos, losas de cimentación, recipientes de presión, (Figura 12), y partes de automóviles. Esta descripción de placa es seguida por una discusión de algunos elementos finitos comúnmente usados como placas.

NODO X (m) M(x)

1 0 -120

2 1 -90

3 2 -60

4 3 -30

(35)

35 Figura 12. Sección de una chimenea modelada como Elemento Finito (Vista rotada de 45º)

(584 vigas y 252 placas planas son los elementos)

4.1 CONCEPTOS BÁSICOS DE LA PLACA A FLEXIÓN

Una placa puede ser considerada como una extensión de una viga en dos dimensiones. Vigas y placas ambas soportan cargas transversales o perpendiculares a sus planos a través de la acción de la flexión. Una placa es delgada (Si esta es curva, esta podría ser un cascaron). Una viga tiene un momento de resistencia simple a la flexión; mientras una placa resiste flexión sobre dos ejes y tiene un momento de torsión.

Nosotros podríamos considerar la teoría clásica de placa delgada o teoría de placa de Kirchhoff. Muchos de las suposiciones de esta teoría son analogías con la teoría clásica para vigas o teorías de Euler- Bernoulli para vigas.

4.1.1 Suposiciones básicas de geometría y deformación

(36)

36 Figura 13.Placa delgada básica que muestra carga transversal y dimensiones

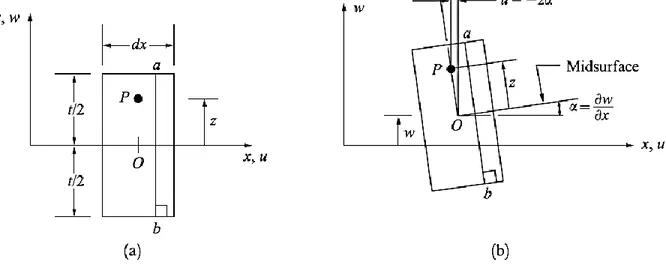
Las superficies de la placa son 𝑧 = ±𝑡/2 , y su punto medio esta en 𝑧 = 0. La geometría básica de la placa asumida es la siguiente: (1) El espesor de la placa es mucho más pequeña que sus dimensiones b y c (es decir 𝑡 ≪ 𝑏 𝑜 𝑐 ). (Si t es mayor que un décimo de la extensión dela losa, entonces la deformación transversal de la sección podría ocurrir para la placa y entonces decimos que es el espesor). (2) La deflexión w es mucho menor que el espesor t (es decir, 𝑤/𝑡 ≪ 1 ).

4.1.2 Suposiciones de Kirchhoff

Considerar un diferencial de un corte de una franja de la placa, al plano perpendicular al eje x como se muestra en la figura 14 (a). La deformación lateral causada por la carga q hacia arriba en la dirección de z, y la deflexión w en el punto P es asumida solamente en función de X y Y, es decir 𝑤 = 𝑤(𝑥, 𝑦) y la placa no se deforma en la dirección z. se dibuja una línea a-b perpendicular a la superficie antes de la carga permanente (Figura 14 (b)) Esta es consistente con las siguientes suposiciones de Kirchhoff:

1. Las normales permanecen normales. Esto implica que los esfuerzos cortantes transversales ϒ_𝑦𝑧 = 0 de la misma manera ϒ_𝑥𝑧 = 0. Sin embargo ϒ_𝑥𝑦 no es igual a cero, ángulos rectos en el plano de la placa no podrían permanecer restos después de la carga. La placa puede doblarse en el plano.

2. El cambio del espesor podría despreciarse y no someterse a extensiones normales. Esto significa deformación normal Ɛ𝑧= 0.

(37)

37 4. Las fuerzas de membrana o en el plano son despreciables aquí, y la resistencia a los esfuerzos puede ser superpuesta después (es decir, las deformaciones permanentes del comportamiento del triángulo del Capítulo 6 pueden ser súper puestas con la resistencia básica del elemento placa a flexión). Es decir, las deformaciones en las direcciones x y y son asumidas como cero en la mitad de la superficie: 𝑢(𝑥, 𝑦, 0) = 0 y 𝑣(𝑥, 𝑦, 0) = 0.

Figura 14.Corte diferencial de placa de espesor t (a) Antes de ser cargada y (b) Desplazamientos del punto P después de ser cargada, basada en la teoría de Kirchhoff

Basados en las suposiciones de Kirchhoff, ningún punto P en la figura 18 tiene desplazamiento en la dirección x debido a una pequeña rotación α

𝒖 = −𝒛𝜶 = −𝒛 (𝜹𝒘 𝜹𝒙)

Sucede lo mismo con el punto que tiene desplazamiento en la dirección y

𝒗 = −𝒛 (𝜹𝒘 𝜹𝒚)

Las curvaturas de la placa están dadas como la razón de cambio del desplazamiento angular de las normales y estas están definidas como:

𝑲_𝒙 = 𝝏𝟐𝒘 𝝏𝒙𝟐 𝑲𝒚=

𝝏𝟐_𝒘

(38)

38 La primera de las ecuaciones es usada en la teoría de vigas. Usando las definiciones para las deformaciones en el plano, y las ecuaciones de desplazamiento se obtiene que:

𝜺_𝒙 = −𝒛𝝏𝟐𝒘 𝝏𝒙𝟐 𝜺𝒚=

𝝏𝟐_𝒘

𝝏𝒚𝟐 𝜸𝒙𝒚 = −𝟐𝒛 𝝏𝟐_𝒘 𝝏𝒙𝝏𝒚

O usando las ecuaciones de razón de cambio tenemos:

𝜺_𝒙 = −𝒛𝑲_𝒙 𝜺_𝒚= −𝒛𝑲_𝒚 𝜸_𝒙𝒚= −𝒛𝑲_𝒙𝒚

La primera de las ecuaciones es usa en la teoría de vigas, las otras son nuevas en la teoría de placas.

4.1.3 Rotaciones Esfuerzos/Deformaciones

Basados en la tercera suposición anteriormente mencionada, las ecuaciones de esfuerzos planos pueden ser usadas para relacionar las deformaciones planas para un material isotrópico así

𝝈_𝒙 = 𝑬

𝟏 − 𝒗𝟐(𝜺𝒙 + 𝒗𝜺𝒚)

𝝈𝒚= 𝑬

𝟏 − 𝒗𝟐(𝜺𝒚+ 𝒗𝜺𝒙)

𝝉_𝒙𝒚 = 𝑮𝜸_𝒙𝒚

(39)

39 Figura 15.Elemento diferencial de una placa con (a) Esfuerzos mostrados en los bordes de

una placa y (b) Diferenciales de momentos y fuerzas

Los momentos actuantes están en función de 𝑥 y 𝑦 son estimados por unidad de longitud en el plano de la placa. Por lo tanto, los momentos son:

𝑴_𝒙 = ∫𝒕/𝟐𝒛𝝈_𝒙𝒅𝒛 −𝒕/𝟐

𝑴_𝒚= ∫𝒕/𝟐𝒛𝝈_𝒚𝒅𝒛 −𝒕/𝟐

𝑴_𝒙𝒚 = ∫𝒕/𝟐𝒛𝝉_𝒙𝒚𝒅𝒛 −𝒕/𝟐

Los momentos pueden ser relacionados con las curvaturas sustituyendo las deformaciones en las ecuaciones de momentos se obtiene

𝑴_𝒙 = 𝑫(𝒌_𝒙+ 𝒗𝒌_𝒚) 𝑴_𝒚= 𝑫(𝒌_𝒚+ 𝒗𝒌_𝒙) 𝑴_𝒙𝒚 = 𝑫(𝟏 − 𝒗) 𝟐 𝒌𝒙𝒚

Donde 𝑫 = _{[𝟏𝟐(𝟏−𝒗}𝑬𝒕𝟑 _𝟐_)] es llamada la rigidez debida a la flexión de la placa.

4.2 DEDUCCIÓN DE LA MATRIZ DE RIGIDEZ Y ECUACIONES DEL ELEMENTO PLACA A FLEXIÓN

(40)

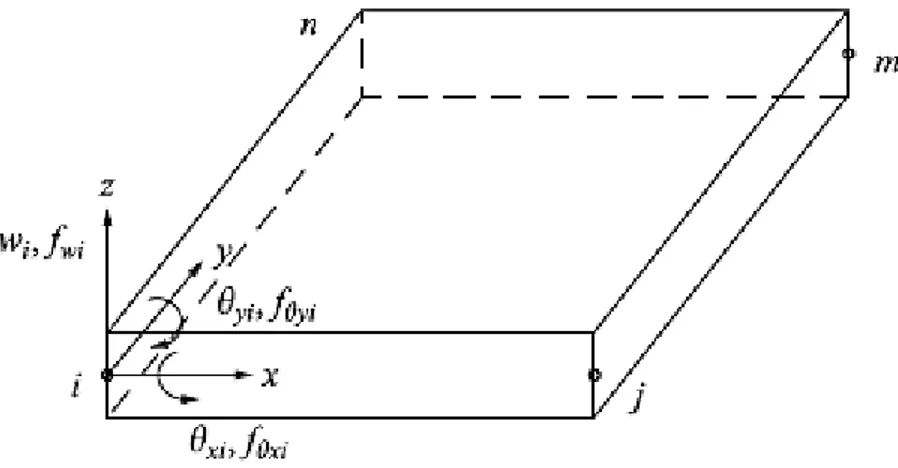
40 Figura 16.Elemento rectangular placa básico con nodos y grados de libertad

La formulación puede desarrollarse consecuentemente con la matriz de rigidez y las ecuaciones del elemento barra, viga, esfuerzos/ deformaciones planas, asimétricos, y otros elementos sólidos.

Paso 1. Seleccionar el tipo de elemento

Consideraremos el elemento placa-plana de 12 grados de libertad mostrada en la figura anterior. Cada nodo tiene tres grados de libertad, un desplazamiento transversal en la dirección z, una rotación 𝜃𝑥 alrededor del eje 𝑥, y una rotación 𝜃𝑦 sobre el eje 𝑦.

La matriz de desplazamiento nodal, en el nodo i está dado por

{𝑑_𝑖} = { 𝑤_𝑖 𝜃_𝑥𝑖 𝜃_𝑦𝑖}

Donde las rotaciones se relacionan con el desplazamiento transversal por

𝜽𝒙 = + 𝜹𝒘

𝜹𝒚 𝜽𝒚= − 𝜹𝒘

𝜹𝒙

El signo negativo de 𝜃_𝑦 se debe al hecho de un desplazamiento negativo w necesario para producir una rotación positiva sobre el eje y.

La matriz total desplazamientos está dada por

{𝒅} = {𝒅𝒊 𝒅𝒋 𝒅𝒎 𝒅𝒏}𝑻

(41)

41 Porque hay 12 grados de libertad, para el elemento, seleccionaremos 12 términos polinomiales en 𝑥 y 𝑦 cómo se presenta:

𝒘 = 𝒂_𝟏+ 𝒂_𝟐𝒙 + 𝒂_𝟑𝒚 + 𝒂_𝟒𝒙𝟐_{+ 𝒂}

𝟓𝒙𝒚 + 𝒂𝟔𝒚𝟐+ 𝒂𝟕𝒙𝟑+ 𝒂𝟖𝒙𝟐𝒚 + 𝒂𝟗𝒙𝒚𝟐+ 𝒂𝟏𝟎𝒚𝟑+ 𝒂𝟏𝟏𝒙𝟑𝒚 + 𝒂_𝟏𝟐𝒙𝒚𝟑

La ecuación anterior es una función incompleta en el contexto del triángulo de Pascal. La función está completa hasta el tercer orden (diez términos), y una elección de dos términos más para los cinco términos restantes para completar la función que debemos hacer. La mejor elección de términos es 𝒙𝟑𝒚 y 𝒙𝒚𝟑dado que ellos aseguran que habrá continuidad en los desplazamientos entre los límites. (Los términos 𝒙𝟒 y 𝒚𝟒 producen discontinuidad en los desplazamientos a lo largo de los límites de los elementos interconectados, y deben ser rechazados). La función planteada anteriormente solo satisface la ecuación básica diferencial del comportamiento a flexión de la placa delgada, sobre la parte descargada de la misma, aunque no es un requerimiento mínimo en la aproximación de la energía potencial.

Además, la función permite el movimiento para cuerpos rígidos y esfuerzo constante, están presentes como términos a tener en cuenta para este fenómeno en una estructura. Sin embargo, es común que en los límites existan las discontinuidades a lo largo de las pendientes de los elementos relacionados no se puedan asegurar.

Se puede observar dicha discontinuidad en la esquina, evaluaremos el polinomio en estas esquinas a lo largo de un lado (es decir, al lado de i-j, del eje 𝑥 de la figura 16), obtenemos

𝑤 = 𝑎₁+ 𝑎₂+ 𝑎₄𝑥2_{+ 𝑎} 7𝑥3

𝛿𝑤

𝛿𝑥 = 𝑎2+ 2𝑎4𝑥 + 3𝑎7𝑥2 𝛿𝑤

𝛿𝑦 = 𝑎3+ 𝑎5𝑥 + 𝑎8𝑥2+ 𝑎12𝑥3

Los desplazamientos w son cúbicos usados para el elemento viga, mientras la pendiente 𝛿𝑤/𝛿𝑥 es el mismo en la flexión de viga, basados en el elemento viga, sustituiremos las cuatro constantes 𝑎1, 𝑎2, 𝑎4y 𝑎7 podemos definirlas recurriendo a las condiciones de los puntos terminales (𝑤𝑖, 𝑤𝑗, 𝛳𝑦𝑖, 𝛳𝑦𝑗). Entonces, 𝑤 y 𝛿𝑤/𝛿𝑥

(42)

42 análisis podría no ser una solución mínima de potencial de energía. Sin embargo, estos elementos proveen resultados aceptables, y la prueba de esta convergencia podría ser mostrada.

Las constantes 𝑎1 hasta 𝑎12 pueden determinarse por las 12 ecuaciones simultáneas enlazando los valores de 𝑤 y estas pendientes de los nodos cuando las coordenadas toman los valores apropiados. Primero escribimos

{ + 𝑤 𝛿𝑤 𝛿𝑥 −𝛿𝑤 𝛿𝑦}

= [10 𝑥0 +1𝑦 0 −1 0

𝑥2 _𝑥𝑦 _𝑦2 0 +𝑥 +2𝑦 −2𝑥 −𝑦 0

𝑥3 _𝑥2_𝑦 _𝑥𝑦2 0 +𝑥2 _+2𝑥𝑦 −3𝑥2 _−2𝑥𝑦 _−𝑦2

𝑦3 _𝑥3_𝑦 _𝑥𝑦3 +3𝑦2 _+𝑥3 _+3𝑥𝑦2

0 −3𝑥2_𝑦 _−𝑦3 ] × { 𝑎1 𝑎₂ ⋮ 𝑎₁₂ }

O en una matriz simple de los grados de libertad matricialmente

{𝝍} = [𝑷]{𝒂}

Donde P es la primera matriz de la derecha de la ecuación matricial anterior con una dimensión de 3 x 12. Luego, evaluamos cada punto nodal como sigue

{𝑑} = { 𝑤_𝑖 𝜃𝑥𝑖 𝜃_𝑦𝑖 𝑤_𝑗 ⋮ } = [

1 𝑥𝑖 𝑦𝑖 0 0 +1

⋮

⋮ … …

𝑥𝑖2 _{𝑥𝑖𝑦𝑖} _𝑦𝑖2 0 +𝑥 +2𝑦𝑖

… … …

𝑥𝑖3 _𝑥𝑖2_𝑦𝑖 _{𝑥𝑖𝑦𝑖}2 0 +𝑥𝑖2 _{+2𝑥𝑖𝑦𝑖}

… … …

𝑦𝑖3 _𝑥𝑖3_𝑦𝑖 _{𝑥𝑖𝑦𝑖}3 +3𝑦𝑖2 _+𝑥𝑖3 _{+3𝑥𝑖𝑦𝑖}2

… … ∙ ∙ … ] × { 𝑎₁ 𝑎2 ⋮ 𝑎12 }

La matriz compacta, la expresamos como

{𝒅} = [𝑪]{𝒂}

Donde C es la matriz de la derecha de 12 x 12 de la ecuación matricial anterior. Por lo tanto, las constantes de a pueden ser resueltas así

{𝒂} = [𝑪]−𝟏_{𝒅}

(43)

43

{𝝍} = [𝑷][𝑪]−𝟏_{𝒅}

{𝝍} = [𝑵]{𝒅}

Donde [𝑵] = [𝑷][𝑪]−𝟏 es la matriz de función de forma. Una manera específica de la función de forma está dada 𝑁_𝑖, 𝑁_𝑗, 𝑁_𝑚 y 𝑁_𝑛.

Paso 3. Definir la función de esfuerzos/ Deformaciones y la relación de momentos de fuerza y curvatura

La matriz de curvatura está dada por

{𝐾} = { 𝐾_𝑥 𝐾_𝑦 𝐾_𝑥𝑦} = {

−2𝑎4− 6𝑎7𝑥 − 2𝑎8𝑦 − 6𝑎11𝑥𝑦 −2𝑎6− 2𝑎9𝑥 − 6𝑎10𝑦 − 6𝑎12𝑥𝑦 −2𝑎5− 4𝑎8𝑥 − 4𝑎9𝑦 − 6𝑎11𝑥2− 6𝑎12𝑦2

}

O expresada en forma matricial, tenemos

{𝒌} = [𝑸]{𝒂}

Donde [𝑄]es la matriz de coeficientes multiplicada por las variables 𝑎, la matriz de curvatura se puede expresar como

{𝒌} = [𝑩]{𝒅}

Donde

[𝑩] = [𝑸][𝑪]−𝟏

Es la matriz gradiente.

La matriz de momento/ curvatura para una placa está dada por

{𝑴} = { 𝑴𝒙 𝑴_𝒚 𝑴_𝒙𝒚} = [𝑫] { 𝒌_𝒙 𝒌𝒚 𝒌_𝒙𝒚} = [𝑫][𝑩]{𝒅}

Donde [𝐷] es la matriz constitutiva dada para materiales isotrópicos

[𝑫] = 𝑬𝒕𝟑 𝟏𝟐(𝟏 − 𝒗𝟐₎[ 𝟏 𝒗 𝟎 𝒗 𝟏 𝟎 𝟎 𝟎 𝟏 − 𝒗 𝟐 ]

(44)

44 La matriz de rigidez está dada por la forma común

[𝑘] = ∬[𝐵]𝑇_{[𝐷][𝐵]𝑑𝑥𝑑𝑦}

Donde [𝐵] y [𝐷] se definieron anteriormente. La matriz de rigidez de un elemento rectangular de cuatro nodos es de orden 12 x 12. Debido a la matriz de fuerzas de la carga distribuida 𝑞 sobre la superficie por unidad de área en la dirección de 𝑧 se obtiene una ecuación estándar.

[𝐹_𝑠] = ∬[𝑁_𝑠]𝑇_{𝑞𝑑𝑥𝑑𝑦}

Para una carga uniforme 𝑞 actuando sobre la superficie de un elemento de dimensiones

2𝑏 × 2𝑐 producen momentos y fuerzas en un nodo 𝑖 asi

{ 𝒇_𝒘𝒊 𝒇_𝜽𝒙𝒊 𝒇𝜽𝒚𝒊 } = 𝟒𝒒𝒄𝒃 {−𝒄/𝟏𝟐𝟏/𝟒 𝒃/𝟏𝟐 }

Con una expresión similar los nodos 𝑗, 𝑚 y 𝑛. Podemos observar que para una carga uniforme producen pares aplicados a los nodos como parte del trabajo equivalente reemplazado, tal como era para el caso del elemento viga. Las ecuaciones del elemento están dadas por

{ 𝑓𝑤𝑖 𝑓𝜃𝑥𝑖 𝑓_𝜃𝑦𝑖 ⋮ 𝑓_𝜃𝑦𝑛} = [

𝑘11 𝑘12 … 𝑘1,12 𝑘21 𝑘22 … 𝑘2,12 𝑘₃₁ ⋮ 𝑘_12,1 𝑘₃₂ … …

… 𝑘_3,12 … … … 𝑘_12,12]{

𝑤𝑖 𝜃_𝑥𝑖 𝜃_𝑦𝑖 ⋮ 𝜃_𝑦𝑛}

El resto de los pasos, incluyendo el ensamblaje total de las ecuaciones, incluyendo las condiciones de frontera (ahora las condiciones de frontera en 𝑤, 𝜃_𝑥, 𝜃_𝑦 ) y resolviendo las ecuaciones para los desplazamientos nodales y pendientes (observar tres grados de libertad por nodo).

4.3 ALGUNAS COMPARACIONES NUMÉRICAS DEL ELEMENTO PLACA

Ahora presentamos algunas comparaciones numéricas de cuadriláteros en las formulaciones del elemento placa. Recordando que hay numerosas formulaciones del elemento placa en la literatura. La figura 17 muestra un número de resultados para formulaciones de elementos placa como una placa cuadrada simulando soportar una carga concéntrica aplicada en el centro de la misma.

(45)

45 elemento placa. Estos resultados incluyen 12 términos polinomiales descritos en la sección anterior. Observemos que los 12 términos polinomiales convergen a la solución exacta desde arriba. Esto produce una solución de límite superior. Porque la continuidad entre elementos de las pendientes no se garantiza para los 12 términos polinomiales, no se obtiene abajo las características clásicas de una formulación de la mínima energía potencial. Sin embargo, como más elementos se usan, la solución converge en una solución exacta.

Figura 17. Comparaciones Numéricas: Formulaciones del Elemento placa cuadrada

Fuente: (Gallagher, R. H., Finite Element Analysis Fundamentals, 1975, p. 345. Reprinted by Permission of Prentice-Hall, Inc., Upper Saddle River, NJ.)

La figure 18 muestra la comparación de una formulación triangular para la misma carga simple centrada que soporta la placa comparada con la formulación cuadrilátera de la figura anterior. Observamos un número de diferentes formulaciones con resultados que convergen desde arriba y abajo en las dos figuras. Algunos de estos elementos producen mejores resultados que otros.

(46)

46 Figura 18.Comparaciones numéricas para una placa cuadrada simplemente soportada sujeta

a la carga central. Formulaciones de elementos triangulares

Fuente: (Gallagher, R. H., Finite Element Analysis Fundamentals, 1975, p. 345. Reprinted by Permission of Prentice-Hall, Inc., Upper Saddle River, NJ.)

4.4 SOLUCIÓN POR COMPUTADORA A UN PROBLEMA DE PLACA A FLEXIÓN

(47)

47 cuatro bordes y sujeta a una carga en el centro de esta, como se muestra en la figura 19.

Figura 19. Placa de evaluación

El elemento placa es un elemento de tres o cuatro nodos formulado en un espacio tridimensional. El elemento permite grados de libertad permitidas en las tres traslaciones (𝑢, 𝑣 𝑦 𝑤) y rotaciones en el plano (𝜃𝑥 𝑦 𝜃𝑦 ). Los grados de libertad rotacionales normales en la placa no son definidos y deben ser limitados.

El elemento formulado en el programa de computadora es de 16 términos polinomiales. La formulación de los 16 nodos converge por debajo del análisis de los desplazamientos, y es basada en la formulación de la compatibilidad de desplazamientos. Este también es mostrado en la figura 16 para la placa restringida y sometida a una carga concentrada.

4.4.1 Ejemplo

Una malla de 2 x 2 fue creada para modelar la placa. Los resultados de los desplazamientos son mostrados en la figura 20.

La solución exacta para los máximos desplazamientos (los cuales ocurren debajo de la carga concentrada) dan como:

𝑤 =0,056𝑃𝐿2

𝐷 = 0,056

(48)

48 Donde D es la matriz constitutiva para materiales isotrópicos que relaciona los esfuerzos y deformaciones

𝐷 =

(206843𝑀𝑃𝑎 )(2.54×10_{[12 (1−0,3}₂_)] −3𝑚)3

= 576.45𝑁 ∗ 𝑚

Figura 20.Desplazamientos de la placa de ejemplo

(49)

49 Figura 21. Modelo de elementos viga y placa combinados en el centro de línea de los

elementos

Esto asegura la compatibilidad entre la placa y los elementos viga. La placa es la misma que se usó en la figura 21. Los elementos viga refuerzan la placa reduciendo su máxima deflexión como se muestra en la figura 22.

Figura 22. Deflexión vertical para una parte del modelo

(50)

50 Otra manera de conectar elementos viga y placa se muestra en la figura 23, donde los elementos viga están compuestos de elementos placa y pequeños elementos viga usados para conectar los elementos viga y placa a los nodos. En este modelo de 5𝑐𝑚 ×

5𝑐𝑚 por 1₄𝑐𝑚.

Figura 23. Modelo que muestra elementos de viga desplazada para el elemento placa

5 DESARROLLO DE ESFUERZOS PLANOS Y DEFORMACIÓN PLANA (ECUACIÓN DE RIGIDEZ)

(51)

51 Figura 24. Esfuerzos en el plano (a) Placa perforada (b) placa extendida

Los esfuerzos y deformaciones de dichos elementos se pueden predecir mediante la matriz de rigidez, bajo la hipótesis de tensión constante sobre estos.

Figura 25.Plano de esfuerzos (a) carga horizontal en una presa (b) carga vertical en un tubo

En la figura anterior se evidencia que para que las tensiones y esfuerzos normales no sean nulos debe existir un espesor unitario en el eje 𝒁 (Principio de discretización del elemento).

A continuación, se presenta un ejemplo detallado utilizando el Método de Elementos Finitos para la obtención de esfuerzos sobre una superficie plana (área).

5.1 EJEMPLO DE ESFUERZOS PLANOS Y DEFORMACIONES PLANAS

(52)

52 Figura 26. Elemento placa, sujeta a esfuerzos de tensión

Fuente: Propia

El primer paso consiste en discretizar la placa, en este caso manejamos dos elementos, y a partir de la tensión que sufre la placa en uno de sus extremos determinamos la resultante de la fuerza a la cual está expuesta.

𝐹 =1 2𝑇𝐴 𝐹 = 1

2 (1 𝑀𝑃𝑎)(0.50𝑚 × 0.10𝑚 ) 𝑭 = 𝟐𝟓 𝒌𝑵

Figura 27. Discretizacion de la placa

Fuente: Propia

(53)

53

[𝐹] = [𝐾][𝛿]

Expandiendo las matrices, obtenemos

| | | 𝐹1𝑋 𝐹_1𝑦 𝐹_2𝑋 𝐹2𝑦 𝐹_3𝑋 𝐹_3𝑦 𝐹_4𝑋 𝐹_4𝑦 | | | = | | | 𝑅_1𝑋 𝑅_1𝑦 𝑅_2𝑋 𝑅_2𝑦 25 0 25 0 | | | = [𝐾] | | | 𝛿_1𝑋 𝛿_1𝑦 𝛿_2𝑋 𝛿2𝑦 𝛿_3𝑋 𝛿_3𝑦 𝛿4𝑋 𝛿4𝑦 | | | = [𝐾] | | | 0 0 0 0 𝛿3𝑋 𝛿_3𝑦 𝛿_4𝑋 𝛿_4𝑦 | | |

Donde la matriz de rigidez tiene una dimensión de 8 x 8(Dos grados de libertad por nodo), antes interpretando que los nodos 1 y 2 no tienen grados de libertad. El tercer paso consiste en ensamblar la matriz general, que consiste en la superposición de las matrices individuales de cada elemento.

[𝑘] = 𝑡𝐴[𝐵]𝑇_[𝐷][𝐵]

De la figura 28 (Discretización) podemos establecer las coordenadas para el elemento 1 ( 𝑥𝑖 = 0 , 𝑦𝑖 = 0, 𝑥𝑗 = 1.00 , 𝑦𝑗 = 0.50, 𝑚𝑖 = 0, 𝑚𝑗 = 0.50). En general el área del elemento 1 (A) se obtiene:

𝐴 =1 2𝑏ℎ 𝐴 =1

2× 1 × 0.50 = 0.25𝑚2

Figura 28. Elemento 1 de la placa discretizada

Fuente: Propia

Siendo [𝑩] la matriz de desplazamientos nodales tenemos:

[𝐵] = 1 2𝐴[

𝛽𝑖 0 𝛽𝑗

0 𝛾𝑖 0

𝛾𝑖 𝛽𝑖 𝛾𝑗

0 𝛽𝑚 0

𝛾𝑗 0 𝛾𝑚

𝛽𝑗 𝛾𝑚 𝛽𝑚 ]

(54)

54

𝛽𝑖 = 𝑦𝑗 − 𝑦𝑚 = 0.50 − 0.50 = 0 𝛽𝑗 = 𝑦𝑚 − 𝑦𝑖 = 0.50 − 0 = 0.50 𝛽𝑚 = 𝑦𝑖 − 𝑦𝑗 = 0 − 0.50 = −0.50

𝛾𝑖 = 𝑥𝑚 − 𝑥𝑗 = 0 − 1.00 = −1.00 𝛾𝑗 = 𝑥𝑖 − 𝑥𝑚 = 0 − 0 = 0 𝛾𝑚 = 𝑥𝑗 − 𝑥𝑖 = 1.00 − 0 = 1.00

Entonces, reemplazando en la forma matricial de [𝑩]

[𝐵] = 1

2 × 0.25[

0.00 0.00 0.50 0.00 −1.00 0.00 −1.00 0.00 0.00

0.00 −0.500.00 0.00 0.001.00 0.50 1.00 −0.50

]1 𝑚

Para esfuerzos planos, la matriz [𝐷] se puede expresar

[𝐷] =_{(1 − 𝑣}𝐸 ₂₎[

1 𝑣 0

𝑣 1 0

0 0 1 − 𝑣₂ ]

Sabemos que 𝑣 = 0.3 y 𝐸 = 200 𝐺𝑃𝑎

[𝐷] =200 × 10_{(1 − 0.3}₂6₎[

1 0.3 0

0.3 1 0

0 0 1 − 0.3

2

] 𝑘𝑃𝑎

Entonces

[𝐵]𝑇_{[𝐷] =} 200 × 106 0.50 (1 − 0.32_{) |}

|

0.00 0.00 −1.00 0.00 −1.00 0.00 0.50 0.00 −0.50 0.00 0.00 0.00 0.00 1.00 0.00 0.50 1.00 −0.50 | | [

1 0.3 0

0.3 1 0

0 0 1 − 0.3

2 ]

Simplificando

[𝐵]𝑇_{[𝐷] =}400 × 106 0.91 |

|

0.00 0.00 −0.35 −0.30 −1.00 0.00

0.50 0.00 −0.50 0.30 0.15 0.00 −0.15 1.00 0.00 0.18 0.35 −0.18 | |

Recordando que la matriz del elemento está dada por:

(55)

55

[𝑘] = (0.10)(0.25)400 × 106 0.91 |

|

0.00 0.00 −0.35 −0.30 −1.00 0.00

0.50 0.00 −0.50 0.30 0.15 0.00 −0.15 1.00 0.00 0.18 0.35 −.18 | | × 1 0.50[

0.00 0.00 0.50 0.00 −1.00 0.00 −1.00 0.00 0.00

0.00 −0.500.00 0.00 0.001.00 0.50 1.00 −0.50

]

Finalmente, la matriz de rigidez está dada por:

[𝑘1] =20 × 106 0.91 _| | 𝑢₁ 0.35 𝑣₁ 0.00 𝑢₃ 0.00 0.00 1.00 −0.15 0.00 −.018 −0.35 0.18 −0.15 0.00 0.15 −1.00 0.25 0.00 −0.25 0.15 𝑣₃ −0.18 𝑢₂

−0.35 0.18𝑣2 0.00 0.15 −1.00 0.00 0.09 0.18 −0.09 −0.25 0.18 0.60 −0.33 0.15 −0.09 −0.33 1.09 | | 𝑘𝑁/𝑚

Cada columna de la matriz de rigidez del elemento 1, indica el grado de libertad asociado en 𝑢 y 𝑣. De la misma manera se procede a generar la matriz del elemento 2.

Figura 29. Elemento 2 de la placa discretizada

Fuente: Propia

De la figura 29 (Discretización) podemos establecer las coordenadas para el elemento 2 ( 𝑥𝑖 = 0 , 𝑦𝑖 = 0, 𝑥𝑗= 1.00 , 𝑦𝑗 = 0, 𝑚𝑖 = 1.00, 𝑚𝑗 = 0.50). Resaltando que el área es la misma que el elemento anterior.

𝛽𝑖 = 𝑦𝑗 − 𝑦𝑚 = 0 − 0.50 = −0.50 𝛽𝑗 = 𝑦𝑚 − 𝑦𝑖 = 0.50 − 0 = 0.50

𝛽𝑚 = 𝑦𝑖 − 𝑦𝑗 = 0 − 0 = 0 𝛾𝑖 = 𝑥𝑚 − 𝑥𝑗 = 1.00 − 1.00 = 0 𝛾𝑗 = 𝑥𝑖 − 𝑥𝑚 = 0 − 1.00 = −1.00

(56)

56 Entonces, reemplazando en la forma matricial de [𝑩]

[𝐵] = 1 2𝐴[

𝛽𝑖 0 𝛽𝑗

0 𝛾𝑖 0

𝛾𝑖 𝛽𝑖 𝛾𝑗

0 𝛽𝑚 0

𝛾𝑗 0 𝛾𝑚

𝛽𝑗 𝛾𝑚 𝛽𝑚 ]

[𝐵] = 1