AP01 Fourier del Tomasi Teleco V10032018

amplificador en la dirección correcta y desactiva al amplificador en la dirección opuesta, evi-tando así que el eco regrese a quien habla. Si la conversación cambia rápidamente de direc-ción, la persona que escucha puede oír cuando el supresor de eco se enciende y se apaga, ya que cada vez que un supresor de eco detecta la voz y se activa, el primer instante de sonido se elimina del mensaje, y se obtiene una voz entrecortada. Con un supresor de eco en el circui-to no puede haber transmisiones en ambas direcciones al mismo tiempo y, por consiguiente, la operación del circuito se limita a semidúplex. Las compañías comunes de larga distancia, como AT&T, por lo general ponen supresores de eco en circuitos de cuatro hilos de longitud mayor a 1500 millas eléctricas (ya que mientras más largo es el circuito, la demora por ida y vuelta es mayor).

ANÁLISIS DE SEÑALES

Cuando se diseñan los circuitos electrónicos de comunicaciones, con frecuencia se tiene que analizar y pronosticar el funcionamiento del circuito con base en la distribución de potencia y la composición de frecuencias de la señal de información. Esto se hace con el método matemá-tico llamado análisis de señales. Aunque todas las señales en las comunicaciones electrónicas no son ondas senoidales o cosenoidales de una sola frecuencia, muchas de ellas sí lo son, y las que no lo son se pueden representar con una combinación de funciones de seno o de coseno. Señales senoidales

En esencia, el análisis de señales implica la realización del análisis matemático de frecuencia, longitud de onda y valor de voltaje de una señal. Las señales eléctricas son variaciones de vol-taje, o de corriente, respecto al tiempo, que se pueden representar por una serie de ondas se-no o cosese-no. La descripción matemática de una onda de voltaje o de corriente con frecuencia única es

v(t) Vsen(2ft ) o v(t) V cos(2ft ) i(t) Isen(2ft ) o i(t) I cos(2ft ) donde v(t) voltaje de la onda senoidal, variable respecto al tiempo t

i(t)corriente de la onda senoidal, variable respecto al tiempo t V voltaje máximo (volts)

f frecuencia (hertz)

desplazamiento de fase (radianes) I corriente máxima (amperes)

2f velocidad angular (radianes por segundo)

El uso de una función seno o coseno para representar una señal es completamente arbitra-rio y depende de cuál se escoge como referencia. Sin embargo, se debe observar que sen = cos(°90°). Por consiguiente, son válidas las siguientes ecuaciones

v(t) Vsen(2ft ) Vcos(2ft °90°) v(t) Vcos(2ft ) Vsen(2ft °90°)

Las fórmulas anteriores son para una onda repetitiva, de una sola frecuencia. A esa forma de onda se le llama onda periódica, porque se repite con rapidez uniforme, es decir, cada ciclo sucesivo de la señal tarda exactamente el mismo tiempo y tiene exactamente las mismas varia-ciones de amplitud que en cualquier otro ciclo; cada ciclo tiene exactamente la misma forma. Una serie de ondas seno, coseno o cuadradas, son ejemplos de ondas periódicas. Las ondas pe-riódicas se pueden analizar en el dominio del tiempoo en el dominio de la frecuencia. De he-cho, con frecuencia se hace necesario pasar del dominio del tiempo al de la frecuencia y vice-versa cuando se analiza el funcionamiento de un sistema.

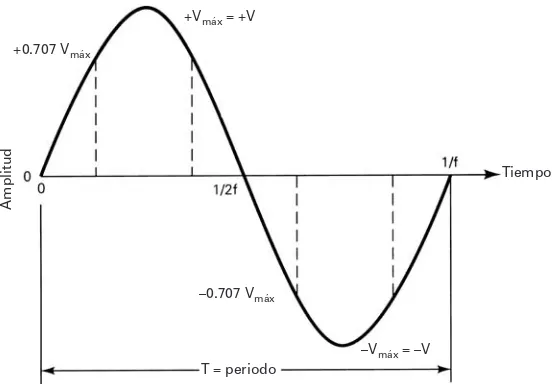
forma de onda de la señal muestra la forma y la magnitud instantánea de la señal con respecto al tiempo, pero no necesariamente indica el valor de la frecuencia. Con un osciloscopio, la des-viación vertical es proporcional a la amplitud de la señal total de entrada, y la deflexión hori-zontal es una función del tiempo (frecuencia de barrido). La fig. 1.9 muestra la forma de onda de una señal senoidal de frecuencia única de fhertz con amplitud máxima de Vvolts.

Dominio de la frecuencia. El analizador de espectro es un instrumento de dominio de la frecuencia. En esencia no se despliega ninguna forma de onda en la pantalla del tubo de ra-yos catódicos. En vez de lo anterior se muestra una gráfica de amplitud contra frecuencia (la cual se conoce comoespectro de frecuencia). En un analizador de espectro, el eje horizontal repre-senta la frecuencia y el eje vertical reprerepre-senta la amplitud. En consecuencia, existirá una defle-xión vertical para cada frecuencia que está presente en la entrada. De hecho, la forma de onda de entrada se “barre” a una frecuencia variable, con la ayuda de un filtro de paso de banda con Q elevado (cuya frecuencia central está sincronizada con la velocidad de barrido horizontal del tubo de rayos catódicos. Cada frecuencia que está presente en la forma de onda entrada produ-ce una línea vertical en la pantalla del tubo de rayos catódicos (éstas son las componentes espec-trales). La deflexión vertical (altura) de cada línea es proporcional a la amplitud de la frecuencia que representa. Una representación en el dominio de la frecuencia de la onda muestra el conteni-do de la frecuencia, pero no indica necesariamente la forma de la onda o la amplitud combinada de todas las componentes de entrada en un instante específico de tiempo. La fig. 1-10 muestra el espectro de frecuencia de una señal senoidal de frecuencia única cuya amplitud pico es Vvolts y la frecuencia es fhertz.

Amplitud

Frecuencia (Hz)

FIGURA 1-10 Representación en el dominio de la frecuencia (espectro) de una onda senoidal de frecuencia única

Amplitud

+0.707 Vmáx

+V_máx = +V

–0.707 Vmáx

–Vmáx = –V

Tiempo

T = periodo

Ondas periódicas no senoidales (ondas complejas)

En esencia, toda onda repetitiva formada por más de una onda senoidal o cosenoidal relaciona-da armónicamente, es una onda no senoidalo una onda periódica compleja. Para analizar una onda periódica compleja es necesario usar una serie matemática inventada en 1826 por el físico y matemático francés, el barón Jean Fourier. Esta serie se llama serie de Fourier.

La serie de Fourier. Esta serie se usa en análisis de señales para representar las com-ponentes senoidales de una onda periódica no senoidal, es decir, para cambiar una señal en el dominio del tiempo a una señal en el dominio de la frecuencia. En general, se puede obtener una serie de Fourier para cualquier función periódica, en forma de una serie de funciones trigono-métricas con la siguiente forma matemática

f(t) A0A1cos A2cos 2 A3cos 3 ⋅⋅⋅An cos n

B1sen B2sen 2 B3sen 3 ⋅⋅⋅Bnsen n (1-6) donde

La ecuación 1-6 indica que la forma de onda f(t) comprende un valor promedio (A0) de cd, una serie de funciones cosenoidales en las que cada término sucesivo tiene una frecuencia que es múltiplo entero de la frecuencia del primer término cosenoidal de la serie, y una serie de funciones senoidales en la que cada término sucesivo tiene una frecuencia que es múltiplo entero de la del primer término senoidal de la serie. No hay restricciones para los valores o los valores relativos de las amplitudes de los términos seno y coseno. La ecuación 1-6 se enuncia como sigue en palabras: Cualquier forma de onda periódicaestá formada por un componen-te promedio y una serie de ondas senoidales y cosenoidales relacionadas armónicamencomponen-te. Una armónicaes un múltiplo entero de la frecuencia fundamental. La frecuencia fundamentales la primera armónica, y es igual a la frecuencia (rapidez de repetición) de la forma de onda. El segundo múltiplo de la fundamental se llama segunda armónica, el tercer múltiplo es la tercera armónica, y así sucesivamente. La frecuencia fundamental es la mínima necesaria pa-ra representar a una forma de onda. Por consiguiente, la ecuación 1-6 se puede escribir co-mo sigue

f(t) dc fundamental 2da. armónica 3ra. armónica ⋅⋅⋅n-ésima armónica Simetría de onda. Dicho en términos sencillos, la simetría de la ondadescribe la sime-tría de una forma de onda en el dominio del tiempo, esto es, su posición relativa con respecto a los ejes horizontal (tiempo) y vertical (amplitud).

Simetría par. Si una forma de onda periódica de voltaje es simétrica respecto al eje ver-tical (amplitud) se dice que tiene simetría especular, o de ejes, y se llama función par. Para to-das las funciones pares, los coeficientes Bde la ecuación 1-6 son cero. Por consiguiente, la se-ñal sólo contiene un componente de cd y los términos cosenoidales (nótese que la misma onda cosenoide es una función par). La suma de una serie de funciones pares es una función par. Las funciones pares satisfacen la condición

f(t) f(t) (1-7)

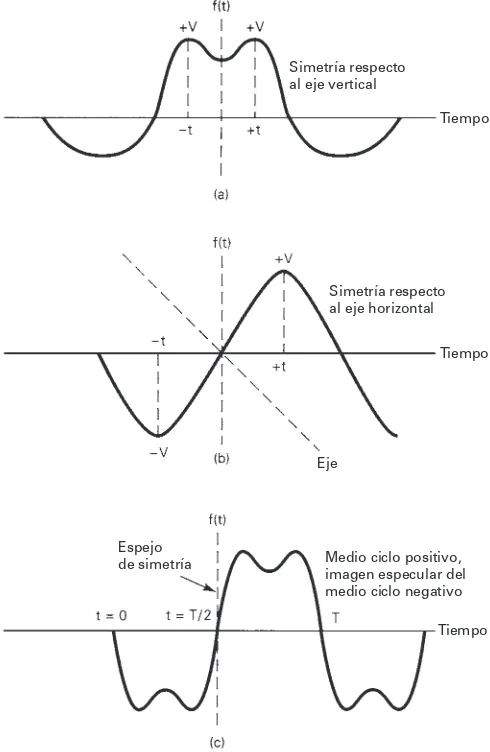
De acuerdo con la ecuación 1-7, la magnitud y la polaridad de la función en tes igual a la mag-nitud y la polaridad en t. En la fig. 1-11a se ve una forma de onda que sólo contiene funcio-nes pares.

suma de una serie de funciones impares es una función impar. A esta forma primero se le debe reflejar en el eje Yy después en el eje Xpara sobreponerla consigo misma. Así,

f(t) f(t) (1-8)

La ecuación 1-8 establece que la magnitud de la función en tes igual al negativo de la magni-tud en t, es decir, que las magnitudes en esos puntos son iguales, pero los signos son opuestos. En la fig. 1-11b se ve una forma de onda periódica que sólo contiene funciones impares.

Simetría de media onda. Si una forma de onda periódica de voltaje es tal que la on-da del primer medio ciclo (t0 a tT/2) se repite, pero con signo contrario, durante el se-gundo medio ciclo (tT/2 a tT), se dice que tiene simetría de media onda. Para todas las formas de onda con simetría de media onda, las armónicas pares de la serie, en los términos en seno y en coseno, son cero. Por consiguiente, las funciones de media onda cumplen con la condición

(1-9)

f(t) f

2t

Simetría respecto al eje vertical

Tiempo

Simetría respecto al eje horizontal

Tiempo

Eje

Espejo

de simetría Medio ciclo positivo, imagen especular del medio ciclo negativo

Tiempo

TABLA 1-3 Resumen de series de Fourier

Forma de onda Serie de Fourier

v(t)

Nimpar

8V (N)2 cos Nt

v(t)8V

2 cos t

8V

(3)2 cos 3t

8V

(5)2 cos 5t

v(t)V

T

N1 2V

T

sen NtT NtT

v(t)

Nimpar

V sen N2 N2 cos Nt v(t)4V

cos t

4V

3 cos 3t 4V

5 cos 5t

v(t)

Nimpar

4V N sen Nt v(t)4V

sen t

4V

3 sen 3t v(t)2V

N1

4V(1)N

[1(2N)2_] cos Nt

v(t)2V

4V 3 cos t

4V

15 cos 2t v(t)V

V

2 sen t

N2

V[1(– 1)N_] (1 – N2₎ cos Nt

v(t)V

V

2 sen t – 2V

3 cos 2t – 2V

15 cos 4t· · ·

En la fig. 1-11c se ve una forma de onda periódica con simetría de media onda. Se debe hacer notar que una forma de onda puede tener simetría de media onda y también puede ser impar o par, al mismo tiempo. Los coeficientes A0, B1a Bn, y A1a Anse pueden evaluar con las siguien-tes fórmulas integrales

(1-10)

(1-11)

(1-12)

Para resolver las ecuaciones 1-10, 1-11 y 1-12 se requiere aplicar el cálculo integral, que sale del alcance de este libro. Por lo anterior, en las descripciones que siguen se presentarán las so-luciones correspondientes.

La tabla 1-3 es un resumen de las series de Fourier para algunas de las formas de onda pe-riódicas no senoidales.

Ejemplo 1-2

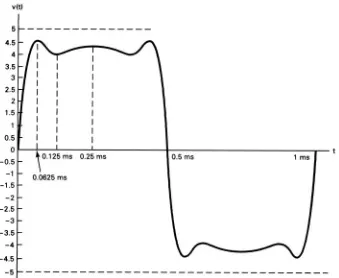
Para el tren de ondas cuadradas de la fig. 1-12:

(a) Determinar las amplitudes máximas y las frecuencias de las primeras cinco armónicas impares.

(b) Trazar el espectro de frecuencias.

(c) Calcular el voltaje instantáneo total, para varios tiempos, y trazar la forma de onda en el dominio del tiempo.

Solución (a) Al inspeccionar la forma de onda de la fig. 1-12 se ve que el componente promedio de cd es 0 V, y que la forma de onda tiene al mismo tiempo simetría impar y de media onda. Si se eva-lúan las ecuaciones 1-10, 1-11 y 1-12 se obtiene la siguiente serie de Fourier para onda cuadrada con simetría impar.

(1-13a)

v(t)V0

4V

1

3 sen 3t 1

5 sen 5t 1

7 sen 7t 1

9 sen 9t. . .

B_n 2

T

T

0

f(t) sen ntdt

An

2

T

T

0

f(t) cos ntdt

A0

1

T

T

0

f(t) dt

Tiempo

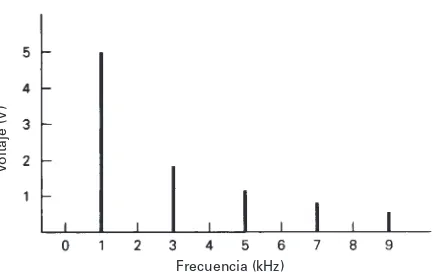
(b) El espectro de frecuencias se ve en la fig. 1-13.

(c) Se sustituyen los resultados de los pasos anteriores en la ecuación 1-13a y se llega a

v(t) 5.09 sen[21000t] 1.69 sen[23000t] 1.02 sen[25000t]

0.73 sen[27000t] 0.57 sen[29000t]

n Armónica Frecuencia (Hz) Voltaje máximo (Vp)

1 Primera 1000 5.09

3 Tercera 3000 1.69

5 Quinta 5000 1.02

7 Séptima 7000 0.73

9 Novena 9000 0.57

en dondev(t) voltaje variable en el tiempo

V0voltaje promedio de cd (volts)

V amplitud máxima de la onda cuadrada (volts) 2f(radianes por segundo)

Tperiodo de la onda cuadrada (segundos)

ffrecuencia fundamental de la onda cuadrada (1/T) (hertz) La frecuencia fundamental de la onda cuadrada es

Se puede ver en la ecuación 1-13a que la frecuencia y la amplitud de la n-ésima armónica impar se determinan con las siguientes ecuaciones

fnnf (1-13b)

nentero positivo impar (1-13c)

siendo n n-ésima armónica (sólo armónicas impares para una onda cuadrada)

f frecuencia fundamental de la onda cuadrada (hertz)

Vn amplitud máxima de la n-ésima armónica (volts)

fn frecuencia de la n-ésima armónica (hertz)

V amplitud máxima de la onda cuadrada (volts) Si se sustituye n1 en las ecuaciones 1-13b y 1-13c, el resultado es

f11 1000 1000 Hz

Al sustituir n3, 5, 7 y 9 en las ecuaciones 1-13b y 1-13c se obtiene

V₁4(4)

5.09 Vp

V_n4V n

f1 T

1

1 ms1 kHz

V

oltaje (V)

Frecuencia (kHz)

Se despeja v(t) para t62.5 s se obtiene

v(t) 5.09 sen[21000(62.5 s)] 1.69 sen[23000(62.5 s)]

1.02 sen[25000(62.5 s)] 0.73 sen[27000(62.5 s)]

0.57 sen[29000(62.5 s)]

v(t) 4.51 V

De igual modo se despeja v(t) para varios otros valores del tiempo, y se obtiene la siguiente tabla

FIGURA 1-14 Señal del ejemplo 1-2 en el dominio del tiempo

Tiempo (s) v(t) (volts máximo)

0 0

62.5 4.51

125 3.96

250 4.26

375 3.96

437.5 4.51

500 0

562.5 4.51

625 3.96

750 4.26

875 3.96

937.5 4.51

1000 0

Serie de Fourier para una forma de onda rectangular

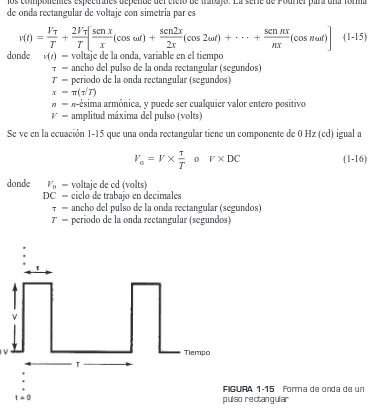
Cuando se analizan los circuitos de comunicaciones electrónicas se hace necesario, con fre-cuencia, usar pulsos rectangulares. En la fig. 1-15 se ve una forma de onda que representa una serie de pulsos rectangulares. El ciclo de trabajo(DC, de duty cycle) en la onda es la relación del tiempo activo del pulso entre el periodo de la onda. En forma matemática, el ciclo de tra-bajo es

(1-14a)

(1-14b) en donde DCciclo de trabajo en decimales

DC(%)ciclo de trabajo en porcentaje

ancho del pulso de la onda rectangular (segundos) Tperiodo de la onda rectangular (segundos)

Independientemente de su ciclo de trabajo, una forma de onda rectangular está constitui-da por una serie de onconstitui-das senoiconstitui-dales relacionaconstitui-das armónicamente. Sin embargo, la amplitud de los componentes espectrales depende del ciclo de trabajo. La serie de Fourier para una forma de onda rectangular de voltaje con simetría par es

(1-15) donde v(t) voltaje de la onda, variable en el tiempo

ancho del pulso de la onda rectangular (segundos) T periodo de la onda rectangular (segundos) x (/T)

n n-ésima armónica, y puede ser cualquier valor entero positivo V amplitud máxima del pulso (volts)

Se ve en la ecuación 1-15 que una onda rectangular tiene un componente de 0 Hz (cd) igual a

o VDC (1-16)

donde V0 voltaje de cd (volts)

DC ciclo de trabajo en decimales

ancho del pulso de la onda rectangular (segundos) T periodo de la onda rectangular (segundos)

V₀V

T

v(t)V

T

2V

T

sen x

x (cos t)

sen2x

2x (cos 2t)

sen nx

nx (cos nt)

DC(%)

T100

DC

T

Tiempo

Mientras menor sea el ancho del pulso, la componente de cd será menor. También, según la ecua-ción 1-15, la amplitud de la n-ésima armónica es

(1-17a)

o sea (1-17b)

donde Vn amplitud máxima de la n-ésima armónica (volts) nn-ésima armónica (cualquier entero positivo)

3.14159 radianes

Vamplitud máxima de la onda rectangular (volts) ancho de pulso de la onda rectangular (segundos) Tperiodo de la onda rectangular (segundos)

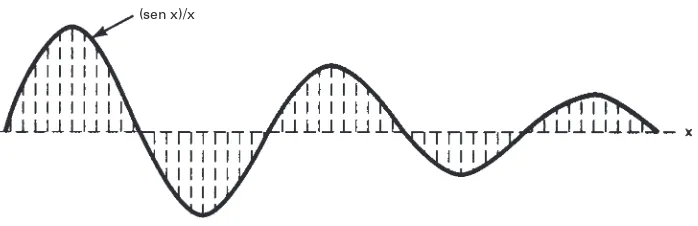
La función (sen x)/xse usa para describir formas de onda de pulsos repetitivos. El sen x es sólo una onda senoidal, cuya amplitud instantánea depende de x, y varía en sentido positivo entre sus amplitudes máximas, con una rapidez senoidal, cuando aumenta x. Si sólo hay xen el denominador, éste aumenta al aumentar x. Por consiguiente, una función (sen x)/xno es más que una onda senoidal amortiguada, en la que cada pico sucesivo es menor que el anterior. En la fig. 1-16 se ve una gráfica de la función (sen x)/x.

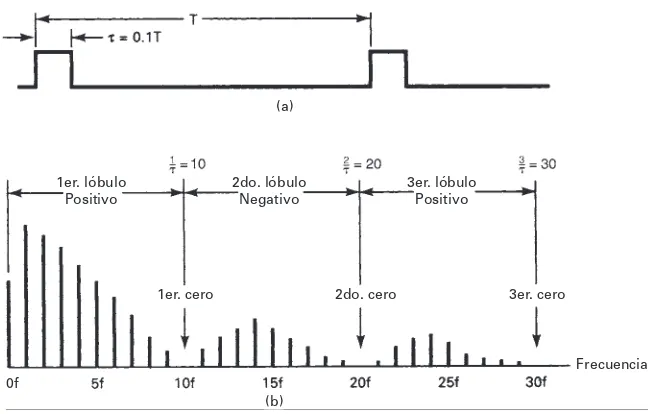
La fig. 1-17 muestra el espectro de frecuencias para un pulso rectangular, con relación de ancho de pulso a periodo igual a 0.1. Se puede ver que las amplitudes de las armónicas son como ondas senoidales amortiguadas. A la frecuencia cuyo periodo es igual a 1/(es decir, a la frecuen-cia 10fhertz), hay una componente de 0 V. Un segundo cero está en 20fhertz (periodo = 2/), un tercero en 30fhertz (periodo 3/), y así sucesivamente. Todas las componentes del espectro entre 0 Hz y la primera frecuencia cero se consideran en el primer lóbulo del espectro de fre-cuencias, y son positivas. Todas las componentes espectrales entre el primero y segundo cero de frecuencias están en el segundo lóbulo, y son negativas; las componentes entre el segundo y el tercer cero están todas en el tercer lóbulo y son positivas, etcétera.

Las siguientes características se cumplen en todas las formas de onda rectangulares repe-titivas:

1. La componente de cd es igual a la amplitud del pulso por el ciclo de trabajo.

2. Hay componentes de 0 V en la frecuencia 1/hertz y en todos los múltiplos enteros de esa frecuencia que cumplan con Tn, siendo ncualquier entero impar.

3. La envolvente de la frecuencia en función del tiempo, de las componentes del espec-tro, tiene la forma de una onda senoidal amortiguada en la que todas las componentes espectrales en lóbulos de número impar son positivas, y todas las componentes espec-trales en los lóbulos pares son negativas.

Vn

2V

T

sen[(n)T] (n)T

Vn

2V

T

sen nx nx

(sen x)/x

Ejemplo 1-3

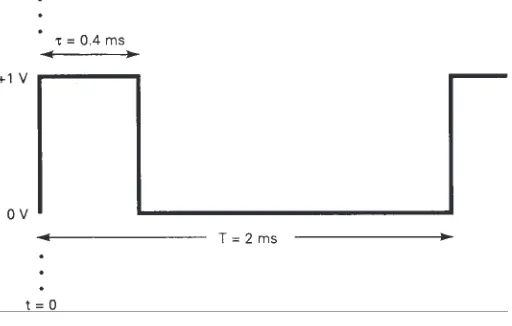
Para la forma de onda de pulsos que se ve en la fig. 1-18:

a)Determine la componente de cd.

b)Determine las amplitudes máximas de las 10 primeras armónicas.

c)Grafique la función (sen x)/x.

d)Trace el espectro de frecuencias.

Solución (a) De acuerdo con la ecuación 1-16, la componente de cd es

(b) Las amplitudes máximas de las 10 primeras armónicas se calculan sustituyendo los valores de , T, Vy nen la ecuación 1-17b, como sigue

V_n2(1)

sen[(n)(0.4 ms2 ms)] (n)(0.4 ms2 ms)

V0

1(0.4 ms) 2 ms 0.2 V

Frecuencia Amplitud

n (Hz) (volts)

0 0 0.2 V dc

1 500 0.374 Vp

2 1000 0.303 Vp

3 1500 0.202 Vp

4 2000 0.094 Vp

5 2500 0.0 V

6 3000 0.063 Vp

7 3500 0.087 Vp

8 4000 0.076 Vp

9 4500 0.042 Vp

10 5000 0.0 V

1er. lóbulo Positivo

2do. lóbulo Negativo

3er. lóbulo Positivo

1er. cero 2do. cero 3er. cero

Frecuencia (a)

(b) 0f

FIGURA 1-17 Función (sen x)/x: (a) forma de onda de un pulso rectangular; (b) espectro de frecuencias

(c) En la fig. 1-19 se ve la gráfica de la función(sen x)/x. (d) El espectro de frecuencias se ve en la fig. 1-20.

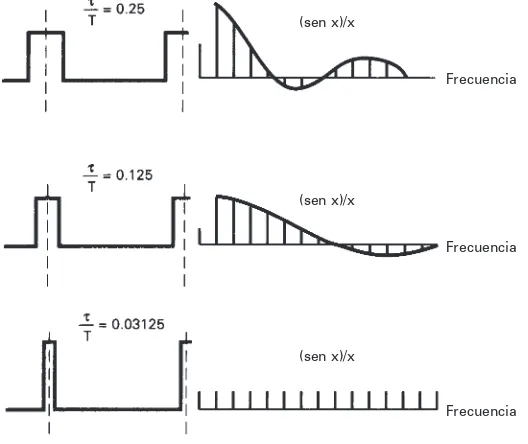
La fig. 1-21 muestra el efecto que tiene el reducir el ciclo de trabajo (es decir, reducir la relación /T) sobre el espectro de frecuencias, para una forma de onda no senoidal. Se puede apreciar que al angostar el ancho del pulso se produce un espectro de frecuencias con amplitud más uniforme. De hecho, para pulsos infinitamente angostos, el espectro de frecuencias abarca una cantidad infinita de frecuencias de igual amplitud, relacionadas armónicamente. Es imposible producir este espectro, y no digamos propagarlo. Eso explica por qué es difícil producir pulsos FIGURA 1-18 Forma de onda del pulso del ejemplo 1-3

Frecuencia (Hz)

V

oltaje (V)

FIGURA 1-19 Función (sen x)/xpara el ejemplo 1-3

Frecuencia (Hz)

V

oltaje (V)

extremadamente angostos. Si se aumenta el periodo de una forma de onda rectangular, mante-niendo constante el ancho del pulso, se obtiene el mismo efecto en el espectro de frecuencias. Espectros de potencia y energía

En la sección anterior se usaron las series de Fourier para comprender mejor la representación de una señal compleja en el dominio de la frecuencia y del tiempo. Ambos dominios se pueden usar para ilustrar la relación de los voltajes (magnitudes) de señal con respecto a la frecuencia o al tiempo, para una señal variable en el tiempo.

Sin embargo, hay otra aplicación importante de la serie de Fourier. El objetivo de un ca-nal de comunicaciones es transferir energía electromagnética de una fuente a un destino. Así, la relación entre la cantidad de energía transmitida y la recibida es una consideración importante. Entonces es importante examinar la relación entre la energía y la potencia en función de la fre-cuencia.

La potencia eléctricaes la rapidez con la cual se disipa, se entrega o se usa la energía, y es una función del cuadrado del voltaje o de la corriente (PE2/Ro PI2R). Para las re-laciones de potencia, la ecuación de Fourier, f(t), se reemplaza por [f(t)]2. La fig. 1-22 muestra el espectro de potencia para una forma de onda rectangular con 25% de ciclo de trabajo. Se pa-rece al espectro de voltaje en función de frecuencia, excepto que tiene más lóbulos y un lóbulo primario mucho más grande. Nótese también que todos los lóbulos son positivos, porque no existe la potencia negativa.

En la fig. 1-22 se puede ver que la potencia de un pulso se dispersa dentro de un espectro de frecuencias relativamente ancho. Sin embargo, nótese que la mayor parte de la potencia está dentro del lóbulo primario. Por consiguiente, si el ancho de banda de un canal de comunicacio-nes tiene la suficiente anchura para pasar sólo las frecuencias del lóbulo primario, transferirá al receptor la mayor parte de la energía que contiene el pulso.

Transformadas de Fourier discreta y rápida

Muchas formas de onda que se manejan en los sistemas normales de comunicaciones no se pue-den definir en forma satisfactoria con ecuaciones matemáticas; sin embargo, es de interés primor-dial su comportamiento en el dominio de la frecuencia. Con frecuencia hay necesidad de obtener este comportamiento de señales que se captan en el dominio del tiempo, es decir, en tiempo real.

Frecuencia

Frecuencia

Frecuencia (sen x)/x

(sen x)/x

(sen x)/x

Ésta es la razón por la que se desarrolló la transformada discreta de Fourier. En esa transfor-mación se muestrea una señal en el dominio del tiempo, en tiempos discretos. Las muestras se alimentan a una computadora donde un algoritmo calcula la transformación. Sin embargo, el tiem-po de computación es protiem-porcional a n2, siendo nla cantidad de muestras. Para cualquier canti-dad razonable de muestras, el tiempo de computación es excesivo. En consecuencia se desarro-lló, en 1965, un nuevo algoritmo, llamado transformada rápida de Fourier(FFT, de fast Fourier transform), por Cooley y Tukey. Con la FFT, el tiempo de cómputo es proporcional a nlog2n, y no a n2. Hoy se cuenta con la FFT en forma de subrutina, en muchas bibliotecas de subrutinas científicas en los grandes centros de cómputo.

Efectos de limitación de banda sobre las señales

Todos los canales de comunicaciones tienen un ancho de banda limitado y, en consecuencia, un efecto limitador sobre las señales que se propagan por ellos. Se puede considerar que un canal de comunicaciones es un filtro ideal de fase linealcon ancho de banda finito. Si una forma de onda repetitiva y no senoidal pasa por un filtro pasabajas ideal, se eliminan los componentes ar-mónicos de frecuencia mayor que la frecuencia superior de corte del filtro. En consecuencia, cambia tanto el contenido de frecuencias como la forma de la onda. La fig. 1.23a muestra la forma de onda en el dominio del tiempo, para la onda cuadrada del ejemplo 1-2. Si esta forma de onda pasa por un filtro pasabajas, con frecuencia superior de corte de 8 kHz, se eliminan las frecuencias superiores a la octava armónica (9 kHz y mayores), y resulta la forma de onda de la fig. 1-23b. Las figs. 1-23c, d y e muestran las formas de onda que se producen cuando se usan filtros pasa-bajas con frecuencias superiores de corte de 6, 4 y 2 kHz, respectivamente.

Se puede ver en la fig. 1-23 que al limitar la bandade una señal cambia el contenido de fre-cuencias y por consiguiente la forma de onda. Si se impone una limitación suficiente de banda, al final la forma de onda sólo comprende a la frecuencia fundamental. En los sistemas de comunica-ciones, la limitación de banda reduce la capacidad de información del sistema y si se impone de-masiada limitación, se puede eliminar la señal de información de la forma de onda compuesta.

MEZCLADO

El mezcladoes el proceso de combinar dos o más señales, y es un proceso esencial en comuni-caciones electrónicas. En esencia hay dos formas en las que se pueden combinar o mezclar las señales: lineal y no lineal.

Suma lineal

La suma linealse presenta cuando se combinan dos o más señales en un dispositivo lineal, co-mo puede ser una red pasiva o un amplificador de señal pequeña. Las señales se combinan de tal manera que no se producen nuevas frecuencias, y la forma de onda combinada no es más que la suma lineal de las señales individuales. En la industria de grabación de audio, a veces se lla-ma mezclado lineal a la suma lineal; sin embargo, en las radiocomunicaciones, el mezclado im-plica casi siempre un proceso no lineal.

Frecuencia