Utilización del método fotoelástico para la determinación de esfuerzos en placas agrietadas

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA SECCION DE ESTUDIOS DE POSGRADO E INVENTIGACIÓN

UTILIZACIÓN DEL MÉTODO FOTOELÁSTICO

PARA LA DETERMINACIÓN DE ESFUERZOS EN

PLACAS AGRIETADAS

T E S I S

QUE PARA OBTENER EL GRADO DE

MAESTRO EN CIENCIAS

CON ESPECIALIDAD EN

INGENIERÍA MECÁNICA

P R E S E N T A :

MARCO ANTONIO AUDELO BENÍTEZ

DIRIGIDA POR : M.C. GABRIEL VILLA Y RABASA

R

R

E

E

S

S

U

U

M

M

E

E

N

N

A

A

B

B

ST

S

T

R

R

AC

A

CT

T

O

O

B

B

J

J

E

E

T

T

I

I

VO

V

O

J

J

US

U

ST

T

I

I

F

F

I

I

CA

C

AC

CI

IÓ

ÓN

N

La falla de los elementos mecánicos, a causa de la presencia de grietas, es muy frecuente, por eso es importante predecir cuando sucederá ésta. Desafortunadamente, el análisis para la predicción de la falla a causa de las grietas no es tan simple, ya que intervienen muchos factores, que intervienen en la propagación de las mismas En primer lugar, la forma y ubicación de las grietas, es importante para su análisis; por otro lado, las grietas no se encuentran aisladas, éstas pueden ser dos o más y, además, presentan diferentes configuraciones, que pueden afectar, en menor o mayor grado, el crecimiento de las mismas. Si, en un principio, el grado de dificultad para predicción de la falla, en la que interviene una sola grieta, es relativamente alto, cuando intervienen más de una grieta, la dificultad es mayor.

Í

Í

ND

N

DI

I

C

C

E

E

G

G

E

E

N

N

E

E

R

R

A

A

L

L

RESUMEN i

ABSTRACT ii

OBJETIVO iii

JUSTIFICACIÓN iv

ÍNDICE DE FIGURAS viii

ÍNDICE DE TABLAS x

SIMBOLOGÍA xii

INTRODUCCIÓN xiv

CAPÍTULO I.

1. Análisis Teórico de Placas Agrietadas. 1

1.1. Estado del arte. 2

1.2. Fundamentos de mecánica de la fractura. 5

1.2.1. Modos de carga. 5

1.2.2. Criterio de Griffith. 7

1.2.3. Planteamiento energético 10

1.2.3.1. Relación de energía liberada de deformación. 10

1.2.3.2. Descripción gráfica de G. 10

1.2.3.3. Resistencia al crecimiento de la grieta. 10

1.2.3.4. Relaciones matemáticas de G. 13

1.2.4. Planteamiento a partir del análisis de esfuerzos. 15 1.2.4.1. Ecuaciones del campo de esfuerzos. 15 1.2.4.1.1. Ecuaciones diferenciales de equilibrio. 15

1.2.4.1.2 Condiciones de frontera. 17

1.2.4.1.3. Ecuaciones de compatibilidad. 18

1.2.4.1.4. La función esfuerzo. 19

1.2.4.4. Limitaciones del análisis lineal de la mecánica de fractura. 32

1.3. Planteamiento del problema. 34

CAPÍTULO II.

2. Principios Básicos de la Luz 36

2.1. Teoría electromagnética. 37

2.2. Espectro electromagnético. 38

2.3. Ecuación de onda. 39

2.4. Superposición de ondas. 42

2.5. Reflexión y refracción. 48

2.6. Polariscopio. 52

2.6.1. Polarizadores planos o lineales. 53

2.6.2. Placas de onda. 54

2.7. Luz polarizada plana. 57

2.8. Luz polarizada circular. 57

2.9. Luz polarizada elípticamente. 58

2.10. Arreglo de los elementos ópticos del polariscopio. 58

2.11. Aplicación al caso de estudio. 60

CAPÍTULO III

3. Fotoelásticidad 62

3.1. Teoría de la fotoelasticidad. 63

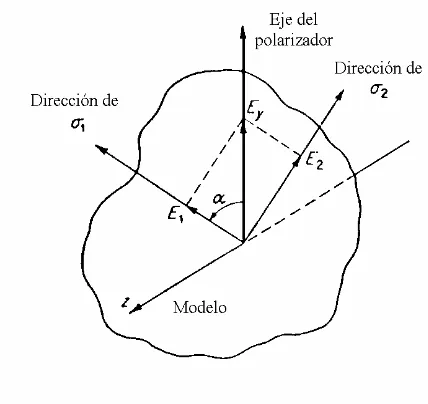
3.2. Efectos de modelos en un polariscopio. 68 3.3. Efecto de la dirección de los esfuerzos principales. 71 3.4. Efecto de la diferencia de los esfuerzos principales. 72 3.5. Frecuencia de respuesta en un polariscopio. 72

3.6. Aplicación al caso de estudio. 72

CAPÍTULO IV

4. Fotoelasticidad Aplicada 74

4.1. Análisis fotoelástico. 75

4.2. Modelo de franjas isocromáticas. 75

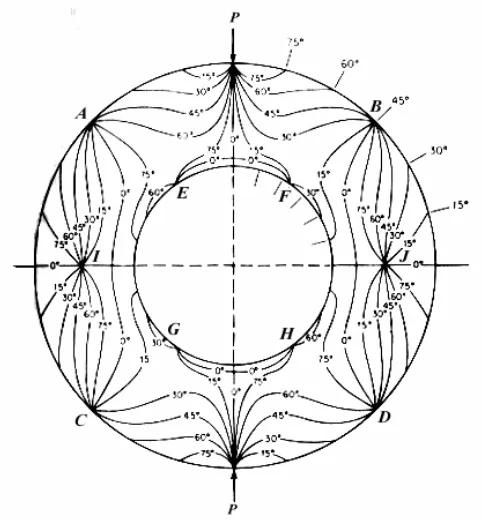
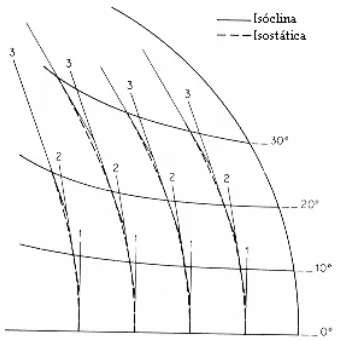
4.3. Modelo de franjas isóclinas. 79

4.4. Técnicas de compensación. 83

4.5. Métodos de calibración. 83

4.6. Métodos de separación. 85

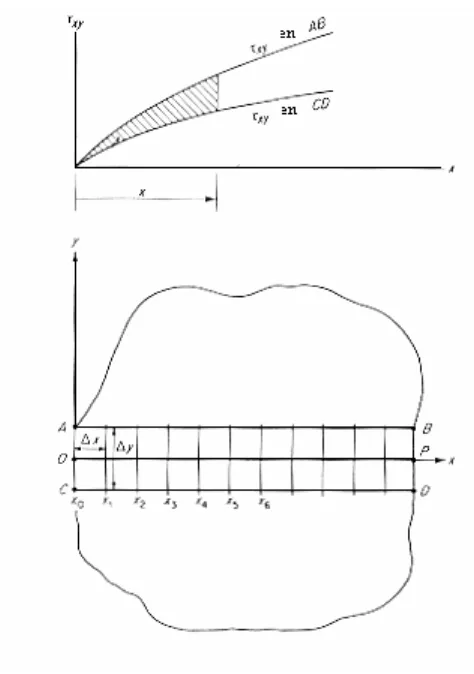
4.6.1. Método de diferencia de cortante. 85 4.7. Método de Irwin para determinar KI a partir de patrones de franjas isocromáticas 88

4.8. Modificaciones al método biparamétrico de Irwin 90 4.9.Método para determinar KI a partir de franjas isocromáticas de dos grietas que se encuentran

interactuando. 92

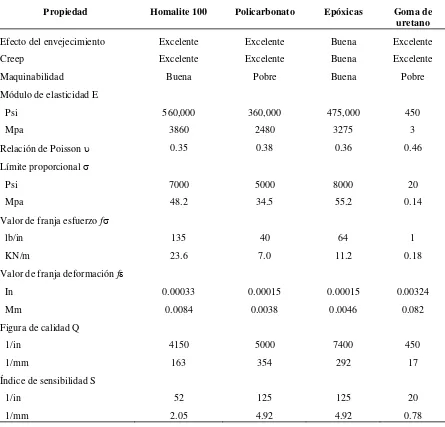
4.10. Materiales empleados en fotoelasticidad. 94 4.10.1. Propiedades de los materiales utilizados en fotoelasticidad. 95

4.10.1.1. Transparencia. 95

4.10.1.2. Sensibilidad. 96

4.10.1.3. Linealidad. 96

4.10.1.4. Homogeneidad e isotropía. 97

4.10.1.5. Fluencia. 97

4.10.1.11. Costo del material. 104 4.10.2. Materiales fotoelásticos más empleados. 104

4.10.2.1. Homalite 100. 105

4.10.2.2. Policarbonato. 105

4.10.2.3. Resinas epóxicas. 106

4.10.2.4. Goma de Uretano. 106

4.10.2.5. Resumen del material modelo. 107

4.11. Aplicación al caso de estudio. 109

CAPÍTULO V

5. Análisis realizados por otros métodos 110

5.1. Análisis numérico. 111

5.1.1. Método iterativo propuesto por J. H. Kuang y C. K. Chen. 111 5.1.2. Modelo de longitud de Grieta Equivalente. 116

CAPÍTULO VI

6. Análisis del estudio experimental 119

6.1. Metodología. 120

6.2. Descripción del equipo. 120

6.3. Desarrollo de la metodología. 120

6.3.1. Selección del material. 120

6.3.2. Fabricación de la probeta. 122

6.3.3. Calibración de la probeta. 122

6.3.4. Determinación del número de franja. 124 6.3.4.1. Caso de la placa centralmente agrietada. 124 6.3.4.2. Caso de una placa con dos grietas apiladas. 125 6.3.4.3. Caso de una placa con dos grietas colineales. 125 6.3.5. Cálculo de los factores de intensidad de esfuerzos. 126 6.3.5.1. Caso de la placa centralmente agrietada. 126 6.3.5.2. Caso de la placa con dos grietas apiladas. 128 6.3.5.3. Caso de la placa con dos grietas colineales. 132

6.3.6. Discusión de resultados. 135

6.3.6.1. Caso para una grieta central. 135 6.3.6.2. Caso de una placa con dos grietas apiladas. 136 6.3.6.3. Caso de una placa con dos grietas colineales. 137

CAPÍTULO VII

7. Análisis de resultados 139

7.1. Análisis de resultados. 140

7.1.1. Caso de una grieta central. 140

7.1.2. Caso de dos grietas apiladas interactuando. 144 7.1.3. Caso de dos grietas colineales. 146

CONCLUSIONES 148

RECOMENDACIONES 150

Í

Í

ND

N

DI

IC

CE

E

D

DE

E

F

F

I

I

G

G

UR

U

RA

AS

S

1.1 Modo de carga I. 6

1.2 Modo de carga II. 6

1.3 Modo de carga III. 6

1.4 Criterio de Griffith. a) placa agrietada con extremos fijos, b) Energía elástica de deformación. 7

1.5 Diagrama carga-desplazamiento. 11

1.6 Crecimiento estable de una grieta bajo la condición de esfuerzo plano. 12

1.7 Curva R para esfuerzo plano. 12

1.8 Placa agrietada. 14

1.9 Esfuerzos sobre un aplaca rectangular en equilibrio. 16 1.10 Prisma triangular sometido a esfuerzos. 17 1.11 Definición del sistema de coordenadas de una placa que contiene una grieta. 21 1.12 Esfuerzos biaxiales en una placa con una grieta central. 24 1.13 Primera estimación del tamaño de la zona plástica. 26 1.14 Segunda estimación del tamaño de la zona plástica. 28 1.15 Forma de la zona plástica. (a) criterio de Von Mises. (b) Criterio de Tresca 30 1.16 Formas de la zona plástica para los modos II y III. 31 1.17 Formas más exactas de la zona plástica para el modo I. (a) de acuerdo con el criterio de Tuba,

(b) de acuerdo a Rice y Rosengren. rP(θ=0) = 0.007 (K/σys)2. rP(θ=100) = 0.24 (K/σys)2.

Relación deformación-dureza = 0.05.

31

1.18 1.18. distancia rK 34

2.1 Vectores eléctricos y magnéticos asociados con una onda electromagnética plana 37 2.2 Dirección de propagación, vector eléctrico y vector magnético en un instante dado. 37 2.3 Espectro electromagnético. Todas las escalas son logarítmicas. Los extremos de las escalas

están en la cercanía de los rayos cósmicos secundarios de más alta energía que se han observado hasta el tiempo presente. [33].

38

2.4 Magnitud del vector luz como una función de su posición a lo largo del eje de propagación en 2

tiempos diferentes. 42

2.5 Dos ondas de luz linealmente polarizadas con la misma frecuencia pero con planos de

vibración mutuamente perpendiculares. 46

2.6 La hélice elíptica formada por las puntas de los vectores a lo largo del eje de propagación en un

instante de tiempo fijo. 47

2.7 Trayectoria de la punta del vector luz sobre un plano perpendicular en la posición z0. 47

2.8 Reflexión y refracción de una onda de luz plana en una interface entre dos materiales

transparentes. 50

2.9 Reflexión y refacción en el ángulo de polarización. 51 2.10 Coeficientes de reflexión para una interface aire-vidro (n21 = 1.5). [7]. 52

3.1 Índice elipsoide. 63 3.2 Modelo fotoelástico sometido a esfuerzos en un polariscopio plano. 69 3.3 División del vector luz cuando entra a un modelo sometido a esfuerzos en un polariscopio

plano.

70 3.4 Componentes de los vectores luz los cuales se transmiten a través del analizador de un

polariscopio plano. 70

4.1 Patrón de franjas isocromáticas en campo claro de un eslabón de cadena sujeto a cargas de

tensión axiales. 76

4.2 Círculo de Mohr para el estado de esfuerzos en un punto (a) σ1> 0, σ2<σ3 = 0;

(b) σ1>σ2>σ3 = 0

77 4.3 Patrón de franjas isocromáticas en campo obscuro para una sección presurizada de un tubo

cuadrado con una perforación circular. [7]. 79 4.4 Patrones de franjas isóclinas de un anillo circular sometido a una carga de compresión

diametral. [7].

80 4.5 Patrón de franjas isóclinas compuesto de un anillo circular sometido a una carga de compresión

diametral. 81

4.6 Técnica para convertir isóclinas en isoestáticas. 82 4.7 Sistema de divisiones empleadas en la aplicación del método de la diferencia de cortante. 87 4.8 Geometría característica de una franja isocromática cerca de la punta de la grieta. 88 4.9 Selección de los puntos sobre una franja isocromática. 93 4.10 Variación típica de KI con respecto a r. 94

4.11 Curvas típicas (a) esfuerzo-deformación y (b) orden de franja deformación para polímeros

utilizados en fotoelasticidad. 98

4.12 Curva típica mostrando el tiempo después de la carga dependiente del valor de franja esfuerzo en un material polímero fotoelástico. [7]. 100 4.13 Curva típica que muestra los cambios en el valor de franja esfuerzo con la temperatura. [7]. 101 4.14 Un ejemplo de la distorsión de franjas cerca de los bordes debidos a esfuerzos producidos por

el tiempo en los bordes de un modelo fotoelástico. [7]. 102 4.15 Maquinado de un modelo fotoelástico con un router. 104 5.1 Principio de superposición de Bueckner para dos grietas paralelas. 111 5.2 Descomposición del problema de la interacción de dos grietas paralelas. 112 5.3 Parámetros geométricos de una grieta simple. 113 5.4 Proceso de iteración para las tensiones en la superficie de la grieta. 114 5.5 Placa con una grieta equivalente sometida a tensión. 118 6.1 Descripción del polariscopio utilizado. 121 6.2 Gráfica para la determinación de KI en una placa sometida a 251.09 N a tensión. 129

6.3 Gráfica para la determinación de KI en una placa sometida a 313.87 N a tensión. 129

6.4 Gráfica para la determinación de KI en una placa sometida a 376.64 N a tensión. 130

6.5 Gráfica para la determinación de KI en una placa sometida a 439.27 N a tensión. 130

6.6 Gráfica para la determinación de KI en una placa sometida a 502.02 N a tensión. 131

6.7 Gráfica para la determinación de KI en una placa sometida a 564.77 N a tensión. 131

6.8 Gráfica para la determinación de KI en una placa sometida a 313.87 N a tensión. 133

6.9 Gráfica para la determinación de KI en una placa sometida a 376.64 N a tensión. 133

6.10 Gráfica para la determinación de KI en una placa sometida a 439.27 N a tensión. 133

6.11 Gráfica para la determinación de KI en una placa sometida a 502.02 N a tensión. 133

6.12 Gráfica para la determinación de KI en una placa sometida a 564.77 N a tensión. 134

6.13 Gráfica para la determinación de KI en una placa sometida a 627.72 N a tensión. 134

7.4 Comparación gráfica de los resultados obtenidos por los dos métodos. 147

Í

Í

N

N

D

D

I

I

C

C

E

E

D

D

E

E

T

T

A

A

B

B

L

L

A

A

S

S

2.1 Espectro visible 39

2.2 4 arreglos diferentes de los elementos ópticos de un polariscopio circular 60 4.2 Resumen de las propiedades mecánicas y ópticas de cuatro materiales fotoelásticos. 108 6.1 Valores de franja fσ obtenidos en el proceso de calibración. 123

6.2 Datos obtenidos a partir de un patrón de franjas isocromáticas para el cálculo de KI en una

placa con una grieta central.

124 6.3 Datos obtenidos a partir de un patrón de franjas isocromáticas para el cálculo de KI en una

placa con dos grietas apiladas. 125

6.4 Datos obtenidos a partir de un patrón de franjas isocromáticas para el cálculo de KI en una

placa con dos grietas colineales. 126

6.5 Factores de intensidad de esfuerzos obtenidos por el método de Irwin. 126 6.6 Factores de intensidad de esfuerzos obtenidos por el método modificado de Irwin por

Bradley – Kobayashi 127

6.7 Factores de intensidad de esfuerzos obtenidos por el método modificado de Irwin por

Schoedl-Smith. 127

6.8 KI obtenidos por los tres métodos basándose en el método fotoelástico. 128

6.9 Valores de KI para diferentes valores de r, en una placa con dos grietas apiladas. 128

6.10 Valores de KI utilizando el método de Rameshian y Chandrasheker, para el caso de dos

grietas apiladas. 132

6.11 Valores de KI para diferentes valores de r, en una placa con dos grietas colineales. 132

6.12 Valores de KI utilizando el método de Rameshian y Chandrasheker, para el caso de dos

grietas colineales. 134

6.13 KI obtenidos por el método aproximado. 135

6.14 KI obtenidos por los tres métodos basándose en el método fotoelástico y basándose en el

método aproximado. 135

6.15 Valores de KI utilizando el método iterativo de Kuang y Chen, para el caso de dos grietas

apiladas. 136

6.16 Resultados obtenidos utilizando el modelo de grieta equivalente para el caso de dos

grietas apiladas. 136

6.17 KI obtenidos por el método fotoelástico, el método iterativo de Kuang y Chen y el modelo

de la grieta equivalente.

7.1. Porcentaje de error mostrado por los resultados obtenidos en comparación con los resultados obtenidos por el método aproximado. 140 7.2. Porcentaje de error mostrado por los resultados obtenidos en comparación con los

resultados obtenidos por el método iterativo, para dos grietas apiladas. 144 7.3. Porcentaje de error mostrado por los resultados obtenidos en comparación con los

S

S

I

I

MB

M

BO

OL

LO

OG

GÍ

Í

A

A

σ Esfuerzo normal aplicado.

ε Deformación unitaria.

π Constante igual a 3.1415...

υ Relación de Poisson.

ρ Densidad.

τ Esfuerzo cortante.

ζ Variable compleja.

α Ángulo de incidencia.

β Ángulo de reflexión.

γ Ángulo de refracción.

∆ Diferencia de fase relativa.

∆ Retardación relativa.

λ Longitud de onda.

ξ Número de onda.

φ Función de esfuerzo de Airy.

ω Frecuencia angular.

α, β, θ, φ Ángulos.

σ1 Esfuerzo principal máximo.

σ2 Esfuerzo principal mínimo.

σc Esfuerzo crítico aplicado.

αp Ángulo de polarización.

σx, σy, σz Esfuerzo normal en las direcciones x, y y z.

εx, εy, εz Deformaciones unitarias en las direcciones x, y y z.

τxy, τyzτzx Componentes del esfuerzo cortante en coordenadas rectangulares.

κ Razón de esfuerzo longitudinal.

µ Módulo de corte.

a Mitad de la longitud de la grieta. A Amplitud de una onda de luz. ac Tamaño crítico de la grieta.

B Ancho de la placa analizada. C Flexibilidad de la placa.

C Coeficiente esfuerzo-óptico relativo. C Velocidad de la luz en el vacío.

c1, c2 Coeficientes esfuerzo-óptico.

G Energía liberada de deformación. Gmáx Razón de la energía máxima liberada.

G Aceleración de la gravedad. H Espesor. I Intensidad de la luz.

KI, KII, KIII Factor de intensidad de esfuerzos para los modos I, II y III.

KIC Factor de intensidad de esfuerzos crítico para el modo I.

L Longitud de la placa. l, m Cosenos directores.

N Índice de refracción. N Número de franja.

n1, n2, n3, Índices de refracción a lo largo de las direcciones principales.

P Carga aplicada. Q Figura de calidad. R Resistencia al crecimiento de la grieta. R Coeficiente de reflexión.

r, θ Coordenadas polares.

rP Tamaño corregido de la zona plástica.

rP* Tamaño de la zona plástica.

T Tensión de superficie o energía de superficie por unidad de área. t Tiempo.

T Periodo

U Energía elástica de deformación interna (energía liberada). u, v Componentes del desplazamiento.

Ue Energía de deformación.

Us Energía de superficie.

Ut Energía total de deformación.

V Volumen.

W Energía requerida para que la grieta crezca. x, y, z Coordenadas rectangulares.

I

I

N

N

T

T

R

R

O

O

D

D

U

U

C

C

C

C

I

I

Ó

Ó

N

N

Las grietas, en la superficie de recipientes a presión y tuberías, son comúnmente observadas en la práctica. Estas grietas pueden generarse por corrosión severa, por fatiga térmica o por los procesos de fabricación utilizados. Es por esto, que resulta difícil evitarlas, por lo que es una mejor opción aprender a vivir con ellas. Por otro lado, las grietas no vienen solas, éstas se encuentran interactuando con otras grietas, las cuales se encuentran en configuraciones aleatorias que influyen en la distribución de esfuerzos que se desarrollan en los cuerpos que presentan dichas configuraciones. La predicción de cuando ocurrirá una falla a causa de una grieta es el objetivo principal de los investigadores que trabajan sobre el comportamiento de las grietas. Cuando una estructura o componente de máquina presenta un defecto, tal como una grieta, los esfuerzos en la vecindad de la punta de la grieta presentan una singularidad. Debido a que estos esfuerzos locales exceden al esfuerzo de fluencia y al esfuerzo de tensión último del material para cargas muy pequeñas, los criterios utilizados para la predicción de las cargas a las cuales falla el material basados en las teorías de falla de Von Mises y Tresca no son factibles. En vez de ésto, se determina un parámetro de fractura, tal como un factor de intensidad de esfuerzos KI, y se compara con la tenacidad de

fractura del material KIc. Este método de análisis estructural utilizado en mecánica de

fractura para predecir se la grieta será estable bajo una carga aplicada o si ésta se convertirá inestable y se propagará para causar una falla abrupta.

En la utilización de la mecánica de fractura en el análisis estructural, es necesario determinar el parámetro pertinente de fractura, KI, como una función de la carga aplicada.

En muchos cuerpos sencillos, KI puede determinarse a partir de datos comprobados

En este trabajo, se propone la utilización del método fotoelástico para la obtención de los factores de intensidad de esfuerzos en el modo I de fractura, KI. Se eligió el modo I de

fractura, porque es el modo que se presenta más frecuentemente en recipientes a presión. El método fotoelástico presenta ventajas sobre otros métodos. Estas ventajas son: la disponibilidad para su realización, la facilidad y rapidez con la que se obtienen resultados prácticos en elementos sometidos a diferentes estados de esfuerzos, que presentan geometrías especiales con más de una grieta, que dificultan el estudio analítico del problema.

El trabajo consta de 7 capítulos. En el capitulo I, se hizo un análisis teórico de las placas agrietadas en base a la Mecánica de Fractura. En un principio se trató a las grietas de manera general, y posteriormente se hizo una descripción más detallada del comportamiento de las mismas cuando se les somete a cargas.

En el capítulo II, se presentan los principios básicos de la luz desde el punto de vista de la teoría electromagnética desarrollada por Maxwell.

El capítulo III, describe en que consiste el fenómeno fotoelástico. Se menciona que es lo que sucede en el polariscopio cuando un modelo fotoelástico se coloca en el campo y se somete a cargas.

El capitulo IV, describe la realización del análisis fotoelástico. Se mencionan algunas técnicas de fabricación de modelo fotoelásticos. Se presenta también algunos materiales fotoelásticos más utilizados, así como sus características de importancia.

Posteriormente, en el capítulo V, se presenta algunos métodos que se utilizan para el análisis de placas con mas de una grieta, esto, con el fin, de poder tener parámetros de comparación para validar los resultados obtenidos a través del método fotoelástico.

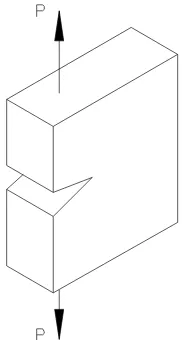
En el capítulo VI se hizo una descripción del procedimiento experimental, que se siguió, para la obtención de resultados. Básicamente, se realizaron 3 pruebas, la primera se hizo en una placa centralmente agrietada, la otra se realizó en una placa con dos grietas apiladas y también se realizó una prueba en una placa con dos grietas colineales.

1.1. Estado del arte.

Existen diferentes trabajos de investigación sobre mecánica de fractura y fotoelasticidad, que preceden a este. Los cuales van desde las primeras aproximaciones que se hicieron sobre mecánica de fractura hasta las realizadas recientemente, lo mismo sucede con la fotoelasticidad. Estos trabajos se utilizan para llevar la línea de investigación en Mecánica de la Fractura y la fotoelasticidad se han mencionado frecuentemente en otros trabajos realizados que tratan con mecánica de fractura y fotoelasticidad. A continuación se presentan algunos de los trabajos realizados durante la última década, ya que muestran la aplicación de los principios básicos ésta línea.

Betanzos [3], trata con las causas representativas de las fallas y algunos fundamentos de análisis de fracturas, así como con una de las muchas teorías del mecanismo de falla de una pieza de metal cuando está sujeta a cargas, haciendo un análisis de la teoría de falla por deslizamiento. Además, trata sobre los dos modos básicos que usualmente siguen las fallas y hace una análisis del reconocimiento de una fractura dada los modos básicos y los factores que la afectan.

García [34] en su tesis de maestría, aplica el método energético basado en los resultados del Método del Elemento Finito para el cálculo del Factor de Intensidad de Esfuerzos en un agrietamiento del modo I. Su metodología propuesta se apoya en dos bases fundamentales en los fundamentos lineales de la mecánica de fractura y en los fundamentos del método del elemento finito aplicados a la mecánica de fractura. Una vez conocidas las bases que justifican esta metodología, la establece y la aplica al caso de interés para obtener el valor del Factor de Intensidad de Esfuerzos. Para validar los resultados obtenidos se comparan con los resultados que proporcionan, por un lado el método experimental fotoelástico y por el otro los métodos analíticos directo y aproximado. Y finalmente concluye que el método energético proporciona resultados aceptables y confiables.

Éste ocurre por una redistribución de las fuerzas internas como resultado de la presencia de la grieta. También observaron un esfuerzo cortante localizado en una zona a flexión pura ocasionado por la presencia de la grieta. El aumento de esta zona se incrementa cuando crece el tamaño de la grieta.

Nakamura [23] ha investigado sobre los diferentes aspectos de los campos de esfuerzos cerca de una grieta interfase en un placa de dos materiales en tres dimensiones. Obteniendo los siguientes resultados. Debido a la naturaleza del campo resultante de deformación, los efectos tridimensionales son más críticos en una placa de dos materiales que en una placa homogénea. En la vecindad de la frente de la grieta interfase, el campo de esfuerzos se caracteriza por campo K de dos materiales asintótico, y su tamaño dominante es una muy pequeña fracción del espesor de la placa. De forma diferente, en el caso homogéneo, el campo asintótico siempre abarca los tres modos de fractura, y una grieta interfase debe propagarse bajo condiciones de modos mezclados. Además, resultados computacionales han mostrado que los dos ángulos de fase que representa las magnitudes relativas de los tres modos son fuertemente dependientes de las propiedades de los dos materiales También se ha observado, que existe una significante deformación antiplana a lo largo del frente de la grieta, especialmente, en la superficie libre. Las investigaciones experimentales han mostrado, que la relación de energía liberada crítica Gc, es altamente dependiente de los

ángulos de fase, una predicción precisa del comportamiento de la fractura interfase requiere no sólo la distribución de G, sino, también, de las variaciones de los ángulos de fase a lo largo de la frente de la grieta.

El factor de intensidad de esfuerzos de una grieta interfase en dos materiales, según Lu y Chiang [22], puede representarse por medio de un vector complejo, cuyos cambios de fase están en función de r, la distancia radial a partir de la punta de la grieta. Propusieron, dos enfoques fotoelásticos para la determinación de la magnitud y el ángulo de fase de este vector complejo. Esto muestra que, dentro de la zona dominada por K, el factor de intensidad de esfuerzos complejo puede determinarse en cualquier r y, para después, convertirlo a cualquier otro r. Para la ilustración de estas técnicas propuestas, utilizaron como ejemplo, el caso de una grieta interfase bajo una tensión lejana.

de la punta de una grieta. Para lo anterior toca aspectos que resultan de importancia para la adecuada comprensión del fundamento matemático de la mecánica de fractura, llegándose a definir tanto las funciones analíticas, como las armónicas que resultan de interés para expresar en una forma conveniente un campo variable. También incluye los fundamentos de mecánica de fractura, enunciando lo que representa efectuar un tratamiento elástico lineal, para desarrollar el planteamiento energético que define la relación de energía liberada G y la resistencia al crecimiento de la grieta R. Además presenta una validación por un método experimental.

Geubelle y Knauss [14] escriben sobre el problema del crecimiento de una grieta localizada en la interfase entre dos sólidos linealmente elásticos cuando las condiciones permiten la propagación a lo largo y/o alejada de la interfase. Examinaron el criterio de la máxima energía de liberación y el criterio de esfuerzos. Encontraron que para el caso contrario del problema del crecimiento de la grieta en un sólido homogéneo, no sólo la dirección de propagación resulta cuando se mantiene sólo consideraciones continuas. Los resultados para este análisis lineal los compararon con observaciones experimentales.

La predicción de la falla, por fractura, es un prerrequisito para evaluar el margen de seguridad para recipientes a presión, que presentan grietas paralelas y se encuentran interactuando. Es por esto que, Kuang y Chen [21], presentaron un método iterativo, que permite la obtención de la longitud de una grieta, equivalente a dos grietas paralelas apiladas. También, utilizaron el criterio de la relación de energía máxima liberada, para convertir problemas de grietas múltiples en problemas de una sola en modo I. Los resultados demostraron, que una grieta paralela secundaria, más corta, puede cubrir a la grieta equivalente en ciertas zonas. Los resultados obtenidos, también, pueden utilizarse para evaluar las reglas aproximadas, que existían anteriormente.

1.2. Fundamentos de mecánica de la fractura. 1.2.1. Modos de carga.

Las grietas, que aparecen en un cuerpo sólido, pueden estar sometidas a cargas en tres formas diferentes, causando los siguientes modos de fractura:

El modo I, es conocido como el de apertura y en éste los desplazamientos de la superficie de la grieta son perpendiculares al plano de la misma, al igual que la carga aplicada.

El modo II, es conocido como de deslizamiento o de corte. En este caso los desplazamientos de la superficie de la grieta están en su plano y son normales al borde de la misma. La dirección de las cargas es perpendicular al borde de la grieta

Figura 1.1. Modo de carga I.

Figura 1.2. Modo de carga II.

Figura 1.3. Modo de carga III.

1.2.2. Criterio de Griffith.

Gran parte de la estructura, sobre la que descansan los conceptos de la mecánica lineal de la fractura, fueron establecidos por A. A. Griffith, con sus trabajos: “Los fenómenos de ruptura y flujo en sólidos [26] en 1921 y La teoría de la ruptura [15] en 1925”.

Para establecer la relación energética de la mecánica lineal de fractura, considérese una placa agrietada de espesor unitario con una grieta de longitud 2a. La placa es sometida a un esfuerzo σ y sujetada en sus extremos como lo muestra la figura 1.4. El diagrama carga-deformación también se indica en la misma figura. La energía de carga-deformación elástica (es decir, el trabajo interno realizado en un cuerpo por fuerzas aplicadas exteriormente) contenida en la placa está representada por el área OAB.

Si la grieta se extiende una longitud diferencial da, la rigidez de la placa disminuirá al

reducirse la sección transversal de la misma. Por lo tanto la energía de deformación restante estará representada por el área OCB. La propagación de la grieta de a a a+da resultará en

una disminución de la energía elástica de deformación (en lo sucesivo se le podrá llamar también energía liberada debido a su disminución al aumentar el tamaño de la grieta), igual al área OAC.

Si se sometiera la placa a un esfuerzo más grande, la energía liberada sería mayor al incrementar el tamaño de la grieta una longitud da. De lo anterior se resume el criterio de

Griffith como sigue:

“La propagación de la grieta ocurrirá si la energía liberada al crecer la

grieta, es suficiente para suministrar toda la energía necesaria para el

crecimiento de la misma”.

El triángulo OCB representa la cantidad de energía disponible si la grieta creciera, Broek [4].

La condición matemática para el crecimiento de la grieta es: dU

da dW

da

= (1.1)

donde:

U = energía elástica de deformación interna (energía liberada). W = energía requerida para que la grieta crezca.

En forma general la energía de deformación elástica está definida como, Popov [24]:

dU= 1 dV

2σε (1.2)

donde:

σ = esfuerzo normal aplicado.

ε = deformación unitaria. V = volumen.

Para este caso particular, la energía de deformación para un espesor unitario está dada por

U a

E

e =

σ π2 2

(1.3)

donde:

E = módulo de Young.

Griffith comparó el cambio en la energía de deformación Ue, con la energía de superficie

Us =4aT (1.4) donde T es la tensión superficial o la energía de superficie por unidad de área.

Griffith argumentó que la grieta se propagaría inestablemente, cuando un pequeño incremento en la extensión de la grieta diera:

dUe > dUs

Así, la condición para que la grieta se extienda es:

(

)

d

da U U

d da

a

E aT

e − s = −

⎛ ⎝

⎜ ⎞

⎠ ⎟ = σ π2 2

4 0

Por lo que la energía de liberación Ue, se iguala a: σ π2

2

a

E = T (1.5) Con lo cual se llega a la relación de Griffith:

σ π c c ET a

= 2 (1.6)

donde los subíndices c indican los valores críticos de esfuerzo y tamaño de la grieta.

1.2.3. Planteamiento energético

1.2.3.1. Relación de energía liberada de deformación.

Las unidades de la energía liberada de deformación G son energía por unidad de longitud (se considera que la placa tiene un espesor unitario), esto es Joules/metro lo cual es equivalente a las unidades de fuerza. De esta forma, G se define por la relación

∂ ∂

U a

Y también se le puede llamar relación de energía potencial liberada.

1.2.3.2. Descripción gráfica de G.

La relación de energía máxima de deformación G puede obtenerse en forma gráfica. Para un cuerpo con una grieta de tamaño a, la relación carga desplazamiento está representada

por la línea OA en la figura 1.5. donde también se muestra la relación carga desplazamiento en la línea OE para el mismo cuerpo con una grieta de tamaño a + da.

Supóngase que la extensión de la grieta cambia de a a a + da. Si los extremos de la placa

están fijos, el desplazamiento de dichos puntos permanece constante y la carga disminuye de A a B. Esto significa que hay una liberación de energía elástica, representada por el área del triángulo OAB

Si la extensión de la grieta se presenta a carga constante, los desplazamientos de los puntos de aplicación de la carga se incrementan una cantidad ∆s. El trabajo hecho por la carga es P

∆s, el cual es igual al área AEFC. La energía de deformación elástica contenida en la placa se incrementa de OAC a OEF. En forma equivalente el incremento puede ser representado por el área OAE; esta energía tiene que ser suministrada por la carga; debido a que el área AEFC es dos veces OAE, permanece una cantidad de energía igual a OAE. Si no se considera el pequeño triángulo AEB, se tiene que OAB = OAE.

Esto significa, que la energía liberada al crecer la grieta es la misma para ambos casos. En el caso de extremos fijos, la energía disponible es suministrada por la energía de deformación elástica. Alternativamente bajo una carga constante, dicha energía es suministrada por la carga al realizar trabajo. Debido a que los resultados son iguales, G puede ser calculada de la energía de deformación elástica y es llamada nuevamente como la relación de energía de deformación elástica liberada.

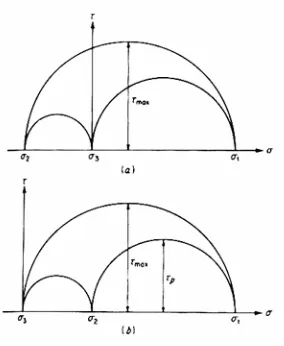
1.2.3.3. Resistencia al crecimiento de la grieta.

Para el caso de esfuerzo plano (σz = 0), la resistencia varía con el crecimiento de la grieta.

el crecimiento de la grieta es estable (de crecimiento predecible) y la fractura no llega a presentarse. Si el esfuerzo se mantiene constante en σj la grieta se propaga solo una

distancia muy pequeña y se detiene. Otro incremento en el esfuerzo es necesario para hacer crecer la grieta, aunque la grieta es de tamaño grande puede resistir un esfuerzo grande. El esfuerzo puede ser incrementado y se tendrá un crecimiento simultáneo de la grieta hasta un esfuerzo σc que corresponde hasta un tamaño de grieta ac y en este momento el

comportamiento de la grieta es inestable.

Figura 1.5. Diagrama carga-desplazamiento.

Al principio de la propagación de la grieta, el criterio energético debe cumplirse; durante su crecimiento estable, la relación de energía de liberación G es igual a la resistencia al crecimiento de la grieta R. Si G es baja la grieta se detiene en su crecimiento; si G es más grande que R, la grieta crece en forma inestable. La relación de energía liberada es:

G a

E

= πσ2 (1.6a)

y tanto σ como a se incrementan durante el crecimiento de la grieta.

Esto significa, que el incremento de G es proporcional a a. Debido a que G = R se concluye

Figura 1.6. Crecimiento estable de una grieta bajo la condición de esfuerzo plano.

Supóngase que para un tamaño de grieta a cargada con un esfuerzo σi,entonces, si la grieta

se ampliara, la energía de liberación disponible está dada por el punto B. Supóngase que este valor es suficiente para el crecimiento de la grieta. Si la grieta fuera a propagarse bajo esfuerzo constante, G se incrementaría de acuerdo a la línea B-H. Esta es menor que la curva R, y por lo tanto el crecimiento de la grieta bajo esfuerzo constante no puede ocurrir.

Figura 1.7. Curva R para esfuerzo plano.

Otro incremento del esfuerzo a σ2 lleva la extensión de la grieta a un valor ∆a2. Tanto G

como R siguen a la curva R del punto B al C. Finalmente, en σc la longitud de la grieta

llega a ser ac y tanto G como R están en el punto D. El incremento de la grieta a esfuerzo

R. Debido a que G permanece más grande que R, la fractura final ocurre en el punto D donde

∂ ∂

∂ ∂

G a

R

a R

= ; G= (1.7)

En otras palabras, la resistencia del material al crecimiento de la grieta y la energía liberada se igualan.

1.2.3.4. Relaciones matemáticas de G.

En el caso de una placa con extremos fijos, las cargas externas no realizan trabajo. La energía requerida para el crecimiento de una grieta debe entonces suministrarse como una energía liberada de deformación. Si los extremos de la placa están libres para moverse durante la extensión de la grieta, entonces el trabajo es realizado por la carga externa. En este caso la energía de deformación elástica contenida aumenta en lugar de disminuir. La condición de crecimiento de la grieta para una placa de espesor unitario es:

(

)

d

da F U

dW da

− = (1.8)

donde:

F = trabajo ejecutado por la fuerza externa. W = energía para la formación de la grieta. Para este caso se definen G y R como:

(

)

G d

da F U

R dW

da

= −

=

A carga constante.

Figura 1.8. Placa agrietada.

Cuando la grieta aumenta de tamaño una cantidad da, los desplazamientos se incrementan

una cantidad dv. Esto significa que el trabajo realizado por la fuerza externa, es P dv. De esta manera se tiene que:

(

)

G d

da F U h

Pdv da

dU da

t

= − = ⎛ −

⎝⎜

⎞ ⎠⎟

1

(1.9)

donde:

h = espesor de la placa.

Ut = energía total de deformación elástica en una placa de espesor h.

Las deformaciones son elásticas; mientras no haya un crecimiento de la grieta, el desplazamiento v es proporcional a la carga:

v = C P donde:

C = flexibilidad de la placa.

Para una placa no agrietada de longitud L, ancho b y espesor h, se tiene que la flexibilidad es igual a:

C L

bhE

=

E = módulo de Young.

La energía de deformación elástica contenida en la placa agrietada, es entonces:

U_t = 1Pv= C

2

1 2

2

P (1.10)

Usando la ecuación (1.10), se puede hacer una evaluación de la ecuación 1.9, quedando:

G h P C a CP dP da P C a CP dP da P h C a = ⎛ + − − ⎝⎜ ⎞⎠⎟ = 1 1 2 2

2 ∂ 2 2

∂

∂ ∂

∂

∂ (1.11)

Los términos con dP

da se cancelan; esto significa que G es independiente de la variación de la carga: G P h C a h dU da h dU da t P t v = = ⎛ ⎝⎜ ⎞⎠⎟ = − ⎛⎝⎜ ⎞⎠⎟ 2 2 1 1 ∂

∂ (1.12)

La relación de energía liberada de deformación G es siempre igual a la derivada de la energía de deformación elástica con respecto al tamaño de la grieta.

1.2.4. Planteamiento a partir del análisis de esfuerzos. 1.2.4.1. Ecuaciones del campo de esfuerzos.

1.2.4.1.1. Ecuaciones diferenciales de equilibrio.

Se considera el equilibrio de un pequeño rectángulo cuyos lados tienen una longitud h y k. Los esfuerzos actúan sobre las caras 1, 2, 3 y 4 y sus direcciones se indican en la figura 1.9. Si X y Y describen las componentes de la fuerza de cuerpo por unidad de volumen, la ecuación de equilibrio para las fuerzas en la dirección x es:

( )

( )

( ) ( )

2 4 0

− + − + =

dividiendo entre hk:

( ) ( )

( ) ( )

h k X

En el límite cuando h → 0, k → 0, se tiene que:

( ) ( )

h

1− 3 _{que es} ∂σ

∂

x

x

Figura 1.9. Esfuerzos sobre una placa rectangular en equilibrio.

En forma similar:

( ) ( )

k

2 − 4 _{que es} ∂τ

∂

xy

y

La ecuación de equilibrio para las fuerzas en la dirección y, es obtenida de la misma manera. Así:

∂σ ∂

∂τ ∂ ∂σ

∂ ∂τ

∂

x xy

y xy

x y x

y x y

+ + =

+ + =

0 0

(1.13)

Estas son las ecuaciones de equilibrio para problemas en dos dimensiones, Timoshenko [28].

La ecuación anterior se debe satisfacer en todos los puntos a través del volumen del cuerpo. Sin embargo, los esfuerzos componentes (σx, σy, τxy) varían sobre el volumen de la placa y

cuando se analiza un punto en la frontera, estos deben estar en equilibrio con las fuerzas externas.

Figura 1.10. Prisma triangular sometido a esfuerzos.

Considérese un pequeño prisma triangular PBC, de tal manera que el lado BC coincida con la frontera de la placa como se muestra en la figura 1.10, y describen las componentes de las fuerzas de superficie por unidad de área en este punto de la frontera. De esta manera se tiene que:

X_ Y_

X l m

Y m l

x

y x

_

_

= +

= +

σ τ

σ τ

xy y

(1.14)

en la que l y m son los cosenos directores de la normal N a la frontera.

Para el caso particular de una placa, considerando un lado paralelo al eje x se tiene la normal N paralela al eje y; por lo tanto l = 0 y m = ±1. De esta manera las ecuaciones anteriores se simplifican a:

X_ = ±τ_xy Y_ = ±σ_y

De forma similar se obtienen las del lado paralelo al eje y, Timoshenko [28].

Es un problema fundamental de la teoría de elasticidad determinar el estado de esfuerzos de un cuerpo sujeto a la acción de las fuerzas. En un problema bidimensional, es necesario resolver las ecuaciones de equilibrio (1.13) y la solución debe satisfacer las condiciones de frontera de la ecuación (1.14). Estas ecuaciones contienen tres esfuerzos componentes σx, σy, τxy, y por lo tanto no son suficientes para su determinación. El problema está

estáticamente indeterminado y para obtener una solución debe considerarse la deformación elástica del cuerpo.

Para problemas bidimensionales se tienen tres deformaciones unitarias:

ε ∂ ∂ ε ∂ ∂ γ ∂ ∂ ∂ ∂ x u x v y u y v x

= _y = _xy = + (a)

Estas tres deformaciones unitarias componentes son expresadas para dos funciones u y v, las cuales representan los desplazamientos en las direcciones x y y respectivamente, por lo tanto estas funciones no pueden considerarse arbitrariamente; existe una relación entre las componentes de la deformación que puede obtenerse de las ecuaciones anteriores.

Diferenciando la primera de las ecuaciones (a) dos veces con respecto a y, la segunda dos veces con respecto a x y la tercera una vez con respecto a x y otra con respecto a y, se tiene:

∂ ε ∂ ∂ ε ∂ ∂ γ ∂ ∂ 2 2 2 2 2 x y

y + x = x y

xy

(1.15)

Esta relación diferencial, es llamada la condición de compatibilidad y debe satisfacerse por las componentes de deformación unitaria, para asegurar la existencia de funciones u y v conectadas por las componentes de deformación unitaria a través de las ecuaciones (a). La condición de compatibilidad anterior puede escribirse en función de los esfuerzos, usando la ley de Hooke para la condición de esfuerzo plano y las condiciones de equilibrio (1.13); por lo que:

(

)

(

)

⎟ (1.16)

(

)

₍

₎

⎟ (1.17)

Las condiciones de equilibrio (1.13), las condiciones de frontera (1.14) y cualquiera de las ecuaciones (1.16) o (1.17), proporcionan un sistema de 3 ecuaciones con 3 incógnitas para determinar el estado completo de esfuerzos en un problema bidimensional, Timoshenko [28].

1.2.4.1.4. La función esfuerzo.

Si se considera el caso, cuando el peso es la única fuerza de cuerpo, las ecuaciones que se deben satisfacer son:

∂σ ∂ ∂τ ∂ ∂σ ∂ ∂τ ∂ ρ x xy y xy x y

y x g

+ = + + = 0 0 (a)

(

)

x + y x y

⎛ ⎝

⎜ ⎞

⎠

⎟ + = (b)

Donde ρ es la masa por unidad de volumen y g es la aceleración de la gravedad.

A estas ecuaciones deben agregarse las condiciones de frontera (1.14). El método usual, para resolver estas ecuaciones, es la introducción de una nueva función llamada función esfuerzo. Como se puede ver, las ecuaciones (a) son satisfechas tomando una función Φ en función de x y de y, y colocando las siguientes expresiones para esfuerzos componentes:

σ ∂ ∂ ρ σ ∂ ∂ ρ τ ∂ ∂ ∂ x y

y gy x gx x y

= 2Φ₂ − = 2Φ₂ − _xy = − 2Φ (1.18)

Sustituyendo las expresiones anteriores en la ecuación (b), se tiene que la función Φ debe satisfacer la ecuación:

∂ ∂ ∂ ∂ ∂ ∂ ∂ 4 4 4 2 2 4 4 2 Φ Φ Φ

de esta manera la solución de un problema bidimensional, cuando el peso es la única fuerza de cuerpo, se reduce a encontrar una solución de la ecuación (1.19) que satisfaga las condiciones de frontera de la ecuación (1.14) del problema, Timoshenko [28].

1.2.4.2. Ecuaciones de campo de esfuerzos en la vecindad de la grieta. 1.2.4.2.1. Estado de esfuerzos en la vecindad de la grieta.

Considérese la porción de un sólido tal y como se muestra en la figura 1.11. La posición de un punto P puede ser definida con respecto a los ejes cartesianos O-X, Y, Z o por las coordenadas (r, θ, z), cuyo origen es el vértice de la grieta. Los esfuerzos que actúan sobre un pequeño cubo de material en P son σx, σy, σz y τxy = τyx, τxz = τzx, τyz = τzy en el caso

general. Cuando el sólido es una placa de espesor muy delgado, el esfuerzo normal σz y los

esfuerzos de corte τyz y τxz son cero en las superficies libres y serán muy pequeños en

comparación con los otros esfuerzos en el interior del sólido. Si se considera que el estado de esfuerzos es independiente de la coordenada z, el problema se reduce a encontrar σx, σy

y τxy para valores de x y y o de r y θ.

La ecuación (1.19) también puede escribirse como:

∇ ⎛ +

⎝

⎜ ⎞

⎠

⎟ = ∇ =

2 2 2

2 2

4 ₀

∂ ∂

∂ ∂

x y Φ Φ (1.20) El problema se reduce, entonces, a encontrar Φ. Debe notarse que la misma solución es válida tanto para esfuerzo plano como para deformación plana.

Si una función armónica, f(x, y), satisface la ecuación:

∇ =2_{f 0 (a)}

se considera que es la solución de la ecuación 1.20, se puede demostrar que: X f(x, y) y Y f(x, y)

Figura 1.11. Definición del sistema de coordenadas de una placa que contiene una grieta.

Considerando una variable compleja:

ζ = x + iy y una función:

( )

( )

( )

Z ζ =ReZ+ImZ a x y= , +ib x y,

donde Re Z = a(x,y) e Im Z = b(x,y), son las partes real e imaginaria de la función Z (ξ).

La derivada de Z está definida de la siguiente forma:

(

) ( )

cuando el límite existe y es independiente de la forma en que (ζ+∆ζ) se aproxima a (ζ), se dice que la función es analítica. La ecuación anterior se puede escribir en términos de x y y:

(

) ( )

[

]

[

(

) ( )

]

Z lim a x x y y a x y i b x x y y b x y

x i y

x y '= + , + − , + + , + − + → → ∆ ∆ ∆ ∆ ∆ ∆ ∆ ∆ 0 0 ,

si el límite es independiente de la forma en que se aproxima, se puede escribir:

(

) ( )

[

]

[

(

) ( )

]

(

) ( )

[

]

[

(

) ( )

]

= _→ + − + + − = − +

→

lim a x y y a x y i b x y y b x y

i y i

a y b y x y ∆ ∆ ∆ ∆ ∆ 0 0 , , , , _∂ ∂ ∂ ∂

se encuentra por lo tanto que cuando la función Z (ζ) es analítica:

∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ a x b y Z x Z y a y b x Z y Z x = = = = o o Re Im Re Im −

Las ecuaciones anteriores son conocidas como las condiciones de Cauchy-Reimann, válidas para Z (ζ) y todas sus derivadas sucesivas. Se puede ver que cuando se cumplen estas condiciones, las funciones Re Z e Im Z son armónicas; de acuerdo a la ecuación (a):

∇ =⎛ + ⎝ ⎜ ⎞ ⎠ ⎟ = − = ∇ =⎛ + ⎝ ⎜ ⎞ ⎠ ⎟ = − − = 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0

Re Re Re Im

Im Im Re Im

Z

x y Z

Z x

Z x y

Z

x y Z

Z x y Z y ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂

Las funciones esfuerzo pueden entonces obtenerse de las partes real e imaginaria de Z (ζ) y sus derivadas; en particular se puede considerar:

Φ =ReZ+ImZ (1.21) sustituyendo esta función en la ecuación (1.18), sin considerar el peso del cuerpo se tienen que: σ ∂ ∂ ∂ ∂ ∂ ∂ x Z y Y Z y Z y

= 2Re₂ + 2Im '₂ +2 Im '

σ ∂ ∂ ∂ ∂ y Z x Y Z x

= 2Re₂ + 2Im '₂

τ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ xy Z

x y Y

Z x y

Z x

= 2 Re + 2 Im '+ Im '

σ σ τ x y xy

Z Y Z

Z Y Z

Y Z

= −

= +

= −

Re ' ' Im ' ' '

Re ' ' Im ' ' '

Re ' ' '

(1.22)

La función Z (ζ) debe ser tal que:

(

)

(

)

2 2 1₂

2 2 2 3₂

Z (1.23)

La función anterior es conocida como la función esfuerzo de Westergaard. Para valores grandes de ζ, es decir para valores alejados del origen:

Z' ' _ζ→∞ =σ, Z' ' ' _ζ→∞ =0

Por lo tanto, σx = σy = σ, τxy = 0 en puntos lejos del origen, donde: σ = esfuerzo de fractura aplicado.

Tomando Y = 0 y -a < ζ< +a, se puede ver que σx = σy = τxy = 0 debido a que:

Re Z’’ = Re Z = 0.

El problema, así solucionado, es para una placa infinitamente larga, uniformemente esforzada en las direcciones x y y con una longitud de la grieta 2a a lo largo de la dirección x como se muestra en la figura 1.12, Ruíz [43].

En la punta de la grieta acercando ζ a a, se tienen que:

(

) (

)

[

(

)

]

(

)

[

]

De la figura 1.12:

(

)

(

)

ζ_{− =a x a− +iy r=} θ_{+i =re}θ

y los esfuerzos en la vecindad de la punta de la grieta llegan a ser: σ σ θ θ θ σ σ θ θ θ τ σ θ θ θ x y xy a r a r a r = ⎛ ⎝⎜ ⎞⎠⎟ ⎛⎝⎜ − ⎞⎠⎟ = ⎛ ⎝⎜ ⎞⎠⎟ ⎛⎝⎜ + ⎞⎠⎟ = ⎛ ⎝⎜ ⎞⎠⎟

2 2 1 2

3 2

2 2 1 2

3 2

2 2 2

3 2

cos sen sen

cos sen sen

cos sen cos

(1.24)

Figura 1.12. Esfuerzos biaxiales en una placa con una grieta central.

La función de esfuerzo, definida en las ecuaciones (1.21) y (1.23), proporciona una solución completa al problema de la figura 1.12, pero debido a que el interés está enfocado en la región que rodea la vecindad de la grieta, se puede usar una aproximación que conduce a una variación de la ecuación (1.24). Considerando que:

KI = σ πa (1.25)

el campo de esfuerzos en la vecindad de la punta de la grieta llega a ser:

σ π θ θ _θ σ π θ θ _θ τ π θ θ _θ x I y I xy I K r K r K r = ⎡ − ⎣⎢ ⎤ ⎦⎥ = ⎡ + ⎣⎢ ⎤ ⎦⎥ = 1

2 2 1 2

3 2 1

2 2 1 2

3 2 1

2 2 2

3 2

cos sen sen

cos sen sen

cos sen sen

Es claro que la condición de fractura es:

σ πa =constante crítica (1.26a) La cual es equivalente a la condición:

KI = KIC

Además, el estado de esfuerzos en cualquier punto P, definido por su distancia r a la punta de la grieta y el ángulo θ, es proporcional a KI con tal de que r sea pequeño.

Procedimientos similares, Broek [4], se emplean para analizar la fractura en los modos II y III. Los resultados son:

Modo II. σ π θ θ _θ σ π θ θ _θ τ π θ θ _θ x II y II xy II K r K r K r = ⎡ + ⎣⎢ ⎤ ⎦⎥ = = ⎛ − ⎝⎜ ⎞⎠⎟

2 2 2 2

3 2

2 2 2

3 2

2 2 1 2

3 2

sen cos cos

sen cos cos

cos sen sen

(1.27)

σz = ν (σx + σy ), τxz = τyz = 0

Para una placa agrietada de tamaño infinito con un esfuerzo de corte en el plano de la grieta:

KII = τ πa (1.28)

Modo III.

De manera similar se tiene que:

τ π θ τ π θ xz III yz III K r K r = − =

2 sen2, 2 cos2 (1.29)

σx = σy = τxy = 0

1.2.4.3. Características de la zona plástica en la punta de la grieta. 1.2.4.3.1. Corrección de la zona plástica de Irwin.

En la práctica los materiales (especialmente los metales) tienden a exhibir un esfuerzo de cedencia, arriba del cual la deformación es plástica. Esto significa, que en un metal siempre hay una región alrededor de la punta de la grieta, donde ocurren las deformaciones plásticas y por lo tanto, un esfuerzo singular no puede existir. La región plástica es conocida como la zona plástica de la punta de la grieta.

Se hará un cálculo, aproximado, del tamaño de esta zona para la condición de esfuerzo plano.

La figura 1.13 muestra la magnitud del esfuerzo σy en el plano θ = 0. Hasta una distancia

rp* de la punta de la grieta; dentro de esta zona, el esfuerzo es más grande, que el de

cedencia σys. Para una primera aproximación, la distancia rp* es el tamaño de la zona

plástica.

Figura 1.13. Primera estimación del tamaño de la zona plástica.

Sea la ecuación, que relaciona los esfuerzos en un punto P de la zona agrietada, con el factor de intensidad de esfuerzos:

( )

σ

π θ

ij I ij

K r f

=

2

sustituyendo en esta ecuación σys, la distancia rp* puede calcularse:

σ

π σ πσ

σ σ

y I p

ys I

ys ys

K r

K

= = = =

2 2 2

2 2

2 2

* o rp

La zona plástica propuesta debe ser más grande, que rp*, ya que ésta sólo considera el

esfuerzo de cedencia del material (representado por el área sin sombrear) por lo que la carga representada por el área sombreada en la figura 1.13 debe ser considerada. Esto se puede llevar a cabo, si el material adelante de la zona plástica soporta más esfuerzo, el cual llevará al material arriba del esfuerzo de cedencia.

Irwin intuyó que la presencia de la plasticidad hacia que la grieta se comportará como si fuera más grande que su tamaño físico. Como resultado de la plasticidad en la punta de la grieta los desplazamientos aumentan y la rigidez disminuye en comparación con el caso elástico. En otras palabras, la placa se comporta como si tuviese una grieta de longitud mayor.

El tamaño efectivo de la grieta, aeff, es igual a a + δ, es decir la longitud física de la grieta

más una corrección δ. La expresión para δ se puede encontrar de la siguiente manera. En la figura 1.14, la grieta física se reemplaza por una de mayor de longitud a + δ, además, de que se proporciona la distribución de esfuerzo elástico σy en la punta de la misma. El

esfuerzo en la punta de la grieta está limitado nuevamente al esfuerzo de cedencia σys.

Similarmente, el esfuerzo que actúa en la parte δ, enfrente de la grieta física es igual al esfuerzo de cedencia. Consecuentemente δ debe ser suficientemente larga para soportar la carga que se tiene en el área A.

Por lo tanto el área A debe ser igual al área B. La distancia λ en la figura 1.14 es igual a:

(

)

K a a

r

= = + = + =

2 2 2

2 2

o *

(1.31)

Debido a que δ es pequeño, con respecto al tamaño de la grieta, esta puede ser despreciada, y por lo tanto λ ≈ rP* al comparar las ecuaciones (1.30 y (1.31). El área B es igual a

Figura 1.14. Segunda estimación del tamaño de la zona plástica.

Despreciando δ al compararlo con a y utilizando la ecuación (1.31), se tiene que:

(

)

(

)

( )

σ

+r_{P ys}= ar_P +r_P = ar = r

ys

P P

* ₂ * * 2 2 * ₄

2 2

2

o *

δ =r_P*

De donde se tiene que:

δ=r_P* _{y rP} = +λ _(1.32)

Se concluye que el tamaño de la zona plástica (rP) es dos veces el tamaño de la primera

estimación (rP*).

Debido a que δ = rP*, la grieta se comporta como si su longitud fuera a + rP*. La cantidad

rP* es conocida como la zona de corrección de Irwin.

Si se ha corregido el tamaño de la zona plástica también debe hacerse lo mismo con el factor de intensidad de esfuerzos:

(

)

K C a r_P C a K

ys

= + = ⎛ +

⎝

⎜⎜ ⎞_⎠⎟⎟

σ π σ π

πσ *

2 2

2 (1.33) 1.2.4.3.2. Forma de la zona plástica.

energía máxima de distorsión), son usualmente aplicados. Tresca predice que: “se inicia la fluencia siempre que, en un elemento mecánico, el esfuerzo cortante máximo se vuelve igual al esfuerzo cortante máximo en una probeta a tracción, cuando ese especimen empieza a ceder.”. Por otra parte, el criterio de Von Mises, en términos de los esfuerzos principales, es como sigue.

(

) (

) (

)

2 2 3 2 3 1 2 ₂ 2

− + − + − = _ys (1.34) donde σys es el esfuerzo de cedencia uniaxial. Para la prueba de tensión σx = σy = 0, y la

cedencia ocurre cuando σ1 = σys.

Las ecuaciones del campo de esfuerzos en función de los esfuerzos principales son:

(

)

3 3 1 2

2 2 1 2

2 2 1 2

0 2 2 2 = ⎛ + ⎝⎜ ⎞⎠⎟ = ⎛ − ⎝⎜ ⎞⎠⎟ = = + = K r K r K r cos sen cos sen cos o (1.35)

En el plano θ = 0 los esfuerzos principales σ1 y σ2 son iguales y actúan en las direcciones x

y y. Para esfuerzo plano σ1 = 0 y τmax = ½ σ1 para una condición de tracción simple.

La frontera o el límite de la zona plástica como una función de θ, se puede obtener de la sustitución de la ecuación 1.35 en la ecuación 1.34, por lo tanto se tiene que:

Deformación plana: K

(

) (

)

2

2 3

2 1 2 1 2

2 2 2

πr sen θ+ + υ +cosθ ys

⎡ ⎣⎢

⎤ ⎦⎥= σ

Esfuerzo plano: K

2

2 1

3

2 2

2 2

πr + θ+ θ σys

⎡ ⎣⎢

⎤ ⎦⎥=

sen cos

De esta manera la extensión de la zona plástica como una función de θ, puede ser dada como:

Deformación plana: K

(

) (

2

4

3

2 1 2 1

2

2 2

πσ_ys sen θ+ + υ +cos ⎡ ⎣⎢ ⎤ ⎦⎥

)

Esfuerzo plano: K2

4 1

3 2

2

2

πσ_ys + θ+

⎡ ⎣⎢

⎤ ⎦⎥

La ecuación (1.36) que limita la frontera de la zona plástica está representada en la figura 1.15. Se puede apreciar, que la zona plástica en la condición de deformación plana es considerablemente más pequeña que la zona plástica en la condición de esfuerzo plano. Para θ = 0 y una relación de Poisson de 1/3 la diferencia tiene un factor de 9.

Figura 1.15. Forma de la zona plástica. (a) criterio de Von Mises. (b) Criterio de Tresca

Si se emplea el criterio de cedencia de Tresca, la forma de la zona plástica cambia ligeramente. Del criterio de Mohr se encuentra, que el esfuerzo máximo de corte en la condición de esfuerzo plano, es igual τmax = ½ σ1 y para la condición de deformación plana τmax = ½ (σ1 - σ3 ) o τmax = ½ (σ1 - σ2 ) , el que sea más grande.

Usando las ecuaciones (1.35), la zona de cedencia de Tresca para esfuerzo plano es igual a:

r_P K

ys = ⎡ ⎛_⎝⎜ + ⎞_⎠⎟ ⎣ ⎢ ⎤ ⎦ ⎥ 2 2 2

2πσ 2 1 2

θ θ

cos sen

Para deformación plana el valor mayor que de cualquiera de las expresiones siguientes:

r K r K P ys P ys = ⎡ − + ⎣⎢ ⎤ ⎦⎥ = 2 2 2 2 2 2

2 2 1 2 2

2 2 πσ θ υ θ πσ θ cos sen cos (1.37)

Figura 1.16. Formas de la zona plástica para los modos II y III.

En la zona plástica que se muestra en la figura 1.16, se limitó el esfuerzo al de cedencia por lo que no se consideró la carga adicional que tiene que ser soportada por el material que se encuentra fuera de la frontera propuesta. La corrección de ésta no es tan fácil, como en el caso de la ecuación (1.30) donde se amplió la zona plástica.

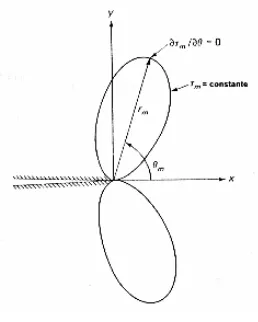
Un análisis más exacto fue realizado por Tuba [29] y por Rice y Rosengren [44], sus resultados se muestran en la figura 1.17. De acuerdo con Tuba el punto más alejado de la frontera plástica está en un ángulo θ = 69°, el cual se muestra en la figura 1.17 para varios valores de σ/σys; es en este ángulo donde se presenta el esfuerzo máximo de corte. Rice y

Rosengren [44] demostraron, que la zona plástica es ligeramente afectada por la relación deformación-dureza, pero que el punto más alejado de la zona plástica está siempre en un ángulo de 100° como se indica en la figura 1.17.

Figura 1.17. Formas más exactas de la zona plástica para el modo I. (a) de acuerdo con el criterio de Tuba, (b) de acuerdo a Rice y Rosengren. rP(θ=0) = 0.007 (K/σys)2. rP(θ=100) = 0.24 (K/σys)2. Relación

deformación-dureza = 0.05.

1.2.4.4. Limitaciones del análisis lineal de la mecánica de fractura.