INVESTIGACION DEL PROCEDIMIENTO DE MUESTREO-RECONSTRUCCION DEL PROCESO EN LA SALIDA DEL CONVERTIDOR EXPONENCIAL CON DIFERENTES ALGORITMOS DE LA RECONSTRUCCION

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA

SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN

INVESTIGACIÓN DEL PROCEDIMIENTO DE

MUESTREO-RECONSTRUCCIÓN DEL PROCESO EN

LA SALIDA DEL CONVERTIDOR EXPONENCIAL

CON DIFERENTES ALGORITMOS DE LA

RECONSTRUCCIÓN

TESIS

QUE PARA OBTENER EL GRADO DE MAESTRO EN CIENCIAS

EN INGENIERÍA DE LAS TELECOMUNICACIONES

PRESENTA:

ING. MÓNICA SEDEÑO JUÁREZ

DIRECTOR DE TESIS:

DR. VLADIMIR KAZAKOV ERASOVA

RESUMEN

El presente trabajo utiliza las propiedades estadísticas de los procesos aleatorios como son la función de la esperanza matemática, la función de la varianza, la función de covarianza para llevar a cabo la realización del procedimiento de Muestreo- Reconstrucción del proceso aleatorio a la salida de un convertidor exponencial del tipo η

( )

t =a e₀ βξ( )t . El proceso de Muestreo-Reconstrucción se realiza utilizando dos algoritmos diferentes: el algoritmo óptimo y el algoritmo no óptimo, el primer algoritmo lleva a cabo el procedimiento de Muestreo-Reconstrucción con las características de los procesos aleatorios no gaussianos, mientras que el algoritmo no-óptimo la realiza mediante el mismo procedimiento con las características de los procesos gaussianos. El tipo de convertidor exponencial se eligió en este trabajo de investigación, debido a que es un filtro no lineal cuyas características tienen la ventaja de hacer que los cálculos se faciliten para llevar a cabo el proceso de Muestreo-Reconstrucción.

Además, se lleva a cabo la descripción estadística de un Procedimiento de Muestreo-Reconstrucción de procesos aleatorios cuando el número de muestras es finito y se determina la Función de Reconstrucción, la cual es representada por la esperanza matemática; y a su vez se determina la Función de Error de Reconstrucción la cual es determinada por la varianza condicional para cierto tipo de procesos aleatorios de tipo no gaussianos. El proceso no Gaussiano se forma a la salida de un convertidor exponencial y por un proceso Gaussiano a la entrada. Esto se puede resolver al utilizar la regla de la estimación de una variable aleatoria llamada Regla de la Esperanza Matemática Condicional.

ABSTRACT

The present work applies the statistical properties of the random processes such as the mathematical expectation, the variance function and the covariance function to realize the Sampling-Reconstruction Procedure of a random process at the output of a exponential converter of the kind of η

( )

t =a e₀ βξ( )t . The Sampling-Reconstruction Procedure is realized using two different algorithms: the optimal algorithm and the non optimal algorithm, the first one, consist on the Sampling-Reconstruction Procedure with the characteristics of the non-Gaussian random process, meanwhile the non optimal algorithm realizes the same Procedure with the characteristics of the Gaussian process.

The type of the exponential converter was selected as a topic of investigation, due to its characteristics, like the no linear filter, and the simplicity of the calculus of its parameters.

And, it is made a statistical description of the Sampling-Reconstruction Procedure of the random processes when the number of samples is finite, and it’s obtained the Reconstruction Function, which is represented by the mathematical expectation, and also it’s obtained the Error Reconstruction Function, that it’s represented by the variance function, for certain types of non-Gaussian random processes. The non-non-Gaussian process is formed at the output of the exponential converter and with a Gaussian process at the entrance of the converter. We can solve this problem with the statistical conditional mean rule.

ÍNDICE

Resumen i

Abstract ii

Lista de Símbolos vi

Índice de Tablas vii

Índice de Figuras vii

Objetivos xiv

Justificación xiv

Introducción xv

CAPÍTULO 1 ANTECEDENTES

1.1 TEOREMA CLÁSICO DE WHITTAKER, KOTELNIKOV Y SHANNON 1

1.2 TEOREMA DE BALAKRISHNAN 1

1.3 DESVENTAJAS DEL TEOREMA DE BALAKRISHNAN 2

1.4 PROCESOS ALEATORIOS 3

1.5 FUNCIÓN DE COVARIANZA 5

1.6 DENSIDAD ESPECTRAL DE POTENCIA 6

1.7 RUIDO BLANCO 7

1.8 REGLA DE LA ESPERANZA MATEMÁTICA CONDICIONAL 8

1.9FUNCIONES DE MOMENTOS CONDICIONALES DEL PROCESO DE 11

SALIDA η( )t

CAPÍTULO 2 PROCEDIMIENTO DE MUESTREO-

RECONSTRUCCIÓN ÓPTIMO DE LOS PROCESOS

GAUSSIANOS.

2.1 INTRODUCCIÓN 13

2.2 PROPIEDADES DE LOS PROCESOS GAUSSIANOS 13

2.3 CASO GAUSSIANO CONDICIONAL 14

2.4 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS RC 15

DE UNA ETAPA. 2.5 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS RC 22

CAPÍTULO 3 ESTUDIO DEL PROCESO EN LA SALIDA DEL

CONVERTIDOR EXPONENCIAL

3.1 INTRODUCCIÓN 33

3.2 NO LINEALIDAD DEL CONVERTIDOR EXPONENCIAL 33

3.3 FUNCIONES DE MOMENTOS CONDICIONALES 34

3.4 CARACTERÍSTICAS DEL CONVERTIDOR EXPONENCIAL: 35

( ) 0 ( )t a eβ ξ t η = 3.4.1 FUNCIÓN DE DENSIDAD DE PROBABILIDAD 35

3.4.2 ESPERANZA MATEMÁTICA DEL PROCESO A LA SALIDA 36

3.4.3 VARIANZA MATEMÁTICA DEL PROCESO A LA SALIDA 37

3.4.4 FUNCIÓN Y TIEMPO DE COVARIANZA 38

3.5 CASOS PARTICULARES 39

CAPÍTULO 4 PROCEDIMIENTO DE MUESTREO-

RECONSTRUCCIÓN CON ALGORITMOS DE

EXTRAPOLACIÓN

4.1 INTRODUCCIÓN 45

4.2 ALGORITMO DE MUESTREO-RECONSTRUCCIÓN DEL PROCESO 46

EN LA SALIDA DE FILTROS RC: CASOS ÓPTIMO Y NO ÓPTIMO 4.3 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 47

RC DE UNA ETAPA USANDO EL ALGORITMO ÓPTIMO. 4.5 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 51

RC DE UNA ETAPA USANDO EL ALGORITMO NO ÓPTIMO. 4.5.1 COMPARACIÓN ENTRE LA RECONSTRUCCIÓN DEL PROCESO 53

EN LA SALIDA DE FILTROS RC DE UNA ETAPA USANDO EL ALGORITMO ÓPTIMO Y EL ALGORITMO NO ÓPTIMO. 4.6 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 55

RC DE DOS ETAPAS USANDO EL ALGORITMO ÓPTIMO. 4.7RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 59

RC DE DOS ETAPAS USANDO EL ALGORITMO NO ÓPTIMO. 4.7.1 COMPARACIÓN ENTRE LA RECONSTRUCCIÓN DEL PROCESO 60

EN LA SALIDA DE FILTROS RC DE DOS ETAPAS USANDO EL ALGORITMO ÓPTIMO Y EL ALGORITMO NO ÓPTIMO. 4.9RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 62

RC DE TRES ETAPAS USANDO EL ALGORITMO ÓPTIMO. 4.10 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 66

RC DE TRES ETAPAS USANDO EL ALGORITMO NO ÓPTIMO. 4.10.1 COMPARACIÓN ENTRE LA RECONSTRUCCIÓN DEL PROCESO 68 EN LA SALIDA DE FILTROS RC DE TRES ETAPAS USANDO EL

CAPÍTULO 5 PROCEDIMIENTO DE MUESTREO-RECONSTRUCCIÓN CON

ALGORITMOS DE INTERPOLACIÓN

5.1 INTRODUCCIÓN 71 5.2 ALGORITMO DE RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA 71 DE FILTROS RC: CASO ÓPTIMO Y NO ÓPTIMO.

5.3 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 73 RC DE UNA ETAPA USANDO EL ALGORITMO ÓPTIMO.

5.4 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 76 RC DE UNA ETAPA USANDO EL ALGORITMO NO ÓPTIMO.

5.4.1 COMPARACIÓN ENTRE LA RECONSTRUCCIÓN DEL PROCESO 78 EN LA SALIDA DE FILTRO RC DE UNA ETAPA USANDO EL

ALGORITMO ÓPTIMO Y EL ALGORITMO NO ÓPTIMO

5.5 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 79 RC DE DOS ETAPAS USANDO EL ALGORITMO ÓPTIMO

5.6 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 82 RC DE DOS ETAPAS USANDO EL ALGORITMO NO ÓPTIMO.

5.6.1 COMPARACIÓN ENTRE LA RECONSTRUCCIÓN DEL PROCESO 83 EN LA SALIDA DE FILTRO RC DE DOS ETAPAS USANDO EL

ALGORITMO ÓPTIMO Y EL ALGORITMO NO ÓPTIMO

5.7 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 84 RC DE TRES ETAPAS USANDO EL ALGORITMO ÓPTIMO

5.8 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS 87 RC DE TRES ETAPAS USANDO EL ALGORITMO NO ÓPTIMO

5.8.1 COMPARACIÓN ENTRE LA RECONSTRUCCIÓN DEL PROCESO 89 EN LA SALIDA DE FILTRO RC DE TRES ETAPAS USANDO EL

ALGORITMO ÓPTIMO Y EL ALGORITMO NO ÓPTIMO

CONCLUSIONES

90

Apéndice I: PONENCIAS EN CONGRESOS

92

Apéndice II: PROGRAMAS EMPLEADOS PARA OBTENER LOS

99

RESULTADOS

REFERENCIAS

107

Lista de Símbolos

α inverso de la constante de tiempo de un filtro RC, donde α = 1/RC.

aij elemento ij-ésimo de la matriz de covarianza inversa.

Bj(t) función básica de la j-ésima muestra.

ΔT intervalo de muestreo.

K( ) función de covarianza.

K matriz de covarianza.

m(t) función de la esperanza matemática.

( )

m t% función de la esperanza matemática condicional. (T_N)

η valor de las muestras a la salida del convertidor.

N número total de muestras. (T_N)

ξ valor de las muestras a la entrada del convertidor.

Rx( ) función de covarianza normalizada. ¡ número real.

2

(t) función de varianza matemática.

( )

2 t

σ% función de varianza matemática condicional.

Sx(ω) densidad espectral de potencia.

variable independiente de la función de covarianza, = t2 - t1 c tiempo de covarianza.

x(t) proceso aleatorio.

( )

x t% proceso aleatorio condicional. ( )j

_{( )}

x t j-ésima realización de un proceso aleatorio x(t). b

ÍNDICE DE TABLAS

2.1 Función de Covarianza Normalizada y Función de Densidad Espectral de un 16

Filtro RC de una etapa. 2.2 Valores de muestreo con cuatro muestras separadas en un intervalo ΔT = 0.5 17

2.3 Valores de muestreo con cuatro muestras separadas un intervalo ΔT = 2 20

2.4 Función de Covarianza Normalizada y Función de Densidad Espectral de un 22

Filtro RC de dos etapas. 2.5 Función de Covarianza Normalizada y Función de Densidad Espectral de un 27

Filtro RC de tres etapas. 4.1 Valores de muestreo con una sola muestra dada en el instante T1 = 0. 47

4.2 Valores de muestreo con una sola muestra dada en el instante T1 = 0. 49

5.1 Valores de muestreo con dos muestras separadas Δ =T 0.1 seg. 73

5.2 Valores de muestreo con dos muestras separadas Δ =T 0.1seg. 75

ÍNDICE DE FIGURAS

1.1Conjunto de posibles realizaciones x(1)(t), x(2)(t),…, x(j)(t),…,x(M)(t) que puede 3

tener un proceso aleatorio continuo. 1.2 Funciones de densidad de probabilidad de primer orden de un proceso aleatorio 4

en dos instantes de tiempo diferentes. 1.3 Función de covarianza K(t) que podría tener a) un proceso aleatorio suave o 5

b) un proceso aleatorio caótico. 1.4 Características del ruido blanco. a) Densidad espectral de potencia. 8

b) Función de autocorrelación. 1.5 Relación funcional entre el proceso de salida η

( )

t y el proceso de entrada ξ

( )

t 12

____________________________________________________________

2.1 Funciones Básicas de un proceso Markoviano considerando sólo cuatro 17

muestras separadas un intervalo ΔT=0.5. 2.2 Función de Reconstrucción m t%( ) de un proceso Markoviano, considerando 18

cuatro muestras (x(T1)=1; x(T2)=1.4; x(T3)=0.6; x(T4)=1.2) separadas un intervalo ΔT=0.5. 2.3 Función de Error de Reconstrucción σ%2

( )

t de un proceso Markoviano, 19

con cuatro muestras separadas un intervalo ΔT=0.5 2.4 Funciones Básicas de un proceso Markoviano considerando sólo cuatro 20

muestras separadas un intervalo ΔT=2. 2.5 Función de Reconstrucción m t%( ) de un proceso Markoviano, considerando 21

cuatro muestras separadas un intervalo ΔT=2. 2.6 Función de Error de Reconstrucción σ%2

( )

t de un proceso Markoviano, 21

dos etapas, considerando sólo cuatro muestras separadas un intervalo ΔT=0.5 seg.

2.8 Función de Reconstrucción m t%( ) de un proceso aleatorio utilizando un 24 filtro RC de dos etapas, considerando cuatro muestras separadas un

intervalo ΔT=0.5 seg.

2.9 Función de Error de Reconstrucción 2

( )

t

σ% de un proceso aleatorio 25 utilizando un filtro RC de dos etapas, con cuatro muestras separadas un

intervalo ΔT=0.5 seg.

2.10 Funciones Básicas de un proceso aleatorio utilizando un filtro RC de dos 25 etapas, considerando sólo cuatro muestras separadas un intervalo ΔT=2 seg. 2.11 Función de Reconstrucción m t%( ) de un proceso aleatorio utilizando un 26 filtro RC de dos etapas, considerando cuatro muestras

x T( )₁ =1, ( )x T₂ =1.4, ( )x T₃ =0.6, ( )x T₄ =1.2 separadas un intervalo ΔT=2 seg.

2.12 Función de Error de Reconstrucción 2

( )

t

σ% de un proceso aleatorio 26 utilizando un filtro RC de dos etapas, con cuatro muestras separadas un

intervalo ΔT=2.

2.13 Funciones Básicas de un proceso aleatorio utilizando un filtro RC de 29 tres etapas, considerando sólo cuatro muestras separadas un intervalo

ΔT=0.5 seg.

2.14 Función de Reconstrucción m t%( ) de un proceso aleatorio utilizando un 29 filtro RC de tres etapas, considerando cuatro muestras separadas un

intervalo ΔT=0.5 seg.

2.15 Función de Error de Reconstrucción σ%2

( )

t de un proceso aleatorio 30 utilizando un filtro RC de tres etapas, con cuatro muestras separadas un

intervalo ΔT=0.5.

2.16 Funciones Básicas de un proceso aleatorio al pasar por un filtro RC de tres 31 etapas, considerando sólo cuatro muestras separadas un intervalo Δ =T 2 seg. 2.17 Función de Reconstrucción m t%( ) de un proceso aleatorio utilizando un filtro 31 RC de tres etapas, considerando cuatro muestras separadas un

intervalo Δ =T 2seg

2.18 Función de Error de Reconstrucción σ%2

( )

t de un proceso aleatorio utilizando 32 un filtro RC de tres etapas, con cuatro muestras separadas un intervalo

Δ =T 2 seg.

3.1 Función de Transferencia Exponencial η

( )

t =a e₀ βξ( )t para 39 a₀ =0.1564673,1,1.5; β =1.

3.2 Función de Transferencia Exponencial η

( )

t =a e₀ βξ( )t para 40 a₀ =1; β =0.5,1,1.5.

3.3 Función de Transferencia Exponencial η

( )

t =eξ( )t para 40 a₀ =1,β =1.

η

3.6 Función de Transferencia Exponencial η

( )

t =0.1564673eξ( )t para 43 a₀ =0.1564673,β =1.

3.7 fdp del proceso aleato o a la salida con los parámetros ri a0=0.1564673, β=1. 43 3.8 Función de covarianza con los parámetros a0=0.1564673, β=1, ση2( )t =0.1143. 44

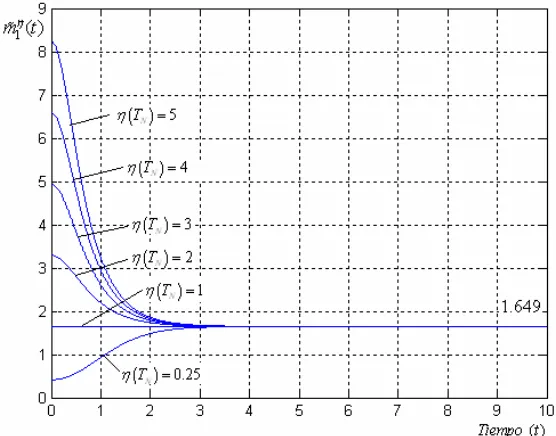
4.1 Gráficas de la Función de Reconstrucción m t%₁η( ) 1.6487= para 48 a₀ =1,β =1. Caso Óptimo.

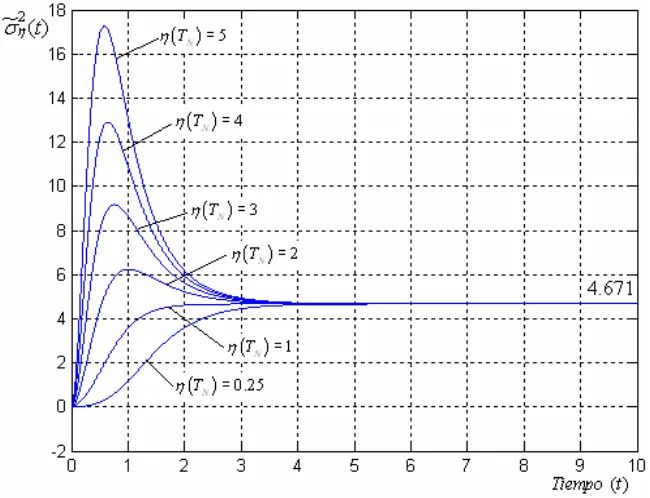
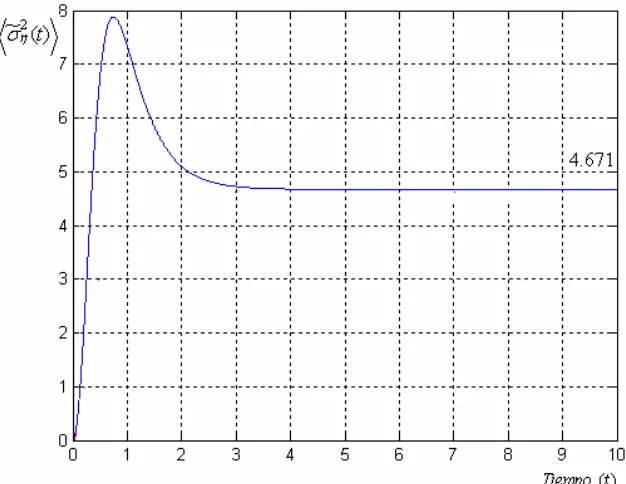
4.2 Gráficas de la Función de Error de Reconstrucciónσ°η2( )t =4.6708 48 para a₀ =1,β =1, valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.

Óptimo.

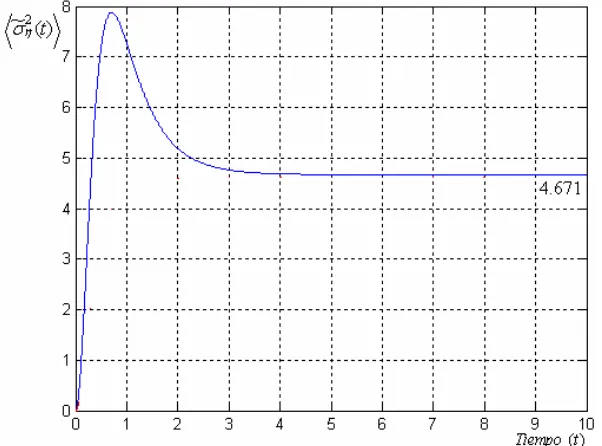
medio de la familia de curvas de la Función de 49 Caso

4.3 Gráfica del Pro

Error de Reconstrucción °2 ( )t

η

σ para a₀ =1,β =1. Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5. Caso Óptimo.

Gráfi

4.4 cas de la Función de Reconstrucción m t%₁η( )=0.2579 50 para a₀ =0.1564673,β =1. Valores de Muestreo

η(T_N) = 0.2, 0.6, 1.2, 1.5, 0

ráfic ción 50

.9. Caso Óptimo.

4.5 G as de la Función de Error de Reconstruc

σ

°η2( )t =0.1143

para a₀ =0.1564673,β =1. Valores de Muestreo η(T_N) = 0.2, 0.6, 1.2, 1.5,

ráfic de la Función de Error 51

0.9. Caso Óptimo. 4.6 G as del Promedio de la familia de curvas de Reconstrucción °2

( )t η

σ para a0 =0.1564673,β =1. Valores de muestreo η(T_N) = 0.2, 0.6, 1.2, 1.5, 0.9.Caso Óptimo.

ción 52 4.7 Gráfica de la Función de Error de Reconstruc σ°η2( )t =4.6708

para a₀ =1,β =1. Caso No Óptimo (No depende de las muestras).

52 4.8 Gráfica de la Función de Error de Reconstrucción σ°η2( )t =0.1143

para a₀ =0.1564673,β =1. Caso No Óptimo (No depende de las muestras).

4.11 Función de Error de Reconstrucción σ°η2( )t =4.6708 para a₀ =1,β =1. 53 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparación entre el

para Caso Óptimo y el Caso No Óptimo.

4.10 Función de Error de Reconstrucción σ°η2( )t =4.6708 a₀ =1,β =1. 53 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparación entre el Caso

Óptim

ción ση( )t =0.1143 para 54 Óptimo y el Caso No o.

2

omparación entre el

54 C Caso Óptimo y el Caso No Óptimo.

4.12 Función de Error de Reconstrucción σ°η2( )t =0.1143 para

a₀ =0.1564673,β =1. Valores de muestreo η(T_N) = 0.2, 0.6, 1.2, 1.5, 0.9. Comparación entre el Caso Óptimo y el Caso No Óptimo.

4.13 Gráficas de la Función de Reconstrucción m t%₁η( ) 1.6487= para 56 a₀ =1,β =1. Caso Óptimo.

4.14 Gráficas de la Función de Error de Reconstrucciónσ°η2( )t =4.6708 56 para a₀ =1,β =1. Caso Óptimo.

4.15 Gráfica del Promedio de la familia de curvas de la Función de Error de 57 Reconstrucción °

σ

η2( )t para a₀ =1,β =1. Caso Óptimo.

4.16 Gráficas de la Función de Reconstrucción m%₁η( )t =0.2579 57 para a₀ =0.1564673,β =1. Caso Óptimo

4.17 Gráficas de la Función de Error de Reconstrucción

σ

°η2( )t =0.1143 58 para a₀ =0.1564673,β =1. Caso Óptimo.

4.18 Gráficas del Promedio de la familia de curvas de la Función de Error 58 de Reconstrucción °

σ

η2( )t para a₀ =0.1564673,β =1. Caso Óptimo.

4.19 Gráfica de la Función de Error de Reconstrucción σ°η2( )t =4.6708 59 para a₀ =1,β =1. Caso No Óptimo (No depende de las muestras).

60 4.20 Gráfica de la Función de Error de Reconstrucción σ°η2( )t =0.1143

para a₀ =0.1564673,β =1. Caso No Óptimo (No depende de las muestras). 4.21 Función de Error de Reconstrucción σ°η2( )t =4.6708 para a₀ =1,β =1. 60

Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparació entre el n

4.22 para

Caso Óptimo y el Caso No Óptimo. °2

Función de Error de Reconstrucción ση( )t =4.6708 a₀ =1,β =1. 61 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparació entre el n

4.23 para 61

Caso Óptimo y el Caso No Óptimo. °2

Función de Error de Reconstrucción ση( )t =0.1143 a₀ =0.1564673,β =1. Valores de muestreo η(T_N) =

62 0.2, 0.6, 1.2, 1.5, 0.9.

Comparación entre e

l Caso Óptimo y el Caso No Óptimo. °2

4.24 Función de Error de Reconstrucción ση( )t =0.1143 para

a₀ =0.1564673,β =1. Valores de muestreo η(T_N) = 0.2, 0.6, 1.2, 1.5, 0.9. omparación entre el

C Caso Óptimo y el Caso No Óptimo.

4.25 Gráficas de la Función de Reconstrucción m%₁η( )t =1.6487 para 63 a₀ =1,β =1. Caso Óptimo.

4.27 Gráfica del Promedio de la familia de curvas de la Función de 64 Error de Reconstrucción °

σ

η2( )t para a₀ =1,β =1, σ°η2( )t =4.6708.

Caso Óptimo.

4.28 Gráficas de la Función de Reconstrucción m t%₁η( )=0.2579 65 para a₀ =0.1564673,β =1. Caso Óptimo.

4.29 Gráficas de la Función de Error de Reconstrucción

σ

°η2( )t =0.1143 65 para a₀ =0.1564673,β =1. Caso Óptimo.

4.30 Gráficas del Promedio de la familia de curvas de la Función de 66 Error de Reconstrucción °

σ

η2( )t para a₀ =0.1564673,β =1,

σ

°η2( )t =0.1143. Caso Óptimo.

ráfica de la Fu Reconstrucción 67 4.31 G nción de Error de σ°η2( )t =4.6708

para a₀ =1,β =1. Caso No Óptimo (No depende de las muestras).

67 4.32 Gráfica de la Función de Error de Reconstrucción σ°η2( )t =0.1143

para a₀ =0.1564673,β =1. Caso No Óptimo (No depende de las muestras). 4.33 Función de Error de Reconstrucción σ°η2( )t =4.6708 para a₀ =1,β =1. 68 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparación entre el

para Caso Óptimo y el Caso No Óptimo.

°2

4.34 Función de Error de Reconstrucción ση( )t =4.6708 a₀ =1,β =1. 68 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparación entre el

para 69 Caso Óptimo y el Caso No Óptimo.

°2

4.35 Función de Error de Reconstrucción ση( )t =0.1143

a₀ =0.1564673,β =1. Valores de muestreo η(T_N) = 0.2, 0.6, 1.2, 1.5, 0.9. paración entre el Ca

Com so Óptimo y el Caso No Óptimo

°2 4.36 Función de Error de Reconstrucción ση( )t =0.1143 para

a

69 ₀ =0.1564673,β =1. Valores de muestreo η(T_N) = 0.2, 0.6, 1.2, 1.5, 0.9.

Comparación entre el Caso Óptimo y el Caso No Óptimo

5.1 Gráficas de la Función de Reconstrucción m t%₁η( ) 1.6487= para 74 a₀ =1,β =1. Caso Óptimo.

5.2 Gráficas de la Función de Error de Reconstrucciónσ°η2( )t =4.6708 para 74 a₀ =1,β =1. Caso Óptimo

ráficas de econstrucción m t%₁η( )=0.2579 para 75 5.3 G la Función de R

β

ráficas de la Función de Error de Reconstrucción para 76

5.4 G σ°η2( )t =0.1143

a₀ =0.1564673, β =1. Caso Óptimo.

5.5 Gráfica de la Función de Error de Reconstrucción σ°η2( )t =4.6708 para 77 a₀ =1,β =1. Caso No Óptimo (No depende de las muestras).

77 5.6 Gráfica de la Función de Error de Reconstrucción

σ

°η2( )t =0.1143

para a₀ =0.1564673,β =1. Caso No Óptimo (No depende de las muestras).

5.7 Función de Error de Reconstrucción σ°η2( )t =4.6708 para a0 =1,β =1. 78 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparación entre el

( )t 0.1143 η

σ = para 78 Caso Óptimo y el Caso No Óptimo.

2

5.8 Función de Error de Reconstrucción °

a₀ =0.1564673, β =1. Valores de muestreo η(T_N) = 0.2, 0.6,0.6,1.2,1.5,0.9 Comparación entre el Caso Óptimo y el Caso No Óptimo.

5.9 Gráfica de la Función de Reconstrucción m t%₁η( ) 1.6487= para a₀ =1,β =1. 80

Función de Error de Reconstrucción para 80 Caso Óptimo.

5.10 Gráficas de la σ°η2( )t =4.6708

a₀ =1,β =1. Caso Óptimo

5.11 Gráficas de la Función de Reconstrucción m t%₁η( )=0.2579 para 81 a₀ =0.1564673,β =1. Caso Óptimo.

5.12 Gráficas de la Función de Error de Reconstrucciónσ°η2( )t =0.1143 81 para a₀ =0.1564673,β =1. Caso Óptimo.

5.13. Gráfica de la Función de Error de Reconstrucción σ°η2( )t =4.6708 para 82 a₀ =1,β =1. Caso No Óptimo (No depende de las muestras).

83 5.14 Gráfica de la Función de Error de Reconstrucción

σ

°η2( )t =0.1143

para a₀ =0.1564673,β =1. Caso No Óptimo (No de uestras).

2

pende de las m

5.15 Función de Error de Reconstrucción σ°η( )t =4.6708 para a₀ =1,β =1 . 83 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparación entre el

Caso Óptimo y el Caso No Óptimo °2

( )t 0.1143 para 84 5.16 Función de Error de Reconstrucción

=

η

σ =

a₀ 0.1564673, β =1. Valores de muestreo η(T_N) = 0.2, 0.6,0.6,1.2,1.5,0.9. No Ó

t

Comparación entre el Caso Óptimo y el Caso ptimo.

5.17 Gráficas de la Función de Reconstrucción m%₁η( )=1.6487 para a₀ =1,β =1. 85

ucción ση t = 8 para 86 Caso Óptimo.

5.18 Gráficas de la Función de Error de Reconstr °2( ) 4.670 a =1,β =1. Caso Óptimo.

2579

0

trucciónση t =

a

5.20 Gráficas de la Función de Error de Recons ( ) 0.1143 para 87 ₀ =0.1564673,β =1. Caso Óptimo

5.21. Gráfica de la Función de Error de Reconstrucción σ°η2( )t =4.6708 para 88 a₀ =1,β =1. Caso No pende de las muestras).

ara a

Óptimo (No de

5.22 Gráfica de la Función de Error de Reconstrucción

σ

°η2( )t =0.1143 88

p ₀ =0.1564673,β 1 s muestras).

para a

= . Caso No Óptimo (No depende de la

5.23 Función de Error de Reconstrucción σ°η2( )t =4.6708 ₀ =1,β =1. 89 Valores de muestreo η(T_N) = 0.25, 1, 2, 3, 4, 5.Comparación entre el

Caso Óptimo y el Caso No Óptimo.

5.24 Función de Error de Reconstrucción

σ

°η2( )t =0.1143 para 89 a₀ =0.1564673,β =1. Valores de muestreo η(T_N) = 0.2, 0.6, 1.2, 1.5, 0.9.

OBJETIVOS

Aplicar la teoría estadística para el Pr treo-Reconstrucción de los procesos aleatorios a la salida de un convertidor de tipo exponencial considerando una cantidad de

uestras limitada.

ritmo óptimo para la reconstrucción de procesos no gaussianos, como el algoritmo no óptimo para la misma reconstrucción en la región de interpolación

no gaussianos, así como el algoritmo no óptimo para la misma reconstrucción en la

JUSTIFICACIÓN

a de Balakrishnan tiene r, este teorema no toma en cuenta i la función de densidad de probabilidad (fdp) que se presenta para cada proceso aleatorio, ni la

nción de covarianza, además la cantidad de muestras debe ser infinita. ocedimien o de Muest

m

Analizar la reconstrucción tomando en cuenta diferentes funciones de covarianza de determinados sistemas para:

a) obtener las funciones de reconstrucción y de error de reconstrucción utilizando tanto el algo

b) obtener las funciones de reconstrucción y de error de reconstrucción utilizando los algoritmos, tanto el algoritmo óptimo para la reconstrucción de procesos

región de extrapolación.

El Teorem n

algunas desventajas, es deci fu

Según este teorema, es suficiente conocer la frecuencia límite ω_b, para obtener la reconstrucción completa de una realización de cualquier proceso aleatorio con un error igual a cero. Todas estas ondiciones no son adecuadas en la práctica. La meta del presente trabajo es investigar cómo un c

proceso no gaussiano, formado a la salida de un convertidor exponencial, puede ser reconstruido con diferentes algoritmos tanto óptimos como no óptimos.

La cantidad de las muestras es limitada, la función de covarianza es tomada en cuenta y para el caso óptimo se usa información acerca de la fdp.

INTRODUCCIÓN

l procedimiento de Muestreo-Reconstrucción basado en la Regla de la Esperanza Matemática ondicional es un buen método para analizar las características de reconstrucción de los procesos

s fundamentos de lo que es un proceso aleatorio, así como las principales E

C

aleatorios con diferentes tipos de filtros realizables al considerar las propiedades estadísticas de la respuesta en el tiempo o en la frecuencia de cada filtro. Y además se puede utilizar en el procedimiento tanto de interpolación como el de extrapolación, a diferencia del Teorema de Balakrishnan.

En el Capítulo I, se presenta el antecedente de los Teoremas de Muestreo-Reconstrucción, y emás se establecen lo

ad

características del mismo, tales como la función de covarianza, la densidad espectral de potencia, el ruido blanco que afecta a los diversos filtros que forman los procesos aleatorios, la regla de la esperanza matemática condicional; así como las funciones de momento condicionales de un proceso a la salida η

( )

t .

En el Capítulo II, se establecen las características de los procesos gaussianos y de los procesos aussianos condicionales, los diferentes tipos de procedimientos de Muestreo-Reconstrucción de

el convertidor exponencial del tipo g

un proceso aleatorio de tipo gaussiano utilizando los filtros RC de una, dos y tres etapas.

En el Capítulo III se presentan las características del proceso aleatorio que se presenta a la salida

( )

( )

0 t a e

η = , como son los momentos condicionales, la

además se t

βξ d

función de densidad de probabilidad, la esperanza matemática, la varianza, la función de covarianza, el tiempo de covarianza; presentan algunos ejemplos para diferentes valores de las constantes a₀ y β.

En el Capítulo IV se d cribes e e procedimiento de Muestreo-Reconstrucción de procesos l leatorios a la salida de un convertidor exponencial con algoritmos tanto óptimo, como el

cial con algoritmos tanto óptimo, como el a

algoritmo no óptimo en la región de extrapolación.

En el Capítulo V se describe el procedimiento de Muestreo-Reconstrucción de procesos leatorios a la salida de un convertidor exponen

a

CAPÍTULO I

ANTECEDENTES

1.1 TEOREMA CLÁSICO DE WHITTAKER, KOTELNIKOV Y SHANNON

El teorema de muestreo de Nyquist-Shannon, también conocido como teorema de muestreo de Whittaker-Nyquist-Kotelnikov-Shannon, (teorema WKS) criterio de Nyquist o teorema de Nyquist, es un teorema fundamental de la teoría de la información y ha sido utilizado para funciones determinísticas con espectro limitado. A continuación se enuncia este teorema [1-4]: .

Toda función de una señal determinística f(t) definida en ¡ , cuyo espectro de amplitud y fase, está limitado dentro de un intervalo [-ωb, ωb] (donde ωb>0) puede ser completamente reconstruida con respecto a toda t∈¡ partiendo de los valores muestreados f ( kπ / ωb ) que son tomados en los puntos kπ/ωb (donde k∈¢ ) igualmente espaciados sobre el eje real ¡ , en base a:

(

)

( ) b

k b b

sen t k

k

f t f

t k ω π π ω ω π ∞ =−∞ − ⎛ ⎞ = _{⎜ ⎟} − ⎝ ⎠

∑

. (1.1) Este teorema demuestra que la reconstrucción exacta de una señal periódica continua en banda base a partir de sus muestras es matemáticamente posible, si la señal está limitada en banda y la tasa de muestreo es superior al doble de su ancho de banda. Es decir, la información completa de la señal analógica original que cumple con el criterio anterior, está descrita por la serie total de muestras que resultaron del proceso de muestreo. Por lo tanto, la evolución de la señal entre muestras está perfectamente definida por la serie total de muestras. La mayoría de sus generalizaciones están relacionadas con la descripción del Procedimiento de Muestreo-Reconstrucción (PMR) de funciones determinísticas con espectro limitado.

1.2 TEOREMA DE BALAKRISHNAN

El teorema clásico WKS ha sido generalizado para procesos aleatorios estacionarios por A. Balakrishnan. El teorema de Balakrishnan toma la esencia del teorema clásico WKS para funciones determinísticas y la retoma para todos los procesos aleatorios estacionarios con espectro finito. Este teorema está dado a continuación [5]:

Sea x(t), un proceso estocástico evaluado real o complejo, estacionario y que posee una densidad espectral de potencia, la cual desaparece fuera del intervalo de la frecuencia angular

t −∞ < < ∞

[

−ω ω_b, _b

]

. Entonces x(t) tiene la representación:

(

)

(

2

)

( ) lim

2 2

b

k b b

sen t k

k

x t x

t k π ω ω π ω ∞ =−∞ − ⎛ ⎞ = _{⎜ ⎟} − ⎝ ⎠

Esto es,

(

)

(

)

2 2

lim ( ) 0

2 2

N

b N

k N b b

sen t k

k

x t x

t k π ω ω π ω →∞ ₌₋ ⎧_{⎡ ⎛ ⎞ − ⎤} ⎫ ⎪ ₋ ⎪ ₌ ⎨⎢ ⎜ ⎟ ₋ ⎥ ⎬ ⎝ ⎠ ⎣ ⎦ ⎪ ⎪ ⎩

∑

⎭

. (1.3)

… se asume que todos los procesos tienen sus varianzas y sus promedios finitos.

De acuerdo con el Teorema de Balakrishnan es suficiente conocer un solo parámetro (la frecuencia de corte del espectro de potencia) de un proceso aleatorio estacionario para obtener una reconstrucción con cero errores. La función de reconstrucción está determinada por una suma lineal de un conjunto de muestras infinitas multiplicadas por las funciones básicas del tipo sen x

x .

1.3 DESVENTAJAS DEL TEOREMA DE BALAKRISHNAN

El Teorema de Balakrishnan no toma en consideración la característica estadística importante llamada función de densidad de probabilidad del proceso aleatorio que se está analizando. Por lo cual, se puede interpretar que el teorema puede aplicarse a cualquier proceso aleatorio que tenga una fdp cualesquiera, ya sea unidimensional o multidimensional [5].

Además, la función básica que se ocupa para muestrear los procesos aleatorios siempre es la función sen x / x independientemente del proceso aleatorio que se esté tratando y ésta no depende del número de muestras. Y de hecho el Teorema admite un número infinito de muestras, ya que considera la realización de los procesos estocásticos en un intervalo infinito de tiempo. También se puede decir, que las características estadísticas importantes que describen un proceso aleatorio Gaussiano y que son las funciones de momento de primero, segundo y tercer orden conocidas como la esperanza matemática, la varianza matemática y la función de covarianza están relacionadas con su correspondiente función de densidad espectral mediante el Teorema de Wiener-Khinchine. Y debido a que el Teorema de Balakrishnan sólo trata con el espectro de potencia y la función de covarianza es utilizada en la demostración de este Teorema, se puede interpretar que el Teorema de Balakrishnan puede ser óptimo para procesos Gaussianos solamente, ya que el autor supone que todos los espectros de mayor orden del proceso estocástico considerado son iguales a cero.

El Teorema de Balakrishnan deja atrás las consideraciones de las características estadísticas importantes mencionadas anteriormente y sólo considera la característica numérica de un proceso estocástico llamada frecuencia límite ω_b, para obtener la reconstrucción completa de las realizaciones de todos los procesos estocásticos con un error de cero.

1.4 PROCESOS ALEATORIOS

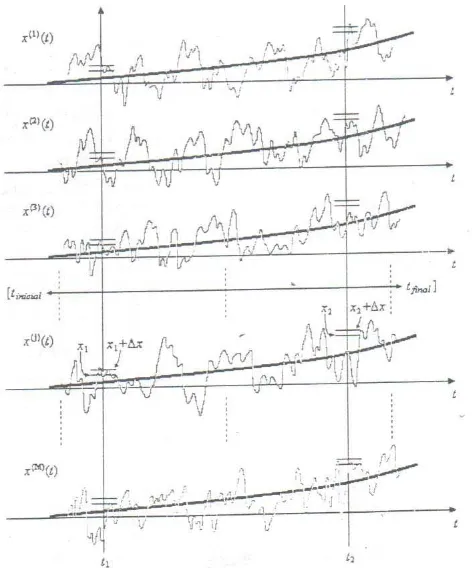
[image:21.612.202.438.211.495.2]

Un proceso aleatorio continuo x(t) tiene muchas realizaciones x(1)(t), x(2)(t),…, x(j) (t),…, x(M) (t) (M finito o infinito) en un tiempo dado y cada realización tiene una medida de probabilidad descrita por las propiedades estadísticas que pueden ser expuestas bajo condiciones similares. Cada realización x(j)(t) puede estar definida en una continuidad de valores de t sobre un intervalo finito (ta, tb) o sobre un intervalo infinito (- ∞,∞)[8].

Fig. 1.1 Conjunto de posibles realizaciones x(1)(t), x(2)(t),…, x(j)(t),…,x(M)(t) que puede tener un proceso aleatorio continuo.

Se puede considerar un conjunto de realizaciones del proceso estocástico que se muestra en la figura 1.1 donde cada realización se especifica en el intervalo (tinicial, tfinal). Después se divide a x en un conjunto de L unidades ( L ≤ M ) cada una con anchura es Δx y se selecciona un intervalo (x1, x1 + Δx). Después se puede medir la probabilidad asociada con dicho intervalo, si se conoce el número de realizaciones x(j) (j=1,…,M) contenidas en el mismo.

P( x1 < x < x1 + Δx; t1). (1.4) Al aplicar el límite, cuando M→∞ y Δx→dx, se obtiene la probabilidad de x en el tiempo t1 dentro del intervalo (x1, x1 + Δx).

Al repetir la operación anterior para cada unidad se encuentra la densidad de probabilidad deseada en cada intervalo. De tal forma, que se puede hallar la densidad de probabilidad existente en cada instante de tiempo t1,t2,…,tm dentro del intervalo (tinicial, tfinal) del proceso aleatorio y hallar su función de densidad de probabilidad (fdp) w1[x(t)]. También se pueden obtener la funciones de densidad de probabilidad de segundo orden w2[x1(t1), x2(t2)] y de mayor orden wm[x(t1), x(t2),…,

x(tm)]. Se deben tomar en cuenta los tiempos t1,t2,…,tm en los cuales las probabilidades se calculan, ya que la estructura actual de las densidades puede ser diferente para tiempos distintos, como se muestra en la figura 1.2

Fig. 1.2 Funciones de densidad de probabilidad de primer orden de un proceso aleatorio en dos instantes de tiempo diferentes.

Si se conocen las fdp unidimensionales (w1[x(t1)], w1[x(t2)],…, w1[x(tm)]) de cada tiempo

t1,t2,…,tm se puede conocer cierta información estadística relacionada con el proceso, como por ejemplo, la función de la esperanza matemática m(t)= <x(t)> en cada instante de tiempo

t1,t2,…,tm expresada por (1.2).

[ ]

( )

( ) ( ) ( ) ( )

m t x t x t w x t dx t

∞

−∞

= =

_∫

. (1.6) así como la función de la varianza matemática σ2( )t =

(

x t( )−m t

( )

)

2 dada por:

( )

(

)

2

(

( )

)

2

[ ]

( )

2

( )t x t( ) m t x t( ) m t w x t dx( )

σ ∞

−∞

= − =

_∫

− t . (1.7)

y las función de momento inicial de orden n:

( )

( )

( )n n( )

x t x t w x t dx

∞

−∞

=

_∫

⎡_⎣ ⎤_⎦ t . (1.8) y además la función de momento central de orden n:

1.5

FUNCIÓN DE COVARIANZA

Consideremos la característica estadística, llamada función de covarianza Kx(t1,t2), la cual refleja las diferencias de la estructura en el tiempo de los diversos procesos aleatorios. Ésta es una función determinística con dos argumentos del tiempo t1 y t2, que demuestran que el momento de covarianza cambia cuando la distancia entre estas dos secciones cambia también[11].

(

)

( ) ( )

( )

( )

(

)

(

( )

( )

)

( ) ( )

( ) ( )

1 2 1 2

1 1 2 2 2 1 2 1 2

,

, .

K t t x t x t

x t m t x t m t w x t x t dx t dx t

∞

−∞

= =

=

∫

− − ⎡_⎣ ⎤_⎦

& &

(1.10)

Fig. 1.3 Función de covarianza K(t) que podría tener a) un proceso aleatorio suave o b) un proceso aleatorio caótico.

La función de covarianza indica si la estructura del proceso en el tiempo es caótico o es suave. Si se fija t1 (por ejemplo t1=0) y movemos a t2 se puede observar el nivel de dependencia estadística que tiene el proceso en el intervalo. La función de covarianza tiende a ser independiente cuando t2 tiende a alejarse de t1. Si la función de covarianza tiende a cero lentamente cuando t2 se aleja, se dice que el proceso es un proceso suave. Sin embargo, cuando la función de covarianza tiende a cero rápidamente, se dice que es un proceso caótico.

a) La función de covarianza tiene su valor máximo cuando t1= t2, en donde = t2 - t1=0:

.

(1.11) b) La función de covarianza es una función par:

K( )= K(- )

.

(1.12) c) La función de covarianza tiende a cero cuando τ → ∞:

K(

∞

)=0

.

(1.13) d) La función de covarianza normalizada Rx( ) está dada por:

(1.14) e) El rango de valores de la función de covarianza es:

|K( )|

≤

K(0)

∴ 0≤ R

( )

τ ≤1. (1.15) f) La función de covarianza está relacionada con el parámetro llamado tiempo de

covarianza _c en función de R( ).

( )

0

c R d

τ =∞

∫

τ τ . (1.16) El tiempo de covarianza c indica el tiempo en que existe dependencia o influencia entre los

mismos valores del proceso y es muy utilizado para medir las características de la respuesta de un filtro. Cuando un proceso es caótico se tiene que el valor del tiempo de covarianza c del proceso

es pequeño comparado con el tiempo de covarianza c de un proceso más suave.

1.6 DENSIDAD ESPECTRAL DE POTENCIA

Existe otro parámetro que sugiere caracterizar las propiedades espectrales de los procesos aleatorios con la distribución de potencia de cada armónico en función de la frecuencia. Esta función espectral debe de caracterizar las propiedades espectrales de todas las realizaciones del proceso aleatorio dado. El Teorema de Wiener-Khinchine sugiere que la función de covarianza

( )

Teorema de Wiener-Khinchine:

( )

1

( )

2

j x

K τ S ω eωτd

π

∞

−∞

=

∫

ω

d

. (1.17)

( )

( )

j

S ω K τ e ωτ

∞

−

−∞

=

∫

τ . (1.18) Se puede percibir que para un proceso suave la densidad espectral de potencia es más estrecha y para un proceso caótico la densidad espectral de potencia es más ancha. Debido a las características espectrales de la función de covarianza K

( )

τ , su transformada de Fourier S

( )

ω tiene las siguientes propiedades:

a) S

( )

ω es real. b) S

( )

ω ≥0.

c) Es una función que tiene una simetría par:S

( )

ω =S

( )

−ω .

1.7 RUIDO BLANCO

La densidad espectral de potencia del ruido blanco es independiente de la frecuencia de operación. El adjetivo blanco se usa porque la luz blanca contiene cantidades iguales de todas las frecuencias dentro de la banda visible de radiación electromagnética. La densidad espectral de potencia del ruido blanco se expresa con una función de potencia denotada por S

( )

ω , como [6]:

( )

0

2

N

S ω = . (1.19)

su gráfica se ilustra en la figura 1.4a Las dimensiones de N0 son watts por hertz. El parámetro N0 casi siempre corresponde con la etapa de entrada del receptor de un sistema de comunicación. Es posible expresarlo como:

espectral de potencia, se concluye que para el ruido blanco:

( )

0

( )

_.

2

N

K τ = δ τ (1.21)

Fig. 1.4 Características del ruido blanco. a) Densidad espectral de potencia. b) Función de autocorrelación.

Esto es, la función de autocorrelación del ruido blanco consiste en una función delta generada por el factor 0

2

N

y que ocurre en τ =0, como se puede ver en la figura 1.4b donde observamos que para

( )

0

K τ = τ ≠0. En consecuencia, cualesquiera dos muestras diferentes de ruido blanco, no importa qué tan próximas se tomen en el tiempo, no están correlacionadas. Si el ruido blanco

también es Gaussiano, entonces las dos muestras resultan estadísticamente independientes. El ruido blanco representa lo último en aleatoriedad y tiene una potencia promedio infinita, por lo que no puede ser físicamente realizable, sin embargo, tiene propiedades matemáticas simples dadas por (1.19)-(1.21), mismas que lo hacen útil en el análisis de sistemas estadísticos.

( )

n t

La utilidad del proceso del ruido blanco es paralela a la de la función impulso o de la función delta de Dirac en el análisis de sistemas lineales. Es posible observar el efecto del ruido blanco, sólo después de que éste ha pasado por un sistema con un ancho de banda finito. Por tanto, es posible establecer que siempre que el ancho de banda de un proceso de ruido en la entrada de un sistema es apreciablemente mayor que el del sistema mismo, entonces se puede modelar el proceso de ruido como ruido blanco.

1.8 REGLA DE LA ESPERANZA MATEMÁTICA CONDICIONAL

Supongamos que un proceso aleatorio x(t) se caracteriza por sus fdp multidimensionales

y una realización del proceso aleatorio se discretiza en instantes de tiempo T ={T1, T2,…,TN}. Por lo que, existe un conjunto de muestras X,T={x(T1), x(T2),…, x(TN)} donde el número de muestras N y sus tiempos de ocurrencia T={T1, T2,…, TN} son arbitrarios. Estos parámetros hacen que cambien las características del proceso aleatorio, esto es, las nuevas funciones y densidades de probabilidad son condicionales o (a posteriori) y dependerán del valor

( ) ( )

1 , 2 ,...,

( )

m

1 2

( ) , ( ) ( ), ( ),..., ( _N)

w x t X T⎡_⎣ ⎤ = ⎡_⎦ w x t x T_⎣ x T x T ⎤_⎦. (1.22)

( )

( ) , ( ) ( ), ( ),..., (1 2 N) ( ) ( ) ,

m t x t X T x t x T x T x T x t w x t X T dx

∞

−∞

= = =

∫

_⎡⎣

% ⎤⎦ . (1.23)

°

( )

(

°

)

(

°

)

2 2

2

( ) ( ) , ( ) ( ) ( ) , .

t x t m t X T x t m t w x t X T dx

σ ∞

−∞

= − =

∫

− ⎡_⎣ ⎤_⎦ (1.24)

Esto es, la reconstrucción del proceso aleatorio depende del conjunto de muestras X,T={x(T1),

x(T2),…, x(TN)} y de la fdp wm⎡⎣x t

( ) ( )

1 ,x t2 ,...,x t

( )

m ⎤⎦, donde N<m.

El conjunto de realizaciones del proceso aleatorio condicional %x t( )=x t X T( ) , pasan a través de todas las muestras X,T={x(T1), x(T2),…, x(TN)}. Cada realización del proceso aleatorio x%(t) es una entre un número infinito de otras. No se puede conocer exactamente una de ellas, pero se puede hacer una estimación de la reconstrucción estadísticamente en un tiempo t. Esto se puede lograr, al seleccionar la regla estadística apropiada, para la función de reconstrucción y después para la función de error de reconstrucción.

La regla de la esperanza matemática condicional es un buen criterio para tener un mínimo de error en la estimación de una variable aleatoria con fdp arbitraria. Acorde con esta regla se puede tener la función de reconstrucción, en términos de la función de la media condicional

°( ) ( ) ,

m t = x t X T y la función de error de reconstrucción, en términos de la función de la varianza condicional °2

( )

(

( )

°

)

2

( ) ,

t x t m t X T

σ = − la cual representa la calidad de la

reconstrucción. Además de estas características utilizadas para el Procedimiento de Muestreo-Reconstrucción, se puede también considerar el parámetro llamado función de covarianza K ( ).

Si se considera el caso general, de un proceso Gaussiano no estacionario x(t) con sus características llamadas esperanza matemática m(t), varianza 2(t) y función de covarianza K( ),

se puede escribir la fdp multidimensional de orden arbitrario m expresado por:

[

]

( )

( )

( )

( )

( ) ( )

1/ 2 / 2 1 2 1 1

( ), ( ),..., ( ) 2 ,

1

exp .

2

m

m m x i

m m

i i ij j j

i j

w x t x t x t Det K t t

x t m t a x t m t

π − −

= =

⎡ _j ⎤

= _{⎣ ⎦} ×

⎧ _{⎡ ⎤}⎫

× _⎨− ⎡_⎣ − ⎤_{⎦ ⎣} − _⎦⎬

⎩

∑∑

⎭

(1.25)

1 1 1 2 1 1 2 ... ... ... ... ( , ) . ... ... ... ... ( , ) ( , ) ... ( , ) m i j

m m m m

t t

K t t K t t

K

K t t

= (1.26)

donde aij es el elemento ij-ésimo de la inversa de la matriz de covarianza.

| a

ij

|=(K

(t

i

,t

j

))

-1

.

(1.27)

Al fijar el conjunto de muestras X,T={x(T1), x(T2),…, x(TN)}, tendremos una fdp condicional Gaussiana. Cuyas características estadísticas del proceso condicional no estacionario son:

°

( )

1 1

( ) ( ) , ( ) ( ) .

N N

i ij j j

i j

m t m t K t T a x T m T

= =

⎡ ⎤

= +

∑∑

_⎣ − _⎦ (1.28)

°2 ₂

( )

1 1

( ) ( , ) ( , ).

N N

i ij j i j

t t K t T a K T

σ σ

= =

= −

∑∑

t

)

.

(1.29)

°

(

)

(

)

(

)

(

1 2 1 2 1 2

1 1

, , , ,

N N

i ij j i j

K t t K t t K t T a K T t

= =

= −

∑∑

(1.30)

Se tienen dos regiones donde se puede llevar a cabo la reconstrucción del proceso aleatorio condicional, la primera es conocida como región de extrapolación, esta región se presenta fuera de la región de muestreo y se da cuando t > tN. Esta región se puede observar cuando el número de

muestras N es finito, como por ejemplo N=1. La segunda región, es conocida como región de interpolación, es decir, la región de muestreo y se presenta cuando Ti < t < TN, donde i=1,…,N. Además, esta regla nos da la pauta para reconstruir las realizaciones sobre todo el eje del tiempo t, a pesar del número limitado N.

Al utilizar la regla de la esperanza matemática condicional, en el proceso de reconstrucción, se pueden resolver dos problemas muy importantes:

a) dado un conjunto de muestras de un proceso estocástico inicial, se puede encontrar la función de reconstrucción y se puede calcular la función de error de reconstrucción;

1.9 FUNCIONES DE MOMENTOS CONDICIONALES DEL PROCESO DE

SALIDA

η( )t =g

(

ξ

( )

t

)

Se tiene un convertidor no lineal de tipo exponencial cuya función de transferencia es

( )

(

)

( ) 0 ( )t g t a eβξt

η = ξ =

.

Para determinar las funciones de momentos condicionales del proceso de salida η( )t , se deben calcular los momentos condicionales de orden n de η( )t cuando el conjunto de muestras

{

1 2

}

( )T ( ), ( ),..., (T T T_N)

η = η η η está fijo, es decir [9-11]:

m%_nn

( )

t =

[ ]

η( )t n η( )T = g_⎣⎡ξ

( )

t ⎤_⎦nη( )T . (1.31)

Como la función inversa ξ

( )

t = ⎡h_⎣η

( )

t ⎤_⎦ es única, se pueden recalcular todos los elementos del conjunto η( )T =

{

η( ), ( ),..., (T₁ η T₂ η T_N)

}

fijo, sobre el conjunto de elementos

{

1 2

}

( )T ξ( ), ( ),..., (T ξ T ξ T_N)

Ξ = , por medio de la dependencia determinística ξ( )T_j = ⎣h⎡η

( )

T_j ⎤_⎦, entonces en lugar de (1.26) se tiene:

( )

( )

1 ( )

n

m t% = g⎡_⎣ξ t ⎤_⎦ ΞT . (1.32)

( )

( )

( )

2

2

2 1 .

t mη t mη t

η

CAPÍTULO II

PROCEDIMIENTO DE MUESTREO-RECONSTRUCCIÓN

ÓPTIMO DE LOS PROCESOS GAUSSIANOS

2.1 INTRODUCCIÓN

Se analizará el procedimiento de Muestreo-Reconstrucción de los procesos aleatorios a partir de sus muestras, las cuales pasan a través de filtros pasa-bajas como son los filtros RC de una, dos y tres etapas. Y además se estudiarán las propiedades estadísticas de los procesos aleatorios como son la esperanza matemática, la varianza y la función de covarianza, para poder describir el proceso aleatorio. En este capítulo se estudiará el caso de un proceso aleatorio de tipo Gaussiano a la entrada de un convertidor lineal en cuya salida se tendrá un proceso aleatorio que se reconstruirá. Para poder determinar la reconstrucción de este proceso aleatorio a la salida del convertidor, se trabaja con la regla de la esperanza matemática condicional, la cual considera varios aspectos como son: la función de covarianza K( ),o la función de densidad espectral S(ω),

el número de muestras y el número del intervalo actual que existe entre dos muestras que se encuentran en medio de un intervalo de N muestras. Posteriormente se estudiará el caso de un proceso aleatorio de tipo Gaussiano a la entrada de un convertidor no lineal de tipo exponencial en cuya salida se tendrá un proceso aleatorio no Gaussiano.

2.2 PROPIEDADES DE LOS PROCESOS GAUSSIANOS

a) Si se tiene un proceso aleatorio Gaussiano u(t) a la entrada de un filtro lineal estable, se tendrá un proceso aleatorio x(t) Gaussiano a la salida.

b) Si se considera un conjunto de variables aleatorias o muestras x(T1), x(T2),…, x(Tn), obtenidas en el proceso aleatorio x(t) en cada instante de tiempo T1, T2,…,Tn, y si este proceso x(t) es Gaussiano, entonces el conjunto de variables aleatorias es conjuntamente Gaussiano por cada n, se describe completamente por su matriz de covarianza K(Ti, Tj) de orden n, donde cada elemento de la matriz es [12-14]:

K(Ti, Tj)= (x(Ti)-mx(Ti))(x(Tj)-mx(Tj)) donde i,j=1,2,..,n (2.1) c) Si la matriz de covarianza K(Ti,Tj) se llegara a transformar en una matriz diagonal,

se tiene que las variables aleatorias son no correlacionadas y por lo tanto, se concluye que las variables aleatorias Gaussianas son independientes.

[ ]

( )

/ 2

[

]

1/ 2

(

( )

)

1

(

( )

1 1

( ) exp

2 2

T

n n x

x

w x t x t m K x t m

Det K

π

−

⎛ _⎡

₎

_⎤⎞

= _⎜− _⎣ − − _⎦⎟

⎝ ⎠ . (2.2)

e) Si un proceso Gaussiano es estacionario en el sentido amplio, entonces el proceso también es estacionario en el sentido estricto.

2.3 CASO GAUSSIANO CONDICIONAL

Se considera el caso general del proceso Gaussiano estacionario x(t) con la esperanza matemática

m, la varianza 2, y la función de covarianza K(ti-tj). En base a la función de covarianza se puede escribir la matriz de covarianza de la siguiente manera:

1 1 1 2 1

1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( m i j

m m m

K t t K t t K t t

K t t

K t t K t t K t t

− − −

− =

− − −

L

L L L L

L L L L

L _m)

. (2.3)

Estas características son completas porque determinan la bien conocida expresión analítica de la fdp Gaussiana multidimensional. Existe una expresión para la fdp gaussiana condicional multidimensional. Basándose en esta fdp condicional uno puede determinar las expresiones para la esperanza matemática condicional y para la varianza condicional . Se establece un conjunto arbitrario de N muestras

( )

m t% 2

( )t

σ%

{

1 2

}

, ( ), ( ),..., ( N)

X T = x T x T x T donde el valor de la muestrax T i( )(_i =1,...,N) está dado en el tiempo . Las expresiones para y tienen la siguiente forma [23]:

i

T m t%( ) 2

( )t

σ%

1 1

( ) ( ) ( ) ( )

N N

i ij j j i j

m t m K t T a x T m T

= =

⎡ ⎤

= +

∑∑

− _⎣ − _⎦

% . (2.4)

2 2

1 1

( ) ( ) ( )

N N

i ij j i j

t K t T a K

σ σ

= =

T t

= −

∑∑

−

% − . (2.5)

donde es el elemento de la inversa de la matriz de covarianza (2.5) con el cambio de designación en lugar de :

ij a

, i j

T T t t_i, _j

1

1

( ) , ( )

N

ij i j ij j i

j

a K t t − a K t t

=

1.

Consideremos el caso más simple donde la esperanza matemática es m=0 y la varianza 2=1, en lugar de (2.4) tenemos:

1 1 1

( ) ( ) ( ) ( ) ( )

N N N

i ij j j j

i j j

m t K t T a x T x T B t

= = =

=

∑∑

− =

∑

% . (2.7)

donde la función básica B t_j( ) está determinada por la siguiente expresión:

1 ( ) ( ) N j i i ij

B t K t T

=

=

∑

− a . (2.8)

De las expresiones (2.7) y (2.8) se puede observar que la función de reconstrucción es una función lineal de las muestras y la función básica no es la función

( )

m t% /

sen x x. La función básica óptima Bj(t) depende del número de la muestra j, ésta depende de la cantidad de las muestras N, y también depende de las diferentes covarianzas que existen entre las secciones del proceso en los momentos Ti y Tj (los elementos de la inversa de la función de covarianza aij incluyen los correspondientes momentos de covarianza K(Ti-Tj)), la covarianza K (t-Ti)) entre la sección actual en el tiempo t y la sección en el tiempo de las muestras Ti.

La fórmula (2.5) muestra que la función de error de reconstrucción no depende de los valores de las muestras, pero sí depende de los tiempos de la muestra T_i.

2.4 RECONSTRUCCIÓN DEL PROCESO EN LA SALIDA DE FILTROS RC

DE UNA ETAPA

Un ejemplo del caso más simple es el proceso Markoviano, el cual es generado a la salida de un circuito integrador RC con el parámetro α=1/RC y cuya función de covarianza se expresa de forma exponencial [15-17]:

2

( ) exp( )

K τ =σ −ατ . (2.9) El tiempo de covarianza c = 1/α es una característica de la respuesta de un filtro, el cual determina el tiempo de influencia entre los mismos valores de un proceso y está dado por la expresión:

( )

(

)

0 0

1 exp

c Rx d d

τ τ τ α τ τ

α

∞ ∞

=

∫

=

∫

− =

. (2.10)

Se puede elegir un tiempo de covarianza como c =1 donde α=1.

El proceso de interpolación depende de las muestras cercanas x(Ti) y x(Ti+1 ) donde

(Ti< t < Ti+1 ) y el proceso de extrapolación es descrito por la última muestra x(TN) donde

(t>TN).

Si consideramos el comportamiento de Muestreo- Reconstrucción de un proceso aleatorio cuando sus muestras se hacen pasar a través de un filtro RC de una etapa. La respuesta de este filtro se exhibe en la Tabla 2.1.

Filtro

RC

Función de Covarianza Normalizada

Gráfica de la Función de Covarianza

Función de Densidad Espectral

Gráfica de la Función de Densidad Espectral

de una Etapa

(

)

exp −α τ 2 2

2 , 1 RC α α ω α + =

Tabla 2.1 Función de Covarianza Normalizada y Función de Densidad Espectral de un Filtro RC de una etapa.

Y su función de covarianza normalizada está determinada por la siguiente expresión:

R( ) = exp (-α | |). (2.11) donde 2 = 1.

Las expresiones de la función básica (2.8), la función de reconstrucción (2.7) y la función de error de reconstrucción para este tipo de función de covarianza R_x

( )

τ son las siguientes:

( )

(

)

1 1

( ) exp

N N

.

j i ij i ij

i i

B t R t T a α t T a

= =

=

∑

− =

∑

− − (2.12)

( )

(

1 1 1

( ) ( ) ( ) exp .

N N N

j j j i ij

j j i

m t x T B t x T α t T a

= = =

=

∑

=

∑

∑

− −

%

)

(2.13)

( )

(

2

1 1

1 exp( ) exp

N N

i ij j

i j

t t T a

σ α = =

)

. T t α = −

∑∑

− − −

% − (2.14)

Considerando sólo cuatro muestras de un proceso aleatorio en los instantes de tiempo T1, T2, T3 y

Valor de la muestra

x(Tj)

Tiempo de Muestreo Tj (seg) x(T1)=1 T1=0

x(T2)=1.4 T2=0.5

x(T3)=0.6 T3=1

x(T4)=1.2 T4=1.5

Tabla 2.2 Valores de muestreo con cuatro muestras separadas en un intervalo ΔT = 0.5.

La función básica (2.8), la función de reconstrucción (2.7) y la función de error de reconstrucción (2.5) en la región de interpolación dependen de las dos muestras más cercanas x (T i) y x (T i + 1) tal como se puede observar en las figuras (2.1), (2.2) y (2.3).

Fig. 2.1 Funciones Básicas de un proceso Markoviano considerando sólo cuatro muestras separadas un intervalo

ΔT=0.5.

La función básica depende principalmente del comportamiento de la función de covarianza y existe una función básica Bj(t) por cada muestra. En la figura 2.1, se observan cuatro funciones básicas si se considera un proceso con cuatro muestras, es decir N=4. Cada función básica Bj(t) se multiplica posteriormente con el correspondiente valor de la muestra x(Tj) y al final se suman todas las ondas resultantes para obtener la función de reconstrucción (2.7).

En la región de interpolación (0 < t < 1.5) la reconstrucción del proceso aleatorio sólo depende de las dos muestras más cercanas, según la posición del tiempo t en la reconstrucción y no existe influencia de las demás muestras restantes para definir su descripción. Mientras que en la región de extrapolación, la reconstrucción del proceso depende de una sola muestra, y esta es la muestra que se encuentra en el extremo inicial en el intervalo t < 0, o en el extremo final en el intervalo

Se pueden observar en la figura 2.2, las dos regiones tanto de interpolación como de extrapolación, donde se realiza la reconstrucción de un proceso Markoviano, tomando solamente las cuatro muestras del la Tabla 2.2.

Fig. 2.2 Función de Reconstrucción m t%( ) de un proceso Markoviano, considerando cuatro muestras (x(T1)=1; x(T2)=1.4; x(T3)=0.6; x(T4)=1.2) separadas un intervalo ΔT=0.5.