Metodología para la medición de la viscosidad de aceites mediante un arreglo óptico

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN

METODOLOGÍA PARA LA MEDICIÓN DE LA VISCOSIDAD DE ACEITES MEDIANTE UN ARREGLO ÓPTICO

T E S I S

QUE PARA OBTENER EL GRADO DE MAESTRO EN CIENCIAS EN INGENIERÍA MECÁNICA

PRESENTA

ING. ROBERTO FLAVIO ARGUELLES ARREDONDO

DIRECTORES DE TESIS

DR. JOSÉ ALFREDO JIMÉNEZ BERNAL

DR. HELVIO RICARDO MOLLINEDO PONCE DE LEÓN

Tesis dedicada a:

Quiero agradecer a las siguientes personas e instituciones el apoyo recibido para la realización de esta tesis.

• A los Doctores José Alfredo Jiménez Bernal y Helvio Ricardo Mollinedo Ponce de León por la profesional dirección de este trabajo, su paciencia y su apoyo.

• A los profesores de la comisión revisora de maestría por la revisión de este trabajo:

Dr. Ignacio Carbajal Mariscal

Dra. Claudia del Carmen Gutiérrez Torres

M. en C. Juan Abugaber Francis

• A la Sección de Estudios de Posgrado e Investigación en la Escuela Superior de Ingeniería Mecánica y Eléctrica (SEPI ESIME) del Instituto Politécnico Nacional (IPN).

• Al Consejo Nacional de Ciencia y Tecnología CONACYT por la generosa beca para cursar la maestría.

• Al Dr. José Ángel Ortega Herrera por el apoyo y consejos cuando llegué a la SEPI de la ESIME.

• Al Ing. Armando Adalid Pineda Hernández por el desarrollo de los programas de procesamiento de imágenes.

• Al M.I. Miguel Ángel Hernández Román por el apoyo recibido.

• A la Universidad Nacional Aeronáutica en Querétaro por el tiempo laboral cedido para la elaboración de esta tesis.

• A mi mamá Irene Arredondo Sosa por su apoyo y su amor.

• A mi papá Roberto Arguelles Robles por su apoyo y su amor.

i

En este trabajo se presenta una metodología para la aplicación del viscosímetro de esfera descendente, el cual se usa para medir la viscosidad de fluidos con valores elevados de dicha propiedad y comúnmente usado también para medir la dependencia de la misma con la temperatura.

Para lograrlo, se mide la velocidad terminal de una esfera sólida, de diámetro “d” y densidad _ρesfera, que cae por efecto de la gravedad, dentro de un

tubo transparente lleno con un fluido Newtoniano de densidad ρfluido, que tiene que ser transparente también o lo suficientemente diáfano como para ver como cae la esfera y se pueda observar como alcanza una velocidad límite o final. La magnitud de esta velocidad terminal debe resultar en un bajo número de Reynolds para que se pueda aplicar este método.

Aunque existen comercialmente equipos que usan el principio del viscosímetro de esfera descendente, es posible implementar uno usando un frasco cilíndrico de vidrio, tomarle un video y así poder medir la velocidad de caída de la esfera.

Además, se hace una comparación de los resultados obtenidos usando el modelo de Oseen para el cálculo de la viscosidad.

ii

valores para verificar su validez: la información de la literatura (manuales y libros) y datos experimentales de un fluido de viscosidad perfectamente conocida.

iii

This work presents a methodology for the application of the falling-sphere

viscometer, which is used for measuring a fluid with a high viscosity and is usually

used also to measure the dependence of the same with temperature.

To perform this measurement, the settling velocity of a solid sphere is

measured. This sphere has a diameter “d” and a density ρsphere, it falls down within

a transparent vessel filled with a Newtonian fluid with density ρfluid. The fluid has to

be transparent or translucent enough to observe the sphere falling down and to

measure its settling velocity. The settling velocity magnitude has to be low enough

to have very low Reynolds numbers; otherwise this method is not applicable.

Although there exist commercial equipment to measure viscosity that use

the same physical principle, it is possible to implement a simple instrument using a

test tube and recording a video to measure the sphere fall velocity.

Furthermore, the results obtained are compared to the Oseen´s model

results to calculate viscosity.

The required tests can be performed in a test tube or a cylindrical vessel.

However, since the Stokes´s expression is only valid for an infinite environment

and it does not consider inertial effects, that’s to say, the effect that produced in the

motion because of the mass of the sphere, and then a correction is needed.

Therefore, the slowing down effect due to the vessel walls and an inertial

iv

validate the results: using values found in literature (books and manuals), and

experimental known viscosity values.

It was found that the proposed technique yields acceptable results within the

same order of magnitude of measured viscosity or data reported in the literature.

Due to it, it is considered that this is a valuable technique for first approximation

v

Contenido

Pág.

Resumen i

Abstract iii

Contenido v

Lista de figuras viii

Lista de tablas xi

Nomenclatura xiv

Introducción xviii

Capítulo 1 Conceptos fundamentales 1

1.1 Viscosidad absoluta 1

1.2 Densidad 3

1.3 Viscosidad cinemática 5

1.4 Número de Reynolds 7

1.5 Ecuaciones principales 9

1.5.1 La ecuación de continuidad 9

1.5.2 Las ecuaciones de Navier-Stokes 11 1.6 Modelos Newtonianos y No Newtonianos 12

1.6.1 El modelo newtoniano 12

1.6.2 El modelo no newtoniano 12

1.7 Índice de viscosidad (IV) 12

1.8 Nomenclatura y clasificación de los aceites 16 1.8.1 Clasificación de los aceites de motor 16 1.9 Tipos de modificadores de viscosidad 18

Capitulo 2 Viscosimetría 20

vi

2.3 Viscosímetros de esfera 22

2.3.1 Viscosímetro de esfera rodante 22 2.3.2 Viscosímetro de esfera rotatoria 25 2.3.3 Viscosímetro de esfera descendente 26 2.4 Aplicaciones del Viscosímetro de esfera descendente 28

2.5 Viscosímetro Saybolt 29

2.6 Flujo a bajos números de Reynolds 31

2.7 Ley de Stokes 45

2.8 Corrección de Oseen 56

2.8.1 La paradoja de Stokes 56

2.9 Consideraciones de diseño del viscosímetro de esfera descendente 63

2.9.1 Velocidad límite 63

2.9.2 Viscosidad de Stokes 65

2.9.3 Tiempo de relajación 68

2.9.4 Energía disipada 70

2.9.5 Calibración 70

2.9.6 Efecto de pared 71

2.9.7 Efecto de fondo 77

2.9.8 Fuerza de sustentación (fuerza perpendicular) 78

2.9.9 Efecto de inercia 79

Capítulo 3 Metodología 81

3.1 Preproceso 82

3.2 Proceso 83

3.3 Postproceso 84

Capítulo 4 Diseño del experimento 91

4.1 Expresión de la viscosidad propuesta 95

4.2 Matriz de pruebas 96

4.3 Incertidumbre 99

vii

Capítulo 5 Resultados experimentales 104

5.1 Cálculo de la densidad de los aceites de prueba 104 5.2 Cálculo de las incertidumbres de la medición 106 5.3 Parámetros involucrados en la medición de la viscosidad 110 5.4 Resultados arrojados por los programas en Matlab 111 5.5 Validación error relativo porcentual 112 5.6 Variabilidad de los resultados debido a la posición de la esfera 119 5.7 Variabilidad de los resultados debido a la temperatura 126 5.8 Variabilidad de los resultados debido a las hojas de los datos del

fabricante

127

Conclusiones 128

Recomendaciones 128

Sugerencias para trabajo futuro 129

Referencias 132

viii

Lista de figuras

Figura Título Pág.

Figura 1.1 Distribución de velocidades en un fluido viscoso que se encuentra confinado entre dos placas paralelas de las cuales una se mueve relativa a la otra

2

Figura 1.2. Densidad en un pequeño volumen de un medio continuo

4

Figura 1.3 Volumen de control infinitesimal 9

Figura 1.4 Curvas típicas de aceites con varios Índices de Viscosidad (IV)

14

Figura 2.1 Diagrama de cuerpo libre de una esfera que cae 23

Figura 2.2 Sistema muelle - amortiguador 25

Figura 2.3 Dispositivo para medir el tiempo de caída de una esfera en un fluido con alta viscosidad y diáfano.

27

Figura 2.4 Esquema del viscosímetro Saybolt 29

Figura 2.5 Sistema coordenado esférico 33

Figura 2.6 Distribución de presión alrededor de la superficie de una esfera sumergida en el flujo de un fluido muy viscoso a muy bajo número de Reynolds

36

Figura 2.7 Distribución de presión alrededor de la esfera en flujo paralelo uniforme.

37

Figura 2.8 Líneas de corriente de la esfera estática dentro de un flujo uniforme

ix Figura 2.9 Líneas de corriente de la esfera en movimiento dentro

de un fluido estático.

44

Figura 2.10 Obtención del elemento diferencial de área en coordenadas esféricas

49

Figura 2.11 Distribución del esfuerzo cortante sobre la superficie de una esfera en un flujo viscoso a muy bajo número de Reynolds

52

Figura 2.12 Comparación entre aproximaciones teóricas y la observación experimental

61

Figura 2.13 Desplazamiento de una masa “m” en un medio resistivo 66

Figura 2.14 Velocidad en función del tiempo de la esfera que cae en aceite.

69

Figura 4.1 Esquema del experimento de medición de la viscosidad 91

Figura 4.2 Pantalla del programa Dif 93

Figura 4.3 Imagen de la esfera en el programa Dif. 93

Figura 4.4 Gráfica de velocidad contra tiempo en el desplazamiento de la esfera.

99

Figura 5.1 Gráfica para el cálculo de la viscosidad. 117

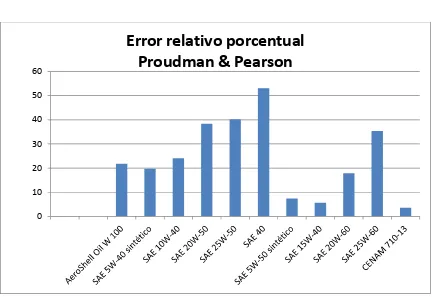
Figura 5.2 Error relativo porcentual usando el modelo de Proudman & Pearson

119

Figura 5.3 Medición de la variabilidad debido a la posición de la esfera

120

x esfera (acercamiento).

Figura 5.5 Medición de la variabilidad debido a la posición de la esfera, cálculo del centro del frasco cilíndrico.

121

Figura 5.6 Medición de la variabilidad debido a la posición de la esfera, distancia positiva y negativa de los diferentes lugares donde cae la esfera.

122

Figura 5.7 Medición de la variabilidad debido a la posición de la esfera, cálculo de la tolerancia

126

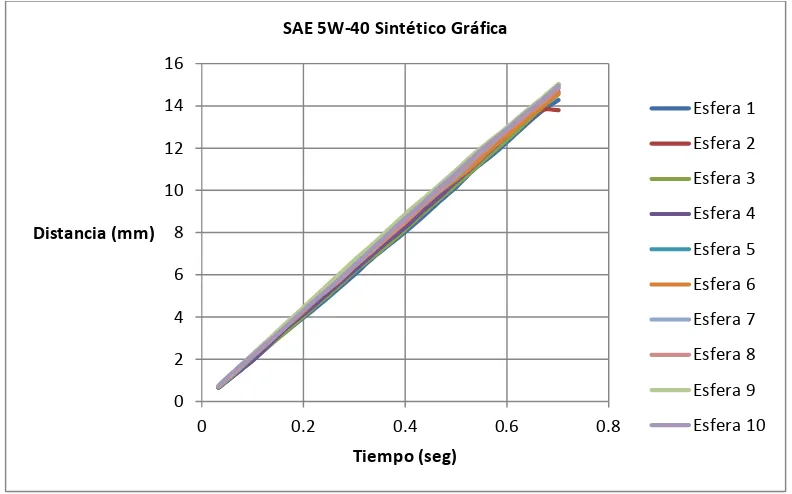
Figura A1.1 SAE 5W-40 Sintético 139

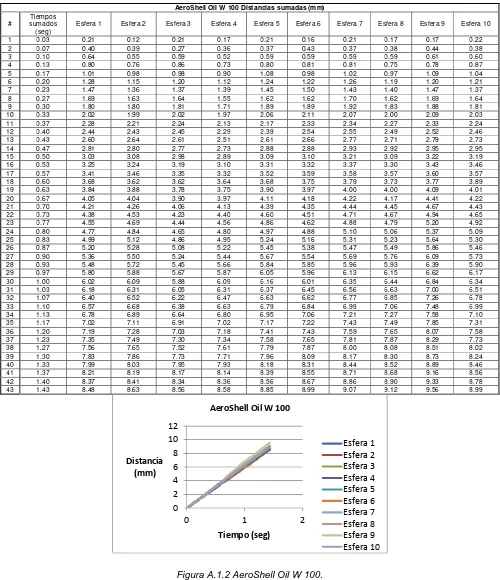
Figura A.1.2 AeroShell Oil W 100 143

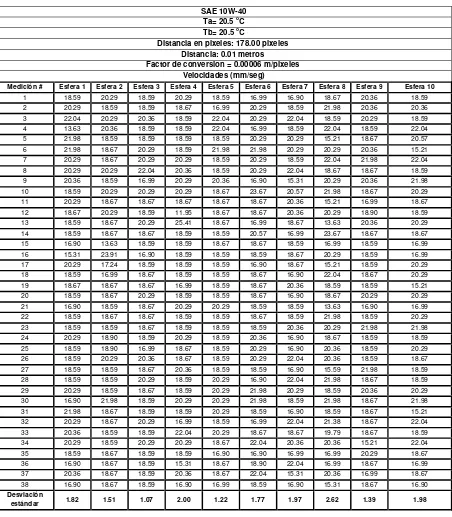
Figura A.1.3 SAE 10W-40 145

Figura A.1.4 SAE 20W-50 148

Figura A.1.5 SAE 25W-50 148

Figura A.1.6 SAE 40 153

Figura A.1.7 SAE 5W-50 Sintético 153

Figura A.1.8 SAE 15W-40 155

Figura A.1.9 SAE 20W-60 155

Figura A.1.10 SAE 25W-60 162

Figura A.1.11 Agua 163

xi

Lista de tablas

Tabla Título Pág.

Tabla 1.1 Equivalencias entre unidades de viscosidad absoluta 3

Tabla 1.2 Equivalencias entre unidades de viscosidad cinemática 5

Tabla 1.3 Estabilidad de los aceites en función del índice de viscosidad.

16

Tabla 1.4 Viscosidades típicas para un aceite de motor multigrado 15W - 40

17

Tabla 4.1 Estadísticas de los fotogramas de los videos. 94

Tabla 4.2 Ecuaciones para el cálculo de la viscosidad 96

Tabla 4.3 Aceites usados en la experimentación 97

Tabla 5.1 Velocidades promedio de cada esfera por aceite 104

Tabla 5.2 Valores para el cálculo de la densidad de los aceites 106

Tabla 5.3 Incertidumbres de entrada y expandidas de los parámetros del cálculo de la viscosidad

110

Tabla 5.4 Resultados de viscosidades 111

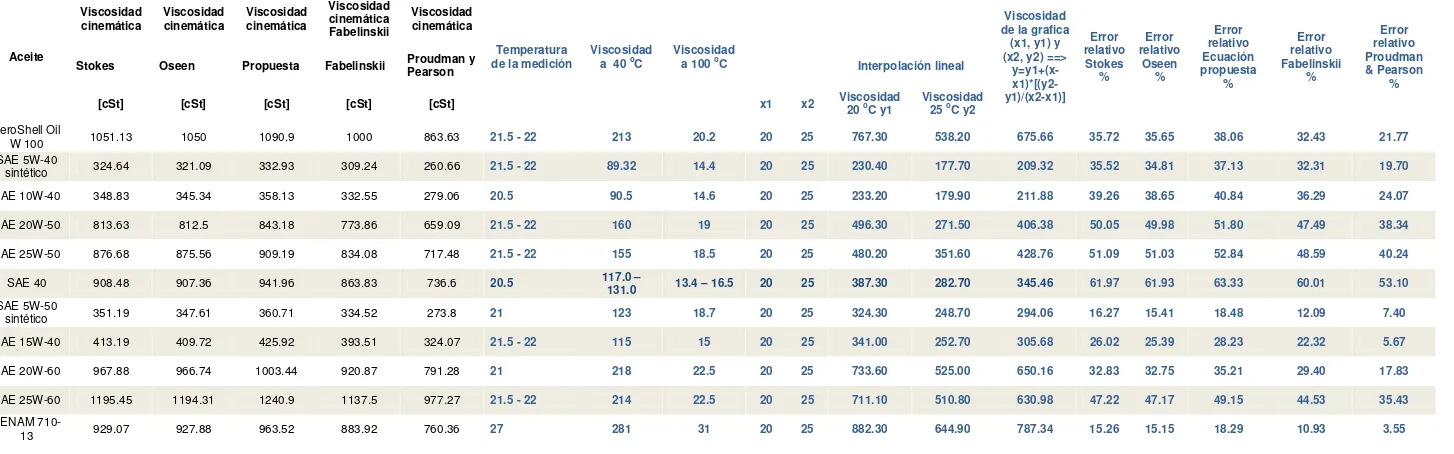
Tabla 5.5 Tabla comparativa de resultados de viscosidades dinámicas

112

Tabla 5.6 Tabla comparativa con el fabricante de los resultados de viscosidades cinemáticas

116

xii

Tabla 5.8 De distancias de caída de la esfera con respecto de la mitad del circulo (boca del frasco)

123

Tabla 5.9 Resultados del estudio de caída de la esfera con respecto de la mitad del circulo (boca del frasco)

124

Tabla A.1.1 Datos experimentales para el aceite SAE 5W-40 Sintético 140

Tabla A.1.2 Datos experimentales acumulativos para el aceite SAE 5W-40 Sintético

141

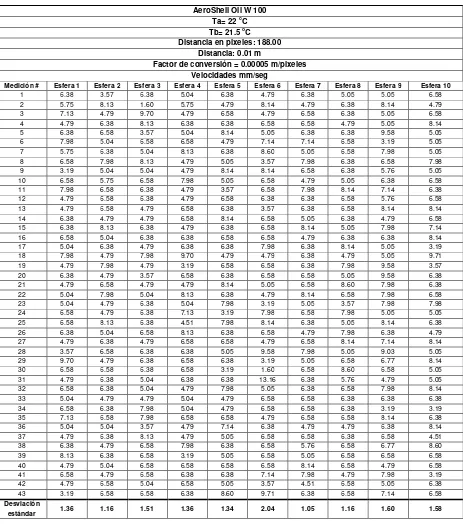
Tabla A.1.3 Datos experimentales para el aceite AeroShell Oil W 100 142

Tabla A.1.4 Datos experimentales acumulativos para el aceite AeroShell Oil W 100

143

Tabla A.1.5 Datos experimentales para el aceite SAE 10W-40 144

Tabla A.1.6 Datos experimentales acumulativos para el aceite SAE 10W-40

145

Tabla A.1.7 Datos experimentales para el aceite SAE 20W-50 146

Tabla A.1.8 Datos experimentales acumulativos para el aceite SAE

20W-50

147

Tabla A.1.9 Datos experimentales para el aceite SAE 25W-50 149

Tabla A.1.10 Datos experimentales acumulativos para el aceite SAE 25W-50

150

xiii

Tabla A.1.12 Datos experimentales acumulativos para el aceite SAE 40 152

Tabla A.1.13 Datos experimentales para el aceite SAE 5W-50 sintético 154

Tabla A.1.14 Datos experimentales acumulativos para el aceite SAE 5W-50 sintético

154

Tabla A.1.15 Datos experimentales para el aceite SAE 15W-40 156

Tabla A.1.16 Datos experimentales acumulativos para el aceite SAE 15W-40

157

Tabla A.1.17 Datos experimentales para el aceite SAE 20W-60 158

Tabla A.1.18 Datos experimentales acumulativos para el aceite SAE 20W-60

159

Tabla A.1.19 Datos experimentales para el aceite SAE 25W-60 160

Tabla A.1.20 Datos experimentales acumulativos para el aceite SAE 25W-60

161

Tabla A.1.21 Datos experimentales para el agua. 162

Tabla A.1.22 Datos experimentales acumulativos para el agua 162

Tabla A.1.23 Datos experimentales para el CENAM 710-13 164

xiv

Nomenclatura

Letras tradicionales

A Área [m2]

a Aceleración [m/s2]

Radio de la esfera [m]

B Flotación [N]

C Constante del aparato (viscosímetro de esfera rodante)

[Kg/ms2_{], coeficiente [Adimensional]} D Fuerza de flotación [N]

Dcil Diametro del recipiente cilíndrico [m]

d Incertidumbre de la báscula CAMRY modelo EK5055 [g] ds Diferencial de desplazamiento [metros]

desfera Diametro de la esfera [m]

E2 Operador Diferencial [Adimensional] F Fuerza [N]

Fs Fuerza de sustentación

f Fuerzas de cuerpo [N]

G Constante de elasticidad de muelle [N/m] g Aceleración debida a la gravedad [m/s2] h Distancia, altura metros [m]

IV Índice de Viscosidad [Adimensional]

k Constante positiva, actúa para impedir el movimiento

[Adimensional]

K₁, K₂ Constantes dependientes de las características del sistema

en el viscosímetro de esfera rodante [Adimensionales]

Kp

xv

Kb

Factor de corrección para los efectos inerciales [Adimensional]

Kac ”Bulk viscosity” (viscosidad de masa) [centipoises]

Kcal

Constante de calibración del aparato para el viscos{imetro de esfera rodante [m2/s2]

L Símbolo dimensional de la distancia [m]

Lcil Distancia entre la superficie del recipiente y el fondo [m]

l Dimensión característica [m] l Longitud del cilindro [m]

M Número de datos [Adimensional]

Mvis Momento viscoso del fluido sobre la esfera [Nm]

m Pendiente [Adimensional], masa [Kg], metro [m]

N Factor a dividir en la ecuación de Oseen Faksen-Ladenburg

[Adimensional]

N Newton [N]

n, n* Parámetro número de replicas y datos [Adimensional] P Potencia desarrollada [W]

p Presión [N/m2] Pa Pascales [Pa]

R Función del cálculo de incertidumbres [mismas unidades de

los datos originales]

r Vector de desplazamiento radial, radio, componente radial

[m]

rc Radio crítico [m]

R2 Coeficiente de correlación [Adimensional] Re Número de Reynolds [Adimensional] Rin Función para calcular las incertidumbres

xvi

St Unidad de medida Stokes [St] (1St=1x10-4 m2/s) T Temperatura [oC]

t Tiempo [s]

U Velocidad promedio [m/s]

u Representación de velocidad [m/s] V velocidad de la esfera [m/s]

v Velocidad de flujo [m/s]

Vsed Velocidad de sedimentación [m/s]

v∞ Velocidad de corriente libre [m/s]

∀ Volumen [m3] W Peso [N]

w Peso específico [N/m3]

w Incertidumbre [mismas unidades de los datos originales] x Abscisa [m]

y Ordenada (coordenada horizontal) [m] z Altura [m]

zcil Distancia entre la esfera y el fondo del recipiente [m]

Letras griegas

ángulo de inclinación en el viscosímetro de esfera rodante [radianes]

Δ Indica un incremento pequeño [Adimensional] Pequeño incremento [Adimensional]

xvii

Κ Coordenada radial establecida [grados]

λ Segundo coeficiente de viscosidad [centipoises] µ Viscosidad dinámica [N*s/m2]

ν Viscosidad cinemática [St]

π 3.1416 [Adimensional] ρ Densidad [Kg/m3]

ρe Densidad de la esfera en el viscosímetro de esfera rodante _[Kg/m3_]

Σ Sumatoria [sin unidades es solo un operador]

σ Desviación estándar [mismas de los datos originales]

τ Esfuerzo cortante [N], tensor de esfuerzos [N/m2]

τ_rel Tiempo de relajación [s]

φ Ángulo acimutal (ángulo que corre con el ecuador de la _{esfera) [Rad]}

Función de corriente [m2_/s]

Ω Vorticidad [J/Kgm2]

ω_rod Velocidad angular de la esfera en el viscosímetro de esfera

rodante [Rad/s]

Otros símbolos

∇ Operador nabla [Adimensional] ∝ Proporcionalidad [Adimensional]

xviii

Introducción

En este trabajo se presenta la propuesta de una metodología de arreglo experimental para medir la viscosidad de ciertos aceites. El fundamento teórico del problema es la ley de Stokes para calcular la viscosidad (ec. 2.101), válida para números de Reynolds muy bajos en un medio ambiente de tamaño infinito. El método propuesto en esta tesis para medir la viscosidad de ciertos aceites, emplea un viscosímetro de esfera descendente junto con un arreglo óptico.

Se mide la velocidad terminal de una esfera sólida, de diámetro “d” y

densidad ρesfera, que cae por efecto de la gravedad, dentro de un tubo

transparente lleno con un fluido Newtoniano de densidad ρfluido, que tiene que

ser transparente también o lo suficientemente diáfano como para ver como cae la esfera y se pueda ver como alcanza una velocidad limite o final. La magnitud de esta velocidad terminal debe resultar en un bajo número de Reynolds para que se pueda aplicar este método.

Aunque existen comercialmente equipos que usan el principio del viscosímetro de esfera descendente, se propone implementar uno usando un recipiente cilíndrico tomando un video y así poder medir la velocidad de caída de la esfera.

xix

El capítulo 1 contiene los conceptos fundamentales necesarios para el estudio de la viscosidad como son las unidades fundamentales y las leyes físicas involucradas, se presentan también las ecuaciones principales que rigen el comportamiento de los fluidos viscosos como la ecuación de continuidad y las ecuaciones de Navier-Stokes. Además hay una descripción de los modelos Newtoniano y No Newtoniano que caracterizan a los diferentes tipos de fluidos y la manera estandarizada de clasificarlos y seleccionarlos.

El capítulo 2 es una recopilación de los tipos de viscosímetros más importantes, sus principales características, su funcionamiento y los modelos matemáticos que los rigen. Hay una introducción del viscosímetro de esfera descendente y las aplicaciones principales en la industria. El desarrollo de las ecuaciones de la viscosidad a bajos números de Reynolds están en este capítulo también así como un esquema del flujo alrededor de la esfera que desciende y las generalidades de como se dedujo la ley de Stokes. Se presentan algunas consideraciones que se deben hacer al diseñar un viscosímetro de esfera descendente como son: el tiempo de relajación, la energía disipada, la calibración del instrumento, el efecto de pared y las fuerzas que actúan sobre la esfera.

La metodología para hacer los experimentos y las mediciones en forma de diagramas de bloques paso a paso para que se explique mejor el proceso están en el capítulo 3. Existen ciertos detalles en el proyecto y en el manejo de los programas de computación que hacen necesario este capítulo y así los investigadores interesados puedan fácilmente reproducir el método.

xx

matriz de pruebas y las ecuaciones que se usaron para calcular la viscosidad y las incertidumbres.

Como apartado especial se hace un resumen del artículo publicado por el profesor Ajay Wadhwa del departamento de Física y Electrónica del Khalsa College de la Universidad Delhi en la India en donde reporta el método para poder calcular la velocidad de caída de la esfera y la estimación del tamaño optimo de las esferas.

El capítulo 5 contiene los resultados obtenidos en los experimentos, la comparación con los otros aceites y con los datos del fabricante. Se hace también un cálculo numérico de los valores obtenidos en las tablas y el error relativo porcentual. Cada una de las 5 expresiones para calcular la viscosidad fue evaluada en detalle para comprobar los resultados con el AeroShell W100.

Finalmente, se presentan las conclusiones y se hacen recomendaciones para la mejora del presente trabajo y propuestas para futuros trabajos.

Las tablas y gráficas con los resultados de cada uno de los experimentos se anexan en el apéndice 1 y el programa generado para el manejo de los cálculos para obtener los valores de velocidad se presentan en el apéndice 2.

Objetivo general.

Se propone una metodología que permita una primera aproximación en la medición de la viscosidad aplicando una variante del método del viscosímetro de esfera descendente. Esta variante es la medición de la velocidad de caída de la esfera mediante un arreglo óptico.

Alcance.

xxi

técnicas de medición de la viscosidad, el estudio aquí presentado es usando el viscosímetro de esfera descendente. Debido a las características ópticas de las pruebas experimentales, se ha seleccionado como fluidos de estudio una clase de aceites automotrices diáfanos; en todos los análisis se ha supuesto un comportamiento de fluido Newtoniano.

Justificación.

1

Capítulo 1. Conceptos fundamentales

En esta tesis se desarrolla una metodología para la implementación de una técnica óptica de medición indirecta de viscosidad absoluta de aceites. Para realizar esta actividad es necesario que se tenga un conocimiento básico de ciertos conceptos, los cuales se describen en los siguientes párrafos.

1.1 Viscosidad absoluta

La viscosidad absoluta (µ) es la propiedad más importante en los lubricantes. Básicamente se define como la oposición que un fluido presenta al movimiento. El valor de ésta y su variación dependiendo de la condiciones del ambiente en el que opere la sustancia determinan el valor de la misma. Este término es empleado cotidianamente para expresar el nivel de fluidez de una sustancia; por ejemplo: al verter miel o agua sobre una superficie plana se observa que una de ellas cubre con mayor rapidez la superficie debido a que tiene una menor viscosidad (agua) que la otra. La viscosidad podría ser atribuida a dos fenómenos:

Fuerza de cohesión intermolecular

Cambio molecular de momento

2

Considere un fluido que se encuentra entre dos placas paralelas, una fija y otra en movimiento (ver figura 1.1). La fuerza requerida para mover la placa es proporcional a la velocidad y al área (plano en contacto con el fluido) e inversamente proporcional a la distancia que separa las placas [1].

Figura 1.1 Distribución de velocidades en un fluido viscoso que se encuentra confinado entre dos

placas paralelas de las cuales una se mueve relativa a la otra.

Esto se puede transformar en la ecuación 1.1, que es conocida como la ley de la viscosidad de Newton [2].

= (1.1)

La constante µ es una constante de proporcionalidad que puede ser encontrada en la literatura con diferentes nombres: viscosidad, viscosidad absoluta o dinámica, módulo de viscosidad, coeficiente de viscosidad.

Las dimensiones de µ están dadas por:

=

× 1 × 1 =

Algunas unidades que se emplean para la viscosidad (µ) son, lbf⋅s/ft2, slug/ft⋅s del sistema inglés y poise, g/cm⋅s, kg/m⋅s y Pa⋅s. Algunas equivalencias entre ellas son:

Placa móvil

Placa fija

y

3

Tabla 1.1 Equivalencias entre unidades de viscosidad absoluta

Las unidades de la viscosidad absoluta o dinámica µ en el SI (Sistema Internacional de Unidades) son el Poise (P) y el centipoise (cP) en honor a J. L. M. Poiseuille, un físico francés que condujo los primeros experimentos de flujo en tuberías.

1.2 Densidad

En esta tesis se considera que cada uno de los aceites que se estudian están continuamente distribuidos a lo largo de la región de interés, es decir que las moléculas de esa región están lo suficientemente juntas como para que el aceite pueda considerarse un medio continuo. La idea de un medio continuo es una abstracción, la materia no es continua sino discreta y sus propiedades mas perceptibles y evidentes se observan de acuerdo a un gran cúmulo de moléculas, las representaciones matemáticas en Mecánica de Fluidos han sido obtenidas de esta forma.

Para saber si las moléculas están suficientemente juntas se usa la trayectoria libre media, que es la distancia promedio que una molécula de fluido viaja antes de que choque con la molécula vecina. Si la trayectoria libre media es pequeña comparada con la dimensión característica de algún dispositivo, entonces la suposición del continuo tiene sentido [3,4].

1 poise 1 !_⋅" 0.1_!%_⋅" 0.1 & ⋅"

4

Para considerar una definición exacta de densidad también se debe considerar un límite.

Si un fluido es un continuo, la densidad promedio se puede definir como:

'( =)*

)∀ (1.2)

Donde ∆m es la masa infinitesimal contenida en el volumen infinitesimal ∆∀.

Al volumen infinitesimal no se le puede permitir que se reduzca a cero debido a que habría muy pocas moléculas en un volumen muy pequeño, entonces se necesita un pequeño volumen límite para que la ecuación (1.2) sea aceptable ya que si físicamente se permite que _{∆∀→ 0}, la masa de _∆∀ tendría una variación discontinua según la cantidad de moléculas contenidas en _∆∀; _∆∀ se haría tan pequeño que la densidad variaría como se muestra en la figura 1.2.

Figura 1.2 Densidad en un pequeño volumen de un medio continuo [2].

.∀ es el volumen más pequeño antes de que la estructura molecular haga que la densidad se vuelva irregular, es la frontera de la hipótesis del continuo. Así, la densidad de un fluido se define como:

' = lim

ρ

'(

5

El valor límite _.∀ para fluidos sometidos a presiones y temperaturas atmosféricas está en el orden de 10-9 mm3. Las propiedades de los fluidos están basadas de acuerdo a la estructura molecular promedio de este volumen.

La densidad depende de la temperatura y la presión, en los gases la dependencia es muy fuerte, en los líquidos y los sólidos es débil.

A la densidad también se le conoce como masa específica [2].

1.3 Viscosidad Cinemática

La razón entre la viscosidad dinámica y la densidad del mismo fluido, se conoce como viscosidad cinemática [5]:

5 =6₇ (1.3)

Y sus unidades son los 38

9 . Algunas de sus unidades para expresarla son el stoke, m2_{/s, mm}2_{/s y el centistoke y las equivalencias correspondientes entre ellas}

son:

Tabla 1.2 Equivalencias entre unidades de viscosidad cinemática

1 stoke 1 !_" 100!!_" 1:10;<!_"

1 cstoke _0.01 !

" 1!!" 1:10;=!"

6

mayor densidad, de aquí se puede observar porque los fabricantes de aceites se interesan más por la viscosidad cinemática, ya que a menor viscosidad cinemática el aceite es más fácil de bombear. Una designación más conveniente para la viscosidad cinemática sería la de “relación de viscosidad” y se le llama también a veces “viscosidad específica”, “difusividad viscosa” o “difusividad de cantidad de movimiento” [7]. A mayor densidad, menor viscosidad cinemática y que tiene las dimensiones de (longitud) x (velocidad) como todas las difusividades [8].

Por lo tanto la viscosidad cinemática es una medida de la resistencia de los fluidos a fluir y al corte bajo fuerzas de gravedad. Aquí también, entre mas grandes sean las moléculas, mayor será la resistencia y por tanto, mayor la viscosidad cinemática.

Es común escuchar que los aceites son fluidos “gruesos”, así por ejemplo el agua es “delgada” porque tiene una viscosidad menor. Todos los fluidos reales tienen alguna resistencia al esfuerzo cortante y los fluidos que no son resistentes al esfuerzo cortante se les conocen como “fluido ideal” o “fluido no viscoso”.

Las unidades de la viscosidad han recorrido un arduo camino para unificarse, aún en la actualidad las unidades empleadas para medir su magnitud no están totalmente estandarizadas y dependen en gran parte de la región y del método con que se mida.

7

1.4 Número de Reynolds

La relación de Reynolds, o mejor conocida como el número de Reynolds (Re), es una cantidad adimensional que se usa para determinar si un flujo es

laminar o turbulento, es la relación de valores típicos de dos entidades físicas. Estas entidades en general son velocidades, fuerzas o energías. Desde el punto de vista de D’Alembert, se puede imaginar una partícula de fluido en movimiento como si estuviera en un estado de equilibrio dinámico bajo la influencia de una “fuerza” inercial (F = - ma), así como también de otras fuerzas reales debidas a la

viscosidad [2, 1, 7]. En un flujo se puede estimar la fuerza de inercia por medio de:

Fuerza de inercia ≈ “Presión dinámica” x Área (1.4)

Un valor típico de presión dinámica es el valor correspondiente a la velocidad de referencia; esto es: un valor típico de área es el cuadrado de la dimensión de longitud _l2_{. Empleando dichas estimaciones se tiene que:}

Fuerza de inercia ≈ 2 2

V l

ρ (1.5)

El símbolo ≈ significa que se estima el valor típico de una cantidad o que se estima su orden de magnitud. La relación no es tan fuerte como una proporcionalidad, que se indica con el símbolo ∝. Los factores multiplicativos tales como el 2, generalmente son irrelevantes para el análisis y se pueden omitir de la

estimación.

Una estimación de la fuerza cortante viscosa es:

Fuerza cortante ≈ Esfuerzo cortante x Área (1.6)

El esfuerzo cortante esta dado por:

     

∂ ∂ =

y u

µ

8

La derivada parcial de la velocidad con respecto a la componente perpendicular al flujo >

> , puede estimarse al suponer que la velocidad cambia de cero al valor típico V a lo largo de una longitud relevante l[2].

l l V 0 V y u y

u _≈ − ₌

∆ ∆ ≈ ∂

∂ _(1.8)

Al usar esta estimación de la derivada, se obtiene una estimación de la fuerza viscosa: l l l V V a cos vis

Fuerza  2 =µ

     µ

≈ (1.9)

Así se puede formar la relación [1, 2, 3]:

friccional Energía cinética Energía Re V V V a cos vis Fuerza inercia de

Fuerza 2 2

= = µ ρ = µ ρ ≈ l l l (1.10)

El número de Reynolds representa los efectos de la viscosidad sobre el flujo, los flujos con valores grandes de Re

(

)

Si se considera una esfera que cae en un fluido de viscosidad µ a bajo número de Reynolds (Re<1):

1 VD

Re ≤

µ ρ

= (1.11)

para D el diámetro de la esfera. En este valor de Re, la ley de Stokes (que se

9

1.5 Ecuaciones principales

1.5.1 La ecuación de continuidad

La ecuación de continuidad es una expresión del principio de conservación de masa, relaciona el cambio de la masa dentro de un volumen de control, esto es la razón de masa que entra y sale del mismo.

En la figura 1.3, se tiene un elemento infinitesimal, es un volumen de control pequeño dentro del cual se tiene un flujo. El flujo de masa esta dado por: m& =ρvA

Donde:

m: razón del flujo de masa

ρ: densidad

v: velocidad

A:área por la que pasa el flujo

Se muestra el plano xy que tiene una profundidad dz. Se asume que el flujo

solo está en el plano xy, así que no se tiene flujo en la dirección z. Puesto que la

masa podría estar cambiando dentro del elemento, la masa que fluye dentro del

Figura 1.3 Volumen de control infinitesimal [9].

udxdy ρ

x y

( )

x u

u 

  

 

∂ ρ ∂ + ρ

( )

y v

v _

  

 

∂ ρ ∂ + ρ

vdxdz ρ

dy

10

elemento menos la que fluye fuera del elemento debe ser igual al cambio en cantidad de masa dentro del elemento. Esto se expresa como:

( )

( )

₍

₎

t dxdz dy y v v dydz dx x u u vdxdz udydz ∂ ρ ∂ =               ∂ ρ ∂ + ρ +       ∂ ρ ∂ + ρ − ρ +

ρ (1.12)

Donde:

(

)

∂

∂ρ _{es la razón con respecto al tiempo del incremento de}

masa.

Considerando que el volumen de control está fijo y simplificando la ecuación (1.12), se tiene:

( ) ( )

∂ _(1.13)

Haciendo las derivadas indicadas y añadiendo la expresión para la dirección en z:

0 z w y v x u z w y v x u

t =

    ∂ ∂ + ∂ ∂ + ∂ ∂ ρ + ∂ ρ ∂ + ∂ ρ ∂ + ∂ ρ ∂ + ∂ ρ

∂ _(1.14)

A los primeros cuatro términos se les conoce como la derivada material o substancial y es la razón de cambio con respecto al tiempo de cualquier propiedad de un elemento de fluido que se mueve con el flujo, y en este caso, esa propiedad es la densidad; por lo que:

0 z w y v x u Dt D ₌       ∂ ∂ + ∂ ∂ + ∂ ∂ ρ +

ρ _(1.15)

La ecuación (1.15) es la forma más general de la ecuación de continuidad en coordenadas rectangulares; usando el operador vectorial gradiente:

11

Así, la ecuación de continuidad expresada en forma vectorial toma la forma:

0 V Dt D = • ∇ ρ + ρ (1.17)

Donde el vector velocidad es: V = u i + v j + w k. A la cantidad escalar ∇•V

se le llama la divergencia del vector velocidad y mide la diferencia entre el flujo entrante y el flujo saliente de un campo vectorial. Si la divergencia es positiva se está ante una fuente y si es negativa se tiene un sumidero [9].

Para un flujo incompresible, y considerando que se analiza una lámina del flujo solamente, la densidad permanece constante mientras viaja a lo largo del campo de flujo, esto es:

0 z w y v x u t Dt D = ∂ ρ ∂ + ∂ ρ ∂ + ∂ ρ ∂ + ∂ ρ ∂ =

ρ _(1.18)

Por lo que si la densidad es constante como sucede generalmente, cada término en la ecuación (1.15) es cero, así:

0 z w y v x u = ∂ ∂ + ∂ ∂ + ∂ ∂ _ó 0 V= •

∇ (1.19)

La ecuación de continuidad contiene las tres componentes de la velocidad de un flujo incompresible. Si se tiene un flujo en el cual el campo de velocidades y el campo de presiones son de interés, la ecuación diferencial de momento proporciona tres ecuaciones más. Las cuatro incógnitas serían u, v, w y p usando un sistema de coordenadas rectangular. Las cuatro ecuaciones proporcionan el equilibrio algebraico necesario con las cuatro incógnitas.

1.5.2 Las ecuaciones de Navier –Stokes

12

g V p

Dt

DV =−∇ +µ∇2 +ρ

ρ (1.20)

Las ecuaciones de Navier-Stokes pueden ser formuladas en varias formas como vectorial y tensorial, en este caso se muestra la forma vectorial por conveniencia al desarrollar la Ley de Stokes.

1.6 Modelos Newtonianos y No Newtonianos

La viscosidad de los aceites está descrita por varios modelos, a decir en general, los modelos newtonianos y los modelos no newtonianos.

1.6.1 El modelo newtoniano

Descrito anteriormente, el modelo newtoniano considera que a cualquier esfuerzo ejercido en el fluido, éste se deforma continuamente, ejemplos de fluidos newtonianos son el agua, el aire y casi todos los gases se pueden considerar newtonianos y muchos aceites también.

1.6.2 El modelo no newtoniano

Algunos fluidos no cumplen con la ley de Newton de la viscosidad y se les analiza desde otra perspectiva, por ejemplo: la pasta de dientes, el yeso o el cemento frescos ya revueltos en agua, en experimentos didácticos es común usar fécula de maíz revuelta en agua para obtener un fluido no newtoniano. La contraparte del fluido newtoniano, para los fluidos no newtonianos se le llama: ley de potencias o modelo de Oscar de Waele, valioso en el apoyo del conocimiento de los esfuerzos cortantes para fluidos no newtonianos llamados pseudoplasticos.

1.7 Índice de Viscosidad (IV)

13

nafténicos1 son más sensibles a los cambios que los aceites basados en parafinas1. Ciertos lubricantes sintéticos son menos sensibles que los aceites parafínicos. Para clasificar esta propiedad de los aceites lubricantes, la Sociedad Americana de Pruebas y Materiales (ASTM por sus siglas en inglés) ha creado un método empírico para proporcionar un número, llamado Índice de Viscosidad (IV) que corresponde a la cantidad de cambio de viscosidad para un aceite dado, comparándolo con dos aceites de referencia que tienen el mayor y el menor índice de viscosidad en la fecha que la escala fue introducida por primera vez (1929). A un aceite parafínico estándar le fue dado un IV de 100 y a un aceite nafténico estándar un IV de 0. Han sido preparadas tablas que muestran la relación entre las viscosidades a 40 y 100º C. Este método ha sido actualizado y revisado muchas ocasiones para incluir IV mayores a 100 [10].

La incorporación de polímeros incrementa los IV basados en el petróleo. SAE no ha usado el IV desde la década de los 60’s porque el término es técnicamente obsoleto, sin embargo la API (Association of Petroleum Engineers) tiene un sistema de clasificación de aceites, basado en el IV como uno de tantos parámetros, para proporcionar una guía de sustitución de aceites con las mismas propiedades químicas y físicas del aceite buscado [10].

Lo valioso del índice de viscosidad es que: un IV bajo significa un cambio de viscosidad relativamente grande con la temperatura y un alto IV denota un cambio pequeño en la viscosidad a un cambio de temperatura. Por lo tanto el índice de viscosidad de un aceite es importante en aplicaciones donde un apreciable cambio en la temperatura del aceite lubricante podría afectar la ignición

1

14

o las características de operación del equipo. Ejemplos típicos de aplicación son la maquinaria a bordo de barcos y equipo de emergencia, así como los bruscos cambios de temperatura, presión y humedad en las diferentes etapas del vuelo de un avión [10].

La figura 1.4 muestra curvas típicas de aceites con diversos índices de viscosidad

Figura 1.4 Curvas típicas de aceites con varios Índices de Viscosidad (IV) [10].

La referencia [10] muestra en su apéndice D un gráfico de la viscosidad cinemática contra la temperatura diversos fluidos.

El índice de viscosidad (IV) se calcula haciendo experimentos con los fluidos a 40 y 100 oC, teniendo como referencia a fluidos de los que se conoce su IV con respecto a los cambios de temperatura. El detalle sobre este tipo de pruebas se encuentra en la norma ASTM (American Society for Testing and

1.0 x 10-6

-20 _{0 20 40} 60 ₁₀₀ 120

Temperatura oC

140 80

2.0 x 10-6 5.0 x 10-6 1.0 x 10-4 1.0 x 10-2

3.0 x 10-5 1.0 x 10-3

1.0 x 10-5

IV = 100

IV = 50 IV = 140

Viscosidad cinemática

15

Materials) D2270-86: “Standard Practice for Calculating Viscosity Index from Kinematic Viscosity at 40 and 100 oC”.

La misma referencia [10], muestra la gráfica de curvas para aceites con índices de viscosidad de 50, 100, 150, 200, 250 y 300.

El índice de viscosidad IV se calcula midiendo la viscosidad cinemática de la muestra fluido de prueba a 40ºC y a 100ºC y relacionando los resultados con dos fluidos de referencia con valores de IV de 0 y de 100.

La siguiente expresión, llamada de Deanny-Davis, se usa para calcular los índices de viscosidad IV a 100ºF para muestras de fluido con índices de viscosidad IV iguales o menores a 100 [10].

@ =

× 100

Donde:

U: SUS del fluido a 40ºC (100ºF aproximadamente)

L: Viscosidad cinemática de un fluido previamente probado a 40ºC, que tiene un índice de viscosidad IV de cero y que a 100ºC tiene la misma viscosidad que el fluido de prueba.

H: Viscosidad cinemática de un fluido previamente probado a 40ºC, que tiene un índice de viscosidad IV de 100 y que a 100ºC tiene la misma viscosidad que el fluido de prueba.

Los valores de L y H se encuentran en una tabla del estándar ASTM D 2270, para aceites con viscosidades cinemáticas entre 2.0 mm2_{/s y 70.0 mm}2_{/s a}

100 o_{C. Este rango comprende la mayor parte de los aceites prácticos que se}

16

Tabla 1.3 Estabilidad de los aceites en función del índice de viscosidad.

IV=0 No estable

IV menor que 75 Poco estable

IV entre 75 y 200 Muy estable

1.8 Nomenclatura y clasificación de los aceites

Es necesario aclarar que la nomenclatura de los aceites que ha sido estandarizada por la SAE, ASTM y API en occidente, no son las únicas organizaciones que realizan la estandarización, ya que existe además la ISO y la contraparte rusa (asociación de certificación) basada en diferentes características de los aceites y fluidos usados en aviación y en la industria pesada [10].

1.8.1 Clasificación de los aceites de motor

Como la selección del grado de viscosidad apropiado es importante, varios sistemas de clasificación de la viscosidad han sido estudiados a través de los años. En occidente la clasificación de la viscosidad para aceites de motor ha sido desarrollada por la Sociedad de Ingenieros Automotrices (SAE por sus siglas en ingles) desde 1911. Este sistema de clasificación, después de muchas revisiones y actualizaciones, sigue siendo usado en occidente [10].

Las normas que a continuación se enlistan, corresponden a la clasificación SAE y sus métodos de prueba ASTM:

SAE J300 Clasificación de viscosidad de aceite para motor

17

ASTM D445 Método estándar de prueba para viscosidad cinemática de líquidos transparentes y opacos.

ASTM D446 Especificaciones estándar e instrucciones de operación para viscosímetros cinemáticos capilares de vidrio.

Los grados SAE desde 0W hasta 25W, donde la W se refiere al invierno (por la inicial W de Winter en ingles), tienen una viscosidad especificada a bajas temperaturas (-5 a –35 o_{C), para asegurar un encendido o arranque fácil a bajas}

temperaturas, y una viscosidad mínima requerida a 100 oC para asegurar una lubricación satisfactoria a la temperatura final de operación. Los grados SAE 20 a 60 solo tienen un limitado espectro a 100 oC ya que estos grados no se diseñaron para trabajo a bajas temperaturas. Para aplicaciones marinas se usan los aceites monogrado SAE 30 y SAE 40 por sus condiciones tan estables de operación a temperatura del cuarto de máquinas [10].

Por otro lado, los aceites automotores son normalmente formulados con sustancias que mejoran el índice de viscosidad (modificadores del IV) para proporcionar un rendimiento multigrado. El uso de estos materiales (polímeros), hace posible alcanzar tanto los requisitos de baja temperatura como los grados W, así como los requerimientos de altas temperaturas.

Las viscosidades típicas para un aceite de motor multigrado 15W – 40 son:

Tabla 1.4 Viscosidades típicas para un aceite de motor multigrado 15W – 40 [10].

Viscosidad a –15o_{C, cP} (2) ₃₀₀₀

Viscosidad a 40 oC, mm2/s (cSt) 105 Viscosidad a 100 o_{C, mm}2_{/s (cSt) 14}

Índice de viscosidad IV 135

18

En este ejemplo se puede observar que un alto índice de viscosidad IV da un cambio en la viscosidad relativamente pequeño con la temperatura, y como resultado del alto IV el aceite multigrado cumple con los requerimientos de baja temperatura 15W, así como, la característica requerida de alta temperatura indicada por el grado 40.

Muchos han sido los sistemas de clasificación usados en el pasado en diferentes partes del mundo. Ha sido muy difícil alcanzar un acuerdo en el número de grados diferentes de viscosidad que deben ser incluidos, los límites de viscosidad de estos grados y la temperatura a la cual deben ser especificados.

Hasta 1972 se acordó el sistema de clasificación de la viscosidad para lubricación industrial (ISO 3448).

Los aceites lubricantes industriales están sometidos a cambios amplios de temperatura y la maquinaria industrial como: cojinetes, sistemas de potencia fluídica, accionadores de engranaje, maquinas eléctricas, ventiladores, sopladores, turbocompresores, turbosopladores y todo equipo con partes en movimiento deben ser lubricados con aceites que faciliten ese amplio intervalo de viscosidades necesarias. Las normas ISO definen un conjunto de 20 grados de viscosidad [10].

1.9 Tipos de modificadores de la Viscosidad

19

como los chocolates, la margarina, los dulces con centro líquido, chicles (en este caso plastificadores), etc.

La estructura química y el tamaño de las moléculas son los elementos más importantes de la estructura molecular de los modificadores de la viscosidad.

Existen muchos tipos de modificadores de la viscosidad dependiendo de la aplicación, las variaciones de la estructura química son las responsables de las propiedades de los modificadores de la viscosidad, tales como la habilidad de endurecimiento, su dependencia de la temperatura, estabilidad frente a la oxidación y características de ahorro de combustible.

Algunos ejemplos de modificadores de la viscosidad de los aceites son: Polyisobutileno (PIB o polibutano), Polimetacrilato (PMA), Polyisopreno hidrogenado radial (STAR), etc. Para más información se puede consultar el sitio web: http://www.lubrizol.com/.

Los aceites usados en la aviación comercial están clasificados con símbolos tales como 80, 100, 120, y 140, los cuales se aproximan a los segundos Saybolt universales (SSU) de viscosidad a 210ºF (99ºF).

20

Capítulo 2 Viscosimetría

Han existido a lo largo de la historia muchos métodos para medir la viscosidad, ya sea midiendo el tiempo que tarda un volumen determinado en pasar por un conducto de diámetro reducido, o ya sea contando las gotas que caen de un cuentagotas por unidad de tiempo, etc. Actualmente, existen viscosímetros industriales muy exactos que aprovechan todas las características viscosas.

Existen muchos tipos de viscosímetros destacándose dos principales grupos: los viscosímetros absolutos y los viscosímetros relativos, la diferencia es que los viscosímetros absolutos son aquellos que su medición de la viscosidad está basada directamente en la ley de viscosidad de Newton. A continuación se describirán brevemente algunos de los tipos de viscosímetros.

2.1 Viscosímetros capilares

Los viscosímetros capilares miden la razón de flujo de un volumen fijo de fluido a través de un pequeño orificio a temperatura controlada. Algunos tipos de viscosímetros capilares y su modo de operación son:

a) Viscosímetro capilar de cristal. El fluido pasa a través de un orificio de diámetro fijo, bajo la influencia de la gravedad. Las viscosidades cinemáticas de los fluidos automotrices se miden con este viscosímetro.

b) Viscosímetro capilar de alta presión. Este viscosímetro funciona aplicando presión mediante un gas a un volumen fijo de fluido al través de un tubo capilar de diámetro pequeño. La razón de corte puede variar hasta 106 _s-1_{. Esta técnica se usa comúnmente para simular las}

21

viscosímetros estándar para la medición de estas viscosidades operacionales descritas en los documentos de la ASTM.

El viscosímetro Saybolt, y en general los viscosímetros capilares, tienen dos desventajas principales: una es el incremento de la incertidumbre a través de la escala de viscosidad y la otra es cuando se calibra el instrumento y se tiene que usar agua doblemente destilada a 20 o_{C para saber que tenemos la viscosidad}

cinemática de 1.0034 mm2/s.

Por eso en este estudio se decide desarrollar una metodología basada en un viscosímetro absoluto de esfera descendente. Existen tres tipos de viscosímetros absolutos: Los de esfera descendente, los rotatorios (cilíndrico, cónico y esférico) y los de plano inclinado.

El tamaño de las esferas puede cambiar, las ecuaciones propuestas para hacer el cálculo de la viscosidad son muy sensibles al tamaño de la esfera, por lo que se puede cubrir un amplio espectro de viscosidades de fluidos de uso general siempre y cuando sean lo suficientemente diáfanos.

2.2 Viscosímetros rotatorios o de cilindros concéntricos

22

Bearing Simulator TBS) y Viscosímetro Ravenfield de conector delgado (tapered Plug viscometer).

La operación y características de todos estos viscosímetros, esta descrita ampliamente en los documentos de la ASTM [10,11].

2.3 Viscosímetros de esfera

Existen varios tipos de viscosímetros que usan esferas en su operación, los de esfera descendente, los de esfera rodante [12] y los de esfera rotatoria [11].

2.3.1 Viscosímetro de esfera rodante

El viscosímetro de esfera rodante consta de un cilindro transparente de diámetro D, ya sea de vidrio u otro material diáfano, en que se le ha introducido una esfera de metal, ya sea, acero, aluminio, cobre, etc. de diámetro “d”, en donde D > d por una muy pequeña cantidad.

Se introduce en el tubo el líquido al que se le va a medir la viscosidad y se tapa.

La esfera rueda a través del tubo debido a que se ha inclinado el tubo un ángulo “α”, después de que la esfera alcanza una velocidad constante, llamada también velocidad terminal, se mide el tiempo que tarda en pasar por dos señalamientos que están a una distancia previamente establecida. Debido a las diferentes densidades de los líquidos y a la temperatura a la que se necesita medir la viscosidad, la distancia de medición varía [12].

La viscosidad se mide mediante la relación:

Ct =

µ (2.1)

23

combinación de las características dinámicas del sistema y se encuentra siguiendo el siguiente desarrollo [12]:

Se propone una expresión lineal del tipo:

= − ∆ (2.2)

Donde:

µ: Viscosidad

ρe: Densidad de la esfera

ρ: Densidad del líquido bajo estudio

∆t: Tiempo en que la esfera pasa entre dos señalamientos en el tubo de vidrio

Kcal: Constante llamada “de calibración del aparato”

Entonces se propone una esfera lisa de radio r y densidad “ρe”, la cual

rueda en un plano inclinado, con ángulo de inclinación “α”. Todo el sistema está inmerso en un fluido de densidad “ρe“ y con viscosidad “µ”. Se está buscando una

expresión para la viscosidad del fluido.

De aquí se hace un diagrama de cuerpo libre, en donde se describen todas las fuerzas que actúan en el sistema, obteniéndose una expresión para la fuerza viscosa que el fluido ejerce sobre la esfera, esto es:

Figura 2.1 Diagrama de cuerpo libre de una esfera que cae.

w B

24

= − + − (2.3)

Para relacionar la fuerza con la viscosidad se propone una solución (parecida a la ley de Stokes que se verá más adelante), sea:

F=K1µrv (2.4)

Donde ”Mvis” es el momento viscoso que produce el fluido sobre la esfera, y está dada por:

! = " # $% (2.5)

Siendo “ωrod” la velocidad angular del rodamiento de la esfera.

Considerando que _{v = #} , se obtiene la expresión:

' v + " v = πr − (2.6)

Observando la ecuación (2.6), se puede ver que ya se tienen juntas en una sola expresión la velocidad y la viscosidad. Despejando:

(

) (

)

x K K

g r

e − ∆

   

 

∆ +

= π α ρ ρ

µ

2 1

2

sen 3

4 _(2.7)

La expresión del lado derecho de la igualdad que está dentro de los paréntesis, se le llama constante del aparato y las constantes “K1“y “K2“ dependen de algunas de las características del sistema, como son: la razón de los diámetros del tubo y de la esfera y de la relación de Reynolds.

Este modelo teórico, es aplicable, siempre y cuando no se cambie el ángulo de inclinación “α”, ni el diámetro de la esfera para usar la expresión (2.2).

25

recordar que el número de Reynolds debe ser pequeño, menor a uno, para que se pueda aplicar este modelo.

2.3.2 Viscosímetro de esfera rotatoria

El viscosímetro de esfera rotatoria es usado principalmente en sistemas donde el fluido de trabajo es un fluido viscoelástico. Un fluido viscoelástico se define como un fluido que tiene propiedades intermedias entre un sólido perfectamente elástico y un fluido perfectamente viscoso. Un sólido perfectamente elástico se puede explicar con el ejemplo de la muelles, en la que una muelle, como la de los automóviles, se deforma con una fuerza “F”, definida como:

x G F = ∆ ∆

Donde G es la constante de elasticidad del muelle.

Y un fluido perfectamente viscoso es aquel que sigue la ley de viscosidad de Newton [11].

Las relaciones aquí descritas son parecidas al siguiente dispositivo mecánico [11, 13]:

Figura 2.2 Sistema muelle - amortiguador

26

medio fluido muy viscoso. Para mover este sistema se tiene que vencer la fuerza ejercida por el muelle más el amortiguador.

Entonces el viscosímetro de esfera rotatoria se usa comúnmente para medir características de los fluidos viscoelásticos, incluida la viscosidad.

El principio de funcionamiento se basa en una expresión del par sobre la esfera producido por el fluido, cuando va girando sobre su eje. Al igual que el viscosímetro de bola descendente, el movimiento rotatorio de la esfera es axisimétrico, y no depende de ninguna manera de la coordenada azimutal “ϕ”

(ángulo que corre con el ecuador de la esfera). Y si se considera que la esfera gira a una velocidad angular pequeña, los términos de inercia en las ecuaciones de movimiento también se pueden despreciar. El resultado de experimentar con un viscosímetro de bola rotatoria es la elaboración de curvas de viscosidad contra rapidez de deformación. El fabricante debe proveer tablas de factores de escala correspondiente al rotor y velocidad usados. Este factor de escala se multiplica por el valor leído en el aparato y se obtiene la viscosidad en centipoises “cp”, unidad descrita más adelante.

2.3.3 Viscosímetro de esfera descendente

El viscosímetro de esfera descendente es especial para fluidos altamente viscosos y transparentes en donde se pueda medir visualmente la caída de la esfera, es especialmente importante que se pueda medir la velocidad por dos razones:

a) Es el parámetro que falta en la ecuación de balance de fuerzas de la viscosidad.

27

El principio básico del viscosímetro de esfera descendente se muestra en la figura 2.3.

Figura 2.3 Dispositivo para medir el tiempo de caída de una esfera en un fluido con alta viscosidad

y diáfano.

El esquema de la figura (2.3) muestra el arreglo básico óptico para medir el tiempo transcurrido entre dos posiciones de la esfera.

Si los fluidos son lo suficientemente diáfanos se puede implementar un dispositivo de videograbación y se mide el desplazamiento de la esfera calculando la distancia entre fotogramas teniendo una escala como referencia.

Los tipos de fluidos que se pueden medir con este dispositivo son los aceites y fluidos con viscosidades tales que permitan a la esfera caer lentamente y puedan ser videograbados por el experimentador; basado en los aceites se tiene un rango de viscosidad dinámica que va desde 0.1 [Pa⋅s], que es aproximadamente la viscosidad de un aceite SAE 10 a 20 o_{C, hasta 20 [Pa⋅s] que}

es la viscosidad de un aceite SAE 140 a 5 o_{C, haciendo notar que el rango de}

temperatura es importante para la medición con este tipo de dispositivo, ya que si la temperatura es elevada la viscosidad disminuye y el número de Reynolds se elevaría, impidiendo el cálculo de la viscosidad por medio de las ecuaciones de Stokes.

g

Fluido viscoso y transparente

28

2.4 Aplicaciones del Viscosímetro de esfera descendente

Las áreas de aplicación de un viscosímetro de esfera descendente son numerosas, se le usa principalmente en:

a) La industria química (Polímeros, solventes y tintas), sedimentación de partículas en fluidos Newtonianos.

b) La industria farmacéutica (materias primas, glicerina)

c) Industria alimentaria (gelatinas, soluciones azucaradas), en particular el método de esfera descendente se puede usar para medir la viscosidad del citoplasma en las células. Una vez homogeneizada la célula, se le pueden introducir microesferas y con las ecuaciones de Stokes u Oseen se puede medir su viscosidad.

d) Industria petrolera (líquidos hidrocarburos y aceites)

e) Educación superior. Al tener un bajo precio y una teoría sencilla se puede mostrar en los laboratorios.

f) Estudios sobre la suspensión de contaminantes.

29

2.5 Viscosímetro Saybolt

Existen muchos tipos de viscosímetros y también diferentes técnicas aparte de las ya mencionadas, por ejemplo: el tiempo de caída de una bola de acero, como ya se ha visto, o una aguja, la resistencia a la vibración usando una sonda, y la aplicación de presión al flujo de un fluido midiendo la fuerza.

Un ejemplo de medición con otro dispositivo es el viscosímetro Saybolt que se ilustra en la figura 2.4.

Figura 2.4. Esquema del viscosímetro Saybolt [14].

El viscosímetro Saybolt es un instrumento estándar en la aviación comercial para probar productos y lubricantes derivados del petróleo, las pruebas generalmente se hacen a 38, 54 y 99º C [14].

Este instrumento tiene un tubo del cual escurre una cantidad específica de fluido ha sido mantenido a una temperatura fija por un baño térmico. El tiempo requerido en segundos para que exactamente 60 ml del aceite escurran a través del orificio de salida cuidadosamente calibrado se registra como segundos universales Saybolt (SUS) de viscosidad.

El método de los segundos Saybolt para probar la viscosidad se divide en dos: los segundos universales Saybolt y los segundos Saybolt Furol, la palabra Furol es una palabra compuesta que significa “Fuel and road oil”, es decir, combustible y aceite para vehículos de carretera, y es la medida que se usa en las

Fluido de

trabajo Baño

térmico

30

pruebas de los automóviles y los aviones [14], el viscosímetro de segundos universales Saybolt se usa para otros aceites y lubricantes industriales.

El orificio para medir los SSU de viscosidad cinemática es de 1/16” de diámetro interior y el de los segundos Saybolt Furol SSF es de 1/8” de diámetro interior.

Los aceites multigrado, usuales para automóviles, usan la nomenclatura de la W, como por ejemplo: 10W-50 que significan la viscosidad del aceite a diferentes temperaturas, los números como en el ejemplo son 10 y 50, y se refieren a los segundos Saybolt, por ejemplo 5W, 10W y 20W determinan la viscosidad del aceite en segundos Saybolt a 0ºF (-18º C), es decir en frio, mientras que los grados 20, 30, 40 y 50 están determinados por su viscosidad a 212ºF (100ºC, es decir: en caliente). Los valores reportados en segundos Saybolt Universales son 10 veces más grandes que los reportados por los segundos Saybolt Furol. El aceite multigrado 10W 50 se comporta como SAE 10 a 0 oF y como SAE 50 a 212 oF.

El método de probar la viscosidad en segundos universales Saybolt esta descrito en la norma ASTM D88 [10].

La norma ASTM D88 recomienda que la viscosidad sea reportada en mm2_{/s, en la referencia [10] se puede encontrar la gráfica en donde se muestra la}

conversión de segundos Saybolt y los mm2_{/s o cSt para un fluido a 100ºF (37.8ºC).}

En la gráfica, si _* >= 75 mm2/s, la curva se hace lineal, expresándose mediante la ecuación: SUS = 4.632 _*. Si el fluido esta a 210ºF (98.9ºC), la ecuación para la sección recta de la curva es: SUS = 4.664 _*.

31

, = 6.061 × 1023 _{+ 0.994}

Donde “t” es la temperatura en grados Fahrenheit

2.6 Flujo a bajos número de Reynolds

En el flujo de un fluido a bajos número de Reynolds, los términos convectivos inerciales (aceleración convectiva) en las ecuaciones de Navier– Stokes carecen relativamente de importancia comparados con las fuerzas viscosas; las características del flujo las determina el balance entre las fuerzas viscosas y los gradientes de presión en el seno del fluido, así que la densidad no está involucrada en ninguna de la expresiones para el arrastre, la velocidad, etc.

Una característica interesante de los flujos a bajos números de Reynolds es que cualquier conato de turbulencia es rápidamente reprimido por las fuerzas viscosas.

Existen varios tipos de flujos a bajos regímenes del número de Reynolds como el fluido confinado entre un cilindro y una pared o el fluido altamente viscoso entre dos placas paralelas, el caso que se estudiará aquí es el flujo de Stokes, que se refiere al flujo alrededor de una esfera que se mueve dentro de un fluido muy viscoso; la acreditación del bajo número de Reynolds se hace calculando el número al final de los resultados.

Partiendo de las ecuaciones de Navier – Stokes [15, 4, 3]:

(

)

(

) (

)

t

V + ⋅∇ = − 1∇ + ′+ ∇∇⋅ + ∇2

∂

∂ _{λ ν ν}

ρ (2.8)

Donde _{* = /} , ₇8 _{= 7/} . “_*” es el coeficiente de viscosidad cinemática, y

al parámetro “λ” se le conoce como el segundo coeficiente de viscosidad, la relación entre las dos es: