2
2 2 1 1 2
(T cos T cos ) x t
2
2 2 2 1 1 1 2
(T tg sen T tg sen ) x t
2
0 ( 2 1) 2
T tg tg
t
ONDAS
ESTACIONARIAS
Escobar, Margarita del Rosario Padulo, Ricardo Javier
Laboratorio 2, Departamento de Física, F.C.E.y N., Universidad de Buenos Aires.
Turno: Sábados de 8 a 14 hs.
RESUMEN
El presente trabajo tuvo como fin el estudio de ondas transversales en una cuerda de nylon y longitudinales en un tubo de Kundt. Para ambos casos, se halló la velocidad de propagación, caracterizando para ello la longitud de la onda, la localización de nodos y frecuencias fundamentales. Para la velocidad del sonido en el tubo, se obtuvieron valores de (312 ± 2) m/s , (359 ± 4)m/s ,(316 ± 3)m/s utilizando tres métodos distintos.
También se midió la densidad en la
cuerda, observando el
comportamiento de la onda en el medio para luego comparar el resultado con la densidad conocida.
I. INTRODUCCIÓN
Con el fin de presentar un marco teórico que explique los fenómenos
observados, se comenzará
deduciendo la ecuación diferencial en derivadas parciales que debe cumplir una perturbación transversal en un medio, como ser el de una cuerda.
Se considera un segmento de cuerda ideal, es decir inextensible de densidad ρ homogénea.
Al aplicarse una tensión T0 en ambos extremos, se desea conocer la condición que debe cumplir una onda que se propaga transversalmente a lo largo de la cuerda.
Sea φ(x,t) una perturbación
transversal, cuya magnitud indica el desplazamiento en el eje y, a lo largo de una cuerda sometida a una tensión T0, (ver figura 1.1.1).
Figura 1.1.1. Perturbación transversal en una cuerda.
Por la segunda Ley de Newton se cumple la expresión 1.1.1.
(1.1.1)
Luego, si se reescriben las componentes x de T1 y T2, resulta la igualdad (1.1.2).
(1.1.2)
Pero T1senθ1 y T2senθ2 son iguales a T0, la tensión aplicada a la cuerda, que puede sacarse de factor
común. Luego, multiplicando y
dividiendo a la izquierda por δx, resulta la expresión 1.1.3.
0 0 2
0 2
( x x x x x)
x x
T
x t
2 2
0
2 2
T
x t
Pero tgθ1 y tgθ2 son iguales a las derivadas parciales de la función φ(x,t) respecto de x por lo tanto, simplificando los diferenciales de x a ambos lados, resulta la expresión 2.1.4.
(1.1.4)
El cociente incremental de la derivada parcial de φ(x,t) respecto de x es la derivada segunda de la función desplazamiento respecto de x. Por lo cual resulta la ecuación 2.1.5 que se denomina ecuación de onda.
(1.1.5)
Las relaciones entre longitud de onda, frecuencia, numero de onda, y velocidad de propagación serán introducidas en secciones posterio-res cuando sea preciso utilizarlas.
II. DESARROLLO DE LAS
EXPERIENCIAS Y DISCUSIÓN DE LOS RESULTADOS
2.1 Perturbaciones transversa-les en una cuerda
En la siguiente sección se analiza
el comportamiento del sistema
formado por una cuerda de longitud y densidad conocidas, sometida a una
tensión dada, estudiándose su
evolución al ser perturbada por un dispositivo mecánico de vibración.
En todos los casos se considerará que el rozamiento del aire es despreciable y la densidad de la cuerda no varía con la tensión, es
decir, que su deformación es
completamente elástica.
Se observarán las frecuencias de sus modos normales así como la
posición de los nodos,
determinándose finalmente la
velocidad de propagación de la perturbación a lo largo de la cuerda.
2.1.1 Disposición experimental
Con el objetivo de observar las frecuencias de los modos normales y la posición de los nodos se procedió a fijar un extremo de la cuerda al vibrador mecánico (figura 2.1.1, A) pasando la cuerda por una polea (figura 2.1.1, B) y sujetándose el otro extremo a un platillo con el fin de colocar pesas y variar la tensión en la cuerda.
Figura 2.1.1. Disposición experimental. A: Vibrador mecánico, B: Polea, C: Panel de
observación.
2.1.2 Resultados y discusión
Las densidades de ambas
cuerdas se determinaron efectuando el cociente entre la longitud total del hilo y su masa.
Para el caso de la primera cuerda la densidad resultó: ρ1= (160 ±
5)mg/m y para la segundaρ2=(355 ±
5)mg/m. A partir de las mediciones de las frecuencias de los modos normales y de la longitud de onda de cada modo se calculará nuevamente la densidad para ambas cuerdas para
luego compararlas con estas
magnitudes conocidas.
Los resultados de las frecuencias de los modos normales para la primera cuerda, sometida a tres tensiones diferentes se observan en el gráfico 2.1.1. Dichas frecuencias se graficaron en función del número de nodos intermedios, esto es, la cantidad de nodos que no están ubicados en los extremos. Por ejemplo, para el caso de la frecuencia del fundamental, con la cuerda fija en los extremos y un máximo en el
centro, la cantidad de nodos
intermedios es 0.
Gráfico 2.1.1. Distribución de frecuencias para la primera cuerda, sometida a tres
tensiones diferentes
Como puede observarse para el caso de las frecuencias la pendiente en los tres casos difiere, esto se debe a la relación entre la frecuencia y la velocidad de propagación en la
cuerda, que depende de la tensión y la densidad como se ha visto anteriormente.
Para cada una de las frecuencias fundamentales se midió la distancia desde un extremo fijo al primer nodo, el resultado para la primera cuerda con tres tensiones diferentes se observa en el gráfico 2.1.2.
Gráfico 2.1.2. Distribución de distancias al primer nodo para la primera cuerda, para tres tensiones diferentes
En este caso las magnitudes no son discernibles puesto que la posición de los nodos para cada frecuencia fundamental no depende de la tensión aplicada.
Luego de linealizar en los tres casos el período de la perturbación con respecto a la longitud de onda se
obtuvieron las velocidades
correspondientes a las diferentes
tensiones. Estos datos pueden
Gráfico 2.1.3. Regresión lineal para el calculo de la densidad
Como puede observarse, se
linealizó esta relación obteniéndose la constante de proporcionalidad que representa la densidad de la cuerda.
El resultado fue de ρ1 = (185 ±
3)mg cuyo intervalo de incerteza no se superpone con la densidad calculada a partir de la longitud y la masa pero dado los errores que
intervienen es razonable esta
discrepancia.
Para el caso de la segunda cuerda, la distribución de frecuencias se observa en el gráfico 2.1.4.
Gráfico 2.1.4. Distribución de frecuencias para la segunda cuerda, sometida a tres tensiones diferentes
Luego, para el caso de
las distancias hasta el primer nodo, los resultados se observan en el gráfico 2.1.5.
Gráfico 2.1.5. Distribución de distancias al primer nodo para la segunda cuerda,
sometida a tres tensiones diferentes
Al igual que en el caso anterior, se graficó la tensión en función de la
velocidad de propagación al
cuadrado, como se observa en el gráfico 2.1.7.
Gráfico 2.1.7. Regresión lineal para el cálculo de la densidad
En este caso, la densidad resultó
ρ2 = (373 ± 5)mg, al igual que en
1A n
n
2.2 Perturbaciones longitudi-nales de presión en un tubo
En esta sección se analiza la propagación y características de ondas longitudinales de presión en el interior de un tubo con aire a presión atmosférica, estudiándose los dos casos: tubo cerrado y tubo abierto1.
Respecto al marco teórico, no se estudiará la ecuación diferencial en
derivadas parciales que debe
satisfacer la perturbación de presión
puesto que se determinará la
velocidad utilizando sólo las
expresiones 2.2.1 y 2.2.3.
2.2.1 Disposición experimental
Para esta experiencia se montó el dispositivo de la figura 2.2.1.
4 8
2 3 1
5
7 6
1.Tubo 2.Micrófono 3.Pistón 4.Varilla 5.Regla 6.Osciloscopio 7.Gen. de func. 8. Parlante
Figura 2.2.1. Dispositivo experimental
El tubo posee una longitud de 90cm para el caso del tubo abierto y 89cm para el caso del tubo cerrado debido al émbolo de 1cm de espesor que lo sella en el segundo caso.
En el extremo izquierdo se colocó
un parlante, emisor de ondas
mecánicas de presión, al cual se le aplicó una tensión pico a pico máxima
1 De aquí en adelante nos referiremos con esta
denominación al caso del tubo abierto en un extremo y el otro cerrado por el parlante.
de 3V, la presión dentro del tubo fue medida a partir de un micrófono deslizable, despreciando los efectos que éste pudiera producir en la propagación de la onda.
2.2.2 Resultados y discusión
a) Tubo abierto
En primer lugar se observó la forma cualitativa de la distribución de presión a lo largo del tubo, en uno de los modos normales, observándose los nodos y las condiciones de contorno (extremo izquierdo presión máxima, extremo derecho, presión nula). Esto puede observarse en la figura 2.2.2.
Figura 2.2.2. Distribución cualitativa de presión para el tubo abierto
Se sabe que se cumple la relación de la expresión 2.2.1.
(2.2.1)
Donde λ1A es la longitud de onda
fundamental para el caso del tubo abierto y n, el número de armónico.
b n a n
T v
de onda n y se procedió a ajustar los datos con la ecuación 2.2.2.
(2.2.2)
El coeficiente a representa la longitud de onda fundamental en el tubo cerrado (λ1C) y b debería ser, por la teoría, igual a -1.
Los resultados de los parámetros linealización fueron de a = λ1C = (379
± 12)cm y b = (-1,2 ± 0,03).
Como puede observarse, la
magnitud λ1C representa cuatro veces
la longitud del tubo, ya que el modo
fundamental corresponde a un
mínimo de presión en un extremo y un máximo en otro, es decir la cuarta parte del periodo de la función seno.
De esta forma, la longitud del tubo
calculada a partir del modo
fundamental resulta de L= (95 ±
3)cm. Esto indica que la longitud efectiva del tubo es mayor que la real. Debido a la falta de precisión y escaso número de datos obtenidos no podemos establecer de qué
parámetros depende la longitud
efectiva, pero sí evidenciarla.
Los datos obtenidos así como la curva de ajuste se pueden observar en el grafico 2.2.1.
Gráfico 2.2.1. Longitud de onda en función del número de nodos y su curva de
ajuste
Por la teoría, se sabe que se cumple la relación de la expresión 2.2.3.
(2.2.3)
Donde T es el período de la perturbación, v su velocidad y λ su longitud de onda.
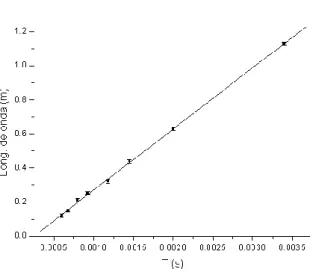
Utilizando esta relación se
procedió a linealizar los datos de longitud de onda en metros en función del período, para determinar el coeficiente de proporcionalidad que representa la velocidad del sonido en aire, la cual resultó ser de v=(312 ± 2) m/s.
Los datos obtenidos para esta medición y la recta de linealización se pueden observar en el gráfico 2.2.2.
Gráfico 2.2.2. Longitud de onda en función del número de nodos y su curva de
b) Tubo cerrado
Al igual que en el caso anterior, se estudió la distribución cualitativa de la presión a lo largo del tubo.
Luego, se midió la longitud de onda de la perturbación en función del número de onda n con el fin de determinar la longitud de onda fundamental para el tubo cerrado (λ1C).
Los resultados, junto con la curva de ajuste (utilizando la expresión 2.2.2), se observan en el gráfico 2.2.3.
Gráfico 2.2.3. Longitud de onda en función del número de nodos y su curva de
ajuste
Los parámetros de la curva fueron de a = λ1C = (114 ± 3)cm y b = (-0.93
± 0.03)
En este caso, la longitud de onda fundamental corresponde al doble de la longitud del tubo, puesto que la forma de onda corresponde a la mitad de período de una función seno, con dos mínimos a ambos extremos del tubo.
Luego, con las mediciones de la frecuencia de cada modo normal se graficó la longitud de onda en función del período (T), para verificar la
relación dada por la ecuación 2.2.2 y obtener v (velocidad del sonido en aire). El valor obtenido fue de v = (359 ± 4)m/s.
Los datos obtenidos para esta medición junto con la recta de linealización se observan en el gráfico 2.2.4.
Gráfico 2.2.4. Longitud de onda en función del número de nodos y su curva de
ajuste
c) Velocidad del sonido- pulso cuadrado
Finalmente se procedió a medir la velocidad del sonido tomando el tiempo de emisión y recepción de una perturbación discreta de presión en el
parlante. Este efecto se logró
presionando y relajando la membrana del emisor con una señal cuadrada que producía una variación discreta de presión en los flancos de subida y bajada de la señal.
sonido, con el fin de diferenciar los pulsos recibidos de los transmitidos. Para evitar errores de disparo se utilizó la señal de sincronización del generador de funciones como trigger
externo del osciloscopio.
La forma típica de la señal recibida puede observarse en la figura 2.2.4 donde se muestran la señal de ida y retorno para tres distancias diferentes (80,60 y 40 cm).
Figura 2.2.3. Señal de ida y retorno del pulso de presión para: A-80cm, B-60cm y
C-40cm. Escala temporal: 0,5mS/DIV
En la figura puede observarse cómo al disminuir la distancia, el pulso recibido llega más rápidamente debido a la menor distancia que debe recorrer.
Los datos obtenidos así como la recta de linealización se observan en el gráfico 2.2.5.
Gráfico 2.2.5. Distancia recorrida en función del tiempo y su recta de linealización
El resultado para la velocidad fue de v = (316 ± 3)m/s.
III. CONCLUSIONES
En el caso de la perturbación transversal en una cuerda se halló que las densidades calculadas a partir de la velocidad de propagación de las ondas en la cuerda eran ligeramente mayores que las medidas a partir del peso y la longitud de las mismas. Es posible que algún fenómeno físico no considerado, o
una mala aproximación esté
involucrado en estas discrepancias.
En el caso de las ondas
mecánicas en aire, se logró calcular a partir de diferentes métodos la velocidad del sonido observando que
las magnitudes variaban,
atribuyéndole la discrepancia a
incertezas del instrumental.
IV. BIBLIOGRAFIA
Resnick- Halliday, Física. Parte ,1
Juan G. Roederer, Mecánica
Elemental, Editorial Eudeba, 1975.
Capítulo
Spiegel y Murria, Estadistica, E. Mc Graw Hill, 2da edición, año 1995.
Sears y Zemansky, Fisica, E.
Aguilar, 1ª edicion, Cap. 35:
Corrientes alternas, págs. 762 a 765, año 1966.
Hecht, Optica, E. Addisson