Instituto Tecnológico y de Estudios Superiores de Monterrey Campus Monterrey
Monterrey, Nuevo León a
", en los sucesivo LA OBRA, en virtud de lo cual autorizo a el Instituto
Tecnológico y de Estudios Superiores de Monterrey (EL INSTITUTO) para que
efectúe la divulgación, publicación, comunicación pública, distribución y
reproducción, así como la digitalización de la misma, con fines académicos o
propios al objeto de EL INSTITUTO.
El Instituto se compromete a respetar en todo momento mi autoría y a
otorgarme el crédito correspondiente en todas las actividades mencionadas
anteriormente de la obra.
De la misma manera, desligo de toda responsabilidad a EL INSTITUTO
por cualquier violación a los derechos de autor y propiedad intelectual que
cometa el suscrito frente a terceros.
de 200
Lic. Arturo Azuara Flores:
Director de Asesoría Legal del Sistema
Por medio de la presente hago constar que soy autor y titular de la obra
c
Detección de Profundidad en Imágenes por Medio de su
Desenfoque y su Implementación en un DSP-Edición Única
Title Detección de Profundidad en Imágenes por Medio de su Desenfoque y su Implementación en un DSP-Edición Única
Authors Alberto Llerena Bejarano Affiliation ITESM-Campus Monterrey Issue Date 2005-12-01
Item type Tesis
Rights Open Access
Downloaded 19-Jan-2017 13:19:55
Instituto Tecnol´
ogico y de Estudios Superiores de
Monterrey
Campus Monterrey
Divisi´
on de Electr´
onica, Computaci´
on, Informaci´
on y
Comunicaciones
Programa de Graduados
Detecci´
on de Profundidad en im´
agenes por medio
de su Desenfoque y su implementaci´
on en un DSP
TESIS
Presentada como requisito parcial para obtener el grado acad´emico de
Maestro en Ciencias en Ingenier´ıa Electr´
onica
especialidad en
Telecomunicaciones
por
Ing. Alberto Llerena Bejarano
Instituto Tecnol´
ogico y de Estudios Superiores de
Monterrey
Campus Monterrey
Divisi´
on de Electr´
onica, Computaci´
on, Informaci´
on y
Comunicaciones
Programa de Graduados
Los miembros del comit´e de tesis recomendamos que la presente tesis de Alberto Llerena Bejarano sea aceptada como requisito parcial para obtener el grado acad´emico de Maestro en Ciencias en Ingenier´ıa Electr´onica, especialidad en:
Telecomunicaciones
Comit´
e de tesis:
Dr. Ram´on Mart´ın Rodr´ıguez Dagnino
Asesor de la tesis
Dr. Gabriel Campuzano Trevi˜no
Sinodal
Dr. Jos´e Ram´on Rodr´ıguez Cruz
Sinodal
Dr. David Garza Salazar
Director del Programa de Graduados
Detecci´
on de Profundidad en im´
agenes por medio
de su Desenfoque y su implementaci´
on en un DSP
por
Ing. Alberto Llerena Bejarano
Tesis
Presentada al Programa de Graduados en Electr´onica, Computaci´on, Informaci´on y Comunicaciones
como requisito parcial para obtener el grado acad´emico de
Maestro en Ciencias en Ingenier´ıa Electr´
onica
especialidad en
Telecomunicaciones
Instituto Tecnol´
ogico y de Estudios Superiores de Monterrey
Campus Monterrey
Reconocimientos
A mis padres por todo su apoyo y por hacer de mi la persona que soy.
Al Dr. Ram´on Mart´ın Rodr´ıguez Dagnino por motivarme a incursionar en esta investigaci´on, por la confianza que siempre me brind´o y por su gran gu´ıa y orientaci´on a lo largo de esta tesis.
A mi amigo Aldo Hern´andez quien colabor´o con los inicios de esta investigaci´on. A mi amigo Ricardo Neri por compartir conmigo sus conocimientos en el ´area de DSP’s.
Alberto Llerena Bejarano
Detecci´
on de Profundidad en im´
agenes por medio
de su Desenfoque y su implementaci´
on en un DSP
Alberto Llerena Bejarano, M.C.
Instituto Tecnol´ogico y de Estudios Superiores de Monterrey, 2005
Asesor de la tesis: Dr. Ram´on Mart´ın Rodr´ıguez Dagnino
´
Indice general
Reconocimientos VI
Resumen VII
´Indice de figuras X
Cap´ıtulo 1. Introducci´on 1
Cap´ıtulo 2. Detecci´on de Profundidad por medio del Desenfoque 5
2.1. An´alisis en el dominio del espacio . . . 9
2.2. An´alisis en el dominio de la frecuencia . . . 11
2.3. Problem´aticas f´ısicas y de implementaci´on . . . 14
2.3.1. Iluminaci´on . . . 14
2.3.2. Aberraciones de la lente . . . 14
2.3.3. Ruido del sensor . . . 15
2.3.4. Captura de las im´agenes . . . 15
2.3.5. Magnificaci´on ´optica . . . 17
2.3.6. Problema delvignetting . . . 18
2.4. M´etodos relevantes de Depth from Defocus . . . 18
2.4.1. Depth from Defocus mediante laTransformada espacial . . . 18
2.4.2. Depth from Defocus medianteFiltros Racionales . . . 27
Cap´ıtulo 3. Implementaci´on 39 3.1. Im´agenes Sint´eticas . . . 41
3.2. Im´agenes Reales . . . 43
3.3. Fuentes de error . . . 49
Cap´ıtulo 4. Conclusiones 50 Ap´endice A. Fundamentos de ´Optica 52 A.1. Caracter´ısticas de una lente . . . 52
A.1.3. Apertura . . . 55
A.1.4. Ecuaci´on de la lente . . . 55
A.1.5. Distancia focal para un sistema de lentes . . . 56
A.2. Point Spread Function . . . 57
A.2.1. Modelo del Pillbox . . . 59
A.2.2. Modelo de Gauss bidimensional . . . 60
Ap´endice B. Equipo 62
Bibliograf´ıa 64
´
Indice de figuras
2.1. Desenfoque en una imagen formada por una lente. . . 6
2.2. Obtenci´on de la distancia d. . . 7
2.3. Dos puntos p1 y p2 presentando el mismo radio de desenfoque R . . . . 9
2.4. Modelo del pillbox en el dominio del espacio. . . 11
2.5. Modelo del pillbox en el dominio de la frecuencia espacial . . . 12
2.6. Gr´aficas del modelo del pillbox para varios valores de R en funcion de fr 13 2.7. Captura simult´anea de las dos im´agenes . . . 16
2.8. ´Optica telec´entrica. . . 17
2.9. Ilustraci´on de α y las distancias (1±α)e . . . 28
2.10. Gr´aficas de M P para varios valores de fr en funci´on deα . . . 31
2.11. Coeficientes racionales en funci´on de fr obtenidos para el modelo prop-uesto de M P y escalados para su mejor ilustraci´on [20] . . . 34
3.1. Diagrama a bloques del algoritmo implementado . . . 40
3.2. Im´agenes i1(x, y), i2(x, y) simuladas computacionalmente . . . 41
3.3. Mapa de 3D, resultado del algoritmo para las im´agenes sint´eticas . . . 42
3.4. Im´agenes simuladasi1(x, y),i2(x, y) con textura real y desenfoque sint´etico 42 3.5. Mapa de 3D para las im´agenes de textura real y desenfoque sint´etico . 43 3.6. Im´agenes de enfoque lejano y cercano de un objeto real . . . 43
3.7. Im´agenes de enfoque lejano y cercano de un objeto real . . . 44
3.8. Efectividad del filtro Gaussiano . . . 45
3.9. Efectividad del suavizado . . . 45
3.10. Efectividad del filtro de moda . . . 46
3.11. Efectividad para filtros de mediana de diferente tama˜no . . . 47
3.12. Filtro de mediana seleccionado . . . 47
3.13. Diagrama a bloques del algoritmo sugerido . . . 48
A.1. Formaci´on de una imagen por medio de una lente . . . 53
A.2. Distancia Focal de una lente. . . 54
A.3. Profundidad de Campo de una lente. . . 54
A.6. Desenfoque en una imagen. . . 58
A.7. Modelo del pillbox . . . 59
A.8. Modelo Gaussiano de dos dimensiones . . . 61
Cap´ıtulo 1
Introducci´
on
La intenci´on de obtener la profundidad en una escena, nace de la necesidad de muchos sistemas de contar con informaci´on m´as completa acerca del entorno que anal-izan, para poder realizar procesos m´as especializados y/o eficientes. Este es uno de los problemas m´as atractivos dentro de la visi´on rob´otica. La primer idea de estimaci´on de profundidad, o bien, tercera dimensi´on (3D) est´a inspirada en la visi´on humana, la cual es una visi´on est´ereo [1].
Los seres humanos usamos la estereoscop´ıa, en donde tenemos la capacidad de reconocer distancias y formas de objetos en la escena que estamos viendo, gracias a los dos puntos de vista que cada uno de nuestros ojos nos proporciona, y es el cerebro el encargado de extraer la profundidad para darnos la noci´on de 3D. Se han desarrollado algoritmos que usan el principio de estereoscop´ıa para detectar la profundidad. Existen otras t´ecnicas tambi´en basadas en estereoscop´ıa, como la de detecci´on de profundidad mediante secuencias de im´agenes [3], en donde se analiza el movimiento relativo entre los objetos para poder calcular las distancias que tienen con respecto al punto de vista. En este caso, se utilizan m´as de dos im´agenes para el an´alisis.
Los m´etodos estereosc´opicos presentan un problema inherente a su naturaleza, el cual es la correspondencia entre sus dos o m´as im´agenes, ya que los algoritmos deben ser capaces de identificar el mismo objeto en las diferentes im´agenes aunque tenga una distinta posici´on para cada imagen, y esto puede significar extensos recursos computacionales.
Los m´etodos monosc´opicos, utilizan un solo punto de vista para detectar la pro-fundidad. Se basan en caracter´ısticas ´opticas, como lo puede ser el grado de enfoque o desenfoque que se presenta en una imagen debido a la naturaleza de la lente con la cual se forma. Aunque no es tan expl´ıcito, se ha demostrado que adem´as de la visi´on est´ereo los seres humanos utilizamos tambi´en la informaci´on de desenfoque para la noci´on de la profundidad [4], [5].
la lente, aunque todas desde el mismo punto de vista [2], [6], [7], [8], [9]. Depth From Defocus (DFD) es otro m´etodo monosc´opico que se basa en el grado de desenfoque que presentan los objetos en una imagen [4], [12], [18], [13], [19], [20], [21]. En este m´etodo se utilizan desde dos im´agenes con diferentes ajustes de la lente tomadas desde el mismo punto de vista. En los m´etodos monosc´opicos se evita el problema de la correspondencia entre im´agenes, ya que los objetos siempre estar´an ubicados exactamente en la misma posici´on, aunque con distinto desenfoque.
Estas dos t´ecnicas monosc´opicas analizan el hecho de que existe una relaci´on entre el grado de desenfoque o enfoque que un objeto presenta en una imagen y su distancia con respecto a la lente a trav´es de la cual dicha imagen fue formada. Si se conocen los par´ametros que tiene la lente, se puede saber la distancia a la cual los objetos estar´an enfocados en la imagen que dicha lente proyecta, y este es el principio b´asico de DFF, en donde se deber´an capturar varias im´agenes con variaciones en los par´ametros de la lente para producir distancias de enfoque ligeramente distintas entre s´ı y consecutivas, de esta manera, para cada p´ıxel, se puede determinar la distancia de enfoque mediante el contraste que presenta, y as´ı obtener un estimado de profundidad.
Cuando los objetos est´an desenfocados, es por que se encuentran a diferente dis-tancia de la disdis-tancia de enfoque, y dependiendo de que tan lejos o cerca est´en de esta distancia de enfoque, los objetos se ver´an m´as o menos desenfocados, respectivamente, en la imagen formada. Por lo tanto, si se mide la cantidad o grado de desenfoque que presenta cada objeto, se puede conocer su distancia a la lente, y este es el principio b´asico de DFD. Sin embargo, medir el grado de desenfoque en una sola imagen no es suficiente, ya que dos objetos a diferentes distancias de la lente pueden presentar la misma cantidad de desenfoque en la imagen proyectada, dependiendo si se encuentran m´as atr´as o m´as adelante de la distancia de enfoque. Adem´as, no se puede asegurar si un objeto ”borroso”en la imagen se ve as´ı por estar desenfocado o simplemente por que el objeto es as´ı aunque est´e perfectamente enfocado. Es por esto que se necesita al menos una segunda imagen con distintos par´ametros de la lente, para tener una referencia.
que esta segunda imagen no presentar´ıa desenfoque, ya que a menor apertura la pro-fundidad de campo aumenta1
, y as´ı se resolv´ıa su sistema de ecuaciones de una manera simple. Aunque estos algoritmos fueron muy innovadores, siendo tal vez los primeros en el ´area, se pod´ıa mejorar la eficiencia de sus resultados.
Subbarao hizo varios trabajos acerca de DFD, pero se pueden destacar dos rele-vantes. En [12] desarroll´o un m´etodo en donde obtiene una ecuaci´on cuadr´atica para el par´ametro de esparcimiento o spread parameter en el dominio de Fourier mediante la densidad espectral de potencia del par de im´agenes y la ecuaci´on de la lente. El par´ametro de distribuci´on proviene de la Point Spread Function (PSF), la cual se dis-cute en el ap´endice. Al resolver la ecuaci´on cuadr´atica se puede obtener un estimado de profundidad mediante el par´ametro de distribuci´on. En [13] Subbarao y Surya aplicaron para DFD una transformada en el dominio espacial que Subbarao desarroll´o en [14] y llam´o Spatial Transform Method (STM). A trav´es de esta transformada, obtienen una expresi´on muy conveniente y simplificada en donde se utiliza el operador Laplaciano. Este ´ultimo trabajo de DFD es muy ingenioso, en el siguiente cap´ıtulo se analizar´a con detalle.
Ens y Lawrence [18] propusieron un algoritmo tambi´en en el dominio espacial, en el cual obtienen mediante iteraciones una matriz de convoluci´on, de tal manera que la convoluci´on, valga la redundancia, entre esta matriz y una de las dos im´agenes da como resultado la otra de las im´agenes. Al final, la matriz de convoluci´on obtenida representa el desenfoque relativo entre el par de im´agenes, con el cual se estima la profundidad. Aunque el algoritmo proporciona un buen c´alculo de profundidad, su naturaleza iterativa utiliza muchos recursos computacionales.
Watanabe y Nayar hicieron trabajos muy eficientes de DFD. En [20] modelan el desenfoque de la imagen como una funci´on racional de dos combinaciones lineales de funciones base en el dominio de la frecuencia, de donde obtienen un conjunto de oper-adores racionales, los cuales son peque˜nos kernels de banda ancha. La salida de estos operadores son coeficientes del par de im´agenes con los cuales se obtiene el estimado de profundidad con una alta resoluci´on espacial. En [21], realizan una implementaci´on en tiempo real que utiliza una proyecci´on de iluminaci´on de patrones de textura a la escena, convirti´endola en un entorno controlado. Mediante la proyecci´on de dicha luz, tienen control sobre las componentes de frecuencia dominantes de las texturas en la escena, evitando el problema de tener un rango amplio en el espectro, enfocando as´ı el an´alisis a tan s´olo las frecuencias fundamentales de dichos patrones de luz. Con un algoritmo relativamente r´apido, desde el punto de vista computacional, son capaces de estimar mapas de profundidad de resoluci´on aceptable a 30 cuadros por segundo, y
despleg´andolos en formato de video, logrando as´ı una implementaci´on en tiempo real muy impresionante.
Cap´ıtulo 2
Detecci´
on de Profundidad por medio del
Desenfoque
En el Cap´ıtulo anterior se dio una breve descripci´on de la detecci´on de profundidad por medio de desenfoque y se mencionaron las caracter´ısticas generales de algunos trabajos en el ´area que se consideran relevantes. En este Cap´ıtulo veremos un an´alisis m´as profundo y formal de este m´etodo.
Los m´etodos de detecci´on de profundidad en general, no s´olo los de DFD, se pueden dividir en dos tipos; m´etodos pasivos y m´etodos activos. Los m´etodos activos afectan de alguna manera la escena de la cual se quiere obtener el c´alculo de profundidad, y aunque esto representa la gran ventaja de que reduce cuantiosamente la complejidad de los algoritmos, tiene la desventaja de tener que condicionar, por as´ı decirlo, la escena en cuesti´on, como en lugares cerrados con condiciones conocidas e informaci´on a priori de las caracter´ısticas de la escena. Por otro lado, los m´etodos pasivos son los que no afectan la escena, y deben ser capaces de analizar cualquier, o casi cualquier tipo de entorno, sin tener limitantes considerables. Esto es una gran ventaja, pero el costo es que se requiere de un an´alisis f´ısico y matem´atico mucho m´as minucioso, ya que se tienen que considerar todos los detalles debido a la incertidumbre que se tiene del entorno. La visi´on humana, por ejemplo, es pasiva, ya que los seres humanos no hacemos modificaciones a la escena que estamos viendo.
Existe un mayor inter´es en la investigaci´on por los m´etodos pasivos, por ser m´as robustos y m´as completos que los activos, aunque en el mundo de la industria, para muchas de las aplicaciones el entorno es conocido, y un m´etodo activo es suficiente, adem´as de que puede ofrecer tal vez mejores resultados que los m´etodos pasivos, debido al control que se tiene de la escena. Sin embargo, los m´etodos activos de alguna manera son casos particulares de los m´as generales m´etodos pasivos, por lo tanto, lo ideal es poder desarrollar los m´etodos pasivos, y adaptarlos dependiendo el caso.
desenfoque. Para formalizarnos con esta idea, necesitamos encontrar una relaci´on entre la distancia que existe entre los objetos y la lente, y la cantidad de desenfoque en la imagen. Partimos de la ecuaci´on de la lente (ver Ap´endice):
1
F =
1
d +
1
d′ (2.1)
donde F es la distancia focal, d es la distancia de un punto en la escena a la lente y
d′ es la distancia de la lente al plano de la imagen donde el punto presenta su enfoque
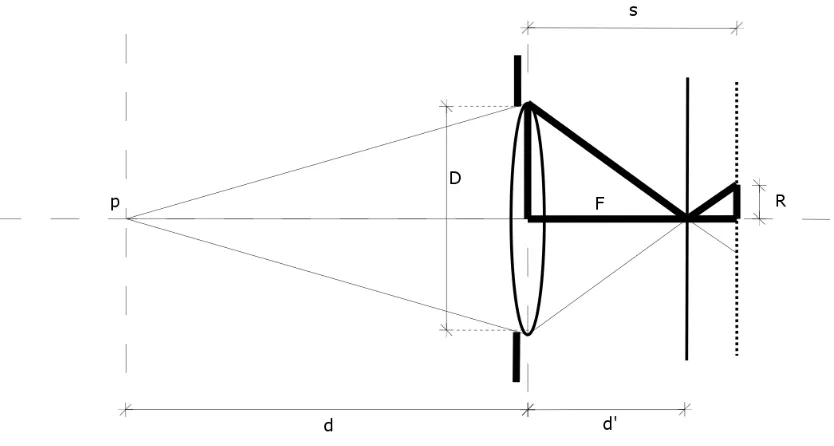
[image:19.612.101.528.325.583.2]perfecto, como se muestra en la Figura 2.1. Esta ecuaci´on nos dice que, si conocemos la distancia focal de la lente y la distancia que existe de la lente al plano de la imagen o sensor, podemos saber la distancia a la cual estar´ıan los objetos enfocados para dicho plano de la imagen.
Figura 2.1: Desenfoque en una imagen formada por una lente.
que es la regi´on de desenfoque, es un circulo que en la Figura 2.1 tiene un radio R. El punto p se proyecta a trav´es de la lente en tres posibles planos, los cuales dan lugar a tres im´agenes; una de enfoque perfecto a una distanciad′, y las otros dos de desenfoque
a las distancias d′
1 y d
′
[image:20.612.114.531.204.427.2]2, y R es el radio de desenfoque, el cual es proporcional al valor absoluto de la distancia que existe entre el plano de enfoque y el plano de desenfoque.
Figura 2.2: Obtenci´on de la distanciad.
De la Figura 2.2 mediante tri´angulos semejantes, podemos encontrar una relaci´on directa entre el radio de desenfoque R y la distancia que nos da la profundidad d. Aunque en la Figura 2.2 se muestra el desenfoque de radio R para el plano que se encuentra a la distancia s, se puede realizar el an´alisis para cualquier plano que tenga cuaquier distancia s distinta a la distancia de enfoque d′:
d′
D/2 =
s−d′
R
d′ 1
D/2 +
1
R
!
= s
R
d′
= sD/2
N´otese que d′ puede ser negativa si s < d′, como por ejemplo si s = d′
[image:21.612.256.383.142.316.2]1 en la Figura 2.1. Si sustituimos esta ´ultima ecuaci´on en la ecuaci´on de la lente (2.1) podemos eliminar d′, y resolviendo para d obtenemos:
1
F =
1
d +
R+D/2
sD/2 1
d =
sD/2−F(R+D/2)
F sD/2 1 d = 1 F − 1 s − R sD/2
d= 1
1
F − 1s − sD/R2
(2.3)
La cual es una ecuaci´on donde conocemos todas las variables del lado derecho excepto por el radio de desenfoque R. De la ecuaci´on del n´umero f (ver Ap´endice) tenemos:
D= F
f/# (2.4)
donde f/# es el n´umero f de la apertura de la lente. Sustituyendo (2.4) en (2.3):
d= 1
1
F − 1s −
2f/#
sF R
(2.5)
La cual es una relaci´on mejor estructurada en donde del lado derecho solo de-sconocemos el radio R. De esta manera, para obtener la profundidad d del punto pen una escena, s´olo necesitamos estimar el radio R del desenfoque en la ecuaci´on (2.5), y este es el problema principal a resolver en DFD.
Figura 2.3: Dos puntosp1 y p2 presentando el mismo radio de desenfoque R una referencia. Algunas t´ecnicas utilizan m´as de dos im´agenes para hacer sus algoritmos m´as robustos.
Para obtener dos im´agenes con distinto enfoque, los par´ametros que se pueden variar son: el di´ametro D de la apertura; la distancia s que existe entre la lente y el plano del sensor; y si se trata de un sistema de lentes, una variaci´on de s provoca un cambio en la distancial que existe entre las dos lentes (ver Ap´endice) y por consiguiente provoca un cambio en la distancia focal F del sistema de lentes.
Hay distintas maneras de atacar el problema de DFD. Se pueden enunciar tres for-mas en general: An´alisis en el dominio del espacio; an´alisis en el dominio de la frecuencia y; an´alisis estad´ıstico. Nos enfocaremos en los primeros dos, dando una explicaci´on de los fundamentos de ambas perspectivas.
2.1.
An´
alisis en el dominio del espacio
Para hacer un an´alisis mas formal, se necesita modelar el efecto que tiene la lente en la imagen, y esto se hace por medio de la Point Spread Function (PSF) (ver Ap´endice), la cual representa la funci´on de transferencia de la luz al pasar por la lente y ser proyectada en un plano, formando una imagen con desenfoque.
Para una imagen en un sistema invariante en el espacio se tendr´ıa la siguiente convoluci´on:
id(x, y, R) = i(x, y)∗h(x, y) (2.6)
donde id(x, y, R) representa a la imagen desenfocada, i(x, y) a la imagen enfocada,
h(x, y) la PSF y ∗ denota la convoluci´on.
Pero como una imagen desenfocada es producto de un sistema variante en el espacio, ya que el radio del desenfoque R var´ıa de p´ıxel a p´ıxel dependiendo de la profundidad, la ecuaci´on (2.6) no es estrictamente v´alida. Sin embargo, si asumimos que el desenfoque, o bien R, es constante en una peque˜na regi´on, ya que el desenfoque no var´ıa abruptamente, la convoluci´on puede considerarse v´alida dentro de esa peque˜na regi´on.
Tomaremos como base el modelo del pillbox para aproximar la PSF de la lente. Este modelo es un cilindro de radio R y de volumen unitario. El pillbox se representa mediante la siguiente ecuaci´on en el dominio del espacio (ver Ap´endice):
h(x, y, R) = 1
πR2 rect
√
x2+y2 2R
!
(2.7)
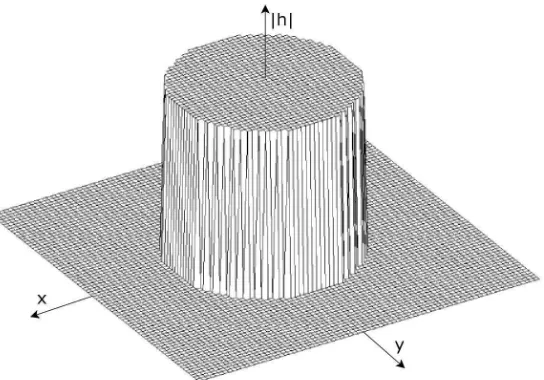
donde x, y son las dimensiones espaciales del plano de la imagen, R es el radio de desenfoque yrectrepresenta la funci´on rectangular. En el modelo del pillbox, se asume que la luz se distribuye uniformemente en la regi´on de desenfoque. La gr´afica del modelo del pillbox en el dominio espacial se muestra en la Figura 2.4.
De tal manera que en la imagen, la informaci´on de la luz est´a esparcida en grupos de p´ıxeles, por lo que se debe estimar el grado de desenfoque para cada p´ıxel o peque˜na regi´on en la imagen. En los algoritmos, esto se hace encontrando una diferencia o variaci´on de enfoque relativo entre el par de im´agenes con diferentes par´ametros, y si se logra medir esta variaci´on, se puede obtener R. Si de alguna forma, se pudiese realizar una convoluci´on inversa en la relacion (2.6), se podr´ıan obtener estimados de
Figura 2.4: Modelo del pillbox en el dominio del espacio.
basados en el dominio espacial. Esta es la perspectiva a grandes rasgos que utilizan los m´etodos fundamentados en este tipo de an´alisis. Mas adelante en este Cap´ıtulo, se analizar´a una t´ecnica basada en estos principios.
2.2.
An´
alisis en el dominio de la frecuencia
Una imagen con desenfoque, a simple vista, presenta menos contraste que la misma imagen cuando est´a enfocada. Desde el punto de vista de la frecuencia espacial, esto quiere decir que el espectro de una imagen enfocada tiene mayor ancho de banda que el de la misma imagen desenfocada. Las t´ecnicas de DFD que utilizan el an´alisis frecuencial se basan en este hecho. Para formalizar esta perspectiva, necesitamos transformar la informaci´on que tenemos al dominio de la frecuencia.
En el dominio de Fourier, por el teorema de la convoluci´on, podemos expresar la ecuaci´on (2.6) de la siguiente manera:
Id(u, v, R) =I(u, v)·H(u, v) (2.8)
Transformamos ahora el modelo del pillbox de la ecuaci´on (2.7) del dominio espa-cial al dominio de Fourier, obteniendo lo siguiente:
H(u, v, R) = 1
πR√u2+v2 J1
2πR√u2+v2 (2.9)
[image:25.612.179.462.288.465.2]dondeJ1 representa la funci´on Bessel del primer tipo y primer orden. La funci´on Bessel tiene una forma de filtro paso bajo, por lo que es evidente de la ecuaci´on (2.9) que el pillbox act´ua como tal. En la Figura 2.5 graficamos la funci´on en (2.9) centrando el origen, y podemos observar claramente el efecto de filtro paso bajo en el dominio de la frecuencia.
Figura 2.5: Modelo del pillbox en el dominio de la frecuencia espacial
Podemos realizar un corte transversal en la Figura 2.5 para ver el efecto del filtro paso bajo de una manera distinta, sin afectar la forma del modelo pues el pillbox es rotacionalmente sim´etrico. Podemos cambiar entonces el sistema de coordenadas del dominio de la frecuencia espacial a coordenadas polares (fr, fθ) donde fr es la
frecuencia radial dada por fr = √u2+v2, y fθ es el ´angulo a la cual la frecuencia radial es expresada, el cual por la simetr´ıa rotacional,fr ser´a constante para todos los valores de fθ. En la Figura 2.6 se grafica el modelo del pillbox de (2.9) en funci´on de la frecuencia radial fr para varios valores de R, y podemos apreciar que la gr´afica con la mayor ca´ıda es aquella para un radio de desenfoque R mayor.
el filtrado es mayor. Entonces, para poder calcular el nivel o grado de desenfoque en cada p´ıxel de la imagen partiendo de estos principios frecuenciales, se necesitar´ıa de alguna manera medir los grados de filtraje que existen en cada p´ıxel o bien grupos de p´ıxeles de la imagen. Si se pudiera obtener esta informaci´on, se pueden establecer relaciones entre el grado de filtraje y el grado de desenfoque, y posteriormente obtener la profundidad. Este es, a grandes rasgos, el enfoque frecuencial que se utiliza para atacar el problema de DFD. M´as adelante en este Cap´ıtulo, se analizar´a una t´ecnica basada en el dominio de la frecuencia espacial.
2.3.
Problem´
aticas f´ısicas y de implementaci´
on
Dentro del desarrollo de las t´ecnicas de DFD nos encontramos con problemas f´ısicos y ´opticos inherentes al m´etodo, los cuales son fuentes de error en los resultados.
2.3.1.
Iluminaci´
on
La iluminaci´on de la escena al momento de capturar las im´agenes es esencial para la calidad de las mismas. Como la formaci´on de la imagen es debida a la luz que refleja la escena y que es recolectada por la lente, una mala iluminaci´on es indeseable en las im´agenes a utilizar en los algoritmos. Se puede llegar a pensar que en un m´etodo originalmente pasivo, al controlar la iluminaci´on de la escena estar´ıamos cayendo en un m´etodo activo de DFD, sin embargo, como la iluminaci´on es independiente de los objetos que hay en la escena, es decir, la iluminaci´on es la misma siempre, y no cambia las caracter´ısticas espaciales o de frecuencia espacial de la escena mas que la cantidad de luz que reflejan, entonces no se cae en un m´etodo activo cuando se proporciona al entorno una buena iluminaci´on.
Ya que se necesitan m´ınimo dos im´agenes de la escena con diferentes par´ametros, si esas im´agenes no son tomadas simult´aneamente, puede tambi´en existir una variaci´on en la iluminaci´on de la escena durante el tiempo que existe entre la captura de cada imagen. Si las im´agenes son capturadas simult´aneamente, no existe este problema.
Colocando alguna fuente de luz con buena intensidad y que asegure no tener variaciones en la iluminaci´on, se pueden controlar en cierto grado estas problem´aticas.
2.3.2.
Aberraciones de la lente
llamados tambi´en aberraciones, las cuales causan que la proyecci´on de la luz no sea en la direcci´on correcta, es decir, que la luz proveniente de la imagen no siempre se proyectar´a a trav´es de la lente en la direcci´on en la cual debe incidir en el plano de la imagen.
Por otro lado, la lente puede absorber luz en el proceso, es decir, que no toda la luz que ”entra”en la lente es proyectada. Desde el punto de vista matem´atico, esto quiere decir que la funci´on de transferencia de la lente, es decir, la PSF tiene una ganancia digamos menor a uno, ocasionando que no toda la luz de entrada llegue a la salida. En una lente sin p´erdidas, en donde la lente no absorbe luz, la PSF cumple lo siguiente:
Z Z
h(x, y)dx dy= 1 (2.10)
La mayor´ıa de las veces estos dos problemas no afectan de una manera relevante la imagen, pero debe tomarse en cuenta al realizar las pruebas antes de ser ignorados.
2.3.3.
Ruido del sensor
En la captura de una imagen digital, como es el caso de las im´agenes que se utilizan en los algoritmos de DFD, se utiliza un sensor de imagen llamado CCD, por sus siglas en ingl´es charge-couple device, el cual muestrea la luz que forma la imagen, y ´este puede a˜nadir ruido en su proceso de cuantizaci´on. Una manera de atacar este problema en una imagen, es tomando varias veces la imagen controlando que no haya cambios en la escena, y promediar el conjunto de im´agenes, de esta manera, el ruido proveniente del CCD se disminuir´ıa. Esta soluci´on requiere de m´as tiempo para la toma de las im´agenes, pero es ´util cuando nuestra principal fuente de ruido es el CCD.
2.3.4.
Captura de las im´
agenes
correcta-captura repetida para cada una de las dos im´agenes, el tiempo total de correcta-captura puede crecer demasiado. El tiempo m´aximo permitido del funcionamiento del algoritmo en total depender´a de la aplicaci´on. La ventaja de la lente motorizada, es que se tiene un solo CCD y una sola lente.
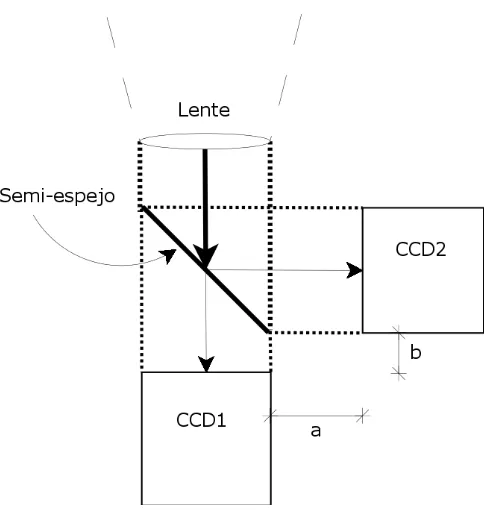
[image:29.612.199.446.318.573.2]Para capturar las im´agenes simult´aneamente, se necesitan dos CCD’s, colocando un semi-espejo detr´as de la lente, el cual es un espejo que refleja la mitad de la luz incidente y deja pasar la otra mitad, de tal manera que la luz que proviene de la imagen llega a dos CCD distintos con par´ametros de la lente diferentes, como lo puede ser la distancia de la lente al sensor, como se muestra en la Figura 2.7, en donde la distancia total de la lente al primer CCD depende dea y la distancia al segundo sensor depende deb. De esta manera, se tienen dos CCD’s y un solo punto de vista, respetando as´ı el principio de monoscop´ıa.
Figura 2.7: Captura simult´anea de las dos im´agenes
2.3.5.
Magnificaci´
on ´
optica
La magnificaci´on ´optica es el cambio entre el tama˜no original de un objeto y el tama˜no que presenta en la imagen. Esta magnificaci´on es proporcional a la distancia que hay entre la lente y el sensor de la imagen. Un ejemplo de este fen´omeno es cuando se toma la fotograf´ıa de una calle recta desde el centro y en direcci´on de la misma; las l´ıneas laterales de la calle, para una distancia muy lejana, parecen juntarse en un punto de la imagen, que en geometr´ıa proyectiva se conoce como vanishing point.
La magnificaci´on en s´ı no es un problema, pero ya que en DFD se necesitan dos im´agenes iguales pero con distinto desenfoque, cuando se cambia el enfoque entre una y otra imagen cambia tambi´en la magnificaci´on si el par´ametro que se var´ıa es la distancia entre la lente y el sensor de la imagen, dando como resultado que las dos im´agenes sean ligeramente distintas entre s´ı, y la correspondencia de p´ıxeles no sea directa.
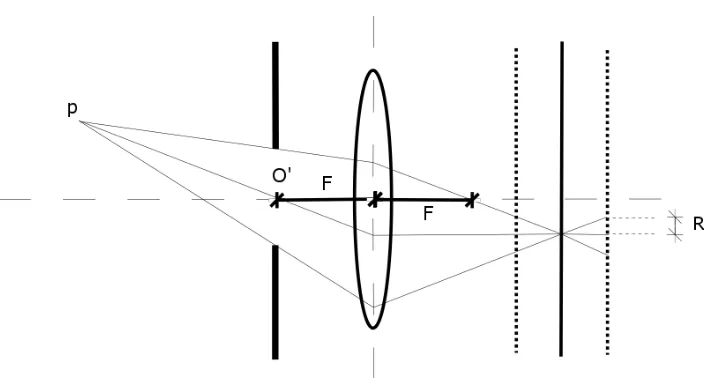
Para contrarrestar este problema, se pueden usar lentes telec´entricas [22], las cuales eliminan totalmente la magnificaci´on en la imagen. Las lentes telec´entricas utilizan la apertura a una distancia focalF de la lente, en lugar de ponerlo justo junto a la lente, como se muestra en la Figura 2.8, en donde podemos observar que el rayo que cruza por el centro telecentr´ıcoO′ se proyecta paralelamente al eje ´optico en el sensor, y esto
[image:30.612.144.499.448.637.2]pasar´a con cualquier rayo de luz proveniente de cualquier punto en la escena que cruce por O′.
Figura 2.8: ´Optica telec´entrica.
me-contrario a la magnificaci´on en una o ambas im´agenes para que la correspondencia de p´ıxeles sea directa. En muchas ocasiones, el problema de la magnificaci´on no afecta de una manera considerable, normalmente se encuentra dentro del 3 % [14], pero es necesario tener presente el concepto durante la implementaci´on de los algoritmos de DFD.
2.3.6.
Problema del
vignetting
El fen´omeno del vignetting se produce en sistemas de lentes. El vignetting es la oclusi´on de objetos en la escena por una o m´as de las lentes o el diafragma, de tal manera que cada una de las lentes o el diafragma bloquea la proyecci´on de la luz en el plano de la imagen debido a la posici´on, por lo que cada elemento puede limitar la luz en este sentido, ocasionando que parte de la escena sea omitida en la imagen. El problema del vignetting en DFD es casi despreciable, pero puede presentarse en casos especiales.
2.4.
M´
etodos relevantes de Depth from Defocus
En esta secci´on se analizar´an dos de las t´ecnicas que se pueden considerar como m´as relevantes dentro de las t´ecnicas de DFD, y cuyos autores tambi´en pueden ser considerados como dos de los m´as importantes investigadores en esta ´area.
2.4.1.
Depth from Defocus mediante la
Transformada
espa-cial
Subbarao y Surya [13] desarrollaron este m´etodo de DFD mediante la Transfor-mada espacial o STM por sus siglas en ingl´es (Spatial Transform Method), el cual es un m´etodo pasivo y en el dominio del espacio. Al inicio de este Cap´ıtulo se present´o medi-ante la ecuaci´on (2.5) una expresi´on directa para la distanciaden funci´on del radio de desenfoqueR, pero dicha ecuaci´on puede ser representada algebr´aicamente de distintas maneras, y los autores la manejan a conveniencia de los algoritmos. De la ecuaci´on (2.3) dejando s´olo el t´ermino deR obtenemos:
d= −
sD
2
R− sD2 F1 − 1s (2.11)
Para encontrar el valor experimental de R es necesario, como ya hemos dicho, utilizar la PSF. El STM es v´alido para cualquier PSF siempre y cuando sea rotacional-mente sim´etrica. Los modelos del pillbox y Gaussiano de dos dimensiones cumplen con esta condici´on (ver Ap´endice). Hay que definir entonces una relaci´on entre un par´ametro obtenible para cualquier PSF, y el radio de desenfoque R; la desvaci´on est´andar es la mejor opci´on. La varianza para alguna PSF est´a dada por la siguiente relaci´on:
σ2
h =
Z Z
(x2 +y2
)h(x, y)dxdy (2.12)
dondeσh es la desviaci´on est´andar de alguna PSF rotacionalmente sim´etrica dada por
h(x, y), y representa el esparcimiento del desenfoque, pues es directamente proporcional al radio de desenfoque R.
Subbarao y Surya [13] comprobaron de manera experimental que el modelo del pillbox es una mejor aproximaci´on que el modelo Gaussiano de dos dimensiones para la regi´on de desenfoque, por lo que se basan en el modelo del pillbox. De (2.11) podemos encontrar la desviaci´on est´andar para el modelo del pillbox en funcion de R, teniendo como resultado:
σh = √R
2 (2.13)
Si sustituimos (2.13) en (2.11) obtenemos:
d=
−sD
2√2
σh − sD
2√2
1
F − 1s
(2.14)
y esta ecuaci´on puede ser expresada, por conveniencia, de la siguiente manera:
d = m
σh−c (2.15)
donde
m= −sD
2√2 , c =
sD
2√2
1 F − 1 s (2.16)
par´amet-(D1, s1, F1) y (D2, s2, F2) respectivamente. Cada imagen presentar´a un valor deσh difer-ente para cada regi´on de la imagen en donde se considera invariante en el espacio, por lo tanto, se obtiene una relaci´on como (2.15) para ambas im´agenes:
d = m1
σ1−c1
(2.17)
donde σ1 es par´ametro de esparcimiento del desenfoque de la imagen i1(x, y) y
m1 = −
s1D1
2√2 , c1 =
s1D1 2√2
1
F1 − 1
s1
(2.18)
as´ı mismo
d = m2
σ2−c2
(2.19)
donde σ2 es par´ametro de esparcimiento del desenfoque de la imagen i2(x, y) y
m2 = −
s2D2
2√2 , c2 =
s2D2 2√2
1
F2 − 1
s2
(2.20)
En las relaciones anteriores, la distancia d de los objetos en la escena no cam-bia para las dos im´agenes, pues lo ´unico que se var´ıa entre ambas im´agenes son los par´ametros de la lente, por lo que podemos igualar (2.17) y (2.19):
d= m1
σ1−c1
= m2
σ2−c2
(2.21)
en donde si despejamos alguno de los par´ametros de esparcimiento del desenfoque, por ejemplo σh1 tenemos:
σ1 =
m
1
m2
σ2−
m
1c2
m2
+c1
σ1 =ασ2+β (2.22)
donde
α= m1
m2
, β =c1−
m1c2
m2
En esta ´ultima ecuaci´on obtenemos una relaci´on entre los par´ametros de es-parcimiento de desenfoque de las dos im´agenes obtenidas, y es la ecuaci´on que hay que resolver.
Transformada espacial
La Transformada espacial es una transformada formal que fue desarrollada por Subbarao en [14], y puede ser utilizada para varias aplicaciones de se˜nalesn-dimensionales tanto continuas como discretas que se puedan representar con polinomios de orden ar-bitrario, en este caso las im´agenes. Mediante esta transformada es como Subbarao y Surya [13] resuelven la ecuaci´on (2.22). Se pretende dar una breve descripci´on de los resultados de esta transformada que son utilizados para el STM.
Sea i(x, y) una imagen la cual es un polinomio c´ubico de dos variables definido en el espacio discreto por:
i(x, y) = 3
X
m=0 3−m
X
n=0
am,nxmyn (2.24)
donde am,n son los coeficientes del polinomio.
Se obtienen ahora por conveniencia los momentos de una PSF:
hm,n =
Z ∞
−∞
Z ∞
−∞
xmynh(x, y)dx dy (2.25)
Desarrollemos ahora la convoluci´on de la imagen i(x, y) y una PSF tal y como se mencion´o en la ecuaci´on (2.6):
id(x, y) =
Z ∞
−∞
Z ∞
−∞
i(x−ζ, y−η)h(ζ, η)dζ dη (2.26)
Comoi(x, y) es un polinomio, se puede representar como una serie de Taylor, dada por:
i(x−ζ, y−η) = X
0≤m+n≤3
(−ζ)m m!
(−η)n n! i
m,n
(x, y)
i(x−ζ, y−η) = X
m n
(−1)m+n m!n! i
m,n
donde
im,n(x, y)
≡ ∂
m
∂xm ∂n
∂yn i(x, y) (2.28)
Si sustituimos (2.27) en (2.26) obtenemos:
id(x, y) =
Z ∞
−∞
Z ∞
−∞
X
0≤m+n≤3
(−1)m+n m!n! i
m,n(x, y)ζmηnh(ζ, η)dζ dη
id(x, y) = X
0≤m+n≤3
(−1)m+n m!n! i
m,n(x, y)Z ∞
−∞
Z ∞
−∞ ζ
mηnh(ζ, η)dζ dη (2.29)
Utilizando la ecuaci´on de los momentos de la PSF (2.25) la expresi´on (2.29) se reduce a:
id(x, y) = X
0≤m+n≤3
(−1)m+n m!n! i
m,n(x, y)hm,n (2.30)
La cual es la convoluci´on de una funci´oni(x, y) con otra funci´onh(x, y) expresada como la suma de las derivadas parciales de i(x, y) y los momentos de h(x, y), y corre-sponde a la Transformada espacial. En esta aplicaci´oni(x, y) es la imagen y h(x, y) es la PSF. Desarrollamos la ecuaci´on (2.30):
id(x, y) = i0,0
(x, y)h0,0−i 0,1
(x, y)h0,1−i 1,0
(x, y)h1,0+i 1,1
(x, y)h1,1 +i
0,2 (x, y)
2 h0,2+
i2,0 (x, y)
2 h2,0−
i1,2 (x, y)
2 h1,2−
i2,1 (x, y)
2 h2,1
− i
0,3 (x, y)
6 h0,3−
i3,0 (x, y)
6 h3,0 (2.31)
Como la PSF tiene la propiedad de ser rotacionalmente sim´etrica, se encuentra que:
h0,1 =h1,0 =h1,1 =h0,3 =h3,0 =h2,1 =h1,2 = 0 (2.32)
h0,2 =h2,0 (2.33)
h0,0 =
Z Z
h(x, y)dx dy = 1 (2.34)
Utilizando estos valores para los momentos de la PSF, la ecuaci´on (2.31) se reduce a lo siguiente:
id(x, y) =i(x, y) + h2,0 2
i2,0
(x, y) +i0,2
(x, y)
i(x, y) = id(x, y)− h2,0 2
i2,0
(x, y) +i0,2
(x, y) (2.35)
Aplicamos ahora por conveniencia las derivadas parciales en los dos lados de la ecuaci´on (2.30). Primero ∂2
∂x2:
i2,0
(x, y) = i2d,0(x, y)− h4,0 2
i4,0
(x, y) +i2,2
(x, y)
i2,0
(x, y) =i2d,0(x, y) (2.36)
ya que las derivadas de orden mayor a 3 son 0, debido a que es un polinomio de orden 3 como se mencion´o cuando se empez´o a definir la Transformada espacial. De igual manera aplicamos ∂2
∂y2:
i0,2
(x, y) = i0d,2(x, y)− h0,4
2
i2,2
(x, y) +i0,4
(x, y)
i0,2
(x, y) =i0d,2(x, y) (2.37)
Se sustituyen ahora (2.36) y (2.37) en (2.35):
i(x, y) = id(x, y)− h2,0 2
i2d,0(x, y) +i
0,2
d (x, y)
i(x, y) =id(x, y)− h2,0 2
∂2
∂x2id(x, y) +
∂2
∂y2 id(x, y)
!
donde ∇2
es el operador Laplaciano. La ecuaci´on (2.38) es una convoluci´on inversa ya que expresa la funci´on originali(x, y) en funci´on de la funci´on convolucionadaid(x, y), sus derivadas parciales y el segundo momento de la PSF. La ecuaci´on (2.38) es la Transformada espacial inversa.
El t´ermino de h2,0 de la ecuaci´on (2.38) es el segundo momento de la PSF, por lo que con (2.12) y (2.25) obtenemos:
h2,0 =h0,2 =
Z Z
x2
h(x, y)dxdy=
Z Z
y2
h(x, y)dxdy= σ 2
h
2 (2.39) Sustituyendo (2.39) en (2.38) obtenemos finalmente:
i(x, y) =id(x, y)− σ 2
h
4 ∇ 2
id(x, y) (2.40)
La cual es una ecuaci´on que nos permitir´a resolver (2.22). Aplicando (2.40) para las dos im´agenes i1(x, y), i2(x, y) con sus respectivos par´ametros de esparcimiento de desenfoque σ1, σ2 obtenemos dos relaciones:
i(x, y) = i1(x, y)− σ 2 1 4 ∇
2
i1(x, y) (2.41)
i(x, y) = i2(x, y)− σ 2 2 4 ∇
2
i2(x, y) (2.42)
en donde ambas ecuaciones tienen la misma imagen i(x, y) como imagen original, ya que ambas im´agenes i1(x, y), i2(x, y) son distintas ´unicamente en el desenfoque, como hemos venido diciendo.
De esta manera, podemos igualar (2.41) y (2.42):
i1(x, y)−σ 2 1 4 ∇
2
i1(x, y) =i2(x, y)− σ 2 2 4 ∇
2
i2(x, y) (2.43)
i1(x, y)−i2(x, y) = 1 4 σ2 1∇ 2
i1(x, y)−σ2 2∇
2
i2(x, y) (2.44)
∇2
i1(x, y) =∇2
i2(x, y) (2.45)
y por lo tanto podemos proponer por conveniencia la siguiente igualdad:
∇2
i(x, y) = (∇ 2
i1(x, y) +∇2i2(x, y))
2 (2.46)
As´ı, podemos sustituir ∇2
i1(x, y) y ∇2
i2(x, y) por∇2
i(x, y) en (2.44):
i1(x, y)−i2(x, y) = 1 4
σ2 1∇
2
i(x, y)−σ2 2∇
2
i(x, y)
i1(x, y)−i2(x, y) = 1 4
σ2 1−σ
2 2
∇2
i(x, y) (2.47)
Finalmente, obtenemos con (2.47) una segunda ecuaci´on para formar junto con (2.22) un sistema de dos ecuaciones con dos inc´ognitas, de donde al sustituir (2.22) en (2.47) obtenemos:
i1(x, y)−i2(x, y) = 1 4
(α σ2+β) 2
−σ2 2
∇2
i(x, y)
i1(x, y)−i2(x, y) = 1 4
α2
σ2
2 + 2α σ2β+β 2
−σ2 2
∇2
i(x, y)
σ2 2
1
4(α 2
−1)∇2
i(x, y)
+σ2
1
2α β∇ 2
i(x, y)
=
i1(x, y)−i2(x, y)− 1 4β
2
∇2
i(x, y) (2.48)
o bien:
a σ2
2 +b σ2+c= 0 (2.49) donde:
a= 1
4(α 2
−1)∇2
b= 1 2α β∇
2
i(x, y) (2.51)
c=i2(x, y)−i1(x, y) + 1 4β
2
∇2
i(x, y) (2.52)
La ecuaci´on cuadr´atica (2.49) se puede resolver en conjunto con sus constantes (2.50), (2.51), (2.52) y estas ´ultimas a su vez utilizan la relaci´on de Laplacianos (2.46) y las constantes (2.23), las cuales se calculan mediante los par´ametros de la lente con las constantes de (2.18) y (2.20).
Los Laplacianos de (2.46) son computados utilizando las im´agenesi1(x, y),i2(x, y) mediante una convoluci´on con un kernel Laplaciano:
∇2
in(x, y) =in(x, y)∗L(x, y) (2.53)
donde L(x, y) es un kernel Laplaciano.
Una vez que se obtiene el valor de σ2, la distancia de la profundidad d puede ser calculada mediante (2.19). Este es el principio b´asico del STM, al cual se le puede hacer una ´ultima modificaci´on, ya que en la igualdad de (2.43) pudiese ser no v´alida en presencia de ruido, por lo que unsuavizado o smoothing es conveniente. Si a (2.47) para peque˜nas regiones se eleva al cuadrado y posteriormente se integra en ambos lados de la igualdad se obtiene:
Z Z
(i1(x, y)−i2(x, y) )2
dxdy= 1
16(σ 2 1 −σ
2 2)
2 Z Z (∇2
i(x, y) )2
dxdy
(σ2 1 −σ
2 2)
2 = 16
R R
(i1(x, y)−i2(x, y) )2dxdy
R R
(∇2
i(x, y) )2
dxdy (2.54)
o bien:
(σ2 1 −σ
2 2)
2 =G2
(2.55)
en donde:
G2 = 16
R R
(i1(x, y)−i2(x, y) )2
dxdy
R R
(∇2
i(x, y) )2
y por lo tanto:
σ2 1 −σ
2 2 =G
′
(2.57)
donde G′ =
±G. El signo de G′ en (2.57) depende en el signo de (σ2 1 −σ
2
2), y se de-ber´a escoger bajo alg´un criterio v´alido. Por ejemplo, si σ1 > σ2 hace que el G′ sea positiva, si σ1 < σ2 tenemos que G′ es negativa. Un par´ametro de esparcimiento del desenfoque mayor representa un desenfoque mayor, por lo que si sabemos cual de las dos im´agenes tiene mayor desenfoque en la peque˜na regi´on en cuesti´on, se puede es-coger correctamente el signo de G′. Sabemos que en una regi´on con mayor desenfoque
los cambios entre p´ıxeles son menos abruptos, por lo que la varianza ser´ıa un buen criterio para conocer cual de las regiones tiene mayor desenfoque, es decir, una var-ianza m´as peque˜na significa que la relaci´on entre p´ıxeles es m´as suave, es decir, con mayor desenfoque, por lo tanto se puede calcular la varianza en ambas regiones y con esta informaci´on se puede tomar una decisi´on para condicionar el signo de G′. Ahora
podemos sustituir (2.22) en (2.57) :
(α σ2+β) 2
−σ2 2 =G
′
σ2 2(α
2
−1) + 2α β σ2+β 2
=G′
(2.58)
Y obtenemos nuevamente una ecuaci´on cuadr´atica paraσ2 que al resolverla y com-putar la distancia mediante (2.19) se obtienen valores de profundidad d m´as precisos, ya que esta modificaci´on ocasiona que el algoritmo sea m´as robusto en la presencia de ruido. Otra manera de obtener la distanciades tener una tabla de valores predefinidos experimentalmente para cada valor deσ2, de tal manera que cuando se obtenga un valor deσ2 la tabla regrese un valor de profundidad, lo cual representar´ıa mejores resultados en la estimaci´on de profundidad.
2.4.2.
Depth from Defocus mediante
Filtros Racionales
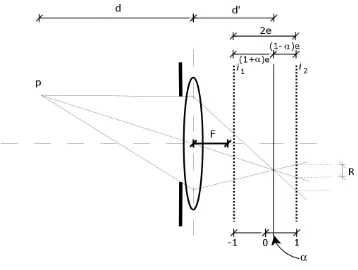
la escena. Introducen una variable llamada profundidad normalizada, la cual es una distancia que describe la posici´on del plano de perfecto enfoque para un punto en la escena y que es relativa a la posici´on de los planos del sensor para las dos im´agenes, como se ilustra en la Figura 2.9.
Figura 2.9: Ilustraci´on de α y las distancias (1±α)e
En la Figura 2.9, 2ees la distancia conocida entre los dos planos del sensor para las im´agenes de enfoque cercano y lejano, yα es la profundidad normalizada la cual puede tomar valores en el rango [−1,1], y es medida desde el punto medio entre los dos planos de las im´agenes de enfoque cercano y lejano a la posici´on donde un determinado punto en la escena tiene su plano de imagen de perfecto enfoque. Por lo tanto, se pueden expresar las distancias entre el plano de imagen de perfecto enfoque para un punto en la escena y los planos de las im´agenes de enfoque cercano y lejano como (1±α)e, donde el signo positivo es para el plano de la imagen de enfoque lejano y el signo negativo para el plano de la imagen de enfoque cercano. De esta manera, si se puede medir la profundidad normalizada α para cada punto en la imagen, se puede obtener la profundidadd. Para medir el valor deα ser´a necesario encontrarle una relaci´on con el radio de desenfoque R el cual a su vez deber´a ser aproximado con la PSF.
Figura 2.2 que dio lugar a la relaci´on (2.2), pero en este caso la ´unica diferencia es de notaci´on, ya que de la Figura 2.9 podemos ver que la distancia (s−d′) de la Figura
2.2 corresponde en este an´alisis alterno a (1±α)e y la distanciad′ al plano de perfecto
enfoque de la Figura 2.2 equivale a γ + (1 +α)e, donde γ es la distancia del plano de la imagen de enfoque lejano, la cual es conocida, de esta manera, la relaci´on que se obtiene es la siguiente:
γ+ (1 +α)e
D/2 =
(1±α)e R
R = (1±α)e D/2
γ+ (1 +α)e (2.59)
en donde podemos observar la relaci´on que existe entre la profundidad normalizada α
y el radio de desenfoque R.
Watanabe y Nayar [20] utilizan tambi´en el modelo del pillbox para la PSF en su algoritmo, por lo que corresponde ahora reescribir la expresi´on del modelo del pillbox en (2.7) en funci´on la profundidad normalizada α por medio del radio R obtenido en (2.59):
h(x, y,(1±α)e) = 4 (γ+ (1 +α)e) 2
π(1±α)2e2D2 rect
(γ+ (1 +α)e)√x2+y2 (1±α)e D
!
(2.60)
Y el modelo (2.60) en el dominio de la frecuencia mediante la Transformada de Fourier tal y como se hizo para (2.9) es:
H(u, v,(1±α)e) = γ+ (1 +α)e
π(1±α)e D/2√u2+v2J1
π(1±α)e D√u2+v2
γ+ (1 +α)e
!
(2.61)
i1(x, y) =i(x, y)∗h(x, y,(1 +α)e)
i2(x, y) =i(x, y)∗h(x, y,(1−α)e) (2.62)
I1(u, v) = I(u, v)·H(u, v,(1 +α)e)
I2(u, v) =I(u, v)·H(u, v,(1−α)e) (2.63)
las cuales, recordemos, son v´alidas para peque˜nas regiones donde se asume que la imagen es invariante en el espacio.
Watanabe y Nayar [20] introducen el concepto delcociente normalizado, el cual es un cociente entre la suma y la resta de los modelados de las im´agenes de enfoque lejano y cercano en el dominio de la frecuencia espacial, como se muestra a continuaci´on:
m(x, y, α p(x, y, α) =
i2(x, y)−i1(x, y)
i2(x, y) +i1(x, y)
M(u, v, α)
P(u, v, α) =
I2(u, v)−I1(u, v)
I2(u, v) +I1(u, v) (2.64) donde M
P es el cociente normalizado. Sustituyendo en (2.64) las relaciones de (2.63) y
factorizando y eliminando el t´ermino com´un se obtiene:
M(u, v, α)
P(u, v, α) =
I(u, v)·H(u, v,(1−α)e)−I(u, v)·H(u, v,(1 +α)e)
I(u, v)·H(u, v,(1−α)e) +I(u, v)·H(u, v,(1 +α)e)
M(u, v, α)
P(u, v, α) =
H(u, v,(1−α)e)−H(u, v,(1 +α)e)
H(u, v,(1−α)e) +H(u, v,(1 +α)e) (2.65) El objetivo del cociente normalizado es el de modelar el comportamiento de la profundidad normalizada frente a la relaci´on de las im´agenes de enfoque cercano y lejano, de tal manera, que si se calcula el valor del cociente normalizado mediante las im´agenes se pueda obtener un aproximado deα, y por consiguiente, de la profundidad
Figura 2.10: Gr´aficas de M
del cociente normalizado M
P en funci´on de la profundidad normalizadaαpara distintos
valores defr se presentan en la Figura 2.10.
En la Figura 2.10 podemos ver que el cociente normalizado M
P es una funci´on
monot´onica en el rango de [−1,1] paraα, y para frecuencias radialesfrno muy grandes. Watanabe y Nayar [20] encontraron que la frecuencia radial m´axima para la cual se cumple la monotonicidad de M
P es aquella en donde el desenfoque es el extremo, por lo
que en la pr´actica no se presentar´a este caso.
Por lo tanto, se puede calcular un estimado de la profundidad normalizada αsi se tiene el valor del cociente normalizado MP, pero como MP est´a en el dominio de Fourier, es necesario encontrar su magnitud a partir del cociente normalizado en el dominio del espacio m
p el cual esta en funci´on de las im´agenes i1(x, y), i2(x, y) con las que se
cuentan. El problema es que la frecuencia de las im´agenes es incierta, pues podr´ıa ser de cualquier tipo al tratarse de un enfoque pasivo. Por lo tanto, se deben utilizar filtros que sean capaces de muestrear todas las posibles frecuencias para las peque˜nas regiones en las im´agenes.
Se necesita encontrar un modelo que aproxime el comportamiento de M
P en la
Figura 2.10. [20] proponen un modelo racional defunciones base, dado por la siguiente expresi´on:
M(u, v, α)
P(u, v, α) =
PnP
i=1GPi(u, v)bPi(α) PnM
i=1GMi(u, v)bMi(α)
+ǫ(u, v, α) (2.66)
donde bPi, bMi son las funciones base, GPi(u, v), GMi(u, v) son sus respectivos
coefi-cientes, y ǫ(u, v, α) es el error residual de correcci´on. Sin embargo, si el modelo es lo suficientemente preciso, podemos reescribir la expresi´on (2.66) de la siguiente manera:
M(u, v, α)
P(u, v, α) =
PnP
i=1GPi(u, v)bPi(β) PnM
i=1GMi(u, v)bMi(β)
= R(u, v;β) (2.67)
donde en el lado derecho encontramos la profundidadβ el cual es un valor estimado de la profundidad normalizada α.
De la Figura 2.10 podemos apreciar que el comportamiento de M
P asemeja a una
recta para valores de α peque˜nos y a un polinomio c´ubico conforme |α| se acerca a 1, por lo que Watanabe y Nayar [20] proponen como funciones base:
M(u, v, α)
P(u, v, α) =
GP1(u, v)
GM1(u, v)
β+ GP2(u, v)
GM1(u, v)
β3
de tal manera que las variables de (2.67) tomaron los siguientes valores:
nP = 2, nM = 1, bP1(β) =β, bP2(β) = β
3
, bM1(β) = 1 (2.69)
En la relaci´on (2.68) podemos observar que el primer t´ermino del polinomio aprox-ima la forma lineal de M
P mientras que el segundo t´ermino del polinomio corrige la recta
para darle la forma c´ubica. Debemos entonces encontrar las formas de los coeficientes racionales de (2.68), para que finalmente podamos resolver la ecuaci´on paraβ y obtener as´ı el aproximado de profundidad. Dichos coeficientes ser´an el conjunto de filtros que deben muestrear todo el rango de frecuencia para las im´agenes de enfoque lejano y cercano. Para encontrarlos, podemos proporcionar informaci´on a priori a la relaci´on de (2.68) y poder describir la forma que tienen, para esto, se asume que β = α, de tal forma que al fijar alguno de los tres coeficientes se pueden obtener los espectros de los otros dos. Reescribamos (2.68) de la siguiente manera:
p0(u, v, α) =p1(u, v)β+p3(u, v)β3
(2.70)
en donde con la suposici´on de que β = α si fijamos alguno de los polinomios del lado derecho podemos encontrar el otro. Es de esta manera como Watanabe y Nayar [20] encuentran las funciones de los coeficientes racionales en el dominio de la frecuencia para el modelo en particular que proponen, y cuyos espectros en funcion de la frecuencia radial fr se muestran en la Figura 2.11.
Una vez encontrados, se puede probar la precisi´on del modelo propuesto mediante un c´alculo deβpara valores deαpredeterminados, utilizando los coeficientes obtenidos. Mediante el m´etodo de Newton-Raphson podemos estimar un valor paraβ desde (2.70). El valor inicial para el m´etodo ser´ıa el que toma la funci´on si despreciamos el t´ermino c´ubico de correcci´on, es decir:
β0(u, v) = p0(u, v, α)
p1(u, v) (2.71)
por lo que el m´etodo despu´es de una iteraci´on queda de la siguiente manera:
β(u, v) = β0(u, v)−−p0(u, v, α) +p1(u, v)β0+p3(u, v)β 3 0
p1(u, v) + 3p3(u, v)β2 0
(2.72)
Figura 2.11: Coeficientes racionales en funci´on defrobtenidos para el modelo propuesto de M
P y escalados para su mejor ilustraci´on [20]
β(u, v) =β0−
p3(u, v)β3 0
p1(u, v) + 3p3(u, v)β02
(2.73)
De esta ecuaci´on se obtiene un valor del estimado de profundidad β mediante los coeficientes racionales dados por los t´erminos p1(u, v), p3(u, v). Watanabe y Nayar [20] encontraron de esta manera que la precisi´on del modelo es muy exacta para un rango de frecuencias radiales fr un poco m´as amplio que el encontrado para que la monotonicidad de M
P sea v´alida, y este rango lo obtuvieron experimentalmente. Sin
embargo, se puede agregar un filtro previo al procesamiento en el algoritmo que remueva todas las componentes de frecuencia fuera de este rango deseado para evitar errores en los estimados de profundidad.
Ya con un modelo preciso para el cociente normalizado de M
P hay que encontrar
la manera de utilizarlo pero en el dominio del espacio. De (2.67) mediante productos cruzados obtenemos:
nM X
i=1
M(u, v, α)GMi(u, v)bMi(β) = nP X
i=1
P(u, v, α)GPi(u, v)bPi(β) (2.74)
Z ∞ −∞ Z ∞ −∞ nM X i=1
M(u, v, α)GMi(u, v)bMi(β) du dv=
Z ∞ −∞ Z ∞ −∞ nP X i=1
P(u, v, α)GPi(u, v)bPi(β) du dv nM X i=1 Z ∞ −∞ Z ∞
−∞M(u, v, α)GMi(u, v)du dv bMi(β) =
nP X i=1 Z ∞ −∞ Z ∞ −∞
P(u, v, α)GPi(u, v)du dv bPi(β) (2.75)
o bien:
nM X
i=1
cMi(α)bMi(β) = nP X
i=1
cPi(α)bPi(β) (2.76)
donde
cMi(α) = Z ∞
−∞
Z ∞
−∞
M(u, v, α)GMi(u, v)du dv
cPi(α) = Z ∞
−∞
Z ∞
−∞
P(u, v, α)GPi(u, v)du dv (2.77)
Para esta ´ultima ecuaci´on, podemos utilizar el teorema de Parseval [24], el cual es el siguiente:
Z ∞
−∞
Z ∞
−∞F(u, v)G(u, v)du dv=
Z ∞
−∞
Z ∞
−∞f(x, y)g(−x,−y)dx dy (2.78)
donde F(u, v), f(x, y) y G(u, v), g(x, y) son pares de Fourier. En el teorema, el lado derecho es una convoluci´on, por lo que para (2.77) utilizando el teorema, obtenemos:
cMi(x, y, α) = Z ∞
−∞
Z ∞
−∞m(x ′
, y′
, α)gMi(x−x
′
, y−y′
)dx′
dy′
cPi(x, y, α) = Z ∞
−∞
Z ∞
−∞p(x ′
, y′
, α)gPi(x−x
′
, y−y′
)dx′
dy′
cMi(x, y, α) = m(x, y, α)∗gMi
cPi(x, y, α) = p(x, y, α)∗gPi (2.80)
las cuales implican que en realidad cMi, cPi tambi´en son funciones del dominio del
espacio (x, y). De esta manera, podemos encontrar las magnitudes de los espectros frecuenciales para el modelo del cociente normalizado M
P mediante convoluciones con los
coeficientes racionales en el dominio del espacio. Aplicando (2.80) para los coeficientes en el modelo de (2.68) obtenemos los coeficientes de inter´es:
cM1(x, y, α) = m(x, y, α)∗gM1
cP1(x, y, α) = p(x, y, α)∗gP1
cP2(x, y, α) = p(x, y, α)∗gP2 (2.81)
y utilizando estos coeficientes en el modelo (2.68) despu´es de realizarle productos cruza-dos, obtenemos:
cM1(x, y, α) = cP1(x, y, α)β+cP2(x, y, α)β
3
m(x, y, α)∗gM1 =p(x, y, α)∗gP1β+p(x, y, α)∗gP2β
3
(2.82)
Y como las relaciones en (2.81) pueden ser obtenidas mediante las convoluciones de las im´agenes de enfoque lejano y cercano con los coeficientes de el modelo en cuesti´on, podemos obtener el estimado de profundidad β resolviendo (2.81).
ancho de banda en el dominio de la frecuencia. Watanabe y Nayar [20] proponen un tama˜no de 7×7 para los kernels, y muestran un ejemplo de kernels para los coeficientes racionales basados en el modelo en particular que se ha utilizado hasta ahora, y se muestran a continuaci´on:
gM1 =
0,00133 0,0453 0,1799 0,297 0,1799 0,0453 −0,00133 0,0453 0,4009 0,8685 1,093 0,8685 0,4009 0,0453 0,1799 0,8685 2,957 4,077 2,957 0,8685 0,1799 0,297 1,093 4,077 6,005 4,077 1,093 0,297 0,1799 0,8685 2,957 4,077 2,957 0,8685 0,1799 0,0453 0,4009 0,8685 1,093 0,8685 0,4009 0,0453
−0,00133 0,0453 0,1799 0,297 0,1799 0,0453 −0,00133
gP1 =
−0,03983 −0,09189 −0,198 −0,259 −0,198 −0,09189 −0,03983
−0,0198 −0,3276 −0,4702 −0,4256 −0,4702 −0,3276 −0,0198
−0,198 −0,4702 −0,3354 1,393 −0,3354 −0,4702 −0,198
−0,259 −0,4256 1,393 3,385 1,393 −0,4256 −0,259
−0,198 −0,4702 −0,3354 1,393 −0,3354 −0,4702 −0,198
−0,0198 −0,3276 −0,4702 −0,4256 −0,4702 −0,3276 −0,0198
−0,03983 −0,09189 −0,198 −0,259 −0,198 −0,09189 −0,03983
gP2 =
0,05685 −0,02031 −0,06835 −0,06135 −0,06835 −0,02031 0,05685
−0,02031 −0,06831 0,05922 0,1454 0,05922 −0,06831 −0,02031
−0,06835 0,05922 0,1762 −0,01998 0,1762 0,05922 −0,06835
−0,06135 0,1454 −0,01998 −0,698 −0,01998 0,1454 −0,06135
−0,06835 0,05922 0,1762 −0,01998 0,1762 0,05922 −0,06835
−0,02031 −0,06831 0,05922 0,1454 0,05922 −0,06831 −0,02031 0,05685 −0,02031 −0,06835 −0,06135 −0,06835 −0,02031 0,05685
Cap´ıtulo 3
Implementaci´
on
En este Cap´ıtulo se muestran los resultados de la implementaci´on realizada dentro de este trabajo1
. La t´ecnica implementada est´a basada en el m´etodo de filtros racionales de Watanabe y Nayar [20]. En la Figura 3.1 se muestra un diagrama a bloques del algo-ritmo implementado para su mejor entendimiento, en donde se muestran las variables presentadas en el Cap´ıtulo 2 para cada etapa del algoritmo.
En el diagrama de la Figura 3.1 el algoritmo base se muestra del lado izquierdo en los bloques de l´ıneas continuas, mientras que los bloques con l´ıneas punteadas son las modificaciones que mejoran los resultados del algoritmo b´asico. Aunque los autores del algoritmo utilizan el filtrado previo y el suavizado de manera permanente en sus experimentos, en la implementaci´on de este trabajo se llegan a omitir estos bloques en algunos casos, ya que no siempre mejoran los resultados de los experimentos realizados. As´ı mismo, los ´ultimos bloques son filtros en la etapa final del algoritmo, y dependiendo el caso, se hizo uso de alguno de estos filtros o alguna combinaci´on de ellos para mejorar los resultados.
la matriz de β. Dependiendo de la combinaci´on de bloques de la Figura 3.1 que se utilice, el c´odigo contiene desde 3 hasta 9 convoluciones, m´as operaciones simples en ciclos anidados que recorren los p´ıxeles de las variables de tama˜no 659×493, m´as la obtenci´on de histogramas y el ordenamiento en sub-m´ascaras utilizadas en los filtros de moda y de mediana.
Se hicieron experimentos con im´agenes sint´eticas y reales para probar la efectividad del algoritmo, y los resultados se presentan a continuaci´on.
3.1.
Im´
agenes Sint´
eticas
Es conveniente hacer uso de im´agenes sint´eticas generadas computacionalmente con las caracter´ısticas requeridas para probar el funcionamiento del algoritmo libre de los errores causados por la captura de las im´agenes que se comentaron en el Cap´ıtulo 2. Primeramente se utilizaron im´agenes sint´eticas con desenfoque sint´etico. Se generaron 2 im´agenes hechas por simples l´ıneas rectas, y se les aplic´o un desenfoque sint´etico, posteriormente se intercalaron segmentos de ambas im´agenes para crear el efecto de que los segmentos de una de ellas estaban m´as lejos que los segmentos de la otra imagen. De esta manera se simularon las im´agenes de enfoque lejano y cercanoi1(x, y),
[image:54.612.209.431.455.634.2]i2(x, y) que utiliza el algoritmo. El par de im´agenes generadas se muestra en la Figura 3.2, y el resultado del algoritmo, es decir, su gr´afica en 3D se muestra en la Figura 3.3.
Figura 3.2: Im´agenes i1(x, y), i2(x, y) simuladas computacionalmente
Figura 3.3: Mapa de 3D, resultado del algoritmo para las im´agenes sint´eticas sint´etico. Se utilizaron 2 im´agenes de texturas reales de arena y piedra, a las cuales se les gener´o un desenfoque sint´etico, y posteriormente fueron intercaladas de la misma manera que con las im´agenes anteriores. El par de im´agenes generadas se muestran en la Figura 3.4, y su mapa de 3D se muestra en la Figura 3.5.
Figura 3.5: Mapa de 3D para las im´agenes de textura real y desenfoque sint´etico
3.2.
Im´
agenes Reales
Ya una vez probado el algoritmo para im´agenes sint´eticas, se realizaron experi-mentos con im´agenes reales capturadas con equipo de video especializado para poder variar los par´ametros de la lente en los pares de im´agenes (ver Ap´endice B). Se pre-sentan los pares de im´agenes de dos objetos en los que se basan los resultados de estos experimentos. Los 2 pares de im´agenes se muestran en la Figura 3.6 y en la Figu-ra 3.7. Se presentan los resultados obtenidos mediante los distintos filtros de mejoFigu-ra que aparecen en los bloques punteados del diagrama en la Figura 3.1, pretendiendo hacer una comparaci´on entre la efectividad de cada uno, ya que dependiendo el caso, los resultados de alguno de los filtros son m´as efectivos.