Ecuaciones Diferenciales Ordinarias EDO

(1)

Ecuaciones Diferenciales Ordinarias EDO

Contenido temático

Primer orden

o Variables Separables o Lineales y Bernoulli

o Exactas y factor integrante

o Homogéneas

o Aplicaciones con Modelado Decaimiento Radiactivo Crecimiento poblacional Ley de enfriamiento y

calentamiento de Newton Circuitos eléctricos

Circuito RL Circuito RC Drenado de un fluido

Cono invertido Orden Superior Lineales

o Coeficientes constantes Homogéneas No homogéneas

por Coeficientes indeterminados Variación de

Parámetros

o Coeficientes x de grado escalonado Ecuación de Cauchi-Euler

Homogéneas

No homogéneas por Variación de Parámetros o Aplicaciones con modelado Transformada de Laplace

o Definición de Transformada de Laplace

o Transformada inversa

o Solución de ecuaciones diferenciales o

Solución de la ecuación diferencial

Se indica el método de solución algunos pasos algebraicos Orden primero se solicita:

o Nombre del Método de solución. o Modelo y algoritmo de solución o Prueba del método

o Integrales realizadas o Solución general o Valor de la constante C o Solución Particular Orden superior se solicita

o Método de solución

o Ecuación auxiliar para la parte homogénea

o Soluciones independientes: y1

y2

yc = C1 y1 + C2 y2 yp

yt = yc + yp ytp

Para problemas de modelado orden primero

o Ecuación diferencial o Integrales

o Soluciones independientes General directa

implícita o explicita Constantes, C, k Particular

(2)

Tema

Ecuaciones Diferenciales Ordinarias de Primer Orden

Ejercicios Resueltos

Variables Separables

Modelo

Solución

A) Cociente (derivada, diferenciales)

𝑑𝑦 𝑑𝑥 =

𝑓(𝑥)

𝑔(𝑦); 𝑑𝑦 = 𝑓(𝑥) 𝑔(𝑦) 𝑑𝑥

𝑑☻

𝑑 = ☻ ; 𝑑☻= ☻ 𝑑

∫ 𝑔(𝑦)𝑑𝑦 = ∫ 𝑓(𝑥)𝑑𝑥 + 𝐶

∫☻𝑑☻= ∫ 𝑑 +©

B) Producto (derivada, diferenciales)

𝑑𝑦

𝑑𝑥= 𝑓(𝑥) 𝑔(𝑦) ; 𝑑𝑦= 𝑓(𝑥) 𝑔(𝑦) 𝑑𝑥

𝑑☻

𝑑 = ☻ ;𝑑☻= ☻ 𝑑

∫ 𝑑𝑦

𝑔(𝑦)= ∫ 𝑓(𝑥)𝑑𝑥 + 𝐶

∫𝑑_☻☻= ∫ 𝑑 +©

Metodología

1. Separar las variables g(y) dy lado izquierdo (de preferencia) y f(x) dx lado derecho 2. Integrar cada lado respecto a su variable. Para determinar la solución general. Se

prefiere cuando sea posible la solución explícita y cuando sea muy complicado se deja como una solución implícita

3. La estructura de la C puede ser: a. Lineal (Se queda igual)

A = 𝐵 + 𝐶

b. Semilogarítmica (se exponencian ambos lados y simplifica)

ln(𝐴) = 𝐵 + 𝐶

𝑒ln (𝐴) = 𝑒𝐵+𝐶 = 𝑒𝐵𝑒𝐶 = 𝐶𝑒𝐵 𝐴 = 𝐶𝑒𝐵

c. Logarítmica (la constante se pone en forma de logaritmo y se exponencian ambos lados y simplifica)

ln(𝐴) = ln(𝐵) + 𝐶; 𝐶 = ln (𝐶) ln(𝐴) − 𝑙𝑛(𝐵) = ln (𝐶)

ln (𝐴

𝐵) = ln (𝐶) 𝑒ln (𝐴/𝐵)= 𝑒ln (𝐶) 𝐴

𝐵= 𝐶 𝐴 = 𝐶𝐵

4. Para EDO con valores de Ci condiciones iniciales (PVI). a. Sustituir los valores de las Ci

𝑦(𝑥₀) = 𝑦₀

(3)

b. Se sustituye el valor de C en la solución general para hallar la solución particular.

Ejemplo 1.

Calcular la solución general y hallar la solución particular. Metodología general: a) Se sustituye, 𝑦′= 𝑑𝑦

𝑑𝑥

b) Se separan las funciones, la función de la variable dependiente g(y) junto a dy en el lado izquierdo y la función dependiente f(x) junto a dx del lado derecho.

c) Se integra ambos lados respecto a su variable correspondiente.

(𝟐𝒙 + 𝟏) 𝒚´ = (𝟒𝒙 − 𝟑)(𝟐𝒚 − 𝟏)

;

y(1)=1, opción: y(0) =0

Separar las variables

𝑑𝑦 𝑑𝑥 =

(4𝑥 − 3)(2𝑦 − 1) (2𝑥 + 1)

1

(2𝑦 − 1)𝑑𝑦 =

(4𝑥 − 3) (2𝑥 + 1) 𝑑𝑥

Integrar (ambos lados más la constante)

∫ 1

(2𝑦 − 1) 𝑑𝑦 = ∫

4𝑥 − 3

2𝑥 + 1 𝑑𝑥 + 𝐶

Lado derecho por división de polinomios

∫ 1

(2𝑦 − 1) 𝑑𝑦 = 2 ∫ 𝑑𝑥 − 5 ∫ 1

2𝑥 + 1+ 𝐶

1

2ln(2𝑦 − 1) = 2𝑥 − 5

2ln (2𝑥 + 1) + 𝐶

Multiplicando (x 2)

ln(2𝑦 − 1) = 4𝑥 − 5 ln (2𝑥 + 1) + 𝐶 ln(2𝑦 − 1) + 5 ln(2𝑥 + 1) = 4𝑥 + 𝐶 ln(2𝑦 − 1)(2𝑥 + 1)5 = 4𝑥 + 𝐶

exponenciando (ambos lados)

𝑒𝑙𝑛(2𝑦−1)(2𝑥+1)5 = 𝑒(4𝑥+𝐶) = 𝑒4𝑥𝑒𝐶 = 𝐶𝑒4𝑥

Simplificando (exponencial/logaritmo)

Modelo estándar para Variables Separables

A) Cociente 𝑑∎

𝑑∆ = ∆ ∎;

∫∎𝑑∎= ∫ ∆𝑑∆ +©

B) Producto 𝑑∎

𝑑∆ = ∆ ∎; ∫𝑑∎

∎ = ∫ ∆𝑑∆ +©

1. División de polinomios

(4𝑥 − 3)

(2𝑥 + 1) = (2 − 5 2𝑥 + 1) 2. Integral (logaritmo). Incluye la

C pero de aquí en adelante se omite por espacio y además ya está considerada en la C de la solución de la EDO

∫𝑑𝑢

𝑢 = ln(𝑢) + 𝐶

∫ 𝑑𝑦

(2𝑦 − 1)= 1

2 ln (2𝑦 − 1)

∫ 𝑑𝑦

(2𝑥 + 1)= 1

(4)

(2𝑦 − 1)(2𝑥 + 1)5 _{= 𝐶𝑒}4𝑥

(2𝑦 − 1) = 𝐶𝑒

4𝑥

(2𝑥 + 1)5

Despejando “y” (solución explícita)

2𝑦 = 𝐶𝑒

4𝑥

(2𝑥 + 1)5+ 1

𝑦 = 𝐶𝑒

4𝑥

2(2𝑥 + 1)5+

1 2=

𝐶𝑒4𝑥 (2𝑥 + 1)5+

1 2; 𝐶 =

𝐶 2

Solución general

𝒚 = 𝑪𝒆 𝟒𝒙

(𝟐𝒙 + 𝟏)𝟓+ 𝟏 𝟐

Condiciones iniciales

𝑦(1) = 1

Sustituir los valores x=1, y=1

1= 𝐶𝑒

4(1)

(2(1) + 1)5+

1 2

Despejar C

1 −1 2=

𝐶𝑒4

35 ; 𝐶 = (

1 2)

35

𝑒4 = 2.225

Solución particular, sustituyendo el valor de C, en la solución general.

𝒚 =𝟐. 𝟐𝟐𝟓 𝒆 𝟒𝒙

(𝟐𝒙 + 𝟏)𝟓 + 𝟏 𝟐

La solución gráfica hay una discontinuidad Infinita en x=(-1/2)

¡Recuérdame!

Álgebra Derivadas Integrales

Propiedades de los logaritmos: ln(𝐴 ∙ 𝐵 ) = ln(𝐴) + ln(𝐵)

ln (𝐴

𝐵) = ln(𝐴) − ln(𝐵) ln(𝐴𝑟_{) = r ∙ ln(𝐴)}

(5)

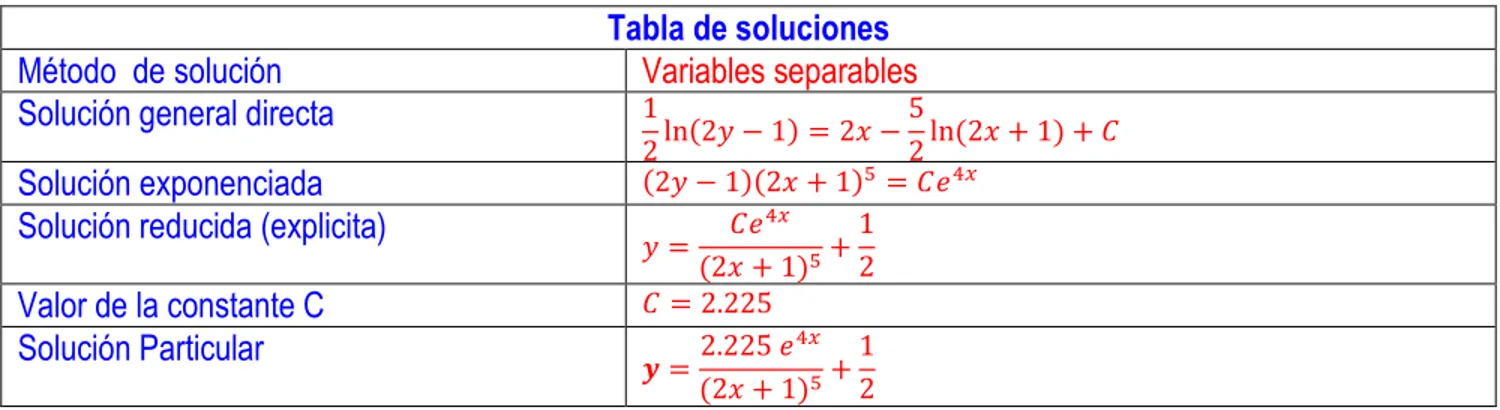
Tabla de soluciones

Método de solución Variables separables Solución general directa 1

2ln(2𝑦 − 1) = 2𝑥 − 5

2ln (2𝑥 + 1) + 𝐶 Solución exponenciada (2𝑦 − 1)(2𝑥 + 1)5_{= 𝐶𝑒}4𝑥

Solución reducida (explicita) _{𝑦 =} 𝐶𝑒4𝑥

(2𝑥 + 1)5+

1 2 Valor de la constante C 𝐶 = 2.225

Solución Particular _{𝒚 =}2.225 𝑒4𝑥

(2𝑥 + 1)5+

1 2

Ejercicio suplementario 1:

(𝒙 + 𝟏) 𝒚´ = (𝟑𝒙 + 𝟏)(𝟐𝒚 − 𝟏) ; 𝑦(0) = 2;

𝒚 = 𝑪𝒆 𝟔𝒙

(𝟐𝒙 + 𝟏)𝟒+ 𝟏 𝟐

𝒚 =𝟑 𝟐

𝒆𝟔𝒙 (𝟐𝒙 + 𝟏)𝟒+

(6)

Ejemplo 2.

Calcular la solución general y hallar la solución particular.

Metodología general: A. Se sustituye, 𝑦′= 𝑑𝑦

𝑑𝑥

B. Se separan las funciones, la función de la variable dependiente g(y) junto a dy en el lado izquierdo y la función dependiente f(x) junto a dx del lado derecho. C. Se integra ambos lados respecto a su variable

(𝟐𝒙 − 𝟏) 𝒚

′

= 𝒚

𝟐

− 𝒚

;

𝑦(1) = −1

𝑑𝑦 𝑑𝑥 =

𝑦(𝑦 − 1) (2𝑥 − 1)

Separar las variables

1

𝑦(𝑦 − 1)𝑑𝑦= 1

(2𝑥 − 1) 𝑑𝑥

Integrar (ambos lados más la constante)

− ∫1

𝑦𝑑𝑦 + ∫ 1

(𝑦 − 1) 𝑑𝑦 = ∫ 1

2𝑥 − 1 𝑑𝑥 + 𝐶

− ln(𝑦) + ln (𝑦 − 1) =1

2ln (2𝑥 − 1) + 𝐶

Multiplicando (x2)

−2 ln(𝑦) + 2ln (𝑦 − 1) = ln (2𝑥 − 1) + 𝐶

Propiedades de C por el formato de la solución

−2 ln(𝑦) + 2ln (𝑦 − 1) = ln (2𝑥 − 1) + ln (𝐶)

Propiedades de los logaritmos

ln ((𝑦 − 1)

2

𝑦2 ) = ln (𝐶(2𝑥 − 1)) exponenciando

Propiedades de la constante C exponenciando (ambos lados)

Modelo estándar para Variables Separables

C) Cociente 𝑑∎ 𝑑∆ =

∎ ∆ ∫1

∎𝑑∎= ∫ 1

∆𝑑∆ +©

1. Por fracciones parciales

1 𝑦(𝑦 − 1)=

𝐴 𝑦+

𝐵 𝑦 − 1; 1 = 𝐴(𝑦 − 1) + 𝐵𝑦 = 𝐴𝑦 − 𝐴 + 𝐵𝑦

1 = 𝑦(𝐴 + 𝐵) − 𝐴;

𝐴 = −1; 𝐴 + 𝐵 = 0; 𝐵 = 1

1 𝑦(𝑦 − 1)=

−1

𝑦 +

1 𝑦 − 1

2. Integral (logaritmo natural).

∫𝑑@

@ = ln(@)

∫ 𝑑@

@ + =

1

ln(@ + )

∫𝑑𝑦

𝑦 = ln(𝑦)

∫ 𝑑𝑦

(𝑦 − 1)= ln (𝑦 − 1)

∫ 𝑑𝑦

(2𝑥 − 1)= 1

2 ln (2𝑥 − 1) 3. Propiedades de C

C = ln(𝐶)

4. Propiedades de los logaritmos ln(∎ ∙ ∆ ) = ln(∎) + ln(∆) ln (∎

(7)

𝑒𝑙𝑛[

(𝑦−1)2

𝑦2 ]

= 𝑒(𝐶(2𝑥−1))

Simplificando (exponencial/logaritmo)

((𝑦 − 1) 2

𝑦2 ) = 𝐶(2𝑥 − 1)

Solución general explícita

(𝑦 − 1)2 _{= 𝐶𝑦}2_{(2𝑥 − 1)}

𝑦(1) = −1

Sustituir los valores x=1, y= -1

(−1 − 1)2 _{= 𝐶(−1)}2_{(2(1) − 1)}

Despejar C

4= 𝐶 ; 𝐶 = 4

Solución particular, sustituyendo el valor de C, en la solución general.

(𝑦 − 1)2 _{= 4𝑦}2_{(2𝑥 − 1)}

La solución gráfica

𝑥 →1

2, 𝑥 = 0.3; 𝑥 = −1

Tabla de soluciones

Método de solución Variables separables Solución general directa

− ln(𝑦) + ln (𝑦 − 1) = 1

2ln (2𝑥 − 1) + 𝐶 Solución general arreglada −2 ln(𝑦) + 2ln (𝑦 − 1) = ln (2𝑥 − 1) + ln (𝐶)

ln ((𝑦 − 1)

2

𝑦2 ) = ln (𝐶(2𝑥 − 1))

Solución exponenciada y reducida

𝑒𝑙𝑛[

(𝑦−1)2

𝑦2 ]

= 𝑒(𝐶(2𝑥−1))

(𝑦 − 1)2

𝑦2 = 𝐶(2𝑥 − 1 Solución general reducida (implícita) (𝑦 − 1)2 _{= 4𝑦}2_{(2𝑥 − 1)}

¡Recuérdame!

Álgebra Derivadas Integrales

Propiedades de los logaritmos: ln(𝐴 ∙ 𝐵 ) = ln(𝐴) + ln(𝐵)

ln (𝐴

𝐵) = ln(𝐴) − ln(𝐵) ln(𝐴𝑟_{) = r ∙ ln(𝐴)}

𝑒ln(𝐴)_{= 𝐴} La constante C

(8)

Valor de la constante C 𝐶 = 4

Solución Particular (𝑦 − 1)2 _{= 4𝑦}2_{(2𝑥 − 1)}

Buscando la solución general explícita a partir de la solución implícita

(𝑦 − 1 𝑦 )

2

= 𝐶(2𝑥 − 1)

𝑦 − 1

𝑦 = ±𝐶√2𝑥 − 1 1 −1

𝑦 = ±𝐶√2𝑥 − 1

−1

𝑦 = ±𝐶√2𝑥 − 1 − 1

Multiplicando por (-1)

1

𝑦= ±𝐶√2𝑥 − 1 + 1

Despejando y

1 = (±𝐶√2𝑥 − 1 + 1)𝑦

𝑦= 1

(1 ± 𝐶√2𝑥 − 1)

𝑦(1) = −1

𝑦 − 1

𝑦 = ±𝐶√2𝑥 − 1

±𝐶 = −1 − 1

(−1)√2(1) − 1= 2 𝐶 = ±2

La solución particular

𝑦= 1

(1 ± 2√2𝑥 − 1)

La gráfica solución no está Determinada para valores

𝑥 <1 2

Ejercicio suplementario 1:

1B. (2𝑥 + 1) 𝑦′ _{= 𝑦}2_{− 𝑦}

𝑦(4) = −1

𝑦= 3

(9)

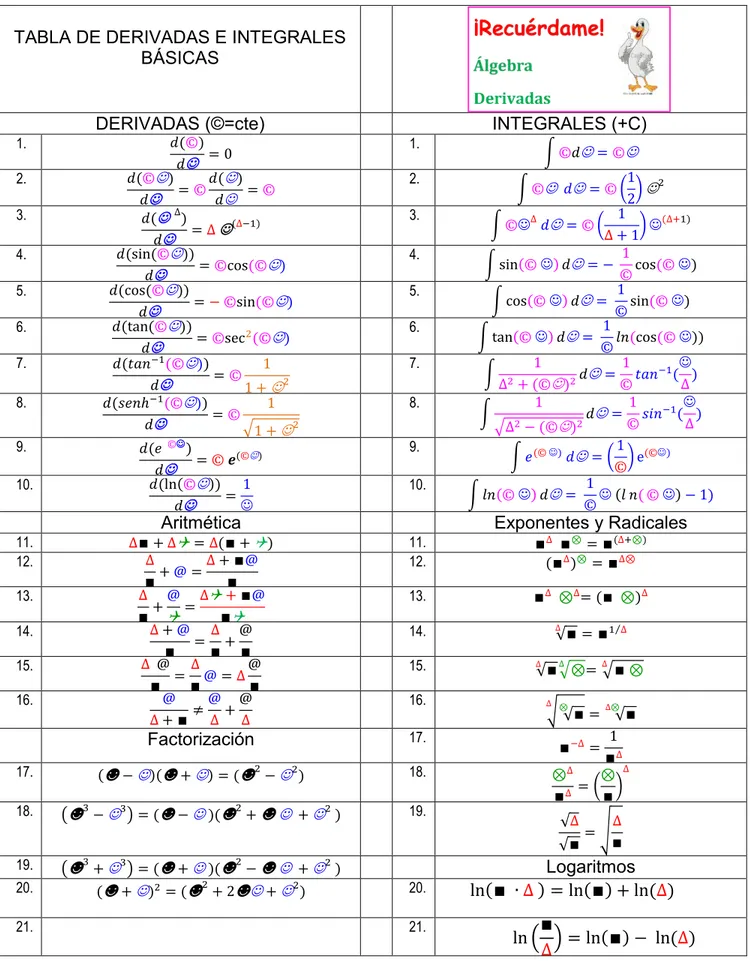
TABLA DE DERIVADAS E INTEGRALES BÁSICAS

DERIVADAS (©=cte) INTEGRALES (+C)

1. 𝑑(©)

𝑑 = 0

1.

∫©𝑑 =©

2. 𝑑(© )

𝑑 =©

𝑑( )

𝑑 =©

2.

∫© 𝑑 =©(1 2)

2

3. _𝑑( ∆

)

𝑑 =∆

∆+ 1)

(∆+1)

4. 𝑑(sin(© ))

𝑑 =©cos (© )

4.

©cos (© )

5. 𝑑(cos(© ))

𝑑 =− ©sin (© )

5.

∫ cos(© )𝑑 = 1

©sin (© )

6. 𝑑(tan(© ))

𝑑 =©sec

©𝑙𝑛 (cos (© ))

𝑑 =©

1 1 + 2

7.

∫ 1

1

©𝑡𝑎𝑛

−1₍

∆)

𝑑 =©

1 √1 + 2

8.

∫ 1

1

©𝑠𝑖𝑛

−1₍

∆)

9. 𝑑(𝑒 © ₎

𝑑 =© 𝒆

©) e

10. 𝑑(ln(© ))

𝑑 =

1 10.

∫ 𝑙𝑛(© )𝑑 = 1

Aritmética Exponentes y Radicales

11. ∆∎ +∆ =∆(∎ + ) 11. ∎∆_∎⊗ _{= ∎}(∆+⊗)

12. ∆

∎+@=

∆+ ∎@

∎

12. (∎∆₎⊗_{= ∎}∆⊗

13. ∆

∎+

@

=∆ +∎@

∎

13. ∎∆ _⊗∆_{= (∎}_⊗₎∆

14. ∆+@

∎ =

∆

∎+

@ ∎

14. ∆_√∎

= ∎1⁄∆

15. ∆ @

∎ =

∆

∎@=∆

@ ∎

15. _√∎∆

√⊗ ∆ = √∎∆ ⊗ 16. @ ∆+ ∎≠ @ ∆ + @ ∆ 16. √ √∎⊗ ∆ = √∎∆⊗

Factorización 17.

∎−∆= 1 ∎∆

17. ₍_☻₋ ₎₍_☻₊ _{) = (}_☻2

− 2) 18. ⊗∆

∎∆ = (

⊗

∎)

∆

18. ₍_☻3

− 3) = (☻− )(☻2+☻ + 2 ) 19. _√∆

√∎= √

∆ ∎

19. ₍_☻3

+ 3) = (☻+ )(☻2−☻ + 2 ) Logaritmos

20. ₍_☻₊ ₎2_{= (}_☻2

+ 2☻ + 2) 20. ln(∎ ∙∆ ) = ln(∎) + ln(∆)

21. 21.

ln (∎

(10)

22. 22. _ln(∎∆_{) =}_{∆ ∙ ln(∎)}

(11)

(12)

(13)

Jea

ne

tt

e

G

on

zá

le

z R

ob

les

S

án

ch

e

z

E

cua

cio

ne

s D

iferenc

ia

les

V

ari

ab

les

S

ep

ara

bl

es