M ´etodo de proyecciones oblicuas incompletas para resolver el
problema de M´ınimos Cuadrados con restricciones de caja
Echebest,N ´elida E. Guardarucci,Mar´ıa T. Scolnik,Hugo
Departamento de Ciencias B ´asicas, Facultad de Ingenier´ıa, UNLP,47 esq.1, La Plata, marite.guardarucci@ing.unlp.edu.ar
Palabras claves: sistemas inconsistentes,proyecciones oblicuas
INTRODUCCI ´ON
En varias aplicaciones de reconstrucci ´on de im ´agenes, mec ´anica computacional , proble-mas de optimizaci ´on, etc. aparecen probleproble-mas que requieren resolver sisteproble-mas de ecuaciones lineales, grandes y esparsos, que a menudo son inconsistentes y requieren que la soluci ´on x∗ ∈ ℜn
, sea acotadali ≤x∗i ≤ui,i= 1, . . . , ny minimice alguna funci ´on de proximidad.
En [9] presentamos el algoritmo IOP que converge a una soluci ´on de m´ınimos cuadra-dos pesada del sistema inconsistente Ax = b, A ∈ ℜm×n
, b ∈ ℜm
,, usando un esquema de proyecciones oblicuas incompletas sobre el conjunto de soluciones del sistema aumentado Ax−r=b. Hemos considerado el problema standart
min
x∈ℜnb−Ax 2
Dm, (1)
donde.Dmes la norma inducida por la matriz diagonal definida positivaDm ∈ ℜ
m×m
bas ´andonos en la equivalencia demostrada entre este problema y el problema
min{p−q2D : para p∈ Py q ∈ Q},
donde
P ={p:p= [x;r]∈ ℜn+m
, x∈ ℜn, r∈ ℜm, Ax−r =b}, y Q={q :q= [x; 0]∈ ℜn+m, x∈ ℜn,0∈ ℜm},
yDis a diagonal matrix of ordern+m, whosenfirst elements are1’s, and the lastmcoincide with those ofDm.
El m ´etodo IOP propuesto para resolver (1) mediante un esquema de proyecciones alter-nadas entreP yQ,, similar al desarrollado por Csisz ´ar and Tusn ´ady [6], reemplaza el c ´alculo de la proyecci ´on exacta sobreP por una proyecci ´on incompleta que aproxima a la soluci ´on de una manera aceptable.
En este trabajo agregamos la condici ´on x ∈ B, dondeB = {x : x ∈ ℜn
, li ≤ xi ≤ ui, i =
1, . . . , n}, lo que lleva a redefinir
Pb =P{(x;r) :x∈ B} y Qb =Q{(x; 0) :x∈ B}, (2)
Algoritmo 1 (Esquema B ´asico Alternante)
Paso Iterativo: Dadopk
= [xk
;rk
]∈ Pb , yqk
= [xk
; 0]∈ Qb , hallarpk+1
r = [x
k+1;rk+1]∈ Pb
tal que:
pkr+1 ≈arg min{p−q k
2D :p∈ P b
}, luego
definirpk+1 =pk+1
r , and q
k+1∈ Qb
qk+1= [xk+1; 0]≡arg min{pk+1 −q2
D : q ∈ Q b
Para computar las proyecciones incompletas sobre Pb aplicamos el algoritmo Halpern-Lions-Wittmann- Bauschke(HLWB) [5]. Cuando HLWB es aplicado para resolver un sistema de desigualdades lineales consistenteSy¯ ≤¯c, la secuencia{yk}generada a partir de un punto inicialy0 converge a una soluci ´on que satisface
¯
y∗= arg min{y∗−y0
2
D, y ∗
∈ ℜn: ¯Sy∗ ≤¯c}.
Presentaremos el algoritmoBIOP basado en el esquema b ´asico, proponiendo una condici ´on para aceptar una soluci ´onpk+1
r enPb que aproxime a la proyecci ´on exacta de manera tal de asegurar convergencia a una soluci ´on de (1)
RESULTADOS
Usaremos la notaci ´on:xD para la norma inducida por una matrizDdefinida positiva,mT i para referirnos a la filaide una matrizM,R(M)para el subespacio generado por las columnas deM,PM and PMD para los proyectores ortogonales y oblicuos sobreR(M),R(M)
⊥
para el subespacio D-ortogonal aR(M)yPD
M⊥ para su correspondiente proyector.
Supondremos que el sistema Ay¯ = ¯b, A¯ ∈ ℜm×n, ¯b ∈ ℜm es compatible y que cada fila de A tiene norma Eucl´ıdea igual a 1. Para cada restricci ´on en el sistema denotaremos
Li={y∈ ℜn:a¯Ti y= ¯bi},ri(y) =¯aTi y−b¯i,and the oblique projection ofyontoLi por
PiD(y) =y− ri(y) ¯aT
i D
−1¯a
i
D−1¯ai. (3)
Dado un sistema deminecuaciones lineales
S :={y∈ ℜn: sTjy≤cj, j= 1,2, . . . , m} (4)
supondremos que tiene soluci ´on, denotaremos con S a la matriz del sistema y llamaremos
y∗
a cualquier soluci ´on admisible deSy ≤ c. Cuando z no pertenezca a alg ´un semiespacio particular Sj, es decir cuando rj = sTjz −cj > 0, la proyecci ´on exacta de z sobre Sj ser ´a calculada poryj =PSj(z) =z+sj(−rj)/sj
2
.
Tal como dijimos, para sistemas acotados, posiblemente inconsistentes, Ax = b, x ∈ B,
A∈ ℜm×n,b∈ ℜm,m≥n, trabajamos con el problema asociado
min
x∈BAx−b 2
Dm. (5)
Usando un esquema de proyecciones alternantes sobre los conjuntosPb yQb. Dadopk∈ Pb, y su proyecci ´onqksobreQb, denotamospD
min(qk)a la proyecci ´on exacta de
qksobrePb, soluci ´on del problema
min{p−qkD : p∈ Pb}. (6)
En el nuevo algoritmo, dado qk ∈ Qb reemplazamos el c ´alculo de pk+1
= pD
min(qk), re-solviendo en forma incompleta (6) y definiendo una proyecci ´on aproximadapk+1
r ,
En [9] hemos presentado la teor´ıa de proyecciones inexactas sobre el conjunto de solu-ciones deAx−r=b. Para definirpk+1
r ≈pDmin(qk), consideraremos la siguiente:
Definici ´on 1 Si pˆ = [zj;µj], z ∈ ℜn ,µ ∈ ℜm, es una soluc ´on aproximada de pDmin(qk),
de-notamos con Pb(ˆp) = [zb;r(zb)], donde zb es la proyecci ´on of z
j sobre xi ≥ li, o xi ≤ ui,
i= 1, . . . , n, yr(zb) =Azb−b.
Definici ´on 2 Condici ´on de Aceptaci ´on.
Dada una sucesi ´on{βk}que tiende a0cuandoktiende a∞, diremos quepˆj = [zj;µj]es
una aproximaci ´on aceptable depDmin(qk)si la proyecci ´on inexactaPb(ˆp) = [zb;r(zb)], satisface:
(i)pˆj−T(pj−1)D ≤βkqk−T(pj−1)D (7) (ii)Pb( ˆpj)−qk2D <pk−qk
2
D,yPb(ˆp)−pˆ
2
D ≤γpk−Pb(ˆp)
2
D, 0< γ <1, (8) En ese caso aceptamospk+1
r =Pb( ˆpj)como soluci ´on aproximada depDmin(qk).
Lema 1 Si el problema (6) es resuelto mediante el algoritmo HWLB entonces es posible hallar un iteradopˆj que satisfaga las condiciones (7) y (8).
Algoritmo 2 Bounded Incomplete Oblique Projections (BIOP)
Inicializaci ´on: Dado 0 < γ < 1; una matriz diagonal, de orden m, definida positivaDm y p0 = [x0;r0], conx0 ∈ B, yr0 =Ax0−b; q0 = [x0; 0]∈ Qbyk= 0.
Paso Iterativo: Dadopk = [xk;rk], definimosqk = [xk; 0],xk∈ B.
• Calculamos p, aproximaci ´on deˆ pD
min(qk) que satisfaga las condiciones (7) y (8), aplicando HLWB como sigue: Definimos y0 = [z0
;µ0] = qk punto inicial. Iteramos hasta hallarpˆj = [zj;µj],que satisfaga las condiciones (7) y (8).
• Definimospk+1
==Pb([zj, µj]) = [xk+1
;rk+1
]
• Definimosqk+1
= [xk+1
; 0]∈ Qb.
• k←k+ 1.
Denominaremos conLsqDm al conjunto de soluciones del problema (1):
LsqD
m ={x
∗∈ B : tal quer∗=Ax∗−bsatisfaceATDmr∗ =µ∗,} (9)
conµ∗
i ≥0six∗i =li, oµ∗i ≤0,siui =x∗i, oµ∗i = 0,cuandoli< x∗i < ui.
DefinimosSDm ={p∗ :p∗ = [x∗;r∗]∈ P
btal que x∗∈Lsq
Dm}
Lema 2 Si{pk}={[xk;rk]}es la sucesi ´on generada por el Algoritmo 2, entonces
(i)pk = [xk;rk]ypk+1 = [xk+1;rk+1]satisfacen
rk+12
Dm ≤ r
k2
Dm− x
k−xk+12.
(ii) La sucesi ´on{rk
Dm}es decreciente y acotada y por tanto convergente
(iii) Las 3 sucesiones que siguen tienden a0
{pk+1
−pk2
D},
{pk+1 −pD
min(qk)
2
D}y{pk−pDmin(qk)
2
D}.
(iv) La sucesi ´on{ATD
mrk−µkmin}tiende a zero, dondeµkmines el vector de los multiplicadores
KKT asociado a las restricciones de cota en la soluci ´on del problema (6).
(v) La sucesi ´on{µk
mini∗min(x
k
i −li, ui−xki)}tiende a zero.
Lema 3 Si{pk}={[xk;rk]}es la sucesi ´on generada por el Algoritmo 2, entonces
(ii) Todo punto l´ımite de{pk}, est ´a enSDm.
(iii) SiSDm es un conjunto unitario, la sucesi ´on{[x
k
;rk]}converge ap∗,p∗ ∈ SDm.
PARTE EXPERIMENTAL
Hemos implementado nuestro algoritmo BIOP en MATLAB con el fin de compararlo con el algoritmoSBLS2para resolver problemas de m´ınimos cuadrados con restricciones de caja del sistema SSL(http://www.math.liu.se/ milun/sls). El algoritmo SBLS2 est ´a basado en el m ´etodo presentado en [1]. Nuestro m ´etodo BIOP est ´a implementado en forma secuencial con γ = 10−2 en la iteraci ´on inicial y γ = 10−1 en las siguientes. La matriz Dm fue elegida
como la matriz Identidad.El punto inicial fue siempre x0 = 0
. La condici ´on de parada para ambos algoritmos es : | rk+1
− rk
|< ǫmax(r0
,1), conǫ= 10−6. Tambi ´en se contempla
parar cuando el residuo se estanca.
Algunos de los problemas usados en los test provienen de RRA(real,rectangular)de la colecci ´on Harwell-Boeing. Del paquete LSQ hemos trabajado con 4 matrices que presentan el mismo patr ´on WELL1033, ILLC1033(real,no sim ´etrica, 1033 x 320), WELL1850 y ILLC1850 (real nosim ´etrica,1850 x 712)pero las segunda y cuarta muy mal condicionadas. Para
proble-mas de grandes dimensiones hemos usado matrices densas generadas al azar con DQRT15(LAPACK), fijando el par ´ametro RKSEL = 2 a fin de que sean de rango deficiente. Indicamos conmel nde
filas ynel n ´umero de columnas de A, con rango= 3
4min(m, n).
Otros sistemas provienen de problemas de reconstrucc ´on de im ´agenes provenientes de geotomograf´ıa y usados por Popa y Zdunek [8] y del paquete SNARK, problemas B1,B4 y B6 conm≥n.
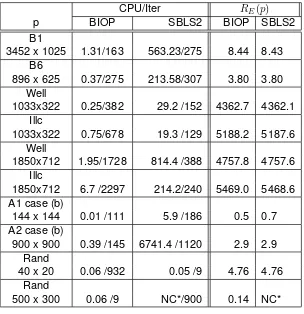
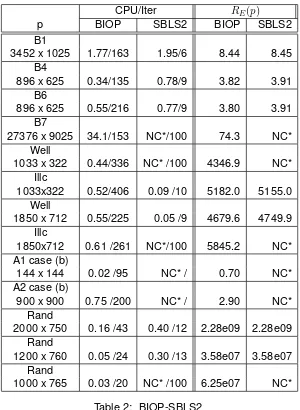
En la tabla 2 mostramos el n ´umero de iteraciones (Iter) y el tiempo de CPU ‘para alcanzar el criterio de convergencia. En la tabla 1 comparamos el n ´umero de iteraciones y tiempo
CPU/Iter RE(p)
p BIOP SBLS2 BIOP SBLS2
B1
3452 x 1025 1.31/163 563.23/275 8.44 8.43 B6
896 x 625 0.37/275 213.58/307 3.80 3.80 Well
1033x322 0.25/382 29.2 /152 4362.7 4362.1 Illc
1033x322 0.75/678 19.3 /129 5188.2 5187.6 Well
1850x712 1.95/1728 814.4 /388 4757.8 4757.6 Illc
1850x712 6.7 /2297 214.2/240 5469.0 5468.6 A1 case (b)
144 x 144 0.01 /111 5.9 /186 0.5 0.7 A2 case (b)
900 x 900 0.39 /145 6741.4 /1120 2.9 2.9 Rand
40 x 20 0.06 /932 0.05 /9 4.76 4.76 Rand
[image:4.595.147.451.444.758.2]500 x 300 0.06 /9 NC*/900 0.14 NC*
CPU/Iter RE(p)
p BIOP SBLS2 BIOP SBLS2
B1
3452 x 1025 1.77/163 1.95/6 8.44 8.45
B4
896 x 625 0.34/135 0.78/9 3.82 3.91
B6
896 x 625 0.55/216 0.77/9 3.80 3.91
B7
27376 x 9025 34.1/153 NC*/100 74.3 NC* Well
1033 x 322 0.44/336 NC* /100 4346.9 NC* Illc
1033x322 0.52/406 0.09 /10 5182.0 5155.0 Well
1850 x 712 0.55/225 0.05 /9 4679.6 4749.9 Illc
1850x712 0.61 /261 NC*/100 5845.2 NC*
A1 case (b)
144 x 144 0.02 /95 NC* / 0.70 NC*
A2 case (b)
900 x 900 0.75 /200 NC* / 2.90 NC*
Rand
2000 x 750 0.16 /43 0.40 /12 2.28e09 2.28e09 Rand
1200 x 760 0.05 /24 0.30 /13 3.58e07 3.58e07 Rand
[image:5.595.148.448.82.492.2]1000 x 765 0.03 /20 NC* /100 6.25e07 NC*
Table 2: BIOP-SBLS2
de CPU en segundos requerido por SBLS2 para alcanzar un residuo RE(p), menor o igual al obtenido por BIOP cuando la tolerancia es ǫ = 10−6
.Para BIOP reportamos el n ´umero de iteraciones internas. Indicamos con N C∗ cuando el algoritmo no converge a una soluci ´on en la caja.
CONCLUSIONES
Hemos presentado resultados mostrando el comportamiento del algoritmo IOP cuando se incluyen restricciones de cota.Los resultados muestran que BIOP es m ´as r ´apido que algoritmos conocidos y capaz de reducir el residuo m ´as r ´apidamente.
Los resultados num ´ericos muestran la efectividad de BIOP respecto de SBLS2 ya que no falla en la convergencia
References
[2] J. A. Browne, G. T. Herman, D. Odhner,SNARK93: A Programming System for Image Re-construction from Projections, Department of Radiology, University of Pennsylvania, Medi-cal Image Processing Group, TechniMedi-cal Report MIPG198, 1993.
[3] Y. Censor and S. Zenios, “Parallel Optimization: Theory and Applications,” Oxford University Press, New York, 1997.
[4] Y. Censor ,Computational acceleration of Projections algorithms for linear best approxima-tion problem, Linear Algebra and its Applications,416(2006), 111–123.
[5] P. L. Combettes,Construction d’un pointfixe commun a famille de contractions fermes, C.R. Acad. Sci. Paris, Ser. I Math. 320 (1995).
[6] I. Csisz ´ar and G. Tusn ´ady,Information geometry and alternating minimization procedures, Statistics and Decisions, Supplement,1(1984), 205–237.
[7] Ortega, J.M. and Rheinboldt, W.C: Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York and London (1970).
[8] C. Popa, R. Zdunek, Kaczmarz extended algorithm for tomographic image reconstruction from limited-data, Mathematics and Computers in Simulation,65(2004), 579–598.
[9] H. D. Scolnik, N. Echebest, M. T. Guardarucci, M. C. Vacchino, Incomplete Oblique Pro-jections for Solving Large Inconsistent Linear Systems, Mathematical Programming B,111 (2008), 273–300.