Andrea’s Reflections: A Microgenetic Analysis of the Understanding of Division in the Context of a Problem
Texto completo
Figure
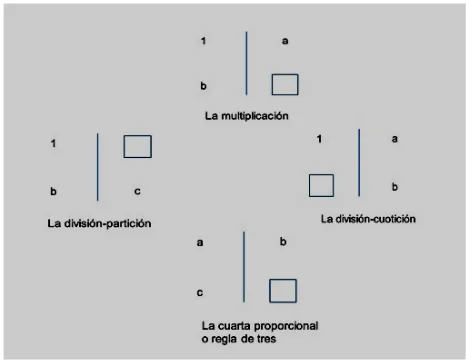
Documento similar
A modern democratic state should guarantee the protection of such human rights as dignity, freedom, and ownership of property, as well as ensure equality and social and
Parameters of linear regression of turbulent energy fluxes (i.e. the sum of latent and sensible heat flux against available energy).. Scatter diagrams and regression lines
2) If the temperature (TCOLD) inside the greenhouse is cold , then it is therefore somewhat below the set temperature then the fuzzy controller sends a signal to automatically
It is generally believed the recitation of the seven or the ten reciters of the first, second and third century of Islam are valid and the Muslims are allowed to adopt either of
In order to study the closed surfaces with constant mean curvature in Euclidean space, Alexandrov proved in 1956 that any embedded closed CMC surface in R 3 must be a round sphere..
In the preparation of this report, the Venice Commission has relied on the comments of its rapporteurs; its recently adopted Report on Respect for Democracy, Human Rights and the Rule
Volviendo a la jurisprudencia del Tribunal de Justicia, conviene recor- dar que, con el tiempo, este órgano se vio en la necesidad de determinar si los actos de los Estados
The purpose of the research project presented below is to analyze the financial management of a small municipality in the province of Teruel. The data under study has