GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS V (504) QUINTO SEMESTRE CICLO LECTIVO: 2016-B

PLANTEL 15 “CONTRERAS”

GUÍA PARA EL EXAMEN EXTRAORDINARIO DE

MATEMÁTICAS V (504)

EMPLEA LA DEFINICIÓN Y TEOREMAS DE LÍMITES EN LA CONTINUIDAD Y DISCONTINUIDAD DE LAS FUNCIONES.

LÍMITES

Definición intuitiva de límite:

El concepto intuitivo de límite es muy simple. Al hablar de límite, hablamos del valor que parece tomar la función f(x) cuando x se aproxima a cualquier x0 que

consideremos. Si tenemos la función − − 2 = 0y queremos analizarla cuando → 3, debemos escribirla en la forma explícita:

= − 2

La variable independiente es x y la y la dependiente. Tabulamos y asignamos valores a x que se aproximen a 3, por la izquierda y por la derecha

Valores por la izquierda son crecientes Valores por la derecha son decrecientes

X Y

2 0

2.9 0.9

2.99 0.99

2.999 0.999

→ 3 → 1

X y

4 2

3.1 1.1

3.01 1.01

3.001 1.001

→ 3 → 1

Para este ejemplo se dice que el límite de la función = − 2cuando x tiende a 3 es 1, esto se expresa así:

lim_→ ( − 2) = 1 Conclusión:

Cuando f(x) tiende hacia un límite, por ejemplo H, a medida que x tiende hacia el punto a, se expresa de la siguiente manera:

lim_→ ( ) = Definición de límite:

Cuando una variable x se aproxima cada vez más a una constante ,de tal manera que la diferencia → ,en valor absoluto, puede ser tan pequeña como se quiera, se dice que la constante es el límite de la variable x. Se expresa así:

→ é lim_→ =

b) Comportamiento no acotado Analice la existencia del límite

2.- crece o decrece sin cota cuando tiende a

3.- oscila entre dos valores fijos cuando tiende a .

En virtud de que no se está aproximando a un número real cuando 0tiende a cero, puede concluir que el límite no existe.

c) Comportamiento oscilatorio Examine la existencia del límite

Solución:Sea la gráfica de la función y

x

En la gráfica se puede ver que, cuando tiende a cero, oscila entre -1 y -1. Por tanto, el límite no existe

Comportamientos comunes asociados con la inexistencia de un límite. 1.- tiende a un número diferente desde la derecha de que al que tiende desde la izquierda de este último.

UTILIZA FUNCIONES Y TEOREMAS DE LÍMITES EN LA RESOLUCIÓN DE PROBLEMAS DE SU ENTORNO ACADÉMICO

TEOREMA PRINCIPAL DE LOS LÍMITES

TEOREMA 1:Si c es una constante, entonces para cualquier número

lim_→ =

Ejemplos:

1) lim

TEOREMA 2:Siaes un número real cualquiera lim

→ =

Ejemplos:

1) lim

→ = 2 2) lim→ x = −4 3) lim→ = 0

TEOREMA 3:Si c es una constante, entonces: lim

→ ( ) = lim→ ( )

Ejemplos:

1) lim

→ 2 = 2 lim→ = 2(1) = 2 2) lim_→ = lim_→ = (−4) = −

TEOREMA 4:Límite de una suma, de un producto y de un cociente. Si son dos funciones tales que: lim

→ ( ) = lim→ ( ) =

Entonces:

lim_→ [ ( ) ± ( )] = lim_→ ( ) + lim_→ ( ) = +

Ejemplos:

1) lim

→ (8 + 3) = lim→ 8 + lim→ 3 = 8 lim x→ + lim 3→ = 8(3) + 3 = 19

2) lim

→ 7 − = 7 − = 3

TEOREMA 5:Limite de una potencia

lim_→ [ ( )] =

Para el caso especial ( ) = ,el resultado da lim

→ =

Ejemplos:

1) lim

→ = 10 = 1000

2) Determinar lim

→ (4 − 1)

Primero se observa que: lim

→ (4 − 1) = lim→ 4 − lim→ 1 = 4(1) − 1 = 3

Luego, por el límite de una potencia: lim

→ (4 − 1) = 3 = 243

Si ( )es polinomial, entonces:lim

→ ( ) = ( )

Para calcular el límite de una función, polimonial cuando x tiende al real a, sólo se necesita calcular la función en

Ejemplo:

1) lim

→ ( − 5 + 6) = lim→ − lim→ 5 + lim→ 6 = 3 − 5(3) + 6 = 0

TEOREMA 7:Límite de una raíz

El límite de la raíz n-ésima de una función, es la raíz n-ésima del límite siempre que el límite exista y tenga una raíz n-ésima real

lim_→ ( )= lim

→ ( )

1) lim

→ √ = lim→ = √9= 3

2) lim

→ √25 − = lim→ (25 − 16)=√9= 3

TEOREMA 8: Límite de una función racional

El límite del cociente de dos funciones cuando → , es igual al cociente de los límites de las funciones cuando → , siempre que el límite del denominadorNO sea igual a cero

Ejemplo: 1) lim → = → ( ) → ( ) = → → → → = ( )

EJEMPLO:

Ejemplos: 1.

2. 3. 4.

5. Sí el límite del numerador es cero y el del

denominador es diferente de cero, el límite del cociente es igual a cero.

6. Sí el límite del numerador es diferente de

cero y el del denominador es cero, el cociente no tiene límite y se establece que tiende a más o menos infinito .

7. Forma indeterminada.

Sí los límites del numerador y del denominador son ambos iguales a cero,

se tiene la forma que se denomina indeterminada. La indeterminación se puede eliminar buscando una función equivalente mediante operaciones algebraicas sencillas

8.

9..

=

=

12.

=

13. se resuelve la división

=40

LÍMITES CON RADICALES EN EL CASO

EJEMPLO:

1.-

2.-=6

LÍMITES AL INFINITO DEL TIPO

Sí los límites del numerador y del denominador son ambas iguales a infinito, se

tiene la forma indeterminada . La indeterminación se puede eliminar dividiendo ambos términos entre la variable de mayor grado que interviene en la expresión.

1.-

2.-3.-

4.-5.-

6.-LÍMITES CON FUNCIONES TRIGONOMÉTRICAS.

Los límites de funciones polinomiales, siempre pueden encontrarse por sustitución y los límites de funciones racionales pueden encontrarse por sustitución, siempre y cuando el denominador no sea cero en el punto límite. Esta regla de sustitución se aplica también a las funciones trigonométricas.

TEOREMA A. Límites de funciones trigonométricas.

Para todo número real c en el dominio de la función.

IDENTIDADES FUNDAMENTALES

RECIPROCAS COCIENTE PITAGORICAS FUNCIONES DEL

ANGULO DOBLE

1.- 1.- 1.- 1.-Sen2x = 2sen.cox

2.- 2.- 2.-

3.-EJEMPLO:

1.-

2.-=4

EJERCICIO: Calcular los siguientes límites:

1.-

2.-

3.-

4.-

5.-

6.-

7.-

8.-

9.-

10.-

11.-

13.-

14.-

15.-

16.-

17.-

18.-LÍMITES CON RADICAL

8.-

9.-

10.-

11.-

12.-

13.-

14.-LÍMITES AL INFINITO

15.-

16.-

18.-

19.-

20.-

21.-

22.-

24.-LÍMITES CON FUNCIONES TRIGONOMÉTRICAS

25.-

26.-

27.-

28.-

29.-

30.-

31.-

32.-

33.-En los siguientes límites calcular lo que se pide en cada inciso.

34.-a) b) c)

Use la información para evaluar los límites

36.-a) b) c) d)

Unidad 2:

Derivada de funciones Algebraicas Competencia particular 2:

Resuelve problemas referentes a la derivada de funciones algebraicas en situaciones de su entorno académico, social y global

OBTIENE DERIVADAS DE FUNCIONES ALGEBRAICAS A PARTIR DE SU FUNCIÓN Y USO DEL FORMULARIO, EN SITUACIONES ACADÉMICAS

LA FUNCIÓN DERIVADA

INCREMENTOS

El incremento Δx de una variable x es el aumento o disminución que experimenta dicha variable, desde un valor a otro . Así,

ó bien +

Δx

Si se da un incremento Δx a la variable x (es decir si x pasa de a + Δx), la

función

y= se verá incrementada

en a partir del

Ejemplo 1. Cuando x aumenta en Δx= 0.5 a partir de =1, la

función se incrementa en

Ejercicio.Si x se incrementa en Δx = -0.1 a partir de 4. ¿Cuál será el incremento que sufre la función

La derivada como pendiente de una curva

Son tres los objetivos sobre los cuales nos centraremos en esta sección:

1. Definir la pendiente de una curva.

2. Definir la derivada y usarla para calcular la pendiente de una curva. 3. Calcular la derivada por su definición como límite.

El cálculo diferencial consiste simplemente en calcular algebraicamente el límite de un cociente. Eso nos proporciona la pendiente de la recta tangente que estamos buscando.

Se sabe que la pendiente viene dada por

Si; (x1, y1) y (x2, y2) son dos puntos cualesquiera de la recta.

En general para una curva no lineal la pendiente no es constante, si no que varía de un punto a otro.

Por ejemplo, en lafigura 1, la recta tangente de la gráfica de f en p es la recta que mejor se aproxima a la gráfica de f en tal punto. El problema es hallar la pendiente a una curva en un punto se convierte así, en el de calcular la pendiente de la recta tangente a la curva en dicho punto.

[image:17.612.195.400.234.369.2]

No es este el caso de la figura 1, como se aprecia en la parte punteada de la recta tangente. De un modo informal, cuando nos referimos a la recta tangente a una curva, entendemos una tangentelocala la curva en un punto concreto, sin que nos interese el que la recta y la curva se corten en algún otro punto.

Figura 1

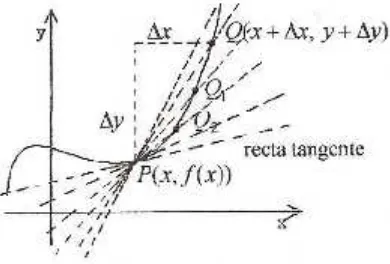
Podemos hallar la recta tangente en un punto de la forma siguiente. Considérese la recta tangente que pasa por los puntosP yQde la gráfica de la función en la figura 2.

Supóngase que el punto Q se mueve hacia el P sobre la curva, definiendo rectas secantes desde P hasta Q, por ejemplo: la recta secante que pasa por P y Q1, la recta secante que pasa por P y Q2 y así sucesivamente. Conforme Q queda más y más cerca de Pnótese como estas rectas secantes tienden a una posición límite. Esta posición límite de las restas secantes es denominadarecta tangentea la curva en el puntoP.

[image:17.612.206.401.553.685.2]

Podemos hallar la recta tangente en P calculando su pendiente. Dado que la recta tangente es la posición límite de las rectas secantes, su pendiente mt es el valor límite de las pendientes m s de las rectas secantes al aproximarseQ aP,

mt=

De la figura 2, la pendiente de la recta secante por Q yP es

Cuando tenemos que . Por lo tanto, la pendientede la recta tangente en

Pes

Ahora se puede definir la pendiente a una curva en uno de sus puntos.

Definición.En la pendiente mde la gráfica de es igual a la pendiente de su recta tangente en y queda determinada por

Si este límite existe.

Para calcular la pendiente de la tangente a una curva mediante su definición por el límite:

Definición

La derivada de una función f es otra función f´ cuyo valor para un número cualquiera

ces

Ejemplo 2.

a) Hallar la fórmula que proporcione la pendiente de la gráfica en cualquier punto.

b) ¿Cuál es la pendiente en (0,3) y en (-2,-1)

Solución.Aplicando la definición de derivada.

1.

Así,

.

Para el punto (0,3);

Así, la gráfica de la función tiene pendiente en el punto (0,3), etc.

Ejemplo 3.Hallar la pendiente de la recta tangente a en cualquier punto.

Solución.Aplicando la regla de los cuatro pasos:

Por lo tanto es la pendiente de la gráfica de la función en cualquier punto.

Ahora nos encontramos en un punto crucial en el estudio del cálculo, pues el límite

DEFINICIÓN DE LA DERIVADA DE UNA FUNCIÓN

El límite se llama derivada de en (si el límite existe) y se denota por:

(Que se lee “f prima de x”

Una función es derivable o diferenciable en , si existe su derivada en , llamándosederivaciónal procedimiento para calcular la derivada. La derivada de una función también es una función.

Las notaciones que se usan más comúnmente para denotar la derivada de una función son:

se lee la derivada de y con respecto a x

y´ se lee “y prima” y denota la derivada de y respecto de la variable x. De forma similar se leen las otras notaciones.

Introducida esta notación, entonces y si :

¿Qué necesito?

Conceptos de la derivada, pendiente

Cálculos Básicos y factorización

EJERCICIOS. Determina la derivada de las funciones siguientes mediante la regla de los cuatro pasos.

DERIVADA DE FUNCIONES ALGEBRAICAS

Si y es una función de u, definida por y = f(u) y Duy existe, y si u es una función de x,

definida por u = g(x) y Dxu existe, entonces y es una función de x y Dxy existe y está definida

por:

Dxy = Duy.Dxu

o en forma equivalente

.

Ejemplo:

= (3 + 5 − 2)

= 3(3 + 5 − 2) (6 + 5)

Resuelve los siguientes ejercicios

1. (2 − 5 + 4) 2. = 7 − 5 + 4

REGLAS DE DERIVACIÓN

En las funciones siguientes: u,v y w son funciones derivables de x.

¿Qué necesito?

Concepto de la derivada Reglas de derivación

Factorización Operatividad

Hallar la primera derivada de las siguientes funciones Sol. 1. 2. 3. 4. 5. .

Un líquido fluye por un agujero en el fondo de un depósito a una velocidad

v

dada por , donde g es la

aceleración de la gravedad (32 ) y h es la profundidad del líquido en el depósito. Hallar la razón de cambio de v

respecto a h cuando: h=9 y h=4.

APLICA LA DERIVADA EN SITUACIONES GEOMÉTRICAS Y FÍSICAS, EN LA RESOLUCIÓN DE PROBLEMAS, DE SU ENTORNO ACADÉMICO

LA DERIVADA COMO RAZÓN DE CAMBIO

Ya se ha visto que la derivada se puede interpretar como la pendiente de una curva.

Existen numerosas aplicaciones de la noción de razón de cambio. Por ejemplo: el índice de crecimiento de una población la tasa (razón de cambio) de desempleo, la tasa de producción, tasa de mortandad, tasa de nacimientos, etc. Las razones de cambio más útiles son las relacionadas con el tiempo, sin embargo, empezaremos investigando la razón de cambio respecto de cualquier variable.

Supóngase que se lanza una pelota al aire de forma que la ecuación que describa

su trayectoria es

Por lo que ahora el cambio que manifiesta la altura de la pelota al cambiar su distancia horizontal alejándose respecto del origen. Es decir, la razón de cambio de la altura y de la pelota conforme crece la distancia horizontal x.

Por ejemplo, si la pelota se ha alejado horizontalmente y se encuentra en

la altura correspondiente de la pelota para este valor de la variable independiente es

La figura muestra en forma explícita las condiciones iniciales del problema, aplicando estas condiciones a la ecuación de movimiento de un objeto en caída libre en el instante , tenemos

.

Despejemos ahora la variable t para conocer el tiempo que transcurre desde el momento en que se suelta la piedra y el impacto en el suelo.

.

Sustituyendo y en la

expresión para conocer la velocidad ene l

momento de impacto, tenemos que

Ayuda:

Solución:40 cm2/s

pies/s.

Unidad 3:

Derivada de funciones trascendentes y diferenciales Competencia 3:

Resuelve Problemas referentes de la derivada de funciones trascendentes y el uso de la diferencial, en situaciones de su entorno académico

OBTIENE DERIVADAS DE FUNCIONES TRASCENDENTES, A PARTIR DE LA DEFINICIÓN DE DERIVADA Y EL USO DEL FORMULARIO, EN SITUACIONES ACADÉMICAS.

DERIVADA DE LA FUNCIÓN SENO.

Así de la misma manera, aplicando la definición de derivada, se obtienen las reglas de derivación de las funciones trascendentes.

FORMULARIO DE LAS REGLAS DE DERIVACIÓN DE LAS FUNCIONES TRASCENDENTES.

FUNCIONES TRIGONOMÉTRICAS

FUNCIONES

TRIGONOMÉTRICAS INVERSAS.

DERIVADAS DE FUNCIONES EXPONENCIALES.

EJEMPLO:

DERIVADA DE FUNCIONES

TRIGONOMÉTRICAS.

1.-10.

11.-

2.-

12.-3.-

13.-4.-

14.-5.-

15.-

6.-

16.-

7.-

17.-

8.-

9.-EJEMPLO:

DERIVADA DE FUNCIONES

TRIGONOMÉTRICAS INVERSAS.

1

.-2.-

6.-

3.-

4.-

9.-

13.-10.- DERIVADA_{EXPONENCIALES.}DE FUNCIONES

1.-

11.-

2.-

12.-

4.-

2.-DERIVADA DE FUNCIONES

LOGARITMICAS.

1.-

3.-EJERCICIOS:

Derivar las siguientes funciones.

1.-

2.-

3.-

4.-

5.-

7.-

8.-

9.-

10.-

11.-

12.-

13.-

14.-

15.-

16.-

17.-

18.-

20.-RESUELVE PROBLEMAS DE OPTIMIZACIÓN CON FUNCIONES TRASCENDENTES, EN SITUACIONES ACADÉMICAS

Problemas: Derivadas Inversas

Un hombre parado en la cima de un acantilado vertical está a 200 pies encima de un lago. Observa un bote de motor que se aleja directamente del pie del acantilado a razón de 25 pies por segundo. ¿Qué tan rápido cambia el ángulo de depresión de su línea visual cuando el bote está a 150 pies de la base del acantilado

a) Comprensión c) Resultado

Datos

y = 200 pies

x

X = 150 y=200 pies

b) Planteamiento

Despejando

Derivando

Sustituyendo

Un avión vuela a 5millas de altitud hacia un punto situado sobre un observador a una velocidad de 600 millas/hora. Calcular el ritmo al que está cambiando el ángulo de elevación

para

a) Comprensión

x

y = 5 millas

Datos

c) Resultados

Sustituyendo, x=

y= 5millas

b) Planteamiento

Despejando

Resolver los siguientes problemas

1. Un avión vuela a 6millas de altitud hacia un punto situado sobre un observador a una velocidad de 600 millas por hora. Calcular el ritmo al que está cambiando el ángulo de

elevación para = 75°

2. Un pescador recoge el hilo del carrete a razón de 1pie por segundo desde un puente de 15 pies de altura sobre el agua. ¿A qué ritmo está cambiando el ángulo entre el hilo y el agua cuando hay 25 pies de hilo fuera del agua?

3. Estas grabando un video de una carrera desde un lugar que está a 40 metros de la pista y sigues a un auto que se mueve a290 km/hr. ¿Con qué rapidez cambiará el ángulo

de tu cámara cuando el auto está exactamente frente a ti?

LA INTEGRAL

La diferencial.

Sea la función y = f(x), entonces su diferencial se define como el producto de la derivada por el diferencial de x.

dy = f´(x) dx

Ejemplos

1) La diferencial de la función y = x3_{- 2x}2_{+ 4x – 5es:}

a) (3x

2

_{– 4x + 4) dx}

b) (6x – 4) dx

c) (6x + 4) dx

d) (3x

2

– 4x - 4) dx

Solución:

Se deriva la función, se multiplica por el diferencial de X: dy = (3x2_{– 4x + 4) dx}

por lo tanto, la opción correcta es el inciso a.

2) La diferencia de la función f(x) = sen 4x es:

a) 4 sen 4x

b) cos 4x

c) 4 cos 4x dx

d) sen 4x dx

Solución:

Se deriva la función y se multiplica por el diferencial de X: dy = 4 cos 4x dx

Por tanto, la opción correcta es el inciso c.

LA ANTIDERIVADA

Es el proceso mediante el cual se determina el conjunto de todas las Antiderivadas de una función dada, el símbolo

∫

(integral),denota la operación de antiderivada y se escribe:

∫

f(x)dx = F (x) + C

INTEGRACION INMEDIATA

1)

∫

= +

2)

∫

= a

∫

3)

∫( + − )

=

∫

+

∫

− ∫

n+1

4)

∫

n

dx =

+ c

5)

∫

= -cos x + C

6)

∫

= sen x + C

Ejemplos:

1) La integral∫ 2_{dx es:}

a

)

+ c

b) x3 _{+ C}

c) x

3 _{+ C}

3 d)

x

2 _{+ C}

3

Solución:

Al aplicar la integral

∫

n

dx, se obtiene:

2+1

∫

2

_dx=

_{+ c}

La opción correcta es el inciso c.

2) La integral

∫(4 sen x + 5 cos x) dx: es

a) 4 cos x + 5 sen x + c

b) 4 sen x – 5 cos x + c c) 4 sen x + 5 cos x + c d) -4 cos x + 5 sen x + c SOLUCIÓN

∫(4 sen x + 5 cos x) dx

= ∫

4 sen x dx +

∫

5 cos x dx = 4

∫

sen x dx + 5

∫

cos x dx = 4(- cos x) + 5(sen x) + C= - 4 cos x + 5(sen x) + C

La opción correcta es el inciso d.

Cambio de variable

FÓRMULAS

1)

∫v

n_{dv =}

v

n+1

+ c

2)

∫

=ln | v |

+ c

3)

∫a

v_{dv =}

v

n+1

+ c

lna

4)

∫

℮v_{dv = ℮}v_{+ C}

5)

∫

sen v dv = - cos v + C 6)

∫

cos v dv = sen v + C

Ejemplos.

1) La integral∫ ( + )3_{dx es:}

a) (2x + 1)4_{+ C}

b) (2x + 1)4_{+ C}

4

c) (2x + 1)3_{+ C}

3

d) (2x + 1)2_{+ C}

2 SOLUCIÓN:

Se utiliza la fórmula

∫v

n_{dv donde:}

V = 2x + 1 y dv = 2dx

Se realiza el cambio de variable

∫ 2(2 + 1)3_{dx =∫(2 + 1)}3_{2dx =}

∫

_v3_{dv =}

∫

_v4 _{+ C = (2x + 1)}4_{+ C}

4 4 La respuesta correcta es el inciso b

3) La integral

∫5 sen (5 x – 3) dx es:

a) –sen (5x – 3) + C

b) – cos (5x - 3) + C c) cos (5x – 3) + C d) sen (5x -3) + C

Se aplica la fórmula

∫

sen v dv, donde: V = 5x – 3 y dv = 5dx

Se realiza el cambio de variable:

∫

5 sen (5 x – 3) dx =

∫

sen (5 x – 3) ▪ 5dx =

∫

sen v dv = - cos v + C = - cos(5x – 3) + C

La respuesta correcta es la b

INTEGRACIÓN POR PARTES

Es uno de los métodos más usados para la resolución de una integral y se define por:

∫

u dv = uv -

∫

v du

Donde la segunda integral es más sencilla de integrar, se aplica cuando se tiene:

 Funciones para las que no existen fórmulas directas, como las logarítmicas o inversas trigonométricas.

Ejemplos:

1) La integral

∫

x ℮x_{dx es:}

a) x ℮x_{+ c}

b) x2 _{+ ℮}x_+c

2

c) x ℮x _{- ℮}x_{+ c}

d) x2_℮x_+c

2

SOLUCIÓN:

Se eligenuydvde la siguiente manera y se obtienendu yv, respectivamente

u= x → du = dx dv = ℮x_{dx → v =}

∫

_℮x_{dx = ℮}x

De acuerdo con la fórmula

∫

u dv = uv -

∫

v du,

∫

x ℮x_{dx = x ℮}x_-

∫

_℮x_{dx = x ℮}x_{- ℮}x_{+ c}

Por tanto la, opción correcta es el inciso C. 2) La integral

∫

x sen x dx es:

a) –x cos x + sen x + c b) –x sen x + cos x + c c) x cos x + sen x + c d) x sen x - cos x + c Solución:

Se eligenuydvpara obtenerduyv, respectivamente

u= x → du = dx

dv = sen x dx → v =

∫

sen x dx = -cosx De acuerdo con la fórmula:

∫

x sen x dx = x ( -cos x) -

∫-

cos x dx = - x cos x +

∫

cos x dx = -x cos x + sen x + c Por tanto, la opción correcta es el inciso a.

INTEGRAL DEFINIDA

Seay = f(x)una función continua en el intervalo cerrado [a, b], entonces la integral definida de f(x) deaabes:

∫ ( ) =

[F(x)]

ba

= F(b) –F(a)

Ejemplos:

1) El valor de la integral definida ∫ ( )3_dxes:

c) - 3 d) -Solución:

3

∫

3_{dx = x}4 _{= (3)}4 _{- (0)}4 _{= 81 - 0 = 81}

4 0 4 4 4 4 4

Por lo tanto, la opción correcta es el inciso d.

Área bajo una curva

Seay= f(x)una función definida en el intervalo [a, b], entonces el área formada por la curva,

el ejeXy las rectasx= ayx=b,está dada por:

Á=

∫ ( )

dx

aybson respectivamente los límites de integración inferior y superior

Ejemplos

l) El área formada por la curvay= 4x-x2,e] ejeXy las rectasx= 0 yx= 4, es:

Referencias Documentales

No. Título del Documento Autor(es) Editorial y Año

1 Cálculo Diferencial e Integral Larson, H. E. Mc Graw Hill

2005

2 Cálculo con Geometría

Analítica

Purcell, E. J. Limusa

2004

3 Cálculo Stewart, J. Thompson

2008

4 El Cálculo Leithold, L. Oxford

2007

5 Cálculo Diferencial e Integral Granville, WW. A.

Limusa

2004

6 Cálculo Diferencial e Integral Taylor, H. E. Limusa

2004

7 Cálculo Diferencial Cuellar, J. A. Mc Graw Hill

Páginas Electrónicas

Dirección Electrónica

Contenido Principal

Clasificación

http.//www.weneslao.com.mx/matematicas/math4/ Texto Consulta

http://umay.edu.mx/ Texto Consulta

http://www.biopsychology.org/apuntes/calculo/calculo1.htm Texto Consulta

http://es.wikipedia.org/wihl/C%c3%A1lcalculo_diferencial Texto Consulta

http://dieumsnh.qfb.umich.mx/DIFERENCIAL/diferencial.htm Texto Consulta

http://platea.pntic.mec.es/jescuder/calcdif.htm Texto Consulta

http://docentes.uacj.mx/sterraza/matematicas_en_movimiento/m athematica.htmk