IACULTAP DE INGENIERIA MECANICA
¥ ELECTBÍCA
IX)CRORADO EN IMGENIERIA DE MATERIALES
E O T P I O DE LA TRANSFERENCIA DE
CALOR-EN LECHO FIJO
{PRIMERA APROXIMACION, CASO UNIDIMENSIONAL)
POR
LIC. CESAR ALBERTO N U Ñ E Z LOPEZ
T E S I S
PRESENTADA PARA LA OBlT3¡CíON DEL GRADO
DE MAÉCTRO EN CIENCIAS EN I N G E N I E N MECANICA
CON ESPECIALIDAD EN n-íGEMEBIA DE MATEBIAI-ES
UNIVERSIDAD AUTONOMA DE NUEVO LEON
FACULTAD DE INGENIERIA
MECANICA-? ELECTRICA
«
DOCTORADO EN INGENIERIA "DE MATERIALES
S T U D I O DE 3LA TRANSFERENCIA DE CALDE
EN LECHO FIJO,
PRESENTADA 'PARA LA OBTENCION DEI GRADO
PE MAESTRO. EN O E N O A S EN INGENIERIA MECANICA
CON ESPECIALIDAD EN INGENIERIA DE MATERIALS
S A N m C D l M D E L O S S A P S l ü H ,
T M
.
K lM
H g
F O N D O T E S J S
UNIVERSIDAD AUTONOMA DE NUEVO LEON
FACULTAD DE INGENIERIA MECANICA Y ELECTRICA
DOCTORADO EN INGENIERIA DE MATERIALES
ESTUDIO DE LA TRANSFERENCIA DE CALOR EN LECHO FIJO
(PRIMERA APROXIMACION, CASO UNIDIMENSIONAL)
por
Lic. César Alberto Núñez López
TESIS PRESENTADA PARA LA OBTENCIÓN DEL GRADO DE MAESTRO EN CIENCIAS EN INGENIERÍA MECÁNICA
CON ESPECIALIDAD EN INGENIERÍA DE MATERIALES
San Nicolás de los Garza, N.L.
AGRADECIMIENTOS
D e s e o agradecer al personal d o c e n t e y admini strati vo del Doctorado en I n g e n i e r í a de M a t e r i a l e s de la Facultad de Ingeniería Mecánica y Eléctrica d e la Universidad Autónoma de Nuevo León por todo el apoyo brindado durante mis estudios.
A HYLSA, S. A. DE C. V. por las f a c i l i d a d e s p r e s t a d a s durante el desarrol1 o d e la mi sma asi c o m o al Dr. L u í s R. Farias por el apoyo b r i n d a d o durante el d e s a r r o l l o de esta tésis.
A todos mis condicipulos y Profesores del D o c t o r a d o en Ingeniería d e Materiales q u e d e una u otra forma participaron en ésta.
M u y especi al mente a mi asesor, el Dr. Raúl ' F u e n t e s Samaniego por su r e s p a l d o y dedicación en mi formación.
A MI ESPOSA,CON A M O R , POR T O D O EL A P O Y O Q U E M E BRINDÓ D U R A N T E M I S E S T U D I O S
A M I M A D R E Y A LA M E M O R I A D E M I P A D R E
T A B L A DE C O N T E N I D O
PAGI N A
AGRADECI MI E N T O S i T A B L A DE C O N T E N I D O i i
RESUMEN i i i I N T R O D U C C I O N i v C A P I T U L O I T R A N S F E R E N C I A D E
CALOR EN EL PELET 1 C A P I T U L O II T R A N S F E R E N C I A DE
CALOR EN EL REFRACTARIO 4 C A P I T U L O III B A L A N C E S DE ENERGIA 6 C A P I T U L O IV F U N C I O N E S D E T E M P E R A T U R A DEL
L E C H O Y DEL G A S 11 C A P I T U L O V SOLUCION POR E L E M E N T O S F I N I T O S
C C A S O U N I D I M E N S I O N A L } 1 5
C A P I T U L O VI R E S U L T A D O S 1 7 C A P I T U L O VII C O N C L U S I O N E S 26
ESTUDIO DE LA TRANSFERENCIA DE CALOR EN LECHO FIJO
(PRIMERA APROXIMACION: CASO UNIDIMENSIONAL)
RESUMEN.
En este trabajo de Tesis se resuelve el problema de
transferencia de calor en el tiempo de un reactor cilindrico,
cuyas p a r e d e s están recubiertas de material aislante refractario,
que se lleva a cabo entre un gas de calentamiento y pelets
esféricos que conforman un lecho fijo.
El problema se plantea a partir de la función Green que
resuelve el problema de transferencia de calor para una partícula
esférica de radio a con un coeficiente de convección Hg y
temperatura incial constante To, determinando con ella la función
de distribución de temperaturas en el pelet. De manera semejante
se deduce la función de distribución de temperaturas en el
refractario conociendo entonces la temperatura del lecho en
cualquier punto.
Por otra parte, se resuelve el problema original pero
utilizando una formulación de diferencias finitas partiendo del
balance energético que debe existir entre el gas de calentamiento
y el sistema" pelets-refractario.
Los resultados obtenidos con la solución del problema
analítico se comparan con la solución proporcionada por el método
de diferencias finitas en una formulación explícita. Se observa la
concordancia de los resultados pero se m a n i f i e s t a n las ventajas
INTRODUCCION
El estudio de la transferencia de calor en lechos fijos es de
interés debido al uso frecuente de reactores químicos con estas
configuraciones ya sea para producir una reacción química o para
transferir calor. Algunas de las operaciones industriales en las
que la fase fluida pasa a través de una fase formada por
partículas sólidas son:
a) Filtración.
b) Transferencia de masa en columnas empacadas.
c) Reacciones químicas utilizando catalizadores.
d) Absorción en torres empacadas.
e) Intercambiadores regenerativos de calor.
en estos procesos se pueden encontrar diferentes configuraciones
de la fase sólida pudiendo estar:
- Estacionaria, como en torres empacadas.
- Fluida, como en reactores catalíticos de lecho fluidizado.
y dependiendo de la velocidad del fluido puede suceder que las
partículas,
i) queden suspendidas,
ii) sean arrastradas con el fluido,
iii) caigan por efecto de la gravedad.
En lechos fijos, el flujo es a través de los espacios entre
las partículas y dado que estos no son uniformes, la fase fluida
Como puede intuirse con todo lo anterior, un análisis de
transferencia de calor en un lecho fijo es un trabajo de gran
complejidad sobre todo si ocurren procesos de transformación
químicos durante el proceso. Para atacar este problema, se toman
en cuenta una serie de consideraciones que si bien, alteran el
sistema físico real, pueden resultar en una muy buena aproximación
siempre y cuando las consideraciones se hagan adecuadamente.
No en todos los procesos mencionados anteriormente se tiene
que tomar en cuenta la transferencia de calor que pudiera existir
entre la fase sólida y el fluido, pero existen una gran cantidad
de ellos en que si es de gran importancia este análisis, por
ejemplo, en los procesos de reducción de minerales utilizando
gases reductores.
Todas las concepciones desarrolladas sobre estos procesos de
reducción (tecnológicamente posibles) se han caracterizado por un
común denominador: obtener la más rápida y completa conversión
química y transferencia de calor en el menor volumen posible; se
ha concluido que una circulación uniforme de los gases alrededor
de las piezas de mineral ofrece las mejores condiciones..
Un ejemplo de este tipo de proceso es el patentado por HYLSA
a finales de los 50's. En este proceso se hace pasar gas reformado
(metano y monóxido de carbono) por un lecho fijo de mineral de
hierro (hematita principalmente). Si bien, lo que interesa en el
proceso es la transformación de hematita a hierro, las reacciones
químicas de reducción solo pueden llevarse a cabo al llegar el
mineral a una cierta temperatura a partir de la cual inician las
proceso de transferencia de calor.
En el trabajo que se presenta a continuación, se da una
primera aproximación al análisis de la transferencia de calor en
un lecho fijo de simetría cilindrica cuyas paredes están
recubiertas de material aislante refractario y la fase sólida está
en forma de pellets esféricos de tamaño uniforme. Se supone que el
gas no reacciona con las partículas por lo que no se considera que
exista generación de calor por reacciones químicas.
Aunque existen di-ferentes trabajos relacionados con este
análisis de transferencia de calor( 1 , 2 , 3 > , la solución a este
problema se dá en función de relaciones empíricas cuyo rango de
aplicación no siempre está bien definido. En este trabajo, se
parte del análisis de la transferencia de calor entre el pelet y
el gas de calentamiento llegando a determinar la función de
distribución de temperaturas en el pelet y por otro lado se
determina un coeficiente de transferencia de calor promedio entre
el pelet y el gas. De una manera similar, se analiza la
transferencia de calor entre el gas de calentamiento y el
refractario determinando la función de distribución de
temperaturas en el refractario y otro coeficiente de transferencia
de calor promedio entre el gas de calentamiento y las paredes del
refractario. Estos coeficientes de tranferencia de calor promedios
se encuentran en función del coeficiente de convección del gas
para la geometría descrita, de acuerdo a lo que se expone en la
mayoría de los textos sobre transferencia de calor.
Me Adams(1) muestra que este coeficiente de transferencia de
flujo de gas y sus propiedades como calor específico,
conductividad, viscosidad, etc.. Se llega a una relación del tipo:
p o
C G A
P O k
en donde h es el coeficiente de transferencia de calor por
convección y n, m y A dependen del gas utilizado. Esta relación es
la más encontrada. El valor esperado para h es de 80 a 150 Watts
por metro cuadrado por grado centígrado.
ORGANIZACION DE LA TESIS.
En el capítulo primero se analiza el problema de
transferencia de calor en el pelet a partir de la función Green
para la transferencia de calor en esferas tomando en consideración
el mecanismo de convección en la superficie. En este capítulo, se
determinará una ecuación para la temperatura del pelet en función
de su radio y de la temperatura del gas de calentamiento, que es
función del tiempo; sin embargo, esta ecuación no toma en cuenta
las pequeñas variaciones de la temperatura del gas de
calentamien-to. La ecuación más general es del tipo,
en donde sí se consideran cambios más finos en la temperatura del
Si se sustituye la relación anterior en la ecuación de
transferencia de calor y tomando en cuenta las consideraciones a
la frontera del pelet, se llega a determinar el valor de los
coeficientes A M , y los cuales se generan a partir de:
. n i, _ _ 2 A
- 1 , KP® a a N ni
I (
1 = 0
A , - > + ? n = 1,2,3,...
11+1,0 KP Hg 21+2 > 21+3
2 a
A = A ; 1 = 1,2,3,...,n
B + 1'1 2 1 ( 2 1 + 1 ) K p n > 1-1
2
a
h t , = A ; n = 1,2,3,
n + 1'n + 1 2 (n+1) (2n+3)KP n'n
en donde los coeficientes de arranque son:
- a2 , 2kp
\o
6KP aHg V aHn
)
a2
An
-6 K p
como se verá en el trabajo de tesis, se desprecian los términos
que contengan derivadas de orden superior o igual a dos. En este
capítulo también se determina una expresión para el coeficiente de
transferencia de calor por convección, promedio, entre el pelet y
En el capitulo segundo se resuelve la ecuación de
transferencia de calor que gobierna la distribución de
temperaturas en el refractario debido al gas de calentamiento.
Al igual que con la función de distribución de temperaturas
en el pelet, se puede demostrar que la solución a este problema,
que toma en cuenta aún cambios pequeños en la temperatura del gas
de calentamiento, es:
Tr(Xít) = T,(t) + l — _ 1
n = 1 8t 1=0
en donde, para cumplir con la ecuación de transferencia de calor y
los valores a la frontera, los coeficientes Bni están dados por,
n B
- 1 n-1,1
B n 0 = — - l — ? 2,3,4,...
KrHg 1=0 1 + 1
~ 1 + 1 i n B , , c
- 1 n-1,1
B = > ; n = 2,3,4,... Kr 1=0 1 + 1
B
n- 1 , 1-2
B = ; 1=2,3,...,2n-l ; n=2,3,4,...
nl K 1 (1 - 1)
B n r - '* n = 2,3,
n , 2 n (2n) !K
-e k r
K H r g
-e
1
en donde c es el espesor del refractario. Al igual y como se
mencionó en el punto anterior, en este trabajo de tesis se
desprecian las derivadas de orden superior o igual a dos.
En este capítulo también se analiza el coeficiente promedio
de transferencia de calor por convección entre el gas de
calentamiento y el refractario.
El tercer capítulo muestra los balances energéticos
considerados y los cuales conducen al plantemiento de las
ecuaciones diferenciales que rigen el problema de transferencia de
calor en lecho; con ellas se determinará la distribución de
temperaturas en el reactor, tanto para los pelets como para el
refractario y el gas de calentamiento.
Por otro lado, se definen algunas relaciones fundamentales
que llevan a la simplificación de las expresiones encontradas;
estas se refieren a Masa de Pelets por unidad de longitud en
dirección paralela al eje del reactor, área de refractario por
Con las relaciones encontradas en el capitulo anterior, en el
capítulo cuarto se establecen las ecuaciones de distribución de
temperaturas en el pelet y el gas de calentamiento y sus
relaciones diferenciales, las cuales se resuelven utilizando la
técnica de transformadas de Laplace; las soluciones encontradas se
normalizan a los valores de temperaturas inicial del gas de
calentamiento y del lecho, de tal forma que las gráficas generadas
a partir de la solución son de caracter más general y por ello no
solamente válidas para ciertos valores de las temperaturas
inciales del gás de calentamiento y del lecho,
A manera de verificar los resultados, en el capítulo
quinto se soluciona el mismo problema de transferencia de calor,
pero utilizando un método numérico de diferencias finitas,
formulación explícita, la cual proporciona soluciones estables
cuando se cumple que,
oc At 1
Ax2 2
en donde a es el valor de difusividad del material (tn2/s) .
La razón por la que se eligió una formulación explícita se
basa en el hecho de que el problema es unidimensional y no se
presentan discontinuidades en la geométria, además de que no se
presentan ni fuentes ni sumideros de energía, por lo que una
solu-ción de este tipo es lo suficientemente precisa y estable para
este problema con un tiempo de cómputo razonable. Sin embargo, es
Cranck-Nicholson, residuos ponderados o Gallerkin por ejemplo.
En el capítulo sexto se analizan los resultados obtenidos con
la modelación matemática analítica y la numérica, basandose en un
ejemplo numérico en el que los datos utilizados son bastante
aproximados a los que se obtendrían en un reactor de unas 80
CAPITULO I.
TRANSFERENCIA DE CALOR EN EL PELET
1.- FUNCION DE DISTRIBUCION DE T E M P E R A T U R A S EN EL P E L E T .
Del estudio de Xa transferencia de calor en e s f e r a s se
o b t i e n e la función Green para u n a e s f e r a de r a d i o a , d e material homogéneo e isotrópico de conductividad térmica k , difusividad
p
K , densidad p y capacidad calori fica C en cuya s u p e r f i c i e p P p e x i s t e transferencia d e calor por convección d e acuerdo a la e c u a
-ción (1) :
a Tp Hg
(jg
- Tp ] , en r = a. (1} d r kpen d o n d e Hg e s el c o e f i c i e n t e de transferencia de calor entre el gas y el pelet , Tg es la temperatura del gas y Tp e s la función
de distribución de temperatura del pelet que e s función de r y del
tiempo.
La función Breen está dada como,
+ ftz
n^l \Z + ftZ + ft n
. X e Kp(t - t ' ) / a2j s e n j x ^ r / a j s e n ^ r ' / aj (2)
con ft =(Hg a/kp) — 1, y la ecuación de e i g e n v a l o r e s ,
U t i l i z a n d o la función Breen en la ecuación de c o n d u c c i ó n d e
c a l a r se e n c u e n t r a la ecuación de distribución de t e m p e r a t u r a s en
el pelet en función de r y del t i e m p o :
2 Hg ® \n / X n + (3*
Tp(r;t) = Y sen(X.n r/ a ) x ..
pe n?i (\n + (l2 + ft)r
P P '
t
2
... x Joe x p[ \ n Kp ( t ' - t ) / a 3 Tg(t') dt' (4)
Désarroilando el integrando en una serie de Taylar y
r e s o l v i e n d o s e llega a q u e :
2 Hg ® \n + (f
Tp(r;t) = y sen(\r> r / a ) x ...
p C n ? l ( \ n + (Ï + P P
... x a |Tg(t) - Tg(t)a - Tg(0) e x p ( - \2 Kp t / ' a2) + ...
... + T g ( O ) exp(-\n KP t / a2 ) a + © CTff(t)3 + . . (5)
2 2
con a — a /(\n Kp) y para un valor de tiempo por encima del cual
el estado transitorio no e s importante. Se llega e n t o n c e s a que, aZ T, r 2 2 Kp
Tp (r; t) = Tgít) + f f——""1 - — ' — - ll Tg( t ) (6) 6 Kp
LL
aJ
a Hg-I
Tp(t> = Tg(t) (7) 5Kp a Hg
2 . - C O E F I C I E N T E DE T R A N S F E R E N C I A DE CALOR P R O M E D I O E N T R E EL P E L E T
Y EL G A S DE C A L E N T A M I E N T O .
Para obtener un coeficiente de t r a n s f e r e n c i a de c a l o r
promedio entre el pelet y el gas de c a l e n t a m i e n t o se debe c u m p l i r
q u e
donde Hp e s el c o e f i c i e n t e de transferencia de calor promedio
entre el pelet y el gas,Tp e s Tp(r;t), Tp es Tp(t) y Tg es Tg(t);
una vez s u s t i t u i d a s las e x p r e s i o n e s e n c o n t r a d a s a n t e r i o r m e n t e
para Tp y Tp se obtiene Hp:
Hp (Tg-Tp) = Hg (Tg-Tp); en r = a ( 8 )
1
(9)
C A P I T U L O II
T R A N S F E R E N C I A DE CALOR EN EL R E F R A C T A R I O
1.- FUNCION DE DISTRIBUCION DE T E M P E R A T U R A S EN EL R E F R A C T A R I O .
Con un procedimiento similar al usado en el a n á l i s i s d e
transferencia de c a l o r en el pelet, se determina la función de distribución de t e m p e r a t u r a s en la pared del lecho la cual se
s u p o n e e s d e un material a i s l a n t e refractario homogéneo e
isotrópico de conductividad térmica kr, difusividad Kr, densidad
pr y c a l o r e s p e c i f i c o Cr, en c u y a s paredes e x i s t e , por un lado,
i n t e r c a m b i o de calor con el gas de c a l e n t a m i e n t o m i e n t r a s q u e por el otro e x t r e m o no o c u r r e ningún intercambio de calor, esto es:
9 Tr H>
9 x
( Tg - Tr ] x = 0 <1 0 )
d Tr
= 0 ; x = e (11) a x
donde e e s el espesor de la pared de r e f r a c t a r i o .
Resolviendo la ecuación de conducción de c a l o r y a p l i c a n d o las c o n d i c i o n e s a la frontera se determina la función de d i s t r i b u
-ción de temperaturas en el refraetarios
2
Tg(t) . x e k. . M 7 . Tr (x; t) = Tg(t) - 1 •• • *
igiLJ , x « K r . + - * K - j
Kr ^ 2 HaHg J
Tr(t) = Tg(t)
2 . - C O E F I C I E N T E DE T R A N S F E R E N C I A DE CALOR P R O M E D I O ENTRE EL R E F R A C T A R I O Y EL G A S DE C A L E N T A M I E N T O .
Igual q u e can el pelet, se debe c u m p l i r que:
Hr (Tg - Tr) = Hg (Tg - Tr); en x = 8 (14)
donde Hr es el c o e f i c i e n t e de transferencia de calor promedio
entre el gas de c a l e n t a m i e n t o y el refractario, Tr e s Tr(x;t), Tr
es Tr(t) y Tg e s Tg(t)..
S u s t i t u y e n d o las ecuaciones e n c o n t r a d a s para Tr y Tr, se
llega a que:
_ 1
Hr = (15) 1 e
+ — • • -Hg 3kr
e r € kr ^ •
+
Kr L 3 Ha '
CAPITULO III
BALANCES DE ENERGIA
El balance de energía entre el calor cedida por el gas de
calentamiento a los pelets y al refractario, lleva al
planteamiento de las ecuaciones d i f e r e n c i a l e s cuya solución
c o n d u c e a las ecuaciones que desc r i ben e1 calentamien to de 1os
pelets y el refractario tomados como uno solo mediante ciertas
c o n s i d e r a c i o n e s .
1.- DEFINICIONES GENERALES.
Para éste análisis se supone una geometria cilindrica del
lecho y una transferencia de calor unidimensional en z, de acuerdo
Se definen los siguientes parámetros dependientes de las
dimensiones del lecho:
2
- Lp, es el área de pelets por unidad de longitud (m /m de cuba)»
que es:
2 Pp ( apar ente) r
3 n
PP a
donde pp{aparente) es la densidad aparente del pelet y pp es
la densidad real del pelet, a es el radio del pelet, y r es el
radio interno del lecho.
— Lr, e s el área de refractario por unidad de longitud (m2/m de
cuba), que es:
n D
donde D es el diámetro interno del lecho (diámetro externo menos
dos veces el espesar del refractario).
- Mp, es la masa de pelets por unidad de longitud (Kg/m de cuba),
que es:
2
pp<apar©ril©> JT r
- Mr, es la masa de refractario por unidad de longitud (Kg/m de
cuba), que es:
2 2 pt n (r© - r )
donde r© es el radio externo de la cuba (radio interno más el
espesor del refractario) y pr es la densidad del refractario.
— Qp, es el calor que ceden o reciben los pelets a través del gas
de calentamiento.
- Qg, es el calor que cede o recibe el gas de c a l e n t a m i e n t o al pasar a través del lecho {pelets y refractario).
La definición de los parámetros a n t e r i o r e s ayuda a s i m p l i
-ficar las e x p r e s i o n e s que describen los balances de e n e r g í a .
2 . - B A L A N C E DE ENERGIA PARA LDS P E L E T S Y EL R E F R A C T A R I O .
Se toma un e l e m é n t o difereneia1 en z y se obtienen las
e x p r e s i o n e s para Qp y para Qr:
Qp = HP LP Ò.Z (Tg - Tp) (16)
Qr = Hr Lr Az (Tg - T r ) (17)
La suma de las e c u a c i o n e s a n t e r i o r e s es la cantidad total de
energia que se intercambia entre el gas de c a l e n t a m i e n t o , el refractario y los pelets; usando las e c u a c i o n e s (7), (9), (13) y
(15), se obtiene -que
Hr = Y Hp (18)
con
1 + a H g / ( 5 kP) r =
1 + e H g / ( 3 k r )
y además,
» Tr = Tp + a Tg con
a2 , 5 k p , *2 r 3 Ki oí = i +
J 3 K r 1 Hg s
y la primera derivada de Tg con respecto al t i e m p o es,
Tg - Tp Tg = ¡
a , 5 kP , 1 +
15 Kp ^ a Hg J
y entonces,
Qr + Qp = Hp Lp Az 3S (Tg - Tp) (19)
donde
L r e p r C r
t = 1 + 3
Lp a pp Cp .
3 . - B A L A N C E DE ENERGIA PARA EL GAS.
Para el gas de c a l e n t a m i e n t o el balance de energía c o n s i s t e
en conocer el aumento o pérdida de la energí a interna del g a s :
ATg
Qg = Mg Cg (20) At
donde ATg es el cambio de temperatura del gas al transcurrir un
interval o de tiempo At y Mg/At es el gasto de g a s e s (Sg), en
Kg/seg.
4 . - B A L A N C E DE ENERGIA AL PASAR EL G A S DE C A L E N T A M I E N T O DE UN
PUNTO z A UN PUNTO z + Az.
Cuando el gas pasa a través de una rebanada de e s p e s o r Az en
el lecho, el gas pierde una cantidad de calor igual a la que se
transfiere a los pelets y al refractario por convección de acuerdo
Gg Cg ATg = - Hp Lp t A z (Tg - Tp) (21)
y c u a n d o los c a m b i o s en z y en el tiempo son s u f i c i e n t e m e n t e pequeños, la ecuación anterior se expresa en su forma diferenciáis
a Tg Hg Lp "S - _ .
Tg - Tp (22)
9 Z Gg Cg 1 J
5.- B A L A N C E DE ENERGIA AL T R A N S C U R R I R U N INTERVALO DE TIEMPO At.
Al transcurrir un tiempo At, el calor perdido por el gas será
igual al calor transferido al refractario y a los pelets durante
é s e tiempo, o sea, el aumento de energía i n t e r n a :
ATp
(Cp Mp + Cr Mr) Az = Mp Lp A z S (Tg - Tp) (23) At
y expresando la ecuación en forma diferencial se llega a que,
é TP Hp Lp S _
= Tg - TP (24)
<? t Cp Mp + Cr «r 1 J
L a s ecuaciones (22) y (24) describen las funciones de
temperatura del gas de c a l e n t a m i e n t o y del lecho en función de z y
CAPITULO IV
1.-FUNCIONES DE TEMPERATURA DEL LECHO Y DEL G A S
E s necesario definir dos v a r i a b l e s £ y x cornos
Hp Lp S
K = z (25-a ) Cg Gg
Hp Lp S
T = t (25-b) Cp Mp + Cr Mr
Usando é s t a s v a r i a b l e s en las e c u a c i o n e s (22) y (24) se
o b t i e n e que,
9 T g ( ? , r )
T g - TPU , T ) I ( 2 6 )
9 K
9 TP( £ , T )
Tg ( ¿f j T ) - Tp(£,r) I (27) » \ s > 4 ' r
T L
con las c o n d i c i o n e s ,
- Tg(0,r) ~ Tg, temperatura del gas a la e n t r a d a del lecho, y
- Tp(^,0) = Tp, temperatura inicial del pelet.
Despejando Tg de la ecuación (27) y s u s t i t u y e n d o en la ecuación
(26) se encuentras
9ZTp 9 Tp 9 Tp
= 0 ( 2 8 )
de donde,
Tp = Tg [ 1 - exp ( - * - r ) 1 (29)
o p 9 *(?»•> T
Tg = Tg 1 - exp ( - ? - r ) (30)
L Q T J
tal que >P(íf,T) e s una función tal que,
,r)
= (31) a? tfr
Sea entonces,
f ( £ ) = condición inicial
r TP( ? , 0 )
= e x p ( ? ) ^ 1 - J (32)
Apiicando la transformada de L a p l a c e en a m b o s lados de la ecuación (31):
4r(fpS) = [ s í ( í ,s) - 1 (33)
d ? L J
con la condición a la frontera
*(0,s) = f(0)/s
tal que
T p ( 0 , 0 ) f(0) = 1
-T |
Al resolver la ecuación (33) se obtienes
f(0) % e x p [ ( ) / s ] df
t í f j S ) = exp(¿f/s) + f dx (34)
J O _
s S dx
a q u e :
df (x)
F Í ^ J T ) * f ( 0 ) I O ( 2 V ? R ) + I O [ 2 V ( ? - X ) T ] d x ( 35
dx
q u e t a m b i é n s e puede e x p r e s a r c o m o :
? I I [ 2 V ( ? - X ) T ]
= f ( < ) + 2t f f ( x ) = Z — dx ( 3 6
2 V ( Í - X ) T '
y e n t o n c e s ,
a T
= JQ f ( x ) Io[2V(£-x)r ] dx ( 37 )
S u s t i t u y e n d o las e c u a c i o n e s (36) y (37) en las e c u a c i o n es
(29) y (30) se e n c u e n t r a n las e x p r e s i o n e s p a r a T p ( £ , r ) y Tg(?,r)s
o r r ? i i C 2 V ( e - x ) T 3 -.>>
Tp(?,r)=Tg Ji - e x p ( - í - r ) f ( ? )+2 r f f (x) r = Z dx (38í
i L 2 V ( e - x ) T JJ
Tg(¿f , T )~Tg jl - e x p ( - í - r ) f ( x ) Io[2V(?-x)T 3 d x j j ( 3 9 )
L a s e c u a c i o n e s (38) y (39) d e s c r i b e n las f u n c i o n e s Q e
t e m p e r a t u r a del lecho y del g a s a p a r t i r d e u n a distribución inicial d e t e m p e r a t u r a s f ) en z. P a r a el c a s o en que
t e m p e r a t u r a inicial e s c o n s t a n t e , las e c u a c i o n e s a n t e r i o r e s S e
reducen a:
oo ^ i l - i ^ n
Tp( ? ,r ) = Tp + (T| - T p ) e x p ( — r T (40)
¿ l! C n!
T g U , r ) = Tp + (TÍ - T^)exp(-?-T) + ^ 2 ] ( 4 1 ) 1=1 n=o
N o r m a l i z a n d o las e c u a c i o n e s a n t e r i o r e s se 1lega a
00 l l -1 „ n r T v K
Tnp(?,T) = e x p ( - £ — r ) ) ) (42)
f l! L ni
1=1 n = 0
00 _l l ^n
T n g ( ? , T ) - e x p ( - f - T ) ] ( 4 3 )
d o n d e
l=i n=o
Tp(*f,r) - Tp
Tnp ( £ , T ) = , (44)
Tg - Tp
T p ( ? , T ) - T p
Tng (? jT ) — (45) Tg - Tp
Si Tnp(¿f,T)=0, la temperatura en é s e punto e s igual a la
temperatura inicia 1 (Tp), m i e n t r a s que si Tnpí £, r) =1, la
t e m p e r a t u r a en ése punto e s igual a la temperatura del gas a la
entrada del lecho (Tg) ; d e forma similar, si Tr>g(£ ,t)=0, la
temperatura del gas en ese punto es igual a la temperatura inicial
del lecho (Tp), m i e n t r a s q u e con un v a l o r de 1 indica q u e la
CAPITULO V
SOLUCION POR ELEMENTOS FINITOS (CASO UNIDIMENSIONAL)
En el caso unidimensional, el método de elementos finitos se
reduce a las ecuaciones de transferencia de calor en forma
diferencial a de incrementos deltas. En éste caso, se considera
una rebanada de espesar Az del lecho, igual que en el capitulo
tres. Dado que,
Gg = QP + Gr (46)
entonces, sutituyendo las expresiones encontradas para cada una de
las variables anteriores, ees. (16), (17) y (20), se obtiene que,
f
l+At t-At . Hp Lp Az . t t^Tg - Tg = - Tg - Tp - .
J Gg Cg J
[T; - TrJ
Hr Lr Az Gg Cg
de la cual se obtiene que,
t+At t _ t
Tg = Hp Lp Tp + Hr Lr Tr + . . .
Gg Cg
(47)
r "9 - _ v t-i
...+ [ — — - Hp Lp - Hr LrJ T g j
GgCg (48)
Por otra parte, el calor que intereambia el gas de
calentamiento con el refractario es igual al aumento de energía
t + At t (Tr - Tr ) Mr Cr Az
At
Hr Lr - t t^
= Tg - Tr | Az (49) Mr Cr ^ J
t+At de donde se obtiene la expresión para Tr
t+At Hr Lr t t t
Tr = (Tg - Tr) At + Tr (50) Mr Cr
Un a n á l i s i s similar para el pelet resulta en q u e :
t+At Hp Lp t t t
Tp = (Tg - Tp) At + Tp (51) Mp Cp
Las e c u a c i o n e s (48), (50) y (51) proporcionan las
temperaturas del gas, los pelets y el refractario a un tiempo t+At en función las temperaturas al tiempo t y de los incrementos A z y
At. Es o b v i o que para poder 1 legar a e s t o s resultados e s
imprescindible c o n o c e r las temperaturas a un tiempo dado para
generar la evolución de las mismas de ahí en a d e l a n t e . Se s u p o n e además que los incrementos en el tiempo, At, y en la al tura, Az,
son razonablemente pequemos de tal manera que se a s e g u r e la
estábilidad de las e c u a c i o n e s y la exactitud de los r e s u l t a d o s asi
C A P I T U L O VI
R E S U L T A D O S
1 . - MODELO MATEMATICO,
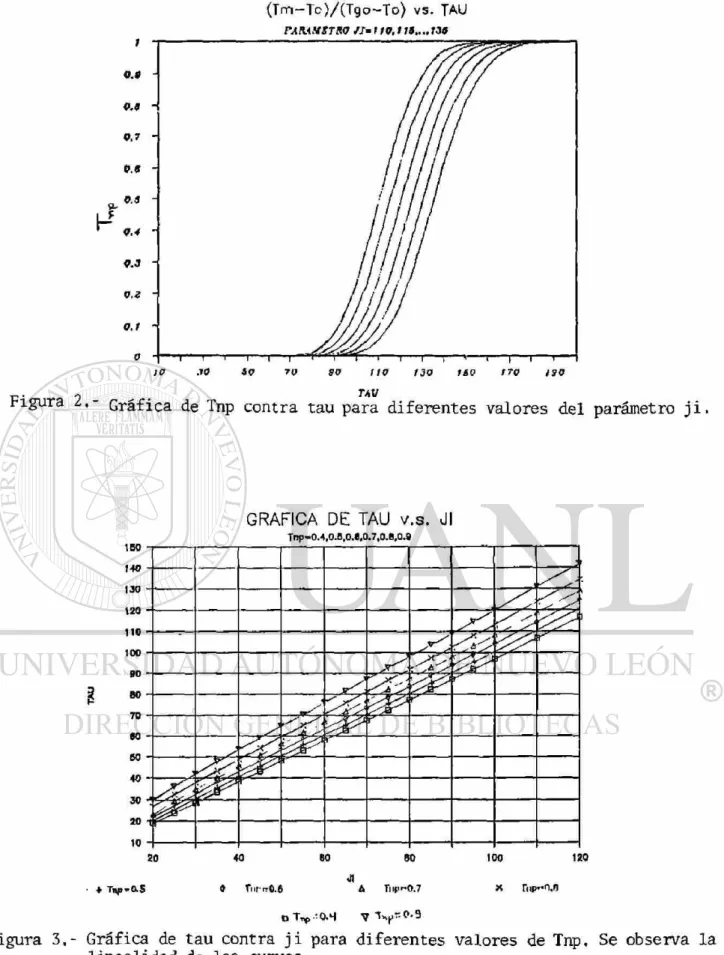
Al graficar Tnp c o n t r a r para d i f e r e n t e s v a l o r e s d e £ d e la ecuación C42D, se o b t i e n e el c o n j u n t o d e curvas m o s t r a d a s en 1 a figura 2.
De la figura 2, s e pueden encontrar los valores de £ y de r par a un val or d a d o de Tnp pudi e n d o segui r se una d e dos a l t e r n a t i v a s :
CID, determinar los valores de £ y de r c o r r e s p o n d i e n t e s a las c a r a c t e r í s t i c a s fisicas del m o d e l o en particular para q u e a par ti r de e s t o s valor es s e pueda deter mi nar el t i e m p o n e c e s a r i o en alcanzar el valor de Tnp.
C 23, hacer una gráf i ca de r contr a £ par a un val or de Tnp y obtener 1 a ecuaci ón que reíaci ona e s t a s var i ables para que, una vez q u e s e sus ti tuyan 1 as expresi ones para; ? y para t se e n c u e n t r e una ecuaci ón q u e r e í a c i o n a el t i e m p o de cal entami ento en funci ón del g a s t o de gases y de 1 as demás variables del sistema.
En e s t e trabajo se escoge 1 a s e g u n d a opción ya q u e no se pierde ninguna generalidad, o b t e n i e n d o s e las curvas mostradas en la figura 3.
M e d i a n t e un a n á l i s i s de regresión lineal» s© o b t i e n e una ecuación q u e reíaci ona a £ y r con un c o e f i c i e n t e de correlación satisfactor io, 1 o cual nos 11eva a una ecuaci ón del ti po:
(Tm-To)/(Tgo-To) vs. TAU
FAXiUSTSO /T*tf<r,tJ»,..,t3B
Figura 2.- Gráfica de Tnp contra tau para diferentes valores del parámetro ji.
1 5 0
1-40
1 3 0
1 2 0
1 1 0
1 0 0
9 0
GRAFICA DE TAU v.s. JI T n p - 0 . 4 , 0 . 8 , 0 . 8 , 0 . 7 , 0 . 8 , 0 . 9
( eo 7 0 6 0 60 4 0 30 20 1 0
+ T n f - O - S
/
• /
r* i r"
r r ^ sZs
> r
•
4 1
•r
Y
\
i r
20 eo 60
di 4 0
$ TMITTO.6 A T i i t " - 0 . 7
O T V - Q . H V ' S - ^ ' S
1 0 0 1 2 0
x r<ip«n.o
Sustituyendo las ecuaciones (25-a,b) en la ecuación anterior, se X lega a que,
(CpMp + C r M r ) (CpMp + CrMr)F f i a ,
t = E z + + (53)
Cg Gg S Lp l Hg 5 kp J
En la figura 4, se grafica la ecuación (53) para diferentes
gastos de gases usándose los siguientes valores a manera de
ejemplo:
pr = 2650 Kg/m9
Cr = 960 J/Kg °C
kr = 2 W/m °C
£
pp<apcur«nte> = 2200 Kg/m
pp = 3700 Kg/m3
Cp = 8 9 0 J/Kg °C
kP = 0.5 W/m °C
a = 6.4 x 10"*9 m
Z m a x = 1 0 m D = 2 m
£ = 0.1 m
Hg/unidad de área = 120 W/m2 °C
Cg = 1160 J/Kg °C
Se aprecia en la figura 4 que las curvas no se alejan mucho
una de otra. En parte esto se debe a que un valor constante de Hg
como el utilizado en este ejemplo no es del todo adecuado, ya
que Hg en realidad depende también del valor de Gg.
Puede observarse también que las curvas se aproximan cada vez
más conforme el gasto de gases aumenta tal como lo predice la
TIEMPO DE CALENTAMIENTO
T n p - 0 . 4 , 0 . 7
\\
\
\\
w
\
4 8 1 2 1 6 2 0 . 2 4 2 a
D Tiip-O.* + Tnp»0.7
Figura 4,- Gráfica del tiempo de calentamiento contra el gasto de gases para Tnp = 0,4 y 0.7,
0
9 0 0
Tp v , s . TIEMPO PARA 1 - 1 1 m r DIFERENTES 89
« OgalB TIEMPO (MIN) t sj®¿0 V Gq-30
4- 'Jg.»tO
infinito debido al cual la transferencia de c a l o r e s t a limitada
s o l a m e n t e por la inercia térmica del m a t e r i a l .
2.~ M O D E L O N U M E R I C O .
El m o d e l o n u m é r i c o se ejecutó con los v a l o r e s n u m é r i c o s de el
e j e m p l o u s a d o para el modelo m a t e m á t i c o de tal manera que se puedan ana1 i zar 1os resu1tados paraleíamen te.
E s obvio que los resultados asi o b t e n i d o s no son de c a r á c t e r
general, ya q u e é s t o s dependerán de los v a l o r e s u t i l i z a d o s y de la discretización en el modelo de e l e m e n t o s finitos.Sin e m b a r g o los
resultadas p r o p o r c i o n a d o s por el método n u m é r i c o están en muy
buena concordancia con los reportados por el modelo m a t e m á t i c o , de
tal manera que la convergencia de los r e s u l t a d o s es
satisfactoria con las c o n s a b i d a s v e n t a j a s del modelo m a t e m á t i c o (solución automática para c u a l q u i e r tiempo y c u a l q u i e r posición
en el lecho sin necesidad de basarse en la historia térmica
del punto a d e t e r m i n a r ) .
En la figura 5 se reporta una grafica de la temperatura del
pelet en la parte alta del lecho (z = 11 m ) en función del tiempo para diferentes v a l o r e s del gasto de gases. L a s curvas
e n c o n t r a d a s poseen la misma forma q u e las curvas de la figura 2,
c o r r e s p o n d i e n t e s al modelo m a t e m á t i c o .
En la figura 6 se grafica la temperatura del refractario para d i f e r e n t e s tiempos tomando como parámetro el g a s t o de g a s e s .
F i n a l m e n t e , en la figura 7 se grafica el tiempo de
c a l e n t a m i e n t o para z = 11 m (salida del lecho) y Tnp igual a 0 . 4 y
Tr v.s. TIEMPO
PARA * » 1 1 m Y DIFERENTES Og
TIEMPO(MIN)
oeg«S t Gs)»IO « (?9«16 A «9-20 X Oj-26 * 09=30
Figura 6,- Gráfica de la temperatura del refractario contra el tiercpo para diferentes valores del gasto de gases (Modelo Numérico).
TIEMPO DE CALENTAMIENTO
Tnp-0.4,0.7
\
\
\
\
\
\
VJ\
\\
\
N
4 8 12 10 20 24 2S
D Tnp«"0.4 + Tnpa0.7
3 . - COMPARACION DE M O D E L O S .
Las g r a f i c a s de la figura 8 muestra las c u r v a s proporcionadas
por a m b o s modelos con Tnp = 0 . 4 y 0.7, o b s e r v á n d o s e que:
a).— C o n f o r m e el gasto de gases aumenta, a m b o s m o d e l o s tienden al
mismo valor de t i e m p o de c a l e n t a m i e n t o .
b).- P a r a gasto d e g a s e s pequeños y v a l o r e s a l t o s d e Tnp, el tiempo de c a l e n t a m x e n t o es mayor en la solución n u m é r i c a que en la so1ución matemá t ic a.
c ) P a r a gastos de g a s e s pequeños y valores bajos de Tnp, el
tiempo de c a l e n t a m i e n t o es m e n o r en la solución numérica q u e
en la solución m a t e m á t i c a .
Sin e m b a r g o , hay q u e notar que estas d i f e r e n c i a s n o son muy
grandes a p r e c i á n d o s e que los resultados de a m b o s m o d e l o s son casi
idénticos. Las d i f e r e n c i a s e n c o n t r a d a s son fácilmente e x p l i c a b l e s
tomando en consideración que en el m o d e l o matemático:
1.— Se supone q u e el c a m b i o de la temperatura con respecto al
tiempo e s igual tanto en el refractario como en los pelets
como se expresa en la ecuación (23). N ó t e s e q u e se trata del
c a m b i o de temperatura promedio.
2.- La temperatura del lecho, Tnp , es una temperatura promedio
que toma en cuenta tanto al refraetario como a 1os pe1ets. Es por ello que a v a l o r e s al tos de Tnp se da tiempo para calentar
al refractario con lo que el v a l o r reportado será menor que el
dado por el modelo numérico, ya que este ú l t i m o si considera
t
&
2 3 p 4.6 5.5 Í5 1.6 O J• S O L MATEMATICA
TIEMPO DE CALENTAMIENTO
COMPARACION DE MODELOS
®9 (Kb/««9) •I SOL NUMERICA
Figura 8a,- Tiempo de calentamiento contra el gasto de gases para un va-lor de Tnp = 0,4, predicho según la solución numérica y la solución matemática exacta, Se observa la consistencia entre los dos modelos,
TIEMPO DE CALENTAMIENTO
COMPARACION DE MODELOS
4.6
3.9
Z9
OJ
4 8
Q SOL MATEMATICA
Gg (kj/a«g)
•I SOLNUMFJUCA
En cambio, para valores bajos de Tnp, no se cuenta con el
tiempo suficiente para calentar al refractario por lo que
estará muy "frío" y la temperatura promedio será más baja en
el modelo matemático que en el numérico, el cual solamente
reporta 1a temperatura del peíet.
Por último cabe seRalar la importancia de determinar el valor
del coeficiente de transferencia de calor entre el gas y los
pelets y el refractario, Hg.
En este trabajo se supone un valor constante para dar mayor
simplicidad al ejemplo numérico pero existen diversos métodos para
encontar un valor de Hg con la simetría utilizada en esta
modelación.
Una consideración muy importante que se debe señalar es el que
se haya supuesto un mismo valor de coeficiente de transferencia de
calor para los pelets y para el refractario, lo cual es bastante
val ido dado el sistema físico con el que se trabajó. Está
C A P I T U L O VII
C O N C L U S I O N E S
Los r e s u l t a d o s q u e proporciona el m o d e l o m a t e m á t i c o aquí p r e s e n t a d o representan v a l o r e s m u y c e r c a n o s a los q u e s e obtendr í an a par ti r d e un m o d e l o n u m é r i c o como el de di ferencias fi ni tas.
El modelo m a t e m á t i c o proporciona resultados en tiempos d e c ó m p u t o insignificantes.
El modelo numér i c o r equi er e de t i e m p o s d e c o m p u t o m u c h o mayores q u e el modelo matemático.
Las curvas mostradas en las f i g u r a s 2 y 3 no dependen de las propiedades de los materiales del lecho.
La ecuación C333 es una e x c e l e n t e a l t e r n a t i v a para el c á l c u l o del t i e m p o de c a l e n t a m i e n t o necesario para llevar un punto del lecho a un valor de Tnp dado.
REFERENCIAS.
[13 Mc. Adams, William H. ; "Heat Transmission"; International
Student Edition, Third Edition, 1954, pp 290-299.
C2] Bugdandy, L. Von, Engel1, H.J.; "The Reduction of Iron Ores,
Scientific Basis and Technology"; Springer-Verlag Berlin
Heiderberg, New York, Verlag Stahleisen m. b. H. Düsseldorf,
1971, pp 203-221.
[33 Mc. Gannon, Har ol d E. ; "The Mafci ng Shapi ng and Tr ©a ti ng of
Steel", United States Steel, Ninth edition, 1971, pp 417-418.
C4] Carslaw, H.S. , Jaeger, J.C. ; "Conduction of heat in Solids",
NOMENCLATURA.
a R a d i o del pelet.
Cp Calor especi fi co del peí©t.
Cr Calor e s p e c i f i c o del refractario.
D D i á m e t r o del 1 echo.
Gg G a s t o de gases.
Hg C o e f i c i e n t e de transferencia de calor entre el lecho
y el gas de calentamiento.
Hp C o e f i c i e n t e p r o m e d i o de transferencia de calor entre
el pelet y el gas de calentamiento.
Hr C o e f i c i e n t e p r o m e d i o de transferencia de calor e n t r e
el r e f r a c t a r i o y el gas de calentamiento.
kP Conductividad del pelet.
kr Conducti vi dad del refractari o.
Lp Area de pelet por unidad de longitud.
Lr Ar ea de refractari o por uni dad de 1ongi tud.
M p Masa de pelet por unidad de longitud.
Mr Masa de r e f r a c t a r i o por unidad de longitud.
Qg Energia c a l o r í f i c a del gas de calentamiento.
Qp Energia calorífica del pelet en un Az d e lecho. Or Energi a cal or i fica del r efr ac tario en un Az
lecho.
Coordenada del pelet; r = a en la s u p e r f i c i e del
Tg Temperatura del gas de cal e n t a m i e n t o en función del
ti empo.
Tp Temper atura del peíet en f unci ón del r adi o del peí et
y del tiempo.
Tr Temperatura del r e f r a c t a r i o en función del espesor y
del tiempo.
Tg Temperatura del gas de c a l e n t a m i e n t o al entrar al
lecho.
Tp Temperatura inicial del pelet.
Tng Temperatura del gas referenciada a Tp y normalizada
a Tg-Tp.
Tnp Temperatura del pelet referenciada a Tp y n o r m a l i z a
-da a Tg-Tp.
x C o o r d e n a d a del r e f r a c t a r i o referenciada a la .pared
en contacto con los pelets; dirección positiva hacia
afuera del 1 echo p e r p e n d i c u l á r m e n t e al eje de s i m e
-tria.
z C o o r d e n a d a del l e c h o referenciada a la base; d i r e c
GRIEGAS.
s Espesor del refractario.
Kp Difusividad del pelet.
Kr Difusividad del refractario, pp Densidad del pelet.
pr Densidad del refractari o.
T Parámetro adimensional del tiempo.