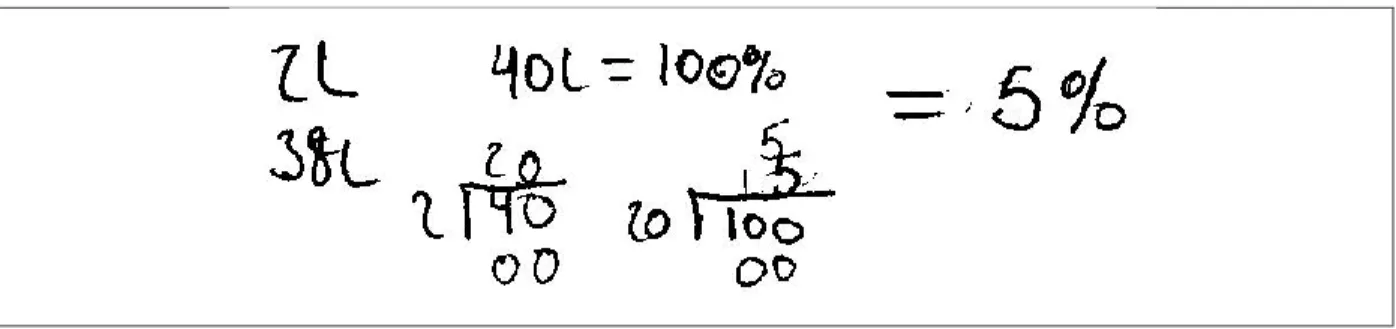UNIVERSIDAD AUTÓNOMA DEL ESTADO DE HIDALGO

UNIVERSIDAD AUTÓNOMA DEL ESTADO DE HIDALGO

INSTITUTO DE CIENCIAS BÁSICAS E INGENIERÍA

ÁREA ACADÉMICA DE MATEMÁTICAS Y FÍSICA

MAESTRÍA EN CIENCIAS EN MATEMÁTICAS Y SU DIDÁCTICA

Entendimient o de la proporcionalida d en

e stu diante s de licenciatura

Tesis

Que para obtener el grado de:

MAESTRA EN CIENCIAS EN MATEMÁTICAS Y SU DIDÁCTICA

PRESENTA:

M a r í a A n t o n i a R a m í r e z B e r n a l

Dirigida por:

Dr. Fernando Barrera Mora

Dr. Aarón Reyes Rodríguez

AGRADECIMIENTOS

Al Creador y Soberano del Universo, Jehová Dios, por

brindarme entendimiento para realizar esta

investigación y permitirme culminar esta meta.

A mi esposo, Mariano Javier Pozas

Cárdenas, por su apoyo económico y

moral durante todo el proceso de esta

maestría.

A los revisores de la tesis, Dr. Roberto

Á

vila Pozos y Dr. Raúl Temoltzi

Á

vila,

por

sus

comentarios;

los

cuales

contribuyeron a mejorar la calidad de

este documento.

A mis asesores, Dr. Fernando Barrera y

Dr. Aarón Reyes Rodríguez, por su

guía, apoyo y experiencia brindados

durante la realización de esta tesis.

DEDICATORIAS

A mi mamita, Sra. María del Carmen Bernal Vda. de

Ramírez, por ser una fuente de superación constante

en mi vida.

A mis hijos, Antares, Altair y Asahel, por ser la ilusión de

mi vida.

A mis hermanos, Nacho, Enri, Lolis y Elena, y a

todos mis sobrinos, por tener confianza en mí.

RESUMEN

En esta investigación se analizan y documentan las formas de razonamiento desarrolladas por 102 estudiantes de nivel licenciatura al resolver problemas de proporcionalidad. El análisis se centró en el nivel de funcionalidad que los estudiantes otorgaron a la fracción, la influencia de diversos sistemas de representación en el desarrollo de estrategias de solución, y el reconocimiento de las relaciones multiplicativas básicas presentes al razonar proporcionalmente; así como la identificación de algunas dificultades para resolver este tipo de problemas.

Considerando el papel fundamental de la fracción como sistema articulador de la red de conceptos relacionados con la proporcionalidad, se consideraron teorías alrededor de los sistemas de representación. En este sentido, las ideas de Lamon sobre la existencia de una base de significados para la fracción como representación de los números racionales, dio consistencia e influyó notablemente en el diseño e interpretación de datos en este trabajo. Se incluyeron ideas complementarias en las que se considera que la proporcionalidad, junto con los cocientes y otras formas de relaciones multiplicativas, se establecen en el sistema matemático intuitivo del niño aún antes que el símbolo mismo como notación formal.

ABSTRACT

ÍNDICE

CONTENIDO

CAPÍTULO 1. EL PROBLEMA DE INVESTIGACIÓN

1.1. Introducción……….. 1

1.2. Revisión de la literatura……… 4

1.3. Planteamiento del problema………..….. 7

1.4. Preguntas de investigación……….. 9

1.5. Hipótesis………..….. 10

1.6. Objetivo general……….….. 10

CAPÍTULO 2. MARCO CONCEPTUAL 2.1. Introducción……….. 11

2.2. Construcción del marco………. 12

2.2.1. Elementos básicos de Razonamiento Proporcional……….. 13

2.2.2. Construcción cualitativa de la noción de proporción……….. 17

2.2.3 Cuantificación de relaciones proporcionales……….. 19

CAPÍTULO 3. METODOLOGÍA 3.1. Introducción……….. 23

3.2. Análisis Previos. Referente teórico/conceptual………..….. 23

3.3. Descripción del Instrumento……….….. 24

3.4. Características de los participantes……….. 30

4.2. Análisis de resultados……… 32

4.2.1. Ojos………. 32

4.2.2. Barda………. 34

4.2.3. Gasolina……… 35

4.2.4. Pastel……….. 44

4.2.5. Planetas………. 54

4.2.6. Edades……….……….. 58

4.2.7. Cuerpo……… 60

4.2.87. Examen………... 63

4.2.9. Naranjas……… 66

4.2.10. Potrero………. 70

CAPÍTULO 5. DISCUSIÓN Y CONCLUSIONES 5.1. Introducción……….. 79

5.2. Conclusiones………. 80

5.3. Implicaciones Didácticas………...…… 83

5.4. Limitaciones……….. 84

5.5. Trabajos futuros………...……… 85

REFERENCIAS……….. 87

APÉNDICES Apéndice A. Hoja de trabajo de la prueba piloto……… 91

Apéndice B. Hoja de trabajo del instrumento final……..………. 94

Apéndice C. Resultados cualitativos - cuantitativos de la prueba piloto……….. 97

EL PROBLEMA DE INVESTIGACIÓN

1

1

1.1. Introducción

La proporcionalidad es una idea central en las matemáticas de todos los niveles escolares, la cual, además de facilitar el desarrollo del pensamiento formal del adolescente (Piaget, citado en Beard, 1971), es considerada por muchos investigadores educativos como una noción que permite la construcción de otros conceptos fundamentales en el estudio y comprensión de las matemáticas (álgebra, trigonometría, cálculo, probabilidad, estadística, etcétera). Además, el concepto de proporcionalidad permite vincular a las matemáticas con otras áreas del conocimiento como la Física, la Química, la Biología, la Geografía, la Economía o el Arte; y constituye la base para resolver diversos problemas de la vida cotidiana.

En la vida diaria razonamos proporcionalmente cuando usamos dibujos a escala, cuando determinamos cuánta gasolina será necesaria para conducir un número grande de millas si se conoce la razón de millas por galón para distancias normales, o cuando se adapta una receta para alimentar a pocas o muchas personas. (Beckmann, Thompson y Austin, 2004, p. 257)

Esta relevancia de la proporcionalidad se ha plasmado en propuestas curriculares como la de los Principios y Estándares para la Educación Matemática (NCTM, 2000) en la que se le considera como uno de los ejes fundamentales del currículo y como un elemento articulador de diversas ideas matemáticas. La proporcionalidad constituye también un antecedente indispensable para comprender conceptos tales como combinación lineal en álgebra lineal; densidad, velocidad, aceleración y fuerza en física; o molaridad en química.

El razonamiento proporcional se emplea en las ciencias de la tierra para entender la relación entre mapas y características geológicas en el mundo real, en química para resolver problemas de estequiometría, y en ingeniería para crear y entender modelos a escala utilizados para evaluar el propósito y apariencia de conceptos de diseño. (Boyer y Levine, 2012, p. 517)

Sin embargo, a pesar de la importancia de este concepto en el aprendizaje de la disciplina y en la resolución de problemas en la vida diaria, por ejemplo al comprar diversos productos, al cambiar divisas o determinar la cantidad de ingredientes en

Capítulo 1

1

2

una receta de cocina (Figueras, López y Mochón, 1994), la investigación en educación matemática aporta evidencia de que los estudiantes muestran dificultades para razonar proporcionalmente (Ben-Chaim et al., 1998). Incluso se ha llegado a estimar que el 90% de los adultos no razonan proporcionalmente (Lamon, 2007) y se ha comprobado que las dificultades de comprensión de este concepto persisten hasta el nivel universitario (Lawton, 1993). Estas dificultades se deben a que, con frecuencia, en la enseñanza de este concepto se enfatiza el desarrollo de habilidades de cálculo, centrando la atención en la representación algebraica de las proporciones y las operaciones simbólicas, más que el entendimiento conceptual (Ye y Perry, 1998; Resnick y Ford, 1998; Lamon, 2001).

¿Qué es la proporcionalidad? La proporcionalidad se refiere a una relación matemática de naturaleza multiplicativa entre dos variables, x y y, la cual se puede expresar mediante una función lineal de la forma 𝑦 = 𝑘𝑥, donde k es una constante,

llamada constante de proporcionalidad. Una relación de proporcionalidad directa también se puede expresar diciendo que el cociente de las dos variables es constante; es decir, y/x = k. Esta forma de considerar una relación de proporcionalidad, permite resaltar que el concepto de fracción juega un papel importante en el desarrollo del pensamiento proporcional, ya que este objeto matemático captura los elementos esenciales de una comparación multiplicativa.

La estructura básica de las tareas de valor faltante que involucran proporcionalidad incluye cuatro cantidades (a, b, c y d), de las cuales se conocen generalmente tres de ellas y se tiene que encontrar la cuarta cantidad (Behr, Harel, Post y Lesh, 1992). También existen problemas de comparación numérica en los que, dadas dos tasas o razones, se debe determinar cuál de ellas es mayor o menor y, finalmente, problemas de comparación cualitativa (ver Tabla 1) en los que se debe realizar una comparación que no depende de valores numéricos específicos (Bem-Chaim et al., 1998; Cramer y Post, 1993).

EL PROBLEMA DE INVESTIGACIÓN

1

3 magnitudes son discretas o continuas (Panizza y Sadovsky, 1992; Fernández, Llinares, Modestou, Gagatsis, 2010).

Tabla 1: Tareas que involucran un razonamiento proporcional

Tipo de tarea Ejemplo

Valor faltante

En una reunión a la que asistieron 20 personas se consumieron 5 pizzas. ¿Cuántas pizzas se deben comprar para una reunión a la que asisten 35 personas?

Comparación numérica

a) Carlos manejó durante 3 horas recorriendo una distancia de 180 km. Mario manejó durante 8 horas y recorrió una distancia de 450 km. ¿Quién manejó más rápido?

b) Un paquete de 6 lápices de la marca A cuesta $20. Un paquete de 15 lápices de la marca B cuesta $57. ¿Cuáles lápices son más baratos?

Comparación cualitativa

Luisa y Paty preparan agua de limón. Luisa utiliza menos azúcar y más agua que Paty. El agua de Luisa es:

(a) más dulce que el agua de Paty (b) menos dulce que el agua de Paty (c) igual de dulce que el agua de Paty

(d) no hay suficiente información para decidir cuál agua es más dulce.

1

4

proporción, porque una proporción es esencialmente una igualdad entre dos

razones.

Figura 1. Red de algunos conceptos relacionados con la proporcionalidad

Tradicionalmente se ha conceptualizado al entendimiento de la proporcionalidad como la habilidad para resolver problemas de valor faltante (Cramer y Post, 1993); sin embargo, el entendimiento de este concepto va más allá de saber determinar proporciones y de poder resolver problemas de valor faltante o de comparación. Entender la proporcionalidad o pensar proporcionalmente implica el identificar y dar sentido a la dependencia lineal entre dos cantidades, discriminar entre relaciones proporcionales y no proporcionales (Cramer y Post, 1993; Lo, et al., 2004; Modestou y Gagatsis, 2009b), así como utilizar diversas formas de representación para pensar acerca de las cantidades y sus relaciones (NCTM, 2000).

1.2. Revisión de la literatura

EL PROBLEMA DE INVESTIGACIÓN

1

5 proporcionalidad, analizar las diferentes estrategias que utilizan los estudiantes para resolver problemas que requieren de un razonamiento proporcional (Harel et al., 1987), clasificar las estrategias utilizadas por los estudiantes (Langrall y Swafford, 2000) o determinar qué factores y en qué medida afectan el desempeño de los estudiantes al resolver este tipo de problemas (Heller, Post y Beer, 1985).

El estudio de los conceptos de razón y proporción fue iniciado por Piaget e Inhelder, quienes realizaron su análisis como parte del campo de la probabilidad y en el estudio de las leyes físicas. Entre los resultados principales de estos estudios y algunos estudios posteriores, se encuentra el descubrimiento de que el concepto de proporcionalidad se adquiere en la adolescencia tardía (Beard, 1971; Noelting, 1980a).

El estudio de las proporciones se relaciona estrechamente con algunos trabajos que analizan la construcción del concepto de fracción. Algunos de estos trabajos revelan que los estudiantes son capaces de pensar en las fracciones como símbolos que representan elementos del campo de los números racionales, pero que son incapaces de adaptar la imaginación que los asocian con fracciones en procesos (Herman et al., 2004).

Subramanian (2008) utiliza la representación de la línea de números dobles como una herramienta para pensamiento y comunicación. En su trabajo destaca que esta estrategia pictórica da soporte visual al razonamiento proporcional, al menos cuando la razón “dentro” o la razón “entre” se refiere a magnitudes con espacios de medida de números enteros, pero que al pasar de una proporción entera a una racional, los estudiantes se encuentran con una barrera conceptual que limita la construcción de nuevo conocimiento.

1

6

Resnick y Ford (1998), por su parte, refieren que el desarrollo del cálculo proporcional requiere de ciertas habilidades tales como la percepción de los datos y la abstracción del proceso.

Lamon (2001), con base en un estudio longitudinal realizado en 5 grupos de niños de grados 5 a 8 en Estados Unidos, determinó que un entendimiento profundo de los números racionales no necesariamente implica el manejo estricto de los modelos presentacionales enseñados en cursos tradicionales. Su estudio se basó en una revisión de las interpretaciones existentes para los números racionales, las actividades de instrucción y los objetivos que se promueven en el salón de clases así como algunas conexiones futuras con otros conceptos. Lamon midió y comparó en su estudio el número de los buenos razonadores, el número de subconstructos usados en problemas y tareas, el logro académico, las habilidades de cálculo y la trasferibilidad de los conocimientos a problemas prácticos tanto de los estudiantes de los 5 grupos como de los estudiantes del grupo de control.

Díaz, Soto y Martínez (2007) concluyen que los estudiantes desarrollan más el razonamiento proporcional en los problemas intuitivos que en los problemas numéricos y que existe una interacción entre el conocimiento formal y el conocimiento intuitivo respecto de las proporciones. Además de caracterizar el pensamiento intuitivo como evidente, flexible y vinculado con la memoria, los autores exponen que un estudiante cuyo pensamiento es primeramente intuitivo, es capaz tanto de construir estrategias nuevas para problemas, como de construir conocimiento matemático.

EL PROBLEMA DE INVESTIGACIÓN

1

7 Díaz, et al., encuentran relevante el trabajo de Chi y Glaser (1982) en cuanto a sus resultados sobre razonamiento cualitativo y los vínculos que tiene con el razonamiento intuitivo, en el cual se evidencia que los expertos razonan de manera cualitativa sobre los componentes de un problema y las relaciones entre ellos antes de describir estos componentes y relaciones en términos cuantitativos. Además, ese razonamiento les permite crear representaciones del problema para determinar cuándo es realmente necesario hacer un análisis cuantitativo del mismo o razonar en términos cualitativos basados en principios científicos. Los novatos, por otra parte, razonan únicamente sobre la estructura superficial del problema. Díaz y Soto hacen un símil del razonamiento cualitativo de Chi y Glaser (1982) con el razonamiento intuitivo señalado por Kieren (1988).

1.3. Planteamiento del problema

Con base en la revisión de la literatura se pudo identificar que existen dificultades para entender la proporcionalidad en todos los niveles escolares, incluyendo el nivel superior. Sin embargo, en el caso específico de México las investigaciones que caracterizan esta problemática en las universidades del país son casi inexistentes. Ante este panorama, el presente trabajo busca ofrecer un diagnóstico de las dificultades que presentan estudiantes de licenciatura al abordar problemas de proporcionalidad, así como identificar el origen de estas dificultades.

1

8

Esta confirmación repetida de la validez de la proporcionalidad—junto con el estatus intuitivo que el concepto recibe gradualmente y la simplicidad intrínseca de las situaciones proporcionales—puede ocasionar una falsa creencia profundamente arraigada de que si hay una relación entre dos variables, probablemente esta relación es proporcional y, en consecuencia, los métodos proporcionales obtienen el estatus de panacea para resolver problemas matemáticos. (Van Dooren, et al., 2005, p. 61)

Las limitaciones mencionadas traen como consecuencia que los estudiantes no desarrollen un pensamiento proporcional. Con la realización de este trabajo se busca determinar si las dificultades mencionadas se encuentran presentes entre los estudiantes universitarios o si existen problemáticas específicas para este nivel educativo.

La mayoría de los investigadores coinciden en señalar que el concepto de proporcionalidad comienza a desarrollarse desde etapas tempranas, aún en niños que no están en edad escolar y que es un proceso largo que ocupa gran parte de su desarrollo1_{, además, aseguran que la madurez del concepto se alcanza durante la} adolescencia. El niño, antes de ingresar a la educación escolarizada, exhibe un sentido común regulado de los objetos del mundo que lo rodean gracias al tipo de percepción intuitiva y empírica que le brindan sus sentidos (Hart, 1988; citado en Ruíz y Valdemoros, 2006), y este conocimiento es la base para la construcción de modos de pensamiento formalizado que se adquirirán en la escuela, lo cual coincide con las ideas de Piaget e Inhelder (1959), para quienes el esquema de la proporcionalidad se organiza de forma previa a que el niño ingrese a la escuela, a partir de un pensamiento cualitativo, el cual es la base para la cuantificación de la proporción. Este pensamiento o razonamiento cualitativo se caracteriza por el uso de palabras de comparación, tales como más grande o más pequeño y más o menos, para relacionar las cantidades involucradas en una tarea (Ruiz y Valdemoros, 2006; Fernández, Llinares, Modestou y Gagatsis, 2010).

1 _{Clarkk y Manii (1996; citados en Bosch, 2007) afirman que el pensamiento multiplicativo aparece de}

EL PROBLEMA DE INVESTIGACIÓN

1

9 Considerando que los estudiantes de licenciatura ya han concluido (o están a punto de concluir) los procesos graduales de madurez del concepto, y han revisado durante su formación escolarizada conceptos y fundamentos en los que se basa la proporcionalidad2_{, deberían ser capaces de resolver sin dificultad una amplia} variedad de problemas sobre este tema. Sin embargo, la experiencia docente de la autora de esta investigación aporta indicios de que en este nivel existen deficiencias de compresión y manejo de las fracciones, particularmente en lo que respecta a sus diferentes interpretaciones. Lo anterior conduce a conjeturar que los estudiantes universitarios en su mayoría tendrán dificultades para abordar problemas de proporcionalidad, al no disponer en su estructura conceptual de la riqueza multifacética de las diferentes significaciones de la fracción. Estas carencias conducen al planteamiento de las siguientes preguntas de investigación, las cuales orientan su desarrollo.

1.4. Preguntas de investigación

1.- ¿De qué manera se coordinan las representaciones mentales internas de los

estudiantes con las representaciones matemáticas institucionalizadas 3 _al

resolver problemas que implican el desarrollo de un pensamiento proporcional?

Con esta pregunta se pretende determinar si el estudiante es capaz de razonar proporcionalmente y si logra utilizar adecuadamente diferentes representaciones para resolver problemas de proporcionalidad.

2.- ¿Cuáles son las principales dificultades u obstáculos a las que se enfrentan los estudiantes al resolver problemas de proporcionalidad?

2 _{De acuerdo con Ruiz y Valdemoros (2006), “se hace referencia al pensamiento proporcional}

cuantitativo del niño cuando puede hacer uso de las razones y proporciones y maneja indistintamente razones internas y externas para enfrentar problemas matemáticos”.

3 _{Con este término se hace referencia al tipo de estructuras de conocimiento que contemplan los}

1

10

La respuesta a esta pregunta será identificar cómo la falta de conocimiento y acceso a las diferentes facetas de la fracción obstaculizan la resolución de problemas de proporcionalidad.

La hipótesis general que se sostiene es la siguiente.

1.5. Hipótesis

Entre los factores que obstaculizan la comprensión de la proporcionalidad en los estudiantes de licenciatura, está la falta de coherencia, articulación y sentido de las distintas significaciones de la fracción, así como el desconocimiento de las relaciones que estas significaciones guardan entre sí, y un manejo limitado de los diferentes sistemas de representación alrededor de la fracción.

1.6. Objetivo General

El objetivo general de este trabajo consiste en analizar y documentar las características del pensamiento proporcional de estudiantes de nivel licenciatura, particularmente analizar el nivel de funcionalidad que otorgan a la fracción en la resolución de problemas de proporcionalidad, así como identificar el origen de las dificultades que muestran al resolver este tipo de problemas.

MARCO CONCEPTUAL

2

11

2.1. Introducción

En una investigación en educación matemática, uno de los elementos principales consiste en establecer un marco de referencia que oriente en primer término el diseño de la investigación y en segundo, la interpretación de los datos obtenidos, con la finalidad de responder a las preguntas de investigación. Una premisa que se debe considerar al desarrollar el marco, es que éste sea propositivo y delimite el proceso investigativo. El marco conceptual ayuda a determinar un camino apropiado para alcanzar los objetivos de la investigación, justificando porqué se han escogido ciertos métodos y no otros, basándonos en experiencias de investigaciones previas y destacando simultáneamente cuál es la base de pensamiento que orientará las prácticas encaminadas a la exploración y descubrimiento de diversas variables que influyen en los procesos de aprendizaje.

Al utilizar un marco conceptual, el investigador cuenta con una mayor flexibilidad para desarrollar el trabajo de investigación, respecto de la utilización de un marco teórico o un marco práctico (Lester, 2005). El uso de un conjunto estructurado de ideas teóricas permite al investigador analizar de forma novedosa un problema, incluso desde puntos de vista distintos pero complementarios. El contar con un marco de investigación, permite también justificar la pertinencia de los métodos aceptables para construir nuevo conocimiento y dar sentido a los datos que por sí solos, no proporcionan información sobre el fenómeno de interés, sino que requieren de interpretación a la luz de una aproximación teórica particular. A continuación se expresan los principios teóricos principales que sustentan este trabajo de tesis.

Teniendo en cuenta el papel fundamental de la fracción en la red de conceptos relacionados con el proceso de desarrollo de la proporcionalidad y razonamiento

Capítulo

2

2

12

proporcional 4 _{, se consideran teorías elaboradas alrededor de los sistemas de} representación. Goldin y Shteingold (2001) afirman que el desarrollo eficaz de sistemas de representación interna en los estudiantes deberá tener una correspondencia coherente y una buena comunicación con el sistema matemático establecido, es decir, con las representaciones externas aceptadas en el ámbito académico. Al respecto, se consideró necesaria una aproximación tanto al dominio de los números así como al sistema de símbolos más frecuentemente usado en este campo. En este sentido, las ideas de Lamon (2001, 2007) dan consistencia e influyen notablemente en el desarrollo del presente trabajo de tesis junto con las ideas de Díaz et al. (2007).

2.2. Construcción del marco

Lamon (2001) reconoce que la enseñanza tradicional de las fracciones privilegia la interpretación parte-todo de la fracción y que esta aproximación no proporciona un punto de partida adecuado para la compresión de éste tipo de números. En su trabajo, Lamon habla de una amplia base de significados para el símbolo de fracción, la cual se oscurece cuando se opera mecánicamente con dichos símbolos. Ella defiende la idea de que las múltiples formas de interpretar a las fracciones, favorecen el desarrollo de significados y permiten establecer conexiones que hacen más robusto el entendimiento de los estudiantes. Kieren (1976,1980; citado en Lamon, 2001) considera que hay 5 subconstructos diferentes e interconectados para el símbolo de fracción, a saber: comparaciones parte-todo, operadores, tasas y razones, cociente y medida. Advierte que cada uno de estos modelos captura algunas, pero no todas las características de los números racionales.

4 _{Panizza y Sadovsky (1992) mencionan un conjunto de conceptos que desempeñan un papel importante}

MARCO CONCEPTUAL

2

13 Por otra parte, se considera que los estudiantes desarrollan un razonamiento proporcional en mayor medida al resolver problemas intuitivos que al resolver problemas numéricos y que existe una interacción entre el conocimiento formal y el conocimiento intuitivo respecto a las proporciones. Las funciones del sistema del símbolo, incluyendo las proporciones, los cocientes y otras relaciones multiplicativas, se establecen en el sistema matemático intuitivo del niño aún antes que el símbolo mismo y las notaciones formales. Un estudiante cuyo pensamiento es primeramente intuitivo, es capaz tanto de construir estrategias nuevas para problemas, como de construir conocimiento matemático (Díaz et al., 2007).

El producto de una revisión amplia sobre la construcción de la noción de proporcionalidad y el desarrollo de un pensamiento proporcional se plasma en los diagramas siguientes, los cuales constituyen la base conceptual para el análisis e interpretación de los datos en este trabajo de tesis.

2.2.1. Elementos básicos de Razonamiento Proporcional

El pensamiento proporcional es más que un concepto, es una forma de pensar en

relación con las proporciones. La mayoría de los estudiantes únicamente desarrolla un pensamiento proporcional al nivel de uso de algoritmos y reglas, sin dar sentido a las operaciones numéricas o a sus resultados. Esto implica que existe una desconexión de los bloques básicos de este tipo de pensamiento y por lo tanto no es posible que avancen en sus construcciones mentales cuando se enfrentan a problemas en los que tienen que razonar proporcionalmente. De acuerdo con Cramer y Post (1993), la componente crítica en situaciones donde está implicada la proporcionalidad, es la relación multiplicativa que existe entre las variables involucradas en la situación.

2

14

comparación es la idea básica sobre la que se construyen los conceptos de la red conceptual de la proporcionalidad (Figueras et al., 1994).

Se puede observar que en el diagrama se establece una diferenciación entre las comparaciones multiplicativas y otro tipo de comparaciones numéricas (bloque A1). Básicamente existen dos maneras de relacionar cualquier cantidad con una cantidad base. La primera es encontrar qué tan mayor es la segunda cantidad comparada con la cantidad base (bloque A2), y la segunda es encontrar cuántas veces es mayor la segunda cantidad que la cantidad base (bloque A3). De acuerdo con Lo et al. (2004), deben distinguirse las comparaciones aditivas de las comparaciones multiplicativas. Por otra parte, los bloques A4 y A5 aluden al hecho de que cuando se comparan dos cantidades por cociente, la cantidad considerada como la cantidad base, toma el lugar del denominador en ese cociente; la única condición es que esa cantidad no sea igual a cero, puesto que el cociente con denominador cero no está definido.

Las cantidades en los bloques A6 y A7 designadas para comparación multiplicativa por cociente, tienen su dominio en los números racionales (bloque Q), ya que se reconoce que en este campo puede darse solución a cualquier cociente5_{, incluso cuando la} cantidad representada por el bloque A7 no sea múltiplo entero de la cantidad representada en A6, siendo ésta siempre distinta de cero. Así mismo, el resultado de tal comparación, representado en el diagrama por el bloque A8, tiene su rango en los números racionales6_{. Cabe destacar el hecho de que el término “racional” viene de} “razón” en el sentido matemático de cociente que expresa una comparación por cociente sin residuo.

De acuerdo con diversos autores (Lo et al., 2004; Chapin y Canavan, 2003; Figueras et al., 1994), las nociones más importantes relacionadas con el concepto de proporcionalidad son las nociones de razón y variación. El término razón se utiliza

5 _{La faceta cociente de la fracción se vincula con la actividad de particionar un todo formado por un objeto}

o varios del mismo tipo en un número de partes disjuntas del mismo tamaño, de tal forma que el todo está incluido en una de las partes.

6 _{En Matemáticas, la idea central del concepto de conmensurabilidad no solo es la posibilidad de}

comparación de dos números a y b, sino la existencia de un factor común que pueda ser expresado. En este sentido, se llama número racional a cualquier número que puede expresarse como el cociente entre

dos números enteros. A su vez, dos números, a y b, se pueden medir (o mensurar) sólo cuando la razón,

MARCO CONCEPTUAL

2

15 para referirse a una relación de carácter multiplicativo entre dos cantidades (bloque A9). Además, ya que se asocia una fracción a una razón que va más allá de una simple escritura (Figueras et al., 1994; Cramer y Post, 1993), se entiende que la razón, al igual que la fracción, posee una cantidad infinita de posibilidades de representarla (bloque A10). Lo más importante de esas representaciones, llamadas fracciones equivalentes, es que el número racional o valor representado por ellas no varía (bloque A8). Los bloques A11, A12 y A13, muestran términos relacionados entre sí: razón entera simplificada, relación multiplicativa de base 1 y factor de proporcionalidad. Se piensa en esta investigación, que estas características de las razones forman parte del fundamento del pensamiento proporcional. Así mismo, se reconoce la importancia de las relaciones multiplicativas presentes cuando se establece una equivalencia de fracciones o igualdad de razones, llamada también una proporción (bloque A14). De acuerdo con Freudenthal (1983; citado en Valverde y Castro, 2009), algunas de esas relaciones importantes para desarrollo de pensamiento proporcional, son la relación interna o escalar (bloque A15), y la relación externa o funcional (bloque A16). Además, de acuerdo con Herman et al. (2004) y Lamon (1999), el concepto de proporcionalidad no es estático, porque al establecerse una proporción, queda implicada la presencia de una variación lineal la cual puede usarse para dar significado a una cantidad al compararla con otra (ver bloque A14).

Otra característica de las razones es que representan una relación de los tamaños relativos de los valores que toman las variables relacionadas linealmente (bloque A17), y aunque al utilizar razones se puede perder información sobre los valores originales de las magnitudes o variables, se gana generalidad y significado al expresar una situación mediante una cantidad relativa que funge como referencia. “Así, un primer acercamiento a la razón, debe tener ideas sobre su carácter relativo junto con el significado de razones equivalentes” (Figueras et al., 1994, p. 87). En esta investigación se considera que ésa es la razón por la cual autores como Lo et al. (2004) consideran importante distinguir y conectar la razón misma con su valor.

2

16

una proporción7_{, se piensa que la relación multiplicativa de base 1 (ver bloque A12), es} un medio de conexión para transitar entre las distintas representaciones numéricas de la razón. Conceptualmente el factor de proporcionalidad (ver bloque A13), constituye un medio para determinar si dos situaciones son proporcionales o bien, permite extender la relación proporcional a otros pares de valores de las variables que estén siendo analizadas; y si existe realmente una relación lineal implicada entre esas variables, el factor de proporcionalidad hace explícito el sentido de dicha variación, trátese de una variación proporcional directa o inversa. El factor de proporcionalidad además constituye una medida del cambio que existe en la variación simultánea de las variables que participan en la situación. De acuerdo con Rodríguez y Pérez (2003), identificar diferentes patrones de cambio cuantitativo constituye una acción precursora para el razonamiento proporcional. Por otro lado, las estrategias unitarias para la resolución de problemas de proporcionalidad, derivadas del cálculo del valor de la razón, constituyen estrategias intuitivas, por vincularse más con las situaciones y experiencias que tienen los estudiantes en la vida real (Cramer y Post, 1993).

Se han resumido aspectos importantes que determinan el concepto de proporcionalidad (ver bloque A18), el cual, es un concepto central en su campo, alrededor del cual aparece una red de conceptos relacionados, los cuales se van adquiriendo durante un período prolongado de tiempo. Se sabe que además de la comprensión de esos conceptos (ver bloque A19), se precisa de experiencia en el desarrollo de estrategias y heurísticas (ver bloque A20), así como de habilidades matemáticas de cálculo para desarrollar pensamiento proporcional efectivo8 _{(ver bloque} A21).

7 _{Esencialmente una razón es una comparación de dos cantidades y puede considerarse como un índice}

que transmite una idea que no puede expresarse con un solo número (Lamon, 1999).

8 _{Entendida la efectividad como una medida de la flexibilidad y la precisión en el desempeño de la}

MARCO CONCEPTUAL

2

17

ELEMENTOS BÁSICOS DE RAZONAMIENTO PROPORCIONAL

2.2.2. Construcción cualitativa de la noción de proporción

El desarrollo del pensamiento proporcional cualitativo se origina durante los primeros años de vida, y sin que el niño se encuentre en una etapa escolar (Piaget e Inhelder, citados en Ruiz y Valdemoros, 2006). Además, las funciones del sistema del símbolo, incluyendo las proporciones, los cocientes y otras relaciones multiplicativas, se establecen en el sistema matemático intuitivo del niño aún antes que el símbolo mismo y las notaciones formales (Díaz et al., 2007). De acuerdo con estos conocimientos, la comprensión de la noción de proporción comienza con el desarrollo de comparaciones cualitativas (ver bloque B1).

2

18

que sustentan los procesos de construcción y desarrollo de razonamiento proporcional, son la interpretación mental de palabras que aluden a una situación de tipo proporcional así como el papel de la percepción de relaciones de tipo multiplicativo existentes en los datos, sin que se establezcan todavía operaciones formales para describirlas.

De acuerdo con Piaget e Inhelder (citados en Ruiz y Valdemoros, 2006), un aspecto importante para el desarrollo del pensamiento proporcional cualitativo, se encuentra en la habilidad del estudiante para crear categorías de clases de palabras (ver bloque B3), mediante reconocimiento lingüístico (ver bloque B4). En cuanto a la percepción de relaciones multiplicativas en los datos (ver bloque B5), los aspectos intuitivos y empíricos que brindan los sentidos (ver bloque B8), son importantes para la asimilación de conocimiento. De acuerdo con Piaget y García (2004), estos aspectos tienen su fuente tanto en formas biológicas como en procesos constructivos sociales. Por ejemplo, algunos autores consideran pertinente el uso de expresiones tales como “por cada”, “de cada” u otras que apoyen la unificación de referentes para favorecer la percepción de algunas razones y su comparación9_{.Por otro lado, la relativización de las} comparaciones cualitativas se logra con el uso de expresiones como “relativamente…”, “en relación con”, “con respecto a” y “si se compara con” (Puig y Fernández, 2002).

La percepción de cambios en las relaciones de los datos (ver bloque B6), se considera como un elemento fundamental en la construcción cualitativa de la noción de proporción, ya que representa la parte variacional existente en situaciones proporcionales. En este elemento están implicados principalmente aspectos perceptuales (ver bloque B9), derivados de procesos incipientes de reflexión y significación que implican captar y abstraer dichos cambios.

9 _{Resnick y Ford (1998) y Lamon (1999) consideran que el proceso cognitivo de subitización ocurre}

MARCO CONCEPTUAL

2

19

2.2.3 Cuantificación de relaciones proporcionales

Es deseable que la cuantificación de relaciones proporcionales (ver bloque C1), sea un proceso posterior a la realización de un análisis cualitativo de la situación10 _{ya que de} acuerdo con Chi y Glaser (1982; citados en Díaz et al., 2007), los expertos razonan de manera cualitativa sobre los componentes de un problema y las relaciones entre ellos, antes de describir estos componentes y relaciones en términos cuantitativos (ver bloque C7).

Este diagrama sugiere que el cálculo proporcional (refiérase al óvalo C2), sea el proceso final de la construcción de un camino que da solución a una problemática, en el cual

10 _{Porque para Herrera (2009), el razonamiento permite al ser humano ampliar sus conocimientos y}

2

20

converjan elementos esenciales tales como estrategias de solución y métodos, (ver bloque C5), habilidades numéricas, (ver bloque C3) y sobre todo que esté sustentado en una visión global y particular de los estudiantes acerca de las relaciones matemáticas existentes entre los datos y otros elementos que describen una situación de carácter proporcional (ver bloque C4); ya que la noción de proporción y proporcionalidad se construye no solamente trabajando con el patrón de proporcionalidad, sino reconociéndolo dentro de un diverso rango de situaciones problemáticas.

MARCO CONCEPTUAL

2

21 En resumen, los diagramas detallan los elementos esenciales en la construcción del concepto de proporcionalidad y los aspectos más relevantes conectados con el desarrollo del pensamiento proporcional. Partiendo de la premisa de que existe una desconexión de los bloques básicos de este tipo de pensamiento en los estudiantes de licenciatura, se muestran los componentes teóricos de tipo matemático y cognitivo entrelazados en el campo conceptual de la proporcionalidad y que sustentan a su vez, la interpretación de los datos obtenidos en esta investigación.

METODOLOGÍA

3

23

3.1. Introducción

La investigación realizada es de corte cualitativo11_{, esto es, se pretende identificar} cualidades de la relación entre el pensamiento proporcional de los estudiantes y las diferentes formas de interpretar una fracción, así como la forma en que estas se estructuran, sin llevar a cabo un análisis estadístico. Con este fin, se realizaron distintos análisis antes y después de recolectar evidencias que soporten la hipótesis principal del trabajo de investigación.

3.2. Análisis Previos. Referente teórico/conceptual

Los primeros análisis necesarios para comprender la complejidad que entraña el campo conceptual de la proporcionalidad fueron dos. El primero fue para averiguar qué significa “razonar proporcionalmente” desde distintos puntos de vista12_{, es decir,} conocer las distintas concepciones acerca del razonamiento proporcional que tienen autores mencionados en la literatura especializada13 _{, así como otros aspectos} directamente relacionados con la estructura interna del “dominio del conocimiento”, tales como definiciones formales y propiedades esenciales de la proporcionalidad. Este primer análisis incluyó una revisión acerca de los tipos de problemas y tareas de proporcionalidad más frecuentemente planteados en el ámbito académico, así como una revisión de situaciones, principios y leyes de corte técnico y científico planteados en el nivel universitario, las cuales alientan a los estudiantes a pensar y razonar proporcionalmente; los posibles procedimientos de solución, los contextos de utilización y los conceptos cercanos subordinados tales como el dominio numérico, magnitudes, medida y variación.

11 _{Relativo a la cualidad, a las características propias de la naturaleza de las cosas.}

12_{Desde un punto de vista psicológico, razonar es la facultad intelectual humana mediante la cual se}

obtienen conclusiones y se resuelven problemas. En el razonamiento lógico deductivo, para razonar se entrelazan proposiciones o se conectan ideas de acuerdo con ciertas reglas o cierta lógica, que apoyan o justifican una idea nueva o un pensamiento (Herrera, 2009).

13 _{En Matemática Educativa destacan los trabajos de Karplus et al. (1983), Behr et al. (1988) y}

Freudenthal (1983) citados en Ben-Chaim et al. (1998), Cramer y Post (1993) y Lamon (1993).

Capítulo

3

3

24

El segundo análisis trató sobre los sistemas de representación más utilizados durante el proceso de abstracción de las ideas matemáticas presentes en este tipo de

razonamiento, por ejemplo, el símbolo 𝑎

𝑏, comúnmente llamado fracción con sus

distintos significados funcionales.

3.3. Descripción del Instrumento

La selección de los problemas que integraron el instrumento de recolección de datos se llevó a cabo después de los análisis descritos y con ellos se elaboró una prueba piloto14_{, la cual consistió de 13 problemas incluyendo: un problema de opción múltiple,} uno de aproximación lineal y once problemas de razones, valor faltante y comparación numérica. Este instrumento se aplicó a un grupo de estudiantes de la Licenciatura en Sistemas Computacionales de la Universidad Autónoma del Estado de Hidalgo.

Los problemas de la prueba piloto se seleccionaron atendiendo la sugerencia de Resnick y Ford (1998) y Panizza y Sadovsky (1992) relacionada con el establecimiento de un criterio general que posibilite la formulación o selección de una secuencia de problemas de tal forma que una vez elaborada cubra las expectativas de la investigación. Para cubrir los objetivos de esta investigación, se determinó que era pertinente aislar o simplificar la complejidad implicada por el manejo de contextos, sobre todo porque se planeaba explorar el pensamiento proporcional de estudiantes universitarios sin introducir el sesgo ocasionado por el dominio de conocimientos previos y lenguaje especializado de las diversas áreas del conocimiento.

Se determinó que el ámbito de los problemas a incluir en el instrumento debería centrarse a la realidad cotidiana15_{, puesto que en este ámbito los estudiantes} reconocen fácilmente los términos lingüísticos empleados por resultarles familiares y

14_{Consultar el apéndice A para conocer los problemas de la prueba piloto.}

15 _{Para Streefland citado en Ruiz y Valdemoros (2006), la realidad cotidiana, es un campo donde se}

METODOLOGÍA

3

25 además porque constituye una fuente rica de información para explorar todas las facetas de la fracción.

El instrumento final16 _{se construyó después de adecuar la prueba piloto. Todos los} problemas del instrumento se eligieron de forma que estimularan y propiciaran que el estudiante razone proporcionalmente, y todos ellos se refieren a proporcionalidad simple y directa. El instrumento final se aplicó a tres grupos de estudiantes de diferentes licenciaturas (Licenciatura en Sistemas Computacionales, Licenciatura en Matemáticas Aplicadas y Licenciatura en Mecatrónica), a los cuales se les dio un tiempo de dos horas para resolverlo.

En la siguiente tabla se organizan los aspectos más relevantes sobre los problemas que forman el instrumento de recolección de datos. En la primera columna aparece la identificación del problema, en la segunda, el propósito del mismo o aspecto a averiguar en el pensamiento del estudiante, enseguida, la noción matemática que subyace al problema, después su complejidad numérica y por último, la clasificación que se hace con respecto a la base de significados funcionales de la fracción.

3

PROBLEMA

SUBYACE COMPLEJIDAD NUMÉRICA

CLASIFICACIÓN Razonamiento Proporcional con

fracciones:

OJOS Plantea una comparación multiplicativa entre dos cantidades que _{forman parte de un “total común”.}

 Cantidad

relativa.

 Carácter

relativo de las razones.

 Simplificación

de fracciones.

Involucra cantidades

discretas. Parte-Todo

BARDA Establece las relaciones implicadas para la mitad, la tercera y la cuarta _{parte de una cantidad no necesariamente entera.}

 Noción precursora: Composición de multiplicación y división.  Representación

simbólica con fracciones.

Solución de

expresiones

aditivas y

multiplicativas fraccionarias.

Operador y Medida

GASOLINA  Establece una comparación numérica por cociente. Representa una relación multiplicativa que implica decrecimiento.

 Plantea una proporción con una de las razones referidas a 100.

 Fracciones

equivalentes.

 Comparaciones a

la base 100.

 Significado de

los factores de proporcionalidad

 Valor de una

razón. Vinculación de los números enteros con los números racionales. Razón

PASTEL



_

 Halla el factor de proporcionalidad de la relación.

Cociente sin

METODOLOGÍA

3

27

PROBLEMA PROPÓSITO Analizar cómo el estudiante:

NOCIÓN QUE

SUBYACE COMPLEJIDAD NUMÉRICA

CLASIFICACIÓN Razonamiento Proporcional con

fracciones:

PLANETAS Determina una cantidad base común como medida de comparación _{multiplicativa entre los tamaños relativos de 2 objetos diferentes.}

 Relaciones

multiplicativas

 Denominador

común.

 Simplificación de

fracciones.

Cantidades

discretas. Medida y _Razón

EDADES  Cuantifica la totalidad de partes que componen un conjunto o integran una cantidad total.  Interpreta una relación de cantidades relativas para determinar las

cantidades reales usando las condiciones del problema.

 Cantidad relativa

 Carácter relativo

de las razones.

Cantidades discretas. Parte-Todo, Operador y Razón DINERO

 Cuantifica la totalidad de partes que componen una cantidad total.

 Plantea proporciones para hallar: una cantidad real asociada a un

“todo” y las cantidades reales de cada uno de sus partes a partir de la cantidad real de uno de ellas.

 Determina una cantidad base a partir de la cantidad real de una de sus

partes.

 Usa la cantidad base y la cantidad real de una de sus partes para hallar las cantidades reales del resto de los subconjuntos.

 Usa la cantidad base para hallar una cantidad real asociada al “todo” y

construye un operador fraccionario para determinar las cantidades reales correspondientes a cada parte.

Cantidades relativas y absolutas. Partición. Cantidades discretas. Parte-Todo, Operador, Medida y Razón CUERPO

 Construye una relación multiplicativa con cantidades de distintas

magnitudes.

 Plantea una proporción con las condiciones del problema.

 Da significado a las unidades de medida que cuantifican las cantidades

de una razón (tasa).

Equivalencia de

3

PROBLEMA

SUBYACE COMPLEJIDAD NUMÉRICA

CLASIFICACIÓN Razonamiento Proporcional con

fracciones:

COSECHA



_

 Plantea una comparación proporcional entre razones.

 Factor de

proporcionalida d fraccionario.  Fracción unitaria Cociente fraccionario. Cociente, Operador y Razón EXAMEN

 Integra el total de partes que conforman un “todo”.

 Determina el número de partes de un todo.

 Determina el tamaño real de cada parte.

 Establece una proporción entre relaciones multiplicativas que

comparan tamaños reales con tamaños relativos de cierto número de partes.

 Relaciones

multiplicativas.

 Cantidad

relativa

 Fracción de un

total.  Unidad múltiple.  Partición.  Medida relativa. Cociente fraccionario y fracción unitaria. Medida, P-T, Razón

INSTALACIÓN  Construye proporciones para determinar las partes de un “todo”. Interpreta un “todo” como la suma de sus partes.

 Establece una relación multiplicativa del tipo “cuántas veces cabe”.

 Cantidades

relativas y

METODOLOGÍA

3

PROBLEMA

SUBYACE COMPLEJIDAD NUMÉRICA

CLASIFICACIÓN Razonamiento Proporcional con

fracciones:

COBRE Utiliza una comparación multiplicativa relativa entre dos cantidades de la _{misma magnitud.} Comparaciones multiplicativas relativas y absolutas. Cantidades racionales fraccionarias y decimales.

Operador y Razón

NARANJAS  Determina una variable común en 2 relaciones lineales. Correlaciona tres variables para obtener un propósito conjunto.

 Coordina el valor de 3 variables para producir un propósito conjunto.

Comparaciones lineales múltiples.

Cantidades discretas enteras

y fraccionarias

Tasa o Densidad y Medida

POTRERO

 Establece relaciones multiplicativas con las dimensiones relativas de dos objetos.

 Construye una proporción de semejanza de dos objetos.

 Realiza un cambio de unidades para comparar longitudes.

 Hace la diferencia entre el concepto de factor de proporcionalidad y factor de semejanza o escala.

 Razón

“dentro” y

razón “entre”

 Semejanza.

 Factor de

proporcionalid ad.

 Factor de

semejanza.

Fracciones con números racionales

decimales. Razón

FERROCARRIL

 Toma en cuenta las unidades de medida en las comparaciones

multiplicativas.

 Construye una proporción con cantidades de distintas magnitudes.

 Conforma un “todo” a partir de sus partes.

 Razón

unitaria.

 Razón al total.

 Simplificación

de fracciones.

 Conversión de

unidades.

Números racionales fraccionarios y

decimales

3

30

3.4. Características de los participantes

La prueba piloto, empleada como medio para determinar y ajustar entre otros aspectos la pertinencia de los problemas, su grado de dificultad, el tipo de lenguaje en los textos para describirlos y el tiempo requerido para concluir la prueba, se aplicó a un grupo de 38 estudiantes del cuarto semestre de la Licenciatura en Sistemas Computacionales de la Universidad Autónoma del Estado de Hidalgo; cuyas edades oscilaron entre 18 y 22 años de edad, un caso de 23 y uno de 25. Los resultados de su evaluación cualitativa-cuantitativa se muestran en el apéndice C.

El instrumento final se aplicó a 64 estudiantes cuyas edades oscilan entre los 18 y los 23 años; todos cursando distintos grados de nivel licenciatura y distribuidos en los siguientes grupos disciplinarios.

 8 estudiantes del séptimo semestre de la Licenciatura en Sistemas Computacionales de la Universidad Autónoma del Estado de Hidalgo.

 20 estudiantes del segundo semestre de la Licenciatura en Matemáticas de la Universidad Autónoma del Estado de Hidalgo.

 36 estudiantes del quinto semestre de la Licenciatura en Mecatrónica de la Universidad Politécnica de Tecamac.

RESULTADOS

4

31

4.1.Introducción

Con los resultados de las pruebas disponibles, el proceso de análisis consistió en

interpretar17 _{dichos resultados, tratando de hallar el sentido de las respuestas de los}

estudiantes desde el referente conceptual considerado en esta investigación, principalmente la base de significados para la fracción de Lamon (2001). Para tal propósito, se llevaron a cabo sistemáticamente los siguientes análisis para cada problema del instrumento:

1.- Un análisis de la relación entre las representaciones del estudiante y las representaciones externas institucionalizadas.

2.- Un análisis cualitativo y cuantitativo de las estrategias empleadas por los estudiantes para resolver los problemas propuestos.

3.- Un análisis cualitativo en torno a las posibles dificultades que presentan los estudiantes al resolver problemas que requieren de un pensamiento proporcional.

En términos prácticos, el proceso general de análisis de resultados fue el siguiente: se evaluaron las respuestas de los estudiantes18_{, al mismo tiempo que se detectaron} casos particulares en cuanto a estrategias utilizadas, representaciones y resultados numéricos o cualitativos inusuales. Se identificaron grupos de respuestas homogéneas

17 _{Al decir interpretar, se está en un plano psicológico, en el sentido de que el principal objetivo es}

determinar cómo y porqué el estudiante contestó de la manera como lo hizo.

18 _{En la prueba piloto se utilizó una escala numérica bivalente con la siguiente clave: A para acierto y E}

para error. Se indicaron los problemas sin contestar con SC. En cuanto a la evaluación del instrumento final se utilizó una escala cualitativa con el fin de dar una visión amplia de las respuestas. Los indicadores fueron: Ro para respuestas ilógicas o incipientes, es decir, con uso de estrategias o representaciones inapropiadas, por ejemplo, estrategias aditivas, mal manejo de números y magnitudes, sin relaciones en los datos y falta de comprensión del problema. Am para respuestas elementales con trabajo de apoyo cualitativo o verbal y comprensión parcial del problema. Az para el tipo de respuestas lógicas, reconocimiento intuitivo de las proporciones y relaciones multiplicativas mediante tabulaciones o dibujos. Ve para respuestas acertadas que denotan dominio de la proporcionalidad, reconocimiento de relaciones multiplicativas funcionales y/o escalares entre los datos del problema o dominio de estrategias formales en trabajo de apoyo. SC se utilizó para indicar los problemas sin contestar.

Capítulo

4

4

32

y patrones de solución novedosos con respecto a lo que se reporta en la literatura. Se separaron en esa primera etapa los casos de respuesta que aportaban aspectos de interés en lo tocante a la caracterización que se hizo de cada problema del instrumento, descrito en el apartado 3.3. Después de realizar los análisis citados en el párrafo anterior, se procedió a detallar los aspectos relevantes de esas respuestas, los cuales contestaron las preguntas planteadas en el apartado 1.4 y sustentaron la hipótesis de esta investigación.

Se hace notar que para los fines que persiguió esta investigación, se consideró prioritario analizar los problemas que involucraban distintas facetas funcionales de la fracción y después aquellos problemas que dieron soporte a los primeros. Así se tiene que fueron 10 los problemas sometidos a distintos análisis cualitativos detallados.

4.2. Análisis de resultados

4.2.1. Ojos

Este problema básico explora esencialmente la formación de una comparación por cociente por parte de los estudiantes de licenciatura. La razón es uno de los conceptos fundamentales para el pensamiento proporcional del estudiante (Figueras, López y Mochón, 1994; Lo et al., 2004) junto con el concepto de variación y el reconocimiento y discriminación de otros tipos de relaciones. Los análisis realizados a las respuestas de los estudiantes de licenciatura a este problema revelan que tienen grandes deficiencias en estos aspectos.

Evidencia que exhibe comparación por cociente.

La figura 4.1 muestra que el estudiante utiliza directamente los datos que se le presentan en el enunciado del problema y que efectivamente los identifica como las partes que componen un todo; sin embargo, es probable que una falta de comprensión global lo induzcan a formar una fracción que no responde a la comparación parte-todo19 _{solicitada. La respuesta mostrada es típica en la muestra y otras razones que}

19 _{En la faceta parte-todo de la fracción, se concibe a ésta como un número que permite cuantificar las}

RESULTADOS

4

33 explican el error son: la tendencia que tienen los estudiantes a operar directamente con los datos proporcionados sin deducir ninguna información adicional dada en forma implícita o bien, a una conceptualización no consolidada sobre la fracción en su faceta parte-todo.

Figura 4.1. Comparación entre partes de un entero común.

Evidencia ilógica con pensamiento aditivo.

El pensamiento que denota cierto estudiante en la figura 4.2 al resolver este problema, es claramente aditivo, una vez que determina con una diferencia el resultado de su comparación entre dos cantidades. Después, es probable que el estudiante se vea influenciado por el enunciado del problema, el cual le pide dar un resultado fraccionario, y por ello intente representar con números fraccionarios su cálculo previo, el cual fue concebido con números naturales o enteros; el resultado es una representación fraccionaria con aritmética entera. La figura mostrada es peculiar porque evidencia que algunos estudiantes usan estrategias centradas en el tipo de respuesta que deben dar más que centradas en procesos lógicos que los conduzcan a respuestas lógicas y coherentes. Se piensa que el estudiante desarrolló un pensamiento absoluto20 _{respecto de los datos del problema, lo cual lo llevó a utilizarlos} directamente en cálculos. Es muy probable hablar de una barrera conceptual surgida por una limitante en la percepción de los datos, en la cual, los datos se miran simplemente como elementos aislados sin relación mutua.

20 _{El pensamiento absoluto es llamado también pensamiento aditivo por Lamon (2001) y se caracteriza}

4

34

Figura 4.2. Pensamiento aditivo y absoluto.

4.2.2. Barda

Los análisis a las respuestas de este problema se caracterizan por una desorganización de lo que los estudiantes extraen por reflexión mental de un plano precedente a uno nuevo en el sentido de la abstracción reflexiva de Piaget21_{; se presume que la razón de} eso se debe en gran medida a un conocimiento limitado de las significaciones que los estudiantes de licenciatura otorgan a la fracción.

Evidencia con desarrollo incompleto de las facetas de la fracción.

La figura 4.3 muestra que inicialmente el estudiante tiene una comprensión adecuada global del problema, puesto que refleja bien las condiciones de éste en su hoja de trabajo. Utiliza dos estrategias de solución, la primera de las cuales es estrictamente aditiva y absoluta; es decir, el estudiante considera que los datos en el problema reflejan directamente las porciones de barda que se pintan y que con cada acción de pintar, el área de la barda sin pintura disminuye simbólicamente con la operación aritmética de una resta. El estudiante abandona su estrategia cuando el resultado que obtiene está fuera del rango concebido en su mente. Su estrategia ha fallado debido a la incapacidad conceptual para plantear y utilizar expresiones para la mitad, la tercera y la cuarta parte de una cantidad, las cuales son nociones precursoras para el razonamiento proporcional; con eso se advierte una limitante en el dominio de la faceta

21 _{Piaget dice que la abstracción reflexiva tiene 2 componentes, una refleja y una reflexiva; la primera de}

RESULTADOS

4

35 operador de la fracción por parte del estudiante22_{. En una segunda estrategia que} utiliza, la cual es puramente multiplicativa, se nota una predominancia de la faceta parte-todo de la fracción que no está consolidada; en este caso, el estudiante cuantifica bien el tamaño de la partición final de la barda, el cual corresponde al denominador de una fracción parte-todo; pero en cuanto al numerador, no visualiza las partes de la barda que faltan por pintar en cada intento y no construye correctamente el numerador de esa fracción. En general, se considera que no hay una buena percepción de los datos implicados para cálculo, los cuales no se dan explícitamente en el enunciado del problema, sino que deben encontrarse mediante operaciones multiplicativas, en este caso, mediante operadores fraccionarios.

Figura 4.3. Acceso restringido a la faceta operador de la fracción y faceta parte-todo incompleta.

4.2.3. Gasolina

El uso de la regla de tres es la estrategia predominante como estrategia de solución en este problema de razones23_{. Otras estrategias de solución presentes fueron las}

22 _{La relación significativa de la fracción en esta faceta, es la comparación entre la cantidad que resulta de}

una operación y la cantidad sobre la que está actuando. Un operador fraccionario puede verse como una función compuesta de una multiplicación y una división que actúa sobre una cantidad.

23 _{Esencialmente una razón es una comparación de dos cantidades y este tipo de relación, la razón, le da}

4

36

unitarias: litros por unidad porcentual y porcentaje por litro; este resultado es peculiar por tratarse de un problema donde lo más natural es realizar comparaciones internas de la situación proporcional antes que comparaciones funcionales24_{, las cuales son} más comunes en problemas que implican tasas o densidades. Sin embargo, éste es uno de los problemas del instrumento de recolección de evidencias que muestran mayor uso de estrategias ilógicas y aditivas y sin ningún sentido de la proporcionalidad. Existe evidencia de un grupo de estudiantes que tiene problemas con el manejo de los números enteros y racionales que dificultan el proceso de solución.

Evidencias ilógicas.

La figura 4.4 presenta un factor que vale 0.2. Se establece la conjetura de que el estudiante probablemente quiso comparar 40 litros con 2 litros y en lugar de

determinarlo con 40

2, lo hizo con 40 x 0.2. Si éste es el caso, entonces el estudiante

tiene un problema con los números, pues piensa que 1

2= 0.2. Su falta de reflexión lo

continúa al utilizar este resultado para transformar un porcentaje (100), probablemente teniendo un pensamiento como el siguiente: “si 40 es 8 veces mayor 2, entonces 100 debe ser 8 veces mayor que la cantidad porcentual que busco”. La figura 4.5 muestra que el estudiante también utiliza el factor 0.2, pero debido a la falta de trabajo de apoyo, se concluye que su estrategia no tiene fundamento.

Figura 4.4. Estrategia ilógica por falta de entendimiento de las relaciones entre los números fraccionarios y decimales.

24 _{Chaim, B. (1998) utiliza el término razón interna o escalar y razón externa o funcional para referirse a}

RESULTADOS

4

37 Figura 4.5. Estrategia ilógica por pérdida del concepto de porcentaje.

La evidencia en la figura 4.6 no tiene sentido proporcional. Los estudiantes realizan operaciones con factores y divisores sin propósito aparente y muchas veces sin involucrar los datos del problema como se aprecia en la figura 4.7.

Figura 4.6. Estrategia ilógica por pérdida conceptual del concepto de porcentaje.

4

38

Evidencias aditivas ilógicas:

Las evidencias en las figuras 4.8 y 4.9 muestran claramente una carencia de sentido proporcional y además una carencia de sentido numérico y/o simbólico, ya que asocian indistintamente números naturales con porcentajes y los operan aritméticamente con sumas y restas.

Figura 4.8. Ausencia de comparación multiplicativa y asociación indebida de magnitudes.

Figura 4.9. Ausencia de comparación multiplicativa y asociación indebida de magnitudes.

Evidencias con rupturas en el pensamiento variacional :