,
UNIVERSIDAD AUTONOMA METROPOLITANA
UNIDAD IZTAPALAPA
I
CARRERA:
LIC. EN COMPUTACI~N
MATERIA:
PROYECTO DE INVESTIGACI~N
11
TÍTULO:
"
APLICACIONES DEL FILTRO DE KALMAN
"ALUMNO:
RAúL
CRUZ QUIRASCO
ASES
DR. HÉCTOR PÉREZ MEANA
TIMESTRE LECTIVO
97-0
CAPÍTULO
l. PRINCIPIOS BÁSICOS.
Principios básicos
de
filtros adaptivos
Filtros adaptivos
La
necesidad
de
un filtro adaptivo
Formulación
del
ecualizador adaptivo
Aplicación de un algoritmo recursivo con mínimos cuadrados para
un ecualizador adaptivo
El
algoritmo fuerte
de
kalman
Simulación
de
los
resultados
Conclusiones
CAPITULO 11. APLICACIONES DE FILTROS ADAPTIVOS
El
combinador lineal de impulso-respuesta-finito.
Ecualización
de
un canal usando un filtro
de
kalman para
la
transmisión rápida de datos.
CAPITULO 111. DIVERGENCIA
Divergencia en el filtro de kalman
Causas
de la
divergencia
Control
de
divergencia
Ejemplo ilustrativo
CAPITULO IV. EL FILTRO ADAPTIVO DE KALMAN
Código fuente
delfiltro adaptivo
de
kalman
2
3
9
IO
14
16
19
20
24
26
29
29
30
31
CAPíTULO I
Este
trabajo presenta una breve explicación
del
funcionamiento
de
los
filtros
adaptivos. Uno de los principales
ymás importante
de
estos filtros es
el
de Kalman.
Gracias a sus investigaciones, los filtros actuales son más precisos en
la eliminación
de
ruido
ygeneración
de
señales puras.
Para poder explicar
de
manera precisa
yclara los funcionamientos
de
estos filtros se
requiere tener conocimientos
de
términos matemáticos avanzados, como son
el
manejos
de
matrices, manejo
de
fórmulas Gaussianas, Integrales,
ymuchos más.
Se
muestra
de
manera esquemática las funciones
ydesarrollo
de
estos filtros por
medio
de
algoritmos computacionales,
yasí poder transferir su proceso
de
manejo a
lenguajes
de
programación avanzado, como Lenguaje
"C",Pascal entre otros.
En
el
capítulo
IVde
este documento se anexa
el
código fuente
de
un filtro adaptivo
de
Kalman, este fue creado por
el
grupo
de
alumnos que desarrollaron este reporte.
El
lenguaje usado fue "C"
ysu compilación se hace por medio
de
archivos "Include",
ya
que
sólo
se tiene un archivo *.c
PRINCIPIOS BASICOS
DE FILTROS ADAPTIVOS.
En la
estructura
básica de
un filtro adaptivo mostrada en
la
figura.
La
serial
de
entrada es filtrada
para
producir una
salida
la cual típicamente es llevada a otro
procesamiento subsecuente.
Lasalida de
este
filtro es también observada por un
circuito
el
cual valora
la calidad de la salida.
Esta medida
de calidad,
o alguna función
de
esta, es
pasada al
circuito que
la
utiliza para modificar
los
parámetros
del
filtro
ycon esto mejorar
la
salida.
En principio, este ciclo
de
procesamiento continua
operando hasta que
los
parámetros
del
filtro son ajustados para que la salida
del
filtro
sea lo
mejor posible. También en principio,
si
las
características
de la
serial
de
entrada o
la calidad de
mejoramiento cambian con
el
tiempo. Entonces este ciclo
mejoramiento/ajuste puede reajustar
los
parámetros
delfiltro hasta que
la
nueva
Los bloques funcionales en
la
figura son bastante generales
ypueden ser
seleccionados
de
diferentes formas para resolver problemas prácticos.
Elfiltro, por
ejemplo, puede ser implementado
deforma analógica o
digital ypuede tener "un
canal
de
retardo", polo cero o estructura enrejada.
Los parámetros disponibles para ajustar pudieran ser
la
secuencia
de
valores impulso-
respuesta o funciones más complicadas
de las
frecuencias
de
respuesta
delfiltro
.
Similarmente, el circuito con el cual se valora la
calidad
de la
salida del
filtro puede
tomar diferentes formas dependiendo
de la
aplicación
del
filtro adaptivo.
La
forma
en
la
que
la
valoración
de la calidad de
salida
es convertida en parámetros
modificados (ajustados).
Las variaciones en
la
estructura
delfiltro,
el
mecanismo
de
valoración
de calidad
yla
actualización adaptiva son comúnmente usados para catalogar las características
de
conducta,
yasí
la
aplicabilidad
de
varios filtros adaptivos.
FILTROS ADAPTIVOS
Los filtros adaptivos tienen una relación estrecha con
los
ecualizadores. En la
practica muchos son
de
hecho, ecualizadores.
Los filtros adaptivos son utilizados (como ecualizadores), para filtrar ruidos
de
banda estrecha
ycomponentes senoidales discretos.
La
discusión
de
filtros adaptivos se hará considerando un filtro general con
entradas múltiples.
Tal
filtro puede también ser usado para nulificar
la
dirección
de
aplicaciones
de
antena
ypara patrones
de
emisión. En este caso
las
entradas pueden
llegar de
múltiples antenas. En
el
sentido más convencional para un filtro transversal,
las
entradas múltiples son simplemente versiones retrasadas
de
una
serial de
entrada
simple 0.e.
las
entradas se originan
de
un cambio de registro).
En algunas aplicaciones, una muestra
dela
serial deseada
puede no ser
habilitada,
pero una muestra
del
ruido puede ser removida.
Podemos utilizar una configuaración donde se tenga
la
serial
más
el
ruido, n l
es
el flujo
de
ruido correlacionado en algún camino con no,
y1es
la salida
delfiltro
adaptivo,
y Ejes la serial
de
error minimizada.
Para
valores reales de
X,sea
la
serial
de
entrada
el
vector:
Wj
=I
W3Q)
w2m(8.93)
La j-esima senal
de salida
es
Esta expresión puede ser más consistente
si la
escribimos en forma
de
matriz:
y ( j >
=W'(j>x(j>
=X'(j>w(j>
(8.95)o bien
y ( j ) =
W ~ ( j ) x ~ ( j ) + W 2 ( j ) x 2 ( j ) + w 3 ( j ) x ~ ( j )
Sea la senal deseada de salida
d(j).Entonces la serial de error es:
El
cuadrado de la senal de error es:
Realizando las multiplicaciones tenemos:
Deseamos encontrar el error cuadrático medio el cual es:
Note que los valores
de
Wno son estadísticos
yson constantes en
la
esperanza.
Asimismo, definimos
la
cual es
la
correlación cruzada entre las senales
de
entrada
yla respuesta deseada.
Para un proceso
de
tiempo estacionario, tenemos:
Una expresión similar
para
cada una
de
las entradas
Definimos también
la
matriz
de
correlación cruzada
de las
variables
de
entrada como:
(8.102)
Puesto que Error[E"cuad"(j)l es una función de segundo orden
de
la
conexión
de
adaptivo es entonces
la
tarea de continuidad observada desde
la
parte superior del
tazón.
Elmétodo de pendiente descendente
usa
el
vector gradiente para
determinar
la
dirección en
la
cual se mueve.
Ahora tenemos:
"delta"[E"cuad"(j)l
=-2"theta"(d,X)
+
2"theta"(x,X)
WCj)(8.104)
Derivando esta ecuación, notamos que
el
primer término, Error[d"cuad"(j)l,
es
una
constante con respecto a W.
Hasta
entonces
la
derivada es cero.
Elsegundo término
es
obtenido multiplicando fuera
de
la
expresión
ydiferenciando con respecto a
Wpara
cada fila.
Elúltimo término también puede ser obtenido por
la
multiplicación
de
las expresiones
ydiferenciándolas. Aquí podemos notar que "theta" sub(iK)
(j) ="theta"
sub(Ki)
(j).Ahora, para encontrar
el
vector
de
peso óptimo,
Wsub(LMS1, inicializamos
el
gradiente a cero. Esta condición
es
satisfecha si:
"theta"(d,X)
= "theta"(X,X) Wsub(LMS1
(8.105)Solucionando para
Wsub(LMS1, tenemos
W SUb(LMS) =
"theta"I-Il(X,X) "theta"(d,X)
(8.106)
Esta es
la
ecuación
de
Weiner Hopf en forma de matriz.
Elerror mínimo cuadrado es
obtenido sustituyendo
la
ecuación
(8.106)en la ecuación
(8..99):Error[E"cuad"(j)l sub(MIN)
=Error[d"cuad"(j)l
-
-
W[transl Sub(LMS)
"theta"(d,X)
(8.107)La
ecuación
8.106puede resolverse directamente después
de
calcular
la
correlación
de
matrices. Usando este método,
los
coeficientes pueden determinarse
donde
Wcj) =
vector
de
pesos antes
de la
adaptación
WCj
+
1) =vector
depesos después
de
la adaptación
"mu"
=constante escalar que controla
la
razón
de
convergencia
"grada"[E"-2"(j)I
=estimación
del
vector gradiente con respecto
a w
La
estimación
del
gradiente está hecha para asumir que
el
gradiente
del
valor
de la
esperanza es igual al gradiente
de
su mismo error.
Así,"grada"[E"-2"(j)I "aproximado" "grada"[E"2"(j)l
Diferenciando
"grada"[E"2"(j)l
= 2E(j)"grada"[E(j)l
(8.110)El
error fue previamente definido (ecuación
8.97)como
Entonces el gradiente es:
"grada"[E(j)l
= -X(j)(8.111)
puesto que
d(j)no es una función
de
WCj).Sustituyendo esta en
la
ecuación
(8.110)"grada"[E"2"(j)l
= -2E(j) XCj) (8.1 12)EI
término
ECj)XCj)es simplemente la serial
de
error multiplicada por cada
entrada. Para
el
ejemplo considerado previamente, tenemos:
Por
Io
tanto:
W1 Cj
+
1)
= WlCj)+
2"mu"ECj)
XlCj)W2(j +I) = W2Cj)
+
2"mu"ECj)
X2Cj)W3Cj +I) = W3(j)
+
2"mU"E(j)
X3Cj)El cual es el algoritmo
de
Widrow-Hoff.
LA NECESIDAD DE UN FILTRO ADAPTIVO
un filtro
adaptivo es definido
de
manera muy general como
un filtro cuyas
características pueden
ser modificadas para alcanzar algún
fin u
objetivo
ygeneralmente es adaptado para llevar a cabo esta modificación automáticamente,
sin
la
necesidad
de
una sustancial intervención del usuario (mientras no se requiera
necesariamente). También usualmente
se asume que la escala de tiempo
de
la
modificación es muy lenta comparado con el ancho
de
banda
de la
serial que se esta
filtrando. Implícitamente con esta suposición es que
el
disenador de un sistema
puede en
realidad
usar un filtro adaptivo
de
tiempo invariable, solo si se conoce
bastante acerca
de
la
serial
de
entrada para disenar
el
filtro.
Esta falta de
conocimiento puede brotar
desde
una incertidumbre acerca
de
las
características
de
la serial
cuando
el
filtro es encendido; o porque las características de
la serial de
entrada pueden cambiar lentamente durante
la
operación
de
"filtración"
.
FORMULACI~N
DEL ECUALIZADOR ADAPTIVO
Durante
el
periodo
de
enseñanza inicial del ecualizador, una sucesión
de
símbolos
d(l),d(2),...,d(n), conocida como
el
arreglo
del
algoritmo
del
ecualizador es
transmitida por un canal, dando como resultado una secuencia
de
salidas ecualizadas
y(l), ~(21,....
...y(n). En un tiempo n
,
el
ecualizador tiene
Nentradas almacenadas, esto
Io
denotamos por
el
vector
Indicaríamos
la
dimensionalidad
de
los vectores
ymatrices por sus subscripciones.
La
ausencia de estos
indicaría una sola
dimensión; por ejemplo; y(n) es un escalar,
x,(n)
es
un vector
de
dimensión
N,A,(n)
es una matriz con
Nrenglones
y pcolumnas.
La
transpuesta
de la
matriz se sobrescribe como
T.EI
ecualizador conecta
los
coeficientes a un tiempo n que son representados
por
el
vector
C , ( n
-1)
ycon
salidas
C ,
( n
-l ) " x N ( n ) ,
que difiere
dela salida ideal
d(n) por un error e(n)
Esta
fórmula
de la salida
delecualizador
ysu error difiere de distintos tipos
de
ecualizador.
Los
más obvios
de
estos ecualizadores son los lineales transversales
con
Nconectores, por tal motivo {y(n)} es
el
canal
desalida
muestra para
los
símbolos
derotación.
La
estructura
delecualizador lineal es también relevante a
reserva del algoritmo
de
detección
de
Viterbi, en
tal
caso, d(n) en
(2)
es reemplazado
por
la
combinación lineal
de
los
datos recientes. Una variación
de la
estructura
delecualizador lineal, son los canales
de salida
muestra a tiempo
pde
los
símbolos
de
- -
( n - l ) T + -
( n - l ) T + -
P
P
(Ver referencia
I111).En caso de una
decidir
retroalimentar
el
ecualizador con
N ,
delante
yN ,
retroalimentado por las conexiones
xN
( n )
esto queda como
donde
N
=N ,
+
N , ,
{y(n)} son las muestras del canal
de
salida
y{d(n)} es
la
decisión
previa
delos
datos.
En este
yen otras muchas estimaciones
yaplicaciones predictivas, las
salidas
de
los vectores
x N
( n )
son tales que
x N
( n
+
1)son obtenidas
de
x N
( n )
para satisfacer
estos componentes, introduciendo
el
viejo componente
p.Por ejemplo para
p = 2nuevos elementos y(n), d(n) entra
la
decisión
de
retroalimentar
el
ecualizador a un
tiempo n
+I,mientras lo permitan los elementos y(n-N,)
yd(n-N2
1.Esta
propiedad
es crucial en
el
algoritmo "fuerte"
de
Kalman
.
Para unificar
la
subsecuente notación, definiremos un vector p-dimensional
$ ( n )
que satisface a nuevos elementos
p yun vector p,(n)especificando
a
p yeliminando los elementos viejos a un tiempo n
+
1;por ejemplo; para un ecualizador
lineal,
6
( n )
=y ( n )
y
p,( n )
=y ( n
-N ) .
Para la
decisión retroalimentada
del
ecualizador,
También definiremos un vector extendido
X M ( n )
,
con
M = N + pdimensiones,
tal
que contiene elementos
de
<,(n)
abriendo un campo
de
orden sobre los
elementos
de
x N ( n ) .
Por ejemplo en el caso
de
una retroalimentación
del
I
- - -I
f
"_"
d ( n
- I)Las
líneas punteadas denotan la partición
de
los vectores
ylas
matrices.
En general
Sm
es la permutación
de
matrices obvias
ye,,
el re-arreglo
de
10s
elementos
delVector extendido
X M( n )
para
desplegar
tP
( n )
,pp (n )
,x N
( n )
yxN
( n
+
I)en una forma
de
partición simple, es decir
APLICACI~N
DE
UN ALGORITMO RECURSIVO CON MINIMOS
CUADRADOS PARA UN ECUALIZADOR ADAPTIVO.
El
problema del ecualizador adaptivo es un clásico problema
de
mínimos cuadrados
recursivos
H31, H41.En particular requeriremos
delalgoritmo
delecualizador
adaptivo para generar las conexiones
de
los
coeficientes
del
vector
C N ( n )
para el
tiempo n
tal
que minimizamos
la
acumulación
del
error cuadrático.
La
minimización
delvector es
la
solución
dela
ecuación
deWiener-Hopf:
donde
\ / 6 > = 0
En
la
práctica,
el
parámetro
6es fijo constante
devalor pequeño positivo para
asegurar
la
no singularidad
de la
matriz
R N N ( n ) .
Entonces esto
puede ser
demostrado por
(41,que en consecuencia
CN (n )
puede ser generada recursivamente
de la
siguiente manera:
La
covarianza inversa
de la
matriz estimada
RNN(n)-'
mostrada en
(10)
acelera
grandemente
la
adaptación
del
ecualizador, independientemente
de
las
características
del
canal
de
dispersión,
141, [51, [61El
vector
k , ( n )
puede ser generada
por el algoritmo recursivo tal que
produciría
Npor
Nde la
matriz
R,,(n)"
sin requerir explícitamente
la
matriz
inversa.
Elalgoritmo resultante, es el caso especial
delalgoritmo convencional
de
Kalman
para
los
ecualizadores adaptivos,
reportado por Godard
.
Elparámetro
6devuelve
salida
que serían estimadas
al
final
de
un mal error cuadrático;
el
estado
del
algoritmo es trascendente
yfirme
yno esta bien sensibilizado para
la
selección
de
6.Esta
complejidad
del
algoritmo, es proporcional a
N2,se
usa matrices
de
arista
de
Npor
Npara computar
k , ( n )
.
El"Algoritmo fuerte
de
Kalman" será presentado
matemáticamente equivalente a esto, por
la
proeza
de
cambiar
la
propiedad para
computar
los
vectores
k , ( n )
recursivamente, sin necesidad
de
computar o
almacenar alguna matriz
de
Npor
N.En
el
algoritmo
de
Kalman (convencional o fuerte) para
el
ecualizador
adaptivo, todos
los
vectores previos
x,,,(n)
ylos
errores previos em) son acordados
de
igual peso en
la
determinación
de
conexiones
de
sus coeficientes estimados. Esta
fuente
de
trabajo para
la
limitación-duración inicial
delarranque
de
fase.
Decualquier modo
el
estado fijo de operación usualmente requiere
de
estos vectores
{
x , ( k )
}para
evitar
la
siguiente variación en
el
canal actual
yevitar los problemas
asociados con
los
errores
digitales
aleatorios. Un criterio conveniente a ejecutar
estos requerimientos
de
caso
de
estudios, es minimizar exponencialmente
el
peso
del
error cuadrático en
el
tiempo n.
donde
A
es algún número positivo cerrado, pero menor que
1.
Elinverso
de
I - hes,
aproximadamente hablando,
la
memoria de
el
algoritmo.
La
minimización
delvector
C ,
( n )
es ahora
donde
Note que
(12a)implica
EL ALGORITMO FUERTE
DE KALMAN
Los
siguientes escalares, vectores
ymatrices
son
almacenadas
yactualizadas
durante cada iteración:
(1) Matrices N por N;
A ,
( n )
y
DNP(n)
con valores iniciales
A,(O)
=D,(O)
=O,
(2) Matriz N por N;
EJn)
con valor inicial
Epp,(0)
=d l ,
( 3 )
Vector con dimension
M;
k,(n)
donde
M=N+p
(4)
Vector con dimension p;
sp
(n),
sP
(n)'
,
rll,
(n),
y
cc,
( n )
(5)
Vector con dimension N;
mN(n)
y
todo x(n)
=Opara n
<
=O.Entonces iniciamos con
n
=I,k , ( n
+
1)este
actualizado con
el
siguiente
algoritmo:
(Multiplicado por
la
permutación
,
,
S
y QMsimplificando la cuenta
de
permutaciones
de
los
componentes
de
cada
vector).
La
línea
de
división
de
la
ecuación
(18)
indica una permutación.
Una vez actualizada
las
conexiones del ecualizador con
los
coeficientes
de
cada
vector
C,(n
+
1)
entonces tomamos
las ecuaciones
(2) y (91,usando
el
vector
K,,, ( n
+
1 ) .
El
conteo
del
numero
de
operaciones necesarias para calcular cada
salida del
ecualizador
ysu actualización, pone a cada coeficiente
de
las
conexiones un nuevo
indicativo como para
el
algoritmo,
7 N p
+
Np2
+
3p2
+
2 N
+
4 / 3 p 3
-p / 3
multiplicado
(ecuaciones
(21, (9) y (14)hasta la
(22)) y7 N p
+
N p 2 + p 2 / 2
+
An
+
4/3p'
+
19/6p
sumas.
Estos conteos
de
divisiones como multiplicaciones
yelementos Guassianos eliminan
la
matriz inversa
ppor
p 1151.La
correspondencia
deconvencíonalidad-
implementación
del
algoritmo
de
Kalman es
de
3 N 2 + 3 N
multiplicaciones
y2 N 2 + 2 N
+
1
sumas. Para un sencillo
algoritmo gradiente tenemos que
C N ( n )
es
actualizado, acordado por:
C N
( n )
=C , ( n
-1)
+
ge(n9xN
( n )
(g una constante)
(23)
2N
multiplicaciones
y 2~sumas son necesarias
para
computar
las
salidas de
ecualizador
yactualizar
los
coeficientes
de
conexión.
De
este
modo para
el
ecualizador lineal
(p=1),el
número de computaciones
por intervalo
de
símbolo es
de:
Kalman fuerte
3N2
+
3NKalman convencional
12N
+ S
ION + 42N2+2N+1
convencionalidad-implementación
del
algoritmo
de
Kalman es
de
aproximadamente
Nveces menor que el del complejo algoritmo
del
gradiente simple.
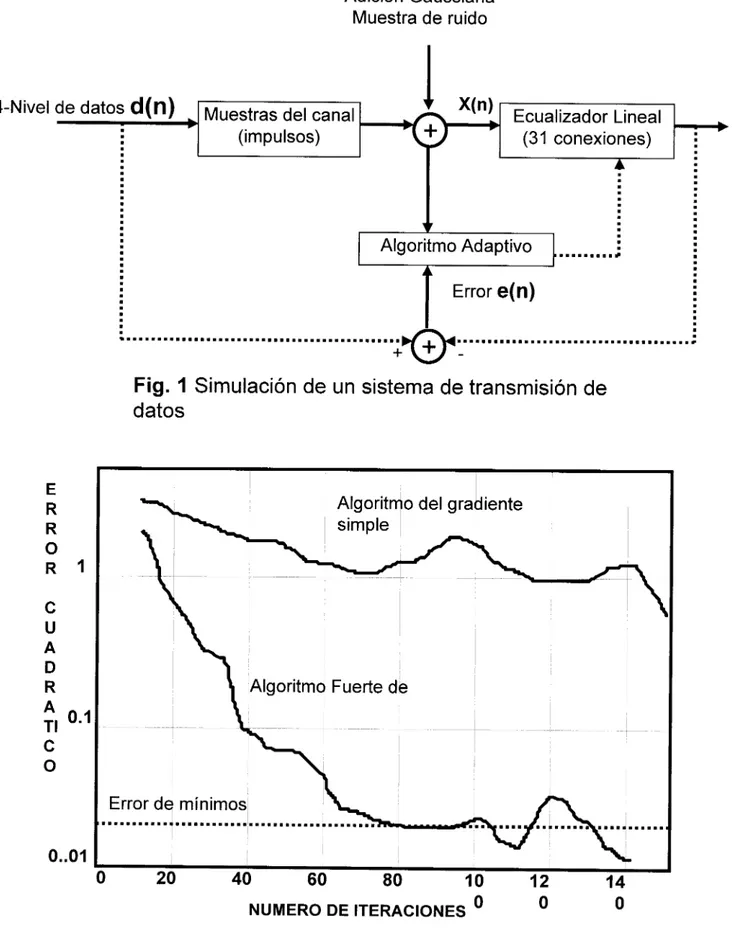
SIMULACION DE LOS RESULTADOS
La
figura
1muestra un esquema
de
los datos
de
un sistema de comunicación
con un ecualizador lineal cuyas conexiones
de
coeficientes podrían adaptarse acorde
con otros algoritmos, por ejemplo el
delfuerte
de
Kalman o
el del
algoritmo
delgradiente simple.
Elprograma
desimulación estaba dado para
el
lenguaje
BASICpero
se puede usar otros tipos
de
lenguajes,
yejecutarlo sobre un tiempo-real.
4niveles
de
datos pseudo-aleatorios estarán generando
yverificando
las
continuas muestras
de
impulsos respondidos para
6600bauds, sistemas
de
datos
de
comunicación
modulados sobre
VSBcon
3455 Hzde
acarreo
de
frecuencia, usado sobre un típico
canal
deteléfono. Los
bits de
rotación correrían a
13200bits/s.
Adicionando ruido de
muestra Gaussianas sumaran al filtro
de salida
una simulación
de
señal-ruido en un
radio
de
31dB.Esta basebanda equivale a la respuesta
de
impulsos
yradios de señal-
ruido que estarán mapeados
por
el
algoritmo
de
adaptación
de
Kalman
151.La
característica de
la
frecuencia
delcanal
del
teléfono
[51,estará
anulando
los
profundos ruidos causados por
la baja
convergencia
del
algoritmo gradiente
121.EI
ecualizador lineal tiene
N =31conexiones. Estas
salidas
estarán
substrayendo
de
referencia lineal la transmisión de datos que corren d(n), a
la
forma
de
la señal
de
error em).
La
secuencia
delerror em) {ecn)}
yla
secuencia
deentradas
del
ecualizador {xcn)} estarán usadas para ajustar
las
conexiones
del
ecualizador
adaptivamente,
ymensurar
el
error cuadrático durante
la adaptación, estarán
desplegando como función,
los
números
de
cada
iteración. Como muestra la figura
2.Note que
(e2)>1 inicialmente porque
los
datos son
(+-)1,(+-)3, con igual
probabilidad.
EI
algoritmo
deadaptación del gradiente sencillo
esta
implementado como
en
la
ecuación
(231,donde
la
constante
g,se
escoge para rotar la gran convergencia,
como
de
0.002. Elcanal
de
impulsos responde
normalmente
al
tener unidad
de
El
algoritmo fuerte de Kalman estará
implementado con
a=1.Porque este
algoritmo es comenzado con todos los vectores
k,
A,etc. a cero
ycon x(n)
= Opara
n
<
=O,esto se encontrará conveniente para empezar
la
actualización
de
kdespués
de
leerlo en
el
corte
del
primer pulso
de
datos recibido. Sin embargo para ambos
algoritmos, los grandes resultados estarán obteniéndose
por
el
comienzo
de
la
conexión
de
los
coeficientes
delecualizador actualizando antes
la
principal parte
de
los
primeros pulsos
de
datos recibidos. “Iteración
de
Números”, en
la
figura
2se
enumeran los comienzos
de
las
conexiones
de
actualización
delos coeficientes
delecualizador.
El
error cuadrático estará estimado por cada iteración como
el
promedio
del
peso
ysu exponencial.
Lamemoria
del
peso exponencial estará sobre las órdenes
de
10
intervalos
de
símbolos. Para ambos algoritmos adaptivos,
el
valor inicial
de
todos
los coeficientes conectados serán cero.
La
convergencia
delalgoritmo
delgradiente
simple estará bien bajo
porque
el
canal
de
frecuencia anulará
las
respuestas.
Elalgoritmo
de
Kalman converge a un valor firme dentro
de
aproximadamente
80intervalos. Esta convergencia comporta a este, como sería esperado un similar
algoritmo convencial-implementado
de
kalman/Godard
151.CONCLUSIONES
El
algoritmo
del
ecualizador adaptivo
de
Kalman tiene una proporcional
complejidad
de
N,justa en
el
caso
de
un algoritmo de gradiente simple, mientras
que se tiene un
rápidaconvergencia con
el
algoritmo
de
convencionalidad-
implementación
de
Kalman, cuya
complejidad es proporcional a
N2. Elrápido
algoritmo es una factor matemáticamente equivalente
para
el
algoritmo
convencional
de
Kalman;
el
solamente requiere
de
esto
(1)
el
cambiar
la
propiedad
deentrada
de
los vectores
(satisface
en todos
los
ecualizadores conocidos
o
cancelaciones
de
aplicaciones
de
eco);
y (2)que actualice el vector inicial
k , ( n )
con
todas
la
muestra previas x(n) asumidas a cero.
Elposterior requerimiento garantiza
una condición
de
comienzo simple, con
el
argumento
deinducción usado en
el
Para un ecualizador lineal,
el
algoritmo rápido
de
Kalman requiere un número
de
operaciones por iteración solo aproximadamente
5veces que para
el
algoritmo
de
gradiente simple. Acordando
la
cantidad
de
números por operación tabulado
anteriormente, una correspondencia
del
algoritmo convencional-implementación
de
Kalman requeriría aproximadamente
45veces
tal
como muchas operaciones haría
el
Adición Gaussiana
Muestra de ruido
4-Nive1 de datos
d(n)
,
M
u
m
Ecualizador Lineal
,~
(impulsos)
(31 conexiones)
i
A
Algoritmo Adaptivo
...;
Error
e(n)
A
...
...
Fig.
1
Simulación de un sistema de transmisión de
datos
E R R
O
RC U A
D
R
1
0.1
C
O
O..Ol
Error de mínimos
...
...
20
40
60
:
80
10
12
14
NUMERO DE ITERACIONES
o
O
O
Fig.
2
Convergencia del error cuadrático, todos
los
CAPITULO
II
EL COMBINADOR LINEAL DE IMPULSO-RESPUESTA-FINITO.
Analizaremos un filtro con una estructura
deimpulso-respuesta finita en tiempo
ydiscreta
(FIR) ,basado en una línea
de
retardo
yun conjunto
de
Ncoeficientes
de
ganancia ajustables
Wohasta
WN-1.
La salida
del filtro
Y(x)es simplemente la suma
de
las entradas retardadas
yescaladas
dada
por
por conveniencia
Y(x)también puede ser escrita como los puntos
(o
interiores)
producto
de
2vectores
:i.
e.
donde
W = [Wl,W2,
...,
W(N-1) 1t
yX(k) = [X(k),X(k-l)
,....,
X(k-N+
111t
El
filtro mostrado en
la
figura también usa una
forma simple
de
valoración
de
calidad de la
senal filtrada.
La salida del
filtro
Y(k)es comparada a una forma
de
onda
degradación de la calidad. La forma de onda d(k) es en algunas veces llamada la serial
deseada, la referencia, o la forma de onda plantilla.
El
objetivo de seleccionar los coeficientes del filtro adaptivo es para forzar a ser
Y(k)igual a
d(k)exactamente.
Uno pudiera cuestionar porque no simplemente pasamos
d(k)en vez de
Y(k),ya que
es la sena1 deseada a la salida
del filtro. Por ahora citaremos
dos
circunstancias
donde la transmisión de
d(k)en vez de Y(k) no es posible.
En ciertas aplicaciones
d(k)esta solo disponible durante una fase de entrenamiento
en conjunción con una secuencia de valores de
entrada predeterminada
.
En tales
casos la adaptación es cesada durante el procesamiento de la actual secuencia de
entrada
X,
para cada d(k) no esta disponible (es imposible).
En otras aplicaciones d(k) es "medible" solo después de que calculamos Y(k). En otras
palabras, nuestra evaluación de calidad es derivada de una "perfecta" retrospectiva.
Alguna diferencia entre
d(k) y Y(k)resulta en una Serial de
error e(k) (distinta de
cero), la cual intentamos usar en
los
parámetros de las reglas de adaptación del filtro.
Como hemos notado, el objetivo del ajuste es buscar un conjunto de coeficientes, un
vector
W;el cual reduce e(k), o alguna función de e(k) al valor más pequeno posible,
cuando esta parametrización
es alcanzada
(ymantenida), es decir el filtro toma
convergencia a el conjunto optimo
dcoeficientes representado por el vector
Ws.Nótese que
si
d(k) =
xt(k)WS, entonces
W = W$implica que e(k)
= Opara todo k.
ECUALIZACI~N DE
UN CANAL USANDO UN FILTRO DE
KALMAN PARA LA TRANSMISI~N
RÁPIDA DE DATOS.
A
continuación se muestra cómo
el
filtro
de
Kalman puede aplicarse en
el
problema
de
establecer
la
ganancia
de
ecualizadores transversales para minimizar la distorsión
cuadrática (mean-square). En presencia
deruido
ysin conocimiento previo
del
canal,
el
algoritmo del filtro conduce a una convergencia más
rápida
que otros métodos, su
velocidad
de
convergencia depende solamente
delnúmero de recursos. Se dan
resultados teóricos
yse
usa una simulación
por computadora para corroborar
la
teoría
ycomparar
el
algoritmo con el método clásico.
Los sistemas
detransmisión
de
datos generalmente usan canales
de
comunicación
de
voz
de
banda. Estos
se caracterizan por un ancho
de
banda relativamente
estrecho.
(de
300a
3000 Hz),una alta razón
de
ruido en
la
señal (aproximadamente
de
20
a
39
dB), yuna amplitud
ydistorsión
de
fase
que varían lentamente con
el
tiempo.
La
alta velocidad
de
transmisión
de
datos requiere entonces ecualización.
Muchos módems receptores usados en
la actualidad, están equipados con
un filtro
para maximizar razón
de
señal/ruido
yun ecualizador para minimizar
la
interferencia
entre símbolos debida a una distorsión. Los ecualizadores generalmente son del tipo
de
filtro transversal, con ganancias
dedicadas
a minimizar algunos errores
de
criterio. Un proceso automático
deecualización requiere un
período inicial
de
entrenamiento durante el cual el ecualizador reduce
el
error. En
la
“ecualización
preestablecida”,
pulsos aislados son
transmitidos previamente a la transmisión
de
datos,
ylas
ganancias
establecidas
derivadas se mantienen constantes durante
la
transmisión
de
datos. Periódicamente,
debe
practicarse
un corto lapso
de
entrenamiento para mantener actualizadas las ganancias.
Una segunda
clase
de
proceso
de
ecualización es conocido como “ecualización
adaptiva”. Aquí el ecualizador establecido es derivado
de la
señal recibida. Durante el
período
de
entrenamiento,
el
ecualizador continuamente busca minimizar
la
desviación estándar
de
la
muestra
de
su señal
de salida
de
una referencia
ideal
generada internamente en sincronía en
el
receptor. Cuando
la
distorsión residual es
ecualizador.
La
ecualización adaptiva tiene muchas ventajas sobre
la
ecualización
preestablecida,
estando entre
ellas la capacidad de
adaptación a
los
cambios en
las
características
del
canal durante
la
transmisión.
Claramente,
hayun retraso en
la
transmisión
de
datos proporcional a
la
longitud del
período de entrenamiento,
yes
deseable
un decremento en este retardo. Muchos
algoritmos
de
ajuste han sido descritos en los libros, generalmente haciendo énfasis
en
la
velocidad
de
convergencia.
Elbien conocido
algoritmo
de
los
mínimos
cuadrados
de
Gersho, muestra que la velocidad
de
convergencia es determinada por
los
valores máximo
ymínimo
del
espectro
de
poder
de la
señal sin ecualizar
.
Resultados similares para algoritmos más sofisticados se han reportado por Chang
yKobayashi.
Aquí, un nuevo algoritmo, basado en
la
teoría
de
filtrado
deKalman, es propuesto
para obtener una rápida convergencia en
la
ganancias
de
ecualizadores transversales
para su óptima configuración. Un filtro
de
Kalman
ha
sido aplicado previamente
al
canal
de
ecualización por Lawrence
yKaufman, pero en una forma enteramente
diferente, comenzando por
el
hecho
de
que en
su estudio
el
ecualizador es
reemplazado por
el
filtro.
Mostraremos que
la
convergencia
demínimos cuadrados se obtiene, bajo
condiciones
de
ruido, dentro
de
un número
de
iteraciones determinado solamente
por
el
número
de
utilizaciones, sin previa información sobre
el
canal. Después
de
revisar
los
fundamentos
de la
teoría
de
Kalman, mostramos cómo aplicar
ése
filtrado
en
la
ecualización
yen
la
derivación
de
una expresión para
la
velocidad
de
convergencia. Finalmente, se usarán simulaciones por computadora para comprobar
CAPíTULO Ill
DIVERGENCIA EN EL FILTRO
DE KALMAN
Bajo ciertas condiciones,
la
órbita estimada por un filtro
de
Kalman tiene errores
mucho más grandes que los predichos
por la teoría. Este fenómeno es llamado
divergencia,
yproporciona la operación insatisfactoria
delfiltro
deKalman
.
La
ejecución
del
filtro
de
Kalman bajo las condiciones actuales
de
operación puede
degradarse seriamente en relación
de la
ejecución teórica indicada por
el
estado
de
la
matriz
de
covarianza.
Elfiltro
deKalman teóricamente produce una estimación
cuya precisión
va
incrementándose con
cada
observación adicional que
es
procesada.
Lamagnitud
de
los errores
de
estimación medida por el determinante
de
la
matriz
de
covarianza
delerror
de
estimación
es una función monótona
decreciente del número de observaciones. Sin embargo,
se ha observado que bajo
las condiciones actuales
de
operación, los niveles
de
error en
el
filtro
de
kalman son
significativamente más altos que los predichos teóricamente. Los errores pueden,
de
hecho, incrementarse continuamente aunque
se estén procesando datos
adicionales.
La
posibilidad
de
dicha inestabilidad o comportamiento divergente fue
sugerida primero por Kalman.
Mástarde fue notada por Pines
yKnoll
yotros en
aplicación
del
filtro
de
Kalman a la navegación espacial
yla determinación
de
órbitas.
CAUSAS DE LA DIVERGENCIA
una causa
de la
divergencia
del
filtro es la discrepancia entre
el
modelo matemático
usado para derivar
las
ecuaciones
delfiltro
ylas
actuales condiciones bajo
las
cuales
el
filtro
debe
operar. Ejemplos
de
tales discrepancias son
el
descuido
de
los
términos
en
el
potencial gravitacional o un conocimiento inexacto
de
las
constante en
el
potencial. Otro origen
dela
divergencia son los errores en
el
coeficiente balístico
o
en
elmodelo
dedensidad
de aire
usado en
el
cálculo
de la
aceleración
de
arrastre.
La
figura
1muestra
la
divergencia causada por un error
del
25 %en
la
aceleración
de
arrastre. Un origen diferente
de
divergencia son los errores "round-off"
inherentes en la implementación
de
las
ecuaciones
delfiltro en una computadora
digital
de
palabras
de
longitud finita.
Lafigura
2muestra
el
efecto
de
los
errores
computacionales inducidos por una singular precisión
aritmética
(IBM7090)
en
el
filtro
de
Kalman.
Una manifestación
de
los errores causados por
la
máquina ocurre en el cálculo
del
estado
de la
matriz
de
covarianza. Después
de
que
el
filtro
de
Kalman
ha
estado
operando por algún tiempo, ésta matriz
deja de
ser definida positiva
ysimétrica.
Los
coeficientes relevantes
del
filtro calculados usando
ésta
matriz son entonces
erróneos
y,consecuentemente,
la
órbita estimada es incorrecta.
J. E.Potter
y R.Battin derivaron una variación del filtro
de
Kalman en la cual la matriz
de
covarianza
permanece
al
menos simétrica no-negativa.
Esta técnica elimina algunos, pero no
todos
los
efectos
de los
errores computacionales
yal
mismo tiempo
el
filtro requiere
un algoritmo más complejo. En filtros
de
procesamiento por lotes, los errores
"round-off"
en
el
filtro se vuelven evidentemente serios como errores
computacionales en
la
operación
dela
matriz
de
inversión.
Varias aproximaciones han sido sugeridas para prevenir
la
divergencia del filtro. Una
aproximación sostiene que
la
divergencia ocurre cuando
el
filtro asigna un peso
demasiado pequeno
al
último dato medido. Así
el
dato actual hace
sólo
una pequena
corrección en
la
estimación,
de
hecho muy pequena,
ésos
errores crecen
actualmente por
la
interacción natural
de
los
errores
de
posición
yvelocidad. Un
"arreglo" obvio es incrementar más o menos arbitrariamente
el
peso del dato actual.
Tal
arreglo implica incrementar
la
matriz
de
covarianza
de
estado mientras
mantenemos constante
el
período
de
órbita incierto. La frecuencia
ycantidad
del
incremento
debe
determinarse empíricamente,
ypuede emplearse tanto en filtros
recursivos como en
los
no recursivos.
Schmidt
yPines han sugerido modificaciones analíticas
a
las
ecuaciones
delfiltro
para representar
parciales
dinámicas sin incrementar
el
número
de
estados a ser
estimados por
el
filtro. Además, Pines
ha
desarrollado una máquina simple
para
“round-off’’ en
la
computadora
digital.
Otras técnicas, tales como
el
borrado
del
filtro
para guardar los elementos
de la
diagonal
de la
matriz
de
covarianza
de
estado en un
“umbral” específico, fueron investigados por Holick.
Ditto experimentó
la
divergencia en
el
corrector diferencial no-recursivo Gemini-
Bayes, donde
los
problemas numéricos aparecen en
la
inversión
de
matrices no
condicionadas, así como en
el
incumplimiento
de
parciales
dinámicas.
La
ocurrencia
de
la
divergencia en un
filtro no recursivo no
es sorprendente en vista
de
la
equivalencia
del
filtro
de
Kalman
yla
mínima varianza no recursiva
del
filtro. Las
modificaciones
del
filtro empleada por Ditto son similares a
las de
Schmidt
yPines.
EJEMPLO
ILUSTRATIVO.
Para
proporcionar
al
lector una comprensión
intuitiva
del
problema
de la
divergencia, daremos un simple ejemplo analítico, donde
el
filtro
de
Kalman estima
cómo diverge una trayectoria
de la
verdadera cuando
el
número
de
observaciones
se incrementa. Éste fenómeno es ocasionado en este caso por
la
omisión
de
una
de
las
componentes
de
estado
delvector que describe
el
sistema. Esta situación ocurre
generalmente in
la
práctica,
yasea deliberadamente para disminuir
la
complejidad
de la
representación
delsistema, o bien
de
forma inadvertida porque se desconoce
la
existencia
de
ciertos estados.
Elejemplo considerado aquí es la estimación
de la
altitud
Xde
un vehículo
de
datos
de
altura. Un filtro
de
Kalman se diseña
primeramente suponiendo que
Xes constante, ¡.e.,
el
vehículo se encuentra
ascendiendo
(o
cayendo) con una aceleración constante. Una pequeña modificación
del
filtro
de
Kalman muestra entonces
la
eliminación
de
ésta divergencia.
Para diseñar
el
filtro
de
Kalman, asumimos que
las
medidas
de
altitud tienden a cero
es
independiente
de
los
errores aleatorios
de
ruido n(k) que poseen una desviación
estándar común
u.
En resumen,
los
errores por ruido se asumen acotados,
J n N l < = B .
+)
=-1
+W ( k ) [ Y O - Y,(k)l
W ( k )
=P(k -)l[P(k
-)+
0 2 1P(k
-)
=P(k
-
1
+)
X ( k
-)
=X ( k
-
1
+)
P(k+)
=P(k-)
-P(k-)[P(k-)
+
0 ' ] " P ( k - )
y ( k )
=X ( k )
+
n ( k )
Y , ( k )
=m - )
Donde
O
=desviación estándar del
P(O-)=
varianza
de
la altura estimada a
pri
error por ruido
de la
altura
or¡;
ylos símbolos
-
y+
que aparec
n
(kl,
Ben en
las
ecuaciones precedentes, denotan
los
estimados inmediatamente al previo e
inmediatamente subsecuentes a una observación.
Supongamos ahora que
el
vehículo, en vez
de
permanecer a una altitud constante,
está
ascendiendo con una aceleración constante
ysu trayectoria está descrita por:
Supongamos también que
las
medidas de altitud son tomadas una vez por segundo.
Un
fácil
cálculo conduce para el filtro
de
Kalman, a
la
altitud observada después
de
Nobservaciones:
VN
1
X ( N + )
=X ( 0 )
+
~+
______C n ( k )
2
N+1,=,
Substrayéndolo
de la
trayectoria real:
X(N) = X(0)
+
VNencontramos que para el error
U(N)VN
1
N2
N + l , = ,
& ( N )
=X ( N )
-
X ( N + )
= -+
~-C n ( k )
CAPITULO
IV
EJEMPLO ILUSTRATIVO.
/ *
DECLARACION DE VARIABLES GLOBALES Y PROTOTIPOS DEL PROGRAMA KALMAN* /
# include
# include
# include
# include
# include
# include # include
# include
# include
<graphics.h> <dos. h> cstdio. h> <conio. h> <bios. h> <stdlib.h> <time
.
h> <mouse. h> <portada.h>#define tam 14 #define muestras 14 #define N 14
#define M 100
#define NumElem 14 #define NumBlock 100 #define NumIter 60
#define NumLoop-Corr 20 #define Num AR 5
#define PI 3.141592
/ *
orden del predictor * // * VARIABLES GLOBALES
* /
double HK [ tam]
,
XK [ tam],
A [ tam] ;double Q[tam] [tam] ,Q1 [tam] [tam] ;
double sena1 Y [muestras] ;
double senal-D[muestras];
double Y2,Y3T D, error;
/ *
salida del filtro* /
double arr [250] ;int opc = 1, uso;
char cadfileout [50] ; / * almacena el archivo datos * /
char cadfileinA[50]; / * almacena el archivo de A * /
char cadfileinX[50]; / * almacena el archivo de X * /
char cadfileinD[50];
/ *
almacena el archivo de D * /char USO='O'; / * O si es Predictor o
char AA='O'; / * O si es aleatorio y
* /
donde se guardaran los
donde se leeran los datos
donde se leeran los datos
donde se leeran los datos
1 si es Estimador
* /
char A1='O1,D1='O';
/ *
PROTOTIPOS DE FUNCIONES * /void inicializa(void); void KALMAN (void) ;
void vector XK(doub1e nvoval); void vector-A(void);
void proyecto (void) ;
void fuera (void) ;
void correr (void) ;
void void void void void void void void
inicial (void) ;
lim vert (void) ;
lim-horiz(void); muestra rat (void) ;
esconde-rat (void) ;
reporta-edo (int *x, int *yI int *edo) ;
ini graf (void) ;
flecha(int x, int y, int clr) ;
void void void void void void void void void void void void void void void void void void void void void void void void void void void void void void void void void void
menu (void) ;
mensa j e-mouse (int x
,
int y) ;mensa j e-tecla (void) ;
detecta opc(int x, int y); checa-opcion (void) ;
mueve-opcion (int k) ;
limpia barra (void) ;
limpia-flechas(void);
func (int xi
,
int yi,
int xf, int yf) ;haz opcion (void) ;
mensaje tecla func2 (void) ;
checa-o&ion-func2 (int x, int y) ;
uso comun mouse (int x, int y, int xi
,
int yi,
int x€, int yf) ;rangomouse (int x, int y, int xi
,
int yi,
int xf, int yf) ;mueve-opcion-uso(int k); limpia barra uso (void) ;
comunlTint xTint y,char *cadl,char *cad2); comun2 (int x, int y, char *cadl, char *cada) ;
flecha2 (int x, int y, int color) ;
guarda imagen(int x1,int y1,int x2,int y2,void **imagen); boton (int x, int y, char *cadena, int clr) ;
boton press(int x,int y,char *cadena,int clr); botonIcirc (int x, int y) ;
fondo (void) ;
esq-sup-izq (int x, int y) ;
esq-sup der (int x, int y) ;
esq-infIizq(int x, int y); esq inf-der (int x, int y) ;
lineas (void) ;
cuadro2 (void) ;
cuadro3 (void) ;
barrido (int xi, int yi
,
int xf,
int yf, int color) ;mensa j e (void) ;
void void void void void void void void void void void void void void void void void void void void
barra(int x, int y, int anch, int alt) ;
barra1 (int x, int y, int anch, int alt, int clr) ;
barra2 (int x, int y, int anch, int alt) ;
titulo (void) ;
cuad men (void) ;
logotipo (int x, int y, int colorl, int co1or2) ;
fondo azul (void) ;
submenus (int x, int y, int x1
,
int yl) ;captura archivo(void); void captura archivo2(void); enbarraT(int x, int y, int anch, int alt, int fondo) ;
captura (int x, int y, int tope, int clr, char *cadena) ;
caja(int x, int y, int taml);
advertencia(char *cadl,char *cad2);
captura muestras(void); void captura aleatorios(void); salida (void) ; void integrantes (void)
y
inicializa cadenas(void);
rango-mousg-horizontal(int x,int y); salida-entrada (void) ;
hacer instalacion (void) ;
restablece(v0id);
void inicializa - cadenas() / * inicializa las cadenas de salida
* /
strcpy(cadfileout, " " ) ; / * numero de muestras a tomar para
* /
strcpy(cadfileinA, " " ) ; / * cada uno de los par metros* /
strcpy(cadfileinX, " ' I ) ;
strcpy(cadfileinD, " " ) ;
strcpy (NUMA, " " ) ;
strcpy (NUMX, ' ' ' I ) ;
strcpy (NUMD, ' " I ) ;
11
I
/ *
las rutas de los archivos y el* /
. . .
. . .
/ *
FUNCIONES GRAFICAS PARA EL AMBIENTE * /# include <kalman.h>
char entro='O'; char entrouso;
char NUMTEMP[S];
/ *
guardamos en el, el numero temp. de muestras * /void menu ( ) {
int edo, i f x, y;
/ * in¡-graf ( ) ;
* /
fondo ( ) ;