CAPITULO II: CÁLCULO VECTORIAL

(1)

IGNACIO ELIZALDE MARTÍNEZ ENERO – JUNIO 2012 22

Capitulo II

CALCULO VECTORIAL

2.1 Cálculo vectorial

El cálculo vectorial se utiliza para el análisis de problemas de ingeniería ya que provee de las herramientas necesarias para describir las variaciones espaciales como desplazamiento, velocidad y aceleración que experimentan las partículas o elementos materiales que se mueven a lo largo de una trayectoria así como también proporciona los elementos para analizar funciones que dependen de más de una variable independiente que aparecen frecuentemente en ingeniería en problemas asociados con optimización entre otras aplicaciones a las ciencias e ingeniería.

2.1.1 Funciones vectoriales de una y varias variables.

Funciones vectoriales de una variable

Una función escalar (o una función de una variable) es una expresión matemática cuyo variable independiente es un escalar y su variable dependiente es un escalar y su regla de correspondencia es: regla

f

:  .

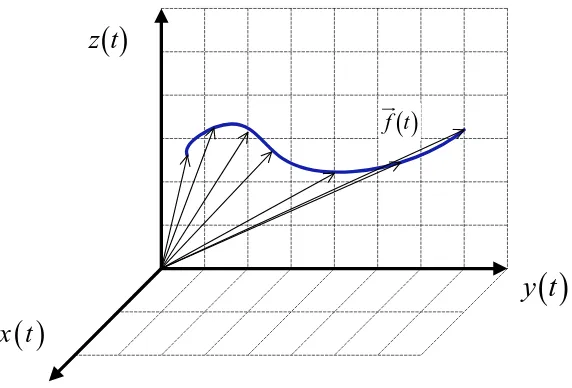
Una función vectorial de variable real tiene como regla de correspondencia

f

:  n, es decir tiene como dominio números reales y como imagen vectores. Por ejemplo, considerando las coordenadas del espacio, la siguiente es una función vectorial:

 



     



f t =

x

t ,

y

t ,

z

t , donde t es un parámetro comprendido en el intervalo

a t b

 

.

La representación de la función vectorial en el espacio euclidiano se muestra en la siguiente figura:

 

x t

 

y t

 

z t

 

f t

[image:1.612.189.475.462.656.2]

(2)

 



cos

 

, e

 

,



f t



t s n t t

, o de forma alternativa:

 

cos

 

e

 

f t



t i s n t j t k

    

 



,



f t



t t

2

₁



t

Grafica de funciones vectoriales.

La gráfica de una función vectorial en el plano o en el espacio se origina uniendo un conjunto de puntos. Dicho gráfico recibe el nombre de gráfico de línea para distinguirlo de los gráficos de superficie que se verán más adelante.

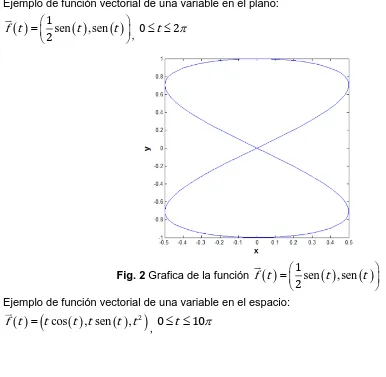
Ejemplo de función vectorial de una variable en el plano:

 

sen

 

,sen

 

f t

_{ }



t



_





1

2

,

0  

t

2 

Fig. 2 Grafica de la función

f t

 

  sen

 

t

,sen

 

t

_

 

1 2

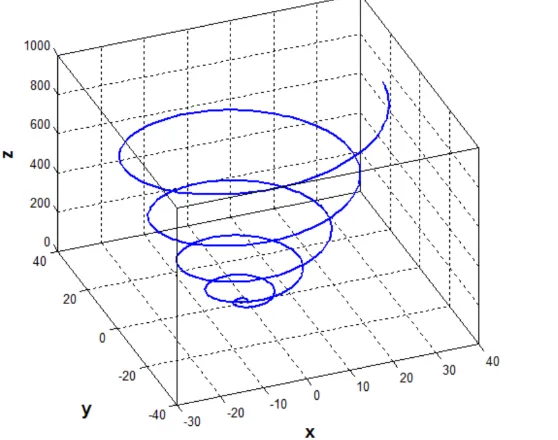
Ejemplo de función vectorial de una variable en el espacio:

 



cos

 

, sen

 

,



f t



t

t t

2

[image:2.612.82.468.227.604.2]

(3)

Fig. 3 Grafica de la función

f t

 





t

cos

 

t t

, sen

 

t t

, 2



.

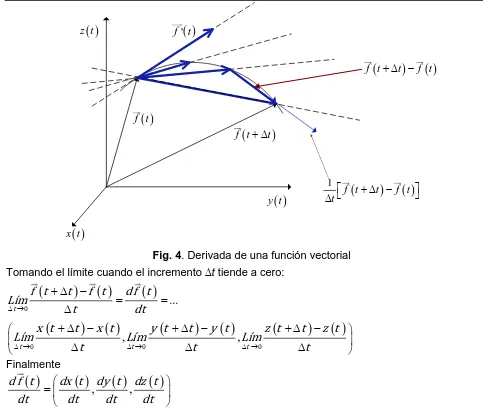
2.1.2 Cálculo diferencial de funciones vectoriales.

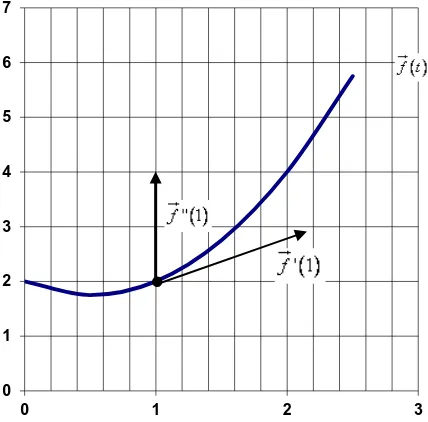
Dado el vector

f t

 





x t y t z t

     

, ,



, si se incrementa la variable en un t, el vector evaluado en el valor incrementado (ver Fig. 4) es:







 

,

 

,



f t

  

t

x t

 

t y t

 

t z t

 

t

Restando de la ecuación incrementada la ecuación original,



  



 

,

 

,





     

, ,



f t

  

t

f t



x t

 

t y t

 

t z t

 

t



x t y t z t



  





  

,



  

,

  



f t

  

t

f t



x t

  

t

x t y t

  

t

y t z t

  

t

z t

Dividiendo por el incremento,



  





  



  

  

, ,

f t

t

f t

x t

t

x t

y t

t

y t z t

t

z t

t

             

  

[image:3.612.205.484.81.301.2]

(4)



 



f t t

 

f t



  



 

f t t f t

 

'

f t

 

y t

 

z t

 

x t





 

1 _ _{  } _

 

t f t t f t

Fig. 4. Derivada de una función vectorial Tomando el límite cuando el incremento t tiende a cero:



  

 

... t

f t

t

f t

d f t

Lím

t

dt

 

  

 



0





 





 



  

,

t t t

x t

t

x t

y t

t

y t

z t

t

z t

Lím

t

     

  







_





0 0 0



Finalmente

 

, ,

d f t

dx t dy t dz t

dt

 

  

 

Es decir, la derivada de una función vectorial de variable real es otro vector cuyas componentes son las derivadas de los componentes de la función vectorial.

Velocidad

Sea

f t

 





f t f t f t

₁

     

, ₂ , ₃



una función que describe la posición de una partícula, entonces su velocidad está dada por

 



'

     

' '



' , ,

v t



f t



f t f t f t

₁ ₂ ₃ ; la rapidez está dada por la magnitud de la velocidad:

 

'

 

'

 

'

 

v t

 _

f t

₁ _2_

f t

₂ _2_

f t

₃ _2

Aceleración

 



''

     

'' ''



'' , ,

a t



f t



f t f t f t

1 2 3 , cuya magnitud se calcula con:

[image:4.612.79.562.75.484.2]

(5)

IGNACIO ELIZALDE MARTÍNEZ ENERO – JUNIO 2012 26 Recta tangente a una trayectoria.

La recta tangente a una trayectoria se calcula como:

 

'

 



l t



f t

0 

f t

0

t t

 0

Reglas de derivación de funciones vectoriales de variable real: Sean

a t b t

   

, funciones vectoriales y



una función escalar:

1) Regla de la suma algebraica

   

'

 

'

 

d

_{a t}

_{b t}

_{a t}

_{b t}

dt















2) Multiplicación por una función escalar

   

'

       

'

d

_{t b t}

dt







 









3) Producto escalar

   

'

     

'

 

d

_{a t b t}

dt



















4) Producto vectorial

   

'

     

'

 

d

_{a t}

_{b t}

_{a t}

_{b t}

_{a t}

_{b t}

dt



















5) Regla de la cadena o derivación de funciones compuestas

 





'



 



'

 

d

_a

_t

_a

_t

dt







 





Geometría diferencial

Vector tangente unitario, vector normal unitario, vector binormal El vector tangente unitario se define como:

 

'

f t

T t

f t



Mientras que el vector unitario es:

 

'

T t

N t

T t



El vector binormal es el producto vectorial del vector tangente y el vector normal:

 

B t



T t X N t

(6)

 

'

/

'

T t

dT

dT dt

dS

dS dt

_{f t}





 





, o bien,

 

'

''

'

f t X f t

f t



 





₃

Mientras que el radio de curvatura se define como el recíproco de la curvatura:







1

Problemas de aplicación de velocidad y aceleración.

Calcule en cada caso la velocidad y la aceleración dadas las siguientes trayectorias en los puntos especificados:

Problema 1:

 

, t

f t



t e

en

t



1

Solución

Derivando:

f t

’

 



V t

 



 

1,

e

t , donde v es la velocidad. Derivando ahora al vector velocidad:

 

’ , t

V t



a t

 0

e

, con a como la aceleración. Evaluando:

   

,

V

1  1

e

;

a

   

1  0,

e

Problema 2:

 



,



f t



t t

2

t

_t

_

₁

Solución

Derivando:

f t

’

 



V t

  

 1 2,

t

1



. Derivando ahora a v:

V t

’

 



a t

   

 0 2, Si se evalúan la velocidad y la aceleración:

V

   

1  1 3, ,

a

   

1  0 2,

Problema 3:

 



cos

 

,

 



f t



t

2

sen t

,

t





/

4

Solución

Derivando:

f t

’

 



V t

 

 



sen t

 

, cos2

 

t



. Derivando ahora a v:

 



 



’ cos ,

V t



a t

 

t

2

sen t

,

V

   _{  }



 _

   

2 2

4 2 ;

a

,



 

     

   

   

2 2

4 2

Problema 4:

(7)

Solución

Derivando:

f t

’

 

V t

 

,

,cos

 

t







_{ }

_







1

2

1

Derivando ahora a v:

 





 

’

,

V t

a t

sen t

t



_













_





3



1

0

4

1

Problema 5:

 



cos

 

, sen

 

,



f t



t

t t

2

Solución

Derivando:

f t

’

 



V t

 





cos

 

t



t

sen

 

t t

, cos

 

t

sen

 

t

,2

t



La representación de la derivada en varios puntos de la curva se muestra a continuación:

Fig. 5. Representación de la función vectorial y su derivada. La aceleración es entonces:

f

’’

 

t

 



cos

 

t

2

t

sen

 

t

, cos2

 

t



t

sen

 

t

,2



Problema 6: Dada la trayectoria en un plano de una partícula descrita por la función vectorial

 



,



f t



t t

2 

t

₂ _{, representar: la trayectoria, el vector velocidad y el vector aceleración en el}

instante t=1

  



' ,

(8)

Fig. 6 Representación de la trayectoria, la velocidad y aceleración del problema 5.

Suponiendo que la partícula de la trayectoria anterior en el instante 1 sale por la tangente, en el instante t=2, ¿Cuál será su posición?

     

, ,

   

, ,

 

,

 

,



l t

 1 2  1 1

t

1  1 2  

t

1

t

   1 1

t

1 2 

t

1 

t t

1

   

,

l

3  3 4

Problema 7. Una partícula se mueve sobre una hipocicloide

 

3 3

cos

c t  t isen t j

. Calcule la velocidad de la partícula en el instante

t





/ 4

. Muestre que la rapidez de la partícula en cualquier instante es

c t

'

 



3 sen t

   

cos

t

Problema 8. La trayectoria de una partícula está dada por:

 

1 cos

 

cos

 

c t  _ t sen t _i_sen t  t _j

. Calcule la velocidad de la partícula en el instante

/ 4

t





_{. Muestre que la rapidez de la partícula en cualquier instante es independiente de}_t_{e igual a}

 

'

2 c t



Halle: vector tangente unitario, normal y binormal dadas las siguientes funciones vectoriales.

Problema 9

 

,

f t



t t

2

_t

_

₁

Solución

Derivando el vector posición y calculando su magnitud:

  



’ ,

f t

 1 2

t

,

f t

’

 

 1 4

t

2; Entonces el vector tangente unitario es: 0

1 2 3 4 5 6 7

[image:8.612.223.437.88.299.2]

(9)

  

,

t



T t

t



 2

1 2

1 4 ; Entonces evaluando el vector tangente unitario en el punto especificado:

 

,

T

1 

1 1 2

5

Para el cálculo de el vector normal ahora se deriva el vector tangente unitario:

 





/



 







/

’

d

,

d

T t

t

dt

 

 

_{1 4}

2 1 2

_{1 2}



_{1 2}

_{1 4}



2 1 2_;

 





/

  







/

’

,

T t

 

_{1 4}

t

2 1 2

_{0 2}



1 _{1 2}

t

_{1 4}



t

2 3 2

₈

t

2  

 









,

’

t t

T t

t

_t







2

_

₂ 3

0 2

1 1 2 8

2 1 4

_{1 4}

o bien

 









j

i

j

’

t

T t

t









2 2 3 2

2 1 4

4

8 1 4

 





i+ j

’

t

T t

t







2 3

4

2 1 4

; Ahora se calcula la magnitud de la derivada del vector tangente unitario:

 







  

’

T t

t







_{ }

_



_

_{ }





_











2 2 2 3 2

1

4

2 1 4

 









’

t

T t

t

   2 3 2

4 4 1

1 4 ; Finalmente:

T t

’

 







t

2



2





t

2

1

2

2 1 4

1 4

Entonces el vector normal de acuerdo a su definición es:

 





i+ j

t

N t

t

    3 2 2 4 2 1 4 2 1 4

,

N t

 

t

i+j

t

 

 2

2

1 4 ; Evaluando el vector normal en el punto especificado:

 

i+j

N

1 



2

5

(10)

 





i

j

k

’

T t

N t

t

_t







2 2

_

1 ₁

₂

₀

1 4

₂

_{1 0}

;

 









k

B t

t

   2 2 2

1 _{1 4}

1 4

;

B t

 

k ; Entonces:

 

k

B

1 

Problema 10

 

,

f t



t t

3

_t

_

₁

Solución

 





’ ,

f t

 _{1 3}

t

2

 

’

f t

 ₁ 2 ₃

t

2 2  _{1 9}

t

4

;

T t

 



,

t



t





2 4

1 3

1 9

_;

   

,

T

1 

1 3

10  





/



 



/

’

d

,

d

T t

t

dt

 

 

_{1 9}

4 1 2

_{1 3}

2



_{1 3}

2

_{1 9}



4 1 2

 





/











/

’

,

T t

 

_{1 9}

t

4 1 2

_{0 6}

t



1 _{1 3}

t

2

_{1 9}



t

4 3 2

₃₆

t

3

2   











,

’

t

T t

t

_t







_

2 3

4 ₄ 3

1 3

36 0 6

1

2 1 9

_{1 9}

;

 







 







,

’

t

T t

t









4 2 3

3 4

0 6

1 9

1 3

18 1 9

 





j

i

’

t

T t

t









 













3 3 4

3

6 1 9

;

 







 







2

’

T t

t











_

_

 











2 2 3 3 4

6

3 1 9

.

 









’

t

T t

t















_







2 4 3 4

6 1 9

1 9

;

’

 





t

T t

t













_









2 2 4 4

6

6 1 9

1 9

 





i+ j

t

N t

t















_











3 3 4 4

3

6 1 9

;

N t

 

t

i+ j

t

   2 4 3

4 9 _;

 

i+ j

N

1 3

13

 





i

j

k

T t

N t

t

_t







_

2 2 4 ₂

1 ₁

₃

₀

1 9

₃

₁

₀

;

B t

 



t



k

t





4 4

1 _{1 9}

(11)

Problema 11

 



t,



f t



e t

2

_t

_

₁

Solución

 





’ t,

f t



e

2

t

;

f t

’

 



e

2t 4

t

2

 



e t

_tt

,



T t

e

t





2 2

2

4

;

   

,

e

T

e





2

1

4

Derivando:

 





/



 



/

’

t

d

t

,

t

,

d

t

T t

e

t

e t

e

t

dt

 



2



₄

2 1 2

₂



₂

2



₄

2 1 2

 



   

/



 

/



’

t t

,

t

,

t t

T t



e

2



₄

t

2 1 2

e

₂



1 e t e

₂

2



₄

t

2 3 2

₂

e

2



₈

t

2

, simplificando:

 

 

 









,

’

t t t t

t

e

t

e t

e

t

T t

e

t











2 2 2

3

2 2

2

4

2

8

2

4

;

 

 

 









,

’

t t t t

t

e

t

e t e

t

T t

e

t











2 2 2

3

2 2

2

4

2

4

, desarrollando:

 

 

  

 











i

j

’

t t t t t t

t

e

t

e

t

e

t

t e

t

T t

e

t















2 2 2 2 2 2

3

2 2

4

2

4

2

4

, simplificando:

 





i

j

’

t t t t t

t

e e

t

e

t

e

t

te

t

T t

e

t































2 2 2 2 2 2 2

3

2 2

4

2

4

4  













i

j

’

t t t

te t

e

t

T t

e

t











2 3 2 2

4

1

2

1

4

;

 













i

j

’

t t t

e t

t

e

T t

e

t







3 2 2

2 1 2

4

.

Magnitud de la derivada del vector tangente unitario:

 











 



’

t t t

e t

T t

t

e

t













_

_

 











2 2 2 3 2 2

2

1

2

4

;

 













’

t t

t

T t

e t

t

e

t







2 2 3 2 2

1

2

1

4

4  









’

t

T t

e t

e

t







2 2 2

1

2

1

4

;

 

(12)

 

















i

j

t t

t t t

e t

t

e

t

N t

e t

e

t











3

2 2

2 1 2

4

2

1

4

;

 

i j t t

t

e

N t

e

t

 



2 2

2

4 _:

 

i

e

j

N

e

 



2

2 1

4

Vector binormal:

 





t

k

t _t

i

j

k

T t

N t

e

t

e

t

_t

_e





 



2

_

2 2

1 ₂

₀

4 ₂

₀

;

B t

 

 k

;

B

 

1  k

Problema 12

 



cos

 

,

 

,

 



f t



t sen t

3

t

Solución

Derivando:

f t

’

 

 



sen t

 

,cos

 

t

,

3 

Magnitud de la derivada:

 

’ cos

f t

 _

sen t

_2_

t

_2_ 3_2,

f t

’

 



sen t

2

 

cos2

 

t

₃_,

_{f t}

_’

 

_

₂

 



 

, cos

 

,



T t



1 

sen t

t

3

2

La derivada del vector unitario es entonces:

 



 



’

cos

,

T t



1 

t



sen t

0

2

Y su magnitud es:

 

’ cos

T t

   _{  }

t



sen t

_  

2

2 2

1

2 ,

T t

’

 



1 2

/

Por lo tanto el vector normal unitario es:

 



cos

 

,

 

,



N t

 

t



sen t

0 y el vector unitario binormal es:

 

cos cos

i

j

k

T t

N t

sen t

t

sen t

  

 

1 ₃

2

0

;

 

cos

 

cos

 

T t



N t



1 

_

₃

sen t i



_



1 

_

₃

t j

_





1 _



sen t

2



2

t k

_



2

2  



 

i

cos

 

j k



B t



1

3 sen t



3 t



2

(13)

IGNACIO ELIZALDE MARTÍNEZ ENERO – JUNIO 2012 34 Sean y conjuntos abiertos. Sean y funciones tales que lleva en de la forma que está definida. Si se supone que es diferenciable en

y que es diferenciable en ( ). Entonces es diferenciable en y ( )( ) ( ) ( )

Primer caso especial de la regla de la cadena

Supóngase que es una trayectoria diferenciable y que . Sea ( ) ( ( )) ( ( ) ( ) ( )) con ( ) ( ( ) ( ) ( )), entonces:

O de forma más compacta:

( ( )) ( )

Segundo caso especial de la regla de la cadena

Sea y , entonces se puede escribir como: ( ) ( ( ) ( ) ( )) Y se define de la siguiente manera:

( ) ( ( ) ( ) ( )) Para esta función, la regla de la cadena es:

[

] [

]

[

]

Derivación implícita

La regla de la cadena expuesta con anterioridad se emplea para hallar la derivada de forma implícita. Por ejemplo, una ecuación de la forma

F x y



,



define a

y

implícitamente como una función diferenciable de

x

es decir,

y f x



( )

, donde

F x f x



,

 



0 para toda

x

en el dominio de

f

. Si

F

es diferenciable se aplica del primer caso de la regla de la cadena para derivar ambos lados de

F x f x



,

 



0 con respecto a

x

. Entonces:



_



_



F dx

F dy

x dx

y dx

0

Si



_



F

y

0

se puede despejar

dy

dx

de donde se obtiene:



 





x y

F

dy

_x

F

dx

F

(14)

Problema 1 Sea:

z x



3



y

2, donde

x

cos

 

t

y

y sen t



 

, halle

dz

zt









dz

z dx

z dy

zt

x dt

 

cos

 

 







dz

_{x sen t}

_y

_t

zt

2

3

2

Problema 2 Obtener

F

y

F

r

t



dada la siguiente función:

F x y



,





xy x

 2, donde

 

cos ,

t t

x e



r

y e sen r



.

Usando segundo caso de la regla de la cadena:

;

F

F x

F y

F

F x

F y

r

x r

y r

t

x t

y t



_

 

_

 



_

 

_

 



 



 

Cálculo de las derivadas parciales:

F

_y

_x

x



 



2  

t

x

_{e sen r}

r



 



cos

 

t

x

_e

_r

t







F

_x

y



_



t

cos

 

y

_e

_r

r







 

t

y

_{e sen r}

t







Sustituyendo

 

cos

   

 

cos

 

cos

 

t t t t t

F

_{e sen r}

_e

_r

_{e sen r}

_e

_{r e}

_r

r



_

_

_

_



_



_





_

_



2

1  

   

cos

 

t t t

F

_{e sen r}

_r

_e

_r

r



_{ }

_

_



2 2

₂

2 2 2

Simplificando

 

   

cos

t t

F

_e

_r

_{sen r}

_{e sen r}

_r

r



_

_



_



_







2 2 2

₂

2

 

cos

t

F

_e

_r

_{sen r}

r







_





_



2

₂

Sustituyendo

 

cos

 

cos

 

cos

 

t t t t t

F

_{e sen r}

_e

_{r e}

_r

_e

_{r e sen r}

t



_

_

_

_

_

_

_











2    

cos

 

   

cos

t t t

F

_{e sen r}

_r

_e

_r

_{e sen r}

_r

t









2

₂

2 2 2

 

cos

 

t

F

_e

_{sen r}

_r

t







_





_



2

₂

₁

F

y

F

r

t



F x y



,





x

cos

 

y

, donde ,

x r t y t r

 

(15)

;

F

F x

F y

F

F x

F y

r

x r

y r

t

x t

y t



_

 

_

 



_

 

_

 



 



 

 

cos

F

_y

x







x

_t

r







x

r

t



_



2  

F

xsen y

y



 



y

t

r







2 y

_r

t







 

cos

F

t

y

t

xsen y

r

t







_



_

 



_



_



2

,

cos

 

F

_t

_{t r}

_{rtsen t r}

r



_

_



1

2  

 

cos

F

_y

r

_{xsen y}

_r

r

t



_

_

_

_{ }

_

_











2

,

cos

 

F

r

_{t r}

_{r rt sen t r}

r

t



_

_



2 dy

dx

dada la siguiente función

x



y

 

2 2

_{1 0}

. Usando la derivación implícita:



x

F

2 x

;

F

y



2 y

 

dy

x

dx

y

2

Problema 5 Usando la derivación implícita obtener R

df

dN

dada la siguiente función





10

1 1 2.51

2log

3.7 D/ _R

f  N f

          . Sol.

 





10 10

 

10.04 log e

3.7 / 2.51 5.02 log e

 

 

   

 

R _R _R

f df

dN N D N f f

Problema 6 Derive implícitamente para hallar

dy

dx

dada







2

2 





y

x

y

x

C

Sol.

y

'

2 xy

xy

x





F

y

F

r

t





,



F x y



xy y

 2

, donde

x e sen r

 t

 

,

y

 

e

t cos

 

r

(16)

 

cos

t

F

_e

_r

_{sen r}

r



 



_





_



2

₂

y

F

e

t

sen r

 

cos

 

r

t



 



_





_



2

₂

₁

F

y

F

r

t



F x y



,





y

tan

 

x

, donde ,

r

t

x

y

t

r

 

R. Parcial

sec tan

F

r

rt

t

r t

t

   

 _{ } _

   

 _ _ _ _

2 3

1 1

2

Problema 9 Aplicando la regla de la cadena, transformar la siguiente ecuación diferencial a su forma adimensional:

z

d c

_u

dc

_kc

dy



2₂   0

Con las siguientes sustituciones:

;

z

uL

kL

c

z

Pe

R

f

y

u

c



L





0

Solución

dc

dc df d

dz df d dz





 

;

z

d

d c f

dc

_c

d

L

df

dz

L



  _{ }

 0   

0

1

, por lo tanto,

dc

df

c

dz

L d



    0_{ }

1

La segunda derivada de “c” respecto a “z” es:

d c

d

dz

dz dz

 

 _ _

 

2

2 ;

d

d d

d

dz d dz

L d





1

Entonces,

c

d c

d f

dz



L d

2 2

0

2 2 2 Sustituyendo en la ecuación

z

c

d f

uc

df

_{kc f}

L d











2

0 0

0

2 2 ; dividiendo por “c0” y multiplicando por “L/u”

z

d f

df

kL

_f

uL d

d

u











2

2 , sustituyendo los grupos de constantes, finalmente se obtiene:

d f

df

_Rf

Pe d





d





2 2

(17)

Problema 10 Aplicando la regla de la cadena, transformar la siguiente ecuación diferencial a su forma adimensional:

A A A A

a r B A

C

u

D

k C

z

r









 







_

 

_



 



_



_

2 2

1

Use:

0

A A

C C f  ;

R r 



;

L z 



;

A

L

R

 ; Pe_a

a

uL

D

 , Pe_r

r

uR

D



Sol.

Pe

_a

Pe

_r B

f

A

f

L k

_f

u







 















_

 

_





_



_

2 2

1

2.1.4 Máximos y mínimos de funciones de 2 variables.

Campos escalares

Una función escalar  que toma valores en los puntos del espacio se dice que es una función escalar de punto o un campo escalar.

A cada punto P(x,y,z), la función  le hace corresponder un número (x,y,z); es una aplicación de R3 en R. Aunque no es necesario que  esté expresada en función de las coordenadas cartesianas, será lo más habitual.

La regla de correspondencia es: : n

f



Por ejemplo

z

  1

x y

(18)

Fig. 7 Gráfica de un plano

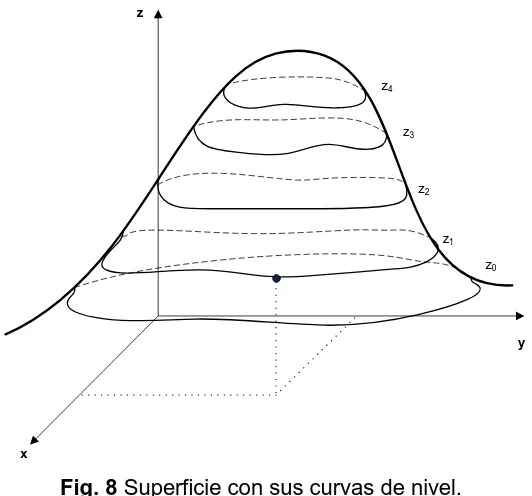
Conjuntos de nivel. Las curvas o conjuntos de nivel de una función de dos variables independientes o campo escalar son las curvas con ecuaciones

f x y



,





k

donde k es una constante. Por ejemplo, en la Figura 8 se muestra una superficie con algunas curvas de nivel (

z

₁,

z

₂, etc.)

z0

z1

z2

z3

z4

x

y z

Fig. 8 Superficie con sus curvas de nivel.

[image:18.612.196.465.84.340.2] [image:18.612.200.466.411.659.2]

(19)

IGNACIO ELIZALDE MARTÍNEZ ENERO – JUNIO 2012 40 Sea la función

f x y



,





x

2



y

2

Algunas curvas de nivel son:





x

2

y

2

₁

,

x



y



2 2

₄

Es decir, circunferencias cuyo radio es 1 y 2 unidades, respectivamente.

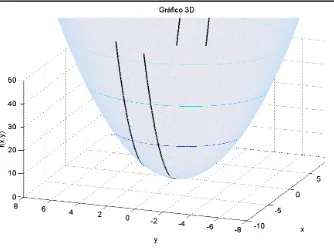
Secciones de una función de dos variables. Se originan en la intersección de los planos en la dirección

x z

 ,

y z

 con la función.

Ejemplo.

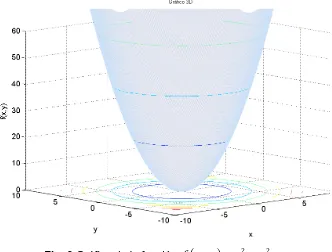
Sea la función

f x y



,





x

2



y

2

Sus secciones son:



,





f x

₀

x

2

;

f



,

y





y

2

0

, también

f x



,0





x

24;

f



0,

y





y

21

Estas secciones corresponden a ecuaciones de parábolas. En efecto la función

f x y



,



es un paraboloide, como se observa en la siguiente Figura 9. Sus correspondientes curvas de nivel están proyectadas en el plano x-y.

Fig. 9 Gráfica de la función

f x y



,





x

2



y

2.

Y las parábolas

f x



,





x

2

0

y

f x



,





x



2

0 4

[image:19.612.171.503.338.590.2]

(20)

[image:20.612.172.506.74.325.2]

Fig. 10 Secciones de la función

f x y



,





x

2



y

2.

Las ecuaciones de algunas superficies importantes junto con sus secciones se muestran en la siguiente Tabla. También se han incluido las parametrizaciones más frecuentes de dichas curvas.

Superficie Ecuación Secciones Parametrización

Elipsoide

x



y



z



a

b

c

2 2 2

1 



x

y

a

b

2 2

1 



x

z

a

c

2 2

1    

cos sen

x a

 

u

v

   

sen sen

y b

 

u

v

 

cos

z c

 

v

u



 

0

2 v



 

0

Esfera

x



y



z



c

2 2 2

1 



x

y

c

2 2

1 



x

z

c

2 2

1    

cos sen

x a

 

u

v

   

sen sen

y a

 

u

v

 

cos

z a

 

v

u



 

0

2 v



 

0

Paraboloide

elíptico





z

x

y

c

a

b

2 2



z

x

c

a

2



z

y

c

b

2 2

 

cos

x a v

  

u

 

sen

y b v

  

u

z c v

  2

u



 

0

2

(21)

IGNACIO ELIZALDE MARTÍNEZ ENERO – JUNIO 2012 42 Paraboloide

hiperbólico





z

x

y

c

a

b

2 2



z

x

c

a

2

 

z

y

c

b

2 2

x a u

 

y b v

 





z c u v

  2 2

< , <

u v





Cono

z



x



y

c

a

b

2 2 2



z

x

c

a

2 2



z

y

c

b

2 2 2 2

 

cos

x a v

 

u

 

sen

y b v

 

u

z c v

 

u



 

0

2 v

   Hiperboloide de una hoja







x

y

z

a

b

c

2 2 2

1 



y

z

b

c

2 2

1 



x

z

a

c

2 2

1  

 

cos cosh

x a



u

v

 

sen cosh

y b



u

v

 

senh

z c

 

v

u



 

0

2 v

    Hiperboloide de dos hojas



x



y



z



a

b

c

2 2 2

1 





y

z

b

c

2 2

1 





x

z

a

c

2 2

1  

 

cos senh

x a



u

v

 

sen senh

y b



u

v

 

cosh

z c

 

v

u



 

0

2 v

   

Cilindro

x

y

c



c



2 2

1 x

c



2 2

1 y

c



2 2

1  

, cos

 

x u v



a

u

 

sen

y a



u

z v



En muchos casos es preferible utilizar las parametrizaciones de las ecuaciones para trazarlas de forma adecuada.

Dado el conjunto de ecuaciones paramétricas

 

e cos cos

u

_v

x

_ _ _ _

u

 

      2 6 2 1 2

 

e sen cos

u

_v

y

_ __{ } _

u

 

      2 6 2 1 2

 

e sen e sen

u u

y

_{ }₁ 3_

v

_ 6

v

Cuyo intervalo para los parámetros es:

u



 

0

6

,

v



 

0

2

Construir su gráfica.

(22)

[image:22.612.224.436.79.260.2]

Fig. 11 Grafica del “Unicornio”.

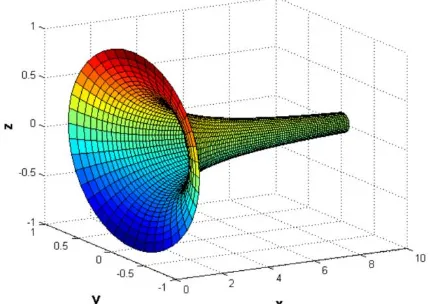
Grafique “La Trompeta de Gabriel” cuyas ecuaciones paramétricas son:

x u



 

cos

y

v

u



1  

z

sen v

u



1

EL intervalo para los parámetros u y v son:

u

 

1

10

,

v



 

0

2

Fig. 12 Grafica del “la Trompeta de Gabriel”. Derivadas parciales

Una forma adicional de analizar una función de dos o más variables independientes además de sus secciones y curvas de nivel es a través de sus derivadas parciales.

[image:22.612.224.439.430.582.2]

(23)

IGNACIO ELIZALDE MARTÍNEZ ENERO – JUNIO 2012 44 es decir,

g x

 



f x b



,



. Si

g

tiene derivada en un punto

a

, entonces ésta recibe el nombre de derivada parcial de

f

con respecto de x en

 

a b

, y se denota por

f a b

_x

 

, , es decir:

 

,  '

 

x

f a b

g a

donde

g x

 



f x b



,



De forma similar la derivada parcial de

f

con respecto a

y

en

 

a b

, , denotada por

f a b

_y

 

, se obtiene dejando a

a

fija (

x a

 ) y calculando la derivada ordinaria de la función

h y

 



f a y



,



. Las notaciones utilizadas para designar las derivadas parciales son:

Sea

z f x y





,





,













,







x x x

f x y

f

f x y

f

D f

x



,



   



,





 

y y y

f x y

f

f x y

f

D f

y

Para hallar la derivada parcial de una función de dos variables se usan las mismas reglas que para derivar funciones univariables ya que el resto de ellas se consideran fijas.

Interpretación geométrica de la derivada parcial de una función de dos variables

Una función de dos variables independientes representa una superficie y sus derivadas parciales



f

x

y



f

y

proporcionan las pendientes de las tangentes a las curvas que se generan entre los

planos x z y

y z