LA E C U A C I ~ N DE POISSON-BOLTZMANN, Y C O R R E L A C I ~ N DE
UN
ELECTROLITO A T R A V ~ SDE UNA PLACA CARGADA
Tesis que presenta el Físico
GABRIEL ELOY AGUILAR PINEDA
Para la obtención del grado de Maestro en Ciencias (Física)
Junio de 1998
UNIVERSIDAD AUT6NOMA METROPOLITANA-IZTAPALAPA
DIVISI6N DE CIENCIAS
BASICAS
E INGENIERÍAA mis padres y hermanos, por su cariño y apoyo, y por mostrarme la belleza e importancia de l a familia y de la vida.
A
todos mis profesores, por enseñarme la belleza e importancia de la ciencia.ÍNDICE
Introducción
Capítulo I
Funciones de Distribución Teoría de Debye-Hückel
Capítulo I1
Solución a la Ecuación de Poisson-Boltzmann Linealizada Resultados
Capítulo I11
Solución a la Ecuación de Poisson-Boltzrnann Para una Placa Resultados
Comentarios y Conclusiones
2
10
10
17
20
20
33
38
38 53
57
Existen en la naturaleza una gran cantidad de sistemas que requieren para su
comprensión el estudio de los fluidos cargados. Es éste u n tema de gran importancia en muchas ramas de la ciencia: en Física de Plasmas, en el estudio de soluciones electrolíticas, y en diversas áreas de Fisicoquímica y Biofisica.
La concentración local de los iones en una solución electrolítica se ve afectada por la presencia de una superficie cargada en el interior de dicha solución. Mientras la concentración de los coiones disminuye, la concentración de los contraiones aumenta debido a la atracción que sobre ellos ejerce dicha superficie. Sin embargo, a una distancia suficientemente lejana, la concentración de ambas especies debe ser la misma.
A
esta distribución de carga se le conoce como Doble Capa Eléctrica (DCE), y su estructura es tal que el potencial químico del fluido debe ser el mismo en todas partes.La comprensión de la estructura de la DCE puede ser muy útil en el estudio de algunos sistemas biofísicos. La cantidad de agua en los líquidos biológicos es considerable, ya que representa en la mayoría de los casos más del 90% del total. En estos líquidos se encuentran una gran cantidad de iones. El ion sodio (Na+) es el que tiene una mayor concentración en el liquido extracelular de un organismo, pues representa aproximadamente el 92% del total de cationes que existen. Aunque en menor cantidad, tambikn existen iones de potasio (K+), de calcio (Ca2+), magnesio (Mg2+), etc. Los principales aniones en los líquidos extracelulares son el cloro (Cl-), iones de bicarbonato (HCO3-), y de fosfato de hidrógeno (POqH2-). Existen algunos más, que se encuentran en concentraciones mucho m u y bajas, aunque su importancia en determinados procesos biológicos es fundamental. Los líquidos intracelulares presentan una composición iónica muy variable, dependiendo del tipo de célula. Sin embargo. se sabe que el principal catión en este caso es el K+, y los principales aniones son fosfatos orgánicos, proteínas y C1-.
La membrana celular es la parte de la cdlula que divide y separa a ésta de sus alrededores. Dependiendo de la cdlula en cuestibn, la membrana puede medir
mismo orden al de las membranas externas, obteniCndose con esto, que los diversos organelos celulares permanezcan aislados de su medio ambiente.
L a s membranas están compuestas principalmente por proteínas y lípidos. Las proporciones relativas entre ambos componentes varía según la naturaleza de la membrana. Los lípidos constituyen del 25 al 80% del peso de una membrana celular, y su composición depende del tipo de célula. Los lípidos son usualmente moléculas anfipúticns: están constituidos por una parte hidrofóbica (no polar) y una hidrofílica (polar). Los más comunes encontrados en las membranas son fosfolípidos, glucolípidos, esfingolípidos, y los esteroles.
Las proporciones de éstos en las membranas varía ampliamente, aunque se desconoce la razón de esta variación en relación con la función que desempeñan en la célula.
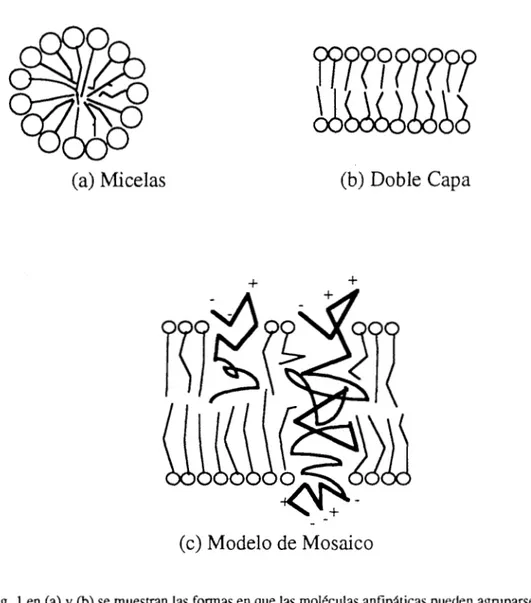
El conocimiento del comportamiento de los lípidos anfipáticos en soluciones acuosas, es muy importante en el estudio de los sistemas biológicos. Se sabe que estas moléculas forman estructuras globulares llamadas Micelas (fig. l.a), en las que la cola hidrofóbica queda inmersa en el interior de ésta, con las cabezas polares hidrofílicas en contacto con el agua. Alternativamente, estas moléculas pueden también ordenarse de tal manera que formen una doble capa, con las cabezas hidrofílicas hacia el medio acuoso (Fig. 1.b).
Las proteínas son el compuesto más complejo que existe en las membranas; la proporción de éstas depende de l a actividad y especialización de l a membrana, pues ellas son las que ejecutan casi todas sus funciones. Así por ejemplo, mientras las membranas de mielina contienen muy pocas proteínas, las de los gl6bulos rojos contienen hasta 20 tipos diferentes, todas con actividad enzimática. Aún cuando no se sabe con exactitud cómo las proteínas se encuentran unidas a las membranas, existen evidencias experimentales basadas en la dificultad para disociarlas, que hacen suponer que éstas se acomodan en dos formas diferentes: las llamadas proteínas "perifiricas" están únicamente adsorbidas ligeramente sobre la superficie de los lípidos de l a membrana, y las proteínas "integrales", que están fuertemente embebidas e incluso atraviesan todo el lípido. Las proteínas integrales dejan alguna parte expuesta en las superficies externa e interna de la membrana, lo que proporciona una distribución asimétrica de carga en las superficies de ksta.
L a mayor parte de los científicos está de acuerdo en que las membranas biológicas estBn formadas por una doble capa de lípidos, pues es el arreglo que explica más
biol6gicas es un arreglo de proteínas globulares dispersas en una matriz de bicapa lipídica fluida. Las proteínas son también moléculas anfipáticas, con sus grupos no polares embebidos en el interior hidrofóbico de la membrana (Fig. 1.c).
En lo que se refiere a la estructura de la membrana, en ésta existen también poros, que permiten las propiedades de transporte vitales en la célula, además de que la membrana misma es altamente permeable a l agua y a algunas moléculas pequeñas. Estos poros pueden s e r originados por dos causas: la primera, el propio movimiento de las moléculas en la membrana puede ser capaz de abrir en ella algunas cavidades de naturaleza transitoria. Alternativamente, algunos poros podrían ser canales formados al agregarse algunas proteínas integrales, dejando entre ellas una cavidad llena de agua. L a entrada y salida sincronizada de iones a través de diferentes canales de una membrana, es la causa de las señales eléctricas producidas en las células nerviosas. Se sabe también que estos poros son altamente selectivos, propiedad debida a su tamaño, a la presencia de grupos polares en las paredes del canal y a la interacción de los iones con las moléculas de agua.
El movimiento de iones a través de las membranas es un proceso controlado que involucra mecanismos m u y específicos, desde movimientos de difusión , hasta un transporte activo en el cual los iones se mueven contra un gradiente electroquímico.
Por último, cabe mencionar que alsmembranas son estructuras móviles y dinámicas, pueden contraerse y expanderse, son capaces de autorepararse. Con frecuencia hay recambios en su flujo constituyente y, además, hay comunicaci6n e intercambio de material físico entre las células a través de sus membranas.
+
+
(c) Modelo de Mosaico
fig. 1 en (a) y (b) se muestran l a s formas en que l a s moleculas anfipkicas pueden agruparse, formando
micelas, o como una doble capa. en (c) se muestra el modelo de mosaico propuesto para
las membranas celulares, en donde las proteínas estan embebidas en el cuerpo de esta o tinimente adheridas a la superficie de la membrana.
Una primera aproximaci6n al estudio de la distribuci6n de partículas cargadas en un fluido en s o l u c i h , fue dada por Gouy y Chapman, a traves de la ecuaci6n de Poisson- Boltzmann (EPB). Se utiliza la ecuaci6n de la electrostdtica de Poisson, que relaciona la divergencia del gradiente del potencial electrice con la densidad de carga en un punto dado, y considerando que la distribucidn de carga sigue una distribuci6n de Boltzmann.
n
v2y(r) = C q i p i e -qiw(r)/kT i=l
donde
Y
es el potencial electrostático en r; la sumatoria se lleva a cabo sobre las n especies de iones existentes en el fluido, qi es la carga de la i-ésima especie, pi la densidad en el bulto de &sa, w(r), el potencial de fuerza media en r, k la constante de Boltzmann, y T la temperatura del sistema.Para construir una teoría basada en esta ecuación, Debye y Hiickel introdujeron dos aproximaciones importantes. L a primera de ellas es considerar que el potencial de fuerza media entre los iones es exclusivamente de carácter electrostático. Además, como la no linealidad de esta ecuación impide la obtención de soluciones analíticas en la mayoría de los casos, la segunda aproximación que utilizaron consistió en linealizar el factor de Boltzmann, y de esta forma resolver la ecuación y obtener las propiedades termodinámicas de los sistemas en estudio.
L a DCE debe satisfacer que el exceso de carga de los iones en una solución electrolítica en presencia de una superficie cargada, sea igual en magnitud y de signo opuesto a la carga que se tenga sobre la placa. Entonces, la integral sobre todo el espacio de la densidad de carga electrostática, debe ser igual en magnitud y de signo opuesto a la carga Q sobre la superficie en cuestión.
[ i-21
donde Pel es la densidad de carga eléctrica de los iones, y l a integral se extiende sobre todo el volumen de l a soIuci6n electrolítica. A este principio se le conoce como la Condición General de Electroneutralidad (GEC, por sus siglas en inglés).
por lo tanto
[i-31
[ i-41
donde Q d es la carga sobre la cara derecha de la placa, A es un elemento de superiicie dado, od
y
oi
son la densidad de carga superficial derecha e izquierda de la placa respectivamente, (3'd yo'i
son la densidad de carga inducida en el fluido a la derecha e izquierda de la placa respectivamente, 2d es el grosor de la misma, a/2 es el radio de los iones, que es la distancia de m&ximo acercamiento de éstos a la pared.I
i
(
I1
Obviamente, existen versiones de la LEC para eIectrodos con otras simetrías. Por ejemplo, para electrodos huecos esféricos o cilíndricos, l a LEC establece que la carga inducida en el fluido localizado en el interior de éstos, debe tener el mismo valor pero diferente signo al
de la carga sobre la superficie interna de estos electrodos, y l o mismo debe suceder con el electrolito localizado en el exterior de los mismos.
L a LEC ha sido ampliamente aplicada en teoría de líquidos; en muchos trabajos teóricos y simulaciones numéricas se ha hecho uso de esta condición[*-30], sin suponer ninguna correlación entre los fluidos en cada lado de la placa, ya que de la forma en que se habían deducido en los primeros estudios sobre el tema las ecuaciones integrales pam fluidos inhomogeneos, no era posible notar este efecto[*-lO1.
Sin embargo, no hay ninguna demostración general de la validez de la LEC; de hecho, bajo ciertas condiciones ésta no se satisface. Se puede demo~trar[33~3~] que si se mantiene el potencial electrostatico constante e igual en ambas superficies del electrodo, la LEC se cumplirá siempre, pero si se impone como condición que la densidad de carga en las superficies de este sea l o que permanezca constante, la LEC no será satisfecha en todos los casos[35].
Este problema y, en general, el estudio de los fluidos homogineos e inhomogineos se pueden atacar a traves de teorías mechico estadísticas miis sofisticadas, con las quc se obtienen mejores resultados a altas concentraciones. Por ejemplo, a traves de ecuaciones integrales para la funci6n de distribuci6n, tales como la Percus-Yevick Aproximation (PY), Hypernetted Chain (HNC), Mean Spherical Aproximation (MSA), etc., cuyos resultados aproximados se obtienen a partir del desarrollo de metodos numericos avanzados. Existen además tknicas de simulación por computadora, como Montecarlo y Dinámica Molecular, sin embargo, los resultados obtenidos con la EPB no lineal para bajas concentraciones, estin de acuerdo con los predichos por la teoría HNC/MSA, por lo que nuestro propósito será resolver la EPB y la EPBL en determinados sistemas, que nos permitan obtener resultados analíticos a traves de los cuales podamos observar directamente la violaci6n a la LEC, y l a existencia de una correlación entre los fluidos a traves de las paredes de los electrodos.
condición de densidad de carga constante. En estudios anteriores, se ha encontrado ya una violación a la electroneutralidad local en estos casos, es decir, para fluidos confinados [317331.
Mostraremos que aún en el modelo de la EPBL, la violación de la LEC puede ser observada, y obtendremos expresiones analíticas que muestran lo anterior. Presentamos también, algunas gráficas de las densidades inducidas en el fluido, y de las funciones de distribución radial de las dos especies de iones, ést0 con el fin de reforzar los resultados analíticos que demuestran la violación de la condición local de electroneutralidad en estos sistemas.
En el capitulo III, obtenemos l a s expresiones para la distribución de iones en presencia de una pared infinita cargada por ambos lados, que resultan de resolver la EPB no lineal, en los casos en que el electrolito es simétrico (1: 1 y 2:2) y no simétrico (1:2 y 2: l), utilizando la teoría de Debye-Hückel pero sin linealizar la ecuación, incluyendo la aproximación de Stem, que consiste en considerar que los iones tienen una distancia de máximo acercamiento a la pared igual al radio de ellos, con lo que estamos suponiendo que interactúan con ella como esferas duras, y como iones puntuales entre ellos.
CAPÍTULO I
FUNCIONES DE D I S T R I B U C I ~ N d
En el estudio de sistemas densos, como los líquidos, es necesario tomar en cuenta la interacción efectiva entre todas las particulas del sistema. L a función de distribución radial nos permite lo anterior. Esta función describe la probabilidad de encontrar dos partículas del sistema en alguna configuracion dada. A continuación haremos una breve introducción hacia ésta.
Si tenemos un sistema de
N
partículas en un volumen V a una temperatura T, la probabilidad de encontrar el sistema en la configuración en la cual l a partícula 1 esté en el elemento de volumen d r l localizado en rl, la partícula 2 en dr2 localizado en r2, etc., está dada pordonde ZN es la integral de configuración
ZN = j...je-U’kTdrl...drN
y U es la energía potencial de interacción total del sistema.
Si consideramos sólo u n subconjunto de h partículas del sistema, la probabilidad de encontrar a la moldcula 1 en el elemento (rl, drl), la 2 en (r2, d q ) , ..., y la h en (rh, drh), independientemente de la posición del resto de las N-h partículas, se obtiene integrando sobre las posiciones de las N-h partículas:
Por otra parte, sea P[h] drh, la probabilidad de encontrar a la h-&sima partícula en
donde l a constante se f i j a a partir del hecho de que esta probabilidad está normalizada
por lo tanto
Si el sistema está compuesto de partículas indistinguibles, debemos tomar en cuenta que existen ahora varias formas de obtener la misma configuración y, en este caso, la probabilidad de observar cualquier molécula de u n conjunto de h partículas en ( r l , d r l ) , otra en (1-2, dr2). etc., es
J J
f h ( q , r 2 , . ... rh)drldr2 ... drh = N! N-h drldr2 ... drh.
( N - h)! ZN
[ 1-71 Note que
De este resultado y del hecho de que la funci6n PN estli normalizada, se encuentra que
Podemos tambikn obtener la probabilidad f[h] drh definida como la probabilidad de
Es necesario notar que l a s h-1 partículas son distinguibles. Además
y de las ecuaciones [I-61, [I-101 y [I- 111 encontramos
[I- 101
[I- 1 11
[I-121
Por otra parte, para un fluido h o m o g h e o e isotrópico en equilibrio, todas las posiciones son igualmente probables, por lo tanto fl será independiente de rl, y entonces
j f l ( r 1 ) d r I = f l j d r l = f l V = N , [I-131
N V
f l
=-=o,
[I-131es decir, fl es l a densidad de numero en el bulto del fluido cuando &e es isotrópico. AdemBs, cuando la energía de interacción entre las partículas del fluido es cero, la integral de configuracion es simplemente
VN,
por lo que obtenemosN!VN-h NI h N !
f h ( q , . . . J h ) = - = P [I- 151 ( N - h ) ! V " - V h ( N - h ) ! N h ( N - h ) ! '
Podemos definir la funci6n de correlaci6n g(h)(r1,r2,...,rh) como
[I- 161
[I- 171
Y si tenemos un número muy grande de partículas, los términos de orden 1/N pueden ser ignorados, asíque g(h) vale 1 y f h ( q ,..., rh) = ph. Entonces, la función g(h) cuantifica la
no independencia entre las partículas del fluido, i.e., el factor por el cual las partículas dejan de ser independientes. De la ecuación [I-71 se tiene que en general
Definamos ahora la función w(h)(rl,...,rh) de la siguiente forma
donde 1
kT
p=-.
[ 1-19]
Sustituyendo esta expresión en la ecuación [I-18], sacando el logaritmo en ambos lados, y tomando el gradiente con respecto a la j-ésima partícula, obtenemos
j . . . j ( - v j u ) e - U/ kT d r h + l ... drN
J... j e - u / k T d r h + l ... drN = (-VjU)
[ 1-20]
N-h
pero -VjU es l a fuerza que actúa sobre la j-esima partícula, así que el lado derecho de esta
ecuaci6n es la fuerza media actuando sobre la partícula j del sistema promediada sobre la posici6n de las N-h partículas, dejando fijas el resto, 1,2 ,..., h. Por lo tanto, w ( ~ ) es el potencial que da la fuerza media actuando sobre la partícula j, i. e., w(h) es el potencial de fuerza media.
experimentalmente mediante técnicas de dispersión de rayos X o de neutrones. De l a ecuación [I- IS] obtenemos
[I-2 11
Si tenemos un fluido con simetría esférica, f2(rl,r2) dependerá únicamente de la distancia entre l a s partículas, y lo mismo para gQ)(rl,r2), así que
Por otra parte, de las ecuaciones [I-101 y [I-211 podemos obtener una relación entre
f[2](W) y g(2)(r12)
[I-221
donde hemos escrito r12=r. Por lo tanto, pg(?-)dr;! es la probabilidad de encontrar una partícula cualquiera en (r, dr), cuando se tiene una partícula específica en el origen. Además, de la ec. [I-221
entonces
Jpg(*)(r)dr =(N - 1) [I-241
Como esta integral es sobre todo el espacio, la expresión pg(?)(r)dr nos da la cantidad de partículas que se encuentran alrededor del ion central en la región comprendida entre r y r+dr. En este sentido, podemos considerar que g(2)(r)es el factor por el que hay que multiplicar a la densidad de bulto para obtener la densidad local:
p(r) = pg(2)(r)dr [ 1-25]
todas las configuraciones.
Otra razón por la que l a función g(r) es importante en teoría de líquidos, es que si suponemos que l a energía de interacción entre las
N
moléculas del fluido es aditiva por pares, es decirN
[I-261
entonces las propiedades termodinámicas del fluido pueden ser expresadas en términos de g(r). Si incluyéramos interacción entre tripletas de partículas, necesitaríamos conocer
g@)(rl,q,r3) para poder obtener l a s propiedades termodinámicas del sistema.
Una forma de obtener g(r) a partir de l a ecuación [I-21], es diferenciarla con respecto a rl. El resultado de esto, utilizando Ia definición de $)(rl,r~,r3) y suponiendo aditividad por pares es:
[I-271
Este resultado es conocido como le ecuación de BGY (iniciales asociadas a Born, Green y Yvon). Para resolver esta ecuación es necesario conocer la función g(3)(r 1 ,r2,r3), la cual, si se calcula de esta forma, quedará en función de g(4)(rl,r2~3,rq), y así sucesivamente. A
este tipo de ecuaciones se les conoce como Jerarquías.
Una forma de resolver este problema es suponer alguna otra relación entre
y de esta forma, la ecuación de BGY puede ser resuelta numéricamente. Sin embargo l a s predicciones sobre las funciones termodinámicas que de ella se obtienen suelen ser poco satisfactorias a densidades altas, debido a que la aproximación por superposición es mala en estas circunstancias. L a ecuación de IOrkwood, que se deduce de una forma similar a la de BGY, introduciendo un factor de acoplamiento en la interacción entre las partículas, y que utiliza la misma aproximación de superposición, presenta también esta limitación.
Por otro lado, se puede deducir una nueva clase de ecuaciones integrales por métodos diferentes a los usados por Kirkwood y BGY. Éstas hacen uso de dos nuevas funciones de correlación, las cuales están relacionadas con g(r). L a primera es la Función de Correlación Total, definida como
[I-291
que mide l a influencia total de la partícula 1 sobre la 2 cuando estin separadas una distancia
1-12. ya que le estamos quitando a g(r) un 1, que corresponde al caso en el que las partículas están descorrelacionadas. L a otra función fué introducida por Ornstein y Zernike (OZ) en 1914, quienes propusieron dividir a la función de correlaci6n total en dos partes, una parte directa y otra indirecta
[I-30]
La Funci6n de Correlación Directa (FCD), c(r12), da el efecto directo de 1 sobre 2 tomando en cuenta que forman parte de un sistema de N partículas; es una función de corto alcance y de estructura más simple que g(r) y h(r). La integral de convolución, que es la parte indirecta, toma en cuenta l a influencia de l a partícula 1 sobre una tercera 3, la cual interacciona directa e indirectamente a travks del resto de las partículas con la partícula 3, este efecto es promediado sobre todas alsposiciones de la partícula 3.
densidad de l a
FCD,
conservando en cada aproximación sÓ10 cierto tipo de diagrama. Estas aproximaciones sonPY
HNC c ( r ) = g ( r ) - l - h g ( r ) - - u(r)
kT
[I-3 13
[I-32]
L a sustitución de estas aproximaciones en la ecuación de Ornstein-Zernike, permite encontrar ecuaciones integrales, cuya resolución numérica da mejores resultados cuando se comparan con resultados experimentales o de computadora, que las ecuaciones de BGY y de Kirkwood.
TEORÍA DE DEBYE-HÜCKEL
Un paso importante en el estudio de la distribución de cargas alrededor de u n ion en soluciljn, fue dado por Debye y Hiickel en 1923. En el modelo que ellos manejaron, se fija uno de los iones en el origen, y se calcula la distribución de carga alrededor de este. El resto de los iones son considerados como cargas puntuales, y el solvente se modcla como un medio continuo con constante dielictrica E. Esta forma de tratar a1 fluido se conoce
como
el Modelo de Ion Puntual (PIM) de la solución electrolítica.
Consideremos primero el potencial electrostAtico en algún punto r de la solución
el promedio canljnico de y ( r ) dejando a la partícula 1 fija en rl es
[I-331
Si tomamos el laplaciano en ambos lados de esta ecuaci6n con respecto a r, obtenemos la ecuación de Poisson
[I-35]
Por otra parte, la distribución de carga cuando hay
más
de una especie de iones, puede ser escrita en tkrminos de la función de distribución radial:donde pi es la concentración de la especie i en el bulto, qi la carga de l a misma, y gil(r,rl) es la función de distribución radial entre la partícula de la especie i, y el ion central. Escribiendo gil(r,rl) en términos del potencial de fuerza media, y considerando que sólo es funcion de Ir - '11, la distancia entre las partículas.
[I-371
La primera aproximación que Debye y Hiickel introdujeron en su modelo, fué considerar al potencial electrostático promedio, como el potencial de fuerza promedio, esto es, considerar a l a energía electrostática como la única energía de interacción entre los iones en l a solución, por lo tanto
y si sustituimos w i l ( r ) en [I-371, obtenemos la ecuación de Poisson-Boltzmann (EPB)
t . 1=1
[ 1-40]
que Debye y Hückel introdujeron en su teoría, fue linealizar el factor de Boltzmann, obteniéndose a primera aproximación
[I-4 11
[ 1-42]
i=l i=l i=l
y si el sistema
es
neutro, el valor absoluto de las cargas positivas y negativas son iguales, por lo tanto, el primer término de la parte derecha de la ecuación vale cero, quedando entonces la ecuación de Poisson-Boltzmann linealizada (EPBL)[I431
[ 1-44]
CAPITULO I1
VIOLACI~N DE
LA
LECS O L U C I ~ N
A
LA EPBLEn este capítulo resolveremos la EPBL para fluidos confinados entre dos placas, un cilindro y una esfera, y para el fluido en el exterior de estos sistemas. Esta ecuación es válida s6l0 en el caso de bajos potenciales, o bajas densidades de carga. Como hemos ya mencionado, cuando se impone que el potencial a la distancia de contacto permanezca constante en ambos lados del electrodo, la LEC se satisface, pues la carga inducida en cada lado del fluido sólo dependerá de la densidad de carga sobre el lado correspondiente del electrodo. En cambio, si suponemos densidad de carga constante sobre los electrodos, la LEC no necesariamente se cumplirá, como se ha demostrado ya en sistemas matemáticamente más cornplejos[351.
Utilizaremos el tratamiento de Stern, en el cual los iones interaccionan con la pared como esferas duras y entre ellos como cargas puntuales; de esta manera, estamos ignorando efectos importantes debidos al tamaño de los iones, que han sido estudiados ya con las teorías de ecuaciones integrales y los mitodos numkicos mencionados anteriormente. Sin embargo, para los propósitos de este trabajo, esta aproximación es suticientcmente buena.
En estos tres casos, dividiremos el espacio en 5 regiones, como se muestra en las figuras (3), (4) y (5), para obtener el potencial electrostático separando las zonas libres de carga de aquellas en donde sí hay.
donde pi, con i igual a
+
o -, es la concentración de l a especie i en el bulto, y gai(r) es la función de distribución radial entre dos partículas de las especies a e i. La especie a es l a especie a la que pertenece el electrodo.Como en los problemas a resolver en éste trabajo tenemos electrodos con cierta simetría, el problema será en los tres casos dependiente de una sola variable. Es decir, pel será sólo función de r, que en el caso de las placas paralelas, es la distancia perpendicular del eje de simetría a cualquier punto en el fluido, y para los electrodos cilíndrico y esfkrico, es la coordenada radial correspondiente a cada caso.
Utilizando l a teoría de Debye-Hiickel, podemos obtener el potencial electrostitico en todo el espacio en los tres casos; resolviendo la EPBL en las zonas donde haya carga, utilizando la geometría correspondiente, y la ecuación de Laplace en las regiones libres de ella.
A.
RegiónV:
r2R+d+a/2Si resolvemos la ecuación [I-401 para las tres diferentes geometrías, con las condiciones de frontera
lim Y 5 ( r ) = O ,
r +=m
Obtenemos, en forma integral: Para las placas
para la esfera
[II-2]
[ 11-31
[II-4a]
[II-4b]
La EPBL en esta región es
[ I I - k ]
ecuación que para las dos placas da
donde
y p 5 (r) = YpHe -~(r-R-d-a/2) 7 [II-6a]
‘€‘pH E Y p ~ ( R + d + d 2 ) .
Para la esfera
R d a / 2 y e-K(r-R-d-a/2)
y, j (r) = sH [II-6b]
r
y para el cilindro
[ I I - ~ c ]
Y c ~ y Y sestán definidos en ~ l a misma forma que Y p ~ , es decir, son los potenciales en la
frontera de las regiones V y IV. En el caso del cilindro, Ko(x) es l a segunda función modificada de Bessel de orden cero, y, x = u .
B. Región IV:R+d+a/2 5 r I R+d
En esta región, dado que está libre de cargas, debemos resolver la ecuación de Laplace, con las condiciones de frontera
Y 4 ( R + d + a / 2 ) = Y 5 ( R + d + a / 3 ) ” f ’ ~ ~ , [ 11-71
[II- 81
para l a esfera
y para el cilindro
resolviendo l a EPBL, obtenemos para el par de placas
y Y p , ( r ) = y p ~ ( 1 - K ( r - R - d - a / 2 ) ) ,
para l a esfera
[II-ga]
[II-gb]
[II-9c]
[11- loa]
[II- lob]
y para el cilindro
[11- 1 Oc]
C. Región 111:
R
5 r 5 R+dEn esta región resolvemos la ecuación de Laplace con l a s condiciones de frontera
Y 4 ( R + d ) = Y 3 ( R + d ) = Y o , [11- 1 11
donde o. es la densidad de carga sobre la superficie externa de las placas, de la esfera y del cilindro, de acuerdo a cada caso.
El potencial electrostático en forma integral para las placas es entonces
o , ( r - R - d ) + J
m
E R+d+al2
para la esfera
[11- 13a]
Ys3(r) = -
""[
E o,(R+
d) 2 ( - - ~ ) + ~ ~ m R + d 1 r r R + d + a / 2 (r-y)ypel(y)dy], [II-l3b]para el cilindro
Yc-(r)=~[o,(R+d)ln(&)+
E Jm R+d+a/2y resolviendola ecuaci6n de Laplace, obtenemos en el caso de l a s placas
Y p 3 ( r ) = ( * - ~ Y p ~ ~ ) ( r - - R - d ) + Y p ~ , E
[ 11- 1 3 4
[ 11- 14a]
para la esfera
[II- 14b] para el cilindro
K1 (K(R
+
d+
a / 2)) x ( R + d + a / ? ) l n ( r ) + I ) - K O ( ~ ( R+
d+
a / 2)) R + d + a / 24x
+-(R
+
d)o, In ED.
Región 11: R-aJ2 I r 2R
Aqu' resolvemos la ecuación de Laplace con l a s condiciones de frontera siguientes
Y2(R) = '4'3(R) E TO, [II- 151
[II- 161
donde oi es l a densidad de carga sobre la superficie interna de las placas, de la esfera y del cilindro, según el caso.
En general, la ecuación integral para las placas paralelas es
para la esfera
+-
E[11- 17b] para el cilindro
y al resolverlas, introduciendo l a forma linealizada para pel, obtenemos
para las placas
[11- 18a]
3 m O ( R + d ) 2
(
1 1) ( R + d + a / 2 ) Y S H +r
"
-E R + d r
[n-
18b] y para el cilindro47t 47t
+-(R
+
d)o, In -E
(
d ) + T R o i 1n(+)
[11- 1 8 ~ 1
E. Región I: O 5 r 5 R - d 2
En esta región. las condiciones de frontera son
En esta ocasión, los resultados en forma integral son, para las placas
[11- 191
[II-201
Por lo tanto, la EPBL para las placas paralelas es
+(
1 - tanh( K(R - a / 2)))e-para l a esfera
para el cilindro
[II-Ea]
[II-22b]
[11-22c]
donde Io(x) es la primera función modificada de Bessel de orden cero.
Las ecuaciones [11-41, [11-91, [11-131, [11-171 y [11-211 se obtuvieron al resolver la ecuación de Poisson sin suponer aún nada acerca de pel, por lo tanto puede decirse que estas ecuaciones son exactas. Para poder resolver l a s integrales que en ellas aparecen, necesitamos conocer pel, i.e., c6mo estin distribuidas las diferentes especies que integran nuestro sistema en el fluido, por lo que en este caso, supondremos que los iones siguen una distribución de Boltzmann que, siguiedo el metodo de Debye y Hückel, luego linealizanos.
LOS potenciales Y H , Yo, (PH y q o e n cada caso, pueden ser relacionados, por lo tanto para las placas
a , + ~ i + [ ~ o ~ - ( d + a / 2 ) + o ; ~ a / 2 ] t a n h ( h - ( R - a / 2 ) )
[II-23a]
qfl =YPH(1+Ka/2+Kd)--, 47cdo0 E
yp~(1+KZi/2i-Kd)-- 47cdo0 E 1
+
- tanh( IC( R - a / 2))T p H = Ka
2
Para l a esfera
o o [ R 2 R o ( d + a / 2 ) - f l ~ 2 ] + o i ( ~ - y R 1 2 )
R o [ l + K ( d + a ) ] - y ( l + ~ R ~ )
donde hemos definido
Ro=R-a/2; Rl=R; R2=R+d; y R3=R+d+a/2. AdemAs
y cuando R tiende a infinito, yse reduce a -rl.
477 ERO
(PsI-r =
-
Para el cilindro
[II-26a]
i'
[II-23b][II-24b]
[II-25b]
[I"c]
donde Ro,Rl,R2 y R3 están definidas en l a misma forma que en el caso de la esfera.
[II-24c]
[ I I - ~ ~ c ] Es necesario notar que cuando R tiende a infinito
Y si hacemos que R tienda a infinito en las ecuaciones [II-23a, b y c], y en las [II-26a, b y c], los potenciales se reducen a
para las placas
o O [ l + ~ ( d + a / 2 ) ] + o i ( l + m / 2 ) 2
+
K ( d+
a)4nd
Y p ~ ~
[
1+
K(d+
a / 2)] - oO -l + ~ a / 2
'PpH = E .1
[II-27a]
[II-28a]
y para el cilindro
4n: o o [ ~ ( d + a / 2 ) + 1 ] + o i ( K a / 2 + 1 )
ycH =
-[
EK 2 + ~ ( d + a ) [II-27c][ I I - ~ ~ c ]
por lo tanto, si d=O, en los tres casos
9-
donde hemos quitado los subindices p,s y c, indicando así que este resultado es el mismo en los tres sistemas. Si en las ecuaciones [11-271 Y [11-281 hacemos que d tienda tambien a infinito, alsexpresiones para los potenciales se reducen a
YH - z o o - 4x Y [ 11- 301
Debemos notar tambien que si o, = oi, se obtiene el resultado anterior sin necesidad
de hacer que el grosor de los electrodos tienda a infinito
Cada uno de los sistemas manejados debe cumplir con l a CEC, que obtendremos a
partir de l a forma linealizada de pel en funcih de l a densidad de carga sobre los electrodos.
Las
expresiones son, para alsplacas paralelaspara el electrodo esf6rico
2 2
[ j
R-al2 rAYsl(r)dr 7+
Jm4x 0 R+d+al?,
1,
[II-3 1 b]R o i + ( R + d ) O , = - r2Yj5(r)dr
y para el cilindro
Donde
o,
y Di son la densidad de carga superficial en las caras externa e interna delelectrodo (placas paralelas, esfera y cilindro) respectivamente.
En
el caso de las placas, únicamente se ha considerado para integrar la mitad del espacio, pues la otra mitad es l aimagen especular de la primera. Resolviendo estas integrales obtenemos:
Para l a s placas
d
.=-- EK(PpH tanh(K(R - a / 2)),P' 4 x [II-32a]
[II-33b]
Donde G'pi y o'po son las integrales interna y externa del sistema respectivamente. De estas ecuaciones y de las ecs [II-27a] y [II-28a], podemos ver que si R tiende a infinito
Y
(o,
+
ai)( 1+
Ka / 2)+
o,Kdd
= -Po 2 + ~ ( a + d ) 7 [II-34a]
[II-35a]
y si o, = oi, las densidades de carga inducidas tanto en el fluido interno como en el externo,
tienden a este valor, independientemente del grosor de la placa. Ademis, si d = O entonces
y si d tiende a infinito tenemos
d =-Go
Po
Y
Pl 1 'd . = - o . [II-37a]
Lo
importante a notar, es que laLEC
sólo se satisface en el límite cuando d y R tienden a infinito en un electrodo cargado asimétricamente.Para el electrodo esférico, sean
S1 .=- EK2 r2Y (r)dr
4xR2 0
Y
por lo tanto, el cumplimiento de la
LEC
requiere que, despuks de resolver las integrales2 R + d + a / 2
( R + d ) d S O = - E [ K ( R + ~ + ~ / ~ ) + ~ ] Y / ~ H .
4x [II-33b]
A
partir de estas expresiones, como los tkrminos que contienen exponenciales tienden a cero al tender R a infinito, y de los resultados obtenidos para Y,H y cps~[, con R tendiendo ;1infinito y d igual a cero; y con d y R tendiendo a infinito, podemos ver que tambiin para una esfera asimktricamente cargada, la
LEC
se satisface sólo cuando el radio y el grosor de ella son muy grandes en comparación con el diámetro de los iones, evidenciando así, la violación de esta condición.Para el cilindro
Y
EKK~(K(R
+
d + a / 2)) ~ K K o ( K ( R+
d + a / 2))con las ecuaciones [II-27c] y [II-28c] y el par anterior, es posible obtener los mismos límites que en los casos anteriores para d y R muy grandes, y encontrar el incumplimiento de la LEC, en éste caso para un electrodo cilíndrico asim6tricamente cargado.
Además, es importante notar que la densidad de carga inducida en cada lado del fluido depende de la densidad de carga sobre ambas paredes del electrodo, lo que indica una correlación entre los dos lados del mismo.
RESULTADOS
Mostramos ahora algunas gráficas de la carga inducida en el fluido en estos tres sistemas.
En
todos los casos, l a densidad de carga sobre los electrodos permanece constante, el diámetro de los iones es a=4.25A, E = 78.5 y la temperatura T=298K. Presentamos los resultados de cada sistema por separado.A . Placas Paralelas
Para poder mostrar gr5ficamente la violación de l a LEC en este sistema, definimos las cantidades
AG,
y AOi de la siguiente maneraY
[ 11- 34a]
[II-35a]
Para establecer la región de validez de la EPBL. mostramos las figuras (6) y (7). En la fig. (6) se tienen las curvas de g para los iones positivos y negativos, medidas con respecto a la superficie de alsplacas, en unidades de didmetros iónicos, para un electrolito 0.05 M, con una densidad de carga sobre las placas de o0 = 0.068C/m2 sobre la cara externa, y sobrc la interior de Gi = -0.0136C/m2; cuando l a distancia entre ellas es igual a 20a. y el grosor de las
positivos, y las otras a las de los negativos. Observamos en esta figura, que las funciones de correlación para los iones positivos localizados en el exterior del sistema tienen valores
negativos, lo que demuestra que con estos parámetros, no es válido usar la EPBL.
La fig. (7) muestra las mismas curvas, ahora para u n electrolito 0.01M, sobre las placas se tiene cs0 = 0.0068C/m2 y Oi = -0.00136C/m2, la distancia entre las placas es igual a 20a. Vemos que la curva de la función de correlación de los iones positivos en el exterior de las placas, para d = 100a, es aún negativa en una pequeña región junto a la placa, pues aunque las densidades de carga son bajas, al serlo tambih la concentración del electrolito, la DCE está lo bastante extendida como para hacer que la correlación sea lo suficientemente fuerte de manera que no se pueda aplicar la EPBL en estas condiciones
En la figura (8), mostramos las funciones de correlación para un electrolito con una concentración de 0 . 0 M y una densidad de carga sobre las placas de cs0 = 0.0068C/m2 y ( 3 i = -0.00136C/m2, cuando la distancia entre las placas es R=lOa, con d=a y d=100a. La (9) tiene los mismos parámetros, salvo la distancia entre las placas, ya que en este caso R=100a. En éstas, las funciones de correlación son siempre positivas, por lo que concluimos que con estos datos l a EPBL funciona bien. Podemos notar en ambas, que la concentración de los contraiones cerca de las placas en la parte externa a ellas, aumenta al aumentar el ancho de las mismas, y prácticamente no se observa ninguna variación con el aumento de la distancia entre ellas. Se puede ver también en las dos figuras, que cuando el grosor de las placas es pequeño, a pesar de que las caras internas están cargadas negativamente, los iones positivos se alejan de ellas y los negativos se acercan, comportamiento debido a la correlación entre los fluidos, ya que al aumentar el grosor de las placas y separar así los tluidos, desaparece este comportamiento, y en la parte interna, aumenta la concentración de los contraiones en las proximidades de las placas.
situación que se consigue a partir de las ecuaciones [11-271 y [11-281. En el caso de las placas paralelas, para un determinado valor de d a una concentración y densidades de c a r p dadas, g
es igual a 1 enmedio de ellas para cualquier valor de r, sin importar cuánto valga R, aunque en general este resultado dependeri de R, d, la concentración de los iones y las densidades de carga sobre las placas. En la figura (10) mostramos las funciones de correlación para o. =
0.0068C/m2 y Oi = -0.00136C/m2, en un electrolito 0.05M, con R= loa, en donde vemos que para d igual a
se consigue que el fluido en el interior de las placas esté descorrelacionado de la placa.
En las gráficas (1 1) y (12) presentamos las curvas de Aopo y AGpi en función de la
mitad de la distancia entre las placas, medida en diámetros iónicos, con diferentes valores de d (d=a, d=lOa, d=100a, y d=1000a), para u n electrolito 0.05M y O.1M respectivamente. En ambas gráficas, las lineas con círculos se refieren a Aow, y las otras a AGpi. El cumplimiento de la LEC, requiere que Aow y AGpi valgan cero, sin embargo en las ecuaciones [11-561 y [II-
571, la densidad de carga inducida en el fluido cuando R tiende a infinito, no tiende a la densidad de carga del lado correspondiente de la placa, a menos que tambikn el grosor de kstas
se haga muy grande. Este comportamiento es el que observamos en las figuras, pues el valor al que convergen las curvas es más cercano a cero a medida que el grosor de las placas aumenta. Podemos ver que el valor de AGpi es siempre negativo cuando la distancia entre las
placas es muy pequeña, pues en estos casos, el electrolito confinado no alcanza a cancelar la carga inducida sobre la cara interna de las placas.
B. Esfera
En este caso, el cumplimiento de la LEC, implica que las expresiones definidas a continuaci6n sean igual a cero
[II-35b]
La región de validez de la EPBL es la misma que en el caso anterior. Las gráficas (13) y (14) presentan curvas de las expresiones anteriores en función del radio de la esfera, para diferentes valores del grosor de ésta. Los parámetros son los mismos que los de las gráficas del par de placas, incluyendo los distintos valores de d que se muestran; las lineas con círculos se refieran a ACT,^ y las otras a ACTsi. En la fig. (13) la concentración es de 0.05 M, y en l a
(14), de 0.1 M Podemos constatar nuevamente la violación de la LEC en este sistema, pues sólo a medida que los valores de d y de R se van haciendo muy grandes, las curvas van tendiendo a cero. Es claro tambi6n la fuerte dependencia con R, pues a pesar de que se tenga un valor grande para d, la violación a la LEC es importante, y de hecho mientras más grande sea d, l a violaci6n es mayor cuando R es pequeña. Además.comparando ambas figuras, es posible notar que a radios pequeños, la violaci6n a la LEC es mlis pronunciada a una mayor concentración para un mismo valor de d, y al aumentar el radio, esta violación es mris notoria a concentraciones menores.
Las funciones de correlación de los iones tienen el mismo comportamicnto que en el caso del par de placas, existe una correlación entre los fluidos localizados dentro y fuera de la esfera, que se manifiesta con una alta concentracion de aniones junto a las paredes dc la esfera en el interior de esta, a pesar de estar cargadas negativamente. Esta concentraci6n va disminuyendo a medida que el grosor de la esfera aumenta.
C. Cilindro
En este caso, las cantidades Aoc0 y ACTci son
[II-35C]
d=1000a). L o s parámetros en estas figuras son los mismos que en los sistemas anteriores, en la fig. (15), la concentración es de 0.05 M, y en la (16), de 0.1 M. Podemos ver que la LEC es sólo satisfecha en el caso en el que d y R son muy grandes, pues no es suticiente con hacer tender el radio del cilindro a infinito, sino que es necesario t a m b i h que el grosor de &te sea muy grande para que
Acto
y AOci converjan a cero.CAPITULO I11
C O R R E L A C I ~ N DE UN FLUIDO CARGADO SEPARADO POR UNA PARED
S O L U C I ~ N A LA E C U A C I ~ N DE POISSON-BOLTZMANN
Utilizando la EPB, mostraremos que para un electrolito asimétrico en presencia de una placa asimétricamente cargada con l a condici6n de densidad de carga constante, la LEC no se satisface, debido a la existencia de una correlaci6n a travks de la pared entre los fluidos localizados a ambos lados de ella. Este fen6meno ha sido estudiado y reportado ya en el caso de una placa inmersa en un electrolito sirnétric0[3~], o para un par de placas paralelas infinitas, bajo la condición de densidad de carga constante e i g u l adentro y &era en presencia de un electrolito asimetrico[31]. Sin embargo, no existen estudios previos en los que se trate un sistema asimktrico tanto en el electrolito como en las densidades de carga. A trav6s de la EPB analizaremos este caso y obtendremos expresiones analíticas en las que se puedan observar- la violaci6n a la LEC y la correlacidn de los fluidos a travtSs de la placa.
Resolveremos la EPBL para un electrolito simktrico, y la EPB para u n sistema formado por u n electrolito y una placa cargada por ambos lados, en los casos en los que el electrolito sea 1:1, 2:2, 1:2 y 2:l.
Con un electrolito asim6trico, se tiene que
en el caso (i), la EPB a resolver es
[111-11
d2Y dY 47t dY dx2
(
d r ) = - r i d x j P e l ,"
por lo tanto
entonces
(g)d(z)
= - I p e , d Y . 47t[III-2]
[ 111-41
Para el caso (ii), se tiene una ecuación similar a la ec. [III-4], y se resuelve de la misma forma.
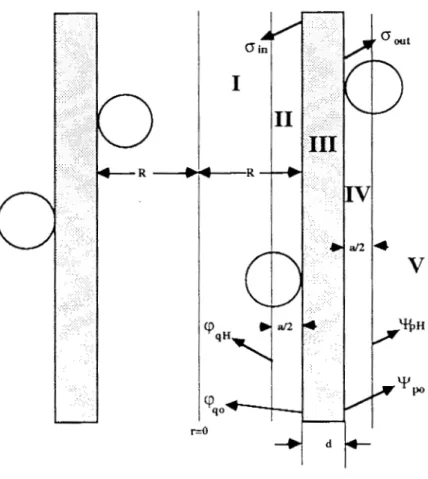
Podemos obtener el potencial electrostático en todas l a s regiones del sistema mostrado en la figura (2), usando la ecuación de Laplace en las zonas libres de cargas (regiones IV, 111 y
L
I
)
,
y la EPB en donde existan iones en solución (regiones V y I).A.
RegiónV:
d+a/2lx<-=La ecuaci6n vaida en esta regi6n es la EPB
con las condiciones de frontera
lim Y5(x) = O ,
x-+-=
En forma integral, el potencial en esta zona es
[ I1 1-51
[ 111-61
[ 111-71
[111-81
A-1) Caso Simétrico
Si
sustituimos l a forma linealizada de Pel, con z+ = 12-1 z, obtenemos",(x) = Y h e - ~ ( x - d - a / 2 ) 9
donde
2 47$
K =-
(=I*
(P; +p-)
E
y si usamos la forma no linealizada de pel
A-2) Caso Asimétrico
Para el caso no lineal asimktrico 1:2
Pi- = 2P-,
con z+ = 1 y z- = -2, obtenemos, de integrar la ecuación [111- 141
por lo tanto
[nI-9]
[III- loa]
[111- 1 11
[ 111- 121
haciendo el cambio de variable
YS (X> = e p y j
(x>
7 y definiendoY
y = \ J .
d3
- (1+
2Cepyhj
1/2 ’ob tenemos
de forma andoga, para el caso 2: 1
p- = 2p+,
con z+ = 2 y z- = - 1, el resul [ado es
donde
Y
B. Región
IV: dlxSd+a/2En esta región, tenemos que resolver la ecuación de Laplace
[rII-14]
[111- 151
[III- 161
[In- lOC]
[ 111- 1 Od]
[ 111- 171
[ 111- 1 81
con las condiciones de frontera
el potencial es entonces:
B-1) Caso Simétrico
Resolviendo la ecuación de Laplace para el caso simétrico linealizado
y para el caso no lineal
Para x=d, Y4(d) Y o donde
y de la ec.[III-9]
En el caso simktrico lineal
y en el caso no lineal
[III-20]
[111-2 11
[111-221
[III-23a]
[III-23b]
[111-241
[111-251
B-2) Caso Asimétrico
Para el caso no lineal asimétrico 1:2
y para el caso 2: 1
además, para el electrolito 1:2
y para el 2: 1
[III-24b]
donde en esta región y en las siguientes, debe tomarse el Yh quc corresponda a cada caso.
C. Región 111: -d<x<d
[III-27]
[111-281
[III-29]
C-1) Caso Simétrico
Con éstas condiciones de frontera, obtenemos para el caso simktrico linealizado
para caso no lineal
[III-30a]
[III-30b]
C-2) Caso Asirnétrico
para el electrolito 1:2
[III-30c] y para el 2: 1
Si x= -d, y definimos Y3(-d)
=
cpo, entonces[III-32]
Si
hacemos 'p0 = Y o en la ec. [111-321, y utilizando la GEC, es claro que la LEC seri satisfecha para cualquier valor de d.Para el caso simétrico lineal, la ecuaci6n anterior queda
en el caso no lineal
[III-33a]
[III-33b]
Para el electrolito asimétrico 1:2
y para el 2: I
'Po(2:I) = Y h
+-
(
1 - e - e p y + 2 e + y h ) l i 2 ( 2d+-1)
---"CJ~. 8 ~ t deB E [III-33d]
D. Región 11: -d-a/2lxS-d
En esta regi6n tenemos l a s condiciones de frontera
Y?(-d) = q o 7 [111-341
[III-35]
D-1) Caso Simétrico
De
la ecuación de Laplace, obtenemos para el electrolito simétrico linealizadoY 2 ( x ) = Y h
[
1 - K(
x-d-- +-[(x-d)o, +(x+d)o,];3 1
[III-37a]y para el no lineal
D-2) Caso Asimétrico
para el asimktrico no lineal 1:2.
+(x+d)Gi]+yh,
[III-37c] y para el 2: 1
Y2(2:1)(x) = I + 2 e e p y h ) 1 ’ 2 ( ~ - d - ~ ) + * [ ( ~ - d ) o d + ( ~ + d ) o i ] + Y h E
[III-37d] En especial, Y2(-d-a/2)
=
(Ph, dondepara el electrolito simétrico no linealizado
[III-39a]
[III-39b]
para el electrolito asim6trico no lineal 1:2
[III-39c] y para el 2: 1
[III-39d]
E. Región I: -c-<xl-d-a/2
Las condiciones de frontera en esta región son
lim Y l ( x ) =
O ,
X+"
y aplicando la ecuaci6n de Poisson-Boltzmann
[III-40]
[111-4 11
[111-421
E-1) Caso Simétrico
Usando la forma linealizada para pel, obtenemos en esta región
usando l a forma no lineal para Pel
I
J
[III-43]
[111-44a]
[III-44b]
E-2) Caso Asimétrico
Resolviendo l a EPB para un electrolito no lineal asimetrico 1:2, usando el mismo procedimiento que en l a región V, obtenemos las ecuaciones
donde
[111-451
donde
[III-44d]
[ HI-461
donde (Ph debe calcularse en cada uno de los casos a travks de [III-43].
Como en el capítulo anterior, es necesario hacer notar que las ecuaciones [III-s], [III- 221, [111-291, [III-36] y [III-42], se obtuvieron al resolver la ecuación de Poisson, y son exactas pues en éstas no se ha supuesto aún ninguna aproximación. Para resolver las integrales involucradas en ellas tenemos que decir algo acerca de la pel, y es aquí cuando empleamos las aproximaciones discutidas ya con anterioridad.
Por otro lado, tenemos que
entonces, si derivamos las ecuaciones [III-36] y [111-421 obtenemos
[ 111-471
[III-48]
y a t a ecuación es precisamente la GEC.
Derivando las ecuaciones para Y 1 y Y 2 en cada caso, y sustituyendo estos resultados en la condici6n de frontera, ec.[ILI-47], podemos obtener otra expresión para los potenciales Yflh y (Ph.
1) Caso Simétrico
y sustituyendo en l a ec. [III-39b]
[III-49a]
[III-501
[III-49b]
2) Caso Asimétrico
Para el caso asimétrico no lineal 1:2, la condición de frontera [III-471 queda
y sustituyendo en l a ec. [ I I I - ~ ~ c ]
( P h = y h + A i 2 d + ” ( i -eePTh)(l+ 2e-epvh eP
para el electrolito 2: 1 no linealizado, la ecuación [III-47] queda
y sustituyendo en l a ec. [III-39d]
linealizada de pel en las integrales que dan la
LEC,
ecs. [i-31 e [i-41, y las expresiones para Y jy Y 1 dadas por las ecs. [111-loa] y [III-44a] respectivamente. De isto, obtenemos las siguientes expresiones para la LEC
h
0.' = "
47c ' 1
[III-53a]
[III-54a]
y si usamos las ecuaciones correspondientes a un fluido cargado sim6trico no linealizado para resolver la ecuación de la LEC, obtenemos
KE
d d n l = "
2nzep
para un electrolito no lineal, 1:2 , la LEC es equivalente a
[ 111-53 b]
[III-54b]
[III-54c]
para un electrolito asimktrico 2:1, los c6lculos son semejantes, y obtenemos las siguientes expresiones para la LEC
algunas manipulaciones matemáticas:
Para el caso simétrico no linealizado, sustituimos los senos hiperbólicos obtenidos en las ecs. de o ’ d y o’i, ecs.[III-53b] y [III-54b], con los de las ecuaciones correspondierltes de
y h y (Ph, ecs. [III-39b] y [III-49b], y obtenemos
[III-55b]
[III-56b]
Por otra parte, si en las ecs. [ I I I - ~ ~ c ] y [ I I I - ~ ~ c ] sustituimos las expresiones que dan o ’ d y o’¡ para el caso 1:2, obtenemos de nuevo las ecuaciones anteriores. Lo mismo sucede si manipulamos de la misma forma las ecs. [III-39d] y [III-49d], correspondientes al caso 2: 1, expresindolas en tirminos de o’d y O ’ i , usando [III-53d] y [III-54d].
Es evidente la dependencia de las densidades de carga inducidas en el fluido con el grosor de la placa en las ecuaciones anteriores, y con la densidad de carga de ambos lados de la misma. Al obtener el límite cuando d tienda a infinito en las expresiones anteriores, veremos que nuestros resultados satisfacen la LEC cuando el ancho de la placa es m u y grande con respecto a l d i h e t r o i6nico a.
Si en las ecuaciones [III-55a] y [III-56a] hacemos Gi = od =
o,
obtenemos[III-57b]
es decir, las densidades de carga inducidas en cada lado del fluido son iguales a las del correspondiente lado de la placa, i.e., la LEC es satisfecha, pues en este caso el sistema es simétrico, y (Ph = y/h. Por otra parte, si sumamos las ecs. [III-Sa] con [III-56a], y [III-55b] con [III-56b], podemos comprobar que se cumple la GEC
Si en las expresiones para od' y ~ i ' (ecs. [III-55a,b] y [III-56a,b]) el grosor de la placa
se hace igual a cero, (?h = y h . , y entonces
y además, si d tiende a infinito,
[111-591
Por lo tanto, la LEC es sólo satisfecha para grandes valores de d con respecto al diámetro de los iones.
RESULTADOS
diámetro de los iones de 4.25 A.
En l a fig. (17) mostramos el negativo de l a densidad de carga.
-o*
izquierda y derecha para los casos no linealizados de los electrolitos 1:1, 2:2, 1:2 y 2: 1, en función del grosor de la placa, en unidades de diámetros iónicos, donde el fluido es Iz-lp- =0.01 M, Cidereclla = 0.68C/m2 y G k q u i e r h = -0.136 C/m2. Es claro que las densidades de carga inducidas dependen del ancho de la placa. Podemos ver que la LEC es válida en todos los sistemas sólo cuando el ancho de la placa es muy grande con respecto al diámetro de los iones. En todos los casos, cuando el ancho de la placa es igual a cero, CT’i es igual a o’d e igual a (od+oi)/2. En la fig. (18) se muestran las mismas curvas, pero ahora para un fluido Iz-lp- = 0.97 1 M. El comportamiento observado es el mismo. La violación de la LEC es ligeramente menor en los casos 1:l y 2:l.En estas gráficas podemos observar tambikn el gran parecido existente entre el tluidos 1:l y el 2: 1, así como entre el 2:2 y el 1:2. Las curvas de éstos estlln pricticamente una encima de l a otra. Esto significa que no se perciben efectos provocados por la diferencia de carga de los cationes. Algo semejante se observa en l a fig. (19), sólo que en este caso, las curvas que coinciden son las de los fluidos 2: 1 y 3:2, y la 1 :3 con la 1: l . Las densidades de carga en la placa son oderecha = 0.-0.012C/m 2 y Crizquierh =
-0.272
Urn’; y Iz-lp- =().O1 M. La violación de la LEC es ahora ligeramente menor en los fluidos 2:2 y 2: 1. En este caso, es la diferencia de carga entre los aniones la que resulta irrelevante. Esto significa que el comportamiento del fluido es dominado por el efecto de la carga de los contraiones de la placa, sin importar cualquier diferencia entre los coiones.Como hemos mencionado, la LEC es satisfecha cuando Odcrecha = CJizquierda,
independientemente del grosor de la placa. En las figs. (20) y (2 I ) , podemos ver de nuevo cl negativo de la densidad de carga, -o’ izquierda y derecha para los casos no linealizados de los electrolitos 1:1, 2:2, 1:2 y 2:1, con u n fluido Iz-lp- =0.01 M. En la fig.(20), oderecha = 0.012 C / m * y o i z q u i e r d a = 0.272 C/m2, mientras que en la fig. (21), Oderccha = 0.250 C/m2 manteniendo los otros pardmetros iguales que en la anterior grifica. En &as podemos ver que si disminuye l a diferencia entre las densidades de carga derecha e izquierda, el intervalo de validez de la LEC se ve aumentado, situación acorde con los resultados deducidos
El perfil de concentración en cada lado de la placa es función de la densidad de carga de ambas supefkies, como hemos visto anteriormente, y como se muestra en las figuras
(22)
-(29).
Las gráficas(22), (23), (24)
y (25) están expresadas en unidades de radios iónicos, y fueron hechas para un electrolito tal que IZ-lp-=0.01
M,
Gderecha = 0.68Um2, oizquierda =-0.136
C/m*, y para d igual a a/2 y 2500a .En
éstas no se representó el grosor de la placa. La (22) y la(23)
corresponden a los aniones y la (24) y(25)
al perfil de concentración de los cationes. Los mismos parámetros se manejan en las curvas(26)
a la(29),
a excepción de la concentración, pues en estos casos,Iz-lp-
=0.97
1M.
Si el ancho de la placa es igual a cero, el perfil de concentración es el mismo en ambos lados de ésta, pero si el grosor se ve aumentado, la concentración de los iones negativos disminuye en el lado de la placa cargado negativamente, sin embargo, la concentración de éstos es mayor que 1 para una pared delgada. Este comportamiento "anómalo", señalado t a m b i h en el capítulo anterior, muestra la correlación entre los fluidos a través de la placa, pues a medida que ésta va haciéndose más ancha, la densidad de aniones junto al lado negativo disminuye, como se observa en la gráfica(23), donde d=2500a.
Un
comportamiento similar es el que muestran los cationes para placas delgadas, pues existe una baja concentración de éstos junto a la placa negativa en la fig.(24)
donde 2d = a, misma que aumenta al hacer el grosor de la pared m u y grande, como se muestra en la fig.
(25).
Se tiene el mismo comportamiento en las grificas (26) - (29), realizadas con diferente concentración.Las curvas correspondientes a los iones negativos para los casos 1: 1 y
2:l
están prácticamente una sobre la otra, lo mismo que las curvas para los casos 2:2 y 1:2, cuando d=a/2,
en las diferentes concentraciones de las figs.(22)
y(26).
Vemos tambi6n que la concentración de los aniones junto a la pared en los casos2:2
y 1:2 es mayor que en los otros dos, pues la doble carga de los aniones hace que sean atraidos por la pared con más fuerza, pero esta concentración disminuye más rapido, pues en ambas hay menos aniones que en los sitemas 1:l y2:
1. Para d=2500a, figs. (23) y(27),
sólo las curvas de concentración en el lado cargado positivamente se comportan de esta forma, pues en el lado izquierdo, podemos distinguir perfectamente los cuatro perfiles, y el caso 1:2 es la curva m i s baja, pues la doble carga del anión, y la existencia de una mayor cantidad de iones positivos que negativos, hace que prácticamente no haya de estos últimos junto a la pared de este lado.correspondientes a
los
fluidos 1 2 con 1:1, y 2: 1 con 3:2 respectivamente; y en el otro lado, se pueden distiguir las cuatro curvas.Todas estas observaciones ponen de manifiesto que el comportamiento de los contraiones en la placa es independiente de la carga de los coiones involucrados en el fluido. Cuando la placa es delgada, como la densidad de carga total de esta es positiva, la distribucion de los aniones junto a la pared da curvas similares para los casos ya mencionados, mientras que en estas mismas circunstancias, las distribuciones de los coiones, o sea, los cationes. son diferentes en cada uno de los sistemas.
COMENTARIOS
Y
CONCLUSIONES
Hemos resuelto la EPBL para un fluido en tres casos diferentes, en presencia de una macroparticula asimétricarnente cargada, formada por una placa infinita, por un par de placas paralelas infinitas, por una esfera, y por un cilindro de gran longitud, considerando como una variable el grosor de estas macropartículas, y tomando en cuenta al líquido localizado fuera y dentro de las mismas, o a l a derecha e izquierda en el caso de la placa.
Además, se resolvió la EPB no lineal, para cuando el electrodo es una placa infinita, de grosor dado, cargada asimétricamente, inmersa en un electrolito simktrico (1: 1 y 2:Z), y no simétrico (1:Z y 2: 1).
De los resultados obtenidos a l tomar los límites requeridos en cada uno de los casos resueltos y de l a s gráficas mostradas, es evidente en primer lugar, que una LEC a densidad de carga constante sobre los electrodos, no será satisfecha en general, aún en este modelo de iones puntuales. En todos los sistemas resueltos, se observa que para el cumplimiento dc la LEC no es suficiente con que los electrodos sean infinitamente anchos, pues la violación de esta condición no desaparece cuando d tiende a infinito, ya que existc tambih una dependencia con la variable R, que es el radio de los electrodos cilíndrico y esferico, y l a mitad de la distancia entre el par de placas. Sólo si R tiende tambikn a infinito, puede satisfacerse la LEC. Obviamente en el caso de una sola placa, el cumplimiento de l a LEC se logra al hacer que el grosor de l a misma tienda a infinito, y en este caso es claro que la violación de esta condición no tiene que ver con el confinamiento del fluido, sino con la correlación a trav6s de la pared de los fluidos localizados a ambos lados de la placa.