, México a de 20
INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY
PRESENTE.-Por medio de la presente hago constar que soy autor y titular de la obra denominada
, en los sucesivo LA O B R A , en virtud de lo cual autorizo a el Instituto Tecnológico y de Estudios Superiores de Monterrey (EL INSTITUTO) para que efectúe la divulgación, publicación, comunicación pública, distribución, distribución pública y reproducción, así como la digitalización de la misma, con fines académicos o propios al objeto de EL INSTITUTO, dentro del círculo de la comunidad del Tecnológico de Monterrey.
El Instituto se compromete a respetar en todo momento mi autoría y a otorgarme el crédito correspondiente en todas las actividades mencionadas anteriormente de la obra.
Implemtentation of Differential Evolution Algorithm to the
Wavelength Converters Placement Problem in a Multichannel
Optical NetworkEdición Única
Title
Implemtentation of Differential Evolution Algorithm to the
Wavelength Converters Placement Problem in a
Multichannel Optical NetworkEdición Única
Authors
Fernando Lezama Cruzvillasante
Affiliation
Tecnológico de Monterrey, Campus Monterrey
Issue Date
20110501
Item type
Tesis
Rights
Open Access
Downloaded
18Jan2017 14:09:09
I n s t i t u t o T e c n o l ó g i c o y d e E s t u d i o s S u p e r i o r e s d e M o n t e r r e y
C a m p u s M o n t e r r e y
I M P L E M E N T A T I O N O F D I F F E R E N T I A L E V O L U T I O N
A L G O R I T H M T O T H E W A V E L E N G T H C O N V E R T E R S
P L A C E M E N T P R O B L E M I N A M U L T I C H A N N E L
O P T I C A L N E T W O R K
by
I n g . F e r n a n d o L e z a m a C r u z v i l l a s a n t e
T h e s i s
Presented to the Program of Graduate Studies in Information Technologies and Electronics In partial fulfillment of the requirements for the degree of
M a s t e r of S c i e n c e
c
Instituto Tecnológico y de Estudios Superiores de Monterrey
C a m p u s M o n t e r r e y
División of I n f o r m a t i o n Technologies a n d E l e c t r o n i c s
P r o g r a m of Gradúate Studies
The members of the committee recommend that the present thesis by Fernando Lezama Cruzvillasante be acccpted in partial fulfillrncnt of the requirements for the academic degree
of Master of Science, in:
Electronic Engineering (Telecommunications)
I M P L E M E N T A T I O N O F D I F F E R E N T I A L E V O L U T I O N
A L G O R I T H M T O T H E W A V E L E N G T H C O N V E R T E R S
P L A C E M E N T P R O B L E M I N A M U L T I C H A N N E L
O P T I C A L N E T W O R K
by
Ing. Fernando L e z a m a C r u z v i l l a s a n t e
Thesis
Presented to the P r o g r a m of G r a d u a t e Studies i n Information Technologies and E l e c t r o n i c s i n p a r t i a l fulfillment to o b t a i n the degree of
M a s t e r of Science
in
E l e c t r o n i c E n g i n e e r i n g ( T e l e c o m m u n i c a t i o n s )
I n s t i t u t o Tecnológico y de E s t u d i o s Superiores de M o n t e r r e y
C a m p u s M o n t e r r e y
Dedication
To my dear family, my parents M. Cristina S. Cruz Villasante Barrita and Mariano Lezama
Olguin, and my brother Alejandro and sister Mariana.
For their love, patience, understanding and support.
Acknowledgment
To my Thesis Advisor Dr. Gerardo Antonio Castańon Ávila, for his guidance, friendship, and
support throughout this work.
To my thesis committee members, Dr. Gabriel Campuzano Trevińo and Dr. Jose Ramón
Rodriguez Cruz, for their valuable comments, readiness, and strategic visión applied to this
research.
To the management of C O N A C Y T and I T E S M scholarships for sponsoring me throughout
my graduate studies.
To all my friends, for their valuable help, good will and friendship.
To my lovely family, for the continuous love and affection.
M y special thanks to God for his endless love.
F E R N A N D O L E Z A M A C R U Z Y I L L A S A N T E
Instituto Tecnológico y de Estudios Superiores de Monterrey
I M P L E M E N T A T I O N OF D I F F E R E N T I A L E V O L U T I O N
A L G O R I T H M T O T H E W A V E L E N G T H C O N V E R T E R S
P L A C E M E N T P R O B L E M IN A M U L T I C H A N N E L
O P T I C A L N E T W O R K
Fernando Lezama Cruzvillasante
Instituto Tecnológico y de Estudios Superiores de Monterrey, 2011
Thesis Advisor: Dr. Gerardo Antonio Castańon Ávila
The wavelength converters placement in an optical communication network is wellknown
that belong to the NPcomplete problem. So far this type of problem is solved using strate
gies known as heuristics, or by applying optimization methods. In this research we study a
novel evolutionary algorithm called differential evolution (DE), and we propose the applica¬
tion of D E to the wavelength converters placement problem. D E is a very simple but very
powerful stochastic global optimizer for a continuous search domain, which represents a very
complex process of evolution. A comparative study has shown that D E generally outperforms
other evolutionary algorithms in terms of convergence speed and quality of solutions. The
major advantage of the D E algorithm rests in the fact that it does not need to build up a
search tree or to create auxiliary graphs. This research present experiments that demonstrate
the effectiveness and efficiency of the proposed algorithm. The computed results show that
only a small population is needed to obtain the optimal solution for the placement of wave¬
length converters in an arbitrary network. In conclusion, D E is an attractive tool for solving
wavelength converter placement problem due to optimization speed, and because it is not
required to change many parameters for handling, outperforming other algorithms in the field
Contents
Abstract vii
List of Tables x
List of Figures xi
Chapter 1 INTRODUCTION 1
1.1 Problem Statement . . . 2
1.2 Objectives . . . 2
1.3 Justification . . . 3
1.4 Scope and Limitations . . . 4
Chapter 2 BACKGROUND 5 2.1 Optical Networks . . . 5
2.1.1 Wavelength Division Multiplexing (WDM) . . . 7
2.1.2 Blocking Probability . . . 9
2.1.3 Wavelength Converters Placement . . . 10
2.2 Optimization . . . 12
2.2.1 Evolutionary Computation . . . 13
2.2.2 Differential Evolution (DE) . . . 13
Chapter 3 DIFFERENTIAL EVOLUTION OPTIMIZATION APPLIED TO THE WAVELENGTH CONVERTERS PLACEMENT PROBLEM IN ALL OPTICAL NETWORKS 15 3.1 Introduction . . . 15
3.3 Differential Evolution (DE) Algorithm . . . 21
3.3.1 Mutation Operator . . . 22
3.3.2 Recombination and Selection Operators . . . 22
3.3.3 Binary-DE Operators . . . 23
3.3.4 Pseudocode of the DE Algorithm . . . 24
3.4 Illustrative Example . . . 25
3.5 Numerical Results . . . 28
3.6 Conclusions . . . 39
Chapter 4 FURTHER WORK 43
Bibliography 45
List of Tables
3.1 Shortest paths 5-node network . . . 25
3.2 Link load 5-node network . . . 26
3.3 Shortest paths for NSFNet . . . 30
3.4 Shortest paths for EON . . . 31
3.5 Optimal states NSFNet . . . 32
3.6 PSO vs. DE NSFNet . . . 34
3.7 Optimal states EON . . . 36
3.8 Exhaustive searching method on USA network . . . 39
3.9 Optimal states USANet . . . 41
List of Figures
2.1 Trends in optical transmission system capacity. . . 6
3.1 5 nodes Network. . . 25
3.2 Illustration of Differential Evolution simulation. . . 28
3.3 NSF network topology, 14 nodes, 21 links. . . 29
3.4 EON topology, 19 nodes, 39 links. . . 29
3.5 USA network topology, 40 nodes, 58 links. . . 29
3.6 Japan network topology, 40 nodes, 65 Links. . . 29
3.7 Number of iterations vs. Number of wavelength converters withRC = 0.7 and M = 1.5 for NSFNetwork. . . 33
3.8 Efficiency vs. Number of wavelength converters with RC = 0.7 and M = 1.5 for NSFNetwork. . . 33
3.9 Number of iterations vs. Number of wavelength converters withRC = 0.7 and N P = 7 for NSFNetwork . . . 35
3.10 Number of iterations vs. Number of wavelength converters with M = 1.5 and N P = 7 for NSFNetwork. . . 35
3.11 Number of iterations vs. number of wavelength converters with RC = 0.7 and M = 1.5 for EON. . . 37
3.12 Number of iterations vs. number of wavelength converters with RC = 0.7 and N P = 9 for EON. . . 37
Chapter 1
INTRODUCTION
At present, it is well known that traffic in telecommunication is developing almost
ex-ponentially worldwide. This development will result in an increase of higher bandwidth and
transmission speed. The force that can cope with this exponential growth is led by optical
systems which have superior characteristics over other systems, in terms of bandwidth (in the
order of terabits), lower signal attenuation, distortion, power consumption, miniaturization
and integration, among other. In this context the most promising technology to address the
aforementioned growth and demand is possible by optical network systems with wavelength
division multiplexing (WDM) technology [1]. WDM technologies have led to substantial
research which has eventually point out the modifications required in the optical network
architectures to achieve their full potential.
In a simple definition, optimization consist in find the best solution to a determinate
problem. However, the problems NP-complete cannot be resolve in a deterministic way. It is
here when Heuristics become fundamentals.
In this context, the wavelength converter placement [2] is of paramount importance in
optical networks optimization. This kind of problems is well known to belong to the class of
NP-complete problem [3], which means that the number of possible solutions grow up in an
exponential manner when the network gets bigger.
Throughout this investigation, an evolutionary algorithm called differential evolution
(DE) will be applied to a problem related to optical networks, particularly the wavelength
converters placement, in search for favorable results and comparing these with other
method-ologies in order to validate them.
The DE algorithm is an algorithm developed by K. R. Price and Storn in 1995 [4] for
parameters that can be applied to different problems.
Particulary, Its really interesting to see how this two trends can be merged to achieve
a common goal, in one way the increasing demand for communication traffic which will be
covered by the multichannel optical networks, but the problems of design and optimization
of these networks will be resolved by heuristics based on evolutionary computation, so there
is a direct dependence of both trends, growth in demand in optical communication networks
and the development of tools for solving problems caused by this growth.
1.1
Problem Statement
The problem of this thesis consist on the application of the DE algorithm to the
wave-length converters placement problem in a wavewave-length routing optical network.
In this thesis we show that DE produce excellent results finding the optimal solution in
arbitrary networks.
1.2
Objectives
The main objective of this research involves the application of an evolutionary algorithm,
namely differential evolution (DE), to the wavelength converters placement problem in a
multi-channel optical network.
Particularly objectives are intended to cover the following points:
• Apply the differential evolution algorithm (DE) to the wavelength converters placement problem in a multichannel optical network.
• Determine the minimal number of wavelength converters and their placement suitable for optimal performance (minimal blocking probability) in a multichannel optical network
using the DE algorithm.
1.3
Justification
In recent years the field of telecommunications has experienced impressive importance,
mainly due to the popularity of the internet. This has led to find alternatives to satisfy the
current consumer demand, which consist in high bandwidth and large transmission distances.
Here is where optical networks play an important role because the development is the best
solution to address the imminent growth of data traffic. However, the implementation of
optical networks result in various problems, for example, network optimization and design,
network planning, among many, because their characteristics (components, architecture, etc)
can be modified so that the network is capable of provide all the needs users require, but
without increasing the cost to levels unaffordable for buyers.
In this research we explore the application of an evolutionary algorithm to one well-known
problem in the design of optical networks, this is the placement of wavelength converters in
multichannel optical network. The current work has an impact not only to society but also
in the field of telecommunications in general, as it present an alternative to solve problems
currently interest in optical telecommunications networks.
Solving the wavelength converters placement problem effectively reduces the blocking
probability of the network, which is of much value when designing and implementing a
telecom-munications network, because a low blocking probability indicates that the network is available
for communication. The problem of wavelength converters placement is critical because
wave-length converters not only decrease the blocking probability when placed in specific network
nodes, but also impact the cost of the network, because it is known that wavelength converters
have a relative expensive price in the market.
In addition, it is fundamental the application of the DE algorithm to well known NP
problems in the telecommunications field, since these NP problems are already solved by other
heuristics, but probably not to optimality, then the idea is to compare research results and
show that this DE algorithm can provide satisfactory or better results than other algorithms
reported in the literature. Indeed, we compare our results using DE algorithm with other
1.4
Scope and Limitations
In the present investigation we implement of an evolutionary algorithm called differential
evolution (DE) to the wavelength converters placement in multi-channel optical networks.
This algorithm could be applied to any arbitrary networks, however, for comparative purposes
with existing literature, we apply it to well-known networks topologies like NSFNet (National
Science Foundation Network), EON (Europe Optical Network), USA and Japan networks.
The analysis is limited to network simulation, since the implementation of network
topol-ogy, and analysis of real networks is too complex for this application. During the simulations,
we execute a large number of numerical calculations, therefore considerations have to be
im-plemented to simplify the testing. As stated above the study of the algorithm applied to a
Chapter 2
BACKGROUND
2.1
Optical Networks
The development of optical systems started in 1960 with the invention of the laser [5]
published by T.H. Maiman. Because of this invention, the researchers focused their attention
on developing systems that take advantage of the use of laser, and this meant the beginning
of the development of optical systems.
In 1966 K. C. Kao and G. A. Hockham suggested that optical fiber is the best option,
to transmit an optical signal, in an article published in the IEEE. In that year laid the
foundations of what optical fibers are and how such a signal can propagate through this. This
study can be found in [6]. The optical fibers are able to guide light in a manner similar to
electrical cable systems guided the electrons. Due to this contribution K.C. Kao was awarded
the Nobel price of physics in 2009.
At first the losses in optical fibers were very high, about 1000 dB/km. But the
develop-ment that occurred in 1970 gave much impetus to these systems, making optical fiber able to
reduce the attenuation below of 20 dB/km. Thereafter began a development with two trends,
first commercial systems were developed, and at the same time investigation to improve and
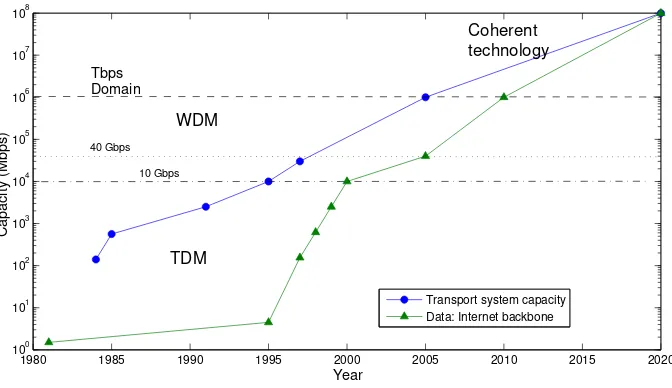
optimize optical systems. Figure 2.1 shows the evolution of transport and service bit rates
capacity of optical transmission systems.
According to Michael J. OMahony [7] two thrusts are driving separate optical network
infrastructure models, namely the need by nations to provide a ubiquitous network
infras-tructure to support all the future services and telecommunication needs of residential and
business users and increasing demands by the scientific community for networks to support
1980 1985 1990 1995 2000 2005 2010 2015 2020 100 101 102 103 104 105 106 107 108 Year Capacity (Mbps)
Transport system capacity Data: Internet backbone
[image:19.612.154.490.94.288.2]TDM 10 Gbps 40 Gbps WDM Tbps Domain Coherent technology
Figure 2.1: Trends in optical transmission system capacity.
from the Figure 2.1 a breakthrough in the capacity around the year 1995 because was around
that year when the WDM (wavelength division multiplexing) technology began to appear and
represented an increase in communication capacity of great importance. Such technology will
be discuss in later chapters.
At present there is an exponential growth in Internet traffic, which results in networks
having problems to support the demand that is requested by users, and requires that
re-searchers and designers of telecommunication systems search for viable and feasible
alterna-tives in order to support this demand, generating systems that provide the bandwidth required
and the desired transmission speed.
Optical networks are systems that promise many benefits, as these are networks based
on large-capacity optical technologies and components that provide routing protection and
restoration at the wavelength level. The success of optical networking technology is due
to WDM which gave additional capacity on existing optical fibers. It is clear that these
technologies offer many advantages compared to electrical networks, and have also evolved,
which is reflected in their development towards even more comprehensive systems. According
to the physical technology employed, the networks can be classified into three generations.
The first generation is based on copper cables or microwave technologies. In the second,
we introduced the use of optical fiber links, but is limited by electronic speeds (a few Gb/s)
entirely) based on WDM, and where both the transmission and the switching of data is done
entirely in the optical domain.
2.1.1 Wavelength Division Multiplexing (WDM)
The most promising technology to address the aforementioned growth and demand
sus-tained by optical network systems is wavelength division multiplexing (WDM) technology. In
principle, the capacity of optical communication systems can exceed 10 Tb/s because of the
large bandwidth associated to optical fiber. In spite of this commercial infrastructure, bit rate
was limited to 10 Gb/s or less until 1995, due to the limitations imposed by the dispersive
and nonlinear effects and by the speed of electronic components [8].
In order to get more transmission capacity, multiple optical channels can be send over
the same fiber using channel multiplexing and this has provide a way to extent the capacity
beyond 1 Tb/s. Channel multiplexing can be done in time and frequency, and in an optical
context it is common to refer to the two techniques as optical time division multiplexing
(OTDM) and WDM.
The concept of WDM has been pursued since the first commercial lightwave system
became available in 1980. In its simplest form, WDM was used to transmit two channels in
different transmission windows of an optical fiber [8]. However, it was during the decade of
the 1990s that WDM systems were developed most aggressively [9, 10]. Commercial WDM
systems first appeared around 1995, and their total capacity exceeded 1.6 Tb/s by the year
2000.
It is therefore important to look a little deeper about WDM systems, to identify the
potential components that generated transmission limitations and are key components to
further enhance the development of optical communications.
In the book Fiber-optic communication systems by Agrawal [8], we can find a detailed
description of the components of a WDM system, however we give a brief description of these:
• Tunable Optical Filters: The role of a tunable optical filter in a WDM system is to select a desired channel at the receiver. The filter bandwidth must be large enough to
trans-mit the desired channel but, at the same time, small enough to block the neighboring
• Multiplexers and Demultiplexers: Are the essential components of a WDM system. De-multiplexers require a wavelength-selective mechanism and can be classified into two
broad categories. Diffraction-based demultiplexers and Interference-based
demultiplex-ers. In both cases, the same device can be used as a multiplexer or a demultiplexer,
depending on the direction of propagation, because of the inherent reciprocity of optical
waves in dielectric media.
• AddDrop Multiplexers: Are needed for wide-area and metro-area networks in which one or more channels need to be dropped or added while preserving the integrity of other
channels. The demultiplexer separates all channels, optical switches drop, add, or pass
individual channels, and the multiplexer combines the entire signal back again.
• Star Couplers: the function of this is to combine the optical signals entering from its multiple input ports and divide it equally among its output ports. Star couplers do not
contain wavelength-selective elements, as they do not attempt to separate individual
channels. The number of input and output ports need not be the same.
• Wavelength Routers: An important WDM component is an N∗N wavelength router, a device that combines the functionality of a star coupler with multiplexing and
demul-tiplexing operations. The WDM signals entering fromN input ports are demultiplexed into individual channels and directed toward the N output ports of the router in such a way that the WDM signal at each port is composed of channels entering at different
input ports. This operation results in a cyclic form of demultiplexing. Such a device is
an example of a passive router since its use does not involve any active element
requir-ing electrical power. It is also called a static router since the routing topology is not
dynamically reconfigurable. Despite its static nature, such a WDM device has many
potential applications in WDM networks.
• Optical Cross-Connects: wide-area WDM networks requires a dynamic wavelength rout-ing scheme that can reconfigure the network while maintainrout-ing its nonblockrout-ing
(trans-parent) nature. This functionality is provided by an optical cross-connect (OXC) which
performs the same function as that provided by electronic digital switches in telephone
networks. The use of dynamic routing also solves the problem of a limited number of
• Wavelength Converters:A wavelength converter is a device capable of changing a wave-length at its input to a different wavewave-length at its output without changing the data
content of the signal
• WDM Transmitters and Receivers: Are the basic component in a telecommunication system.
All these components are interconnected to result in the WDM systems of optical
net-works.
2.1.2 Blocking Probability
In the third generation networks, which are all optical, WDM technology is used to
transmit different wavelengths in a fiber. To send information from one node to other node
in the network the signal has to pass through several links (fiber) and nodes (routers). It is
possible that some lightpaths (source-destination light circuits) can be created using the same
wavelength through different links. This creates a problem of routing, with the constraint
that in WDM systems without wavelength conversion capability the same wavelengths can
not share the same link simultaneously. Eliminating wavelength conversion capability reduces
the cost of the switch; however it may lead to reduced network efficiency because the same
wavelength must be available on each link of a route for a call to be established. For example,
there may be a route which has a wavelength available on each of its links but they may not
be the same wavelength, thereby causing the call to be rejected. The performance metric to
measure the non-availability of the resources to establish a communication is typically the call
blocking probability. This is a very important parameter in the network, since the blocking
probability is related largely to the efficiency of the network.
Many studies have been performed to calculate the blocking probability within an
op-tical network, so we can briefly mention two of them. A. Birman who in 1996, published a
paper about the calculation of the blocking probability in all-optical network. His study was
conducted using a generalized scheme of load reduction in the net in [11].
The paper of A. Birman has been a reference in many publications, and may be one
of the first approaches to reduce blocking probability and calculation of it in an optical
the blocking probability for optical networks with limited range wavelength converters. They
took the model proposed by Birman and extended for networks with limited range wavelength
converters in [12].
In the paper published by Tripathi and Sivarajan, we can observe how models emerge to
study more complex problems, this time related to optical networks and wavelength
convert-ers, which reflects the interest of researchers to look into the optimization of optical networks.
Their main contribution was to derive an analytic expression for calculating the blocking
probability in networks with composite routes.
Finally one of the most interesting work in terms of blocking probability in an optical
network with wavelength converters were those proposed by Suixiang Gao et al in 2003 [13],
which found an optimization model of the wavelength converter placement to minimize the
blocking probability.
This work consider the success probability on the network as a geometric mean of the
success probabilities between links, and can be extended to include the contributions of
wave-length converters in the network, which results in an optimization of blocking within the
network, since this probability is minimized.
2.1.3 Wavelength Converters Placement
A wavelength converter is a device capable of changing a wavelength at its input to a
different wavelength at its output without changing the data content of the signal. During
the 90’s researchers developed several schemes for wavelength converters.
As mentioned in [8] pages; there are four configurations considered the most important.
The first one is based on an optoelectronic regenerator, the second is based on the saturation
gain of a semiconductor laser amplifier (SLA), the third is based on the phase modulation in
a SLA, and the fourth is based on a nonlinear effect called 4-wave mixing (FWM ) of a SLA.
These technologies have been changing and improving. One recent publication is the
one by Vikrant Lal [14] in 2007, which describes the design and demonstration of advanced
40-Gb/s return-to-zero (RZ) tunable all-optical wavelength converter technologies for use in
packet-switched optical networks. Other work done by Yong Liuet al [15] in 2009, presents
a high-speed optical wavelength converter that is capable of converting the data to the same
is demonstrated at a bit-rate of 40 Gb/s. This kind of work shows that the evolution of
wavelength converters is latent, and that researchers and telecommunication companies are
very interested in develop them.
A point of considerable importance is the fact that these devices are expensive in the
market, this is the reason why researchers are interested on improving the performance and
also to decrease its cost. Wavelength converters improve network performance because help
to decrease the blocking probability at expenses of increase the cost of the network.
In the wavelengths routed optical networks (WRON), the wavelength should be assigned
to all the lightpath along its route. and those who share one or more fiber links through their
routes should be assigned to different wavelengths.This is known as the wavelength continuity
constraint.
This constraint has no impact if the network has wavelength conversion capability. The
wavelength converters transfer a signal from a specific channel to another, without loss of
information. This is the reason why a lightpath may use different wavelengths through its
route source-destination. Networks with this characteristic are equivalent to traditional circuit
switched networks. Besides the wavelengths converters can be of two types: optoelectronic
type and all-optical type.
However, if you want to equip the network with a limited number of wavelength converters
(due to their hight cost), the problem becomes in where to put them in order to get the highest
efficiency. This kind of problem it is well-know to belong to the class of the NP-complete
problems, because the number of possible combinations rise in an exponential way when the
network is large.
For this reason it is not possible to make a deterministic analysis that assure the optimal
solution to the problem, and is when the heuristics acquire great significance in
optimiza-tion, being the evolutionary algorithms the most powerful tools in this context, due that DE
algorithm are multi-objective oriented.
One of the works that combine wavelength converters placement and an evolutionary
algorithm is there by Choon Fang Teoet al in collaboration with Dr. Gerardo Casta˜non [16]
in 2005. They used an evolutionary algorithm called particle swarm optimization (PSO) in
the solution of this problem. This was the first time that PSO was used in the wavelength
The use of this heuristics makes that the space of research become big enough, let us to
find different approaches for a particularly problem, getting several results according to the
schema.
2.2
Optimization
The main objective of any optimization technique is to find the global optimum (for
example, the best solution) of a problem. But not all of those optimization techniques can
guarantee convergence to the global optimum. Mathematically, the problem can be expressed
as follows:
minimize f(X) subject to (2.1)
gi(X)≤0; for i= 1, ..., p
hj(X) = 0; forj = 1, ..., n
where:
X: is the solution vector
f(X) : is the objective function
gi: is the set of inequality equation
hj : is the set of equality equations
It is interesting to see how a particular branch of mathematics can be applied to different
problems, as in this case, where it is attractive to bring the math programming approach to the
design of optical networks, as in Lena Wosinka’s work [17], which seeks to optimize networks
focusing on the price of network reliability.
The majority of the recent work done in 2008 mark this trend. For example the paper by
M. Fontana [18] in 2008 presents a software development for application in optical networks, in
which genetic algorithms are used to optimize network performance, with satisfactory results.
The following chapter discusses the development of evolutionary computation, which
leads the optimization efforts of many problems today, particularly the optimization of optical
2.2.1 Evolutionary Computation
Evolutionary computation encompasses a set of heuristics that base their operation on
the mechanism of natural selection proposed by Charles Darwin and later extended to the
so-called Neo-Darwinism.
This is to bring natural laws of evolution and applying computational algorithms to solve
optimization problems, such as those seen in previous sections.
In evolutionary computation, a population is composed of several individuals, an
indi-vidual is a solution to a problem and is encoded according to the needs of the problem, the
environment where it develops is represented by the objective function and restrictions on
the problem tell us how the individual is able to survive in that environment based on their
performance within it.
Probabilistic operators are applied to individuals referred to as parents of the population.
These operators are called crossing and mutation and are used to generate new individuals
known as children, which maintain certain properties of their ancestors.
A comparison is then made between parent and children, and the children are retained
or eliminated by selection (deterministic or probabilistic). This process is conducted for each
individual of the population to form a new population with new individuals.
The process is repeated for a given number of iterations, which are called generations in
evolutionary computation.
2.2.2 Differential Evolution (DE)
Differential Evolution is a very simple mathematical model, which represents a very
complex process of evolution. Intelligently using the differences in the population generated,
a simple but fast linear operator called differentiation makes the DE unique.
The genetic annealing developed by K. Price [19] was the beginning of the differential
evolution algorithm. The article about genetic annealing was first published in October 1994
and would mark the beginning of the development of DE.
Shortly after, K. Price was contacted by S. Storm, who was interested in solving the
Chebychev polynomials using this technique. After some experiments they were able to
develop a technique; the DE algorithm.
Kenneth Price [4], and since then the algorithm has developed, at present is very popular
because is very effective when attacking multiobjective problems.
In DE, the variables are represented by real numbers. The initial population is generated
randomly (for most of the cases) and three individuals are selected as parents. One parent is
the main parent and he is disturbed leading to the vector of the difference between the two
other parents. If the resulting value is better than the primary parent, then it replaces it.
Otherwise, it is retained.
The DE generates these new vectors when adding the weight difference between two
members of the population vectors to a third vector member. This simple operation is the
Chapter 3
DIFFERENTIAL EVOLUTION OPTIMIZATION APPLIED
TO THE WAVELENGTH CONVERTERS PLACEMENT
PROBLEM IN ALL OPTICAL NETWORKS
The placement of wavelength converters in an arbitrary mesh network is known to belong
to the class of NP-complete problems. So far, this problem has been solved by heuristic
strategies or by the application of optimization tools such as genetic algorithms (GA). In
this paper we introduce the application of Differential Evolution (DE) to the placement of
wavelength converters problem to obtain the optimal solution. Many comparative studies
confirm its robustness and efficiency, showing that in many cases DE outperforms many other
well known evolutionary computational approaches in terms of convergence speed and quality
of solutions. The major advantage of the DE algorithm rests in the fact that it does not need
to build up a search tree or to create auxiliary graphs. Furthermore, the method typically
requires few control parameters, and the computed results show that only a small population
is needed to obtain the optimal solution for the placement of wavelength converters in an
arbitrary network. We present experiments that demonstrate the effectiveness and efficiency
of the proposed evolutionary algorithm.
3.1
Introduction
Wavelength routed optical networks (WRON) promise to meet the high transmission
quality and large bandwidth desired by end users for transmitting multimedia traffic. In view
of this, the routing and wavelength assignment (RWA) issue is of paramount importance in
reducing the network blocking probability [2, 20]. This issue can be generally categorized
routing strategies may be divided into static routing and adaptive routing, whereby the latter
always outperforms the former but causes longer connection setup delays and higher control
overhead [21,22]. To further improve the WRON, wavelength converters are placed in network
nodes to reduce the network call blocking probability [11, 23]. It is well understood that
wavelength converters are presently very expensive and exhibit only a limited wavelength
conversion range. Due to these reasons, a network in which selected nodes are equipped with
wavelength conversion capabilities is economically more practical. These networks are often
referred to as networks with sparse wavelength conversion [24]. However, a sparse wavelength
convertible network has risen up other problems, i.e., where should the wavelength converters
be placed and how many converters are needed?
K.R. Venugopal et al. [25] used a new heuristic approach for placement of wavelength
con-verters to reduce blocking probabilities . Their study includes both, static and dynamic light
paths establishments. C. Vijayanand et al. [26] proposed new integer linear program (ILP)
formulations for the static and dynamic RWA problems to reduce the number of conversions.
In their study, a genetic algorithm (GA) was used for placing limited-range wavelength
con-verters in an arbitrary mesh WRON. This was one of the first evolutionary algorithm applied
to the wavelength converters placement problem. Li et al. [27] have proven that the optimal
solution on a path could be achieved when all the segments (a path segment between two
consecutive converters or between an end node and its nearest converter) on the path have
equal blocking probabilities. Based on this theorem, some algorithms of linear complexity
were proposed to obtain near-optimal solutions for converter placement on a path. In short,
most of the proposed techniques are either complicated, need large storage capacity, or
re-quire massive computation time. Considering these factors, C. F. Teo et al. [16] have proposed
a novel evolutionary algorithm named particle swarm optimizer (PSO) to find the optimal
placement of wavelength converters to achieve minimum blocking probability. More recently,
Kuntal Roy et al. [28] proposed a genetic evolutionary algorithm for efficient allocation of
wavelength converters in WDM optical networks. The distinguished feature of their approach
lies in that they considered various practical aspects (i.e., spatial problem, connectivity of a
node with other nodes) rather than arbitrarily to possibly improve the overall blocking
per-formance of WDM optical network. In this paper we present the application of DE to the
evolutive algorithms such as PSO and GA.
DE is a very simple but very powerful stochastic global optimizer for a continuous search
domain. It was proposed by Storn and Price [29], to represent a very complex process of
evolution. Using intelligently the differences between populations (a population is a set of
candidate solutions) and with the manipulation of few control parameters, they created a
simple but fast linear operator called differentiation, which makes DE unique.
Additionally, studies show that DE in many instances outperforms other evolutionary
algorithms [30]. More specifically DE exploits a population of potential solutions to effectively
probe the search space. The algorithm is initialized with a population of random candidate
solutions, conceptualized as individuals. For each individual in the population, a descendant is
created from three parents. One parent, the main, is disturbed by the vector of the difference
of the other two parents. If the descendant has a better performance resulting in the objective
function, it replaces the individual. Otherwise, the individual is retained and is passed on to
the next generation of the algorithm. This process is repeated until it reaches the termination
condition. A complete theoretical analysis of the algorithm is presented in [29].
The paper layout is as follows, the system model is introduced in Section 3.2. The
proposed search algorithm is presented and discussed in Section 3.3. An illustrative example
is presented in Section 3.4. Results of DE applied to realistic networks are presented and
explained in Section 3.5. Section 3.6 presents the conclusions.
3.2
System Model
We assume that either only one or none full range converter is placed in a node. Our
analysis is also based on the assumption that the routing in the network is done by using a
shortest path routine and that there is a random wavelength assignment. Moreover, for
sim-plicity we are considering that there is no losses in the converters or the link due to physical
impairments. Hence, the model can be formulated as a binary programming problem and
expresses the overall system success probability as a polynomial function of binary variables
Directed link from nodezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA i to node j.
Number of wavelengths on each link.
Number of wavelength converters. We
will assume one converter per node;
therefore variable k also represents the
number of nodes to be equipped with
conversion.
Endtoend traffic rate from node s to
node t. It is the arrival probability of
a call from s to t.
Traffic matrix of the network.
Amount of traffic XzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAst going through
link lij
Load per wavelength over linkzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA 1 ^ .
is the probability that a given wavelength on link 1^ is occupied, which is called the
blocking probability on 1 ^ . The traffic model can be computed by [16]:
Under the condition that Xs 3
t is small such that pij < 1. (x\, X2, • • •, xn) is the state
vector, indicating the placement of converters. Xi is defined as:
By using variables Xi where (i = 1,2,... ,n), and the given traffic matrix T and k
converters, we can determine the values in (x\, X2, • • •, xn), such that the overall blocking
probability of the network is minimized.
Before the overall success probability is formulated, we need to consider the endtoend
between node s and node t and there are some converters which have been placed in this route,
we define a segment of the path to be the set of links between two consecutive converter nodes
or between an end node and its nearest converter node in the path. In the case where the
load on the links is nonuniform with pathzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA Pst = i0,i1,i2 •••izyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAd where ij is a network node
(1 < j < d) and d is the number of segments in a path.
When i 0 = s and i d = t, the length of Pst = d. Subsequently, let qij = 1 — pij, be the
probability that a given wavelength is idle on link and each link consists of F channels.
Then, the endtoend success probability of a call on path Pst, S(Pst) is formulated, under
the converter placement state (x1,x2, •••,xn), as follows [13]:
when d = 1,
(3.2)
whenzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA d > 2,
In order to formulate the overall success probability, we consider the geometrical average
of all endtoend success probabilities in the system, which is defined as:
(3.7)
wherezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA XzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAst is the traffic flow from s to t. Note that we assume the traffic between two
endnodes to take the same path. Substituting Eq. (3.2) Eq. (3.4) into Eq. (3.5), the
overall success probability becomes a function of variables xzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA\,X2, • • • , xn. Eq. (3.6) represents
the binary constraint variable, which is limited to a given k converters in the system. The
optimization goal is to find an assignment of binary variables x\,X2,--- ,xn such that the
objective function in Eq. (3.5) is maximized. Thus, the overall success probability objective
function after taking the logarithm of Eq. (3.5) will be:
3.3 Differential Evolution (DE) Algorithm
We propose to apply the D E algorithm to determine the optimal placement of wavelength
converters in the network. As mentioned above, this algorithm uses a population of individuals
and iterates by creating new populations until an optimal solution is obtained. A n individual
in the algorithm is a vector of dimension D (where D is the problem's dimension), individuals
represent specific solutions to the problem. At the beginning of the algorithm, individuals
are created randomly. D E employs repeated cycles of recombination and selection to guide
the population towards the vicinity of a global optimum. In the algorithm, we apply the
probability operators which are crossing and mutation to each individual in a population
to obtain new individuals (children). These new individuals have some properties of their
ancestors, these ancestors are kept or deleted by selection. The term generation is used to
designate the conversion of all individuals into new ones, i.e., to move from one population to
another.
The algorithm is run for a limited number of generations. D E has three crucial control
parameters: the mutation constant ( M ) , controlling the mutation strength, the recombination
constant (RC) and the population size (NP). Throughout the execution process, the user
defines the population size NP. At each generation, all individuals in the population are
individuals are randomly chosen from the population and are mixed, this operation is referred
to as mutation, and results in a mutant individual (which is also a vector). The mutant
individual is then mixed with the current target vector by an operator called recombination,
the result of this recombination process is a vector called the trial vector.
Finally the selection operator is applied. If the trial vector improves the objective func
tion, it is accepted and replaces the current target vector in the new population that is being
created. Otherwise, it is rejected and the current target vector passes on to the next genera
tion, in this case the trial vector is not retained.
Next, we present a description of the operators used in the D E algorithm that find the
most promising region in the search space.
3.3.1 M u t a t i o n O p e r a t o r
For each individualzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA x%
,i = 1, • • • , NP, the mutant individual m% is generated according
to the next equation:
(3.9)
are three random individuals
from the population, mutually different and also different from the current individual xl
, and
M is a scaling factor called the mutation constant which must be M > 0. The mutation
operator is used to control the magnitude of the difference between two individuals, this
operator allows us to manage the trade off between exploitation and exploration on the search
process. This operator is the one that guides the convergence of the algorithm.
3.3.2 R e c o m b i n a t i o n a n d Selection O p e r a t o r s
The recombination operator is applied to increase the diversity of the mutation process.
As mentioned before, this operator is the last step in the creation of the trial vector. To
create the trial vector, the mutant individual, m%
, is combined with the current target vector.
Particularly, for each component j, where j = {1,2,-zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA• • , D } , of the mutant individual m',
we choose a random number rand in the interval [0,1]. Next, we compare this number rand
to the parameter RC, which is called the recombination constant. If rand < RC, then we
ti
,zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA otherwise, we select the j — th element of the target vector as the j — th element of the
trial vector. It is important to note that a small value in RC yields to the cancelation of the
mutation operator, since the target vector will become the new trial vector. This is because
rand < RC may not be true in most cases if RC is large. Finally, the selection operator
is applied, this operator is a simple rule of elitist selection of the vectors that improve the
objective function. This is done by comparing the fitness between the trial vector and the
target vector in the objective function using:
(3.10)
Where pop is the population of the next generation, that changes by accepting or rejecting
new individuals.
The best individual in the population and the global best individual are kept at the end
of each generation, to keep track of the best solution found so far.
3.3.3 B i n a r y - D E O p e r a t o r s
Note that in the wavelength converter placement problem, the optimization goal is to
find an assignment of the binary variables x1, x 2 , x n . Therefore, we have applied the binary
version of D E algorithm (BDE). A '1' indicates a converter is needed at a particular node
and a '0' represents a converter is not needed at the node. With the same framework of D E ,
tree new operators are used to expand the continuous field of the original D E to the discrete
field [31]. A new mapping operator, denoted by /1, was constructed to map the variable x in
a discrete domain into a continuous domain. The operator is defined as follows:
(3.11)
The boundary constraints of the wavelength converter placement problem might be v
olated as a result of the mutation and recombination operators of the continuous D E . T
avoid this problem, the S operator, which is a Sigmoid function, is used to make the mutatio
Finally, we defined the inverse mapping operator, which makes the transformation from
the continuous domain into the discrete domain:
(3.12)
(3.13)
Under these considerations we can establish the pseudocode for the problem of the place¬
ment of wavelength converters in an optical network, which is presented in the next subsection.
3.3.4 P s e u d o c o d e of t h e D E A l g o r i t h m
Create an initial population ofsize NP and set the control parameters;
Evaluate the fitness of every individual;
Repeat:
For each individual x e [ 1 , 2 , N P ] , where NP is the number of individuals;
Generate the trial individual:
Select tree individuals from the population;
To each one ofthese three individuals apply the following operators:
mapping operator eq. (3.11)
mutation operator eq. (3.9)
S operator eq. (3.12)
inverse mapping operator eq. (3.13)
select the best individual ofthe target vector and the trial vector eq(3.10);
update the fitness;
update the population;
continue the process for each individual
3.4 Illustrative Example
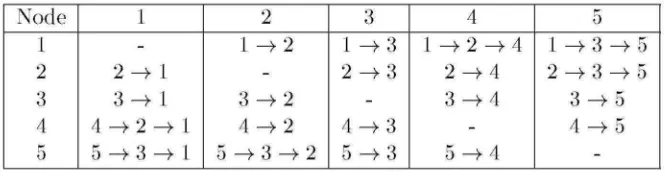
Table 3.1: The shortest paths for a simple 5node bidirectional graph.
A simple bidirectional graph with five nodes (D = 5) is shown in Figure 3.1. It is assumed
that a fiber link (F) consists of five channels, and Aij = 0.05 for any node pair (i, j) where
The shortest paths of each node pair are shown in Table 3.1. The
traffic load on each link pij and the endtoend success probabilityzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA S(Pst) of any node pair Si
which is based on Eqs. (3.2) and (3.3) are given in Table 3.2. For example,
according to Table 3.1, the traffic flows passing through the node pair 2 — 3 are 2 — 3 and
2 — 3 — 5. Hence, according to E q (3.1), p23 = (A23 + A2 5)/F = (0.05 + 0.05)/5 = 0.02.
From Eqs. (3.2) and (3.3), the endtoend success probability of the node pair 2 — 3 becomes
1 — 0. 025. A l l pzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAij and endtoend success probabilities are calculated in this way. Table 3.2
According to E q . (3.8), we can formulate the converter placement problem as a linear
function of variablezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA Xi for f <zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA i < 5 since the number of hops in this example is two (i.e.,
d < 2). Note that max(ln(s)) = min|Zn(a;)|, when 0 < x < I.
This equation is the D E objective function and can be written as:
(3T4)
last vector indicates that the overall minimum blocking probability will be obtained when a
wavelength converter is placed in node 3.
The capability of the applied binary D E is illustrated in Figure 3.2. The D E algorithm
found the optimal placement of the converter within three iterations, two iterations faster
than the PSO algorithm applied to the same example [16]. Also, according to Table 3.2, the
summation gives the highest load at node 3, which is a relatively good
indication that node 3 is the most promising location to place a wavelength converter. It is
important to mention that the optimal placement of the first converter is at the node with the
largest load. However, if we want the optimal placement of several converters it is absolutely
necessary to use a search algorithm such as the one proposed in this work because traffic load
Figure 3.2: Illustration of Differential Evolution simulation.
3.5
Numerical Results
We have tested the validity of the proposed DE algorithm in four real sized networks,
NSFNet (National Science Foundation Network), EON (European Optical Network), USA and
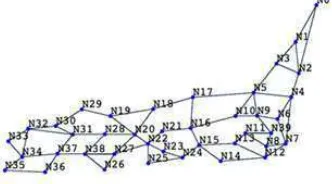
Japan, their topologies are shown in Figures 3.3, 3.4, 3.5, 3.6 respectively. More specifically,
we focused our analysis in the 14-nodes NSFNet (Figure 3.3) and 19-nodes EON (Figure 3.4),
because these two networks offer the advantage of being big and complex enough to show the
advantages and subtleties of the DE algorithm and at the same time, allow us to perform a
higher number of tests, which gets cumbersome with larger networks such as USA and Japan.
Furthermore, for comparison purposes we had to consider that most of the studies are done
Figure 3.3: NSF network topology, 14 nodes, 21 links.
Figure 3.4: EON topology, 19 nodes, 39 links.
Figure 3.5: USA network topology, 40 nodes, 58 links.
Figure 3.6: Japan network topology, 40 nodes, 65 Links.
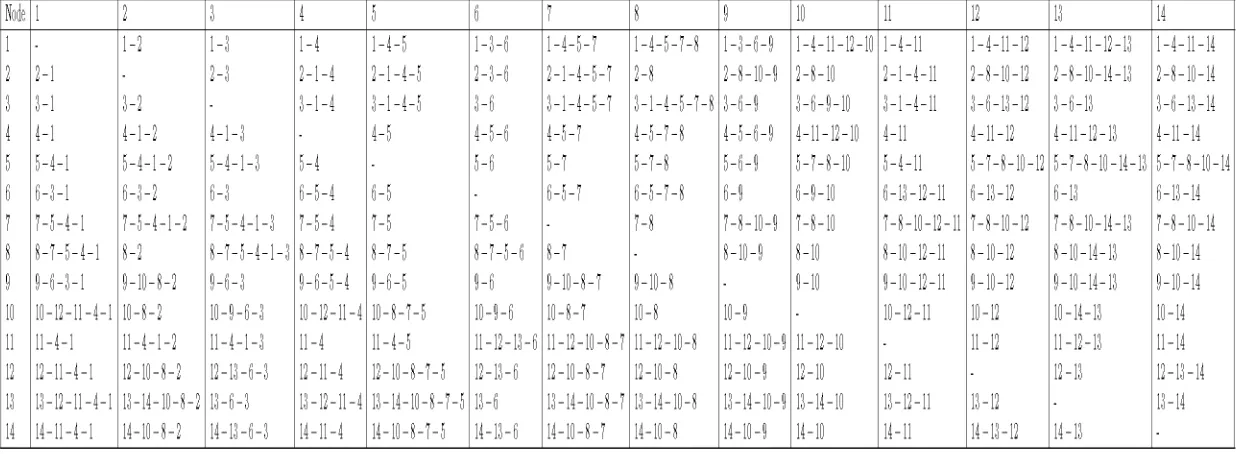
The shortest path routes from every node to any other node on these two networks
are given in Tables 3.3 and 3.4 respectively. Additionally, to simplify our analysis we have
[image:42.612.238.400.390.460.2] [image:42.612.239.405.517.609.2]The proposed D E algorithm is used to find the best placement of wavelength converters
in the network that will result in the minimum blocking probability. This best placement is
the one obtained from the optimization of equation (3.8), with the constraint of one converter
per node at most.
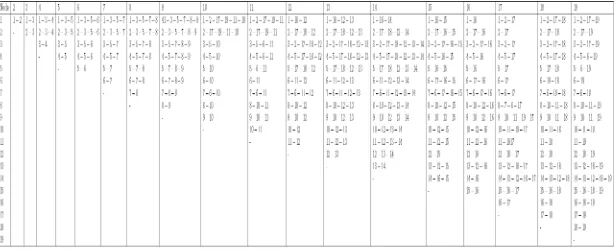
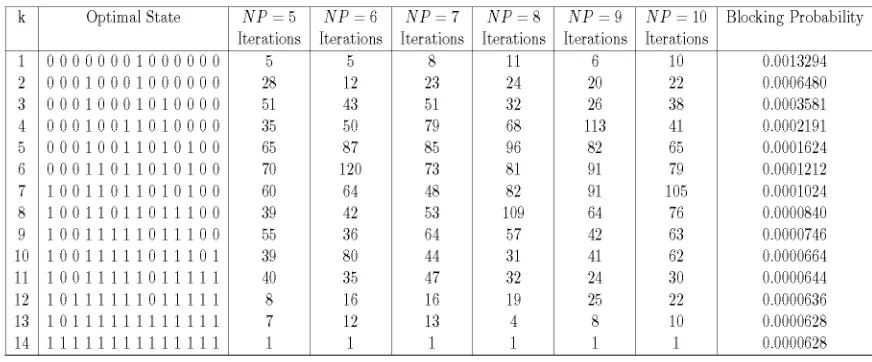
Table 3.5 presents a summary of the results obtained from the optimization of the
NSFNet. In our analysis the following values were fixed: number of channels F = 5, crossover
constant R C = 0.7, and mutation constant M = 1.5, the population has been increased from
10 to observe the convergence of individuals. As in other evolutionary algorithms,
the determination of the initial population size in D E is of critical importance, because it
may cause stagnation in a local optima. For example, when N P = 5 and k = 12 converters,
the optimal solution was not reached, this in spite of the fast convergence of our algorithm.
However the optimal solution was reached for the other values of N P and k, shown in the
[image:45.612.102.538.391.572.2]table.
Table 3.5: Results of NSFNetwork, F = 5, R C = 0.7, M = 1.5.
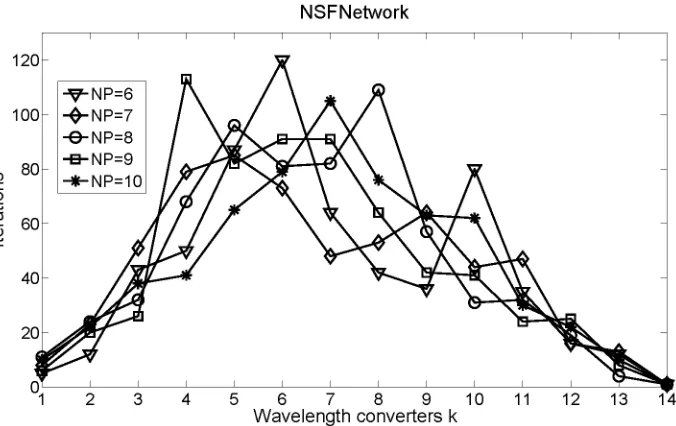
Figure 3.7 shows the number of iterations required to achieve the optimum state vs.
number of wavelength converters k for the NSFNet. Note that despite the increase on the
number of individuals in the population, the number of iterations required is fairly consistent,
however it is favorable to handle a population size as small as possible, as this reduces the
Figure 3.7: Number of iterations vs. Number of wavelength converters with R C = 0.7 and M = 1.5 for NSFNetwork.
Figure 3.8 shows the efficiency vs the number of wavelength converters. The algorithm
efficiency n (in percentage) is calculated according to [16]:
Figure 3.8: Efficiency vs. Number of wavelength converters with R C = 0.7 and M = 1.5 for NSFNetwork.
WherezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA D is the number of nodes in the network, k is the number of wavelength converters
placed, Cj? is the binomial coefficient and a is the number of iterations required to find the
optimal state. Consistency is evident in the efficiency of the algorithm, regardless of the
number of individuals in the population, it is also important to note that the efficiency for
exceeds 80 percent.
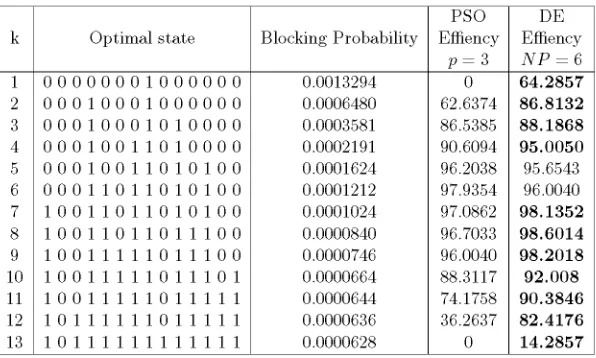
In order to prove the high efficiency of the D E algorithm in this problem, we have
[image:47.612.171.473.288.471.2]compared our results to those achieved by the P S O (particle swarm optimization) in [16].
Table 3.6 shows the comparison of efficiencies between these two algorithms with p = 3 (size
of the population) in P S O and NP = 6 in D E . The results in bold in Table 3.6 are those in
[image:47.612.174.472.290.469.2]which D E is better than P S O for this particular network.
Table 3.6: Results of NSFNetwork, Effiency P S O vs. D E
We have also investigated the impact of the parameters RC and M in the performance
of the D E algorithm to find the optimal state for the placement of wavelength converters in
the network. Figure 3.9 shows the results obtained when we vary the parameter M . Note how
the increase of M (M = 2) makes the number of iterations required to achieve the optimal
state to increase as well, but at the same time, it helps individuals to not remain trapped in
local optima. Experiments with N P = 7 and M = 0.9 showed an stagnation when k = 11, in
this state the optimal solution was not reached (not shown in the figure), therefore requiring
an increase in the population size. In Figure 3.10 we investigated how the RC parameter
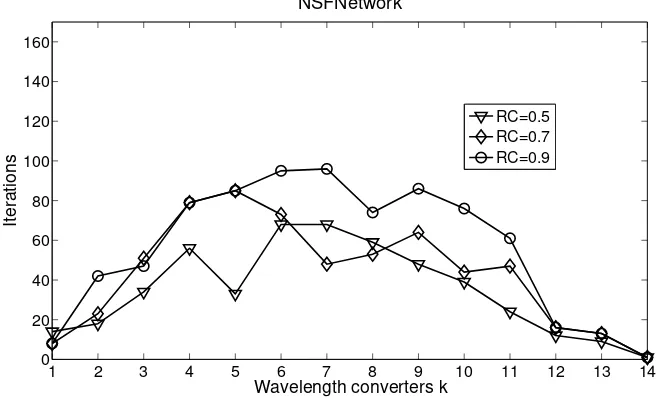
affects the convergence, and noticed that the increase of this constant makes the convergence
1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 20 40 60 80 100 120 140 160 NSFNetwork
Wavelength converters k
Iterations
[image:48.612.151.481.87.288.2]M=1.2 M=1.5 M=1.8 M=2
Figure 3.9: Number of iterations vs. Number of wavelength converters with RC = 0.7 and
N P = 7 for NSFNetwork
Table 3.7 shows the number of iterations required to achieve the optimal state when
7 ≤ N P ≤ 12 for the EON network. For the NSFNet the stopping criterion was set for a maximum of 3,000 iterations or when convergence of all individuals to the optimal state was
achieved, whichever occurred first. For the EON network an additional stopping criterion was
required, which is to stop the optimization process if after N iterations the optimal value so
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 20 40 60 80 100 120 140 160 NSFNetwork
Wavelength converters k
Iterations
[image:48.612.152.481.468.667.2]RC=0.5 RC=0.7 RC=0.9
Figure 3.10: Number of iterations vs. Number of wavelength converters with M = 1.5 and
far obtained is not improved, even when not all the individuals have converged to the same
state.
The reason for this is explained as follows, we observed that (for the E O N ) the global
optimum is reached when k = 14, therefore to consider more converters is unnecessary, this
also indicates that for k = 15 there are five different positions for k which would yield the
same minimum blocking probability. In general, for k > 14 there exist more than one state
for the optimal placement of the wavelength converters. This means that individuals are
leaping from one optimal region to another, without a unique convergence of them all, even
after 3,000 iterations of the algorithm. We considered a value of N = 100 for the E O N , but
we recommend to consider a higher value for the analysis of a larger network, since an small
value can lead to stagnation.
Figure 3.11 shows the number of iterations vs. number of wavelength converters k for
the E O N . As with the NSFNet, we observe that the number of iterations is fairly consistent
[image:49.612.104.537.82.260.2]even when N P increases.
Figure 3.12 shows the relationship between M and the number of iterations required to
reach the optimal state, we observe that the larger the M the slower the convergence. Again,
as with the NSFNet, Figure 3.13 shows a small increment in the number of iterations when
the parameter R C increase in the E O N .
In order to test the performance of the proposed algorithm on a more realistic stage, we
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 0 50 100 150 200 250 300 EONetwork
Wavelength converters k
[image:50.612.151.481.86.290.2]Iterations NP=8 NP=9 NP=10 NP=11 NP=12
Figure 3.11: Number of iterations vs. number of wavelength converters with RC = 0.7 and
M = 1.5 for EON.
networks. It is clear that as the network size increases, the number of iterations required to
reach the optimum increases as well. The number of individuals in the population needs to
increase also to avoid stagnation in local optima.
The recommended population size in GA, is 1.65∗20.21L [32], where Lis the parameter that defines the problem size, for the networks we are considering with 40 nodes (L= 40), GA
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 50 100 150 200 250 300 EONetwork
Wavelength converters k
Iterations
M=1.2 M=1.5 M=1.8 M=2
Figure 3.12: Number of iterations vs. number of wavelength converters with RC = 0.7 and
[image:50.612.152.480.468.668.2]1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 0 50 100 150 200 250 300 EONetwork
Wavelength converters k
Iterations
[image:51.612.163.473.84.280.2]RC=0.5 RC=0.7 RC=0.9
Figure 3.13: Number of iterations vs. Number of wavelength converters with M = 1.5 and
N P = 8 for EON.
would suggest a population size of 1.65∗2(0.21∗40) ≈557. From our analysis we realized that in DE we do not need such a big population, however, a significant increase in the population size
(compared to the NSFNet and EON) is required, therefore for the USA and Japan networks
we set the population size to N P = 50. To run the algorithm for 3,000 iterations with this population size would be computationally too expensive, therefore we lowered the number of
iterations to 500.
It is evident that DE outperforms GA in terms of population size, which in turn has an
impact on computing time, as the number of evaluations needed in each generation is reduced.
Table 3.9 and 3.10 show results for the two networks respectively, for a simulation run with
a maximum number of iterations of 500,F = 10, RC = 0.7,M = 1.5 and N P = 50.
In [13] the authors argue that the optimal placement of thek converters in the network can be obtained by maintaining the placement ofk−1 converters unchanged and finding the optimal placement for the k-th converter in one of the remaining available nodes. We have verified that this is true in the analysis of the NSFNet (Table 3.5) and EON (Table 3.7).
However, for more realistic sized networks this fundamental idea does not hold in many cases.
For instance, for the USA and Japan networks, the optimal solution for k= 8 andk= 18 is not obtained if we maintain the state k−1 (k= 7 and k = 17 ) unchanged and search for the optimal placement of the eighth and seventh converter as shown in Tables 3.9 and 3.10
indispensable to find the optimal state.
Also, note that for small networks an exhaustive searching method (which evaluates
all possible combinations) could be used to find the global optimum. Such a technique is
impractical when the network grows in size and complexity, i.e for a network with fourteen
nodes, having 7 converters available would exist C1 4 = 3432 possible combinations to test,
which is not a very large number of evaluations and computation time, either. However,
for larger networks such as shown in this research, evaluate all possible combinations to find
the optimum is impractical, i.e. in a network with 40 nodes and 20 converters will exist
C o = 137846528820 possible combinations, which represents a large number of evaluations
and computation time. The problem becomes critical as the number of evaluations grows
exponentially. For example, if the network grows only over one node, say 41 instead then, the
number of combinations grows to C4 1 = 269128937220.
In order to show the effect aforementioned, Table 3.8 shows the number of evaluations
and how the computation time grows for the U S A network. Note that we only used k < 5 for
[image:52.612.101.540.394.463.2]an illustrative purpose.
Table 3.8: Computation time for an exhaustive searching method on U S A network.
So, if we evaluate larger networks will come a point where computing capacity to be
insufficient to achieve the global optimum. For this reason is preferable to use a technique as
the D E algorithm to approach or find the global optimum when the problem gets too complex,
because, it reduces drastically the number of evaluations and computation time.
3.6 Conclusions
In this article we have presented the application of a differential evolution (DE) algorithm
to solve to optimality the problem of the placement of wavelength converters in an optical
network. We have confirmed the high capability of the algorithm in terms of convergence speed