Notas de Matem ´atica B ´asica

(1)

Notas de Matem ´atica B ´asica

Jorge Delgado

Sebasti ˜ao Firmo

Pedro N ´

obrega

Depto. de Matem ´atica Aplicada

Instituto de Matem ´atica - UFF

(2)

(3)

Conte ´

udo

1 Conjuntos 1

2 Os Inteiros 19

(4)

Cap´ıtulo 1

Conjuntos

1.1 Introduc¸ ˜ao

As teorias estudadas em matem ática s ão constru´ıdas sempre partindo de alguns fatos con-siderados b ásicos. Tais fatos s ão chamadosaxiomas. Os axiomas junto com asdefiniç õesdos conceitos que a teoria pretende estudar d ão lugar, ap ós racioc´ınios l ógicos, a resultados cha-mados proposiç ões. A seq ü ência de conclus ões l ógicas utilizadas para chegar a um resultado determinado partindo das definiç ões, axiomas e outros resultados, é chamada demonstraç ão. A palavra teorema é reservada a proposiç ões de car áter relevante na teoria em quest ão, da mesma maneira, umlema é uma proposiç ão que ser á usada como ferramenta fundamental para provar outras proposiç ões. Oscorol árioss ão proposiç ões que se obt êm como conseq ü ência di-reta de proposiç ões e teoremas importantes.

Todo lema, proposiç ão, teorema e corol ário, tem umenunciado. Todo enunciado se divide em duas partes, as hip óteses e as teses. A demonstraç ão do resultado (seja um lema, uma proposiç ão, um teorema ou um corol ário) pode ser descrita da seguinte maneira: usar os axio-mas, definiç ões e resultados pr évios da teoria para chegar às teses partindo das hip óteses por meio de um racioc´ınio l ógico. Isto se resume dizendo quea hip ótese implica a tesee escreve-se

Hip ´otese =⇒ Tese

O s´ımbolo =⇒ significa que partindo da parte da esquerda (Hip ótese) e usando um ra-cioc´ınio l ógico baseado nos axiomas, definiç ões e resultados anteriores da teoria, se obt ém como conseq ü ência o lado direito (Tese).

(5)

Conjuntos 1.2 Conjuntos

Teorema.(Pit ágoras) SejaT um tri ângulo ret ângulo cujos catetos medemaebrespectivamente e cuja hipotenusa medec. Ent ãoa2+b2 =c2.

A hip ótese diz que a, b e c s ão respectivamente os catetos e a hipotenusa de um tri ângulo ret ânguloT, e a tese diz quea2+b2 = c2. Mais tarde no texto veremos uma demonstraç ão do teorema de Pit ágoras.

Devemos observar tamb ém a validade das hip óteses dos nossos resultados, assim como a veracidade de cada um dos passos l ógicos nas demonstraç ões. Veja por exemplo a passagem de B. Russell citada nas primeiras p áginas desta apostila, na qual uma hip ótese falsa d á origem a conclus ões absurdas.

Em matem ática é freq üente o uso de quantificadores. Estes s ão apenas um simbolismo que nos permite descrever a abrang ência de fatos ou propriedades sobre uma determinada coleç ão de objetos. Temos dois tipos de quantificadores: oquantificador de exist ência, escrito simbolicamente∃(leia-se “existe...” ou “existem...”), e o quantificador de universalidade, escrito

∀(leia-se “para todo...”). O quantificador de exist ência é algumas vezes usado com o ponto de exclamaç ão∃!para indicar que certo objeto existe e é o únicoque possui as propriedades que o determinam.

1.2 Conjuntos

Neste cap´ıtulo introduziremos algumas noç ões b ásicas da teoria de conjuntos. N ão apre-sentaremos uma exposiç ão axiom ática e rigorosa da teoria, mas sim uma exposiç ão intuitiva e simples, incluindo apenas o material e a terminologia que usaremos mais adiante.

Para n ós umconjuntoser á qualquer coleç ão dada de objetos.

Embora esta “definiç ão” do termo “conjunto” seja intuitivamente clara, ela n ão é formal-mente correta, pois a palavra “coleç ão” é ainda indefinida. Na verdade, a noç ão de conjunto em matem ática é uma noç ão indefinida (da mesma maneira que a noç ão de ponto na Geometria Euclidiana) e é necess ária uma lista de axiomas para trabalhar com conjuntos e suas propri-edades. Na pr ática, uma introduç ão heur´ıstica, como a que apresentamos a continuaç ão, é suficiente.

(6)

que n ão pertence ao conjunto A escrevemos a /∈ A e dizemos que a n ão é um elemento do conjuntoA. Sea, b∈A, a notaç ãoa=bsignifica queaebs ão o mesmo elemento deA.

Os conjuntos podem ser descritos de duas maneiras:

A.Escrevendo numa lista os seus elementos, e englobando tal lista entre chaves{. . .}. Por exemplo,

A = {azul, verde, vermelho, laranja, maç ã}, B = {banana, morango, maç ã, azul}.

Quando representamos um conjunto por extens ão mediante uma lista, as repetiç ões e a ordem na qual aparecem os elementos na lista s ão irrelevantes. Por exemplo, o conjunto A

acima ´e tamb ´em representado como

A = {azul,verde, vermelho, laranja, azul, mac¸ ˜a, verde},

ou ainda

A = {vermelho,laranja azul, mac¸ ˜a, verde}.

B.Por meio de uma propriedade que caracteriza dos elementos do conjunto. Por exemplo

C ´e o conjunto que consiste dos nomes das cores do arco-´ıris,

D ´e o conjunto dos nomes das frutas tropicais.

SeP ´e uma propriedade sobre objetos, dizemos que o objetox satisfaz a propriedade P

e escrevemosP(x)se a propriedadeP ´e verdadeira parax.

Designamos por{x; P(x)}o conjunto formado pelos objetosx para os quaisP(x).

Por exemplo, segundo os exemplos acima,

C = {x; x ´e o nome de uma cor do arco-´ıris}

D = {x; x ´e o nome de uma fruta tropical}.

A caracterizaç ão (b) é principalmente útil quando o conjunto tem tantos elementos que seria praticamente imposs´ıvel coloc á-los numa lista. Consideremos por exemplo:

E={x; x é o nome de um assinante do cat álogo telef ônico do Rio de Janeiro},

ou pior ainda,

F={x; x é o nome de um assinante de algum cat álogo telef ônico de alguma cidade do mundo}.

(7)

A6⊂B. Dizemos tamb ém queAn ão é subconjuntodeBou queBn ão cont émAe escrevemos

B6⊃A.

Nos nossos exemplos vemos que,

A={azul, verde, vermelho, laranja, maç ã}6⊂B={banana, morango, maç ã, azul},

e nos conjuntos dos assinantes dos cat ´alogos telef ˆonicosE⊂F.

Dizemos que dois conjuntos s ãoiguaisquando cont êm exatamente os mesmos elementos. Neste caso escrevemosA=B. Quando os conjuntosAeBn ão s ão iguais escrevemos A6=B.

QuandoA⊂BmasA6=Bdizemos que A ´e umsubconjunto pr ´opriodeB.

A partir das definic¸ ˜oes acima podemos inferir que

i. Qualquer que seja o conjuntoAvaleA⊂A.

ii. SeA⊂BeB⊂C, ent ˜aoA⊂C.

iii. SeAeBs ˜ao conjuntos, (A=B) ⇐⇒ (A⊂BeB⊂A).

Vamos explicar o significado do s´ımbolo ⇐⇒, se p e q s ão proposiç ões ou afirmativas. Escreverp ⇐⇒q significa que, tomando como hip ótesep podemos obter como conseq ü ência l ógicaq (isto é “pimplicaq”, que se escreve p=⇒ q) e similarmente, tomando como hip ótese

q podemos obter como conseq ü ência l ógica p (isto é q implica p, que se escreve q =⇒ p). Resumindo,p⇐⇒qequivale às duas afirmativas simult âneasp=⇒qeq=⇒p.

Dado um conjunto A podemos considerar o conjunto {x; x ∈ Aex 6= x}. Tal conjunto é chamado osubconjunto vazio deAe se designa por∅A. É claro da definiç ão que∅A ⊂A.

Vamos apresentar agora a nossa primeira proposiç ão. A sua demonstraç ão ser á feita pelo m étodo do absurdo. Tal m étodo consiste em negar a tese e ap ós uma seq ü ência de conclus ões l ógicas, obter uma afirmativa que seja claramente falsa ou que entre em contradiç ão com as nossas premissas ou conhecimentos anteriores.

Proposiç ão 1.2.1. SeAeBs ão conjuntos quaisquer, ent ão _∅A=∅B.

Demonstrac¸ ˜ao. Procedendo pelo absurdo, vamos supor que A e B sejam conjuntos tais que

∅A6=∅B.

Segundo o item iii. acima, _∅A6=∅B significa que∅A6⊂∅B ou que∅B 6⊂∅A.

Caso_∅A 6⊂∅B, dever ´a existir um elementox∈∅A tal quex /∈∅B.

Pela definiç ão de∅Avemos quexser á um elemento deAtal quex 6=x, “o qual é absurdo,

(8)

Conjuntos 1.3 Operac¸ ˜oes com Conjuntos

Caso seja∅B 6⊂∅Ase procede da mesma maneira.

O absurdo indica ent ˜ao que a nossa hip ´otese de existirem conjuntosAeBtais que∅A 6=

∅B é errada. A conclus ão disto é a veracidade da proposiç ão. C.Q.D.

O quadrado que temos colocado no extremo direito da última linha acima indica que a demonstraç ão est á terminada. Alguns autores escrevem as letras CQD que significam “Como Queria-se Demonstrar” para indicar o fim de uma demonstraç ão.

Como conseq ü ência da proposiç ão anterior obtemos o seguinte resultado.

Corol ário 1.2.2. Existe um único conjunto _∅, chamado o conjunto vazio, que n ão cont êm elementos e est á contido em qualquer conjunto.

Demonstrac¸ ˜ao. Para provar este resultado simplesmente consideramos um conjunto qualquer

A e definimos _∅ = _∅A. Pela definiç ão de ∅A obtemos que ∅ n ão cont ém elementos, pela

proposic¸ ˜ao,∅=∅B ⊂Bqualquer que seja o conjunto B. Isto prova que o conjunto∅existe.

Agora provaremos que ele ´e ´unico. Seja_∅0 um conjunto com as mesmas propriedades de

∅. Pela proposic¸ ˜ao anterior, ∅ = ∅∅0 ⊂ ∅

0_{. Como}

∅0 possui as mesmas propriedades de ∅,

temos que∅0 ⊂∅. Logo∅0 =∅, e portanto o conjunto ∅existe e ´e ´unico. C.Q.D.

O corol ário acima é um exemplo de um resultado de “Exist ência” e “Unicidade”. Ele diz que sob certas hip óteses, certos objetos “existem” e s ão “ únicos”. A demonstraç ão deste tipo de resultados divide-se em duas partes: provar a exist ência do objeto e depois demonstrar que ele é único. Existem v ários procedimentos para provar a exist ência de um certo objeto, um deles é construir ou exemplificar um objeto com as propriedades requeridas. A demonstraç ão da parte da unicidade pode ser feita, por exemplo, das seguintes maneiras

(a) Mostrando que qualquer objeto com as mesmas propriedades do nosso ter á ne-cessariamente que ser igual ao nosso (como foi feito na demonstraç ão acima).

(b) Pelo absurdo, isto é, sup õe-se a exist ência de outro objeto (“outro” significa dis-tinto) com as mesmas propriedades do objeto em quest ão e chega-se a um absurdo.

1.3 Operac¸ ˜

oes com Conjuntos

Nesta parte vamos introduzir as leis b ásicas de formaç ão e operaç ão com conjuntos.

Definiç ão. Dados dois conjuntosAeB, definimos auni ãoA∪Be ainterseç ãoA∩Bde

(9)

A∪B={x; x ∈Aoux ∈B} e A∩B={x; x∈Aex ∈B}.

Dito em palavras, A∪ B ´e o conjunto cujos elementos pertencem ao conjunto A ou ao conjunto B. O conjunto A∩B ´e o conjunto cujos elementos pertencem ao conjunto A e ao conjuntoBsimultaneamente.

Na figura abaixo vemos dois conjuntosAeB, a sua uni ãoA∪Be a sua interseç ãoA∩B

respectivamente.

Fig. 1 (a).Representaç ão deA∪B. Fig. 1 (b).Representaç ão deA∩B.

Por exemplo, seAeBs ão os conjuntos dos exemplos da seç ão anterior, tem-se

A∪B = {azul, verde, vermelho, laranja, maç ã, banana, morango}, A∩B = {azul, maç ã}.

Observe que os elementos repetidos foram eliminados.

Da definic¸ ˜ao acima vemos que A e Bpossuem elementos em comum se, e somente se,

A∩B6=_∅.

Dois conjuntosAeBs ão chamadosdisjuntosseA∩B=_∅, isto é, seAeBn ão possuem elementos em comum.

Outro fato evidente da definiç ão é que, qualquer que seja o conjuntoAvalem as igualdades

A=A∪_∅ _∅=A∩_∅.

Tamb ém da definiç ão obt ém-se diretamente a seguinte proposiç ão:

Proposiç ão 1.3.1. SejamA, B, C, Dconjuntos quaisquer. Ent ão

(a)A∩B⊂A⊂A∪B.

(b)SeA⊂CeB⊂D, ent ˜aoA∪B⊂C∪DeA∩B⊂C∩D.

Demonstrac¸ ˜ao. Exerc´ıcio.

(10)

Teorema 1.3.2. Para quaisquer conjuntosA, B, C, valem as seguintes propriedades:

(1)Idempot ˆencia: A∪A=A=A∩A.

(2)Associatividade: A∪(B∪C) = (A∪B)∪CeA∩(B∩C) = (A∩B)∩C.

(3)Comutatividade: A∪B=B∪AeA∩B=B∩A.

(4)Distributividade: A∩(B∪C) = (A∩B)∪(A∩C)eA∪(B∩C) = (A∪B)∩(A∪C).

Demonstraç ão. N ão é dif´ıcil provar (1)-(3), exerc´ıcio. Vamos provar apenas a primeira das f órmulas de distributividade.

Lembramos que dois conjuntos s ão iguais se, e somente se, um est á contido no outro. Portanto, provar a f órmula em quest ão equivale a provar que o conjunto do lado esquerdo est á contido no conjunto do lado direito e que este, por sua vez, est á contido no primeiro:

Prova da inclus ˜aoA∩(B∪C)⊂(A∩B)∪(A∩C):

x∈A∩(B∪C) =⇒ (x∈A)e(x∈B∪C)

=⇒ (x∈A)e[(x∈B)ou(x ∈C)]

=⇒ [(x ∈A)e(x∈B)]ou[(x ∈A)e(x ∈C)] =⇒ [(x ∈A∩B)ou(x ∈A∩C)]

=⇒ x∈(A∩B)∪(A∩C).

Prova da inclus ˜aoA∩(B∪C)⊃(A∩B)∪(A∩C):

As implicaç ões =⇒ da prova da inclus ão anterior podem ser invertidas a ⇐=(verifique!). Leia ent ão a prova de baixo para cima.C.Q.D.

O seguinte resultado relaciona os s´ımbolos⊂,∪e∩.

Proposiç ão 1.3.3. SejamAeBconjuntos quaisquer. As seguintes afirmativas s ão equivalen-tes:

(1) A⊂B.

(2) A=A∩B.

(3) B=A∪B.

Demonstraç ão. Primeiramente vejamos o significado do enunciado: Dizer que duas proposiç ões

peqs ão equivalentes significa quep⇐⇒q, isto é,p=⇒qeq=⇒p. Temos que provar, ent ão, que(1)⇐⇒(2),(1)⇐⇒(3)e(2)⇐⇒(3). Basta provar(1)⇐⇒(2)e(1)⇐⇒(3).

(11)

Prova de (1) ⇐⇒(3): Se (1) é verdadeira, B =B∪B ⊃A∪B⊃ B, isto é,B =A∪B. Se (3) é verdadeira,B=A∪B⊃A, provando (1).C.Q.D.

Embora as operaç ões ∩ e ∪ foram definidas para dois conjuntos, podemos generalizar e reescrever a definiç ão para mais de dois conjuntos, mesmo parafam´ılias de conjuntos:

Definiç ão. SejaΛum conjunto n ão vazio. Se a cada elementoλ∈Λcorresponde um conjunto

Aλ, dizemos que a coleç ão F ={Aλ; λ ∈ Λ} (que tamb ém se designa porF ={Aλ}λ∈Λ) é uma

fam´ılia de conjuntos indexada porΛ. O conjuntoΛ ´e chamado oconjunto de ´ındicesda fam´ılia.

Observamos que qualquer conjunto n ão vazioApode servir como conjunto de ´ındices de uma fam´ılia de conjuntos. Com efeito, para cadaa ∈AsejaAa ={a}e consideremos a fam´ılia F = {Aa}a∈A. Tamb ém todo conjuntoF, cujos elementos s ão conjuntos, pode ser considerado

como uma fam´ılia de conjuntos indexada porF (i.e. auto-indexada). De fato,F ={AF}F∈F, onde

AF =Fpara todoF∈ F.

Definic¸ ˜ao. Seja X um conjunto dado e F = {Aλ}λ∈Λ uma fam´ılia de subconjuntos de X. Se

define auni ãoe ainterseç ãoda fam´ıliaF como

[

λ∈Λ

Aλ={x∈X; ∃λ∈Λtal quex∈Aλ} e

\

λ∈Λ

Aλ={x∈X; x∈Aλ∀λ∈Λ}

Por exemplo, se X ´e um conjunto qualquer, e para cada x ∈ X escrevemos Ax = {x}

podemos considerar a fam´ılia{Ax}x∈X indexada porX. Resulta que

[

x∈X

Ax =Xe

\

x∈X

Ax=∅.

Observando com cuidado, podemos ver que a uni ão e a interseç ão de uma fam´ılia inde-pende da maneira como est á indexada. Isto é, seΛ=Γ eF ={Aλ}λ∈Λ é uma fam´ılia indexada

porΛ, ent ˜ao

[

λ∈Λ

Aλ=

[

γ∈Γ

Aγ e

\

λ∈Λ

Aλ=

\

γ∈Γ

Aγ.

Pode-se provar com um pouco de esforço, que a uni ão de fam´ılias distribui sobre a interseç ão e que a interseç ão de fam´ılias distribui sobre a uni ão. Para enunciar este fato usaremos a noç ão de produto cartesiano que introduziremos em breve.

Definimos a seguir uma outra operac¸ ˜ao entre conjuntos

Definiç ão. Sejam AeBconjuntos. Definimos o conjunto diferençaA−Bcomo sendo o conjunto que consiste dos elementos deAque n ão s ão elementos de B, i.e.

(12)

´

E importante observar que, seAeBs ão conjuntos,A−BeB−As ão, em geral, conjuntos diferentes. Tamb ém é claro que A−B⊂A.

Fig. 2 (a).Representaç ão deA−B. Fig. 2 (b).Representaç ão deB−A.

Por exemplo, seAeBs ˜ao os conjuntos dos exemplos anteriores, ent ˜ao

A−B={verde, vermelho, laranja} e B−A={banana, morango}.

Definiç ão. Se A, X s ão conjuntos e A ⊂ X, o complementar de A com respeito a X é o conjunto{XA=X−A.

Por exemplo, seA={azul, verde, vermelho, laranja, maç ã} é o conjunto dos nossos exem-plos anteriores eB={azul, verde, vermelho}, ent ão{AB={laranja, maç ã}.

A figura abaixo é uma representaç ão da noç ão de complementar.

Fig.3.O complementar deAem relac¸ ˜ao aX.

Proposiç ão 1.3.4. Sejam A, B eC conjuntos quaisquer e X um conjunto que cont ém A∪B. Ent ão

i. A−_∅=Ae A−A=_∅.

ii. B⊂C=⇒A−C⊂A−B.

iii. A−B=A− (A∩B).

iv. A−B=A∩_{XB.

Demonstraç ão. Prova dei. J á que_∅n ão cont ém elementos,

A−_∅={x; x∈Aex /∈_∅}={x; x∈A}=A.

E observando que nenhum objetox pode ser tal quex ∈Aex /∈A, obtemos queA−A=_∅.

Prova deii. Observe que,

(13)

Portanto

(x∈A−C)=⇒(x∈Aex /∈C)=⇒(x ∈Aex /∈B)=⇒x ∈(A−B),

isto é, todo elemento deA−C é tamb ém elemento de A−B. LogoA−C⊂A−C.

Prova de iii. A inclus ãoA−B ⊂A− (A∩B) é conseq ü ência deii., poisA∩B⊂ B. Para a outra inclus ão observamos que

(x∈A− (A∩B))=⇒(x ∈Aex /∈A∩B)=⇒(x∈Ae(x /∈Aoux /∈B))=⇒

((x ∈Aex /∈A)ou(x ∈Aex /∈B))=⇒((x∈A−A)ou(x ∈A−B)).

Como, pori.,A−A=_∅, obtemos

((x ∈A−A)ou(x∈A−B))=⇒(x ∈A−B),

e portanto A− (A∩B) ⊂ A−B. Observe que as implicaç ões =⇒ do argumento podem ser invertidas a⇐=, isto é, substitu´ıdas por⇐⇒para provar as duas inclus ões simultaneamente.

Prova deiv. J ´a queA∪B⊂X, isto ´e,(x∈A∪B)=⇒x ∈X, obtemos

A−B = {x; x∈Aex /∈B}={x ∈X; x ∈Aex /∈B}

= {x∈X; x∈A}∩{x ∈X;x /∈B}={x; x∈A}∩{x; x∈Xex /∈B}

= A∩(X−B) =A∩_{XB.C.Q.D.

As propriedades b ´asicas do complementar s ˜ao dadas no seguinte resultado:

Proposiç ão 1.3.5. SejamAeBconjuntos eXum conjunto que cont émA∪B. Ent ão:

(a)A∩_{XA=∅,e A∪{XA=X.

(b)_{X({XA) =A.

(c)_{X∅=X,e {XX=∅.

(d)A⊂B⇐⇒_{XB⊂{XA

(e)(Leis de De Morgan) As relaç ões entre as operaç ões∪e∩com_{Xs ão:

{X(A∪B) = ({XA)∩({XB) e {X(A∩B) = ({XA)∪({XB).

Demonstraç ão. Os itens (a)-(d) s ão simples e os deixaremos como exerc´ıcio para o leitor. Provemos a primeira das leis de De Morgan:

(14)

⇐⇒ (x ∈Xex /∈A)e(x∈Xex /∈B)

⇐⇒ (x ∈_{XA)e(x∈{XB)⇐⇒x∈({XA)∩({XB).

A segunda das f ´ormulas de De Morgan pode ser provada de maneira similar, mas tamb ´em pode ser obtida da primeira com ajuda do item(b). De fato, como

{X({XA∪{XB) ={X({XA)∩{X({XB) =A∩B,

temos que{XA∪{XB={X({X({XA∪{XB)) = {X(A∩B).C.Q.D.

As leis de De Morgan podem ser generalizadas, sem dificuldade, a uni ões e intersecç ões de fam´ılias de conjuntos da seguinte maneira: Se F = {Aλ}λ∈Λ é uma fam´ılia de subconjuntos

de um conjuntoX, ent ˜ao

{X

[

λ∈Λ

Aλ

= \

λ∈Λ

(_{XAλ), e {X

\

λ∈Λ

Aλ

= [

λ∈Λ

(_{XAλ).

Vamos introduzir outra operaç ão entre conjuntos, oproduto cartesiano. O resultado desta nova operaç ão ser á um conjunto de natureza diferente da natureza dos conjuntos envolvidos. Na definiç ão a seguir, a noç ão de par ordenado desempenha papel fundamental. Se a e b

s ão dois objetos quaisquer (n ão necessariamente pertencentes ao mesmo conjunto), podemos considerar o objeto(a, b)no qual os elementosaebser ão denominados aprimeira coordenada e asegunda coordenada do par(a, b), respectivamente.

Dizemos que os pares ordenados(a, b)e(c, d)s ãoiguaise escrevemos(a, b) = (c, d)se, e somente se,a=ceb=d, isto é, dois pares ordenados s ão iguais se, e somente se, as suas coordenadas correspondentes s ão iguais.

Observemos ent ão que, se(a, b) é um par ordenado, ent ão

(a, b) = (b, a)se, e somente se,a=b.

Definiç ão. Sejam A e B dois conjuntos quaisquer. Designamos por A×B o conjunto cujos elementos s ão todos os poss´ıveis pares ordenados(a, b)ondea∈Aeb∈B. Isto é,

A×B={(a, b) ; a∈Aeb∈B}.

Na Fig.4. mostramos uma representaç ão gr áfica do produto cartesiano, na qual o conjunto

(15)

Fig.4. O produto cartesiano representado graficamente

Por exemplo, sejamA={a, b, c}eB={?,•}. Ent ˜ao

A×B={(a,?), (a,•), (b,?), (b,•), (c,?), (c,•)}.

Observe por exemplo, que os pares ordenados(?, a), (a, a), (•,?)n ˜ao pertencem aA×B.

De maneira similar podemos definir o produto cartesiano de tr ˆes ou mais conjuntos. Se A,

B, eCs ˜ao conjuntos, definimosA×B×Ccomo sendo o conjunto(A×B)×Ce similarmente, se

A1, A2, . . . , An s ˜ao conjuntos, definimosA1×A2×. . .×Ancomo sendo o conjunto(A1×A2×

. . .×An−1)×An. Os elementos deA1×A2×. . .×Ans ˜ao asn- ´uplas ordenadas(a1, a2, . . . , an)

ondea1 ∈ A1, a2 ∈ A2, . . . , an ∈ An, e duasn- ´uplas(a1, a2, . . . , an) e(b1, b2, . . . , bn) de A1×

A2 ×. . .×An s ˜ao consideradas iguais se, e s ´o se, a1 = b1, a2 = b2, . . . , an = bn. Todas as

propriedades que estudaremos sobre o produto cartesiano de dois conjuntos continuam v ´alidas para o produto cartesiano de mais de 2 conjuntos.

A seguinte proposiç ão descreve duas propriedades b ásicas do produto cartesiano.

Proposiç ão 1.3.6. SejamA,B,C,Dconjuntos. Ent ão:

(a) A×B=_∅⇐⇒(A=_∅)ou(B=_∅).

(b) SeC×D6=_∅, tem-se: (C×D⊂A×B)⇐⇒( (C⊂A)e(D⊂B) ).

Demonstrac¸ ˜ao.

(a)A propriedade do enunciado (a) equivale1_a

(A×B6=_∅)⇐⇒(A6=_∅)e(B6=_∅).

SeA×B 6=_∅, existe(a, b)∈ A×B, e pela definic¸ ˜ao de A×B,a ∈A eb∈ B. LogoA 6=_∅e

B6=_∅.

1_Se_p_e_q_{s ão proposiç ões l ógicas, a proposiç ão}₍_p_⇐⇒_q₎_⇐⇒ ₍_q_p_⇐⇒q_q₎ _{é sempre verdadeira}

(16)

Reciprocamente, seA 6= _∅ e B 6= _∅, existem elementos a ∈ A e b ∈ B. Portanto o par ordenado(a, b)pertence ao produto A×B, i.e.,A×B6=_∅.

(b)Suponhamos primeiro queC×D⊂A×B. Como, por hip ótese,C×D6=_∅, pelo item (a),C6=_∅eD6=_∅. Sejad0 ∈Dum elemento fixo. Pela definiç ão do produto cartesiano temos

c∈C=⇒(c, d0)∈C×D⊂A×B=⇒(c, d0)∈A×B=⇒c∈A,

logoC⊂A. Similarmente verifica-se queD⊂B(exerc´ıcio).

Reciprocamente, para todo(c, d)∈ C×D, tem-sec∈ Ced∈ D, e por hip ´otese,c∈ Ae

d∈B. Logo(c, d)∈A×B, provando queC×D⊂A×B.C.Q.D.

No item (b) da proposiç ão acima, é importante observar que a hip ótese C× D 6= _∅ é fundamental. Por exemplo, sejam A ⊂ C, A 6= C, B qualquer conjunto n ão vazio e D = _∅. Ent ãoC×D=_∅⊂ A×B, mas é falso queC ⊂A. A hip ótese C×D6=_∅ é usada apenas na implicaç ão=⇒.

O último resultado desta seç ão diz que o produto cartesiano verifica apropriedade distri-butivasobre as operaç ões ∪,∩e−.

Proposiç ão 1.3.7. SeA,B,Cs ão conjuntos, valem as seguintes f órmulas de distributividade:

(a) A×(B∪C) = (A×B)∪(A×C).

(b) A×(B∩C) = (A×B)∩(A×C).

(c) A×(B−C) = (A×B) − (A×C).

Demonstrac¸ ˜ao. Prova de(a): Para todo(a, b)tem-se

(a, b)∈A×(B∪C) ⇐⇒ (a∈A)e(b∈B∪C)⇐⇒(a∈A)e(b∈Boub∈C)

⇐⇒ (a∈Aeb∈B)ou(a∈Aeb∈C)

⇐⇒ (a, b)∈A×Bou(a, b)∈A×C

⇐⇒ (a, b)∈(A×B)∪(A×C).

Os itens(b)e(c)podem ser demonstrados de maneira similar.C.Q.D.

Consideremos, de novo, duas fam´ılias de conjuntosF = {Aλ}λ∈Λ e G = {Bγ}γ∈Γ. Pode-se

provar, sem dificuldade, que valem as seguintes propriedades distributivas:

[

λ∈Λ

Aλ

∩ [

γ∈Γ

Bγ

= [

(λ,γ)∈Λ×Γ

(Aλ∩Bγ), e

\

λ∈Λ

Aλ

∪ \

γ∈Γ

Bγ

= \

(λ,γ)∈Λ×Γ

(Aλ∪Bγ),

(17)

Conjuntos 1.4 O Conjunto Pot ˆencia

indexada pelo conjuntoΛ×Γ. Mais ainda, ao inv és de considerar duas fam´ılias podemos con-siderar uma fam´ılia de fam´ılias e provar propriedades similares, mas este ponto é bem mais delicado e o deixaremos para um curso avançado.

De maneira similar, podemos demonstrar que as uni ões e intersecç ões de fam´ılias se distribuem sobre o produto cartesiano, isto é, seF eG s ão as fam´ılias acima, ent ão

[

λ∈Λ

Aλ

× [

γ∈Γ

Bγ

= [

(λ,γ)∈Λ×Γ

(Aλ×Bγ), e

\

λ∈Λ

Aλ

× \

γ∈Γ

Bγ

= \

(λ,γ)∈Λ×Γ

(Aλ×Bγ),

1.4 O Conjunto Pot ˆencia

Finalizamos o nosso primeiro cap´ıtulo com um exemplo muito importante.

Definiç ão.SeA é um conjunto qualquer, designamos porP(A)ou2A_{o conjunto cujos}

elemen-tos s ãotodos os subconjuntos deA. Tal conjunto é chamado oconjunto pot ência de A. Isto é, o conjunto pot ência é determinado pela propriedadeB⊂A⇐⇒B∈ P(A).

Resumimos alguns fatos b ásicos sobre o conjunto pot ência de um conjunto dado na se-guinte proposiç ão:

Proposiç ão 1.4.1. SejamA,BeXconjuntos quaisquer, tais que A⊂X. Ent ão:

(a) a∈A⇐⇒{a}∈ P(A).

(b) ∅, A∈ P(A). Em particularP(A)6=∅.

(c) A⊂B=⇒P(A)⊂ P(B).

(d) P e∩comutam, isto ´e, P(A∩B) = (P(A))∩(P(B)).

(e) P e ∪ N ˜AO comutam. Mais exatamente, vale que P(A∪B) ⊃ (P(A))∪(P(B))

mas a igualdade nem sempre se verifica.

(f) P(A)∩ P(_{XA) =P(∅) ={∅}.

Demonstraç ão. Os itens (a)-(c) seguem facilmente da definiç ão. O item (f) é conseq ü ência direta de(d)e do fato de queAe_{XAs ão conjuntos disjuntos.

Prova de(d): Para todo conjuntoCtem-se que

C∈ P(A∩B) ⇐⇒ (C⊂A∩B)⇐⇒(C⊂AeC⊂B)

(18)

Conjuntos Exerc´ıcios

Prova de(e): Observamos que, como A ⊂ A∪B eB ⊂ A∪Btem-se, em virtude de (c), queP(A)⊂ P(A∪B)eP(B)⊂ P(A∪B). Logo,

P(A)∪ P(B)⊂ P(A∪B).

Para mostrar que a igualdade nem sempre ´e verdadeira basta dar um exemplo (isto ´e, um contra-exemplo para a igualdade da afirmativa):

ConsideremosA ={?} eB ={•}, ent ˜ao P(A) = {_∅, A},P(B) = {_∅, B}, e portanto, P(A)∪ P(B) = {_∅, A, B}. Por outro lado, A ∪ B = {?, •} e P(A ∪ B) = {_∅, A, B, A ∪ B}. Como

A∪B /∈ P(A)∪ P(B), os conjuntosP(A∪B)eP(A))∪(P(B)s ˜ao distintos.C.Q.D.

´

E interessante observar aqui que(e)e(f)podem ser generalizados a fam´ılias de conjuntos. Isto é, seF ={Aλ}λ∈Λ é uma fam´ılia de conjuntos, ent ão valem as relaç ões:

\

λ∈Λ

P(Aλ) =P \

λ∈Λ

Aλ

!

e [

λ∈Λ

P(Aλ)⊂ P [

λ∈Λ

Aλ

!

.

Exerc´ıcios

1.Prove que a relaç ão⊂ é uma relaç ãotransitiva, i.e., seA,BeCs ão conjuntos tais queA⊂B

eB⊂C, ent ãoA⊂C. Prove, dando um contra-exemplo, que a relaç ão∈n ão é transitiva.

2.SejamA,BeCconjuntos. Prove que

(a) SeB⊂A, ent ˜aoB∪C⊂A∪CeB∩C⊂A∩C.

(b) As operaç ões ∩e∪s ão comutativas e associativas:

A∩B=B∩A e A∪B=B∪A,

A∩(B∩C) = (A∩B)∩C e A∪(B∪C) = (A∪B)∪C.

3. Sejam A = {?} e B = {?,•}. Diga se as afirmaç ões abaixo s ão falsas ou verdadeiras, e justifique sua resposta:

(a)A⊂B (b)A∈B (c)?∈A (d)• ⊂B

4.SejamAeBsubconjuntos de um conjunto X. Prove que:

(a)A∩B=_∅⇐⇒A⊂_{XB⇐⇒B⊂{XA.

(19)

5.SejamAeBconjuntos quaisquer. Prove que:

(a) Os conjuntos(A∩B)e(A−B)s ˜ao disjuntos eA= (A∩B)∪(A−B).

(b) Os conjuntosAeB−As ˜ao disjuntos eA∪B=A∪(B−A).

6.Prove queA⊂{A}se, e somente se,A=_∅.

7.Prove as seguintes relac¸ ˜oes:

(a) (A−C) − (B−C) = (A−B) −C, (b) (A−C)∪(B−C) = (A∪B) −C,

(c) (A−C)∩(B−C) = (A∩B) −C, (d) (A−B) − (A−C) =A∩(C−B),

(e) (A−B)∪(A−C) =A− (B∩C), (f) (A−B)∩(A−C) =A− (B∪C).

8. Sejam A e B conjuntos quaisquer. Prove que existe um ´unico conjunto X que verifica as igualdadesA∪X=A∪BeA∩X=_∅simultaneamente.

9.Sejam A={0, 1, 2,{2}, 3} e B={{1}, 1, 4}.

(a) Determine A∪B e A∩B.

(b) Diga se as afirmaç ões abaixo s ão falsas ou verdadeiras, e justifique sua resposta:

•2∈A •{2}∈A •{2}⊂A

•{2,{2}}6={{2}, 2} •{2,{2}} ⊂A •2⊂A.

10. Dados dois conjuntos A e B sua diferença sim étrica é definida como sendo o conjunto

A∆B= (A−B)∪(B−A). Prove queA∆B= (A∪B) − (A∩B). Interprete a diferenc¸a sim ´etrica por meio de um desenho.

11.SejamAeBconjuntos n ˜ao vazios. Prove que, se(A×B)∪(B×A) =C×C, ent ˜aoA=B=C.

12.SejamA, B⊂XeC, D⊂Y conjuntos. Prove que:

(a)(A×C)∩(B×D) = (A∩B)×(C∩D).

(b)(A×C)∪(B×D)⊂(A∪B)×(C∪D).

(d)(A∪B)×(C∪D) = (A×C)∪(B×D)∪(A×D)∪(B×C).

(e)_{X×Y(B×D) = (({XB)×Y)∪(X×({YD)).

(e) D ˆe um contra-exemplo para mostrar que a igualdade em (b) nem sempre ´e verdadeira.

13. Designamos por _N o conjunto dos n úmeros naturais _N = {0, 1, 2, 3, . . .}. Dizemos que um conjuntoA é finito se podemos fazer uma correspond ência entre os elementos deA e os ele-mentos de um subconjunto de N da forma {1, 2, 3, . . . , n} para algumn ∈ N. Convencionamos

(20)

{1, 2, . . . , n}, dizemos queApossuinelementos. O naturaln é ocardinaldeAe o designamos por #A. O conjunto vazio tem cardinal 0, isto é, #_∅ = 0. Os conjuntos com cardinal 1 s ão chamadosconjuntos unit ários.

Se A e B s ˜ao conjuntos finitos mostre que

#(A∪B) =#(A) +#(B) −#(A∩B).

14. Sejam A um conjunto com 10 elementos e B um conjunto com 15 elementos. O que se pode dizer do cardinal de A∪B,A∩B e A×B?

(21)

(22)

Cap´ıtulo 2

Os Inteiros

2.1 Notac¸ ˜ao

Este cap´ıtulo ser ´a dedicado a estudar as propriedades do conjuntoZdosn ´umeros inteiros:

Z={. . . ,−4,−3,−2,−1, 0, 1, 2, 3, 4, . . .}.

Dentre os subconjuntos de Zdestacamos os seguintes:

•O conjunto dosn ´umeros naturais_N={0, 1, 2, 3, . . .}.

•O conjunto dosn ´umeros naturais n ˜ao nulosN∗ =N−{0}={1, 2, 3, . . .}.

Este conjunto tamb ém é chamado o conjunto dos n úmeros inteiros positivos e se designa por

Z+.

•O conjunto dosn ´umeros inteiros n ˜ao nulos_Z∗ ₌

Z−{0}={. . . ,−3,−2,−1, 1, 2, 3, . . .}.

•O conjunto dosn ´umeros inteiros negativosZ− ={−1,−2,−3, . . .}.

Do acima estabelecido segue que o conjunto dosinteiros n ˜ao positivos ´e o conjunto

{ZZ

+

=_Z−_Z+ ={0,−1,−2,−3, . . .}.

Analogamente, o conjunto dosinteiros n ˜ao negativos ´e o conjunto

{ZZ

−

=_Z−_Z− ={0, 1, 2, 3, . . .}.

(23)

Os Inteiros 2.2 Operac¸ ˜oes

Dados a, b ∈ _Z, dizemos que a e b t êm o mesmo sinal quando ambos t êm sinal positivo ou ambos t êm sinal negativo, isto é, ambos pertencem a _Z+ _{ou ambos pertencem a}

Z−. Diremos

queaebt êmsinais contr áriosquando um deles é positivo e o outro é negativo.

2.2 Operac¸ ˜

oes

No cap´ıtulo anterior estudamos algumas operaç ões sobre conjuntos. Estas operaç ões nos per-mitiram construir, a partir de conjuntos dados, um novo conjunto. Nesta seç ão vamos introduzir a noç ão de operaç ão desde um ponto de vista global e depois enfocar a nossa atenç ão em operaç ões definidas no conjuntoZdos n úmeros inteiros.

Definiç ão. Seja A um conjunto n ão vazio. Uma operaç ãosobre A é uma lei que a cada par ordenado de elementos de A faz corresponder um elemento de A. Se ? é uma operaç ão em

A e (a, b) ∈ A×A, escrevemos ?(a, b) ou a?b para designar o elemento de A determinado ao aplicar a operaç ão ao par ordenado (a, b). Dizemos que a ?b é o resultado de aplicar a operaç ão?ao par ordenado(a, b)∈A×A.

Em s´ımbolos escrevemos

?:A×A −→ A

(a, b) 7−→ a?b .

Da definiç ão de operaç ão obtemos que:dadosa, b ∈A, sea=a0 eb=b0 ent ão,a?b=a0?b0.

Por exemplo, consideremos um conjunto A = {α, β} contendo dois elementos. Definimos uma operac¸ ˜ao?:A×A−→Amediante a seguinte tabela:

? α β

α α β

β β α

Nesta tabela, escrevemos a primeira coordenada dos pares ordenados de A ×A na coluna embaixo de ?, e a segunda coordenada na fila `a direita de ?. A primeira fila da tabuada se lee: α?α =α, α?β =β, e a segunda filaβ?α=βeβ?β=α.

Neste exemplo observamos que, quaisquer que sejam x, y ∈ A tem-se x ?y = y? x. Uma operaç ão verificando esta propriedade é chamada comutativa. Tamb ém, quaisquer que sejam

x, y, z∈A, valex?(y?z) = (x?y)?z(verifique este fato!). Uma operaç ão com esta propriedade é chamadaassociativa. O elementoαdeAtem a propriedade de que α?x=x?α=x, isto é,

α é um elementoneutropara a operaç ão?.

Vejamos outro exemplo. Seja B = {0, 1, 2, 3, 4} e consideremos a operac¸ ˜ao ? : B ×B −→ B

(24)

? 0 1 2 3 4

0 0 0 0 0 0

1 0 1 2 3 4

2 0 2 4 1 3

3 0 3 1 4 2

4 0 4 3 2 1

Segundo esta tabela vemos que1?x=x?1=xqualquer que seja x ∈ B, isto é, 1 é um elemento neutro para a operaç ão?. Observando com cuidado vemos que a tabu-ada é sim étrica em relaç ão à diagonal, logo a operaç ão? é comutativa. Podemos verificar que a operaç ão ? é as-sociativae que para cadax ∈B−{0}, existey∈Btal que

x?y=1, pois1?1=1,2?3=3?2=1e4?4=1.

Vamos agora enfocar a nossa atenç ão no conjuntoZdos n úmeros inteiros.

Sobre o conjunto Z dos n úmeros inteiros podemos definir muitas operaç ões. As operaç ões

de soma e de multiplicaç ão, com as quais j á estamos familiarizados, ser ão de fundamental import ância no resto deste cap´ıtulo:

+ :_Z×_Z−→_Z (m, n)7−→m+n (operaç ão desomaouadiç ão)

· :_Z×_Z−→_Z (m, n)7−→m·n (operaç ão de multiplicaç ãoouproduto)

A multiplicaç ão de dois n úmeros inteiros a e b ser á tamb ém designada pela justaposiç ão ab, isto é, colocando um n úmero ap ós o outro. Esta terminologia dever á ser usada com cuidado, por exemplo: 15 é o inteiroquinzee n ão1·5. Por outro lado, sea∈_Z,2ase entende como2·a.

Da noç ão geral de operaç ão, tem-se a seguinte regra que utilizaremos com freq ü ência:

Dadosa, b, c∈_Ztemos que

• (i)sea=bent ˜aoa+c=b+c,

• (ii)sea=bent ˜aoa·c=b·c.

Mais tarde voltaremos a falar sobre esta regra, ou mais especificamente, sobre a sua rec´ıproca (vide as leis de cancelamento para adiç ão e multiplicaç ão).

Na pr ática fazemos uso das operaç ões de soma e multiplicaç ão, junto com uma s érie de pro-priedades ou regras de manipulaç ão, que na maioria dos casos aplicamos de maneira quase autom ática sem reparar muito nos detalhes.

(25)

Propriedades das operaç ões de soma e de multiplicaç ão emZ:

• (1)Comutatividade:

•a+b=b+apara todoa, b∈_Z,

•a·b=b·apara todoa, b∈_Z.

• (2)Associatividade:

•(a+b) +c=a+ (b+c)para todoa, b, c∈_Z,

•(a·b)·c=a·(b·c)para todoa, b, c∈_Z.

• (3)Distributividade:

•a·(b+c) =a·b+a·cpara todoa, b, c∈_Z,

•(a+b)·c=a·c+b·cpara todoa, b, c∈_Z.

• (4)Exist ência de elementos neutros (0 para a adiç ão e 1 para a multiplicaç ão):

•0+a=a=a+0para todoa∈_Z.

•1·a=a=a·1para todoa∈_Z.

• (5)Exist ˆencia de sim ´etricos:

•a+ (−a) =0= (−a) +apara todoa∈_Z.

Notaç ão. Dadosa, b ∈ _Z, escrevemosa−bpara significara+ (−b), isto é, a soma dea com o sim étrico deb. O n úmeroa−bse l êamenos b.

Observamos que a propriedade descrita no item (5) diz respeito apenas à operaç ão de soma. Dadoa∈_Z, o n úmero−a∈_Z é chamado osim étricodea.

Como dito anteriormente, podemos definir v árias operaç ões sobre Z. Uma delas, com a

qual estamos bastante familiarizados é a operaç ãodiferençadada pela notaç ão acima:

− :_Z×_Z −→ _Z

(a, b) 7−→ a−b=a+ (−b),

Outro exemplo de operaç ão definida sobre o conjunto_Z é:

:_Z×_Z −→ _Z

(26)

Muita atenc¸ ˜ao!!

• Observe que n ós sabemos somar apenas dois elementos de cada vez. O que significa ent ão uma express ão t ão conhecida como a+b+c onde a, b, c ∈ _Z? Melhor dizendo, faz sentido a express ão acima? De fato, mantendo a ordem em que a, b, c aparecem na express ão s ó podemos oper á-los como a+ (b+c) ou (a+b) +c o que d á na mesma, segundo a propriedade de associatividade da soma. É por esta raz ão quea+b+c faz sentido. Se quisermos alterar a ordem em que a, b, c aparecem na express ão tamb ém podemos faz ê-lo, desta vez, lançando m ão da propriedade de comutatividade.

Em virtude das propriedades associativa e comutativa da multiplicaç ão, as mesmas consideraç ões acima podem ser aplicadas ao produto de tr ês ou mais inteiros, isto é, sea, b, c∈_Z, o produtoa·b·cpode ser entendido comoa·(b·c)ou como(a·b)·c, ou ainda comob·(a·c)etc. Outro exemplo, sea, b, c, d, e, f, g∈_Z,

a+b+c+d+e+f+g = (a+ (b+ (c+ (d+ (e+f))))) +g

= ((a+b) + (c+d)) + ((e+f) +g) =etc.

a·b·c·d·e·f·g = ((a·b)·(c·(d·(e·f))))·g

= ((a·b)·(c·(d·(e·f))))·g=etc.

• Do item anterior conclu´ımos que nas express ˜oesa+ (b+c)e(a+b) +ccoma, b, c∈_Z

podemos ignorar o par ênteses, isto é, a+ (b+c) = a+b+c = (a+b) + c. Ser á que podemos fazer isto na express ão a − (b−c), escrevendo a − (b−c) = a −b− c = (a−b) −c? Se a operaç ão diferença fosse associativa, poder´ıamos faz ê-lo mas isto n ão é verdade (prove!). Exatamente por esta raz ão tamb ém n ão podemos ignorar o par ênteses na express ãoa−(b+c), escrevendoa−(b+c) =a−b+c. De fato,a−(b+c) = (a−b)−c. O que é intrigante é que apesar da operaç ão diferença n ão ser associativa n ós bem que entendemos o que significa a− b− c ! Bem, neste caso quando lemos a express ão

a−b−cde fato estamos lendo(a−b) −ce n ãoa− (b−c). Isto é uma convenç ão que, evidentemente, respeitaremos.

Trabalhando com as operaç ões de soma e multiplicaç ão sobre Z n ós utilizaremos com

freq ü ência as propriedades de (1) à (5). Al ém delas, utilizaremos tamb ém v árias de suas con-sequ ências, listadas abaixo e de f ácil demonstraç ão.

(27)

Demonstraç ão. Das propriedades acima descritas temos que0·a = (0+0)·a =0·a+0·a. Agora, somando−(0·a) a cada membro da equaç ão 0·a = 0·a+0·a n ós conclu´ımos que

0·a=0para todoa∈_Z. Da´ı segue que0·a=0=a·0para todoa∈_Z. C.Q.D.

Conseq ¨u ˆencia 2. (−1)·a= −a , ∀a∈_Z.

Demonstrac¸ ˜ao. Temos que (−1) · a +a = (−1) · a + (1) · a = (−1 +1) · a = 0 · a = 0.

Agora, somando−aa cada um dos membros da equaç ão(−1)·a+a=0n ós conclu´ımos que

(−1)·a= −a, ∀a∈_Z. C.Q.D.

Destas duas conseq ¨u ˆencias temos: 0= (−1)·0= −0.

Conseq ü ência 3. Mais geralmente, repetindo adequadamente os argumentos acima, n ós conclu´ımos que

a·(−b) = (−a)·b= −a·b , ∀a, b∈_Z.

´

E esta propriedade que nos permite garantir que

a·(b−c) =a·b−a·c , ∀a, b, c∈_Z.

De fato,

a·(b−c) =a·(b+ (−c)) =a·b+a·(−c) =a·b+ (−a·c) =a·b−a·c.

Conseq ¨u ˆencia 4. a−b=0⇐⇒a=b.

Demonstrac¸ ˜ao. Com efeito,

a−b=0 ⇐⇒ a+ (−b) =0 pela definiç ão da diferençaa−b

⇐⇒ (a+ (−b)) +b=0+b somandobem ambos lados da igualdade

⇐⇒ a+ ((−b) +b) =b pela propriedade associativa

⇐⇒ a+0=b pela propriedade dos sim ´etricos

⇐⇒ a=b pela propriedade do elemento neutro aditivo. C.Q.D.

Conseq ¨u ˆencia 5. (−1)(−1) =1e portanto,−(−a) =a, para todoa∈_Z.

Demonstrac¸ ˜ao. Com efeito, tem-se

(−1)(−1) −1= (−1)(−1) + (−1) = (−1)(−1) + (−1)·1= (−1)(−1+1) = (−1)·0=0.

e ent ˜ao, pelo item anterior(−1)(−1) =1.

(28)

Repare que, se a ∈ _Z+ _{ent ˜ao} ₋_a _∈

Z− e reciprocamente, se a ∈ Z− ent ˜ao −a ∈ Z+.

Portanto devemos ter cuidado com o seguinte: ´

E falso que: Sea é um inteiro, ent ão−a é um inteiro negativo.

Com efeito, observe que

−(−1) = (−1)[(−1)1] = [(−1)(−1)]1=1·1=1

−(−(−3)) = (−1)[(−1){(−1)3}] = (−1)[{(−1)(−1)}3] = (−1)[1·3] = (−1)3= −3

−(−(−(−(−n)))) = −n, para todon∈_Z, e assim por diante.

Conseq ü ência 6. Lei do cancelamento para a adiç ão.

Dadosa, b, c∈_Ztemos:

a+c=b+c=⇒a=b

Demonstrac¸ ˜ao. Sejama, b, c∈_Ze suponhamos que a+c=b+c. Assim , obtemos:

a+c=b+c=⇒a+c+ (−c) =b+c+ (−c)=⇒a+0=b+0=⇒a=b,

e a demonstraç ão est á terminada. C.Q.D.

Para demonstrar a lei do cancelamento para a multiplicac¸ ˜ao precisamos do seguinte lema.

Lema 2.2.1. Sejama, b∈_Z. Sea·b=0ent ˜ao a=0oub=0.

A demonstraç ão deste lema ser á feita mais tarde quando introduzirmos o conceito de divisi-bilidade. Vamos agora utiliz á-lo para demonstrar a lei do cancelamento para a multiplicaç ão.

Conseq ü ência 7. Lei do cancelamento para a multiplicaç ão.

Dadosa, b, c∈_Z com c6=0temos:

a·c=b·c=⇒a=b

Demonstrac¸ ˜ao. Sejama, b, c∈_Ze suponhamos que a·c=b·c. Assim , obtemos:

a·c=b·c=⇒a·c−b·c=0=⇒(a−b)·c=0=⇒a−b=0 ou c=0.

Comoc6=0por hip ótese, segue do lema acima quea−b=0, isto é,a=be a demonstraç ão est á terminada. C.Q.D.

Definiç ão. Sejaa∈_Z. Ovalor absolutooum ódulodea, denotado|a|se define por

|a|=

        

a , sea ´e positivo

0 , sea=0

(29)

Os Inteiros Exerc´ıcios

Desta definiç ão temos que, sea∈_Z∗_{, ent ão}_|_a_| _{é um inteiro positivo. Al ém disso,}

|a|=0⇐⇒a=0.

Por exemplo,|2|=2= −(−2) =|−2|.

´

E importante observar que,|−a|=ase, e somente se,a ´e um inteiro positivo.

Exerc´ıcios

1.Calcule

(a)2−2(3− (−1)) + (−5−3(5−2(−1(2−4)))).

(b)−3+ (−3− (4−2(1−2)2)(2−3(−1+ (−3·2+2))(−2))).

(c)−2−|2(−2+ (5−2(3−|−4|)))|− | −|3−|2| |−1| |.

2. Sejama ∈ _Z∗ _e _b_∈

Z. Diga se as afirmaç ões abaixo s ão falsas ou verdadeiras e justifique

suas respostas.

(i)−a ´e um inteiro negativo,

(ii)a+b ´e um inteiro positivo,

(iii)2a ´e um inteiro positivo,

(iv)a·a ´e um inteiro positivo,

(v)−100−a ´e um inteiro n ˜ao negativo,

(vi)0e2t ˆem o mesmo sinal,

(vii)1+ (a−b)(a−b) ´e um inteiro positivo,

(viii)|b| ´e n ˜ao negativo,

(ix)|a+3|=a+3,

3.Elimine os par ˆenteses nas express ˜oes abaixo.

(i)a−3(2a− (−a+b) −a(b−2(−a+b))a−b),

(ii)2(−a+1−b(2−2a(1−b)) −3b−2(−4− (a−2))),

(iii)(2−|a|+3(a− (a−1) +|a+1|) −2(1−|a+3|)).

(30)

5. Considere dois inteiros de soma S, de diferenc¸a D e de produto P. Responda as quest ˜oes seguintes selecionando a resposta correta dentre as propostas.

(a) Adicionamos5a um dos inteiros e3ao outro. O que acontece comS?

(b) Adicionamos4a cada um dos inteiros. O que acontece comS? E comD?

(c) Multiplicamos cada inteiro por2. O que acontece comS? E comD? E comP?

(d) Multiplicamos um dos inteiros por5e o outro por3. O que acontece comP?

Respostas propostas.

(i) N ˜ao varia.

(ii) Aumenta de5.

(iii) Diminui de 8.

(iv) Dobra.

(v) Fica multiplicada por15.

(vi) Triplica.

(vii) Fica multiplicada por4.

(viii) Aumenta de8.

6.Um filho tem11anos e sua m ãe35anos. Daqui a quantos anos a idade da m ãe ser á o triplo da idade do filho.

7.A idade de duas pessoas somam 120 anos. Subtraindo-se 10 anos da idade da mais velha e acrescentando-os `a da mais moc¸a, as idades tornam-se iguais. Qual a idade de cada uma?

8.Um r ádio e uma televis ão custam juntos R$ 1.500,00. Comprando apenas o r ádio me sobraria R$ 200,00mas para adquirir a televis ão precisava ter mais R$ 300,00 do que possuo. Quanto custou o r ádio, a televis ão e quanto possuo?

9.Duas cidades A e B distam 200 km. Às 8 horas, parte de A para B, um trem com velocidade de 30 km por hora e, duas horas depois, parte de B para A um outro trem com velocidade de 40 km por hora. A que dist ância de A, dar-se- á o encontro dos trens?

10.Determine o valor de a∈_Zna equac¸ ˜ao

2(a− (2−a) + (1−2a)(2−3(5−2))) =3a− (a−2(a−3(a−1))).

(31)

b=0ouc=0.

12.Determine todas as soluç ões inteiras das equaç ões:

(i)(a+2)(2−a)(a−2(a−2)) = 0,

(ii)(a−2)(3+b)ab=0,

(iii)(a−1)(3+b)(a−b) =0,

(iv)ab+3a−2b=6,

(v)|a|=1,

(vi)|a−2|=3,

(vii)|2−a|·|b+3|=0,

(ix)|a|+a=0.

13.Use a lei de cancelamento da multiplicaç ão para determinar todas as soluç ões inteiras das equaç ões:

(i)2a=2, (ii)2a=a, (iii)ab=b.

14.Mostre que a hip ótese,a6=0na lei de cancelamento para a multiplicaç ão, é essencial.

15. Da associatividade da operac¸ ˜ao soma podemos concluir que (a−b) + c = a− (b+c)? Justifique sua resposta.

16.Mostre que o Lema 2.2.1 usado para demonstrar a lei do cancelamento para a multiplicaç ão é de fato equivalente a tal lei, i.e., mostre que a lei implica o lema e que o lema implica a lei. Ali ás, esta última parte n ós j á fizemos.

17.Sejama, b ∈_Z. Mostre que|a|=|b|se, e somente se,a=boua= −b.

18.Considere dois inteiros iguaisaeb.

Temos ent ˜ao que:

a=b=⇒a2 =ab =⇒a2−b2 =ab−b2 =⇒(a−b)(a+b) = (a−b)b.

Usando a lei do cancelamento para a multiplicac¸ ˜ao, obtemosa+b=b. agora tomandoa=1=

bconclu´ımos que2=1.

(32)

2.3 Pot ˆencias Naturais de N ´

umeros Inteiros

Definic¸ ˜ao:

• a0 ₌₁_{para todo}_a_∈

Z∗

• ak ₌_a_·_{. . .}_·_a

| {z }

k vezes

para todoa∈_Zek∈_N∗_.

Nesse contexto temos: a1 = a , a2 = a·a , a3 = a·a·a = a2 ·a , e assim por diante. Na definiç ão acima, n ós dizemos que an é uma pot ênciatendo como base o inteiroa e como expoenteo naturaln.

Propriedades das pot ˆencias.

Dadosa, b∈_Z∗ _e_{m, n} _∈

Ntemos:

1. am+n =am·an

2. (a·b)n ₌_an_·_bn

3. (an₎m ₌_an·m

Voc ê entendeu o porque da condiç ão a, b ∈ _Z∗ _{ao inv és da condiç ão}_{a, b} _∈

Z ? Ela serve

apenas para evitar a pot ˆencia 00 _{que n ˜ao foi definida. Uma outra forma de enunciar a primeira}

regra, poderia ser, por exemplo:

Sejama∈_Zem, n∈_Ntais queam+n_{, a}m _e _an _{est ˜ao definidos. Ent ˜ao}_am+n₌_am_·_an_.

Exerc´ıcios

1.Sejama, b∈_Z. Mostre que:

(i)(a+b)2 ₌_a2₊_2ab₊_b2_,

(ii)(a−b)2 ₌_a2₋_2ab₊_b2_,

(iii)(a+b)(a−b) =a2 −b2,

(33)

2.Use o desenvolvimento de(a+b)3 _{para concluir que}

(a−b)3 =a3−3a2b+3ab2−b3.

3.Diga se ´e falso ou verdadeiro e justifique sua resposta:

(a)2k+1+6=2(3+2k)para todok∈_N,

(b)6n+1₋₆n ₌₂n_·₃n+1₊₂n+1_·₃n_{para todo}_n_∈

N,

(c)2n₊₁₀m ₌₂n₍₁₊₁₀m−n_·₅n₎_{para todo}_{m, n} _∈

Ncomm ≥n.

4.Sejaa∈_Z. Mostre quea2 ₌₁_{se, e somente se}_a₌₁ _ou_a_{= −}₁_.

Demonstrac¸ ˜ao. Temos que a2 ₌ ₁ _⇐⇒ _a2 ₋₁ ₌ ₀ _⇐⇒ ₍_a₋₁₎₍_a₊₁_{) =} _0. _{Agora, usando o}

Lema 2.2.1 obtemos

(a−1)(a+1) =0⇐⇒a+1=0 ou a−1=0⇐⇒a= −1 ou a=1. C.Q.D.

5.Use o Lema 2.2.1 para mostrar que sea2 ₌₀_,_a_∈

Z, ent ˜aoa=0.

6.Use uma das leis de cancelamento para demonstrar que sea2 ₌₀_com_a_∈

Z ent ˜aoa=0.

7.Determine os valores da vari ´avelnpara os quais as express ˜oes abaixo fazem sentido em_Z.

(a)2n_,

(b)(−5)n−2,

(c)2n−3_{+ (}₂₊_n₎n+1_,

(d)(2+n)2+n_,

(e)2n−1,

(f)32(n−4)_·₅3n−n2

.

8.Determine as soluç ões inteiras das equaç ões:

(a)(a−1)2 ₌₀_,

(b)(a−2)2 =1,

(c)a2₋_b2 ₌₀_,

(d)a2₋_a₊₆₌₀_,

(e)a2(b+1) =a(b+1),

(34)

Os Inteiros 2.4 O Bin ˆomio de Newton

(g)a4₋₁₆₌₀_.

9.Sejama, b∈_Ze coloquemosc=a−b. Temos ent ˜ao quea=b+c. Multiplicando ambos os membros pora−btemos:

(a−b)a= (a−b)(b+c) =⇒ a2−ab=ab+ac−b2−bc =⇒a2−ab−ac=ab−b2−bc

=⇒ a(a−b−c) =b(a−b−c).

Agora, pela lei do cancelamento para a multiplicac¸ ˜ao conclu´ımos quea=b.

E voc ˆe, o que acha disto?

2.4 O Bin ˆ

omio de Newton

Muitas vezes temos necessidade de considerar somas com um grande n úmero de parcelas, ou somas com um n úmeronde termos, onden é um inteiro positivo qualquer. Por exemplo,

a1+a2+a3+a4+a5+a6 +a7+a8+a9 +a10,

b1+b2+. . .+b7,

b1+. . .+b8+b9,

c1+. . .+cn, onden∈Z+,

a0+a1+. . .+ak, ondek∈N.

Fixaremos agora uma notaç ão que facilitar á a manipulaç ão destas somas.

Sejamn∈_Z+ _e_a

1, a2, . . . , an∈Z. Escrevemos n

X

i=1

ai (l ê-sesomat óriodeai variandoi de1at én)

para indicar a soma a1 +a2+. . .+an.

De forma similar, escrevemos:

n+1

X

i=0

ai = a0+a1+. . .+an+1, onde n∈Z+,

k

X

j=2

bj = b2+. . .+bk, onde k∈{2, 3, 4, . . .},

mX+2

k=−4

(35)

Os Inteiros 2.4 O Bin ˆomio de Newton

p

X

n=0

a2n = a0+a2+a4+. . .+a2(p−1)+a2p, onde p∈Z+.

Note que cada uma das quatro últimas somas possui um n úmero m´ınimo de termos e um n úmero total (n ão confundir com m áximo) de termos: a primeira delas possui no m´ınimo 3

termos e um total den+2termos, a segunda possui um m´ınimo de1termo e um total dek−1

termos, a terceira possui um m´ınimo de 8 termos e um total de ...

Atenç ão! Ainda com relaç ão às últimas quatro somas, é importante voc ê perceber que, na primeira delas, o resultado da adiç ão de suas parcelas depende denmas n ão dei, na segunda o resultado depende dek mas n ão dej, na terceira o resultado depende de mmas n ão dek, e na quarta o resultado depende depe n ão den.

Lema 2.4.1 Para quaisquera, b ∈_Z∗ _e_n_∈

Z+, vale a seguinte identidade:

an−bn = (a−b) n−1

X

i=0

an−1−i·bi.

Demonstraç ão. Para demonstrar o lema efetuamos as operaç ões indicadas no segundo mem-bro da identidade com o objetivo de obter o primeiro memmem-bro.

Temos:

n−1

X

i=0

an−1−i·bi =an−1b0+an−2b1+an−3b2+. . .+a2bn−3 +a1bn−2+a0bn−1.

Multiplicando ambos os membros desta identidade pora−be efetuando as operac¸ ˜oes:

(a−b) n−1

X

i=0

an−1−i·bi = a· n−1

X

i=0

an−1−i·bi

!

−b· n−1

X

i=0

an−1−i·bi

!

= (anb0+an−1b1+an−2b2 +. . .+a3bn−3+a2bn−2+a1bn−1) −(an−1b1+an−2b2 +an−3b3+. . .+a2bn−2+a1bn−1+a0bn) = anb0−a0bn=an−bn,

e a demonstraç ão est á terminada.C.Q.D.

Teorema (do bin ˆomio de Newton). Dadosa, b ∈_Z∗ _e_n_∈

Z+ temos:

(a+b)n= n

X

k=0

n k

(36)

onde

n k

é o n úmero de combinaç ões de nelementosk àk.

Veremos mais tarde uma f órmula para a combinaç ão denelementosk àkmas, voc ê pode concluir com facilidade que:

1. combinar n elementos0 à 0s ó podemos faze-lo atrav és da coleç ão com zero elementos, isto é, da coleç ão vazia, e ent ão

n 0

=1,

2. podemos combinar nelementos1 `a1denmaneiras diferentes, e ent ˜ao

n 1

=n,

3. podemos combinar nelementosn ànde uma única maneira, e ent ão

n n

=1,

4. podemos combinarnelementosn−1 àn−1denmaneiras diferentes, para isto basta ver que uma combinaç ão comn−1elementos é constru´ıda retirando um elemento da coleç ão comnelementos, e ent ão

n n−1

=n.

Por enquanto, vamos nos contentar com isso.

Exerc´ıcios

1.Quantas parcelas t ˆem as express ˜oes escritas abaixo:

(a)a1+a2+. . .+an, onden∈Z+,

(b)am+am+1+. . .+am+s, ondem∈Zes∈Z+,

(c)

n−1

X

i=0

ai+1, onden−3∈Z+,

(d)am−1+am+. . .+am+s, ondem∈Zes∈Z+.

(37)

3.Reescreva as express ˜oes abaixo sem usar o s´ımbolo de somat ´orio.

(a)

n

X

j=0

aj+3, onden∈N,

(b)

2n

X

i=0

(−1)i·ai+1, onden∈N,

(c)

n−1

X

k=−4

δk+2, onden∈N.

4. Qual o n úmero m´ınimo de parcelas que poder á ocorrer em cada uma das express ões do exerc´ıcio anterior?

5.Sejamp∈_Zen∈_Z+_{. Mostre que:}

(a)(a−b)n₌ n

X

k=0

(−1)n−k

n k

akbn−k,

(b)(1+a)n₌ n

X

i=0

n i

ai,

(c)

n

X

k=0

ak = n−p

X

i=−p

ai+p,

(d)

n

X

i=0

ai =a0+ n−1

X

i=0

ai+1,

(e)

n

X

i=0

n i

=2n,

(f)

n

X

k=0 (−1)k

n k

=0.

6.Mostre que

(a)

n

X

i=0

(ai+bi) = n

X

i=0

ai+ n

X

i=0

bi,

(b)

n

X

i=0

(c·ai) =c

n

X

i=0

ai,

(c)

n

X

i=1

(ai−ai−1) =an−a0.

(38)

Os Inteiros 2.5 A Reta Orientada e os N ´umeros Inteiros

(a)

100

X

n=0

n2 = 100

X

n=1

n2,

(b)

n

X

k=0

(1+k) =1+ n

X

k=0

k, onden∈_Z+_,

(c)

n

X

i=1

(i+1)4 = n−1

X

i=0

i4, onden∈_Z+_,

(d)

n

X

k=1

k2 = n−s

X

j=1−s

(j+s)2.

8.Mostre que

n 2

= n−1

X

k=1

(n−k) =n(n−1) − n−1

X

k=1

k,

para todon∈{2, 3, 4, . . .}.

9.Compare n p e n n−p

.

10.SejaAum conjunto comnelementos (n∈_N). Mostre que o n ´umero de subconjuntos deA

´e2n_{. Isto ´e, #}_P₍_A_{) =}₂n_.

11.Qual ´e o coeficiente de a2_x2 _{no desenvolvimento de}₍_2x₊_a₎4_?

12.Qual ´e o coeficiente de x4 no desenvolvimento de(x+3)5?

13.Qual ´e o coeficiente de ax3 _{no desenvolvimento de}₍_a₋_x₊₁₎4_?

Indicac¸ ˜ao: Desenvolva(a−x+1)4como((a−x) +1)4.

2.5 A Reta Orientada e os N ´

umeros Inteiros

Considere uma reta e sobre ela fixemos uma orientaç ão, isto é, fixemos um sentido de percurso.

Representaç ões gr áficas:

reta sem orientac¸ ˜ao

sentido de percurso fixado

−−−−−−−−−−→

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−_{reta anterior com orientac¸ ˜ao fixada}→

(39)

Uma reta sobre a qual fixamos uma orientaç ão (i.e. um sentido de percurso) ser á dita uma reta orientada. Assim, uma reta orientada é constitu´ıda de dois ingredientes: da reta e da orientaç ão escolhida sobre ela.

Os tr ês pontinhos colocados à direita e à esquerda nas representaç ões gr áficas acima ser-vem apenas para indicar que estamos representando graficamente uma parte da reta ou da reta orientada. Daqui para frente vamos propositadamente esquec ê-los, n ão esquecendo no entanto que estamos representando graficamente uma parte da reta ou da reta orientada.

Numa reta orientada podemos falar em pontos `a direita (resp. `a esquerda) de um ponto dado, da seguinte maneira.

Seja P um ponto de uma reta orientada. Os pontos à direita de P s ão aqueles que podem ser atingidos a partir de P, seguindo o sentido de percurso fixado. Os pontos à esquerda s ão aqueles que podem ser atingidos a partir de P, seguindo o sentido de percurso oposto àquele fixado.

pontos `a direita de P

◦

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→

reta orientada P

pontos `a esquerda de P

Pois bem, fixemos em definitivo uma reta orientadar, um ponto arbitr ´arioOsobre ela (cha-mado deorigem) e um segmento de retau (dito,unidade de comprimento).

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→

O u r

(segmento de reta)

| {z }

unidade de comprimento

Agora, vamos inserir os n úmeros inteiros na reta orientada, colocando o n úmero0(zero) na origem, os inteiros positivos à direita da origem e os inteiros negativos à esquerda da origem, como mostrado na figura a seguir.

u u u u u u u u

· · · z }| { · · · z }| {z }| {z }| {z }| {z }| {z }| { · · · z }| { · · ·

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→

−n −n+1 −3 −2 −1 0 1 2 3 (n−1) n r

Isto ´e feito da seguinte maneira:

1e−1s ˜ao colocados `a uma unidade da origem,

2e−2s ˜ao colocados `a2unidades da origem,

3e−3s ˜ao colocados `a3unidades da origem, ..

. ... ...

(40)

Diremos que n e −n foram colocados na reta orientada, simetricamente em relaç ão a ori-gem. Tamb ém diremos que o n úmero 1 foi obtido da origem por translaç ão à direita de uma unidade, que o n úmero−1foi obtido da origem por translaç ão à esquerda de uma unidade, que

2 foi obtido da origem por translaç ão à direita de 2unidade (ou de1 por translaç ão à direita de uma unidade), que−2foi obtido da origem por translaç ão à esquerda de2unidade (ou de1por translaç ão de 3 unidades), e assim por diante.

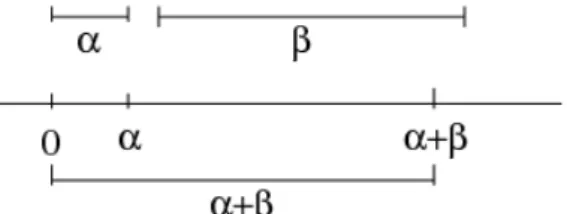
De forma mais geral, dadosa∈_Zeb∈_Z+ _{diremos que}

1. a+b (na reta orientada) foi obtido de a(na reta orientada) pela translaç ão à direita deb

unidades, ou simplesmente,a+bfoi obtido transladandoadeb,

2. a−b(na reta orientada) foi obtido de a(na reta orientada) pela translaç ão à esquerda de

bunidades, ou simplesmente,a−bfoi obtido transladandoade−b.

Assim, dados a, b ∈_Z entenderemos quea+b é obtido transladandoa deb(translaç ão à direita seb é positivo, à esquerda seb é negativo e translaç ão nula se b=0).

Uma outra propriedade importante desta forma de inserir os inteiros na reta orientada, ou digamos assim, de mergulhar os inteiros na reta orientada, ´e a seguinte.

Dados dois pontos P,Q da reta orientada, existem no m ´aximo um n ´umero finito de inteiros entre eles.

Em particular,

dado um ponto P da reta orientada, sempre existem inteiros `a direita de P e inteiros `a esquerda deP.

Mais precisamente,

i. dado um pontoPda reta orientada, existen0 ∈Z+ tal quen0 est ´a `a direita deP, P

• ◦

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→

n0∈Z−

ii. dado um pontoPda reta orientada, existen0 ∈Z− tal quen0 est ´a `a esquerda deP. P

◦ •

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→

n0∈Z−

(41)

Agora, seja A um subconjunto de Z. Diremos que A ´e limitado inferiormente (ou, cotado

inferiormente) se existe um ponto P da reta orientada tal que todo elemento deAest á à direita de P. Diremos queA élimitado superiormente(ou,cotado superiormente) se existe um ponto Q da reta orientada tal que todo elemento deAest á à esquerda de P.

Exemplos.

a. O conjuntoN ´e limitado inferiormente. Para ver isso, fixe um ponto P da reta, `a esquerda

da origem. Neste caso, todo elemento de N est á à direita de P, o que mostra que N é

limitado inferiormente.

b. O conjunto_Z+ _{n ão é limitado superiormente, pois, j á vimos que dado um ponto Q das reta} orientada sempre existe um inteiro positivo à sua direita.

c. O conjunto Z− é limitado superiormente, pois, todo elemento de Z− est á à esquerda da

origem.

d. O conjunto_Zn ão é limitado inferiormente nem superiormente. Isto segue do fato que dado um ponto P sempre existem inteiros à direita e à esquerda de P.

Na pr óxima seç ão falaremos de uma outra propriedade deZenquanto subconjunto da reta

orientada. Esta importante propriedade estar ´a relacionada com o conceito de subconjuntos limitados inferiormente e superiormente.

Exerc´ıcios

1.Diga se ´e falso ou verdadeiro e justifique sua resposta.

(a) O conjunto dos inteiros n ˜ao positivos ´e limitado inferiormente,

(b) O conjunto dos inteiros n ˜ao negativos ´e limitado inferiormente.

2.SejamA, B⊂_Z. Mostre que

(a) SeAeBs ão limitados superiormente ent ão,A∪BeA∩Bs ão limitados superiormente.

(b) SeA é limitado inferiormente eB é limitado superiormente ent ão,A∩B é limitado superior-mente e inferiorsuperior-mente.

3.Diga se ´e falso ou verdadeiro e justifique sua resposta.

(42)

Os Inteiros 2.6 A Relac¸ ˜ao de Ordem

(b) Dado um ponto P da reta orientada existe um inteiron0 ∈Z+ tal quen0 −5est ´a `a direita de

P,

(c) Dado um ponto P da reta orientada existe um inteiron0 ∈Z+tal quen0+100est ´a `a esquerda

de P.

4. Seja P um ponto da reta orientada eM∈_Z. Mostre que existe n0 ∈ Z+ tal que n0−Mest ´a

`a direita de P.

5. Mostre que subconjuntos de conjuntos limitados superiormente (resp. inferiormente) s ˜ao limitados superiormente (resp. inferiormente).

6.Nesta seç ão, n ós definimos o que significa um subconjunto de Zser limitado superiormente.

Colocamos agora uma nova definiç ão: Dizemos que um subconjunto n ão vazioA⊂_Z élimitado superiormente quando existe um n úmero inteiroNtal que todo elemento deAest á à esquerda deN.

Mostre que a definiç ão antiga e a nova s ão de fato equivalentes, isto é, mostre que todo sub-conjunto n ão vazio deZque é limitado superiormente em relaç ão a uma das definiç ões tamb ém

ser á limitado superiormente em relaç ão à outra.

2.6 A Relac¸ ˜ao de Ordem (primeiro contato)

Ap ós representar o conjunto _Z na reta orientada vamos utilizar a orientaç ão fixada na reta para introduzir em Zuma ordenaç ão.

Definiç ão. Sejam a, b ∈ _Z. Diremos que a é menor que b (notaç ão a < b) quando a est á à esquerda de b na reta orientada. Equivalentemente, diremos que a é maior que b(notaç ão

b > a) quandobest ´a `a direita dea.

Neste contexto, os inteiros positivos s ão aqueles que s ão maiores do que zero e os inteiros negativos s ão aqueles que s ão menores do que zero.

Esta forma de comparaç ão entre elementos de_Z, introduzida pela definiç ão acima, ser á dita relaç ão de ordem.

Observe que, definida a relaç ão “<”ao definir a relaç ão “>”n ão introduzimos nada de novo, a n ão ser uma nova notaç ão. Dizer que b > a é, exatamente, dizer quea < b.