aplider

(1)

Aplicaciones

de las

derivadas

(estudio de funciones)

Matemáticas de

2º de Bachillerato

Por Javier Carroquino Ca

Z

as

Catedrático de matemáticas

del I.E.S. Siete Colinas

(2)

(estudio de funciones)

(3)

–•–

Ciencias de la Naturaleza y la Salud

Tecnología

Aplicaciones de las derivadas

( estudio de funciones )

Por

Javier Carroquino Cañas Catedrático de matemáticas

I.E.S. Siete Colinas (Ceuta)

Departamento de Matemáticas

(4)

I.E.S. Siete Colinas (Departamento de Matemáticas) Aplicaciones de las derivadas(estudio de funciones)

(5)

E

l título de este tema “Aplicaciones de las derivadas (estudio de funciones)” es suficientemente elocuente. Veremos como el conocimiento de la derivada de una función y sus derivadas sucesivas nos brinda una información que permitirá conocer el comportamiento de esa función en un punto concreto, en un intervalo o en todo su dominio, es decir, las derivadas sucesivas constituyen una herramienta para el estudio completo de funciones, entendiendo por tal el conocimiento de su forma en un punto concreto &crecimiento, decrecimiento, extremos, puntos de inflexión, concavidad , convexidad, etc.& o en un intervalo

& crecimiento, decrecimiento, concavidad , convexidad, etc.& de tal modo que podamos tener un conocimiento exhaustivo de ella para poder trazar su gráfica con exactitud. Evidentemente, es imprescindible abordar este tema con el estudio previo del tema “Derivadas de funciones”, así como los relativos a “Funciones Reales de Variable Real”, “Gráficas de Funciones Reales de Variable Real”, “Propiedades y formas de las Funciones Reales de Variable Real”, “Límites de funciones” y “Continuidad de funciones”, pertenecientes a esta colección de apuntes.

(6)

Índice

Página

Introducción ... 1

1.Función creciente en un punto. ... 1

2.Función decreciente en un punto... 5

Ejemplo 1 ... 8

3.Función creciente en un intervalo ... 8

Ejemplo 2 ... 11

4.Función decreciente en un intervalo ... 13

Ejemplo 3 ... 15

Ejemplo 4 ... 17

5.Condición suficiente de función creciente en un punto... 17

Ejemplo 5 ... 19

Ejemplo 6 ... 19

Ejemplo 7 ... 20

6.Condición suficiente de función decreciente en un punto... 21

Ejemplo 8 ... 22

Ejemplo 9 ... 22

Ejercicio nº1... 24

Ejercicio nº2 ... 25

Ejemplo 10 ... 27

Ejemplo 11 ... 27

7.Extremos (máximos y mínimos) de una función... 29

7.1.Máximo relativo de una función en un punto ... 29

7.2.Máximo absoluto de una función en un punto ... 31

Ejemplo 12... 31

Ejemplo 13 ... 31

7.3.Mínimo relativo de una función en un punto ... 31

7.4.Mínimo absoluto de una función en un punto ... 33

Ejemplo 14... 33

Ejemplo 15 ... 33

8.Condición necesaria para la existencia de un extremo ... 34

Ejemplo 16 ... 35

Ejemplo 17 ... 35

Ejemplo 18 ... 36

9.Condiciones suficientes para la existencia de un extremo... 36

Ejemplo 19 ... 38

Ejemplo 20 ... 40

10.Concavidad y convexidad de una función en un punto ... 41

10.1.Función cóncava hacia arriba o convexa abajo en un punto... 41

10.2.Func. cóncava hacia arriba o convexa abajo en un intervalo.. 42

10.3.Func. cóncava hacia arriba o convexa abajo en su dominio ... 44

10.4.Func. cóncava hacia abajo o convexa arriba en un punto... 44

10.5.Func. cóncava hacia abajo o convexa arriba en un intervalo.. 45

10.6.Func. cóncava hacia abajo o convexa arriba en su dominio.... 46

11.Determinación de la concavidad-convexidad ... 46

Ejemplo 21 ... ...50

(7)

Página

Ejemplo 23 ... 51

Ejemplo 24 ... 52

12.Puntos de inflexión ... 57

13.Condiciones suficientes para determinar la inflexión ... 57

Ejemplo 25 ... 60

Ejemplo 26 ... 64

14.Asíntota oblicuas de una función ... ... 66

15.Forma de hallar las asíntotas oblicuas de una función ... 70

Ejemplo 27 ... 71

Ejemplo 28 ... 73

16.Estudio exhaustivo de una función ... 74

17.Problemas de optimización ... 79

Problema nº1 ... 79

(8)

Introducción.-Con este tema pretendemos que el alumno comprenda y valore la información que aporta el conocimiento de la derivada y las derivadas sucesivas de una función y sus valores en un punto

x = a, para conocer el comportamiento de dicha función en ese punto, en un intervalo o en todo su dominio.

Cuando nos referimos a la idea “comportamiento de una función”, nos referimos a conceptos vistos en temas anteriores, esto es, “crecimiento”, “decrecimiento”, “concavidad”, “convexidad”,”máximo”, “mínimo”, “puntos de inflexión”, etc.

Generalmente, el estudio de una función, esto es, su comportamiento, referido a un punto

x = a, se denomina “estudio local de una función”, ya que dicho estudio está localizado en un punto. Debe entenderse que para conocer el comportamiento general sea necesario la localización de puntos concretos de la función, tales como máximos, mínimos, inflexiones etc.

Recordemos que para comenzar este tema es necesario el estudio previo de los siguientes:

L Funciones reales de variable real

L Derivadas de funciones

L Gráficas de funciones reales de variable real

L Propiedades y formas de las funciones reales de variable real.

En el presente tema recordaremos y ampliaremos muchos de los conceptos explicados en los temas mencionados.

1.Función creciente en un

punto.-(NOTA: Es recomendable ver el tema “Propiedades y formas de las funciones reales de variable real”) Z Sea y = f (x) una función real de variable real.

Z Sea Df su dominio y sea a un número de ese dominio, es decir, a0Df

Vamos a definir el concepto de función creciente en el punto a :

Vamos a expresar la definición anterior matemáticamente (y) :

Aplicaciones de las derivadas

(estudio de funciones)

(9)

figura1 figura2

En la figura 1 se aprecia como la gráfica de y = f (x) “atraviesa” la recta vertical x = a

de “izquierda a derecha” y “subiendo”.

La figura 2 explica el concepto viendo como se verifica que f (a&_{) <}_f₍_a_{) <}_f₍_a+_{) en un}

entorno de centro a y radio ε

Gráficamente, una función que es creciente en el punto x = a, “atraviesa” la recta vertical “situada” en

x = a “pasando” del “lado izquierdo” al “lado derecho” “subiendo”.

Observa la gráfica de la izquierda e intenta comprender la coherencia de esta con la definición de que y = f (x) es creciente en el punto x = a.

Nótese que la “franja” delimitada por el entorno E_g = (a&g, a+g) es “atravesada” por la función de izquierda a derecha “subiendo”.

Fuera de esa “franja”, es posible que la función cambie de tendencia, es decir, “baje”

figura 3

El tamaño del entorno no tiene ninguna importancia, puede ser grande, pequeño, infinitamente pequeño, etc.

La forma de la gráfica de la función creciente en x = a puede ser muy distinta. Veamos: En la figura 3 tenemos “trozos”de cuatro funciones imaginarias. Todas ellas son crecientes en el punto a0ú. Hagamos las siguientes observaciones:

( La función y = f (x) atraviesa la recta vertical en x = a de forma horizontal, es decir, ni sube ni baja (obsérvese que cumple la definición).

( La función y = g (x) es una recta (al menos en un entorno de centro a) que tiene pendiente positiva.

y f x es creciente en a E a a a si x verifica que a x a entonces f x f a si x verifica que a x a entonces f a f x

= ⇔ ∃ = − + − < < ≤

< < + ≤

( ) ( ) ( , ) ( ) ( )

( ) ( )

ε ε ε

ε ε

(10)

( Las otras dos gráficas son curvas.

Otra forma de expresar que una función y = f (x) es creciente en un punto x = a, es :

(yy)

Aunque la expresión anterior no es una definición rigurosa de función creciente en a, si es bastante intuitiva y útil para resolver ejercicios. Nos dice lo siguiente:

Hemos definido el concepto de función creciente en un punto. Ahora vamos a modificar ligeramente esta definición y tenemos la de “función estrictamente creciente en un punto”.

Matemáticamente sería (yyy) :

La figura 3 nos aclara la diferencia entre función creciente y estrictamente creciente en un punto x = a :

) Las cuatro funciones representadas son crecientes en el punto x = a , pero las funciones y = g (x), y = h(x) e y = r(x) son, además, estrictamente crecientes. ) Observa que la función y = f (x) cumple la definición de función creciente en el

punto x = a, pero no cumple la de función estrictamente creciente. ) Nótese que f (a&_{) =}_f₍_a_{) =}_f₍_a+₎

g (a&_{) < g (}_a_{) <}_g₍_a+₎

h (a&_{) <}_h₍_a_{) <}_h₍_a+₎

r (a&_{) <}_r₍_a_{) <}_r₍_a+₎

La definición (y) la podemos modificar ligeramente y quedaría (IV y):

Se dice que la función y = f (x) es estrictamente creciente en el punto a si existe un entorno de centro a y radio g tal que si x está en la mitad izquierda del ese entorno, su imagen es menor que la de a y si x está en la mitad derecha, su imagen es mayor que la de

a

.

y f x es creciente en a R f a f a f a f a

= ∈ ⇔ ≤

≤

  

−

+

( ) ( ) ( )

( ) ( )

y f x es estric crec en a E a a a si x verifica que a x a entonces f x f a si x verifica que a x a entonces f a f x

= ⇔ ∃ = − + − < < <

< < + <

( ) . . ( ) ( , ) ( ) ( )

( ) ( )

ε ε ε

ε ε

y f x es creciente en a E a x E a si x verifica que x a entonces f x f a si x verifica que x a entonces f x f a = ⇔ ∃ ∀ ∈  _>< ≤_≥



( ) ( ) ( ) ( ) ( )

( ) ( )

ε ε

(11)

De la definición (IV y) sacaremos otra nueva:

( La expresión x < a equivale a la expresión x&a < 0

( La expresión f (x)# f (a) equivale a la expresión f (x)&f (a) # 0 Entonces:

{ x a

f x f a

f x f a x a

negativo o cero negativo

equivale

− <

− ≤

 

 ⇔

−

− = ≥

0

0 0

( ) ( )

) La expresión x > a equivale a la expresión x&a > 0

) La expresión f (x)$ f (a) equivale a la expresión f (x)&f (a) $ 0 Entonces:

{ x a

f x f a

f x f a x a

positivo o cero positivo

equivale

− >

− ≥

 

 ⇔

−

− = ≥

0

0 0

( ) ( )

Por tanto,

∀ ∈

x

E a se verifica que

_ε

( )

f x( )_{x a}−₋ f a( )

≥

0

De este modo, definimos (V y):

Veamos la interpretación gráfica de esta última definición:

Obsérvese lo siguiente:

3 Si a&ε < x < a se verifica que: f x( )_{x a}−₋ f a( )= negativo_negativo= positivo

3 Si a < x < a+ ε se verifica que: f x( )_{x a}−₋ f a( )= positivo_positivo= positivo

Es decir:

,

∀ ∈

x E a es

_ε

( )

f x( )_{x a}−₋ f a( )

≥

0

condición que debe cumplir una función

f (x) para ser creciente en x = a. Si la condición fuese :

∀ ∈

x E a es

_ε

( )

f x( )_{x a}−₋ f a( )

>

0

tendríamos la definición de función estrictamente creciente en x = a.

Por tanto (VI y):

y f x es creciente en a E a x E a se verifica que f x f a

x a

= ⇔ ∃ ∀ ∈ −

− ≥

( ) _ε( ) _ε( ) ( ) ( ) 0

y f x estric creciente en a E a x E a se verifica que f x f a

x a

= ⇔ ∃ ∀ ∈ −

− >

(12)

2.Función decreciente en un

punto.-(NOTA: Es recomendable ver el tema “Propiedades y formas de las funciones reales de variable real”) Z Sea y = f (x) una función real de variable real.

Z Sea Df su dominio y sea a un número de ese dominio, es decir, a0Df

Vamos a definir el concepto de función decreciente en el punto a :

Vamos a expresar la definición anterior matemáticamente (i) :

figura 5 figura6

En la figura 5 se aprecia como la gráfica de y = f (x) “atraviesa” la recta vertical x = a

de “izquierda a derecha” y “bajando”.

La figura 6 explica el concepto viendo como se verifica que f (a&_{) >}_f₍_a_{) >}_f₍_a+_{) en un}

entorno de centro a y radio ε

Gráficamente, una función que es decreciente en el punto x = a, “atraviesa” la recta vertical “situada” en x = a “pasando” del “lado izquierdo” al “lado derecho” “bajando”.

Observa la gráfica de la izquierda e intenta comprender la coherencia de esta con la definición de que y = f (x) es decreciente en el punto x = a.

Nótese que la “franja” delimitada por el entorno Eg = (a&g, a+g) es “atravesada” por la función

de izquierda a derecha “bajando”.

Fuera de esa “franja”, es posible que la función cambie de tendencia, es decir, “suba”

Se dice que la función y = f (x) es decreciente en el punto a si existe un entorno de centro a

y radio g tal que si x está en la mitad izquierda del ese entorno, su imagen es mayor o igual que la de a y si x está en la mitad derecha de ese entorno, su imagen es menor o igual que la de a.

y f x es decreciente en a E a a a si x verifica que a x a entonces f x f a si x verifica que a x a entonces f a f x = ( ) ⇔ ∃ ( )=( − , + ) _{< < +}− < < ( )≥_≥ ( )

( ) ( )

ε ε ε

(13)

El tamaño del entorno no tiene ninguna importancia, puede ser grande, pequeño, infinitamente pequeño, etc.

La forma de la gráfica de la función decreciente en x = a puede ser muy distinta. Veamos:

En la figura 7 tenemos “trozos”de cuatro funciones imaginarias. Todas ellas son decrecientes en el punto a0ú. Hagamos las siguientes observaciones:

Z La función y = f (x) atraviesa la recta vertical en x = a de forma horizontal, es decir, ni sube ni baja (obsérvese que cumple la definición).

Z La función y = g (x) es una recta (al menos en un entorno de centro a) que tiene pendiente negativa.

( Las otras dos gráficas son curvas.

Otra forma de expresar que una función y = f (x) es decreciente en un punto x = a, es :

(ii)

Aunque la expresión anterior no es una definición rigurosa de función decreciente en a, si es bastante intuitiva y útil para resolver ejercicios. Nos dice lo siguiente:

Hemos definido el concepto de función decreciente en un punto. Ahora vamos a modificar ligeramente esta definición y tenemos la de “función estrictamente decreciente en un punto”.

Matemáticamente sería (iii) :

La figura 7 nos aclara la diferencia entre función decreciente y estrictamente decreciente en un punto x = a :

; Las cuatro funciones representadas son decrecientes en el punto x = a , pero las funciones y = g (x), y = h(x) e y = r(x) son, además, estrictamente decrecientes. Se dice que la función y = f (x) es estrictamente decreciente en el punto a si existe un entorno de centro a y radio g tal que si x está en la mitad izquierda del ese entorno, su imagen es mayor que la de a y si x está en la mitad derecha, su imagen es menor que la de

a

.

y f x es decreciente en a R f a f a

f a f a

= ∈ ⇔ ≥

≥

   

−

+

( ) ( ) ( )

( ) ( )

y f x es estric decrec en a E a a a si x verifica que a x a entonces f x f a si x verifica que a x a entonces f a f x

= ( ) . . ⇔ ∃ ( ) (= − , + ) _{< < +}− < < ( )>_> ( ) ( ) ( )

ε ε ε ε _ε

“La función y = f (x) es decreciente en el punto x = a sí y sólo sí para valores de x

(14)

; Observa que la función y = f (x) cumple la definición de función decreciente en elpunto x = a, pero no cumple la de función estrictamente decreciente.

; Nótese que f (a&_{) =}_f₍_a_{) =}_f₍_a+₎

g (a&_{) > g (}_a_{) >}_g₍_a+₎

h (a&_{) >}_h₍_a_{) >}_h₍_a+₎

r (a&_{) >}_r₍_a_{) >}_r₍_a+₎

La definición (i) la podemos modificar ligeramente y quedaría (IV i):

De la definición (IV i) sacaremos otra nueva:

( La expresión x < a equivale a la expresión x&a < 0

( La expresión f (x)$ f (a) equivale a la expresión f (x)&f (a) $ 0 Entonces:

{ x a

f x f a

f x f a x a

positivo o cero negativo

equivale

− <

− ≥

 

 ⇔

−

− = ≤

0

0 0

( ) ( )

) La expresión x > a equivale a la expresión x&a > 0

) La expresión f (x)# f (a) equivale a la expresión f (x)&f (a) # 0 Entonces:

{ x a

f x f a

f x f a x a

negativo o cero positivo

equivale

− >

− ≤

 

 ⇔

−

− = ≤

0

0 0

( ) ( )

Por tanto,

∀ ∈

x

E a se verifica que

_ε

( )

f x( )_{x a}−₋ f a( )

≥

0

De este modo, definimos (V i):

A la derecha tenemos la interpretación gráfica: Obsérvese lo siguiente:

3 Si a&ε < x < a se verifica que: f x( )_{x a}−₋ f a( )= _negativopositivo = negativo

3 Si a < x < a+ ε se verifica que: f x( )_{x a}−₋ f a( )= negativo_positivo = negativo

Es decir:

,

∀ ∈

x E a es

_ε

( )

f x( )_{x a}−₋ f a( )

≤

0

condición que debe cumplir una función

f (x) para ser decreciente en x = a. Si la condición fuese :

y f x es decreciente en a E a x E a si x verifica que x a entonces f x f a si x verifica que x a entonces f x f a

= ⇔ ∃ ∀ ∈  _>< ≥_≤



( ) ( ) ( ) ( ) ( )

( ) ( ) ε ε

y f x es decreciente en a E a x E a se verifica que f x f a

x a

= ⇔ ∃ ∀ ∈ −

− ≤

(15)

tendríamos la definición de función estrictamente decreciente

∀ ∈x E a es_ε( ) f x( )_{x a}−₋ f a( )<0 en el punto x = a.

Por tanto (VI i):

Ejemplo

1.-Consideremos la función f x( )= −x2 + 9. Queremos estudiar su crecimiento decrecimiento en el punto x = 2.

Veamos

P Comprobemos si cumple alguna de las definiciones (VI y) o (VI i): P Imaginemos un entorno Eε(2) = (2&ε , 2+ε)

P Tomemos un número de su mitad izquierda, 2&_{y otro de su mitad derecha, 2}+

( )

x f f

= ⇒ −

− =

− + −

− = = <

= ⇒ −

− =

− + −

− = = <



  

   

− −

−

+

− +−

+ +

+

−

+ −+

2 2 2

2 2

2 9 5

2 2

0

0 0

2 2 2

2 2

2 9 5

2 2

0

0 0

2

( ) ( )

P A la vista de lo anterior tenemos que:

∃

E

_ε

( )

2 tal que x

∀ ∈

E

_ε

( )

2 se verifica que

f x( )_x₋−₂f( )2

<

0

Por tanto: “La funciónf x( ) = −x2 + 9 es estrictamente decreciente en el punto x = 2 “

NOTA: Aplicar la definición para averiguar si una función es creciente o decreciente en un punto no es el método más adecuado, aunque hemos visto con el ejemplo anterior que hay casos en los que es factible. Veremos a lo largo de este tema como el uso de la derivada es el método más adecuado para este fin.

3.Función creciente en un

intervalo.-(NOTA: Es recomendable ver el tema “Propiedades y formas de las funciones reales de variable real”) º Sea y = f (x) una función y sea D_f dú su dominio.

º Sea A un intervalo de su dominio. Es decir, A dDf .

Vamos a definir el concepto “ f (x) creciente en A” ) Una forma de definirlo:

Matemáticamente:

“La función y = f (x) es creciente en el intervalo A si lo es en todos los puntos de A”

y f x estric decreciente en a E a x E a se verifica que f x f a

x a

= ⇔ ∃ ∀ ∈ −

− <

(16)

f x creciente en A

( )

⊂

D

_f

⇔ ∀ ∈

a

A f x creciente en a

, ( )

f x estr crec en A

( )

.

⊂

D

_f

⇔ ∀ ∈

a

A f x estr crec en a

, ( )

.

f x es creciente en A D

a b A a b entonces f a f b

f

( )

, , ( ) ( )

⊂

∀ ∈ < ≤

1444442444443

c

64444444744444448

) Otra forma de definirlo: (e)

Es decir, y = f (x) es creciente en A si dados dos números de A, el que está a la izquierda (a) tiene una imagen (f (a)) menor o igual que la imagen (f (b)) del que está a la derecha (b).

Matemáticamente será:

Š Gráficamente se interpreta del siguiente modo: figura 9 En la figura de la derecha tenemos:

 A = [α,β] intervalo cerrado.  Cualesquiera que sean los números

a y b del intervalo A , tales que sea

a < b, entonces se verifica que

f (a) # f (b). En este caso concreto es

f (a) < f (b).

 Nótese como la gráfica de la función atraviesa la franja existente entre la rectas x = α y x = β ”subiendo” de izquierda a derecha.

 Nótese como en cualquier punto del intervalo A la función y = f (x) es creciente.

 En este caso la función es estrictamente creciente en todos los puntos del intervalo

A, es decir, es estrictamente creciente en todo el intervalo A.

La definición de función estrictamente creciente en un intervalo A es la siguiente:

Matemáticamente:

NOTA: El intervalo A puede ser abierto o cerrado. Otra forma de definirlo:

“La función y = f (x) es estrictamente creciente en el intervalo A si lo es en todos los puntos de A”.

(17)

f x es estrictamente creciente en A D

a b A a b entonces f a f b

f

( )

, , ( ) ( )

⊂

∀ ∈ < <

1444444442444444443

c

64444444744444448

Es decir, y = f (x) es estrictamente creciente en A si dados dos números de A, el que está a la izquierda (a) tiene una imagen (f (a)) menor que la imagen (f (b)) del que está a la derecha (b)

Vamos a distinguir de un modo gráfico la diferencia existente entre función creciente y estrictamente creciente en un intervalo:

figura 10

En la figura 10 tenemos cuatro gráficas de funciones trazadas en un intervalo de extremos α y β.

La función y = f (x) es estrictamente creciente en todo el intervalo [α , β].

Las funciones y = g (x) , y = h (x) e y = r (x) son crecientes en el intervalo [α , β], pero no son estrictamente crecientes.

La función y = g (x) es constante en todo el intervalo (aunque sea constante, cumple la definición de ser creciente). Se entiende así que una función constante es creciente, aunque no estrictamente.

(18)

La expresion

&

& ( ) ( )

( ) ( )

a b equivale a que

a b y b a

f a f b equivale a que

f a f b y f b f a <

− <

− >   

 

≤

− ≤

− ≥

  

 

0

Ejemplo 2

.-Demuestra que y f x que es estrictamente creciente en el intervalo A = (& 4 , 0).

x

= ( )= 1₂

Veamos:

Si construimos la gráfica de esa función tendremos:

Por tanto, hemos demostrado que

∀

α β

,

∈ −∞

(

,

0 )

tales que

α β

<

,

es f

( )

α

<

f

( )

β

(Nótese que hemos llamado α =&a y β = &b ).

Conclusión: La función y f x es estrictamente creciente en el intervalo A = (& 4 , 0)

x

= ( )= 1₂

Modificando la definición (e) podemos obtener otra definición de función creciente en un intervalo. Veamos:

La definición quedará:

figura 11

Gráfica de la función y f x x = ( )= 1₂

Obsérvese como todo número real, excepto el cero tiene imagen.

Q En la gráfica, a simple vista se aprecia que la función es estrictamente creciente en todo el intervalo (& 4,0), ya que la curva “viaja” por todo el intervalo de izquierda a derecha subiendo.

Q V a m o s a d e m o s t r a r l o matemáticamente:

,Sean &a y &b dos números negativos, es decir, &a,&b0 (& 4,0) tales que

&a<&b.

, Es evidente que a y b son positivos. Además a > b.

, Es evidente que (&a)2₌_a2 _>b2₌₍_&_b)2

, Entonces: f a

a a b b f b ( )

( ) ( ) ( )

− =

− = < = − = −

1 1 1 1

2 2 2 2

f b f a b a

o

f a f b a b

o

( ) ( ) ( ) ( )

−

− ++

− −

= = +

0

De las equivalencias de la derecha deducimos que:

(19)

f b f a b a f a f b

a b

( ) ( )

−

− ++

−

− −−

= = + = = +

(ee)

Para el caso de una función estrictamente creciente será:

(eee)

Vamos a interpretar gráficamente estas últimas definiciones:

Observando la figura 12 apreciamos:

3 Tenemos un intervalo de

extremos α y β (cerrado o abierto) y una función f(x) definida en él.

3 T o m a m o s d o s p u n t o s cualesquiera a y b de ese intervalo.

3 Notamos que:

3 Es decir, si tomamos dos puntos cualesquiera x1 y x2 del intervalo, el cociente de la forma

es positivo, sin importar que x1 < x2 o que x1 > x2 (en el caso de la figura

f x f x

x x

( )₁ ( ₂)

1 2

− −

12, la función es estrictamente creciente en el intervalo [α ,β] ).

En la figura 13 tenemos la gráfica de una función que no es creciente en el intervalo [α , β] ya que a,b

0[α ,β] y sin embargo:

f b( )_{b a}−₋ f a( )

=

negativo_positivo

<

0

Puede apreciarse que en unos puntos del intervalo la función es creciente y en otros decreciente. Si en vez de considerar un intervalo, consideramos el dominio de la función, podemos definir el concepto de función creciente (o estrictamente creciente) en su dominio D.

(IVe) f x es creciente en el( ) intervalo A ⇔ ∀a b, ∈ A es f b( )_{b a}−₋ f a( ) ≥0

f x es estric creciente en el( ) . intervalo A⇔ ∀a b A es, ∈ f b( )_{b a}−₋ f a( ) >0

(20)

f(x) decrec. en A ⊂ D _f ⇔ ∀ ∈ a A, f(x) decrec en a.

f x es decreciente en A D

a b A a b entonces f a f b f

( )

, , ( ) ( )

⊂

∀ ∈ < ≥

144444424444443 c

64444444744444448

(Ve)

4.Función decreciente en un

intervalo.-(NOTA: Es recomendable ver el tema “Propiedades y formas de las funciones reales de variable real”) º Sea y = f (x) una función y sea Df dú su dominio.

º Sea A un intervalo de su dominio. Es decir, A dDf .

Vamos a definir el concepto “ f (x) decreciente en A” ; Una forma de definirlo:

Matemáticamente:

) Otra forma de definirlo: (q)

Es decir, y = f (x) es decreciente en A si dados dos números de A, el que está a la izquierda (a) tiene una imagen (f (a)) mayor o igual que la imagen (f (b)) del que está a la derecha (b).

Gráficamente se interpreta del siguiente modo:

Dibujamos la gráfica de una función que es decreciente en un intervalo A = [α,β]

Observa la gráfica de la derecha (figura 14): 9 A = [α,β] intervalo cerrado.

9 Cualesquiera que sean los números reales a y b

del intervalo A , tales que a < b, se verifica que

f (a) $ f (b).En este casoconcreto es f (a) > f (b) 9 Nótese como la gráfica de la función atraviesa la franja existente entre las rectas de ecuaciones

x = α y x = β ”bajando” de izquierda a derecha. 9 Nótese como en cualquier punto del intervalo A

la función y = f (x) es decreciente.

9 En este caso la función es estrictamente decreciente en todos los puntos del intervalo A, es decir, es estrictamente decreciente en todo el intervalo A.

“La función y = f (x) es decreciente en el intervalo A si lo es en todos los puntos de A”

“La función y = f (x) es decreciente en el intervalo A si dados dos números cualesquiera a y b de ese intervalo, tales que a < b, entonces f (a)$f (b)”.

(21)

f x estrictamente

decreciente en A D_f a A f x estrictamente decreciente en a

( )

, ( )

⊂  

⇔ ∀ ∈

f x es estrictamente decreciente en A D

a b A a b entonces f a f b

f

( )

, , ( ) ( )

⊂

∀ ∈ < >

144444444424444444443

c

64444444744444448

La definición de función estrictamente decreciente en un intervalo A es la siguiente:

Matemáticamente:

Otra forma de definirlo:

Es decir, y = f (x) es estrictamente decreciente en A si dados dos números de A, el que está a la izquierda (a) tiene una imagen (f (a)) mayor que la imagen (f (b)) del que está a la derecha (b).

figura 15

Distingamos de un modo gráfico la diferencia que existe entre función decreciente y estrictamente decreciente en un intervalo En la figura 15 tenemos cuatro gráficas de otras cuatro funciones.

La función y = f(x) es estrictamente decreciente en todo el intervalo [α , β] Las funciones y=g(x),

y=h(x) e y = r(x) son decrecientes, pero no en sentido estricto.

La función y = g (x) es constante en todo el intervalo [α , β]. Nótese que es creciente y decreciente.

“La función y = f (x) es estrictamente decreciente en el intervalo A si lo es en todos los puntos de A”.

(22)

[ ]

f

x f x x

: ,

( ) cos

0

π

 →

 → =

   

R

La expresion

&

& ( ) ( )

( ) ( )

a b equivale a que

a b y b a

f a f b equivale a que

f a f b

y

f b f a

<

− <

− >

  

 

≥

− ≥

− ≤

  

 

0

Ejemplo 3

.-Consideremos la función coseno definida en el intervalo cerrado de extremos 0 y π :

Veamos que es estrictamente decreciente en todo el intervalo [0 , π]. 3 f (0) = cos 0 = 1 ; f (π) = cosπ = &1

3 œx0[0 , π] , se verifica que &1 #f (x) #1

3 Sabemos que œα,β 0 [0 , π] tales que α<β , se verifica que f (α) = cos α < cosβ = f (β) (Recordar la definición de coseno de un ángulo y su interpretación gráfica en la circunferencia goniométrica o círculo trigonométrico).

Dibujemos su gráfica:

figura 16

En la gráfica de la izquierda, correspondiente a la función f (x) = cos x , definida en el intervalo cerrado [0,π], apreciamos que:

∀

a b

,

∈

[ ]

0 ,

π

a b es f a

<

,

( )

>

f b

( )

La gráfica “recorre” todo el intervalo [0,π], de izquierda a derecha, “bajando”.

Nótese que la gráfica corta al eje de abcisas en el punto (π/2 , 0)

Modificando la definición (q) podemos obtener otra definición de función creciente en un intervalo. Veamos:

La definición quedará:

(qq)

Para el caso de una función estrictamente decreciente será:

f x es decreciente en el( ) intervalo A ⇔ ∀a b, ∈ A es f b( )_{b a}−₋ f a( ) ≤0

f b f a b a

o

f a f b a b

o o o ( ) ( )

( ) ( ) − −

− + −

−

+ −

= = −

0 0

0

De las equivalencias de la derecha deducimos que:

(23)

f b f a b a f a f b

a b

( ) ( )

−

− −+

−

− +−

= = − = = −

(qqq)

Vamos a interpretar gráficamente estas últimas definiciones:

Observando la figura 17 apreciamos: 3 Tenemos un intervalo de

extremos α y β (cerrado o abierto) y una función f(x) definida en él.

3 T o m a m o s d o s p u n t o s cualesquiera a y b de ese intervalo.

3 Notamos que:

3 Es decir, si tomamos dos puntos cualesquiera x₁ y x₂ del intervalo, el cociente de la forma

es negativo, sin importar que x1 < x2 o que x1 > x2 (en este caso la figura

f x f x

x x

( )₁ ( ₂)

1 2

− −

17 la función es estrictamente decreciente en el intervalo [α ,β]).

En la figura 18 tenemos la gráfica de una función que no es decreciente en el intervalo [α , β] ya que a,b 0[α ,β] y sin embargo: f a( )_{a b}−₋ f b( )

=

positivo_positivo

>

0

Puede apreciarse que en unos puntos del intervalo la función es creciente y en otros decreciente. Si en vez de considerar un intervalo, consideramos el dominio de la función, podemos definir el concepto de función decreciente (o estrictamente decreciente) en su dominio D.

(IVq)

(Vq) f x es estric decreciente en el( ) . intervalo A⇔ ∀a b, ∈ A es f b( )_{b a}−₋ f a( ) <0

f x es decreciente en D( ) _f ⇔ ∀a b D, ∈ _f es f b( )_{b a}−₋ f a( ) ≤ 0

(24)

Supongamos que a b

a b e e

b a a b

f b f a b a

b e a e b a f a f b

a b

a e b e a b

a b

b a

a b

< ⇒

< < − > − <



  

  



  

  

⇒

−

− =

−

− =

+ + > −

− =

−

− =

− − >



  

  

3 3 3 3

3 3

0 0

0

( ) ( )

Ejemplo 4

.-Queremos averiguar si la función f x( )= x e3 x es creciente o decreciente en todo su dominio.

Veamos:

O Observamos que œx0ú , f (x) = x3_ex_{0ú. Por tanto, D} f = ú.

O Imaginemos dos números cualesquiera a, b 0ú= Df

Es decir, œx1, x2 0Df se verifica que , es decir, la función f (x) es

f x f x

x x

( )1 ( 2)

1 2 0

−

− >

estrictamente creciente en todo ú.

Al ser estrictamente creciente, ya no puede ser decreciente.

5.Condición suficiente de función creciente en un

punto.-L Sea y = f (x) una función de dominio Df

L Sea a un punto de su dominio, es decir, a0Df y tal que f es derivable en a.

Queremos saber si f (x) es creciente en a, es decir, ¿qué condición debe cumplir la función f (x) para que podamos asegurar que es creciente en el punto a?

Pues bien:

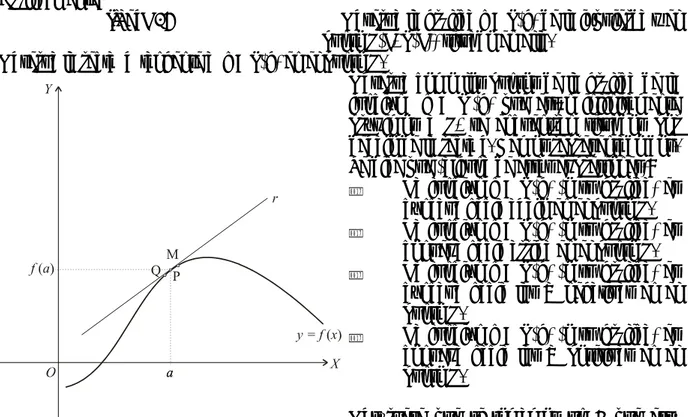
Expresado de otra forma:

Matemáticamente:

Nota: La idea de “condición suficiente” viene porque “para asegurar que f es creciente en el punto a, es suficiente con que f ´(a) sea positiva”. Nótese que se exige que f ´(a) exista. Antes de demostrar esta importante propiedad, lo veremos gráficamente, es decir, aunque lo siguiente no es una demostración rigurosa, si nos permite relacionar la condición de que la derivada f ´(a) sea positiva con que f (x) es creciente en x = a.

“Para asegurar que f (x) es creciente en el punto x = a es suficiente que f ´(a) > 0 “

“Si la derivada de f en el punto a es positiva, entonces la función f es creciente en a”

(25)

f ′( )a = tg

α

=m_r >0

figura 19.a

Sabemos que por el punto P(a,f (a)) pasa la gráfica de la función f, pero queremos saber si pasa por ese punto creciendo o decreciendo, es decir, queremos saber si “atraviesa” la línea vertical “subiendo” o “bajando”.

figura 19.b

Supongamos que hemos averiguado que la derivada de f en el punto x = a es positiva, es decir, la recta tangente a la gráfica de f (x) en el punto P(a,f (a)) tiene pendiente positiva, lo que significa que:

siendo mr = pendiente de la recta r.

figura 19.c

Considerando que r es tangente a f (x), en P, una forma aproximada de la gráfica de

f (x) podría ser como aparece en esta figura, es decir, creciente estrictamente. En este caso se ha dibujado de forma que la gráfica es cóncava hacia arriba (convexa hacia abajo) en el punto x = a.

figura 19.d

En esta figura tenemos otra forma posible de la gráfica de f (x) a su paso por el punto P(a,f (a)), es decir, estrictamente creciente. En este caso la tangente “va” por encima de la curva en un entorno del punto a, es decir, la gráfica de f (x) es cóncava hacia abajo (convexa hacia arriba) en el punto a.

figura 19.e

Puede apreciarse en este caso otra posibilidad de la gráfica de f (x), es decir, estrictamente creciente en x = a, pero la recta tangente atraviesa a la gráfica. Nótese que el punto P(a,f (a)) es un punto de inflexión de f (x).

Debe quedar clara la idea de que:

(26)

Observación: Nótese que la condición expuesta es una condición suficiente pero no necesaria, es decir, “sif ´(a) > 0, podemos asegurar que f es creciente en a, pero puede ocurrir que f ′( )a /> 0 y, sin embargo, f sea creciente en a”.

Veamos la idea gráfica de esta observación:

En la figura 20 tenemos la gráfica de una función f (x) que “pasa” por el punto P(a, f (a)) y cuya recta tangente en ese punto es horizontal, es decir:

f ′( )a =m_r = pendiente de r= 0 Nótese que la función es estrictamente creciente en el punto a, es decir, a pesar de que la derivada de

f en el punto a no es positiva, la función es estrictamente creciente en dicho punto.

Lo anterior se interpreta como que para ser creciente en un punto, no es necesario que la derivada sea positiva

Ejemplo 5

.-Sea la función f x e .

x x ( )=

Queremos averiguar si es creciente en los puntos x = 0, x = 1 y x = 2. Veamos:

K Hallamos la función derivada de f (x) :

f x e x e

x

e x x

x x x

′( )= −₂ = ( ₂−1)

K Veamos el valor de la derivada para cada caso:  Para x = 0 no existe f (0), es decir, 0 óDf

Por tanto, f no es creciente en el punto x = 0, simplemente porque la función no existe en ese punto.

 Para x=1⇒ f( )1 = e₁.0= =0₁ 0

En este caso la derivada no nos informa sobre el crecimiento de la función f (x) en el punto x = 1

 Para x= 2⇒ f ′ 2 = e

( )

2 1− = e > ⇒ f x es creciente en x=

2 4 0 2

2

( ) ( )

Ejemplo 6

.-Sea la función f x( ) (= x−5)3

Queremos averiguar si es creciente en el punto x = 5. Veamos:

(27)

( ) ( ) ( )

( )

( ) ( ) ( )

( )

f f f

f f f f es creciente

en x

5 5 5 0 0

5 5 5

5

3 3

3 ₃

3 3

− − − −

+ + + +

− +

= − = =



  

  

⇒ < < ⇒

= 



 _

R Hallemos el valor de la derivada en x = 5: f ′( )5 = ⋅ −3 5 5( )2= ⋅ =3 0 0 La derivada no nos informa sobre el crecimiento de f en el punto x = 5. R Intentemos aplicar otro método :

$ Imaginemos un entorno de centro 5 y radio tan pequeño como queramos y estudiemos las imágenes de f (x) en ese entorno .

R El punto anterior nos indica que la función es creciente estrictamente en x = 5. R Representemos gráficamente la función:

x y = (x&5)3

5 0

5& ₀&

5+ ₀+

4 &1

6 1

3 &8

7 8

&4 &4

%4 %4

La gráfica de f (x) (figura 21) nos muestra como la función es estrictamente creciente en

x = 5 y como la recta tangente en P(5,0) es el eje de abcisas. Nótese que dicho punto es de inflexión (en este caso pasa de cóncava hacia abajo a cóncava hacia arriba).

Ejemplo 7

.-Sea la función f x( )=2x2 − 5x + 4

Queremos saber en que puntos de su dominio es creciente. Veamos:

W La función f (x) es una función polinómica de grado 2 ( su gráfica es una parábola) y, por tanto, su dominio es ú.

W En los punto a0ú tales que f ´(a) > 0, la función f (x) es creciente. W Hallemos la función derivada: f ´(x) = 4 x - 5

(28)

4 5 0

5 4

x inecuacion x

x

Si x entonces f x

− > > >

  

  

⇒ > ′ >

&

( )

W De lo anterior deducimos que

si

a

>

₄5

entonces f

′

( )

a

>

0 y f creciente en x

=

a

.

Conclusión:

(

)

f x( )=2x2 − 5x + 4 es creciente en el intervalo 5₄,+ ∞

Demostración:

Hemos “demostrado” de un modo gráfico la condición suficiente para que una función sea creciente en un punto x = a. Ahora veremos la demostración formal.

Debemos demostrar que f ´(a) > 0

Y

f es creciente en a

Veamos:

{

f a f a f a

el

es positivo es decir en un entorno E

h

f a h f a h

llamando a h x_{h x a} h

f a h f a

h _x _a

f x f a x a

f(x) - f(a) x-a

′ > ⇒ ′ = > ⇒ ′ = = > ⇒

⇒

>

   

    ⇒

→

+ −

+ = = −

 

→

+ −

→ − −

( ) ( ) lim ( ) lim lim

,

, , (

( ) ( ) ( ) ( ) ( ) ( )

0 0 0

0

0 0

Para valores de x infinitamente proximos a " a"

cociente ε a es

f x es creciente en x a

f(x)- f(a) x-a

)

( ) .

>



  ⇒

⇒ =

0

6.Condición suficiente de función decreciente en un

punto.-L Sea y = f (x) una función de dominio Df

L Sea a un punto (un número real) de su dominio, es decir, a0Df y tal que f ´(a) existe.

Queremos saber si f (x) es decreciente en a, es decir, ¿qué condición debe cumplir la función f (x) para que podamos asegurar que es decreciente en el punto a?

Pues bien:

Expresado de otra forma:

Matemáticamente:

“Para asegurar que f (x) es decreciente en el punto x = a es suficiente que f ´(a) < 0 “

“Si la derivada de f en el punto a es negativa, entonces la función f es decreciente en a”

(29)

Nota: La idea de “condición suficiente” viene porque “para asegurar que f es decreciente en el punto a, es suficiente con que f ´(a) sea negativa”. Nótese que f ´(a) debe existir. Demostración:

En este caso veremos la demostración forma y posteriormente la demostración gráfica.. Debemos demostrar que f ´(a) < 0

Y

f es decreciente en a

Veamos:

{

f a f a f a

el

es negativo es decir en un entorno E a es

h

f a h f a h

llamando a h x_{h x a} h

f a h f a

h _x _a

f x f a x a

f(x) - f(a) x-a

f(x)- f(a) x-a

′ < ⇒ ′ = < ⇒ ′ = = < ⇒

⇒

<

   

  

 ⇒ <

→

+ −

+ = = −

 

→

+ −

→ − −

( ) ( ) lim ( ) lim lim

,

, , ( )

( ) ( ) ( ) ( ) ( ) ( )

0 0 0

0 0

Para valores de x infinitamente proximos a " a"

cociente  ε

  ⇒ ⇒ f x es decreciente en x a( ) = .

Ejemplo 8

.-Sea la función g x( ) = x e−x.

Queremos estudiar su crecimiento o decrecimiento en los puntos x = 0, x = &1 y x = 1 Veamos:

3 Hallamos la función derivada: g x′( )=e−x −x e−x=e−x(1− x)

3 Hallemos su valor en cada uno de los puntos a estudiar:

g e g es creciente en x

g e No podemosdecidir aun sobre el

crecimiento decrecimiento en x

g e e g es creciente en x

e

′ = − = ⋅ = > ⇒ =

′ = − = = ⇒

− =

 

 _

′ − = + = > ⇒ = −

−

( ) ( )

( ) ( ) &

( ) ( )

0 1 0 1 1 1 0 0

1 1 1 0

1

1 1 1 2 0 1

0

1 0

1

Ejemplo 9

.-Sea la función f x( )=2x2 − 5x + 4Queremos saber en que puntos es decreciente. Veamos:

W La función f (x) es una función polinómica de grado 2 y, por tanto, su dominio es ú. W En los punto a0ú tales que f ´(a) < 0, la función f (x) es decreciente.

W Hallemos la función derivada: f ´(x) = 4 x - 5

W Veamos donde es f ´(x) < 0 : 4x− <5 0; 4x<5 ; x < ₄5

W De lo anterior deducimos que

si a< 5₄ entonces f ′( )a <0 y f decreciente en x= a. Conclusión:

(

)

f x( )=2x2 −5x + 4 es decreciente en el intervalo − ∞,5₄

(30)

f ′( )a = tg

α

=m_r <0

figura 22.a

Sabemos que por el punto P(a,f (a)) pasa la gráfica de la función f, pero queremos saber si pasa por ese punto creciendo o decreciendo, es decir, queremos saber si “atraviesa” la línea vertical “subiendo” o “bajando”.

figura 22.b

Supongamos que hemos averiguado que la derivada de f en el punto x = a es negativa, es decir, la recta tangente a la gráfica de f (x) en el punto P(a,f (a)) tiene pendiente negativa, lo que significa que:

siendo mr = pendiente de la recta r.

figura 22.c

Considerando que r es tangente a f (x), en P, una forma aproximada de la gráfica de

f (x) podría ser como aparece en esta figura, es decir, decreciente estrictamente. En este caso se ha dibujado de forma que la gráfica es cóncava hacia abajo (convexa hacia arriba) en el punto x = a.

figura 22.d

En esta figura tenemos otra forma posible de la gráfica de f (x) a su paso por el punto P(a,f (a)), es decir, estrictamente decreciente. En este caso la tangente “va” por debajo de la curva en un entorno del punto a, es decir, la gráfica de f (x) es cóncava hacia arriba (convexa hacia abajo) en el punto a.

figura 22.e

Puede apreciarse en este caso otra posibilidad de la gráfica de f (x), es decir, estrictamente decreciente en x = a, pero la recta tangente atraviesa a la gráfica. Nótese que el punto P(a,f (a)) es un punto de inflexión de f (x).

Debe quedar clara la idea de que:

(31)

f x

como x x

x

′ > − > >

> >

    

    

⇒ > ′ >

( )

, ( )

0

1 0

1

0 1

1 0

1

f x

como x x

x

′ > − > >

> >

    

    

⇒ > ′ >

( )

, ( )

0

1 0

1

0 1

1 0

1

f x x por ser x x

Es decir Si x entonces f x

x x xx

′ < − < < < > <

< ′ <

( ) ; ; ; ( ) ;

: ( )

0 1 0 1 0 1

1 0

1 1

Observación: Nótese que la condición expuesta es una condición suficiente pero no necesaria, es decir, “sif ´(a) < 0, podemos asegurar que f es decreciente ena, pero puede ocurrir que f ′( )a /< 0 y, sin embargo, f sea decreciente en a”.

Veamos la idea gráfica de esta observación:

En la figura 23 tenemos la gráfica de una función f (x) que “pasa” por el punto P(a, f (a)) y cuya recta tangente en ese punto es horizontal, es decir:

f ′( )a =m_r = pendiente de r= 0 Nótese que la función es estrictamente decreciente en el punto

a, es decir, a pesar de que la derivada de f en el punto a no es negativa, la función es estrictamente decreciente en dicho punto.

Es decir, para ser decreciente en un punto, no es necesario que la derivada sea negativa.

Ejercicio nº 1

.-Sea la función

f x

( )

= −

x Lx

( Lx es logaritmo neperiano de x). Se pide:

a) Determina su dominio.

b) Determina en qué puntos es creciente.

c) Determina en qué puntos es decreciente. Solución:

a) Es evidente que f (x) no existe si x # 0. Por tanto: Dominio de f = Df = ú+ = (0, +4)

b) f es creciente en los puntos x tales que f ´(x) > 0 Hallamos f ´(x) :

f

′

( ) 1

x

= −

_x1

c) f es decreciente en los puntos x tales que f

´(x) < 0

De lo anterior deducimos que f es decreciente en el intervalo (0,1)

Por tanto, si x > 1 función f tiene derivada positiva en x, es decir, la función es creciente.

Expresamos que:

(32)

Una forma de expresar los resultados es:

&4 < x # 0 0 < x < 1 1 < x < +4

f no existe f es decreciente f es creciente

Ejercicio nº 2

.-Sea la función

f x

( )

=

x₃3

−

x₂2

−

20 x

Se pide:

a) Determina donde es creciente.

b) Determina donde es decreciente.

c) Indica si es creciente o decreciente en los puntos x = &6 , x = 0 , x = 7´5 , x = &4,

x = 5 Solución:

a) En los punto x tales que f ´(x) > 0, la función es creciente. Hallemos la función derivada de f :

f ′( )x = 3₃x − 2₂x− simplificando   → f ′( )x = x2 − −x 2

20 20

Debemos averiguar qué puntos x verifican la desigualdad x2_&_x_&_{20 > 0}

Como se trata de una inecuación de segundo grado con una incógnita, factorizamos el polinomio x2_&_x_&_20.

Para factorizar el polinomio, debemos resolver la ecuación de 2º grado x2_&_x_&_{20 = 0}

x x x x

x

2 1

2

20 0 1 1 80

2

1 9 2

5 4

− − = ⇒ = ± + = ± =  =_{= −}



Ahora podemos factorizar: f ´(x) = x2_&_x_&_{20 = (}_x_&_{5) (}_x_{+ 4)}

Ahora resolvemos la inecuación (x&5) (x + 4) > 0 :

(x ) (x )

obien

x x

y y

x x

x

obien

x x

y y

x x

x

− + > ⇒

− > ⇒ > + > ⇒ > − 

   

   

 ⇒ > − < ⇒ <

+ < ⇒ < − 

   

   

 ⇒ < − 

   

    

5 4 0

5 0 5

4 0 4

5

5 0 5

4 0 4

4

Por tanto:

f

′

( ) 0

x

> ⇔

x

< −

4 o x

>

5

Conclusión:

b) En los punto x tales que f ´(x) < 0, la función es decreciente. Debemos resolver la inecuación x2_&_x_&_{20 < 0}

Como hemos factorizado en el apartado anterior, resolvemos (x&5) (x + 4) < 0 Efectuamos un razonamiento similar al del punto a):

(33)

(x ) (x )

obien

x x

y y

x x

obien

x x

y y

x x

x − + < ⇒

− > ⇒ >

+ < ⇒ < −

  

 

  

  ⇒

− < ⇒ <

+ > ⇒ > −

  

 

  



 ⇒ − < < 

   

    

5 4 0

5 0 5

4 0 4

5 0 5

4 0 4

4 5

Imposible

Por tanto:

f

′

( ) 0

x

< ⇔ − <

4 x

<

5

Conclusión:

Una forma de resumir los resultados sería:

&4 < x < &4 &4 < x < 5 5 < x < +4

f es creciente f es decreciente f es creciente

c) Determinemos el crecimiento-decrecimiento en los puntos que nos dan: Q f (x) es creciente en x = &6 porque &4 < &6 < &4

Q f (x) es decreciente en x = 0 porque &4 < 0 < 5 Q f (x) es creciente en x = 7´5 porque 5 < 7´5 < + 4 Q f (x) tiene un máximo en el punto x = &4

Q f (x) tiene un mínimo en el punto x = 5

Para comprobar los resultados obtenidos, representamos gráficamente la función:

La figura 24 nos muestra la gráfica de la función dada

f x

( )

=

x₃3

−

x₂2

−

20 x

En ella pueden apreciarse los resultados obtenidos.

Además, hemos señalado el punto M, que se llama

máximo relativo de f (x) y el punto P que se denomina

mínimo relativo de f (x). En el punto M la curva pasa de

creciente a decreciente y en P

de decreciente a creciente. Nótese que la función no está acotada ni superior ni inferiormente.