UNA APLICACIÓN DEL TEOREMA DEL PASO DE
MONTAÑA
Trabajo de Grado
Proyecto Curricular de Matemáticas
Javier David Moreno Paris
Director: Arturo Sanjuán
Universidad Distrital Francisco José de Caldas Bogotá D.C.
Agradecimientos
Quiero agradecer principalmente al profesor Arturo Sanjuán, ha sido un excelente mentor, del cual he aprendido mucho en estos 2 últimos años y me ha colaborado en gran medida en mi formación académica, su ayuda y colaboración en este trabajo han sido fundamentales.
También quiero agradecer a mis padres, que me han dado todo lo necesario para llegar a donde me encuentro hoy, junto con su apoyo incondicional. A mi hermano Manuel que siempre me ha ayudado en todo y a mi novia Julieth que estuvo a mi lado durante toda la realización de este trabajo.
Índice general
INTRODUCIÓN IV
1. PRELIMINARES 1
1.1. Notación y Teoremas Previos . . . 1
1.2. Espacios Lp . . . 6
1.3. Espacios de Sobolev . . . 19
1.4. Teorema Espectral . . . 44
2. TEOREMA DEL PASO DE MONTAÑA 49 2.1. Condiciones Palais-Smale . . . 49
2.2. Principio Variacional de Ekeland . . . 71
2.2.1. Redes . . . 71
2.2.2. Semicontinuidad . . . 78
2.2.3. Enunciado y Demostración del Principio . . . 86
3. UNA APLICACIÓN DEL TEOREMA DEL PASO DE MONTAÑA 98
3.1. El Resorte con Forzamiento . . . 98
3.2. El Lagrangiano . . . 100
3.3. Solución al Problema . . . 104
CONCLUSIONES 106
INTRODUCIÓN
Desde la aparición de un incipiente concepto de función en el siglo XVII, la matemática ha servido para modelar situaciones físicas o abstractas en todos los campos, desde las ciencias naturales hasta la economía y muchas veces en esas situaciones ha aparecido la necesidad de optimizar estos modelos. Eso llevó a los matemáticos, a preguntarse cómo crear un método de encontrar máximos y mínimos, pero las herramientas matemáticas de la época eran muy escasas y la búsqueda de este método se convertiría en uno de los principales problemas abiertos de la matemática de todo el siglo XVII.
Este problema ha sido trabajado por muchos. Fermat (1601-1665) dio el primer método para calcular máximos y mínimos pero no fue publicado si no hasta después de su muerte [Jabri, 2003, pag. 7]. La necesidad de responder esta pregunta de ¿cómo hallar máximos y mínimos?, fue uno de los motores para la creación de la derivada y el cálculo diferencial. Esta teoría que fue creada por la colaboración de muchos (Fermat, Galileo, Cavalieri, Barrow, etc) y que una primera idea del cálculo fue desarrollada por Newton (1660) y Leibniz (1670) y continuada por muchos más matemáticos hasta el día de hoy [Wussing, 1998, pag 137]. Con el cálculo diferencial y el cálculo vectorial el problema de hallar máximos y mínimos se volvió relativamente fácil para una gama amplia de funciones.
más general e incluso puede llegar a ser olvidada. Por esta razón son importantes las aplicaciones. El cálculo variacional (en dimensión infinita) encontró rápidamente aplicaciones en las ecuaciones diferenciales y por ende esta teoría puede ser útil a todos los campos de la ciencia[Jabri, 2003, pag. 9-11].
En este trabajo mostraremos como el cálculo variacional es utilizado para garantizar la existencia de soluciones (débiles) de ecuaciones diferenciales generales que los métodos básicos no pueden resolver, lo haremos a partir delEl Teorema Del Paso De Montañademostrado por Antonio Ambrosetti y Paul Rabinowitz en 1973, Este es un extraordinario resultado y es una de las puntas angulares del cálculo variacional y la teoría de minimax [Jabri, 2003, pag. 12].
CAPÍTULO
1
PRELIMINARES
1.1.
Notación y Teoremas Previos
Para la lectura de este texto se asumen conocimientos generales de análisis, topología y de la teoría de la medida por parte del lector, principalmente la integral de Lebesgue.
Denotamos con(X,X, µ) a un espacio de medida, o mas brevementeX donde Xes laσ-álgebra. Los elementos deXson llamados conjuntos medibles yµes la medida sobre ese espacio. Notamos con M(X,X) al conjunto de funciones medibles a valor real. Tiene sentido definir M+(X,X)
como el conjunto de funciones medibles no negativas y serán de suma importancia los siguientes teoremas tomados de [Bartle, 2014, pag. 31] y [Bartle, 2014, pag. 44]
Teorema 1.1(Teorema de la Convergencia Monótona). Si (fn)es una sucesión monótonamente
creciente de funciones enM+(X,X) que convergen a f c.t.p. X, entonces
Z
f dµ= l´ım
Z
fndµ
Teorema 1.2 (Teorema de la Convergencia Dominada de Lebesgue). Sea (fn) una sucesión
de funciones integrables que convergen a f c.t.p. X. Si existe una función integrable g tal que
|fn(x)| ≤g(x) para casi todon y para casi todo x∈X, entonces f es integrable y Z
f dµ= l´ım
Z
Este teorema es de mucha importancia y es más fuerte que el teorema de integración (en el sentido de Riemann) término a término para sucesiones de funciones uniformemente convergentes. Más precisamente dada una sucesión de funciones (fn) reales Riemann-integrable que convergen uni-formemente a una funciónf, entoncesf es Riemann-integrable yR f dx= l´ımRfndx. Ilustramos lo anterior con los siguientes ejemplos.
Ejemplo 1. Si(fn)es una sucesión enL(X,X, µ)que converge uniformemente enXa una función
f y siµ(X)<∞entonces
Z
f dx= l´ım
Z
fndx.
Demostración. Por la convergencia uniforme tenemos que existeN ∈Ntal que sin≥N entonces
|fn(x)−f(x)|<1.
Por tanto|f(x)|<1 +|fN(x)|para todox, lo que implica que
Z
|f(x)|dµ <
Z
(1 +|fN(x)|)dµ
=
Z
1dµ+
Z
|fN(x)|dµ
=µ(X) +
Z
|fN(x)|dµ <∞.
Por endef es integrable, por otro lado también se tiene que |fn(x)|< 1 +|f(x)| paran≥ N y como1 +|f(x)|es integrable por el Teorema de la Convergencia Dominada obtenemos
Z
f dx= l´ım
Z
fndx.
Ejemplo 2. Existe una sucesión de funciones (fn) de valor real que convergen a una función f c.t.p.X tal que
Z
f dµ= l´ım
Z
fndµ
pero la convergencia no es uniforme
Demostración. Tomemos a X= [0,1]con la medida usual defínase(fn) como sigue
fn(x) =
0 six∈[0,12)
Es claro quefn(x) es continua para todon y además de eso converge puntualmente c.t.pX a
f(x) =
(
0 six∈[0,12) 1 six∈[12,1].
Ahora, la función g(x) = 1 es integrable sobre X y además |fn(x)| ≤ g(x) para todo n y para todox∈X así por el teorema de la convergencia dominada
Z
f dµ= l´ım
Z
fndµ
sin embargo la convergencia no es uniforme puesto que si lo fuera como fnes continua para todo
nse tendría quef es continua, lo cual no es cierto.
También denotamos a (E,k · k) como un espacio normado, en caso de ser completo se le llama espacio de Banach y denotamos a (E∗,k · kE∗) su espacio dual topológico o mas brevemente su
espacio dual, el cual consiste en todos los funcionales lineales continuos (acotados),Φ :E→R, y tiene norma
kΦkE∗ = sup
x∈E−{0} |Φ(x)|
kxk .
El dual de cualquier espacio normado, con esta norma, es siempre un espacio de Banach. Más aún, si definimos aL(E, F) como el conjunto de todos los operadores lineales continuos,Φ :E→F y
(F,k · k1)un espacio normado, estos operadores tienen norma
kΦkL(E,F)= sup
x∈E−{0}
kΦ(x)k1 kxk
y de esta manera(L(E, F),k · kL(E,F)) es siempre un espacio normad, además es de Banach siF
es completo.
Necesitaremos de un teorema de gran importancia del análisis funcional, conocido como el teorema de Hahn–Banach. Este teorema tiene varias versiones. Nosotros utilizaremos una consecuencia de la forma análitica del teorema de Hahn–Banach sobre espacios normados. Tomado de [Brezis, 2010, pag. 3], que se enuncia de la siguiente manera.
Teorema 1.3 (Teorema de Hahn–Banach). Sea G un subespacio vectorial de E. Si Φ : G→ R
es un funcional lineal continuo, entonces existe Φ∈E∗ una extension de Φ tal que
kΦkE∗ = sup
x∈G−{0} |Φ(x)|
kxk =kΦkG∗.
Proposición 1.1. Sea G un subespacio vectorial de E y Sea Φ : G → R un funcional lineal
continuo, entoncesΦ tiene una única extensiónΦ∈G∗ tal que
kΦkG∗=kΦkG∗.
Demostración. Sea x∈ Gentonces existe (xn) en G tal que xn → x. Veamos que (Φ(xn))es de Cauchy. En efecto, sea >0entonces existe N ∈N tal que sin, m≥N entonces
kxn−xmk< /kΦkG∗,
luego
|Φ(xn)−Φ(xm)|=|Φ(xn−xm)| ≤ kΦkG∗kxn−xmk< .
Por tanto(Φ(xn))es de Cauchy y comoRes completo,(Φ(xn))converge a un único puntoax∈R,
esto es,
l´ım
n→∞Φ(xn) =ax.
Definimos a
Φ : G −→ R
x 7→ ax.
Veamos que Φ está bien definida, es decir, que no depende de la escogencia de la sucesión. Sea
(xn) y(yn)en Gtal que xn→x yyn→x y definamos a
(vn) = (x1, y1, x2, y2,· · ·),
entonces vn →x y por el razonamiento anterior(Φ(vn)) converge. Ya que (Φ(xn))y(Φ(yn)) son subsucesiones de(Φ(vn)), convergen y convergen al mismo límite, por tantoax no depende de la escogencia de la sucesión.
Por otro ladoΦ es lineal, pues parax, y∈Gy α∈Rexisten (xn) y(yn) en Gtal que xn →x y
yn→y, luego xn+αyn→x+αy y
Φ(x+αy) = l´ım
n→∞Φ(xn+αyn)
= l´ım
n→∞Φ(xn) +αΦ(yn)
= l´ım
n→∞Φ(xn) +αnl´ım→∞Φ(yn)
Por otro lado,Φ es acotada puesto que parax∈Gexiste (xn) enG tal quexn→xy
|Φ(x)|=| l´ım
n→∞Φ(xn)|
= l´ım
n→∞|Φ(xn)| ≤ l´ım
n→∞kΦkG ∗kxnk
=kΦkG∗k l´ım
n→∞xnk
=kΦkG∗kxk.
Por tanto es acotada y
kΦkG∗≤ kΦkG∗,
y como
kΦkG∗ = sup
x∈G−{0} |Φ(x)|
kxk ≤x∈supG−{0} |Φ(x)|
kxk =kΦkG∗,
se obtiene que
kΦkG∗=kΦkG∗.
Por último veamos queΦes única. Supongamos que existe Ψ :G→Rtal que Ψ(x) = Φ(x) para todo x ∈ G y Ψ es un funcional lineal acotado entonces para x ∈ G existe (xn) en G tal que
xn→x y por ser Ψcontinua tenemos que
Ψ(x) = l´ım
n→∞Ψ(xn) = l´ımn→∞Φ(xn) =ax= Φ(x),
comox era arbitrario, obtenemos que Ψ = Φ, por tantoΦ es única.
Note que esta proposición se podía demostrar mucho más fácil a partir del Teorema de Hahn–Banach, pero dimos una demostración más artesanal puesto que la demostración solo utilizó la completitud de R. Por tanto se puede poner en vez de R cualquier espacio F de Banach y la demostración sería análoga. Así obtenemos la siguiente proposición.
Proposición 1.2. SeaGun subespacio vectorial deE y seaF un espacio de Banach y Φ :G→F
un funcional lineal continuo, entonces Φ tiene una única extensión lineal continua Φ sobreG tal que
kΦkL(G,F)=kΦkL(G,F).
1.2.
Espacios
L
pDefinición. Si 1 ≤ p < ∞, el espacio Lp = Lp(X) = Lp(X,X, µ) consiste de todas las clases
µ-equivalentede las funciones de valor real mediblesf para las cuales |f|p tiene integral finita con respecto a µsobre X. Dos funciones son µ-equivalente si son iguales en casi toda parte, es decir, salvo un conjunto de medida cero. Se define
kfkp =
Z
|f|pdµ
1/p
.
Las operaciones vectoriales sobreLp están definidas puntualmente. Ahora las propiedades básicas de estos espacios están dadas por el siguiente teorema tomado de [Bartle, 2014, pag. 59].
Teorema 1.4. Si 1≤p <∞ entonces se tienen las siguientes propiedades
1. Con las operaciones anteriormente definidas, Lp es un espacio vectorial.
2. k · kp es una norma sobre Lp.
3. (Lp,k · kp) es completo.
En pocas palabras (Lp,k · kp) es un espacio de Banach.
Mostramos a continuación algunos ejemplos y ejercicios para familiarizarnos con estos espacios y algunas de sus propiedades.
Ejemplo 3. El conjunto de las funciones medibles simples es denso en Lp para todo1 ≤p <∞. Se entiende por función simple a una función que toma finitos valores.
Demostración. Basta con demostrar que para cada f ∈Lp existe (φn)una sucesión de funciones medibles simples tal queφn→f en el sentido de||.||p. En efecto, supongamos primero quef ∈Lp es no negativa entonces existe una sucesión (φn) en M(X,X) tal que:
(φn) es monótona creciente no negativa.
φn(x)→f(x) para cadax∈X.
Entonces (f −φn) es una sucesión monótona decreciente y por otra parte al ser (φn) monótona creciente tenemos que
l´ım
n→∞φn(x) = supn∈
N
φn=f(x)
para todox∈X, luego
0≤f(x)−φn(x)≤f(x).
Es decir
(|f(x)−φn(x)|)p ≤(|f(x)|)p
para todox ∈X y para todo n. Como (f(x)−φn(x))p →0 para todo x ∈X obtenemos por el teorema de la convergencia dominada que
l´ım
n→∞
Z
|f−φn|pdµ=
Z
0dµ= 0.
Esto equivale a
l´ım
n→∞||f−φn||p = 0.
Esto esφn→f en el sentido deLp. Ahora sif no necesariamente es no negativa entonces
f =f+−f−,
pero como la parte positiva y la parte negativa de una función son no negativas entonces por lo demostrado anteriormente existen(φ1n) y(φ2n) sucesiones de funciones medibles simples tal que
φ1n→f+ yφ2n→f−.
Luego
φ1n−φ2n→f
y es claro que(φ1n−φ2n)es una sucesión de funciones medibles simples pues la resta de funciones simples es simple y la resta de funciones medibles es medible.
Ejemplo 4. Sif ∈Lp con 1≤p <∞ yE={x∈X :|f(x)| 6= 0}entonces E esσ-finito
Demostración. : Sea
En={x∈X:|f(x)|p >1/n}
entonces se tiene que
E=
∞
[
Veamos queµ(En)es finito para cada n∈N. En efecto, tenemos que|f(x)|p>(1/n)χEn luego
Z
|f(x)|pdµ >
Z
(1/n)χEndµ= (1/n)µ(En).
Es decir
µ(En)< n
Z
|f(x)|pdµ.
Pero R
|f(x)|pdµ <∞ por hipótesis. Es decirµ(E
n)<∞.
Ejemplo 5. Sif ∈Lp y si En={x∈X :|f(x)| ≥n} entonces µ(En)→0 cuandon→ ∞
Demostración. Tenemos que |f(x)|p ≥npχ
En luego
Z
|f(x)|pdµ≥npµ(En),
es decir
0≤µ(En)≤
R
|f(x)|pdµ
np .
Comol´ımn→∞
R
|f(x)|pdµ
np = 0, puesto que
R
|f(x)|pdµ existe y es finita, obtenemos que
l´ım
n→∞µ(En) = 0.
Para finalizar veamos que parap∈(0,1)la definición deLp deja de ser un espacio normado.
Ejemplo 6. Para0< p <1 yLp =Lp(X)como se definió anteriormente, entonces
kfkp=
Z
|f|pdµ
1/p
no es una norma.
Demostración. ConsideremosX = [0,1]. Basta demostrar queB(0,1), la bola cerrada con centro en 0y radio 1, no es convexa. En efecto, tomemos f(x) = 1 yg(x) =g(x;p) = (2x)1/p entonces
Z 1
0
|1|pdx= 1
y
Z 1
0
|(2x)1/p|pdx=
Z 1
0
Esto es que f, g∈B(0,1). Por otro lado siB(0,1)fuera convexo entonces para todo 0≤λ≤1
λf+ (1−λ)g∈B(0,1)
pero paraλ= 1/2
1 2 +
1 2(2x)
1/p∈/ B(0,1).
En efecto, definamos
h(x) =h(x;p) =
1 2 +
1 2(2x)
1/p
p
y veamos queR1
0 h(x)dx >1. Entonces
h0(x) =p
1 2+
1 2(2x)
1/p
p−1
1 2p(2x)
1/p−1(2)
=
1 2+
1 2(2x)
1/p
p−1
(2x)1/p−1.
Luego
h0(1/2) =
1 2 +
1 2
p−1
= 1,
por tanto la recta tangente ah(x) en x= 1/2 tiene pendiente 1. Esto es de la forma
y=x+b
y esta pasa por(1/2,1)puesto que h(1/2) = 1, así la recta tangente ah(x) es
l(x) =x+1 2.
Nótese queh00(x)>0 y por consiguiente es cóncava hacia arriba como ilustra la siguiente gráfica, donde muestra al(x) y a h(x) =h(x;p)variando ap.
Comoh(x) es cóncava hacia arriba, implica que
h(x)> l(x),
por ende
Z 1
0
h(x)dx >
Z 1
0
(x+ 1/2)dx= 1.
Es decir, 1 2f+
1 2g p
>1.
También será de suma importancia la siguiente desigualdad tomada de [Bartle, 2014, pag. 56].
Teorema 1.5 (Desigualdad de Hölder). Sea f ∈ Lp y g ∈Lq donde p >1 y (1/p) + (1/q) = 1. Entoncesf g∈L1 y
kf gk1 ≤ kfkpkgkq.
El elemento q es llamado el conjugado de p, y se denota como q = p0. Es claro que (p0)0 = p. Veamos el siguiente ejemplo que será de gran utilidad.
Ejemplo 7. Lp2(X)⊆Lp1(X) con p1 < p2 siµ(X)<∞
Demostración. Sea f ∈Lp2(X) entonces
Z
|f|p2dµ <∞.
Ahora defínamos E={x∈X:|f(x)|<1} por tanto|f|p1χ
E <1 luego
Z
E
|f|p1dµ <
Z
E
1dµ=µ(E)≤µ(X)<∞.
Parax∈Ec
|f(x)| ≥1.
Es decir
|f(x)|p1 ≤ |f(x)|p2,
por consiguiente
|f|p1χ
Ec ≤ |f|p2χEc. Esto es
Z
Ec
|f|p1dµ≤
Z
Ec
|f|p2dµ≤
Z
por tanto
Z
|f|p1dµ=
Z
X
|f|p1dµ
=
Z
E∪Ec
|f|p1dµ
=
Z
E
|f|p1dµ+
Z
Ec
|f|p1dµ <∞
luegof ∈Lp1(X).
Esta proposición anterior también puede ser demostrada a partir de la desigualdad de Hölder como sigue.
Demostración. (Usando la desigualdad de Hölder ) Sea f ∈Lp2(X) y seap02 tal que p21 + 1
p02
= 1.
Veamos que|f|p02(p1−1)∈Lβ(X)con β = p2−1
p1−1 >1. En efecto, como
p02(p1−1)
p2−1
p1−1
=p02(p2−1) =p2,
entonces
Z
(|f|p 0
2(p1−1))βdµ=
Z
|f|p2dµ <∞.
Por otro lado, como µ(X) < ∞, 1 ∈ Lp(X) para todo 1 ≤ p < ∞. Por tanto 1 ∈ Lβ0(X) con
1
β +
1
β0 = 1. Por la desigualdad de Hölder |f|p 0
2(p1−1)(1)∈L1(X) y
Z
(|f|p 0
2(p1−1))dµ≤
Z
(|f|p 0
2(p1−1))βdµ
1/βZ
1β0dµ
1/β0
=
Z
|f|p2dµ
1/β
(µ(X))1/β0.
Esto es |f|p1−1 ∈ Lp02(X). Nuevamente por la desigualdad de Hölder |f|p
1 ∈ L1(X), esto es, f ∈Lp1(X) como queríamos demostrar y además
Z
|f|p1dµ=
Z
|f||f|p1−1dµ
≤ kfkp2
Z
|f|p 0
2(p1−1)dµ
1/p
0
2
≤ kfkp2
" Z
|f|p2dµ
1/β
(µ(X))1/β0
#1/p
0
2
peroβ = p2p1−−11 = (p2p2−(p11)(−p21)) = p2
p02(p1−1)
, es decir 1β = p
0
2(p1−1)
p2 ,por ende
Z
|f|p1dµ≤ kfkp2
Z
|f|p2dµ
1/βp
0
2
(µ(X))1/β0p
0
2
=kfkp2
Z
|f|p2dµ
(p1−1)
p2
(µ(X))1/β0p
0
2
=kfkp2kfkp1p2−1(µ(X))
1/β0p0
2
=kfkp1p2(µ(X))1/(β0p
0
2).
De donde
kfkp1 ≤ kfkp2(µ(X))1/β
0p0
2p1
Aunque la primera demostración es más natural, la segunda, a pesar de ser muy técnica, da una información extra sobre la existencia de una constante realC que cumple
kfkp1 ≤Ckfkp2
esto implica que la inclusión
i:Lp2 −→Lp1
es continua. Además de esto se conoce explícitamente cual es la constanteC ya que 1 p02 =
p2−1
p2 y
1
β0 = β−1
β =
p2−1
p1−1 −1
p2−1
p1−1
=
(p2−1)−(p1−1)
p1−1
p2−1
p1−1
= p2−p1
p2−1 .
De este modo
1
β0p0 2p1
=
p2−p1 p2−1
p2−1 p2
1
p1
= p2−p1
p2p1
obtenemos que
C =µ(X)
p2−p1 p2p1 .
Es decir
kfkp1 ≤µ(X) p2−p1
p2p1 kfkp2.
En el caso de normas enRn dadas por
kxkp = n
X
i=1 |xi|p
con 1≤p <∞, se sabe que
l´ım
p→∞kxkp = l´ımp→∞
n
X
i=1 |xi|p
!1/p
= sup
1≤i≤n
|xi|
para todo x∈Rn, donde el resultado del límite es a su vez una norma para
Rn. Ésta es llamada
la norma del sup y es denotada por
kxk∞= sup 1≤i≤n
|xi|.
De modo que es natural definir el siguiente espacio como una generalización deRn con la norma del sup, el cual esta relacionado con los espaciosLp, que al igual que estos espacios, será de suma importancia.
Definición. El espacioL∞=L∞(X) =L∞(X,X, µ)consiste de todas las clasesµ-equivalente de funciones de valor real medibles f las cuales están acotadas en casi toda parte sobre X. Es decir acotadas salvo un conjunto de medida cero.
Sif ∈L∞ yN ∈Xcon µ(N) = 0 se define
S(N) = sup{|f(x)|:x /∈N}
y
kfk∞= ´ınf{S(N) :N ∈X, µ(N) = 0}.
Un elemento deL∞es llamadofunción esencialmente acotadaykfk∞es llamado elsupremo
esencial de|f|y se denota también conessup|f|.
Al igual que enLp,L∞tiene algunas propiedades, que se enuncian en el siguiente teorema tomado de [Bartle, 2014, pag. 61 ]
Teorema 1.6. El espacioL∞ tiene las siguientes propiedades:
1. Es un espacio vectorial con las mismas operaciones definidas sobre Lp.
2. k · k∞ es una norma sobre L∞.
3. (L∞,k · k∞) es completo.
Para terminar con los espacios Lp con 1 ≤ p ≤ ∞, introduciremos dos teoremas más de suma importancia. Uno de ellos esEl Teorema de Representación de Riesz para Lp tomado de [Bartle, 2014, pag. 89 ].
Éste teorema se divide en dos partes, que se enuncian a continuación.
Teorema 1.7 (Teorema de Representación de Riesz para L1 ). Si (X,X, µ) es un espacio de medida σ-finito y G es un funcional lineal acotado sobre L1(X,X, µ), entonces existe un g ∈ L∞(X,X, µ) tal que
G(f) =
Z
f g dµ
para todo f ∈L1. Más aun, kGk=kgk∞ y g≥0 siG es un funcional lineal positivo.
Teorema 1.8 (Teorema de Representación de Riesz paraLp con1< p <∞). Si(X,X, µ) es un espacio de medida σ-finito y G es un funcional lineal acotado sobre Lp(X,X, µ), con 1< p <∞
entonces existe un g∈Lq(X,X, µ) donde 1p +1q = 1 tal que
G(f) =
Z
f g dµ
para todo f ∈Lp. Más aun, kGk=kgkq.
El libro [Bartle, 2014] de donde es tomado la primera version del Teorema de Representación de Riesz no demuestra que kGk=kgk∞, sino que lo deja como ejercicio. Por ello lo demostraremos
a continuación.
Ejemplo 8. Si se define aG sobreLp por
G(f) =
Z
f g dµ
con g∈L∞ entonces Ges un funcional lineal acotado sobreLp con kGk=kgk∞.
|G(f)|= Z
f g dµ
≤ Z
|f||g|dµ
≤
Z
|f|kgk∞dµ
=kgk∞
Z
|f|dµ
=kfk1kgk∞.
Por tantoG es acotado ykGk ≤ kgk∞.Por otro lado demostramos que
Z
|f||g|dµ≤ kfk1kgk∞.
Esta es la desigualdad de Hölder en el caso p = 1 y q = ∞. Generalizándola para todo p. Por último, veamos quekGk ≥ kgk∞ para concluir con la demostración.
Sean c > 1 y Ec = {x ∈ X : |g(x)| ≥ ckGk}. Defínase a Ec+ = {x ∈ X : g(x) ≥ ckGk} y
Ec−={x∈X:−g(x)≥ckGk}. Entonces es claro que Ec=Ec+∪Ec− yEc+∩Ec−=∅. Por tanto definamos
fc(x) =
1 six∈Ec+ −1 six∈Ec−
0 six /∈Ec. Por consiguiente
G(fc) =
Z
fcg dµ
=
Z
Ec
fcg dµ
=
Z
E+c
fcg dµ+
Z
E−c
fcg dµ
=
Z
E+c
g dµ+
Z
E−c
g dµ
≥ckGkµ(Ec+) +ckGkµ(Ec−) =ckGkµ(Ec).
Por lo que
Por otro lado tenemos que
G(fc)
kfck1
≤ kGk,
perokfck1 =R
fcdµ=
R
Ec1dµ=µ(Ec). Es decir que
G(fc)≤ kGkµ(Ec).
De lo anterior y de (1.1) obtenemos
ckGkµ(Ec)≤G(fc)≤ kGkµ(Ec).
Comoc >1la desigualdad anterior es contradictoria, a menos que µ(Ec) = 0, luego
|g(x)| ≤ckGk
c.t.pX. Esto implica que
kgk∞≤ckGk
para todoc >1. Por ende
kGk ≤ kgk∞.
Para introducir el último teorema que necesitamos sobre los espaciosLp es necesario la siguiente definición.
Definición. Dada una funciónf : Ω→R con Ωun abierto deRn se define a
suppf ={x∈Ω :f(x)6= 0}
como elsoporte de f, y se denotan aCc(Ω)yCc∞(Ω)como el conjunto de funciones f : Ω→R continuas con soporte compacto e infinitamente diferenciables con soporte compacto respectiva-mente.
A continuación enunciamos el último teorema relacionado con los espacios Lpque es de gran importancia para los fundamentos de nuestro trabajo, tomados de [Brezis, 2010, pag. 109].
Teorema 1.9(Teorema de la Densidad). Dado un abiertoΩ⊆RnconLlaσ- álgebra de Lebesgue
Un ejemplo clásico de una funciónCc∞(Rn) es el siguiente
ρ(x) =
(
e1/(|x|2−1) si|x|<1 0 si|x|>1
Que en el cason= 1 tiene la siguiente gráfica.
Figura 1.2: gráfica deρ(x)
Ahora bien, existe un tipo especial de sucesión de funcionesCc∞(Rn)llamadasmolificadoresque
se definen de la siguiente manera.
Definición. Una sucesión demolificadores (ρm)∞m=1 es una sucesión de funciones sobreRn tal
queρm∈Cc∞(Rn),suppρm⊂B(0,1/m),
R
ρmdµ= 1yρm(x)≥0para todo x∈Rn.
Es fácil construir una sucesión de molificadores a partir de unaρ ∈Cc∞(Rn) tal queρ ⊂B(0,1)
yρ(x)≥0 para todox∈Rnyρ no idénticamente 0. Por ejemplo si tomamos nuevamente a
ρ(x) =
(
e1/(|x|2−1) si|x|<1 0 si|x|>1
obtenemos una sucesión de molificadores dejando a
ρm =Cmnρ(mx)
con C = 1/R
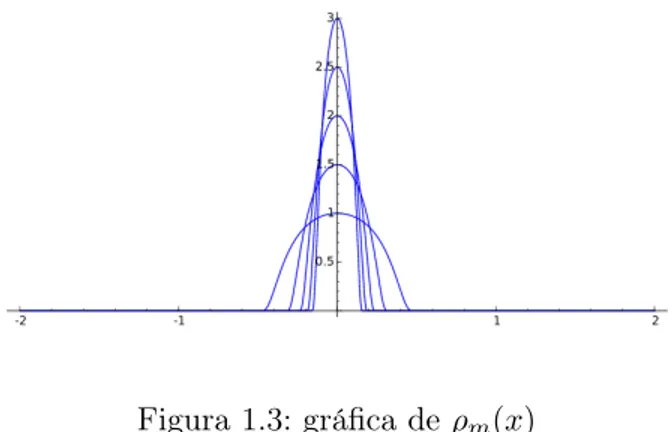
Figura 1.3: gráfica deρm(x)
Son de importancia estas sucesiones de molificadores porque es a partir de ellas que se puede construir una sucesión(fm)de funciones enCc∞(Ω)tal quefm →f enLp(Ω), conf ∈Lp(Ω)con
1≤p <∞. Para poder construir esta sucesión debemos definir la siguiente operación.
Definición. Dadas dos funciones f y g definidas sobre Rn. La convolución de f y g se define como
f ∗g=
Z
Rn
f(x−y)g(y)dy.
En seguida definimos agm =χKmf, donde
f(x) =
(
f(x) si x∈Ω 0 si x /∈Ω
y(Km) es una sucesión de compactos sobreRn tal que
∞
[
m=1
Km= Ω y dist(Km,Ωc)≥2/n.
Por último se define la sucesión deseada como sigue
fm =ρm∗gm.
Se puede encontrar en [Brezis, 2010, pag. 109] la demotración de que esta suseción (fm) así definida, efectivamente converge af en Lp. La siguiente gráfica muestra los primeros 3 elementos de esta sucesión si se toma aΩ = (−1,1)y
f(x) =
(
Figura 1.4: gráfica de fm(x)
1.3.
Espacios de Sobolev
Además de los espacios Lp, también es necesario definir unos subespacios que serán de suma importancia y mencionaremos algunas de sus propiedades más importantes.
Definición. Sea I = (a, b) un intervalo abierto, no necesariamente acotado. Sea 1 ≤p ≤ ∞, el espacio de SobolevW1,p =W1,p(I) es definido como
W1,p(I) ={u∈Lp(I) :∃g∈Lp(I) tal que
Z
I
uϕ0dµ=−
Z
I
gϕdµ, ∀ϕ∈Cc1(I)}.
También defininos a
H1(I) =W1,2(I)
y para unu∈W1,p(I) denotamos ag=u0, ésta es llamada la derivada débil deu.
Mostraremos dos ejemplos para familiarizar al lector con este espacio. Con el fin de ver que esta derivada débil es una generalización de la derivada usual.
Ejemplo 9. Sea u una función deRen Rdiferenciable enI, conI un intervalo acotado, entonces
u∈W1,p(I) y la derivada usual coincide con la derivada débil.
Demostración. Dado ϕ∈Cc1(I), tenemos por integración por partes que
Z
I
uϕ0dx=uϕ|I−
Z
I
u0ϕdx
con u0 la derivada usual de u. Ya que ϕes de soporte compacto obtenemos que
Z
I
uϕ0dx=−
Z
I
u0ϕdx
Con este ejemplo mostramos que las funciones derivables, con la derivada usual, están contenidas en el espacio de SobolevW1,p. Veamos que esta contenencia es propia.
Ejemplo 10. Existe una función enW1,p pero ésta no es derivable en el sentido usual.
Demostración. ConsidereI = (−1,1). Veamos que la funciónu(x) =|x|pertenece aW1,p(I), para cualquier 1 ≤p ≤ ∞. En efecto, Como u(x) ∈C(I) entonces está acotada, luego u ∈ L∞(I) ⊆ Lp(I) pues al serI acotado tiene medida finita. Veamos ahora que u tiene derivada débil.
Sea ϕ ∈Cc1(I) entonces por integración por partes y usando que ϕ se anula en la frontera de I
obtenemos que
Z 1
−1
|x|ϕ0(x)dx=
Z 0
−1
−xϕ0(x)dx+
Z 1
0
xϕ0(x)dx
=−
Z 0
−1
−ϕ(x)dx−
Z 1
0
ϕ(x)dx.
Por tanto, si definimos a
g(x) =
(
−1 si x∈(−1,0) 1 si x∈[0,1)
obtenemos que
Z 1
−1
|x|ϕ0(x)dx=−
Z 1
−1
g(x)ϕ(x)dx,
de dondeu(x) =|x|pertenece aW1,p(I), pero esta función no es derivable en I.
Ya tenemos que Lp es un espacios de Banach y, aunque no lo mencionamos, con el Teorema de Representación de Riez se puede demostrar que Lp con 1 < p < ∞ es reflexivo. Por otro lado este espacio también es separable para 1 ≤ p < ∞ y la demostración de esto se puede ver en [Brezis, 2010]. Con el siguiente teorema se tiene que los espacios de Sobolev también tienen estas propiedades, el cual es tomado de [Brezis, 2010, pag. 203].
Teorema 1.10. El espacio W1,p equipado con la siguiente norma
kukW1,p =kukLp+ku0kLp
es un espacio de Banach para 1 ≤ p ≤ ∞, es reflexivo para 1 < p < ∞, y separable para
1≤p <∞. Además el espacio H1 equipado con el siguiente producto interno
(u, v)H1 = (u, v)L2+ (u0, v0)L2
Ahora, la derivada débil conserva varias propiedades importantes de la derivada usual, como es de esperarse al ser una generalización de la derivada normal. No es difícil demostrar la linealidad de la derivada débil. Esto es, para todou, v∈W1,p y cualquier real α, se tiene que
(u+v)0 =u0+v0 y(αu)0 =αu0.
las demás propiedades se encuentran demostradas en [Brezis, 2010, pag. 205,206,215 y 216] las cuales enunciaremos a continuación con el siguiente teorema.
Teorema 1.11 (Propiedades de la Derivada Débil). Sea u, v ∈ W1,p(I) para 1 ≤ p ≤ ∞ y I
acotado o no acotado entonces se tienen las siguientes propiedades:
1. Si u0 = 0 entonces existe una constanteC tal que u=C c.t.p I.
2. Primer Teorema Fundamental del Cálculo: Dado g ∈Lploc(I) si se define para un y0
fijo enI a
w(x) =
Z x
y0
g(t)dt, x∈I
entonces w∈C(I) y
Z
I
wϕ0dt=−
Z
I
gϕdt, ∀ϕ∈Cc1(I)
esto es, si g∈Lp(I) entonces w tiene derivada débil (w∈W1,p(I)) y w0=g.
3. Segundo Teorema Fundamental del Cálculo: Existe una única función u ∈ C(I) tal que
u=u c.t.p I
y
Z y
x
u0(t)dt=u(y)−u(x)
para todo x, y∈I
4. Regla del producto: uv∈W1,p y
(uv)0 =u0v+uv0,
además se tiene la fórmula de integración por partes
Z y
x
u0vdt=uv|yx−
Z y
x
uv0dt
5. Regla de la cadena:Sea G∈C1(I) tal que G(0) = 0 entonces G◦u∈W1,p y
(G◦u)0 = (G0◦u)u0.
Como W1,p(I) ⊆ Lp(I) yLp(I) es un conjunto de clases de equivalencia donde u = v en Lp(I)
si y solo si u = v c.t.p I, entonces en el Segundo Teorema Fundamental del Cálculo tendremos queu=u enLp(I). Es decir, son indistinguibles en este espacio. Por otro lado, por este teorema tenemos que u es continuo, entonces cada u ∈ W1,p tiene un representante continuo, el cual es indistinguible de u; y más aun si u0 ∈C(I) entonces u ∈ C1(I) y por tanto u ∈ C1(I), por ser indistinguibles.
Con todo lo mostrado anteriormente podemos decir que la derivada débil es, en efecto, una ger-neralización de la derivada usual o fuerte. Sin embargo, no hemos hablado de qué propiedades tiene el espacio de BanachW1,p. Para empezar demos el siguiente resultado, éste es un importante prototipo de ladesigualdad de Sobolev. El cual es tomado de [Brezis, 2010, pag. 212].
Teorema 1.12. Sea I un intervalo no necesariamente acotado entonces existe una constante C
tal que para todo 1≤p≤ ∞y para todo u∈W1,p(I) se tiene que
kukL∞(I) ≤CkukW1,p(I).
En otras palabras, la inclusión i : W1,p(I) −→ L∞(I) es continua. Además, si I es acotado
entonces las inclusiones
i:W1,p(I)−→C(I) y i:W1,1(I)−→Lq(I)
son compactas para todo1< p≤ ∞ y1≤q <∞.
Ahora daremos algunos ejemplos. Con el fin de presentrar una información extra de este importante teorema, además de algunas aplicaciones.
Por la desigualdad de Sobolev tenemos quei:W1,p(I)−→C(I)es compacta para1< p≤ ∞. Es natural preguntarnos si el teorema es cierto para el caso p= 1. La respuesta es no. Para mostrar esto, es decir, que i:W1,1(I)−→C(I) no es compacta, se da el siguiente ejemplo.
Ejemplo 11. Sea I = [0,1]entonces la sucesión
un(x) =
0 si x∈[0,12]
nx−n2 si x∈(12,12+ 1n) 1 si x∈[12+n1,1]
Demostración. Veamos e primer lugar queun∈W1,1(I)para todon∈N. Seaϕ∈Cc1(I)entonces
Z
I
unϕ0 =
Z 1/2+1/n
1/2
n(x−1/2)ϕ0(x)dx+
Z 1
1/2+1/n
ϕ0(x)dx
=n(x−1/2)ϕ(x)|11//2+12 /n−
Z 1/2+1/n
1/2
nϕ(x)dx+ϕ(x)|11/2+1/n
=−
Z 1/2+1/n
1/2
nϕ(x)dx.
Por tanto si se define
gn(x) =
0 si x∈[0,12]
n si x∈(12,12 +n1) 0 si x∈[12 +n1,1]
queda que
Z
I
unϕ0 =−
Z
I
gnϕ.
Por endeun∈W1,1(I)para todon∈Nyun0 =gn. Ahora veamos que(un)es acotada enW1,1(I). En efecto,
kunkW1,1(I) =kunkL1(I)+ku0nkL1(I)
=
Z 1
0
un(x)dx+
Z 1
0
u0n(x)dx
=
Z 1/2+1/n
1/2
n(x−1/2)dx+
Z 1
1/2+1/n
1dx+
Z 1/2+1/n
1/2
ndx
= (1/2n) + (1−(1/2 + 1/n)) +n(1/n)
= 1/2n+ 1/2−1/n+ 1
= 3/2−1/2n
≤3/2.
Por último veamos que(un)no admite subsucesiones convergentes enL∞(I). En efecto, seam > n, entonces
kun−umk∞= sup
x∈(12,12+m1)
mx− m
2 −nx+
n
2
+ sup
x∈[12+m1,12+n1)
1−nx+n 2
= sup
x∈(12,12+m1)
(m−n)x−1
2(m−n)
+ sup
x∈[12+m1,12+n1)
1−nx+n 2
= (m−n)
1 2+ 1 m −1
2(m−n) + 1−n
1 2+ 1 m + n 2
= (m−n)1
m + 1− n
2 −
n m +
n
2 = 2−2
Ahora, supongamos que existe una subsucesión (unk) de (un) convergente en L∞(I) y por tanto de Cauchy. Luego, existeK0 ∈N tal que sik, l≥K0 entonces
kunk−unlk∞<
1 2.
Pero, si tomamosk≥K0 yl∈Ntal que nl ≥2nk, tenemos que
kunk −unlk∞= 2−2 nk
nl
≥2−2nk
2nk
= 1,
lo cual es una contradicción. Por tanto se concluye que(un)no admite subsucesiones convergentes enL∞(I), es decir, i:W1,1(I)−→L∞(I)no es compacta.
Se tiene inmediatamente por el ejemplo anterior quei:W1,1(I)−→C(I)no es compacta. Ahora, aunque ya mostramos que una sucesión (un) en W1,1(I) acotada no necesariamente tiene una subsucesión convergente en L∞(I), que es equivalente a tener una subsucesión uniformemente convergente c.t.pI, pero se puede demostrar que (un) siempre tendrá una subsucesión (unk)que converge puntualmente c.t.pI. Demostramos esto en el siguiente ejemplo.
Ejemplo 12. Sea(un)enW1,p(I)conI acotado, si(un)es acotada entonces existe una subsucesión
(unk) de(un)tal que converge puntualmente c.t.p I.
Demostración. Sea (un) en W1,p(I) acotada. Por la desigualdad de Sobolev tenemos que i :
W1,1(I) −→ L1(I) es compacta, por ende existe una subsucesión(unk) de (un) tal queunk → u en L1(I)para algún u∈L1(I). Ahora, no es dificíl demostrar que si una sucesión (f
n) enLp(X) converge a una función f en Lp(X) entonces fn → f en medida. Una demostración de esto se puede encontrar en [Bartle, 2014, pag. 69].
Por tantounk →u en medida y una de las propiedades de la convergencia en medida, tomada de [Bartle, 2014, pag. 69,70], nos dice que dada una sucesión (fn) de un espacio de medidaX y si
fn→ f en medida entonces existe una subsucesión (fnk) de (fn) tal que fnk → f puntualmente c.t.pX. En conclusión, existe una subsucesión(unkl)de(unk)y por ende de(un), tal queunkl →u puntualmente c.t.pI.
Como dato curioso, para demostrar el teorema anterior pudimos tomar sin perdida de generalidad queun es monótona creciente, como ilustra el siguiente ejemplo.
Si(un) en W1,p(I) es acotada y un es monótonamente creciente para todo n∈N entonces
existe una subsucesión (unk) de (un) tal que unk → u puntualmente c.t.p I, para alguna funciónu.
Entonces la afirmación es cierta para toda(un) enW1,p(I) acotada.
Demostración. Sea(un)enW1,1(I)acotada y definamos avn(x) =
Rx
0 |u 0
n(t)|dt. Como|u0n(t)| ≥0 entonces si y ≤ x implica que Ry
0 |u 0
n(t)|dt ≤
Rx
0 |u 0
n(t)|dt por tanto vn(x) es monótonamente creciente para todon∈N.
Definamos awn(x) =vn(x)−un(x) y ya que
u(x)−u(0) =
Z x
0
u0n(t)dt
entonces
wn(x) =
Z x
0
|u0n(t)|dt−u(0)−
Z x
0
u0n(t)dt.
Es decir,
wn(x) +u(0) =
Z x
0
|u0n(t)| −u0n(t)dt.
Y comofn(t) =|u0n(t)| −un0(t)≥0para todo t∈I, si y≤x, entonces
Z y
0
fn(t)dt≤
Z x
0
fn(t)dt.
Esto es,
wn(y) +u(0) =
Z y
0
fn(t)dt
≤
Z x
0
fn(t)dt
=wn(x) +u(0).
Es decir, wn(y)≤wn(x) siempre que y≤x, luego wn(x) es monótonamente creciente para todo
n∈N.
Ahora, por hipótesis existe una subsucesión(v(1,n)) de (vn) convergente puntualmente en c.t.p I a una funciónv y comownes monótonamente creciente para todonentoncesw(1,n) es
En resumen, tenemos que v(2,n)(x) → v(x) y w(2,n)(x) → w(x) para todo x ∈ I−N con N un
conjunto de medida0, luego
u(2,n)(x) =v(2,n)(x)−w(2,n)(x)→v(x)−w(x).
Es decir(un)tiene una subsucesión convergente puntualmente en c.t.p I.
Se deja como ejercicio dar una demostración del teorema tomando, sin perdida de generalidad, queun es monótonamente creciente. Obteniendo así una demostración que no utilice tanta teoría de la medida, como la que se dio en el ejemplo 12.
Por la desigualdad de Sobolev tenemos quei:W1,p(I)−→L∞(I) es continua, es natural pregun-tarnos ¿es compacta? La repuesta es no, como ilustra el siguiente ejemplo.
Ejemplo 14. Sea una función ϕ ∈ Cc∞(R), con ϕ 6= 0, y sea un(x) = ϕ(x+n) entonces (un) es acotada en W1,p(R) con 1 ≤ p ≤ ∞ y no admite subsucesiones convergentes en Lq(R) con
1≤q≤ ∞.
Demostración. Puesto queϕ∈Cc∞(R)implica queϕ∈Lq(R). Veamos queϕ0 ∈Lq(R). En efecto,
comoϕ= 0sobreKc, conK un compacto, entoncesϕ0= 0sobre Kc. Por tanto ϕ0 ∈Cc∞(R) así
ϕ0∈Lq(R). Por consiguiente ϕ∈W1,q(R) para todo1≤q ≤ ∞. De dondekϕkW1,q<∞. Ahora un ∈ Cc∞(R) ⊆W1,q(R) para todo n∈ N, pues un es sólo una traslación de ϕ. Por otro lado
kunkq =
Z ∞
−∞
|ϕ(x+n)|qdx
1/q
=
Z ∞
−∞
|ϕ(v)|qdv
1/q
=kϕkq.
Comou0n(x) =ϕ0(x+n) obtenemos análogamente queku0
nkq =kϕ0kq. Así
kunkW1,q =kϕkW1,q <∞,
por tanto(un) es una sucesión acotada enW1,q(R) para todo1≤q ≤ ∞. Veamos ahora que (un) no admite subsucesiones convergentes enLq(R). En efecto,
kun−umkqq =
Z ∞
−∞
|ϕ(x+n)−ϕ(x+m)|qdx
=
Z ∞
−∞
|ϕ(x)−ϕ(x+ (m−n))|qdx
=
Z
K∪Km−n
con K = suppϕ y Kn = suppun para todon ∈ N. Debemos tener que Kn = K+{−n}, como ilustra la Figura 1.5, pues un es sólo una trasalación deϕ.
Figura 1.5: Comparación deϕ(x) con un(x)
Por otra parte mostremos que paransuficientemente grandeKn∩K=∅.ComoKes un compacto, existe I = [a, b]tal que K ⊆I y por propiedad arquimediana existe N ∈N tal que
b−a < N.
Luego, six∈K yx∈KN entoncesx=y−N cony ∈K, asíy−x=N, pero como x, y∈K⊆I entonces N = y−x ≤ b−a, lo cual es una contradicción. Por tanto si tomamos n, m tal que
m−n≥N tenemos que
K∩Km−n=∅,
de esta manera
kun−umkqq =
Z
K
|ϕ(x)−ϕ(x+ (m−n))|qdx+
Z
Km−n
|ϕ(x)−ϕ(x+ (m−n))|qdx
=
Z
K
|ϕ(x)|qdx+
Z
Km−n
|ϕ(x+ (m−n))|qdx
=kϕkqq+kum−nkqq
= 2kϕkqq.
Es decir, para todo n∈N y para todom∈N tal que m≥N+nse tiene que
kun−umkq = 21/qkϕkq.
Por tanto (un) no admite subsucesiones convergentes en Lq(R) con 1 ≤ q < ∞. Para el caso
q=∞la demostración es análoga.
decir, ¿La clausura deCc∞(I), con la topología inducida por la norma deW1,p, es igual al espacio de Sobolev? La respuesta es no. Sin embargo existe un resultado más debíl en estos espacios, éste se muestra a continuación y es tomado de [Brezis, 2010, pag. 211].
Teorema 1.13 (Teorema de la Densidad paraW1,p). Seau∈W1,p(I) con 1≤p <∞. Entonces existe una sucesión(un) enCc∞(R) tal que un|I →u en W1,p(I).
Como ya mencionamos, en general no existe una sucesión(un)enCc∞tal queun→uenW1,p(I), como si ocurre en Lp(I). Más aun, el conjunto Cck(I) tampoco es denso en W1,p(I) para todo
k∈N. En particular,C1
c(I) no es denso, pero su clausura sí es un espacio importante, por ello lo mencionamos a continuación.
Definición. Dado1≤p <∞, se denota aW01,p(I)por la clausura deCc1(I)enW1,p(I)y además se define
H01(I) =W01,2(I).
El espacioW01,p(I)es equipado con la norma de W1,p(I).
Ya que Cc1(I) es un subespacio vectorial de W1,p(I) obtenemos que W01,p(I) es un subespacio normado de W1,p(I) y como es cerrado, por definición, entoncesW1,p
0 (I) es completo. Por tanto W01,p(I) es un espacio de Banach para 1≤p≤ ∞.
Ahora como todo subconjunto de un espacio separable es a su vez separable, queda queW01,p(I)
es un espacio separable para1≤p <∞y de igual manera todo subespacio de un espacio reflexivo es reflexivo, implica queW01,p(I) es un espacio reflexivo para1< p <∞.
Existe una importante propiedad de este espacio que además de ser muy útil, con toda la teoría anteriormente expuesta, su demostración no resulta larga y por esto enunciaremos este resultado a continuación con su respectiva demostración.
Teorema 1.14(Desigualdad de Poincaré). SeaI un intervalo acotado. Entonces existe una cons-tanteC tal que
kukW1,p(I)≤Cku0kLp(I)
para todo u∈W01,p(I), con1≤p≤ ∞. En otras palabras, si sobre W01,p(I) se define la siguiente norma
kuk=ku0kLp(I),
ésta es equivalente a la norma de W1,p.
Comoun ∈Cc1(I) implica que un = 0sobre ∂I, entonces u= 0 sobre∂I, por tanto u(a) = 0, de donde
|u(x)|=|u(x)−u(a)|=
Z x
a
u0(t)dt
≤ ku0kL1(I),
esto es,
kukL∞(I)≤ ku0kL1(I). (1.2)
Como ya demostramos, cuando la medida del espacio es finita, la inclusión
i:Lp2(X)−→Lp1(X)
es continua con p1 ≤p2. En particular
i:Lp(I)−→L1(I) y i:L∞(I)−→Lp(I)
son continuas para todo1≤p≤ ∞. Por tanto existen constantes C1 yC2 tal que
ku0kL1(I)≤C1ku0kLp(I) (1.3)
y
kukLp(I)≤C2kukL∞(I). (1.4)
De (1.2) y (1.3) se tiene que
kukL∞(I)≤C1ku0kLp(I)
y junto con (1.4) se obtiene que
kukLp(I)≤C1C2ku0kLp(I).
De modo que
kukW1,p(I) =kukLp(I)+ku0kLp(I)
≤C1C2ku0kLp(I)+ku0kLp(I)
=Cku0kLp(I).
ConC =C1C2+ 1.
Corolario 1.1(Desigualdad de Poincaré-Wirtinger). SeaI un intervalo acotado y sea1≤p≤ ∞, entonces existe una constanteC tal que para todo u∈W1,p(I)
ku−uIkW1,p(I)≤Cku0kLp(I)
con uI una constante definida por
uI=
1
µ(I)
Z
I
u(t)dt.
Demostración. Definamos aI = (a, b) entonces
uI =
1
b−a
Z b
a
u(t)dt
y como u ∈ W1,p(I) entonces existe u ∈ C(I), tal que u = u c.t.p I. Por tanto, sin perdida de generalidad supongamos queu=u, es decir u∈C(I) y definamos
w(x) =
Z b
a
u(t)dt.
Luego, por el Teorema Fundamental de Cálculo (clásico), w es diferenciable en el sentido usual enI yw0=u. Así por el teorema de valor medio, existec∈I tal que
w(b)−w(a)
b−a =w 0
(c).
Es decir,
uI=
1
b−a
Z b
a
u(t)dt
=u(c),
por tanto
|u(x)−uI|=|u(x)−u(c)|=
Z x c
u0(t)dt
≤ ku0kL1(I)
esto es,
ku−uIkL∞(I)≤ ku0kL1(I).
Y usando que la inclusión
i:Lp2(X)−→Lp1(X)
es acotada con p1 ≤ p2, como se uso en la demostración anterior, se obtiene que existe una
constante C tal que
Ahora note que para demostrar la desigualdad anterior sólo necesitamos el hecho de queuI =u(c) para algúnc∈I. A partir de esto obtenemos el siguiente corolario.
Corolario 1.2. Sea I un intervalo acotado y sea1≤p≤ ∞, entonces existe una constanteC tal que para todoc∈I y para todo u∈W1,p(I)
ku−u(c)kW1,p(I)≤Cku0kLp(I).
Ahora mostraremos los siguientes ejemplos, para ilustrar al lector de algunas propiedades más de estos espacios y familiarizarlo un poco más de cómo se trabaja en esta teoría.
Ejemplo 15 (Desigualdad de Sobolev-Gagliardo-Nirenberg para L∞). Sean I = (0,1),1≤q <∞
y1< r≤ ∞entonces existe una constante C =C(q, r) tal que
kukL∞(I)≤CkukaW1,r(I)kuk1
−a Lq(I) para todou∈W1,r(I), donde 0< a <1es definido por
a
1
q + 1−
1
r
= 1
q.
Demostración. Para empezar definamos de una forma más clara a a. Ya que 1 ≤ q < ∞ y
1< r≤ ∞entonces 0< 1q ≤1y0≤ 1
r <1 y por tanto0≤
1
q <
1
q+ 1−
1
r, luego
1< q
1
q + 1−
1
r
.
Por consiguiente si definimos a α = q1q + 1−1
r
tendremos que existe α−1 y 0 < α−1 < 1 y definimosa:=α−1.
En primer lugar veamos que se cumple la desigualdad para el casou(0) = 0. DefinamosG(t) =
|t|α−1tentonces
G(u(x)) =|u(x)|α−1u(x).
No es dificíl demostrar queGes diferenciable y
G0(t) =α|t|α−1.
ComoG(u(0)) =G(0) = 0 obtenemos
G(u(x)) =
Z x
0
G0(u(t))u0(t)dt
=
Z x
0
Por ende
|u(x)|α =
Z x 0
α|u(t)|α−1u0(t)dt
≤ Z I
α|u(t)|α−1|u0(t)|dt.
Entonces por la desigualdad de Hölder aplicado ar queda que
|u(x)|α≤α
Z
I
|u|(α−1)r0
1/r0Z
I
|u0|r
1/r
(1.5)
con r0 el conjugado der. Por otro lado
(α−1)r0 = (α−1)
1−1 r
=
1 +q−q r
−1
1−1 r
=q
1−1 r
2
< q.
Luego, por el ejemplo 7, tenemos que
kuk(α−1)r0 ≤µ(I)
1 (α−1)r0−
1 qkuk
q =kukq. Esto es,
Z
I
|u|(α−1)r0
1/r0
≤ kukαq−1. (1.6)
De (1.5) y (1.6) se obtiene que
|u(x)|α ≤αkukαq−1ku0kr ≤αkukαq−1kukW1,r.
Es decir,
kuk∞≤(α)1/αkukq(α−1)/(α)kuk
1/α W1,r
= (1/a)akuk1q−akukaW1,r.
Ahora veamos que la desigualdad se cumple en el caso general. Seau∈W1,r(I) y seaϕ∈C1(I)
con ϕ(0) = 0. Entonces para v = uϕ, tenemos que v ∈ W1,r(I) y v(0) = 0, luego por el caso anterior
con C= (1/a)a. Por otra parte, parag∈Lp(I) con 1≤p≤ ∞yf ∈C(I) se tiene que
Z
|f|p|g|p ≤ kgpk1kfpk∞
=kgkppkfpk∞
y por tanto
kf gkp ≤ kgkpkfpk1/p
∞ .
Comof es continua en I implica que
kfk∞= sup
x∈I
|f(x)|
y por propiedades delsuptenemos que
kfpk∞= sup
x∈I
|f(x)|p =
sup
x∈I
|f(x)|
p
=kfkp∞.
Se concluye que para todof ∈C(I) y para todog∈Lp(I) con1≤p≤ ∞se cumple que
kf gkp≤ kgkpkfk∞.
Luego obtenemos que
kvk1q−a=kϕukq1−a≤ kϕk1∞−akuk1q−a
y
kvkaw1,r =kϕukaw1,r
= (kϕukr+kϕ0u+ϕu0kr)a
≤(kϕk∞kukr+kϕ0k∞kukr+kϕk∞ku0kr)a
= ([kϕk∞+kϕ0k∞]kukr+kϕk∞ku0kr)a
≤(kϕk∞+kϕ0k∞)a(kukr+ku0kr)a
=kϕka
W1,∞kukaW1,r.
Es decir, para todo ϕ∈C1(I) con ϕ(0) = 0 tenemos
Ckvkaw1,rkvk1q−a≤
CkϕkaW1,∞kϕk1∞−a
kukaW1,rkuk1q−a. (1.8)
Supongamos ahora que para todoϕ∈C1(I)conϕ(0) = 0y para todob >0existe unu0 ∈W1,r(I)
tal que
pero esto ocurre sólo sikϕu0k∞ = 0 para todo ϕ∈ C1(I) con ϕ(0) = 0, luego ϕu0 = 0c.t.p I.
Pero u0(x)6= 0 c.t.pI, pues si suponemos lo contrario entonces
0 =ku0k∞> bkϕu0k∞≥0
y esto es una contradicción, por ende ϕ= 0c.t.pI. Además comoϕ∈C1(I) implica que ϕ= 0, lo cual es una contradicción ya queϕera arbitrario. Por tanto existe almenos unϕ0 6= 0∈C1(I)
con ϕ0(0) = 0 y existe unb0 >0 tal que para todou∈W1,r(I)tenemos que
kuk∞≤b0kϕ0uk∞. (1.9)
De (1.7), (1.8) y (1.9) obtenemos que
kuk∞≤b0kϕ0uk∞
≤b0Ckϕ0ukaw1,rkϕ0uk1q−a
≤[b0Ckϕ0kaW1,∞kϕ0k∞1−a]kukaW1,rkuk1q−a,
es decir,
kuk∞≤C0kukaW1,rkuk1q−a
con C0 =b0Ckϕ0kWa 1,∞kϕ0k1∞−a.
Ejemplo 16 (Desigualdad de Sobolev-Gagliardo-Nirenberg paraLp). Sean I = (0,1),1≤q < p < ∞ y1≤r≤ ∞entonces existe una constante C=C(p, q, r) tal que
kukLp(I) ≤CkukbW1,r(I)kuk1L−q(bI)
para todou∈W1,r(I), donde 0< b <1 es definido por
b
1
q + 1−
1
r
= 1
q −
1
p.
Demostración. Al igual que en la demostración anterior, definamos de una forma más clara a b. Tenemos por el ejemplo anterior que
1< q
1
q + 1−
1
r
y comoq < p entonces0< p−q < py así
1< p p−q,
luego
1< pq p−q
1
q + 1−
1
r
Por consiguiente si definimos aβ = ppq−q1q + 1−1
r
tendremos que existe β−1 con 0< β−1 <1, por lo que definimos a b:=β−1. Por otro lado
kukpp =
Z
I
|u|q|u|p−qdt
≤ kuqk1kup−qk∞
=kukqqkukp∞−q
por otro lado, por el ejemplo anterior tenemos que existe una constanteC tal que
kukp∞−q ≤Cp−qkukWa(p1,r−q)kuk
(1−a)(p−q)
q con a= 1/αyα =q1q + 1−1
r
. Luego
kukpp≤Cp−qkukWa(p1,r−q)kuk
(1−a)(p−q)+q
q . (1.10)
Ahora note que β= p−pqα, es decir,a= p−pqb, por tanto
a(p−q) =pb (1.11)
y
(1−a)(p−q) +q= (p−q−(p−q)a) +a
= (p−q−pb) +q
=p−pb.
Es decir,
(1−a)(p−q) +q=p(1−b). (1.12)
De (1.10), (1.11) y (1.12) obtenemos que
kukpp ≤Cp−qkukpbW1,rkuk p(1−b)
q ,
esto es,
kukp ≤C p−q
p kukb− W1,rkuk
(1−b)
q .
Ejemplo 17. (Desigualdad de Sobolev-Gagliardo-Nirenberg caso especial) SeanI = (0,1),1≤q < p≤ ∞y1≤r≤ ∞entonces existe una constante C=C(p, q, r) tal que
kukLp(I)≤Cku0kbLr(I)kuk1L−q(bI)
para todou∈W1,r(I) con RIu= 0, donde b= 1/β y
β = pq
p−q
1
q + 1−
1
r
Demostración. Por la desigualdad de Sobolev-Gagliardo-Nirenberg tenemos que existe una cons-tanteC1 tal que
kukLp(I) ≤C1kukbW1,r(I)kuk1L−q(bI) (1.13)
y por la desigualdad de Poincaré-Wirtinger, existe una constante C2 tal que
ku−uIkW1,r(I)≤C2ku0kLr(I)
con uI = µ(1I)
R
Iu(t)dt. Por hipótesis obtenemos que uI= 0 y por ende
kukW1,r(I)≤C2ku0kLr(I).
Reemplazando en (1.13) queda que
kukLp(I)≤C1C2ku0kbLr(I)kuk1L−q(bI).
Necesitaremos algunas propiedades del dual de W1,p, pero antes de poder enunciar algunas pro-piedades de este espacio tenemos que trabajar el dual de un espacio de Hilbert. Para empezar necesitaremos del siguiente teorema tomado de [Brezis, 2010, pag. 135].
Teorema 1.15(Teorema de Representación de Riesz-Fréchet). Sea(H,(,))un espacio de Hilbert y seak · ksu correspondiente norma asociada a su producto interno. Dado ϕ∈H∗ existe un único
v∈H tal que
ϕ(u) = (v, u)
para todo u∈Hy además
kvk=kϕkH∗.
De este teorema se desprenden dos resultados. Por un lado, todo funcional lineal continuo deϕ
de H se comporta como un producto interno pues si identificamos a ϕcon v obtenemos, con un abuso de la notación,
ϕ(u) = (ϕ, u).
Esto inspira a la notación de que todo funcional linealϕevaluado enu, se escribe
hϕ, ui.
Sea(H,(,))un espacio de Hilbert y seak·ksu correspondiente norma asociada a su producto interno. Dadoϕ∈H∗ existe un único v∈H tal que
hϕ, ui= (v, u)
para todou∈H y además
kvk=kϕkH∗.
Así es como muchas veces se encuentra en la literatura.
Por otro lado, a partir de este teorema se puede probar fácilmente queH es isométricoH∗, donde diremos que dos espacios normados son isométricos o isomorfos si existe una aplicación lineal biyectiva isométrica entre ellos, la cual en este caso será
IH : H −→ H∗
v 7→ ϕ,
con ϕ(u) = (u, v) para todo u ∈H. A esta aplicación lineal biyectiva isométrica la llamamos la isométria canónica deH en H∗. Por lo tanto es legítimo identificar a H con H∗, es decir
H 'H∗.
Usualmente se hace esto, pero no siempre. Ahora una situación típica que manejaremos adelante, donde tenemos que tener cuidado con esta identificación, es la siguiente:
Sea H = (H,(,)) un espacio de Hilbert y sea k · k1 su correspondiente norma asociada a su
producto interno. Asumamos que V ⊂ H es un subespacio vectorial denso en H. Supongamo además queV tiene su propia norma k · k2, con la cual V es un espacio de Banach. Por último
supongamos que la inclusión i : (V,k · k2) → (H,k · k1) es continua. Con la teoría que llevamos
hasta aquí tenemos varios ejemplos de esta situación. Por ejemplo.
H=L2(X) yV =Lp(X) con p >2yX un espacio de medida con medida finita.
H=L2(Ω)yV =C(Ω)con lak · k∞y Ω⊆Rn medible y acotado.
H=L2(I)yV =W1,2(I), con I un intervalo.
No es dificíl demostrar que estos ejemplos cumplen todas las hipótesis anteriormente dichas.
Ahora definimos la siguiente función
con V∗ el dual de V asociado a la normak · k2 yϕ|V la restricción deϕ sobreV. Es decir, para todov∈V
T(ϕ)[v] =ϕ(v),
o con la notación anteriormente mencionada
hT(ϕ), vi=hϕ, vi.
AT se le llama el mapeo canónico deH∗ en V∗ y tiene las siguientes propiedades.
Proposición 1.3. Sean H y V como se definieron anteriormente y T el mapeo canónico de H∗
enV∗ entonces
1. T es una aplicación lineal continua y más aun para toda constante C tal que kvk1 ≤Ckvk2
para todo v∈V, se cumple que
kT ϕkV∗ ≤CkϕkH∗
para todo ϕ∈H∗.
2. T es inyectiva.
3. R(T) es denso en V∗ siV es reflexivo.
Demostración. En primer lugar veamos que T esta bien definida, para esto basta ver que T ϕ=
ϕ|V ∈V∗ para todo ϕ∈H∗. En efecto, sea v∈V y ϕ∈H∗, como i: (V,k · k2) →(H,k · k1) es continua existe C >0 tal que
kvk1≤Ckvk2
para todov∈V, entonces
|(T ϕ)[v]|=|ϕ(v)| ≤ kϕkH∗kvk1≤CkϕkH∗kvk2. (1.14)
AsíT ϕes acotada en(V,k · k2)y como es lineal, puesto que es la restricción de una transformación
lineal, queda que T ϕ∈V∗. Veamos que T es una aplicación lineal continua. Es lineal pues para todoϕ1, ϕ2 ∈H∗ yα∈R
T(αϕ1+ϕ2) = (αϕ1+ϕ2)|V =αϕ1|V +ϕ2|V =αT(ϕ1) +T(ϕ1),
y de (1.14) tenemos que
|(T ϕ)[v]|
para todov∈V − {0}. Luego
kT ϕkV∗ = sup
v∈V−{0}
|(T ϕ)[v]|
kvk2 ≤CkϕkH∗.
Por tantoT es una aplicación lineal continua. Veamos que es inyectiva. Para esto recordemos que
(V,k · k2) es un espacio de Banach con su respectivo espacio dualV∗ asociado a la k · k2. Pero a su vez(V,k · k1) es un subespacio normado denso en(H,k · k1) y por tanto podemos hablar de su
espacio dual asociado a la norma k · k1 que notaremos por V0. Este es un espacio de Banach con
la norma k · kV0. Ahora, seanϕ1, ϕ2 ∈H∗ tal que T(ϕ1) =T(ϕ2) = Φ, esto es,
ϕ1|V =ϕ2|V = Φ.
Tenemos que Φ ∈ V0 y por lo anterior ϕ1 : H → R y ϕ2 : H → R son dos extensiones de Φ
con ϕ1, ϕ2 operadores lineales acotados, pero por la Proposición 1.1Φ tiene una única extención
Φ :V =H →R, con Φun operador lineal acotado. Por tanto
ϕ1 =ϕ2= Φ.
Es decir,T es inyectiva. Por último veamos que es densa. Para ver queR(T)es densa enV∗ basta ver que para todo funcional lineal continuo sobreV∗ que se anula enR(T), tiene que anularse en todoV∗ [Brezis, 2010, pag. 8].
Sea g0 ∈V∗∗ tal que g0(Φ) = 0 para todo Φ∈R(T), comoV∗ es reflexivo entonces la inmersion
canonica deV en V∗∗
C: V −→ V∗∗ x 7→ gx
con gx(Φ) = Φ(x) para todoΦ ∈V∗, es una isometría lineal biyectiva. Luego existe x0 ∈ V tal queg0(Φ) = Φ(x0) para todoΦ∈V∗. Ahora por hipótesis tenemos que
Φ(x0) = 0
para todo Φ ∈ R(T). Esto implica que para todo ϕ ∈ H∗,ϕ(x0) = T(ϕ)[x0] = 0. Luego por el Teorema de Representación de Riesz-Fréchet, para todox∈H
(x, x0) = 0.
En particular parax0 se tiene que(x0, x0) = 0luegox0 = 0y por consiguiente para todoΦ∈V∗,
De la proposición anterior, se escribe usualmente que
H∗⊂V∗.
Hay que recordar que no son subconjuntos sino que existe entre ellos una inmersión canónica acotada y densa en caso de V ser reflexivo, adicionalmemte si identificamos aH con su espacio dual se escribe normalmente
V ⊂H'H∗ ⊂V∗,
donde las inmersiones son continuas y densas (en caso de V ser reflexivo). Sin embargo siempre se debe recordar que lo que ocurre es el siguiente diagrama
(V,k · k2)−−−→i (H,k · k1)
IH
−−−−→(H∗,k · kH∗)−−−→T (V∗,k · kV∗).
Ahora, siV es un espacio de Hilbert y si identificamos aV con V∗, llegaríamos a que
V ⊂V,
esto no es una contradicción, esta diciendo que existe una inmersión acotada densa deV en V no sobreyectiva
h: (V,k · k2)−→(V,k · k2)
conh=IV ◦T◦IH◦i. Por tanto para no escribir cosas confusas y aparentemente contradictoras como éstas, sólo se identifica a uno de los dos espacios de Hilbert.
Finalmente con toda esta teoría expuesta podemos trabajar sobre el espacio dual deW01,p(I) con
1≤p <∞el cual denotamos porW−1,p0(I)y al espacio dual deH01(I)lo denotamos porH−1(I). Para empezar veamos queH =L2(I) yV =H01(I), conI un intervalo cualquiera, cumplen todas las hipótesis de lo anteriormente expuesto.
Ya tenemos que H1
0(I) es un subespacio vectorial de L2(I), y comoCc1(I) ⊆H01(I) entonces H01
contiene un espacio denso deL2(I) y por tanto él es denso enL2(I). También tenemos que es un espacio de Banach con su propia norma y ya que la inclusióni:W1,p(I)→Lp(I)es acotada para todo1≤p≤ ∞, tenemos que la inclusión deH01 es acotada. Por tanto identificando aL2(I) con su dual, pero no identificando aH01(I) con su dual, obtenemos que para todo intervalo I
H01(I)⊂L2(I)⊂H−1(I),
donde la inclusiones representan inmersiones continuas y densas.
Por un lado tenemos que
W01,p(I)⊂C(I)⊂L∞(I)⊂L2(I),
siI es acotado, y como Cc1(I)⊆W01,p(I) yCc1(I)es denso enL2(I)entoncesW01,p(I)es denso en
L2(I). Esto es, W01,p(I) es un subespacio vectorial denso deL2(I), el cual ya sabemos que con su propia norma es un espacio de Banach.
Por otro lado como la inclusióni1 :W1,p(I)→L∞(I)es continua por la desigualdad de Sobolev y
la inclusióni2 :L∞(I)→ L2(I) es continua por el Ejemplo 7 entonces la inclusióni:W01,p(I)→ L2(I) es continua.
Por tanto, siI es un intervalo acotado y1≤p≤ ∞obtenemos que
W01,p(I)⊂L2(I)⊂W−1,p0(I),
donde las inmersiones son continuas (y densas para1< p <∞). Ahora análogamente siI no es acotado y1≤p≤2 obtenemos que
W01,p(I)⊂L2(I)⊂W−1,p0(I),
donde las inmersiones son continuas (y densas para 1 < p≤2). Por último, al igual que hay un Teorema de la Densidad para los espacios de Sobolev, existe un Teorema de Representación de Riesz para estos espacios tomado de [Brezis, 2010, pag. 219], el cual no resulta difícil demostrar y por tanto lo presenta mos con su demostración.
Teorema 1.16(Teorema de Representación paraW1,p). SeaF ∈W−1,p0(I) entonces existen dos funcionesf1, f2∈Lp
0
(I), con p0 el conjugado de p, tal que
hF, ui=
Z
I
f1u+
Z
f2u0
para todo u∈W01,p y
kFkW−1,p0 = m´ax{kf1kp0,kf2kp0}.
Demostración. Sea E =Lp(I)×Lp(I) equipado con la norma
khk=kh0kp+kh1kp,
donde h = (h0, h1). El mapeo T :W01,p → E definido por T(u) = (u, u0) es una isométria lineal.
Por tanto G = T(W01,p) es un subespacio normado de E, equipado con la norma de E. Sea
S=T−1 :G→W01,p y Definamos