CONTROL DE SISTEMAS MECATRONICOS

INSTITUTO POLITÉCNICO NACIONAL

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA

Y ELÉCTRICA

UNIDAD PROFESIONAL ADOLFO LÓPEZ MATEOS

CONTROL DE SISTEMAS MECATRÓNICOS

T E S I S

QUE PARA OBTENER EL TÍTULO DE

INGENIERO EN COMUNICACIONES

Y ELECTRÓNICA

P R E S E N T A

Leonardo López Antonio

Litzahaya Tzitzintly Salas García

ASESORES

Dr. CARLOS VÁZQUEZ AGUILERA Dr. RODRIGO LÓPEZ CÁRDENAS

ESIME ZAC

I OBJETIVO

Analizar y diseñar un controlador PID aplicado a sistemas actuados y sub-actuados, así como el diseño de trayectorias de un robot manipulador de tres grados de libertad y una grúa viajera de cinco grados de libertad desarrollando sus modelos matemáticos y empleando la cinemática directa e inversa.

JUSTIFICACIÓN

Una de las principales preocupaciones de las empresas en materia de producción, consiste en incrementar los niveles de productividad, aumentando la efectividad y eficiencia de sus procesos. En la búsqueda de mantener la competitividad en el mercado y mejorar dichos factores, deben abrir sus perspectivas hacia la integración de sus operaciones con sistemas automatizados y mecatrónicos.

Uno de los inconvenientes en estos procesos, es el transporte de piezas involucradas dentro de dicho proceso, por lo general, esta tarea es llevada a cabo por un operario, que transporta manualmente las piezas o productos. La automatización industrial no es un fenómeno reciente, desde que la actividad artesanal comenzó a ser sustituida por la industria, las empresas han procurado la obtención del máximo rendimiento del trabajo mediante la acción combinada de herramientas, máquinas y organización, tales como el empleo de robots manipuladores o grúas donde los procesos exigen una detallada ejecución del mismo, traslado de grandes masas de un lugar a otro, siendo estos elementos indispensables en una gran parte de los procesos de manufactura.

ESIME ZAC

II AGRADECIMIENTOS

“A nuestros padres por estar siempre a nuestro lado, por su paciencia, dedicación, apoyo, amor, confianza, que nos brindan a cada momento, y darnos la oportunidad de culminar esta etapa de nuestras vidas.”

“A nuestros Profesores del Instituto Politécnico Nacional, compañeros y amigos que con su cariño y sus enseñanzas hicieron posible este sueño.”

“Al profesor Carlos Vásquez Aguilera por el apoyo, y consejos ofrecidos durante las largas jornadas de asesorías y consultas.”

“Al profesor Rodrigo López Cárdenas por el interés mostrado y apoyo brindado durante el desarrollo de este trabajo.”

ESIME ZAC

III ÍNDICE

Objetivo _______________________________________________________________________ I

Justificación ____________________________________________________________________ I

Agradecimientos ______________________________________________________________ III

Índice _______________________________________________________________________ IIII

Índice de Figuras ______________________________________________________________ VI

Índice de Tablas _______________________________________________________________ IX

CAPITULO 1

Introducción a los Sistemas Mecatrónicos

1.1 Morfología de un Robot Industrial _______________________________________________________ 5 1.2 Principales Caracteristicas _____________________________________________________________ 8 1.3 Cinemática y Dinámica _______________________________________________________________ 11 1.4 Aplicaciones Industriales _____________________________________________________________ 12

CAPITULO 2

Fundamentos Matemáticos

ESIME ZAC

IV

CAPITULO 3

Modelado de Sistemas

3.1 Cinemática Directa de un Robot Manipulador de 3 GDL __________________________________ 32 3.2 Cinemática Inversa de un Robot Manipulador de 3 GDL _____________________________________ 34 3.3 Dinámica de un Robot Manipulador de 3 GDL ____________________________________________ 38 3.4 Expresiones Generales para Obtener la Energía Cinética y la Energía Potencial _____________ 41 3.5 Ecuaciones de Movimiento ____________________________________________________________ 43 3.6 Modelo de una Grúa de 5GDL en 3 Dimensiones __________________________________________ 48

CAPITULO 4

Controlador PID

4.1 Conceptos Básicos de Sistemas de Control ________________________________________________ 58 4.2 Controlador PID ____________________________________________________________________ 62 4.3 Reglas de Sintonización de Controladores PID ____________________________________________ 68 4.4 Control de Seguimiento de Trayectoria __________________________________________________ 80

CAPITULO 5

Análisis y Resultados

5.1 Robot Manipulador __________________________________________________________________ 86

ESIME ZAC

V

CAPITULO 6

Conclusiones

Conclusiones _________________________________________________________________________ 113

Bibliografía _________________________________________________________________________ 115

Anexo A Cinemática Directa del Robot __________________________________________________ 117

Anexo B Cinemática Inversa del Robot __________________________________________________ 118

Anexo C Modelo Dinámico del Robot ____________________________________________________ 119

Anexo D Modelo Dinámico de la Grúa ___________________________________________________ 121

Anexo E Espacio de Trabajo del Robot __________________________________________________ 123

ESIME ZAC

VI ÍNDICE DE FIGURAS

Figura 1.1 Estructura Mecánica ____________________________________________________________ 5

Figura 1.2 Tipos de Articulaciones __________________________________________________________ 6 Figura 1.3 Diagrama de Bloques de un Sistema de Control de Robots _____________________________ 8

Figura 1.4 Configuraciones y Espacios de Trabajo _____________________________________________ 9

Figura 2.1 Espacio Vectorial 2D __________________________________________________________ 16

Figura 2.2 Producto Punto de Dos Vectores Cartesianos _______________________________________ 17

Figura 2.3 Regla de la Mano Deracha ______________________________________________________ 18

Figura 2.4 Utilización de la Ley de Cosenos _________________________________________________ 20

Figura 2.5 Sistemas de Referencia y ___________________________________________________ 20

Figura 2.6 Sistemas de Referencia y ___________________________________________________ 22

Figura 2.7 Sentido Positivo de los Ángulos ____________________________________________ 24

Figura 2.8 Condiciones para obtener los Parámetros de D-H ____________________________________ 25

Figura 2.9 Sistema de un Grado de Libertad _________________________________________________ 26

Figura 3.1 Kuka KR 40 PA ______________________________________________________________ 30

Figura 3.2 Grúa Viajera _________________________________________________________________ 31 Figura 3.3 Configuración de Sistemas de Referencia para un Robot de 3GDL _______________________ 32

Figura 3.4 Configuración Geométrica de un Brazo Manipulador de 3GDL _________________________ 34

Figura 3.5 Configuración Geométrica de los Eslabones 2 y 3 ____________________________________ 35

Figura 3.6 Cuerpo Rígido ________________________________________________________________ 41

Figura 3.7 Sistema Coordenado de una Grúa ________________________________________________ 48

Figura 4.1 Configuración Típica de un Diagrama de Bloques de un Sistema de Control _______________ 58

Figura 4.2 Sistema de Control en Lazo Abierto _______________________________________________ 59 Figura 4.3 Sistema de Contro en Lazo Cerrado _______________________________________________ 60

Figura 4.4 Controlador PID ______________________________________________________________ 63

Figura 4.5 Diagrama de Bloques de un Controlador Proporcional ________________________________ 64

Figura 4.6 Diagrama de Bloques de un Controlador Integral ____________________________________ 65

Figura 4.7 Diagrama de Bloques de un Controlador Derivativo __________________________________ 66

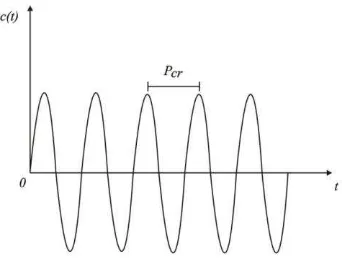
Figura 4.8 Oscilación Sostenida con un Periodo ___________________________________________ 68

ESIME ZAC

VII

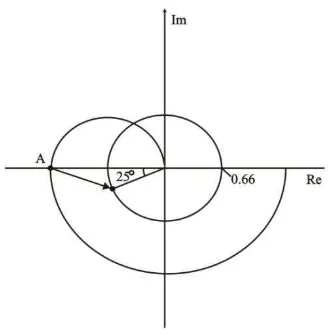
Figura 4.10 Cambio del Punto en el Plano Complejp Causado por un PID _______________________ 70

Figura 4.11 Cambio del Punto a para la Asignación del Margen de Ganancia _________________ 71 Figura 4.12 Curva de Respuesta en Forma de S ______________________________________________ 74

Figura 4.13 Parámetros Característicos de la Respuesta al Escalón por el Método de la Tangente ______ 74

Figura 4.14 Parámetros Característicos de la Respuesta al Escalón por el Método de la Áreas _________ 76

Figura 4.15 Trayectoria Típica del Espacio Común ___________________________________________ 84

Figura 5.1. Robot Manipulador 3GDL ______________________________________________________ 86

Figura 5.2 Área de Trabajo del Robot Manipulador de 3GDL ___________________________________ 87 Figura 5.3 Descripción de la Trayectoria del Robot Manipulador de 3GDL _________________________ 88

Figura 5.4 Trayectoria de Simulación ______________________________________________________ 89

Figura 5.5 Modelo del Robot Manipulador en Matlab Simulink __________________________________ 89

Figura 5.6 Simulación de la Señal de Velocidad Promedio Estimada ______________________________ 91

Figura 5.7 Simulación de la Señal de Velocidad Estimada para T=0.01 ____________________________ 91

Figura 5.8 Simulación de la Señal de Velocidad Estimada para T=0.1 _____________________________ 92

Figura 5.9 Simulación de la Señal de Velocidad Estimada para T=1 ______________________________ 92 Figura 5.10 Controlador PID en Configuración Paralelo _______________________________________ 93

Figura5.11 Implementación de la Función Saturación _________________________________________ 94

Figura 5.12 Diagrama de Bloques de Simulación del Control PID para el Robot ____________________ 94

Figura 5.13 esultados de Simulación 1 del Robot ______________________________________________ 96

Figura 5.14 Resultados de Simulación 2 del Robot ____________________________________________ 97

Figura 5.15 Área de Trabajo de una Grúa de 5GDL ___________________________________________ 98 Figura 5.16 Grua 5GDL _________________________________________________________________ 99

Figura 5.17 Descripción de la Trayectoria de una Grúa de 5GDL ________________________________ 99

Figura 5.18 Trayectoria en Coordenadas Rectangulares 1 _____________________________________ 100

Figura 5.19 Modelo de la Grúa Viajera en Matlab-Simulink ____________________________________ 100

Figura 5.20 Diagrama de Bloques de Simulación del Control PID para la Grúa ____________________ 101

Figura 5.21 Resultados de Simulación 1 de la Grúa __________________________________________ 102 Figura 5.22 Simulación 1 de las Oscilaciones Presentadas en la Carga ___________________________ 103

Figura 5.23 Trayectoria en Coordenadas Rectangulares 2 _____________________________________ 104

Figura 5.24 Resultados de Simulación 2 de la Grúa __________________________________________ 105

ESIME ZAC

VIII

Figura 5.26 Resultados Experimentales 1 de la Grúa _________________________________________ 107

Figura 5.27 Oscilaciones Presentadas en la Carga ___________________________________________ 108

Figura 5.28 Error RMS y Fuerzas (Interpolación Lineal) ______________________________________ 109

Figura 5.29 Resultados Experimentales 2 de la Grúa _________________________________________ 110 Figura 5.30 Oscilaciones Presentadas en la Carga ___________________________________________ 111

ESIME ZAC

IX INDICE DE TABLAS

Tabla 3.1 Especificaciones del Robot Kuka KR 40 PA __________________________________________ 30

Tabla 3.2 Parámetros de Denavit-Hartenberg para un Robot de 3GDL ____________________________ 32

Tabla 4.1 Parámetros , y Basados en la Ganancia Critica y Periodo Crítico _________________ 69

Tabla 4.2 Calibrado del PID con Asignación del Margen de Ganancia o de Fase ____________________ 73

Tabla 4.3 Parámetros , y Basados en la Respusta Escalón de la Planta _____________________ 75

Tabla 4.4 Reglas de Calibrado de Cohen y Coon ______________________________________________ 77

Tabla 4.5 Reglas de Calibrado IMC ________________________________________________________ 77 Tabla 4.6 Reglas de Calibrado ITAE _______________________________________________________ 78

Tabla 4.7 Efecto de las Ganancias en los Controladores ________________________________________ 79

Tabla 5.1 Parámetros del Robot Manipulador de 3GDL ________________________________________ 86

Tabla 5.2 Ganancias PID ________________________________________________________________ 94

Tabla 5.3 Parámetros de la Grúa de 5GDL __________________________________________________ 99

1

Capítulo 1

Introducción a los Sistemas

Mecatrónicos

El campo de la mecatrónica consiste en la integración sinérgica de tres campos de la ingeniería tradicional para el proceso de diseño a nivel de sistema. Estos tres campos son:

1. Ingeniería Mecánica, de donde se toma el prefijo “meca”

2. Ingeniería Eléctrica o Electrónica, de donde se toma el sufijo “trónica”

3. Informática

2

El diseño mecánico forma el “esqueleto” del producto electromecánico sobre el cual se construye el resto

de las funcionalidades (como “ojos, músculos, cerebro”). Estos mecanismos se analizan en términos de su funcionalidad y parámetros comunes de diseño.

Cada sistema mecatrónico tiene algún sensor para medir el estado de las variables del proceso, los

sensores son los ”ojos” de un sistema controlado por computadora, los actuadores son los “músculos” del

sistema.

Los conceptos fundamentales de hardware y software para computadoras, microprocesadores y procesadores digitales de señales (DSP) se analizan teniendo presente aplicaciones para el control de dispositivos mecánicos.

Como ejemplo de estos cambios, la industria Automotriz se ha transformado a sí misma en términos de sus productos como en sus métodos de producción desde la introducción de los microprocesadores. El uso de controladores embebidos basados en microprocesadores ha aumentado de manera significativa los procesos de manufactura programable basados en robótica, como en las líneas de ensamble, maquinas-herramientas CNC (Control Numérico por Computadora) y manejo de materiales.

El manipulador robótico es un buen ejemplo de un sistema mecatrónico. Los manipuladores robóticos, el mecanismo de movimiento reconfigurable, programable y con grados múltiples de libertad se han aplicado en muchos procesos de manufactura (Cetinkunt, 2007).

El robot es, sin duda, uno de los inventos más populares del siglo XX. El fuerte desarrollo experimentado por la robótica se debe a las crecientes necesidades de automatización de la industria del siglo XX (Usategui, 2000).

Los robots actuales son obras de ingeniería y como tales concebidas para producir bienes y servicios o explotar recursos naturales. Desde esta perspectiva son máquinas con las que se continua una actividad que parte de los propios orígenes de la humanidad, y que desde el comienzo de la Edad Moderna se fundamenta esencialmente en conocimientos científicos (Fu, 1988).

También desde la antigüedad, el hombre ha sentido fascinación por las maquinas que imitan la figura y los movimientos de seres animados. Existe una larga tradición de autómatas desde el mundo griego hasta nuestro siglo, pasando por los autómatas de los artesanos franceses y suizos del siglo XVIII, que ya incorporaban interesantes dispositivos mecánicos para el control automático de movimientos.

3

La actualización industrial con utilización de sistemas de control automático comienza también en el siglo XIX pero no es hasta el siglo XX y muy especialmente, después de la segunda guerra mundial, cuando empieza a extenderse de forma importante en todos los sectores industriales. De esta manera, se generalizan los sistemas de control automático de variables de procesos industriales y, en particular, sistemas de control de posición y velocidad (Fu, 1988).

Una definición oficial de un robot viene de ROBOTICS INSTITUTE OF AMERICA (RIA):

Un robot es un manipulador multifuncional reprogramable diseñado para mover materiales, piezas, herramientas o dispositivos especializados para realizar diversas tareas (Craig, 2006).

Los robots no son los únicos sistemas macatrónicos que podemos mencionar, por otro lado podemos encontrar a grúas, sistemas que de igual forma son muy empleados en la industria, éstas son máquinas de elevación de movimiento discontinuo y su uso está destinado a elevar y distribuir cargas en el espacio de manera horizontal o vertical.

Las grúas son clasificadas de acuerdo a los modos en que transportan la carga de manera horizontal, de tal forma que encontramos los siguientes grupos (Towne, 1883).

 Rotary

 Swing Cranes

 Jib Cranes

 Colum Cranes

 Pillar Cranes

 Derrick Cranes

 Walking Cranes

 Rectilinear

 Bridge Cranes

 Tram Cranes

 Traveling Cranes

 Gantries

 Rotary Bridge Cranes

De acuerdo al Comité de Normalización de Petróleos Mexicanos y Organismos Subsidiarios en el documento número NRF-183-PEMEX-2007 disponible en http://www.pemex.com/files/content/NRF-183-PEMEX-20071.pdf, las grúas las podemos clasificar como se menciona a continuación.

 Por su accionamiento

 Manual: El puente, el polipasto y el carro son accionados con rueda y cadena de mando.

 Motorizada: El puente, el polipasto y el carro son accionados con motor eléctrico o neumático.

4

 Por su tipo de servicio

 Clase A: Servicio poco frecuente.

 Clase B: Servicio ligero.

 Clase C: Servicio moderado.

 Clase D: Servicio Pesado.

 Por su construcción

 Mono-puente.

 Bi-puente.

 Por su forma de soporte

 Apoyadas: Las ruedas de translación de la grúa se apoyan sobre la trabe carril.

 Suspendidas: Las ruedas de translación de la grúa se apoyan sobre la cara superior del patín inferior de la trabe carril.

A continuación describiremos los tipos de articulaciones que podemos encontrar en los diferentes sistemas macatrónicos, se define el término de grados de libertad, el sistema de accionamiento, sistema sensorial y sistema de control, sin perder generalidad dichos conceptos son explicados tomando en cuenta uno de los sistemas de mayor estudio.

5

1.1 MORFOLOGÍA DE UN ROBOT INDUSTRIAL

Un robot está constituido por los siguientes elementos:

 Estructura Mecánica (eslabones y articulaciones)

 Transmisiones y Reductores

 Sistemas de Accionamiento (actuadores)

 Sistema Sensorial

 Sistema de Control

 Elementos Terminales (pinzas o herramientas)

La estructura mecánica o brazo de un robot es una cadena formada por eslabones (ejes) consecutivos, unidos entre sí por medio de articulaciones que permiten el movimiento relativo entre ellos, ver figura 1.1 Generalmente, la cadena de eslabones tiene uno de sus extremos fijo, también llamado base, y en el extremo opuesto se coloca un efector final para realizar operaciones.

Figura 1.1 Estructura Mecánica

6

Las características quedan determinadas por su estructura, tales como su configuración, espacio de trabajo, volumen o de alcance del robot, la velocidad o la capacidad de carga.

Las articulaciones son elementos de unión entre los ejes del robot y es en ellas donde se origina el movimiento del mismo. El movimiento de cada articulación puede ser de desplazamiento, de giro o de una combinación de los tipos de movimiento.

Se distinguen seis tipos de articulaciones: prismáticas, de rotación, cilíndrica, esférica o rotula, planar y de tornillo, ver figura 1.2.

Figura 1.2 Tipos de Articulaciones

Las articulaciones prismáticas nos ayudan para su posicionamiento, alta precisión y gran robustez y las de rotación poseen envolventes de trabajo mayores con un menor espacio.

Las transmisiones son los elementos encargados de trasmitir el movimiento desde los actuadores hasta las articulaciones, los reductores adaptan el par y velocidad de la salida del actuador para el movimiento de los eslabones del robot.

7

Para que un robot realice una tarea con la adecuada precisión, velocidad e inteligencia, será necesario que tenga conocimiento tanto de su propio estado como del estado de su entorno.

La información relacionada con su estado (posición de las articulaciones) la adquiere a través de los sensores internos, mientras que el estado de su entorno lo adquiere a través de sensores externos.

A continuación se mencionan algunos tipos de sensores en forma resumida.

 SENSORES INTERNOS

 Sensores de presencia

 Sensores de posición

 Sensores de velocidad

 Sensores de fuerza

 SENSORES EXTERNOS

 Sensores de presencia

 Sensores de distancia

 Sensores para

reconocimiento de formas

 Sistemas de imagen

 Sistemas táctiles

El control de cualquier sistema significa aplicar/ejercer fuerza(s) para que el sistema se mueva/trabaje de acuerdo con las instrucciones ordenadas para ejecutar una tarea específica mediante el movimiento de su efector final en forma precisa y repetida. El control requiere el conocimiento del modelo matemático del mismo, así como de un sistema inteligente que actué sobre él.

Este tipo de control puede clasificarse como lineal y no lineal, y la teoría de control lineal sirve de base para sistemas de control no lineales, el modelo matemático necesario se obtiene de las leyes físicas que rigen el movimiento del sistema, el sistema inteligente requiere de dispositivos sensoriales y medios para accionar y reaccionar ante las variables detectadas.

Existen diferentes técnicas aplicadas a resolver un problema de control, tanto la técnica que se emplea como la manera de su implementación podrá tener una influencia sobre el desempeño del sistema. Por otro lado, el problema de control es de múltiples entradas y múltiples salidas, ver figura 1.3, mediante los vectores dimensionales a lo largo de cada línea de señal. Para simplificar el problema se considera cada articulación como independiente y controlada por separado, a continuación se mencionan las diferentes maneras de controlarla (Saha, 2010).

 Control de encendido/apagado o control de dos pasos

 Control Proporcional

 Control Derivativo

 Control Integral

8

Figura 1.3 Diagrama de Bloques de un Sistema de Control de Robots

Los elementos terminales, también llamados efectores finales son los encargados de interactuar directamente con el entorno del robot.

Existe una amplia gama de efectores finales necesarios para realizar una gran variedad de funciones. Estos tipos se pueden dividir en pinzas o herramientas.

Las pinzas se utilizan para agarrar y/o sostener los objetos.

Las herramientas son los efectores finales diseñados para realizar el trabajo sobre la pinza mejor de lo que lo haría solamente la pinza. Los efectores finales, requieren de otros tipos de artefactos y herramientas en algunas aplicaciones de robótica industrial. Existen otros dispositivos de agarre, de soldadura y otros tipos de dispositivos de agarre que posicionan la pieza de trabajo o la herramienta durante el ciclo de trabajo.

1.2 PRINCIPALES CARACTERÍSTICAS

Cada movimiento independiente que es capaz de realizar una articulación se le denomina grado de libertad (GDL) en la figura 1.2 se muestran los grados de libertad de cada articulación.

Considerando en un espacio 3D, el máximo GDL que se tiene es de seis grados, tres de desplazamiento y tres de giro, de ahí que la mayor parte de los robots tengan seis articulaciones.

El espacio de trabajo o campo de acción, es el volumen espacial al que puede llegar el extremo del robot. Este volumen está determinado por el tamaño, forma y tipo de los eslabones que integran el robot así como por las limitaciones de movimiento impuestas por el sistema de control. No se debe considerar el efector final colocado en la muñeca para la obtención del espacio de trabajo, ya que se trata de un elemento añadido al robot.

9

la figura 1.4d, cuando el robot tiene dos articulaciones de rotación y una prismática, se le llama de tipo esférico o polar y su espacio de trabajo es mostrado en la figura 1.4a, cuando el robot consiste en articulaciones de rotación, se le llama de tipo articulado o de rotación y su espacio de trabajo se muestra en la figura 1.4b. Tales robots son más sencillos de fabricar y mantener, ya que los actuadores del robot están directamente acoplados mediante transmisores de engranes o bien por bandas, pero su superficie interna de trabajo es más difícil de determinar (Saha, 2010).

Figura 1.4 Configuraciones y Espacios de Trabajo

a) Esférico o Polar c) Cartesiano

10

La precisión se define como una función de tres características:

 Resolución espacial

 Exactitud

 Repetibilidad

La resolución espacial de un robot se define como el más pequeño incremento de movimiento en el que el robot puede dividir su volumen de trabajo. La resolución espacial depende de dos factores:

 Resolución de control del sistema: Viene determinada por el sistema de control de posición del robot y su sistema de medida de realimentación.

 Inexactitudes mecánicas del robot: Se encuentran estrechamente relacionadas con la calidad de los componentes que conforman las uniones y las articulaciones.

La exactitud se refiere a la capacidad de un robot para situar el extremo de su muñeca en un punto de destino deseado dentro del volumen de trabajo.

La repetibilidad está relacionada con la capacidad del robot para situar su muñeca, o un efector final unido a su muñeca, en un punto en el espacio que se hubiera enseñado con anterioridad al robot.

La repetibilidad y la exactitud se refieren a los aspectos diferentes de la precisión del robot. La exactitud se relaciona con la capacidad del robot a programar para conseguir un punto destino determinado. El punto programa real es probable que sea diferente del punto destino debido a las limitaciones de la resolución de control. La repetibilidad se refiere a la capacidad del robot para volver al punto programado cuando se le ordena que lo haga.

La capacidad de carga de un robot viene condicionada por el tamaño, la configuración y el sistema de accionamiento del propio robot. Al evaluar la capacidad de carga se considera el peso de las piezas a manipular y el peso propio de la herramienta o pinza que emplee el robot colocada en la muñeca.

La velocidad de respuesta se refiere a la capacidad del robot para desplazarse a la siguiente posición en un breve periodo de tiempo. Este tiempo de respuesta esta evidentemente relacionado con la velocidad de movimiento del robot. También es una función del sistema de control. En robótica la estabilidad se suele definir como una medida de las oscilaciones que se producen en el brazo durante el movimiento desde una posición a la siguiente.

11

1.3 CINEMÁTICA Y DINÁMICA

Para controlar la posición debemos conocer las propiedades dinámicas del sistema con el fin de saber cuánta fuerza se requiere para lograr moverlo, ya sea poca fuerza, el sistema responderá de una forma muy lenta; mientras tanto si aplicamos demasiada fuerza, el sistema puede golpear contra objetos o oscilar sobre la posición deseada (Craig, 2006).

La obtención de las ecuaciones dinámicas de movimiento no es una tarea sencilla debido al gran número de grados de libertad y no linealidades del sistema.

La cinemática de los sistemas que se desarrollaran en esta tesis tratan con el estudio del movimiento con respecto a un sistema de coordenadas de referencia fijo sin considerar las fuerzas que lo originan. En la ciencia de la cinemática se estudia la velocidad, posición y aceleración y todas las derivadas de alto orden de las variables de posición con respecto al tiempo. Existen dos problemas fundamentales en la cinemática del robot.

1. Problema cinemático directo 2. Problema cinemático inverso

Específicamente, dado un conjunto de posiciones articulares, el problema cinemático directo calcula la posición y orientación del sistema coordenado de la herramienta o efector final relativo al sistema de referencia fijo. En la cinemática inversa se obtienen los valores de los posiciones articulares, que son realmente los que se envían al sistema de control, a partir de la posición y orientación deseada para el punto terminal del sistema dado. La cinemática inversa define el espacio de trabajo de un manipulador dado.

Denavit y Hartenberg en 1955 propusieron un enfoque sistemático y generalizado de utilizar algebra matricial para describir y representar la geometría espacial de los elementos del brazo del robot con respecto a un sistema de referencia fijo (Denavit, 1955).

12

El problema cinemático inverso se puede resolver mediante algunas técnicas. Los métodos utilizados más comúnmente son el algebraico matricial, iterativo o geométrico. (En esta tesis se emplea el método geométrico).

El modelo dinámico real de un brazo se puede obtener de leyes físicas conocidas como las leyes de Newton y la mecánica lagrangiana. Esto conduce al desarrollo de las ecuaciones dinámicas de movimiento para las distintas articulaciones del sistema en términos de los parámetros geométricos e inerciales especificados para los distintos elementos. Se pueden aplicar sistemáticamente enfoques convencionales como las formulaciones de Euler-Lagrange y de Newton para desarrollar las ecuaciones de movimiento del sistema.

1.4 APLICACIONES INDUSTRIALES

Los robots como las grúas son muy usados en la industria donde los procesos exigen una detallada ejecución del mismo, traslado de grandes masas de un lugar a otro, siendo estos elementos indispensables en una gran parte de los procesos de manufactura.

La Federación Internacional de la Robótica (IFR) estableció en 1998 una clasificación de las aplicaciones de la robótica en el sector manufacturero:

 Manipulación en función

 Moldes

 Otros

 Manipulación en moldeado de plásticos

 Manipulación en tratamientos térmicos

 Manipulación en la forja y estampación

 Soldadura

 Por arco

 Por puntos

 Por gas

 Por láser

 Otros

 Aplicación de materiales

 Pintura

 Adhesivos y secantes

13

 Mecanización

 Carga y descarga de maquinas

 Corte mecánico, rectificado, desbardado y pulido

 Otros

 Otros procesos

 Láser

 Chorro de Agua

 Otros

 Montaje

 Montaje mecánico

 Inserción

 Unión por adhesivos

 Unión por soldadura

 Manipulación para montaje

 Otros

 Paletización

 Medición, inspección, control de calidad

 Manipulación de materiales

 Formación, enseñanza e investigación

 Otros

Esta clasificación engloba la mayor parte de los procesos robotizados en la actualidad, aunque se puede encontrar aplicaciones particulares que no aparecen de manera explícita en esta clasificación.

En el documento número NRF-183-PEMEX-2007 disponible en http://www.pemex.com /files/content/NRF-183-PEMEX-20071.pdf, Marzo, 201, las aplicaciones para grúas de acuerdo a su clase son:

14

 Clase B (Ligero): Cubre las grúas para talleres de reparaciones, operaciones de ensamble ligero, edificios de servicio, almacenes ligeros entre otros, donde los requisitos del servicio son ligeros y la velocidad lenta.

 Clase C (Moderado): Cubre las grúas usadas en talleres de maquinaria o fábricas de papel, entre otros, donde los requisitos de servicio son moderados.

15

Capítulo 2

Fundamentos Matemáticos

A lo largo de la historia la ingeniería y las matemáticas se han desarrollado en forma paralela. Todas las ramas de la ingeniería dependen de las matemáticas para su descripción, es por eso que en este capítulo se da una exposición elemental de las características particulares de algebra lineal y trigonometría así como algunos conceptos sobre las ecuaciones de Euler-Lagrange útiles para describir los modelos dinámicos de los sistemas desarrollados en el capítulo 3.

16

2.1 ALGEBRA LINEAL

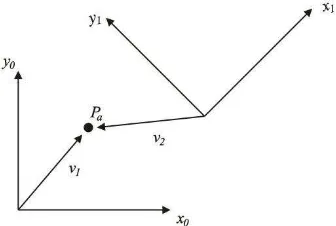
El álgebra lineal y la geometría están fundamentalmente relacionadas de tal forma que pueden ser empleadas para el estudio de cualquier tema. La idea fundamental es que un vector columna pueda ser usado para representar la posición de un punto en relación con otro punto en un sistema de coordenadas dado, ver figura 2.1, aplicado a una geometría de dos o tres dimensiones.

Figura 2.1 Espacio Vectorial 2D

La posición relativa de respecto a puede ser especificada por un par de números determinados por la magnitud y direcciones de las líneas y , el signo de los números depende de las direcciones que se elija (de a o de a ), y de esta manera podemos asociar un par ordenado (Hamilton, 1987).

̅̅̅̅ [ ] (2-1)

Para el caso de un espacio vectorial de tres dimensiones, se tiene

̅̅̅̅ (2-2)

donde la magnitud o norma del vector se determina por

| ̅̅̅̅| √ (2-3)

Dado un vector se define un vector unitario como aquel que su magnitud es igual a uno.

_{| |} (2-4)

Ahora, si denota los vectores unitarios a lo largo de los ejes respectivamente, cualquier vector tridimensional puede expresarse como

17 donde tienen las siguientes representaciones

[ ] [ ] [ ] (2-6)

El producto escalar de dos vectores también llamado producto punto representan cantidades físicas, y se determina por

| || | (2-7)

donde es el ángulo entre y (Hamilton, 1987).

La representación física del producto punto es que el vector se proyecta al vector multiplicado por la magnitud de , ver figura 2.2.

Figura 2.2 Producto Punto de Dos Vectores Cartesianos

El producto vectorial entre dos vectores tridimensionales denotado se determina por

|

|

(2-8)

18

Figura 2.3 Regla de la Mano Derecha

El determinante de una matriz se define para matrices cuadradas, sea A una matriz de elementos, con filas, columnas y elementos denotados como para , el determinante de la matriz,

o | | es un escalar que se determina por

| | |

| ∑

| (2-9)

donde | es el cofactor que resulta de eliminar la fila y la columna .

El determinante depende linealmente de una fila o columna según se elija, de esta manera, como ejemplo se tiene el determinante de tercer orden, utilizando los elementos de la primera columna.

|

|

_|

| | | | |

(2-10)

Los cofactores se calculan como el producto de los elementos de la diagonal principal menos el producto de los elementos de la otra diagonal. Es decir, por definición

|

| (2-11)

|

| (2-12)

19

Para mayor referencia, características y propiedades sobre los determinantes puede consultar el libro de Strang, “Linear Algebra and its Applications”, 1988.

Sea una matriz A de tamaño , definimos la matriz adjunta como una matriz cuadrada que resulta de sustituir cada elemento por su cofactor ; es decir, obtener la matriz de cofactores y después transponer los elementos de la matriz de cofactores (Hamilton, 1987).

| | | | (2-14) donde

_{| (2-15)}

La inversa de A, se define como

(2-16)

2.2 ATAN2

Es una variante de la función arco tangente inversa, devuelve un valor de ángulo en el rango

de ( ). La función devuelve el arco tangente de la función en el rango completo

de ángulos de ( ) (Saha, 2010).

La función , está definida para todos los ( ) y es igual al ángulo único de tal manera que

√ √ (2-17)

también puede definirse de la siguiente manera

√ (2-18)

(√ )

20 Ley de los cosenos

Ésta ley se puede considerar como una extensión del Teorema de Pitágoras aplicable a todos los triángulos, ver figura. 2.4.

(2-20)

(2-21)

(2-22)

Figura 2.4 Utilización de la Ley de Cosenos

2.3 REPRESENTACIÓN DE POSICIONES

La figura 2.5 muestra dos sistemas de referencia que difieren en orientación un ángulo .

21

La posición del punto respecto a cualquiera de estos sistemas de referencia fijo puede describirse mediante el vector cartesiano tridimensional (Spong, 2005).

[

] (2-23)

[

]

(2-24)

donde el superíndice 0 y 1 representan el sistema de referencia , respectivamente. También podemos asignar coordenadas para representar la posición desde el origen de uno de los sistemas de referencia con respecto al otro, por ejemplo

[ ] (2-25)

[ ] (2-26)

En este caso la ecuación (2-25) describe las coordenadas del punto del sistema de referencia con respecto del sistema de referencia , la ecuación (2-26) describe las coordenadas del punto del sistema de referencia con respecto del sistema de referencia .

Como se ha mencionado anteriormente, la orientación de un cuerpo rígido se analiza con respecto al sistema fijo, las cuales pueden representarse por cosenos directores o representación por los ángulos de Euler.

La figura 2.6 muestra un sistema de referencia orientado un ángulo con respecto a

22

Figura 2.6 Sistema de Referencia y

La matriz de rotación del sistema está dada por _[ ]

[ ] [ ] [ ] (2-27)

[ ] [ ] (2-28)

De igual forma se tiene para un sistema de referencia orientado un ángulo sobre el eje , y un ángulo sobre el eje .

[

] [

] (2-29)

Las matrices mencionadas en las ecuaciones (2-28) y (2-29) se llaman rotaciones elementales y son útiles para describir cualquier rotación arbitraria donde se conozcan los ángulos respecto a los ejes de coordenadas.

Los ángulos de Euler constituyen una representación mínima de la orientación, obtenida al componer las tres rotaciones elementales respecto a los ejes de los sistemas de referencia actuales. Existe la posibilidad de doce conjuntos distintos de ángulos de Euler (

) de todos ellos se utiliza más comúnmente el conjunto ; esto implica que el

23 [ ] (2-30)

2.4 TRANSFORMACIÓN HOMOGÉNEA

La matriz de transformación homogénea es una matriz que transforma un vector de posición desde un sistema de coordenadas hasta otro que ha sido rotado y trasladado.

[ ] (2-31)

Algunas transformaciones básicas se muestran a continuación

[

_{] [}

] (2-32)

[

_{] [}

] (2-33)

[

_]

[

_{] (2-34)}

La posición y orientación del efector final en el sistema de referencia fijo está dada por la siguiente expresión

(2-35)

donde cada transformación homogénea es de la forma

24

2.5 PARÁMETROS DE DENAVIT-HARTENBERG (D-H)

Como se mencionó anteriormente un manipulador robótico consiste en varios eslabones, usualmente conectados por articulaciones de un solo grado de libertad. Con el fin de controlar el efector final con respecto a la base, es necesario encontrar la relación entre los sistemas de referencia adjuntos al efector final y la base.

Una forma de elegir estos sistemas de referencia es mediante la convención de D-H.

En esta convención cada transformación homogénea es representada como un producto de cuatro transformaciones básicas.

(2-37)

[

_]

(2-38)

donde es la longitud del eslabón, es el ángulo de torsión, es el desplazamiento de la articulación y es el ángulo de la articulación, representados en la figura 2.7.

25 Condiciones para obtener los parámetros de D-H

 DH1: El eje es perpendicular al eje

 DH2: El eje intersecta al eje

Estas dos condiciones son ilustradas en la figura 2.8.

Figura 2.8 Condiciones para obtener los Parámetros de D-H

26

2.6 ECUACIONES DE EULER-LAGRANGE

El modelo dinámico de un robot puede derivarse de manera sistemática por medio del concepto de coordenadas generalizadas y de una función escalar llamada lagrangiano, que se define de la diferencia de la energía cinética y la energía potencial del sistema (Saha, 2010).

Figura 2.9 Sistema de un Grado de Libertad

La figura 2.9 muestra un sistema de una partícula con masa constante y desplazamiento ejercido por una fuerza en el eje , Las ecuaciones de Euler-Lagrange se pueden deducir a partir de aplicar las leyes de Newton (Spong, 2005).

Aplicando la segunda ley de Newton, la ecuación de movimiento de la partícula está dada por

(2-39)

La ecuación (2-39) puede ser escrita como

₍ ) (2-40)

donde se le conoce como la energía cinética.

Por otro lado podemos expresar la fuerza gravitacional que actúa sobre la partícula

(2-41)

27 definiendo

(2-42)

y derivando parcialmente, respecto a podemos notar que

(2-43)

Por lo que la ecuación (2-39) puede ser escrita como

(2-44)

29

Capítulo 3

Modelado de Sistemas

En este capítulo se estudia con mayor detalle los modelos del robot manipulador y de la grúa para obtener los modelos matemáticos cuantitativos útiles para el análisis y diseño del sistema, se establece la posición y la orientación del efector final de un robot manipulador de tres grados de libertad (3DGL), así como el análisis de la posición de la carga para una grúa de cinco grados de libertad (5GDL) en relación con su base, para esto es necesario encontrar la relación entre la posición y orientación; es decir, la posición de un punto en el efector final y su orientación con los ángulos de las articulaciones y la posición de un punto de la masa con respecto a la base. Para realizar el análisis, primero se obtienen los modelos de la cinemática directa e inversa correspondientes al robot manipulador y a la grúa, posteriormente se obtiene la energía cinética, energía potencial y el modelo dinámico de cada uno de los sistemas y se desarrollan por el método de Euler-Lagrange.

El desarrollo de éste capítulo se basa principalmente en tres referencias: Saha, ”Introducción a la Robótica”, 2010

30

Actualmente en la industria se pueden encontrar una gran variedad de robots manipuladores con articulaciones así como también se encuentran diversos tipos de grúas, cada sistema con propiedades en particular según el trabajo a desempeñar.

Un robot manipulador con más de 6 articulaciones es conocido como manipulador cinemáticamente redundante, y la dificultad de controlar este tipo de robot se incrementa en cuanto más articulaciones tengan.

En la figura 3.1 se muestra un ejemplo de un robot de 4 GDL.

Figura 3.1 Kuka KR 40 PA

Extraído de www.robots.com/kuka.php?robot=kr+40+pa, Marzo 2011

Especificaciones Robot Motion Speed Robot Motion Range

Axes: 4

Payload: 40 kg

H-Reach: 2091 mm

Repeatability: ±0.25 mm

Robot Mass: 700 kg

Mounting: floor

Axis 1: 183 °/s (3.19 rad/s)

Axis 2: 153 °/s (2.67 rad/s)

Axis 3: 212 °/s (3.7 rad/s)

Axis 6: 374 °/s (6.53 rad/s)

Axis 1: ±155°

Axis 2: +15°, -120°

Axis 3: +15°, -145°

Axis 6: ±350°

Tabla 3.1 Especificaciones del Robot Kuka-KR 40 PA Efector Final

Eslabones Articulaciones

Actuadores

31

En la figura 3.2 se muestra el ejemplo de una grúa viajera prototipo de laboratorio.

Extraído de

www.inteco.com.pl/new1/index.php?option=com_content&view=article&id=6&Itemid=12, Abril Dimensiones 1000 x 1000 x 800mm.

Figura 3.2 Grúa Viajera.

Esta grúa de prototipo tiene dimensiones a escala, las grúas empleadas en la industria son de mayor tamaño, son modelos que posibilitan el trabajo en altura. Se pueden obtener maquinarias que van desde 13 metros, con extensión del brazo de alcance horizontal hasta 8 metros, con canastillas con capacidad de carga de hasta 140 kg.

Dentro de la industria encontramos grúas de arrastre, dentro de ésta línea de grúas podemos encontrar subtipos definidas por su caracterización y uso. Los modelos de grúas de arrastre vienen adaptables a todo tipo de uso y necesidad. Traen además tecnología avanzada. Vienen con equipos opcionales como radio control remoto, rotación continúa, protección de sobrecarga, y capacidades que oscilan hasta 20 toneladas como máximo.

32

Existe una amplia línea de grúas industriales las cuales son utilizadas para el mantenimiento de plantas y trabajos de manejo de materia. Las grúas de operación sencilla exhiben plataformas de cargo, doble capacidad de combustible, y varias maneras de conducción.

3.1 CINEMÁTICA DIRECTA DE UN ROBOT MANIPULADOR DE 3 GDL

En la cinemática directa, las posiciones de las articulaciones ( ) ya están determinadas y el problema radica en encontrar la configuración del efector final ( ), ver figura 3.3.

Figura 3.3 Configuración de Sistemas de Referencia para un Robot de 3GDL

La tabla 3.2 muestra la configuración que se emplea para obtener los parámetros D-H. Definido en la sección 2.5.

Articulación i

1 90° 0 0.297

2 0 0.297 0

3 0 0.297

33 Matriz de Transformación Homogénea

Sustituyendo los parámetros de D-H de la tabla 3.2 en la ecuación (2-38) se obtienen las matrices de transformación homogénea ( ) que describen la posición y orientación de cada articulación con respecto a

la base .

[ ] (3-1)

[ ] (3-2) [ ] (3-3)

[ ] (3-4)

Se emplea la notación

[ ] (3-5) [ ] (3-6)

Finalmente las ecuaciones que describen la posición del efector final se expresan en la cuarta columna de la Matriz ; es decir,

(3-7)

34

(3-9)

Las ecuaciones (3-7), (3-8) y (3-9) nos muestran la relación que existe entre las coordenadas generalizadas y las coordenadas cartesianas, esto es, si se definen las posiciones angulares del sistema podemos conocer la posición en la que se encuentra el efector final del sistema.

3.2 CINEMÁTICA INVERSA DE UN ROBOT MANIPULADOR DE 3 GDL

En la cinemática inversa, la posición del efector final ( ) ya están determinadas y el problema radica en encontrar las posiciones de las articulaciones ( ), ver figura 3.4 y figura 3.5 para visualizar el planteamiento del problema.

35

Figura 3.5 Configuración Geométrica de los Eslabones 2 y 3

Calculo de las posiciones de las articulaciones para un robot manipulador de 3GDL

Como se muestra en la figura 3.4 y 3.5 aplicando el método geométrico, se puede obtener como

(3-10)

donde la función se define en la sección 2.2 Para calcular , ver figura 3.4, podemos afirmar que

(3-11)

(3-12)

además

(3-13)

Sustituyendo las ecuaciones (3-11) y (3-12) en (3-13)

(3-14)

Otra forma de calcular , es aplicando la ley de los cosenos. Definida en la sección 2.2

36 Igualando las ecuaciones (3-14) y (3-15) se obtiene

(3-16)

despejando

(3-17)

(3-18)

Por lo tanto, podemos simplificar escribiendo

(3-19)

de la cual existen dos soluciones

₍ √ _{) (3-20)}

reescribiendo la ecuación (3-20)

√ (3-21)

Podemos observar que , aplicando nuevamente la ley de los cosenos para obtener tenemos

(3-22)

despejando

√ (3-23)

(3-24)

Despejando a de la ecuación (3-24)

37 de la cual existen dos soluciones

₍ √ _{) (3-26)}

de la figura 3.5 se deduce que se obtiene con la siguiente expresión

_(3-27)

Finalmente restando las ecuaciones (3-27) y (3-26) obtenemos el valor de

√ (

√

) (3-28)

Reescribiendo la ecuacion (3-28)

√ √ (3-29)

38

3.3 DINÁMICA DE UN ROBOT MANIPULADOR DE 3 GDL

Hasta este momento, hemos analizado los modelos cinemáticos del robot manipulador, sin considerar las fuerzas requeridas para producir movimiento.

En esta sección consideraremos las ecuaciones de movimiento para un robot manipulador; es decir la manera en que se produce el movimiento del manipulador debido a los momentos de torsión aplicados por los actuadores o fuerzas externas aplicadas al manipulador.

Las ecuaciones dinámicas describen la relación existente entre la fuerza y el movimiento, son importantes para el diseño de robots, simulación y animación de robots así como en el diseño de algoritmos de control (Spong, 2005).

La ecuación de Euler-Lagrange (definida en la sección 2.6) describe la evolución de un sistema mecánico objeto de Holonomic Constraints1_{, la ventaja de usar este planteamiento es que elimina las fuerzas de} restricción de las ecuaciones de dinámica de movimiento.

Matemáticamente las ecuaciones de la cinemática directa definen una función entre el espacio de posiciones cartesianas y el espacio de posiciones articulares, la relación que existe entre sus velocidades son determinadas por una función conocida como Jacobiano. En este caso el Jacobiano o matriz jacobiana es uno de los parámetros de estudio más importante para el análisis y control de robots, en la planeación, seguimiento de trayectorias, obtención de las ecuaciones dinámicas, en la transformación de torques y fuerzas del efector final a las articulaciones del robot manipulador.

Para un robot manipulador de articulaciones, la matriz jacobiana es una matriz resultante de

elementos, velocidades lineales y velocidades angulares.

Considerando un robot manipulador de articulaciones con variables y matriz de transformación

[ ] (3-30)

La velocidad lineal del punto está definida como la derivada temporal del vector de posición

(3-31)

Así que, por la regla de la cadena

(3-32)

39

∑

(3-33)

Como se determinó anteriormente, por la elección de los sistemas de referencia de cada articulación para obtener los parámetros D-H, ver figura 3.3, gracias a que la articulación siempre gira sobre el eje la ecuación (3-33) puede ser escrita como

∑[ [ ] ]

(3-34)

donde si la articulación es de revolución y si es prismática. Con lo anterior definimos el Jacobiano de la velocidad angular

[ [ ] [ ] ] (3-35)

Simplificando tenemos que la velocidad lineal puede ser escrita de la siguiente forma

(3-36)

de igual manera se expresa la velocidad angular como

(3-37)

donde y son matrices de , donde las ecuaciones (3-36) y (3-37) pueden escribirse como

(3-38)

y estan dadas como

[ ] (3-39)

[ ] (3-40)

Ahora bien la velocidad angular en el efector final puede ser determinada como la suma de la velocidad angular de cada articulación, si la articulación es de revolución y el eje de rotación es el eje la velocidad angular se expresa como

(3-41)

40 Si la articulación es prismática entonces

_(3-42)

La velocidad angular en el efector final será

∑

(3-43)

donde si la articulación es de revolución y si es prismática, además

Con lo anterior definimos el Jacobiano de la velocidad angular y así llegamos a obtener la ecuación (3-37) mencionada con anterioridad.

[ ] (3-44)

Sustituyendo valores en las ecuaciones (3-35) y (3-44) respectivamente, para (Jacobiano de la primera articulación con respecto a la base), posteriormente se hace para y .

De esta manera los Jacobianos del robot manipulador son

[ ] [ ] [ ] [ ] [ ] [ ]

41

3.4 EXPRESIONES GENERALES PARA OBTENER LA ENERGÍA CINÉTICA Y LA ENERGÍA POTENCIAL

Una vez que tenemos calculados los Jacobianos de cada articulación respecto a la base, el siguiente paso es obtener las ecuaciones dinámicas del robot manipulador, para esto es necesario conocer el lagrangiano del sistema; es decir, la diferencia entre la energía cinética y la energía potencial, (definido en la sección 2.6).

La energía cinética de un objeto rígido es la suma de dos términos: la energía de traslación obtenida por la concentración de la masa del objeto en su centro de masa y la energía cinética rotacional del cuerpo alrededor de su centro de masa, ver figura 3.6.

Figura 3.6 Cuerpo Rígido

La energía cinética del cuerpo rígido está dada por

(3-45)

42 y está dada como

(3-46)

[

] (3-47)

donde

∭

∭

∭

∭

∭

∭

Los elementos de la diagonal de la matriz de tensores de inercia son llamados momentos de inercia principales y los que están fuera de la diagonal son llamados producto cruz de inercia, si la distribución de la masa en todo el cuerpo rígido es simétrica el producto cruz de inercia es cero.

De esta manera la energía cinética de un robot manipulador está dada por la expresión

∑[ ]

(3-48)

En otras palabras la energía cinética del manipulador se resume en la forma

(3-49)

43

Ahora consideremos el término de la energía potencial debida a la fuerza de gravedad. La energía potencial de la articulación puede considerarse como la energía concentrada en el centro de masa del cuerpo y está dada por la expresión

_∑

(3-50)

donde es el vector de gravedad y es el vector que da las coordenadas del centro de masa de la articulación.

3.5 ECUACIONES DE MOVIMIENTO

La ecuación de Euler Lagrange (2-44) puede escribirse como

∑ ∑ { }

(3-51)

Intercambiando el orden de la suma y el aprovechando la simetría del sistema, podemos demostrar que

∑ { } ∑ { } (3-52)

por lo tanto

∑ { } (3-53) ∑ _{ } (3-54)

_{ } (3-55)

44 Finalmente si definimos

(3-56)

Podemos escribir las ecuaciones de Euler-Lagrange como

∑ ∑

_(3-57)

Comúnmente la ecuación (3-57) se escribe como

(3-58)

La ecuación (3-58) es la forma matricial de la expresión dada por la ecuación (3-57), se le conoce como matriz de inercias del sistema, es una matriz con elementos que involucran el producto de términos del tipo , a los que se les conoce como términos centrífugos, y productos del tipo , a los que se les conoce como términos de coriolis, es el vector de fuerzas de gravedad, es vector de fuerzas de fricción y son las fuerzas que afectan al sistema.

Cada elemento de la matriz está definido como

∑

(3-59)

_{ } (3-60)

Ahora bien comparando las ecuaciones (3-48) y (3-49) se observa que

(3-61)

Para y de las matrices de transformación definidas por las ecuaciones (3-4), (3-5) y (3-6) se tienen las siguientes matrices de rotación.

[

]

45

[

]

Se define la matriz de inercia considerando articulaciones simétricas

[

] (3-62)

Empleando la ecuación (3-61) y sustituyendo las matrices jacobianas del sistema y las matrices de rotación obtenidas anteriormente para el caso se forma la matriz de inercia de la siguiente manera

[

]

(3-63)

₍ )

Ahora calculamos los Símbolos de Christoffel de la ecuación (3-55) para calcular la matriz dada por la ecuación (3-59), para el análisis del robot de 3GDL

46

Finalmente se tiene que la matriz centrifuga y de coriolis tiene la siguiente forma

[

]

Para calcular el vector de gravedad dado por la ecuación (3-56), de acuerdo a la figura 3.3 podemos expresar la energía potencial de cada articulación de la siguiente forma

(

)

( )

Ahora bien por la ecuación (3-56) tenemos que

47

Con lo que definimos el vector de gravedad de la siguiente manera

[

( )

]

Por ultimo tenemos el vector de fuerzas de fricción definido de la siguente forma

[

]

48

3.6 MODELO DE UNA GRÚA DE 5GDL EN 3 DIMENSIONES

Las grúas son ampliamente utilizadas en la industria para el transporte de cargas pesadas. Sin embargo, la aceleración de la grúa requerida para el movimiento siempre induce oscilación de carga indeseable, cuanto mayor sea la aceleración mayor será la oscilación de carga.

La capacidad de carga de la grúa también tiende a agravar la oscilación de la carga. El control de la grúa consiste en regular de movimiento de la carga, controlar su elevación y la supresión de la oscilación de la carga.

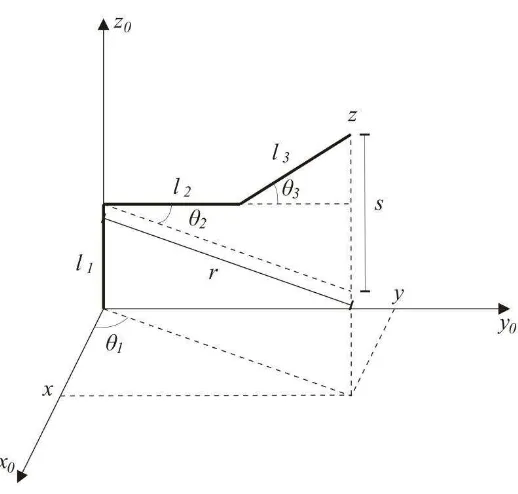
En esta sección se presenta una solución para el modelado y control de una grúa en tres dimensiones.

Figura 3.7 Sistema Coordenado de una Grúa

La figura 3.7 muestra el sistema coordenado de una grúa en tres dimensiones ( , ), las coordenadas del carro del sistema son ( ), es el ángulo existente entre la carga y una orientación arbitraria en el espacio, éste tiene dos componentes ( , ), (Lee, 1998).

La posición de la carga estará representada por ( ), las cuales se expresan como:

49

(3-65)

(3-66)

La energía cinética y potencial está dada por

₍ ) (3-67)

( ) (3-68)

donde cada termino cuadrático de la velocidad de la ecuación (3-67) se desarrolla a continuación.

(3-69)

(3-70)

(3-71)

(3-72)

(3-73)

(3-74)

50

El lagrangiano del sistema; es decir, la diferencia de la energía cinética y la potencial esta dado como

(3-75)

(3-76)

( )

( ) ( )

Una vez conocido el lagrangiano del sistema procedemos a obtener cada uno de los términos de la ecuación de Euler-Lagrange, ver ecuación (2-44), empezando con la variable , posteriormente

.

(3-77)

(3-78)

Por la ecuación (2-44) para tenemos

(3-79)

(3-80)

51

Por la ecuación (2-44) para tenemos las siguientes expresiones

(3-81) (3-82) (3-83) (3-84)

Por la ecuación (2-44) para tenemos las siguientes expresiones

52

Por la ecuación (2-44) para tenemos las siguientes expresiones

(3-89) ( ) (3-90) (3-91) (3-92)

Por la ecuación (2-44) para tenemos las siguientes expresiones

53

(3-96)

La matriz de inercias del sistema está formada por

[ ] [ ] (3-97)

Donde cada término es de la forma

54

De igual forma se obtiene que la matriz centrifuga y de coriolis esta dada por

[ ] [ ] (3-98)

Donde cada uno de sus términos se muestran a continuación

55

El vector de gravedad se define por

[

]

(3-99)

Y finalmente tenemos el vector de fuerzas de fricción definido de la siguiente forma

[

]

(3-100)

donde son las fuerzas de fricción de coulomb y son las fuerzas de fricción viscosa del actuador (Reyes, 2005).

De esta forma se tiene la dinámica del sistema de acuerdo a la ecuación (3-58).

57

Capítulo 4

Controlador PID

Los sistemas de control son parte integral de la sociedad moderna y sus numerosas aplicaciones están alrededor de nosotros: en casa, en los automóviles, en las fábricas, y hasta en los transbordadores espaciales que se lanzan para ponerlos en órbita terrestre, en el agua de enfriamiento que salpica etc.; el control se ha vuelto una parte importante e integral de los procesos industriales. Una de las ventajas de un sistema de control, es la capacidad de compensación debido a las perturbaciones. En general, controlamos variables como la temperatura en los sistemas térmicos; la posición y velocidad en los sistemas mecánicos, y voltaje, corriente o frecuencia en los sistemas eléctricos (Dorf, 2005).