UNIVERSIDAD AUTÓNOMA DEL ESTADO DE HIDALGO
INSTITUTO DE CIENCIAS BÁSICAS E INGENIERÍA ÁREA ACADÉMICA DE MATEMÁTICAS Y FÍSICA
“EFECTO DE LA ACTIVIDAD DOCENTE EN EL
DESARROLLO DE TAREAS DE GENERALIZACIÓN DE PATRONES”
T E S I S
QUE PARA OBTENER EL GRADO DE MAESTRA EN CIENCIAS EN MATEMÁTICAS Y SU
DIDÁCTICA PRESENTA:
Dévora Escorcia Custodio
Dirigida por:
Dr. Fernando Barrera Mora
Dr. Aarón Reyes Rodríguez
3
AGRADECIMIENTOS
A Dios Por los momentos buenos y también los complicados, por los errores que he cometido y me dejaron enseñanza, por lo bueno que tengo hoy y por lo que está por venir. Pero sobre todo porque está a mi lado.
A mis Maestros Por su tiempo, el cual es valioso, por enseñar de la mejor forma, con el ejemplo. Por acercarme a una de las muchas partes sutiles de la matemática.
A mi Familia Por estar en mi vida, por darme fuerza, por hacer cualquier cosa por verme sonreír, por amarme sin importar nada.
4 RESUMEN
La literatura de investigación en educación matemática incluye gran cantidad de trabajos que han abordado los procesos de identificación y generalización de patrones, en los niveles educativos básico y medio superior. Tales trabajos aportan evidencia en cuanto a que los estudiantes mejoran su capacidad para representar algebraicamente procesos de abstracción y generalización, a partir del análisis de representaciones figurales. Sin embargo, solo algunas de estas investigaciones han centrado la atención en el efecto que tiene, sobre el entendimiento de los estudiantes, el apoyo del docente durante la implementación de las tareas.
En este contexto, el presente trabajo tiene como objetivo documentar y analizar el efecto que tienen las preguntas que formula el profesor a los estudiantes durante la realización de tareas con patrones. Esto se llevó a cabo con estudiantes de bachillerato de una escuela pública en el estado de Hidalgo. La hipótesis de trabajo sostiene que el tipo de preguntas que formula el docente a sus estudiantes son de gran importancia para determinar las rutas y características de aprendizaje, que los estudiantes construyen.
5 ABSTRACT
The research literature in mathematics education includes a large number of works that have addressed the processes of identification and generalization of patterns, in the basic and upper secondary education levels. Such works provide evidence that students improve their ability to algebraically represent processes of abstraction and generalization, based on the analysis of figurative representations. However, only some of these investigations have focused attention on the effect that, on the students' understanding, has the support of the teacher during the implementation of the tasks.
In this context, the present work aims to document and analyze the effect that the questions that the teacher formulates to the students during the accomplishment of tasks with patterns. This was carried out with high school students from a public school in the state of Hidalgo. The working hypothesis argues that the type of questions that the teacher asks his students are of great importance to determine the routes and characteristics of learning, which the students construct.
6 ÍNDICE
CAPÍTULO 1. EL PROBLEMA DE INVESTIGACIÓN ... 8
1.1 INTRODUCCIÓN ... 8
1.2 REVISIÓN DE LA LITERATURA ... 10
1.3 PLANTEAMIENTO DEL PROBLEMA ... 15
CAPÍTULO 2. MARCO CONCEPTUAL ... 17
2.1 INTRODUCCIÓN... 17
2.2 DIMENSIÓN ONTOLÓGICA ... 18
2.2 MATEMÁTICAS: LA CIENCIA DE LOS PATRONES ... 19
2.3 DIMENSIÓN EPISTEMOLÓGICA ... 19
2.4 DIMENSIÓN DIDÁCTICA ... 20
2.4.1 APRENDIZAJE CON ENTENDIMIENTO ... 20
2.4.2 CICLO PARA DESARROLLAR UN APRENDIZAJE CON ENTENDIMIENTO ... 21
CAPÍTULO 3. METODOLOGÍA ... 24
3.1 INTRODUCCIÓN... 24
3.2 PARTICIPANTES ... 24
3.3 DISEÑO Y PRUEBA PILOTO DE UNA TAREA ... 25
7
3.5 IMPLEMENTACIÓN DE LAS TAREAS ... 29
3.6 INSTRUMENTOS DE RECOLECCIÓN DE LA INFORMACIÓN ... 30
CAPÍTULO 4. RESULTADOS ... 31
4.1 INTRODUCCIÓN... 31
4.2 ANÁLISIS DE LA PRUEBA PILOTO ... 31
4.3 RESULTADOS DE LA TAREA “BLOQUES DE MADERA” ... 33
4.5 RESULTADOS DE LA TAREA “PALILLOS DE COLORES” ... 41
4.6 ANÁLISIS DEL EFECTO DE LAS PREGUNTAS QUE EL PROFESOR FORMULA A LOS ESTUDIANTES ... 48
CAPÍTULO 5. CONCLUSIONES ... 53
5.1 INTRODUCCIÓN... 53
5.2 RESPUESTAS A LAS PREGUNTAS DE INVESTIGACIÓN ... 53
5.3 LIMITACIONES ... 55
5.4 POSIBLES TRABAJOS A FUTURO ... 55
6. REFERENCIAS ... 56
8
CAPÍTULO 1. EL PROBLEMA DE INVESTIGACIÓN
1.1Introducción
Diversos trabajos de investigación reconocen que las tareas de instrucción determinan las características del conocimiento que los estudiantes construyen, y son el medio principal con el que cuentan los profesores para apoyar el aprendizaje (Stein y Smith, 1998). Desde una perspectiva de resolución de problemas, promover un entendimiento matemático requiere que las tareas de instrucción permitan a los estudiantes “hacer matemáticas”1, así como
establecer conexiones entre diversos conceptos, procedimientos o ideas (Hiebert, et al., 1997). Tareas planteadas en contextos motivadores pueden despertar el interés por conocer cosas nuevas, y desarrollar habilidades para reflexionar, comunicar ideas y formular problemas o preguntas de manera sistemática (actitud inquisitiva); esto es, poner en práctica las actividades fundamentales del quehacer matemático.
Aprender matemáticas con entendimiento requiere de construir habilidades para la resolución de problemas, así como desarrollar un lenguaje para expresar ideas o puntos de vista; y para construir y sustentar argumentos visuales, empíricos o deductivos (Santos Trigo, 2015). Durante el proceso de aprendizaje, el profesor puede apoyar a los estudiantes mediante preguntas que orienten su actividad o mediante sugerencias que le permitan seguir avanzando en el descubrimiento de conjeturas, en la construcción de rutas novedosas de solución o en la formulación de nuevos problemas.
Una de las estrategias de enseñanza más antiguas, la enseñanza socrática (método de la mayéutica), consiste esencialmente en realizar preguntas. Cuando Sócrates se enfoca en formular preguntas al esclavo de Menón, en vez de ofrecerle respuestas, advierte sobre la importancia de las preguntas para que, quien aprende, encuentre las respuestas él mismo (Platón, 1987, pp. 302-311). En Latinoamérica, Paulo Freire también apoya una pedagogía
1John Mason (1999), menciona que las modas de enseñar pueden cambiar, pero la esencia de aprendizaje
9
basada en formular preguntas, en contraposición a una enseñanza basada en responder preguntas que los estudiantes no han planteado ni les interesan (Freire y Faundez, 2013). En este contexto, el favorecer una actitud inquisitiva es central en el aula de matemáticas como medio para construir conocimiento estructurado (Forero, 2014).
Para promover el entendimiento matemático los profesores deben conocer qué es lo que saben sus estudiantes y, a partir de ese conocimiento, proponer tareas y escenarios de instrucción que apoyen y fomenten la construcción de formas matemáticas de pensar. Se propone la resolución de problemas como una aproximación relevante para desarrollar un aprendizaje con entendimiento, pues al resolver problemas se llevan a cabo actividades fundamentales del quehacer matemático, entre las que se encuentran: exploración de relaciones, identificación de patrones, formulación de conjeturas, empleo de distintas representaciones, justificación y comunicación de resultados (NCTM, 2000).
El profesor es un actor fundamental en el proceso de aprendizaje, debido a que sus conocimientos y, en consecuencia, el tipo de actividades que propone en el salón de clase, moldean las características del aprendizaje que los estudiantes construyen (Barrera y Reyes, 2013). Para lograr que los estudiantes tengan una sólida formación matemática se requiere de un currículo flexible, y de profesores con amplios conocimientos disciplinares, de teorías de aprendizaje y aproximaciones didácticas.
De acuerdo con Hiebert et. al., (1997), entendemos algo cuando podemos ver cómo ese algo se relaciona o conecta con otras cosas que conocemos. Cuando se promueve la construcción de conexiones robustas, el conocimiento se organiza en redes conceptuales que permiten extender y aplicar este conocimiento. Tales redes se estructuran mediante los procesos de reflexión y comunicación de ideas que se ejecutan durante la actividad de resolver y formular problemas. Estos autores argumentan que el logro de un aprendizaje con entendimiento está determinado por cinco elementos: (i) las tareas, (ii) el papel del maestro, (iii) la cultura social en el salón de clase, (iv) las herramientas disponibles y (v) la equidad.
10
identificación y generalización de patrones es parte esencial de la formación matemática de toda persona y, por ello, debiera de considerarse en el currículo de todos los niveles escolares (NCTM, 2000).
Por lo regular, las tareas de instrucción propuestas en los materiales educativos de bachillerato en México, no promueven el desarrollo de actividades relevantes relacionadas con el quehacer matemático, y se enfocan en procesos de memorización, repetición y desarrollo de fluidez en la aplicación de algoritmos. Sin embargo, el aprendizaje con entendimiento matemático debiera orientarse en fomentar formas de pensar que permitan a los estudiantes ver el mundo a través de los lentes de un matemático (Schoenfeld, 1992), lo cual significa desarrollar habilidad para interpretar y analizar fenómenos mediante herramientas y lenguaje propios de la disciplina. En este contexto, el presente trabajo pretende determinar si las preguntas que realiza un docente, para orientar la actividad de estudiantes, al implementar tareas de identificación y generalización de patrones, contribuye a que ellos conecten ideas, formulen preguntas, exploren diversas rutas para resolver problemas. Es decir, se busca identificar cómo las acciones docentes contribuyen al desarrollo de formas matemáticas de pensar (Schoenfeld, 1992) y la construcción de un aprendizaje con entendimiento (Hiebert et al., 1997).
1.2 Revisión de la literatura
La revisión de la literatura para el desarrollo de este trabajo se llevó a cabo en dos vertientes. En la primera de ellas se revisaron trabajos cuyo eje son las tareas con patrones, mientras que la segunda se enfocó en investigaciones que analizan el efecto de la intervención docente en el aprendizaje de los estudiantes.
11
constantes. Además, se reconoció una prevalencia de las generalizaciones empíricas, y que los apoyos visuales facilitaron la solución de la tarea.
Por otra parte, Mouhayar y Jurdac (2016), realizaron un estudio con 1232 estudiantes de los grados 4 al 11, en cinco escuelas en el Líbano, cuyo objetivo fue explorar el tipo de razonamiento empleado por los estudiantes en tareas de identificación y generalización de patrones. El análisis de los datos mostró que el razonamiento numérico fue más empleado respecto al razonamiento figurativo, en lo que respecta a la generalización de patrones denominados “cercanos” y “lejanos”; pero no para el tipo denominado “inmediato”. Los
resultados mostraron que para la estrategia recursiva, el enfoque de razonamiento numérico parece predominar sobre el enfoque de razonamiento figurativo. Sin embargo, el enfoque de razonamiento figurativo prevalece sobre el enfoque de razonamiento numérico, en el caso de la estrategia funcional. Otro resultado relevante es que el razonamiento numérico fue preponderante entre los estudiantes de grado 4-5 y el razonamiento figurativo para los grados 10-11.
En el caso de la educación secundaria (grados 7-9), Cañadas (2012), describe el tipo de patrones y la forma de expresar la generalidad que llevan a cabo 359 estudiantes de grado 9 y 10 en la resolución de un problema en el que debían identificar y generalizar patrones, denominado “problema de baldosas”. Entre los resultados se identificó un predominio de la
generalización verbal y, el apoyo de ésta, a otras formas de expresar la generalidad, diferente de la algebraica. Particularmente, se concluyó que la generalización verbal es una forma más accesible de generalización que la algebraica.
En esta línea de ideas, Chua y Hoyles (2014) obtuvieron las tasas de éxito de 104 estudiantes de secundaria en Singapur, al abordar tareas de generalización de patrones. Se implementó una prueba escrita que incluyó cuatro tareas en las que debían generalizar patrones lineales en secuencias figurales. Se asignó un tiempo de 45 minutos para que los estudiantes contestaran la prueba. Los autores concluyen que la mayoría de los estudiantes producen, correctamente, una variedad de reglas funcionales expresadas algebraicamente después de analizar una representación figurativa.
12
ciertas sucesiones numéricas. Las tareas consistieron en generar patrones figurales basados en la sucesión 2, 6, 12, 20, 30... Se pidió a los estudiantes que escribieran el proceso que siguieron para abordar la tarea. Los resultados del estudio indicaron que los participantes produjeron diferentes patrones figurativos mediante diversas rutas y utilizaron estrategias de generación de patrones tales como contar, determinar una figura, dibujar, y dividir. Se concluyó que el análisis de patrones numéricos puede apoyar el desarrollo de un pensamiento algebraico. Por lo tanto, es importante utilizar múltiples estrategias de solución al abordar tareas que involucran patrones figurativos.
Roig y Linares (2008), aplicaron una tarea de patrones a 511 estudiantes de secundaria, de entre 15 y 16 años, con la finalidad de identificar los procesos de abstracción que se llevaron a cabo. Se entrevistó a 71 estudiantes para que explicaran los procesos de razonamiento que siguieron al abordar las tareas. El marco teórico del trabajo se construyó con base en el constructo de abstracción reflexiva propuesto por Piaget y el de Reflexión sobre la relación actividad-efecto, de Simon y Tzur. Los resultados permitieron identificar dos fases en el proceso de abstracción, las cuales se denominan proyección y anticipación local. En la fase de proyección se construyen diferentes términos de la sucesión sin que se produzca la abstracción del patrón. Mientras en la anticipación local, se abstrae el patrón y se usa para anticipar el valor de nuevos términos de la sucesión. El mecanismo clave en el paso de la fase de Proyección a la fase de Anticipación Local es el cambio en el foco de atención desde el conjunto de datos particulares de los primeros términos, hacia la estructura de la secuencia.
13
Al igual que la variedad de estudios de patrones, encontramos una amplia diversidad de investigaciones relacionadas con el análisis de la actividad docente. Al respecto, Montenegro, Costa y Lopes (2018) realizaron un estudio con 18 estudiantes portugueses, de edades entre 10 y 13 años, quienes asistían a una escuela pública. La finalidad de la investigación fue analizar el impacto de las representaciones visuales en la enseñanza y aprendizaje del álgebra. Se implementó una tarea diseñada para explorar un patrón figurativo. Los instrumentos de colección de datos fueron audios de la clase, el trabajo escrito de los alumnos y notas de elaboradas por el profesor del grupo. Los resultados confirman que realizar conversiones entre representaciones permitió a los estudiantes entender las tareas. Por otra parte, una función importante del docente consistió en ayudar a los alumnos por medio de preguntas tales como: ¿Qué es lo mismo entre las figuras 1 y 2? ¿Y qué es diferente? ¿Cómo es la figura 1? ¿Cómo es la figura 2? Este tipo de preguntas apoyó el tránsito entre diferentes registros de representación. Varios autores han identificado dificultades en las actividades de conversión entre representaciones (por ejemplo, Duval, 2006a). En este trabajo se confirma que la exploración dinámica de las representaciones visuales facilitó las conversiones entre registros de representación y brindó flexibilidad para convertir las representaciones simbólicas y verbales, lo que resultó beneficioso para los estudiantes. Otra conclusión relevante fue que los maestros deben considerar durante el diseño de tareas aspectos relacionados con la transformación de las representaciones semióticas, con la finalidad de apoyar el aprendizaje de los estudiantes.
14
argumentaciones. Sin embargo, se requieren unas condiciones tanto de los docentes como de los contextos en el aula, para que preguntas de ese tipo sean parte de la actividad escolar.
Kilic (2017b), investigó la capacidad de conversión entre sucesiones numéricas y figurales que muestran 25 profesores de matemáticas. Durante el estudio, se pidió a los participantes que generaran patrones figurativos basados en patrones numéricos. Los resultados del estudio indican que muchos participantes podían generar diferentes patrones figurales, cuando estos son lineales. Los docentes utilizan diferentes estrategias para generar patrones lineales, pero tienen problemas en el caso de los patrones no lineales. Van De Walle (2004) considera que relacionar diferentes representaciones tales como materiales físicos, palabras, números o expresiones simbólicas es importante al trabajar con patrones.
Lima (2018), buscó identificar de qué manera, tareas que involucran generalizar patrones, utilizando modelos de área, pueden favorecer el entendimiento de la propiedad distributiva. Diseñó dos tareas que involucran análisis de sucesiones figurales en las cuales estudiantes debían representar áreas de rectángulos de dos formas diferentes, identificar un patrón y generalizarlo. El rol del instructor consistió en guiar a los estudiantes para centrar su atención en las operaciones y no en los resultados. Las tareas se implementaron con un grupo de 27 estudiantes de bachillerato. Entre las conclusiones se considera que durante el desarrollo de las tareas de instrucción, es importante que el docente pida a los estudiantes argumentar sus resultados.
Stein (1996), identificó que los niveles bajos de participación y logro de los estudiantes que habitan en comunidades urbanas de escasos recursos no se deben principalmente a la falta de capacidad o potencial intelectual, sino más bien a un conjunto de prácticas educativas que no les proporcionan oportunidades de aprendizaje con entendimiento. En la investigación se examinó cómo las variaciones en la calidad de la instrucción se relacionan con las características del conocimiento que los estudiantes logran construir, a partir de observaciones de tres clases.
15
de un pensamiento algebraico, por lo que, las tareas con patrones son fundamentales en la formación matemáticas de los estudiantes. Se identifican dos fases en el proceso de abstracción, las cuales se denominan proyección y anticipación local. Los estudiantes construyen, desarrollan, refinan, o transforman sus formas de comprender y resolver problemas como resultado de formular preguntas relevantes y responderlas con el uso de distintos medios. El papel del docente debiera ser fundamental para el diseño e implementación de tareas de instrucción con alta demanda cognitiva (Stein y Smith, 1998), orientadas al desarrollo de significados.
1.3 Planteamiento del problema
Mediante la revisión de la literatura se ha podido constatar que varios trabajos de investigación se han interesado en el análisis de los procesos de identificación y generalización de patrones, desde primaria hasta el bachillerato. En diversas investigaciones se puede observar que el apoyo visual facilita a los estudiantes la resolución de las tareas, además de que es mucho más sencillo expresar la generalidad de forma verbal más que de forma algebraica. Otros trabajos concluyen que el análisis de patrones numéricos puede apoyar al desarrollo del pensamiento algebraico, pero no tantos trabajos centran su atención en el apoyo que pueda brindar el docente. Se logró identificar una problemática interesante, la cual se refiere a que uno de los objetivos por los que los docentes hacen preguntas es con la finalidad de que los estudiantes emitan una respuesta correcta, más que entender el pensamiento de los estudiantes, o apoyarlos en el proceso de solución de problemas, al ofrecerles sugerencias para centrar su atención en aspectos relevantes que le permitan avanzar en una ruta de solución. Las preguntas despiertan el deseo de conocer cosas nuevas y, en muchas ocasiones, el profesor se olvida de ellas, cuando la base para promover el entendimiento debiera ser preguntar. Según Polya (1945, p.46) “el estudiante adquiere en su trabajo personal la más amplia experiencia posible, pero si se deja solo ante su problema, sin ayuda alguna o casi ninguna, puede ser que no progrese”.
16
17
CAPÍTULO 2. MARCO CONCEPTUAL
2.1 Introducción
Cualquier investigación requiere de una estructura de conceptos teóricos básicos, para orientar el logro del objetivo planeado. No basta conocer qué se quiere investigar, sino que es necesario explicitar las hipótesis, métodos y teorías utilizadas en el análisis de un objeto de estudio. Un marco de investigación es un conjunto de ideas, principios, acuerdos o reglas que proporcionan la base o estructura para sustentar un trabajo de investigación. En este contexto, Lester (2005) utiliza la metáfora de un andamio para referirse a un marco de investigación:
Me gusta pensar en un marco como un andamio construido para hacer posible las reparaciones en un edificio. Un andamio encierra el edificio y permite a los trabajadores alcanzar regiones que de otro modo son inaccesibles. Por lo tanto, un marco de investigación es una estructura básica de las ideas (es decir, abstracciones y relaciones) que sirven de base de un fenómeno que debe investigarse. (p. 458).
Un marco de investigación puede clasificarse en uno de los siguientes tres tipos: teórico, práctico y conceptual (Eisenhart, 1991). Un marco teórico guía las actividades de investigación con base en una teoría formal; es decir una teoría que ha sido desarrollada para explicar ciertos fenómenos y sus relaciones, como la epistemología genética de Piaget o la teoría sociocultural de Vygotski. El uso de un marco teórico se orienta a la recopilación de datos relevantes, cuya interpretación y los hallazgos correspondientes se utilizan para apoyar, ampliar o modificar la teoría. Al utilizar un marco teórico, el investigador está decidiendo conformarse a las convenciones aceptadas de argumentación y experimentación asociada con la teoría. Algunos investigadores consideran que elegir un marco teórico fuerza a los investigadores a ajustar los datos a la teoría (Eisenhart, 1991).
Un marco práctico, guía una investigación utilizando aquello “qué funciona” en la
18
Un marco conceptual se basa en investigaciones previas, pero se construye a partir de una variedad de fuentes, las cuales se estructuran mediante un conjunto de justificaciones. Puede basarse en diferentes teorías y varios aspectos del conocimiento práctico del investigador. Así, un marco conceptual consiste en una estructura de conceptos y justificaciones de por qué esos conceptos son apropiados para abordar e interpretar un fenómeno que se está investigando.
Este trabajo se fundamenta en un marco conceptual, integrado por tres dimensiones: ontológica, epistemológica y didáctica. La perspectiva ontológica consiste en adoptar una postura con respecto a lo que son las matemáticas y su aprendizaje. En la perspectiva epistemológica se presentarán las ideas de cómo consideramos que se aprende, finalmente en la perspectiva didáctica se expondrá cuáles son, para nosotros, las características deseables que debe incluir el aprendizaje, así como los medios para lograr que el aprendizaje tenga esas características deseables.
2.2 Dimensión Ontológica
Durante el aprendizaje de las matemáticas es importante el proceso y el sentido que los estudiantes muestran en el desarrollo o construcción de las ideas matemáticas. Romberg (1992) ilustra la idea de desarrollar o hacer matemáticas mediante una analogía con la música. Afirma que la música, al igual que las matemáticas, posee varias ramas categorizadas en una variedad de formas (clásica, jazz, rock, instrumental, vocal), también tiene un sistema para preservar información (notas, claves), y teorías que describen la estructura de las composiciones (escalas, patrones). Sin embargo, no importa cuántos artefactos de la música uno aprenda, esto no es lo mismo que hacer música. De forma análoga, en matemáticas uno puede aprender conceptos acerca de los números y las operaciones aritméticas, resolver ecuaciones, graficar funciones, etcétera; pero eso no es hacer matemáticas. “La razón
19 2.2 Matemáticas: la ciencia de los patrones
La comunidad matemática ha debatido la pertinencia de adoptar una posición respecto a lo que es la disciplina y esbozar las características de un plan de estudios que refleje las necesidades sociales actuales (Schoenfeld, 1992). Existen diferentes perspectivas de lo que son las matemáticas, pero en este trabajo, adoptamos aquella que la concibe como la ciencia de los patrones (Steen, 1988). Esta perspectiva se relaciona con una postura didáctica en la cual es importante que el estudiante participe activamente en la generación de ideas y conceptos centrales de la disciplina, como un cuerpo dinámico de conocimientos en constante expansión. En esta perspectiva, el estudiante, al resolver problemas, recopila información, descubre o crea relaciones, discute sus ideas, plantea conjeturas, y constantemente evalúa y contrasta resultados. La actividad matemática no consiste en aplicar reglas o algoritmos de manera automatizada, sino construir esas reglas y procedimientos que nos permitan entender los patrones y regularidades que aparecen en nuestro mundo (Barrera y Reyes, 2013).
2.3 Dimensión epistemológica
20
práctica (Wenger, Mc. Dermott y Snyder, 2002), se negocian significados, para construir esos significados considerados como compartidos (Cobb et al., 1991; Simon, 1994).
2.4 Dimensión Didáctica
2.4.1 Aprendizaje con entendimiento
En esta investigación consideramos importante que los estudiantes desarrollen un aprendizaje con entendimiento. El entendimiento es una idea complicada porque es algo que siempre está cambiando y está creciendo, razón por la cual existen diferentes niveles de entendimiento respecto de temas o tópicos particulares. “El conocer no es una proposición de todo o nada”,
sino que hay varios niveles del dominio de conocimiento (Schoenfeld, 1992, p. 343). Entendemos algo, si podemos ver como ese algo se relaciona o conecta con otras cosas que conocemos. Entre mayor sea el número de conexiones estructuradas que se pueden realizar, será mayor nuestro nivel de entendimiento (Hiebert et al., 1997).
21
2.4.2 Ciclo para desarrollar un aprendizaje con entendimiento
22
Figura 1. Ciclo básico para promover un aprendizaje con entendimiento.
23
entendimiento, orientando el proceso de construcción de conexiones mediante preguntas que permitan a los estudiantes resolver problemas y desarrollar aspectos esenciales del pensamiento matemático. En un escenario de resolución de problemas el estudiante es un sujeto activo y el profesor favorece la construcción de conexiones entre conceptos (entendimiento) a través de tareas que representan un reto intelectual.
24
CAPÍTULO 3. METODOLOGÍA
3.1 Introducción
La investigación cualitativa es una categoría de diseños de investigación en la que se extraen descripciones de significados a partir de observaciones, las cuales adoptan la forma de entrevistas, narraciones, notas de campo, grabaciones, transcripciones de audio, registros escritos de todo tipo, fotografías o películas. Taylor y Bogdan (1986, p. 20) consideran que la investigación cualitativa es “aquella que produce datos descriptivos: las propias palabras de las personas, habladas o escritas, y conductas observables”. Estos autores señalan las
siguientes características propias de la investigación cualitativa: (i) es inductiva, (ii) el investigador ve al escenario y a las personas desde una perspectiva holística, (iii) los investigadores son sensibles a los efectos que ellos mismo causan sobre las personas que son objeto de estudio, (iv) los investigadores tratan de comprender a las personas dentro del marco de referencia de ellas mismas, (v) para el investigador todas las perspectivas son valiosas, (vi) los métodos cualitativos son humanistas, (vii) todos los escenarios y personas son dignos de estudio, (vii) la investigación cualitativa es un arte.
Este trabajo de investigación es de carácter cualitativo, se analizó el efecto de las preguntas que formula el profesor, durante la realización de tareas con patrones, sobre el proceso de entendimiento de ideas algebraicas de estudiantes. La investigación se realizó en tres momentos, el primer momento fue el diseño y aplicación de una prueba piloto, el segundo momento el diseño y aplicación de tres tareas, finalmente el análisis de las tareas. Los instrumentos para la recolección de datos fueron tareas escritos elaboradas por los estudiantes y videograbaciones de las sesiones, las cuales posteriormente se transcribieron. Mediante las soluciones de las tareas que reportaron los estudiantes, se analizó el efecto de las preguntas formuladas por el docente sobre el proceso de entendimiento.
3.2 Participantes
25
especialidades (Diseño gráfico digital, puericultura, mantenimiento en equipo de cómputo y preparación de alimentos y bebidas). La razón por la cual se eligió a estos alumnos fue porque tienen especial interés en la exploración de patrones y porque estoy a cargo de estos grupos. Debido a que los participantes eran menores de edad, se solicitó la autorización, por escrito, de los padres de familia para filmar en video el trabajo de los participantes, indicando que para mantener confidencial su identidad se ocultaría mediante seudónimos.
3.3 Diseño y prueba piloto de una tarea
Retomando la revisión de la literatura se identificaron cuatro aspectos relevantes a considerar para el diseño de una tarea, el primer aspecto es que los docentes generalmente hacen preguntas con la finalidad de que los estudiantes emitan una respuesta correcta, más que para entender cómo piensan, o apoyarlos en el proceso de solución de problemas, al ofrecerles sugerencias para avanzar o centrar su atención en aspectos relevantes en una ruta de solución. El segundo, que las variaciones en las preguntas o sugerencias se relacionan con el desempeño o dificultades mostradas por los estudiantes. El tercer aspecto es que la construcción de entendimiento requiere que los estudiantes desarrollen sucesivos ciclos de acción, observación, formulación de conjeturas y justificación de resultados y, finalmente el cuarto aspecto, que una actividad sobre identificación de patrones en secuencias figurales puede promover procesos característicos del pensamiento algebraico tales como la abstracción, la generalización y la simbolización.
26 3.4 Las Tareas
Las tareas que se utilizaron en este trabajo fueron diseñadas con base en el ciclo básico para promover un aprendizaje con entendimiento (Figura 1), las cuales se basaron en la identificación y generalización de patrones a partir de secuencias figurales. Una tarea guiada es aquella que contiene una serie de preguntas elaboradas por el docente, las cuales orientaron a los estudiantes para que transitaran entre las diferentes fases de ciclo, favoreciendo el desarrollo de una actitud inquisitiva. Las tareas no guiadas únicamente cuentan con indicaciones generales para transitar por cada fase. Se construyeron tres tareas, una de ellas guiada para reconocer un patrón lineal y las otras dos no guiadas, una para reconocer un patrón lineal y la otra para reconocer un patrón cuadrático.
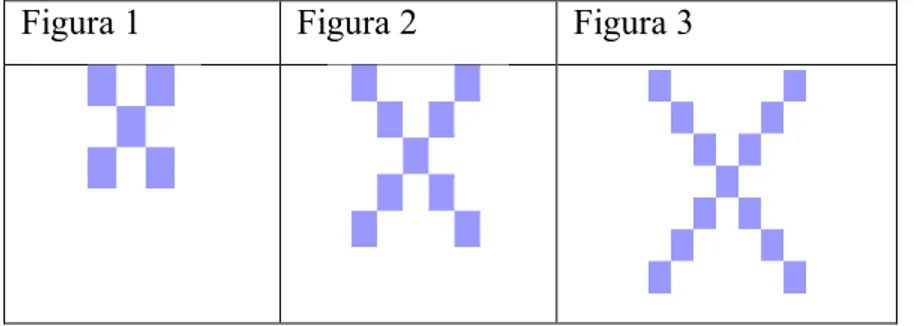
Bloques de madera (Apéndice C) Es una tarea no guiada, resuelta individualmente, en la que los estudiantes deben identificar y generalizar un patrón de orden lineal (4𝑛 + 1). En la fase de acción se proporcionó las hojas de trabajo y bloques de madera, con la cual los estudiantes construyeron las tres figuras indicadas en la hoja de trabajo (Apéndice C). Posteriormente, se solicitó dibujar las figuras 4 y 5, observando cuántos bloques se necesitan para formar cada una de ellas (Figura 3).
Figura 1 Figura 2 Figura 3
Figura 3. Secuencia figural de la tarea “bloques de madera”.
Para el desarrollo de la fase de observación se propuso que el estudiante identificara el número de piezas de una figura cercana. Si así lo deseaba, podía construirla con los bloques de madera que se le proporcionaron (por ejemplo la figura 4). También se le solicitó determinar el número de bloques de una figura lejana (como la figura 73) con la finalidad que el material manipulable no fuera suficiente para su construcción. Para la fase de
27
formulación de conjeturas se pidió la representación algebraica de la cantidad de piezas de cualquier figura. Y en la fase de justificación de resultados se solicitó calcular el total de piezas de una figura cercana (como la figura 5) y una lejana (como la figura 100), con la finalidad de que tuviera elementos para determinar la corrección de la expresión algebraica que obtuvo.
Fichas (Apéndice D) Es una tarea no guiada, resuelta individualmente, en la que los estudiantes debían identificar y generalizar un patrón de orden cuadrático 𝑛(𝑛 + 1). En la fase de acción se pidió a los estudiantes construyeran las tres primeras figuras (figura 4) y dibujaran las figuras indicadas en la tabla. En la fase de observación se pidió que identificaran el número de piezas de las figuras en la posición 7 y 65. En la formulación de conjeturas solicitamos la representación algebraica del patrón y para la fase de justificación tuvieron que explicar el proceso que siguieron para identificar y generalizar el patrón.
Figura 1 Figura 2 Figura 3
Figura 4. Secuencia figural de la tarea “fichas”.
28
Figura 1 Figura 2 Figura 3
Figura 5. Secuencia figural de la tarea “palillos de colores” versión A.
En la fase de acción se solicitó a los estudiantes que dibujaran las dos figuras siguientes con la finalidad de reconocer la construcción del patrón. En la fase de observación se orientó el trabajo de los estudiantes, por medio de preguntas acerca de la posición de los palillos, como las siguientes: Menciona las posiciones que tienen los palillos, ¿Cuántos palillos horizontales tiene la figura 1?, ¿Cuántos palillos horizontales tiene la figura 3?, ¿Cuántos palillos horizontales tendrá la figura 20?, ¿Tiene alguna relación la cantidad de palillos horizontales con el número de figura?, ¿Cuál?, ¿Cuántos palillos están en posición inclinada en la figura 2?, ¿Cuántos palillos están en posición inclinada en la figura 4?, ¿Cuántos palillos estarán en la posición inclinada en la figura 20?, ¿Tiene alguna relación la cantidad de palillos con el número de la figura?, ¿Cuál? Para orientación hacia la formulación de conjeturas utilizamos las siguientes preguntas: ¿Cuántos palillos tendrá la figura 500 en posición horizontal?, ¿Cuántos palillos tendrá la figura 500 en posición inclinada?, ¿Cuántos palillos tendrá en total la figura 500? Si deseo referirme a la figura 2 sería: Figura 2, Si deseo referirme a la figura 5 sería: Figura 5, para referirme a la figura 20 sería la figura____. Si deseo referirme a alguna figura que desconozco el número, sería __________. ¿Cuántos palillos horizontales tendrá cualquier figura que desconozco su número? ¿Cuántos palillos inclinados tendrá cualquier figura que desconozco su número? ¿Cuántos palillos tendrá en total cualquier figura que desconozco su número? Finalmente para justificar representan los siguiente. ¿Cómo representas el número de palillos de la figura 513? No obtengas el resultado, solamente se necesita que utilices alguna forma de representar la cantidad de piezas. Calcula el total de piezas para la figura 1027. ¿Cómo representas el número de palillos de la figura 312? ¿Cómo representas la cantidad de piezas de la figura 13 más la cantidad piezas de la figura 270?
FIGURA 1 FIGURA 2 FIGURA 3
FIGURA 1 FIGURA 2 FIGURA 3
29 3.5 Implementación de las tareas
La aplicación de las tareas se llevó a cabo con un grupo de estudiantes de segundo semestre. Estas se realizaron en un salón para asesorías dentro de la institución, es un lugar cómodo con buena ventilación e iluminación. Se entregaron las hojas de trabajo impresas, además de material concreto (bloques de madera, palitos de colores, fichas) para la fase de acción. Se realizaron videograbaciones durante la aplicación de las diferentes tareas, utilizando una tableta, estas fueron realizadas por la profesora.
La aplicación de las tareas se realizó en un periodo de dos meses debido a que se tuvo que adaptar las fechas de implementación, en función de los horarios de alumnos, y así evitar interferir en sus diversas actividades escolares. Cabe hacer mención que se solicitó permisos con anticipación a los docentes con los que tenían clase, y si estos no lo otorgaban o los estudiantes tenían algunas prácticas en los diferentes laboratorios, se re-agendó la aplicación (Tabla 1 y 2). Se decidió, en primera instancia, implementar la tarea de orden lineal no guiada, para poder observar como respondían los estudiantes ante una tarea relativamente sencilla que contaba únicamente con instrucciones generales. Posteriormente, se decidió aplicar una tarea un poco más compleja, de orden cuadrática no guiada. Finalmente se aplicó la tarea guiada para comparar las tres tareas e identificar hasta que fase del ciclo habían progresado.
Para abordar las tareas 1 y 2 los estudiantes trabajaron individualmente. El único material del que dispusieron fueron las hojas de trabajo impresas y el material concreto (bloques de madera) para la fase de acción, el espacio entre la implementación entre tareas fue de un mes. La tarea 3, se aplicó en el mismo mes de la actividad dos, esta actividad se trabajó en equipos.
Tabla 1. Aplicación de tareas 1 y 2.
ESTUDIANTE FECHA DE
APLICACIÓN DE LA TAREA 1 NUEVA FECHA FECHA DE APLICACIÓN DE LA TAREA 2 NUEVA FECHA
A 4-2-19 4-3-19 6-3-19
B 6-2-19 6-3-19
C 6-2-19 21-2-19 6-3-19 Operación
D 7-2-19 7-3-19
30
Tabla 2. Aplicación de tarea 3.
EQUIPO FECHA DE
APLICACIÓN DE LA TAREA 3
NUEVA FECHA
A,B,H 25-3-19
E,F,J 27-3-19 3-4-19
C,D,G 28-3-19 8-4-19
I Problemas económicos
3.6 Instrumentos de recolección de la información
Los métodos y las técnicas de recolección de información son herramientas con que cuenta el investigador para documentar la información recabada de la realidad. Los instrumentos de recolección de datos que se utilizaron para este trabajo fueron las tareas escritas realizadas por los estudiantes así como grabaciones en video de las sesiones de trabajo, las cuales se transcribieron posteriormente. El análisis de la información incluyó la elaboración de cuadros comparativos.
F 13-2-19 13-3-19 14-3-19
G 14-2-19 20-2-19 13-3-19
H 18-2-19 14-3-19
I 20-2-19 20-3-19 Problemas
31
CAPÍTULO 4. RESULTADOS
4.1 Introducción
En este capítulo se exponen los resultados obtenidos del análisis de los datos recabados durante el proceso de implementación de las tareas. En primer lugar se analizó de forma individual la prueba piloto aplicada a los 10 estudiantes de primer semestre. Posteriormente, se exponen los resultados derivados de la implementación de tareas no guiadas que abordaron de forma individual, los 10 estudiantes de segundo semestre, seguido del análisis de la tarea guiada realizada por los tres equipos que se formaron. Se comparan los dos tipos de tareas, para finalmente analizar el efecto de las preguntas que realicé como apoyo para los estudiantes.
4.2 Análisis de la prueba piloto
Considerando las investigaciones previas se diseña una prueba piloto de una tarea guiada. La primera versión se aplicó a 6 de los 10 estudiantes de primer semestre (Apéndice E), la cual arrojó problemas de redacción y ambigüedad en algunas preguntas e indicaciones, por ejemplo se solicitaba que dibujaran dos figuras más y algunos estudiantes dibujaron otras dos figuras que no tenían nada que ver con el patrón. Por mencionar otro ejemplo al solicitar el número de piezas del origen de simetría, había estudiantes que consideraban 5 y otros uno. Era necesario especificar y aclarar tanto indicaciones, preguntas y el exceso de tablas. (Tabla 3):
Tabla 3. Primera modificación de la prueba piloto.
Fase
Indicación,
pegunta o tabla
Modificación
32
rectángulos debe tener cada figura.
Observación ¿Observas simetría en las figuras?
Marca el origen de la simetría de cada figura.
¿Cuántas piezas conforman el origen de la simetría?
Tabla 1. (Número de piezas del origen de la simetría).
Tabla 2. Se encontraba fragmentada
¿Identifica simetría en las figuras, explica?
Si encuentras simetría, indica el origen de la simetría de cada figura.
¿Cuántas piezas tiene el centro de simetría?
Tabla 1. (Número de piezas en el origen de la simetría).
Tabla 2. Se ajustó
Conjeturas En todas las preguntas se hace mención del origen de simetría.
Se modifica origen de simetría por centro de simetría.
Justificación de
resultados
¿Cómo representas la cantidad de la figura 200?
33
Considerando la investigación de Stein (1996), la variación en la calidad de la instrucción se relaciona con las características que los estudiantes logran construir, por lo que consideramos realizar una segunda versión de la tarea con modificaciones, la cual se aplicó a los 4 estudiantes restantes (Apéndice F). Con la finalidad de que la tarea quedara clara y pudiera guiar al estudiante durante las diversas fases del ciclo para promover el aprendizaje con entendimiento, así que nuevamente realizamos modificaciones en algunas fases (Tabla 4).
Tabla 4. Segunda modificación de la prueba piloto.
Fase Pregunta, indicación o
tabla
Modificación
Observación ¿Cuántas piezas hay en cada
rama que parten de los
vértices de la figura central?
¿Cuántas piezas hay en cada
rama que parten de los
vértices de la figura central
para los siguientes casos?
Conjeturas Si deseo referirme a
cualquier figura ¿Cómo la
puedo representar?
Si deseo referirme a la figura
1. Es figura 1
Si deseo referirme a la figura
2. Es figura 2
Si deseo referirme a alguna
figura que desconozco el
número, sería _________
4.3 Resultados de la tarea “Bloques de madera”
34
cercanas pero cuando se solicita el número de piezas de alguna figura lejana como la 73 no lograron realizar el cálculo. Sin embargo, algunos de ellos sí lograron generalizar el patrón pero no pudieron escribir la representar algebraicamente. Finalmente, dos de ellos en la fase de acción pudieron representar con el material concreto, pero cuando se solicitó que dibujaran dos figuras siguiendo el patrón anterior, cambian la imagen (Tabla 5).
Tabla 5. Fases del ciclo que abordaron los estudiantes en la tarea “bloques de madera”. ESTUDIANTE ACCIÓN OBSERVACIÓN CONJETURAS JUSTIFICACIÓN
DE RESULTADOS A
B C D E F G H I J
Se encontraban algunos de ellos tensos, probablemente por la filmación, intentaron preguntar, sin que el docente respondiera, invirtieron tiempo en tratar de entender lo que se solicitaba y después de realizar algunos intentos, terminaron diciendo “ya no puedo”. Sin
35
Estudiante B Estudiante C
Figura 6. Dificultades de los estudiantes para construir otros elementos de la secuencia. Cuartas (2015), al igual que Chua y Hoyles (2014), reportan que el apoyo visual facilita la resolución de tareas; sin embargo en los casos anteriores, las imágenes no apoyaron a los estudiantes en la identificación de regularidades. Aunque este posible error de los estudiantes se deba a la forma en que se planteó la indicación, ya que pudiese ser confuso para los estudiantes el significado de la expresión “el patrón de las figuras anteriores”.
36
Figura 7. Intento del estudiante D por expresar regularidades.
En la fase de observación, la estudiante E, identificó que las primeras diferencias de la secuencia eran constantes e iguales a cuatro. Al respecto, Cuartas (2015) indica que una estrategia inicial utilizada por los estudiantes consistió en identificar que las primeras diferencias de los elementos consecutivos de una sucesión son constantes, pero el estudiante olvida corroborar con las figuras previas, lo cual impide que llegue a conjeturas verdaderas (Figura 8).
37
En la fase de observación el estudiante G realizó algunas operaciones que lo llevan de forma errónea al cálculo de las piezas por un error aritmético. En el momento de solicitar la representación algebraica no entendió que le solicitan, pues dibuja un triángulo, pero cuando justifica resultados él utiliza la generalización o representación algebraica de forma adecuada (Figura 9).
Figura 9. Sin conjeturas expresadas, pero generalización adecuada.
El estudiante F únicamente logró transitar por la fase de acción, mientras que la estudiante H solamente llegó a la de observación, pero las observaciones que realizó fueron erróneas, probablemente porque la figura se encontraba lejos de su alcance para construirla con el material (Figura 10).
38
Alumno I: Las figuras cercanas las logró identificar e intentó utilizar letras para las representaciones pero no sabe cómo. Identificó que existe una figura central rodeada de más figuras (Figura 11).
Figura 11. Identifica una parte central.
Alumno J: Identificó con facilidad el patrón y su representación algebraica.
Se puedo observar que todos los estudiantes cuentan con elementos para reconocer el patrón y lo intentan, pero la orientación que se da hacia el reconocimiento de este no es la apropiada. Según (Polya 1945, p.46) “el estudiante adquiere en su trabajo personal la más amplia experiencia posible, pero si se deja solo ante su problema, sin ayuda alguna o casi ninguna, puede ser que no progrese”.
4.4 Resultados de la tarea “Fichas”
39
Tabla 6. Fases del ciclo que abordaron los estudiantes en la tarea “fichas”. ESTUDIANTE ACCIÓN OBSERVACIÓN CONJETURAS JUSTIFICACIÓN
DE RESULTADOS A
B
C No asistió debido a problema de salud D
E F G H
I No asistió debido a problemas económicos. J
Resulta relevante la forma en que algunos estudiantes intentaron comunicarse en la fase de justificación de resultados, les solicitamos describir cómo reconocieron el patrón y expresaron la generalidad con las siguientes frases:
Alumno B: “Se aumenta el doble de la figura, haciendo que aumenta más de 2 veces”, el
alumno sabe que saldrá más del doble de cada figura, por ejemplo si es la figura 5, con seguridad será una cantidad mayor a 10.
Alumno D: “Según la secuencia y patrón que puede observar en las figuras previas”,
40
Figura 12. Sin representación algebraica.
Alumno E: “Utilizando las fichas me di cuenta de que manera iba incrementado”, reflejó que
el material es importante, de hecho realiza algunas diferencias ente algunas cantidades de piezas de algunas figuras. Para realizar el cálculo de la figura 100 lo realizó con la multiplicación (100x99). Figura 13. Sin embargo la alumna H llega a la observación errónea que todas las figuras van aumentando 6 piezas más.
Figura 13. El material fue importante pero no suficiente
Alumno F: “Por las filas e hileras de la figuras anteriores”, el estudiante reconoció que tienen relación las filas y las hileras
41
Figura 14. Propuesta de representación algebraica.
Los estudiantes intentaron argumentar lo que observaron en la medida de sus posibilidades, pero en su mayoría se pierde en el intento, no logran llegar a los patrones sugeridos, dadas estas dificultades, la necesidad de apoyo y ayuda externa son fundamentales para que estos retos no se conviertan en enormes muros que los diferencien de una minoría. Aprender matemáticas con entendimiento requiere desarrollar un lenguaje para expresar y defender ideas o puntos de vista; así como para construir y sustentar argumentos de diferente tipo, visuales, empíricos o deductivos (Santos Trigo, 2015). El docente jugará un papel fundamental en la proposición de tareas inquisitivas, es aquí donde el tipo de pregunta e instrucción será crucial.
4.5 Resultados de la tarea “Palillos de colores”
42
Tabla 7. Fases del ciclo que abordaron los equipos en la tarea “palillos de colores”. EQUIPO ACCIÓN OBSERVACIÓN CONJETURAS JUSTIFICACIÓN
DE RESULTADOS A,B,H
E,F,J C,D,G
EQUIPO ABH
Fue un equipo que en su mayoría prefirió leer las actividades en silencio, sin embargo uno de los estudiantes estaba muy atento a los comentarios de otros integrantes del grupo. En este apartado se analiza la actividad del equipo por fase. En la fase de acción iniciaron la construcción de forma individual, posteriormente decidieron construir todas la figuras sobre una. Llegaron a acuerdos para construir y dibujar. En la fase de observación uno de los estudiantes realizó movimientos con la mano para indicar horizontales, pues a uno de los compañeros no le quedaban claras las posiciones (Figura 15). Los estudiantes lograron ver las relaciones que existen entre los palillos horizontales y diagonales con la posición de la figura, a través de las preguntas. Pero su forma de redactar no es muy clara, por ejemplo en la pregunta, ¿Tiene alguna relación la cantidad de palillos con el número de la figura? Contestan si, suma uno.
43
En la fase de formulación de conjeturas, después de las observaciones pudieron imaginar la cantidad de palillos que conformaban las figuras lejanas como la 500, claro que tuvieron que retomar la figura 1, para llegar a la cantidad de palillos horizontales y diagonales en una figura. Uno de los estudiantes comentó que la pregunta se refería a de todos los palillos de la figura, no únicamente horizontales y diagonales. Por lo que realizaron el cálculo del total de palillos. Fue importante la aclaración del estudiante, porque en la generalización les solicitan la cantidad de piezas total de las figuras, nuevamente retomando la cantidad de horizontales y diagonales. Por su parte, en la fase de justificación de resultados cuando se preguntó, ¿Cómo representas la cantidad de piezas de la figura 13 más la cantidad de piezas de la figura 270? Vertieron algunas sugerencias para la representación, el estudiante A escribió que pudiera quedar (2(13) + 1)+ (2(270) + 1) a lo que respondió el estudiante B que mejor (2(13)+2(270))+2. El estudiante A comentó que era lo mismo, pero el estudiante B insistió que está simplificada (Figura 16).
Figura 16. Representación de los estudiantes.
44
aumenta 3, y ahí se aprecia una regularidad en la secuencia, 1 + 2 igual a 3, 3 + 2 igual a 5. El docente solicita que si lo puede escribir porque está imaginando una tabla. El estudiante accedió pero aclaró que no es una tabla (Figura 17).
Figura 17. Argumentos del estudiante. EQUIPO CDG
En la fase de acción construyeron cinco figuras, el docente intervino para preguntar, ¿Qué logran observar? Los estudiantes comentaron que cada figura va cambiando, que ya pueden imaginar la figura 6. Se pusieron de acuerdo para dibujar las figuras solicitadas. En la fase de observación uno de los estudiantes comentó las posiciones de los palillos, son horizontales y verticales, a lo que el docente intervino para preguntar ¿Cuáles serían las verticales? y ¿Qué piensan los demás? El estudiante retomó diciendo no, no, no, perdón no son verticales son diagonales. Su redacción no fue muy clara, pero de manera oral se refirieron adecuadamente (Figura 18).
45
En la fase de formulación de conjeturas los estudiantes no tuvieron problemas para realizar el cálculo de la cantidad de horizontales y diagonales en la figura alejada como la 500, ni para el cálculo total de piezas de dicha figura. Cuando se solicitó referirse a alguna figura que desconozco el número, inicia un pequeño debate entre los que consideraban que era x y la estudiante que consideraba que era n, finalmente el estudiante que consideraba a x, comenta que es lo mismo pues ambas son variables. Una vez aclarando este punto para establecer cantidad de horizontales, diagonales y total de piezas no tuvieron problema. El docente intervino preguntando ¿Por qué 2x+1?, uno de los estudiantes intervino contestando que se basan en lo anterior, sumando la cantidad de palillos horizontales y verticales. Una estudiante preguntó ¿No sería n +2?, el docente pregunta ¿Por qué n+2?, la estudiante argumentó, porque la figura 1 es n+2 igual a 3. El docente volvió a preguntar ¿Sirve para los demás? Y la alumna contesta, no esperen, si es 2x+1.
46 EQUIPO EFJ
En la fase de acción uno de los estudiantes comentó que las figuras van aumentando de dos en dos, porque se pone la primera figura y después solo dos (Figura 19). En la fase de observación identificaron las posiciones de los palillos, pero constantemente regresaron a las imágenes para realizar el conteo de palillos. Antes de llegar a las preguntas de la relación de palillos horizontales con la figura, ya habían observado que eran la misma cantidad. Cuando llegan a la relación de los palillos inclinados con la figura, regresaron nuevamente a las figuras para concluir que siempre será 1 más que la figura.
47
Figura 20. Identificación de que las primeras diferencias son constantes.
48
Figura 21. Reducción de términos que realiza el equipo.
En la fase de comunicación de resultados los estudiantes comentaron, la cantidad de palillos horizontales es igual al mismo número de la figura y las diagonales 1 más que la figura. Volvieron a tener dudas en la representación de las piezas de la figura 13 más las piezas de la figura 270. La docente apoyó sugiriendo que den inicio con la 13 y posteriormente con la 270. Se puedo observar en los 3 equipos dadas las condiciones de la actividad, que el brindarles preguntas les permitió acercarse paulatinamente hacia una idea, la cual es cuestionable, los estudiantes intercambiaron ideas, externar dudas y pueden ayudarse. Compartimos la idea que plantea Forero (2014), quien expresa que cuando los estudiantes participan activamente en las tareas con preguntas que puedan discutir, la discusión posibilita enriquecer las explicaciones y argumentaciones, ya que se intercambian ideas, se construyen significados para los objetos matemáticos conjuntamente. Pero se requiere condiciones que el docente propicie para que aparezcan esas preguntas movilizadoras del pensar.
4.6 Análisis del efecto de las preguntas que el profesor formula a los estudiantes
49
Tabla 8. Preguntas de la tarea no guiada “bloques de madera”
FASES PREGUNTAS O INSTRUCCIÓN EFECTO
Acción 1. Forma las siguientes figuras utilizando bloques de madera.
2. Dibuja dos figuras más siguiendo el patrón de las figuras anteriores.
1. La construcción de las figuras. 2. Si logró ver el comportamiento puede dibujar las siguientes, de lo contrario puede elaborar otro patrón.
Observación 3. Número de piezas de la figura 4
4. Número de pieza de la figura 73 3. Puede realizar el conteo porque es una figura cercana. 4. Será complicada si no reconoció el patrón, pues no tiene al alcance la cantidad necesaria de material concreto para poder realizar la figura.
Conjeturas 5.Representación algebraica de cualquier figura
5. Esta indicación está formada de 2 elementos, debido a que en primera instancia debió reconocer el patrón y en segunda tiene que tener elementos para representar. Así que si no lo reconoció no tendrá que representar, o puedo reconocerlo pero no saber cómo representar. La instrucción te brinda ayuda nula.
Justificación
de Resultados
6. Representa el cálculo del total de piezas de la figura 5. No indiques el resultado, solamente se necesita que utilices alguna forma de representar la cantidad de piezas.
7. Representa el cálculo del total de piezas de la figura 100. No indiques el resultado, solamente se necesita que utilices alguna forma de representar la cantidad de piezas.
8. Representa la cantidad de piezas de la figura 50 más la cantidad de piezas de la figura 200.
6, 7 y 8. Para llevar a cabo estas instrucciones, se requiere de una representación. Puede ser no necesariamente la algebraica, de hecho como muestra las evidencias pueden ser propiamente imágenes como algunos estudiantes lo hacen.
50
les es clara. Al realizarla de forma individual te quita aún más la posibilidad de externar alguna idea de la probabilidad de intentar algo más.
Tabla 9. Preguntas de la tarea guiada “palillos de colores”
FASES PREGUNTAS O INSTRUCCIÓN EFECTO
Acción 1. Construye las primeras tres utilizando el material.
2. Observa la cantidad de palillos de las figuras y dibuja dos figuras más.
1. Permite manipular el material y construir el patrón.
2. Al solicitar que observes la cantidad de palillos, restringe la posibilidad de realizar otro patrón y permite acercarse al reconocimiento del patrón que se le está presentando.
Observación 3.Menciona las posiciones que tienen los palillos
_______ ____________
4. ¿Cuántos palillos horizontales tiene la figura 1?_____________
5. ¿Cuántos palillos horizontales tiene la figura 3?______________
6. ¿Cuántos palillos horizontales tendrá la figura 20?____________ 7. ¿Tiene alguna relación la cantidad de palillos horizontales con el número de figura?_______
¿Cuál?_________________________ ___________
8. ¿Cuántos palillos están en posición inclinada en la figura 2?___________ 9. ¿Cuántos palillos están en posición inclinada en la figura 4?___________ 10. ¿Cuántos palillos estarán en la posición inclinada en la figura 20?____________
11. ¿Tiene alguna relación la cantidad de palillos con el número de la figura?____________
3. Realizar conexiones.
4, 5, 6. Observar comportamiento.
7 y 8. Establecer relación de la cantidad de palillos en posición horizontal con la figura.
9 y 10. Establecer relación de la cantidad de palillos en posición inclinada con la figura.
51 12. ¿Cuál?______________ Conjeturas Primera Parte
13. ¿Cuántos palillos tendrá la figura
500 en posición
horizontal?______________
14. ¿Cuántos palillos tendrá la figura
500 en posición
inclinada?____________
15. ¿Cuántos palillos tendrá en total la figura 500?___________
Segunda Parte
16.Si deseo referirme a la figura 2 sería: Figura 2
17.Si deseo referirme a la figura 5 sería: Figura 5
18.Si deseo referirme a la figura 20 sería ____________
19.Si deseo referirme a alguna figura que desconozco el número, sería ________________
20. ¿Cuántos palillos horizontales tendrá cualquier figura que desconozco su número?_______
21. ¿Cuántos palillos inclinados tendrá cualquier figura que desconozco su número?_________
22. ¿Cuántos palillos tendrá en total cualquier figura que desconozco su número?__________
Nota: Hasta el momento ha tenido contacto con figuras cercanas, las cuales puede manipular con material concreto. En la primera parte de conjeturas se brinda la oportunidad de alejarse, es decir, pensar en alguna figura como la 500, la cual ya no se encuentra a su alcance para trabajar con material concreto.
13. A partir de lo observado con la relación de la cantidad de palillos en posición horizontal con la figura puede predecir, sin necesidad de construir y contar.
14. A partir de lo observado con la relación de la cantidad de palillos en posición inclinada con la figura puede predecir, sin necesidad de construir y contar.
15. Reflexionar que la figura está conformada de la suma de los palillos de ambas posiciones, horizontales e inclinadas.
Nota: En la segunda parte se pretende que a partir de sus primeras conjeturas y de forma
paulatina llegue a
generalizaciones.
16, 17, 18. Proporcionar elementos para referirme a la figura considerando su número de posición.
19. Representar cualquier figura. Por ende la necesidad de utilizar los símbolos algebraicos.
52
21. Realizar conexiones entre lo que había hecho y observado en relación a la cantidad de palillos en posición vertical de varias figuras con cualquier figura.
22. Generalizar la cantidad de palillos de cualquier figura.
Justificación de Resultados
23. ¿Cómo representas el número de palillos de la figura 513? No obtengas el resultado, solamente se necesita que utilices alguna forma de representar la cantidad de piezas.
24. Calcula el total de piezas para la figura 1027
25. ¿Cómo representas el número de palillos de la figura 312?
26. ¿Cómo representas la cantidad de piezas de la figura 13 más la cantidad piezas de la figura 270?
23. Representar el proceso que generalizó, después del ciclo que realizó donde interviene de forma directa la comunicación.
24. Probar la validez de la generalización.
25. Verificar si su proceso es el adecuado
26. Operar el proceso
53
CAPÍTULO 5. CONCLUSIONES
5.1 Introducción
El docente es un actor fundamental en el proceso de aprendizaje de los estudiantes debido a que su conocimiento y actitud, y, en consecuencia las características de las actividades que propone en el salón de clase, son determinantes en el tipo de aprendizaje que los estudiantes logran construir. Por otra parte, las tareas de instrucción son el vehículo para que los estudiantes desarrollen entendimiento de las ideas matemática, y por ello deben dar lugar a procesos inquisitivos de discusión y reflexión. Pero ¿Cómo construir esas tareas?, después de la experiencia de realizar la prueba piloto de una de las tareas, identificamos algunos aspectos que pueden ser importantes durante el proceso de diseño: (i) Incorporar todas las fases del ciclo para desarrollar aprendizaje con entendimiento, (ii) Es importante que la hoja de trabajo de las tareas incluya una serie de preguntas que permitan al alumno identificar estructuras en las secuencias figurales que le permitan generalizar y simbolizar el patrón, (iii) Cuidar la redacción de las indicaciones y de las preguntas, de forma que sean claras y precisas, (iv) No suponer que el estudiante conoce algún término por muy sencillo que lo parezca, pues entender las indicaciones es fundamental para que transite por todas las fases del ciclo, (v) Utilizar algún material concreto en la fase de acción, ya que las experiencias sensoriales son la base de todo conocimiento; (vi) Realizar una prueba piloto de la tarea antes de realizar la implementación definitiva, y (vii) Ser consciente de que una tarea nunca queda terminada, cada implementación permite realizar ajustes y mejoras.
5.2 Respuestas a las preguntas de investigación
Mediante la aplicación de las tareas, se pudieron identificar de forma clara algunos de los errores y las dificultades de los estudiantes para reconocer, generalizar y representar un patrón mediante una expresión simbólica; además se pudo reconocer la relevancia de preguntas durante el proceso de instrucción. Con base en las preguntas de investigación ¿Qué
54
tareas será determinante para poder guiar al alumno, las preguntas serán la llave para pensar, reflexionar, construir, promoviendo el intercambio de ideas, al preguntar a los estudiantes se deposita la responsabilidad en ellos, los estas invitando a actuar.
Cuestionarnos nos permite explorar, indagar, curiosear, interactuar, realizar conexiones. Pero algo es claro, pocos estudiantes se cuestionan, la mayoría siguen en el mejor de los casos instrucciones. Como docentes muchas ocasiones preguntamos esperando una respuesta correcta, pero no con la finalidad de orientar. Sugerimos que los estudiantes se cuestionen, pero cómo aprenderán a cuestionarse si no promovemos tareas inquisitiva, indudablemente gran cantidad de ellos no lo habrá por si solos. Fue claro en la comparación de tareas guiadas y no guiadas, el avance de los estudiantes en las diferentes fases del ciclo de aprendizaje con entendimiento, mientras que en las tareas que no contaban con preguntas en su mayoría únicamente podían llegar a la fase de acción, pues desconocían como avanzar, de hecho no reconocían lo que les solicitaban, mientras que en las tareas con preguntas orientadoras les permitía ir realizando conexiones y formular nuevas preguntas.
Es notoria la diferencia entre las tareas individuales y en equipo, mientras en las tareas individuales no tienen oportunidad de exteriorizar con alguien sus ideas o dudas, no se atreven a tomar riesgos, por lo que prefieren dejar las tareas hasta donde se sientan seguros. Las tareas por equipo les permite cometer errores, los cuales pueden ser reorientados por algún compañero o propiamente por el docente a través de alguna pregunta, realizan consensos entre ellos para continuar o detenerse, en algunas ocasiones algún estudiante toma el control, pero llegan algunos momentos que decide pedir opinión, ya sea para asegurarse o porque propiamente tiene dudas.
Se puede visualizar que para aprender el lenguaje algebraico es importante que los estudiantes tengan algo que comunicar; para ello necesita percibir un patrón o una regularidad y después intentar expresarlo y comunicarlo a alguien. No podrá realizarlo solo, requiere de ayuda externa que el docente puede brindar, por medio de preguntas, pero estás no pueden ser arbitrarias, tendrán que ser en las diferentes fases del ciclo de aprendizaje con entendimiento.