y producto punto
2012
–
2013
Índice
Vectores y combinaciones lineales
1
Vectores en
R
2y producto por un escalar
1
Combinaciones lineales de vectores
3
Vectores en
R
33
Longitud y producto punto
5
Producto punto
5
Longitud y vectores unitarios
6
Ángulo entre dos vectores
8
Trabajo práctico
11
Ejemplos con Sage
12
Operaciones con vectores de
R
n12
Representación gráfica de vectores en
R
2y
R
313
Vectores y combinaciones lineales
Vectores en
R
2y producto por un escalar
Vector columna deR2
v=
v
1
v2
v
1=primera componente
v2=segunda componente ¿Qué es un vector?
Tenemos dos números separadosv1yv2.
Este par produce unvector de dos dimensionesv.
Vector columna
v= v1 v2
!
v1= primera componente v2= segunda componente
Escribimosvcomo unacolumna, no como una fila.
Decimos quev∈R2(tiene dos números reales).
Suma de vectores
Podemossumar dos vectoresvyw.
La primeras componentes devywno se mezclannuncacon las segundas componentes.
Suma de vectores
v= v1 v2
!
y w= w1 w2
!
suman v+w= v1+w1 v2+w2
!
La resta de vectores sigue la misma idea, las componentes de
v−wsonv1−w1yv2−w2.
Suma de vectores columna enR2
v+w=
v1+w1
v2+w2
Multiplicación de un vector columna deR2por un escalarc∈R
cv=
cv
1
cv2 Multiplicación por un escalar
La otra operación básica es lamultiplicación escalar.
Los vectores pueden ser multiplicados por2, por−1, o por
cual-quier otro númeroc∈R.
Hay dos maneras de duplicar un vector: sumarv+vo (más fácil) multiplicar cada componete por2.
Multiplicación escalar
2v= 2v1
2v2 !
y −v= −v1 −v2 !
Las componentes decvsoncv1ycv2.
El númeroces llamadoescalar.
Comentarios sobre la suma y la multiplicación escalar
Hay que notar que la suma de−vyves el vector cero.
¡Esto es el vector0= 0
0
!
, que es distinto del número0!
Todas las ideas delálgebra linealse basan en operacionesv+wy
cv(suma de vectores y multiplicación por escalares).
El orden de la suma no altera el resultado:v+wes igual a w+v.
v+w= 1
5
!
+ 3
3
!
= 4
8
!
w+v= 3
3
!
+ 1
5
!
= 4
8
Combinaciones lineales de vectores
Combinación lineal de dos vectores columna enR2
cv+dw=
cv
1+dw1
cv2+dw2 ¿Qué es una combinación lineal?
Combinando la suma vectorial y la multiplicación por un escalar se forman combinaciones lineales devyw.
Esto se hace multiplicandovporc, multiplicandowpord, y luego sumandocv+dw.
Definición1. La operacióncv+dwes unacombinación linealde
vyw.
Hay cuatro combinaciones lineales especiales: suma, resta, cero y múltiplo escalar.
1v+1w= suma de vectores 1v−1w= resta de vectores
0v+0w= vector cero
cv+0w= vectorcv múltiplo dev
Comentarios sobre las combinaciones lineales
El vector0(cero) siempre es un resultado posible de una combi-nación lineal de vectores.
Siempre que hablemos de unespacio(lleno)de vectores, el vector cero estará incluido.
El álgebra lineal consiste en trabajar sobretodaslas posibles combinaciones lineales devyw.
−1 1 2 3 4 y
−1 1 2 3 4
x v 3v w 2w u=
3v+ 2w
Figura1: representación de
una combinación lineal de vec-tores columna deR2.
Representación de vectores enR2
v= −
1 3 2 3
!
w= 2
1
!
3v+2w=3 −
1 3 2 3
!
+2 2
1
!
= 3·
−13
+2·2 3·2
3+2·1 = 3 4 ! =u
Vector columna deR3
v=
vv12
v3
vv12==primera componentesegunda componente
v3=tercera componente Vector columna deRn
v= v1 v2 .. . vn
v1=primera componente
v2=segunda componente ..
.
vn=n-esima componente
Vectores en
R
3Extensión de la idea de vector a más dimensiones
El plano xyes reemplazado por el espacioxyz.
Una combinación lineal de dos vectores enR3es
2 1 0 3 +4
1 2 1 =
2·1+4·1 2·0+4·2 2·3+4·1
= 6 8 10
v = (4, 2)ow = (1, 2, 1)son vectores columna, deR2yR3, representadoscomo números separados por coma para simplificar la escritura.¡No son vectores fila!
Vector fila deR3
a= a1 a2 a3
a1=primera componente
a2=segunda componente
a3=tercera componente ¡Sin separar con comas!
Vector fila deRn
a= a1 a2 · · · an ¡Sin separar con comas!
Combinación lineal de dos vectores columna enR3
cv+dw= cv1
+dw1
cv2+dw2
cv3+dw3 Representación de vectores enR3
v= 1 1 2 1
w=
1 3 2 1
2v+12w=2 1 1 2 1 +12
1 3 2 1 =
2·1+12·13
2· 12+12·2
2·1+12·1
= 13 6 2 5 2 =u
Figura2: representación de
una combinación lineal de vec-tores columna deR3.
Ejemplo1. Las combinaciones lineales de estos vectores deR3
v= 1 1 0
y w=
0 1 1
llenan un plano.Describir este plano. Encontrar un vector queno seauna combinación lineal devyw.
Los vectores en el plano corresponden atodaslas combinaciones lineales posibles de la forma
cv+dw=c 1 1 0 +d
0 1 1 = c c+d
d
para números cualesquieracydpertenecientes aR.
Los vectores del plano son entoncesu= (c,c+d,d).
La segunda componentec+des siempre la suma de la primera
y la tercera.
El vector(2, 0, 1)no esuna combinación lineal devyw, debido a que 06=2+1.
Figura3: vectores que
pertene-cen al planocv + dw(verdes), y un vector que no pertenece a este plano (azul).
Ejemplo2. Encontrar dos ecuaciones para las incógnitascydtales
que la combinación linealcv+dwsea igual al vectorb
v= 2
−1
!
w= −1
2
!
b= 1
0
!
Laecuación vectorialdel problema es
c 2 −1
!
+d −1
2
!
= 1
0
!
Elsistema de ecuaciones linealesparacydes 2c− d=1 −c+2d=0
Repaso de ideas clave
1. Un vectorven el espacio de vectoresR2tiene dos componentes v1yv2.
2. v+w= v1+w1 v2+w2 !
ycv= cv1 cv2 !
3. Un vectorven el espacio de vectoresR3tiene tres componentes v1,v2yv3.
4. v+w=
v1+w1 v2+w2 v3+w3
ycv=
cv1 cv2 cv3
5. Una combinación lineal de tres vectoresu,vyw,en cualquier espacio de vectores, escu+dv+ew.
Longitud y producto punto
Producto punto
El producto punto de dos vectores de
R2es el número
v·w=v1w1+v2w2
El producto punto de dos vectores de
R3es el número
v·w=v1w1+v2w2+v3w3
El producto punto de dos vectores de
Rnes el número
v·w=v1w1+v2w2+· · ·+vnwn
=
n
∑
i=1viwi Una nueva operación con vectoresEn la sección anterior no hablamos de multiplicación entre vecto-res.
Ahora definiremos unproducto puntoentrevyw.
Esta multiplicación implica calcular los productosv1w1yv2w2,
pero no solo eso.
Estos dos números deben sumarse para obtener un único núme-rov·w.
Definición del producto punto
Definición2. Elproducto puntode dos vectores columna deR2
v= v1 v2
!
y w= w1 w2 !
es el númerov·w
v·w=v1w1+v2w2
Ejemplo3. Los vectoresv = (−1, 2)yw = (4, 2)tienen producto
punto cero
v·w= −1
2
! · 42
!
= (−1)·4+2·2=−4+4=0
En matemáticas, el número cero suele tener un significado espe-cial.
Con el producto punto, significa que estos dos vectores son per-pendiculares (simbolizado con⊥).
Osea que el ángulo entre ellos es de π
2 radianes (=90◦).
1 2 3 4
y
−1 1 2 3 4
x
v
w
Figura4: el producto punto de
dos vectores perpendiculares esv·w=0.
1
y
1
x
i
j
Figura5:iyjson los vectores
estándar o canónicos enR2. Comentarios acerca del producto punto
El ejemplo más evidente de vectores⊥esi= (1, 0), a lo largo del
ejex, yj= (0, 1), a lo largo del ejey
El productoi·j = 1·0+0·1 = 0. Estos vectores forman evidentemente un ángulo recto.
Longitud y vectores unitarios
Según el contexto, y según la biblio-grafía, los vectores estándar se escriben de diversas formas (todas equivalen-tes)
i=~i=ex=e1=~ex=~e1
j=~j=ey=e2=~ey=~e2 Producto punto de un vector con sí mismo
Un caso importante es el producto punto de un vector con sí mismo. En este casovywson iguales.
Si tenemosv = (1, 3, 2), el producto con sí mismo esv·v = |v|2=14.
Longitud al cuadrado
|v|2=
1 3 2
·
1 3 2
=1·1+3·3+2·2=1+9+4=14
En vez de 90◦, entre los vectores tenemos 0◦. El producto punto
es 146=0, porquevno es⊥a sí mismo.
Longitud de un vector
Definición3. Lalongitud(o norma)|v|de un vectorves la raíz cuadrada dev·v
longitud dev =|v|=√v·v
En dos dimensiones la longitud esqv2 1+v22.
En tres dimensiones esqv2
1+v22+v23.
En el ejemplo la longitud dev= (1, 3, 2)es|v|=√14.
La|v| = √v·ves simplemente la longitud de la flecha que representa al vector.
La longitud de un vectorv∈R2es
|v|=√v·v= q
v2 1+v22
La longitud de un vectorv∈R3es
|v|=√v·v=qv2
1+v22+v23
La longitud de un vectorv∈R4es
|v|=√v·v=qv2
1+v22+v23+v24
La longitud de un vectorv∈Rnes
|v|=√v·v=qv2
1+v22+· · ·+v2n
=
sn
∑
i=1v2 i Los vectores unitarios
Definición4. Un vector unitarioues un vector cuya longitud es
igual a1. Entoncesu·u=1.
Un ejemplo enR4esu=1 2,12,12,12
.
Tenemos que|u|=√u·u=q14+14+14+14 =√1=1.
Para obtenerupodríamos haber dividido el vectorv= (1, 1, 1, 1)
por su longitud
|v|=p12+12+12+12=√4=2
u= v |v| =
v
2
−1 1
y
−1 1
x
cos
θ
sin
θ
θ
i
j
u
|
u
|
=
1
Figura6: vectores unitarios en
el planoR2. Vectores unitarios en el planoR2
Ejemplo4. Los vectores unitarios a lo largo de los ejesxeyse
es-cribeniyj. En el planoxy, aquel vector unitariouque forme un ánguloθcon el ejexesu= (cosθ, sinθ).
i= 1
0
!
j= 0
1
!
u= cosθ
sinθ
!
Siθ=0 el vector horizontaluesi.
Siθ= π2 radianes (=90◦), el vector verticaluesj.
A cualquier ángulo, las componentes cosθy sinθhacen que
u·u=1, porque sin2θ+cos2θ=1.
Los puntos que representan estos vectores unitarios forman un
Vectores unitarios en el planoR2
Vector unitario
u= |vv| es un vector unitario en la misma dirección quev.
Ángulo entre dos vectores
−1
1
y
−1 1
x
u
=
√
v
2
u
=
1√
2 1
√
2
!
v
=
1
1
|
u
|
=
1
|
v
|
=
√
2
Figura7: para encontrar un
vectorucon el mismo sentido y dirección quev, pero que sea unitario, hay que dividirvpor su longitud.
Teorema1. El producto puntov·w=0cuandoves perpendicular aw.
w
v
−1 1 2 3 4
y
−1 1 2 3 4
x
v w
v+ w
|v| |v +w
| |w|
Figura8: la fórmula de
Pitágo-ras aplicada a la suma de dos vectores⊥.
Demostración:
1. Siv ⊥ w, entoncesvywforman dos catetos de un triángulo
rectángulo, y la hipotenusa es|v+w|. Por ejemplo
v= −1
2
!
w= 4
2
!
v+w= 3
4
!
|v|2=5 |w|2=20 |v+w|2=25
2. La fórmula de Pitágoras esa2+b2=c2, entonces
|v|2+|w|2=|v+w|2
v21+v22+w21+w22= (v1+w1)2+ (v2+w2)2
v21+v22+w12+w22=v21+2v1w1+w21+v22+2v2w2+w22
0=2v1w1+2v2w2
0=v1w1+v2w2
0=v·w
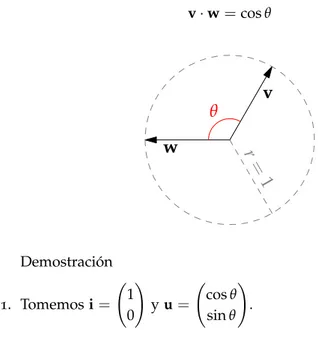
Teorema2. Sivywson vectores unitarios, entonces
v·w=cosθ
w
v
r
=
1
θ
Demostración
1. Tomemosi= 1
0
!
yu= cosθ
sinθ
!
2. El producto punto esi·u=cosθ.
3. Si rotamos ambos vectores un ánguloαobtenemosv= (cosα, sinα)
yw= (cosβ, sinβ), dondeθ=β−α. Sigue siendo cierto quevy
wsonunitarios.
i
u
θ
v
w
θ
α
β
4. v·w=cosαcosβ+sinαsinβ=cos(β−α) =cosθ.
La fórmula del coseno
v·w=|v||w|cosθ permite encontrar el ángulo entre dos vectores.
Teorema3. Sivywson un par de vectores no nulos cualesquiera, entonces
v·w=|v||w|cosθ
w
v
r
=
1
θ
Utilización de la fórmula del coseno
Ejemplo5. Encontrar cosθparav= (2, 1)yw= (1, 2).
El producto punto esv·w=4.
Tantovcomowtienen longitud√5.
El coseno es 45
cosθ= v·w |v||w| =
4
√
5√5 = 4 5
Entonces el ángulo será
θ=arc cos
4
5
Repaso de ideas clave
1. El producto puntov·wmultiplica cadavi porwi y luego suma
todos losviwi.
2. La longitud|v|de un vector es la raíz cuadrada dev·v.
3. u= v
|v| es unvector unitario. Su longitud es1.
4. El producto puntov·w = 0 cuando los vectoresvywson
perpendiculares.
5. El coseno deθ(el ángulo entre dos vectoresvywno nulos)
puede calcularse a partir de
Trabajo práctico
1. Representar gráficamentev = 4
1
!
yw = −2
2
!
, así como
tambiénv+wyv−w, todos en el mismo plano xy.
2. Dadosv = 2
1
!
yw = 1
2
!
, calcular las componentes de
3v+wy decv+dw.
3. Calcular los productos puntou·v,u·w,u·(v+w)yv·w
u= −0, 6
0,8
!
v= 3
4
!
w= 8
6
!
Dados dos vectoresuyvcualesquiera, siempre se cumple la desigualdad de Schwarz
|u·v| ≤ |u||v|
4. Calcular las longitudes|u|,|v|y|w|de los vectores del ejercicio
anterior. Luego comprobar que efectivamente se cumplen las siguientes desigualdades
a) |u·v| ≤ |u||v|
b) |v·w| ≤ |v||w|
5. Calcular vectores unitarios en las direcciones de los vectoresvy wdel ejercicio anterior, y el coseno del ánguloθformado entre
ellos. Pensar y escribir tres vectoresa,bycque formen 0◦, 90◦y
180◦con el vectorw(representar gráficamente los vectores en el
planoxypuede ayudar).
6. Dados un par de vectores unitariosvywcualesquiera, calcular
el valor de los productos punto siguientes
a)v·w b)(v+w)·(v−w) c)(v−2w)·(v+2w)
Pista: se debe trabajar “con letras”, recordando quev = (v1,v2),
w= (w1,w2)y que|v|=1 y|w|=1 (por ser vectores unitarios).
7. Calcular el ánguloθ, a partir del valor de cosθ, entre estos pares
de vectores:
a)v= √1
3
!
yw= 1
0
!
b)v=
2 2
−1
yw=
2
−1 2
c)v= √1
3
!
yw= √−1
3
!
d)v= 3
1
!
yw= −1 −2
Ejemplos con Sage
.
El código Sage en los siguientes recuadros puede ser seleccionado, copiado y pegado en una hoja de trabajo de Sage, para ejecutarlo y así obtener los resultados y los gráficos.Operaciones con vectores de
R
nHacer combinaciones lineales de vectores
# crear el vector u∈R3 u = vector((1,1,0)) # crear el vector v∈R3 v = vector((0,1,1))
# producto por un escalar: a=√2u a = sqrt(2)*u
# suma: b=u+v b = u+v
# resta: c=v−u c = v-u
# combinación lineal: d=2u+3v d = 2*u+3*v
# mostrar los resultados
print a;b;c;d
.
Puede utilizar estos ejemplos de código Sage como base para compro-bar los resultados de los ejercicios del trabajo práctico.Calcular el producto punto y la longitud
# crear el vector u∈R5 u = vector((1,1,1,-1,3)) # la longitud es |u|=√13
print u.norm()
# crear dos vectores v y w de R2 v = vector((4,2))
w = vector((2,-4))
# la longitud es |v|=2√5
print v.norm()
# el producto es v·w=0
print v.dot_product(w)
Calcular el vector unitario
# crear el vector u∈R3 u = vector((1,-2,2))
print u
# la longitud es |u|=3
print u.norm()
# crear el vector U= |uu| unitario # en la dirección de u
U = u/u.norm()
Calcular el ángulo entre dos vectores
# crear dos vectores de R2 u = vector((2,1))
v = vector((1,2))
print u;v
# calcular cosθ= |uu||·vv|
c = u.dot_product(v)/u.norm()/v.norm()
print c
# resultado en rad (con decimales)
print acos(c).n()
# resultado en grados (con decimales)
print (180/pi*acos(c)).n()
Representación gráfica de vectores en
R
2y
R
3 Graficar vectores enR2# crear dos vectores de R2 v = vector((-1/3,2/3)) w = vector((2,1)) # calcular u=v+w u = v + w
# crear "flechas" para cada vector fv = arrow2d((0,0), v, color="red") fw = arrow2d((0,0), w, color="red") fu = arrow2d((0,0), u, color="blue") # crear el gráfico
grafico = fv + fw + fu # mostrar el gráfico grafico.show()
Graficar vectores enR3
# crear dos vectores de R3 v = vector((1,1/2,1)) w = vector((1/3,2,1)) # calcular u=v+w u = v + w
# crear "flechas" para cada vector fv = arrow3d((0,0,0), v, color="red") fw = arrow3d((0,0,0), w, color="red") fu = arrow3d((0,0,0), u, color="blue") # crear el gráfico