EFINICIÓN DE UN CRISTAL

C

1:

C

─

D

Sólido.- Sustancias elásticas rígidas, tienen un comportamiento elástico cuando se someten a fuerzas hidrostática y esfuerzos de tensión y cortantes. Existen materiales cuyo comportamiento es tanto elástico como plástico ó viscoso, por lo que esta definición no es del todo rigurosa, sin embargo se adopta como criterio. Los sólidos, de acuerdo con esta definición se dividen en dos grupos. Los amorfos y cristalinos.

Amorfos: Los átomos ó moléculas pueden estar enlazados con bastante fuerza entre si, pero poseen poca regularidad ó periodicidad geométrica en la forma en que los átomos están dispuestos ó acomodados en el espacio, y se pueden considerar como líquidos sobre enfriados, es decir al enfriar un material de su estado líquido no muestra cambios discontinuos, pero llega a ser más rígido a través de un incremento progresivo en su viscosidad. Materiales con una viscosidad superior a 1012 Ns/m2 se le llama vidrio. Los materiales amorfos ó vidrios poseen un orden atómico únicamente sobre rangos del orden de una separación interatómica, fig. 21.

Cristales: Los materiales cristalinos se caracterizan por una periodicidad regular en el arreglo geométrico de los átomos ó moléculas, fig. 22.

Policristales : Los materiales sólidos no siempre se componen de un solo cristal, sino que a menudo están formados por un conjunto ó conglomerado de pequeñas unidades de cristal, cada una con diferente orientación, separadas entre si por fronteras de grano, a estos materiales se les conoce como policristales.

Red cristalina: Un cristal ideal esta compuesto de átomos acomodados en una red cristalina, definido por los vectores fundamentales ar,br,cr, tal que el arreglo atómico es el mismo visto en el punto rr como desde otro punto cualquiera rr,:

c

w

b

v

a

u

r

r

r

=

r

+

r

+

r

+

r

donde u, v, y w son enteros arbitrarios.

El conjunto de puntos rr,para todos los valores de u, v, y w definen una red cristalina, fig. 23, es decir una red se puede definir como un arreglo periódico regular de puntos en el espacio definidos por rr,, siendo de esta forma una red, una abstracción matemática.

Una estructura cristalina se forma cuando una base de átomos ó moléculas es ubicada idénticamente

en cada punto de la red, con lo que: Fig. 23 Red cristalina.

Cristal = red + base

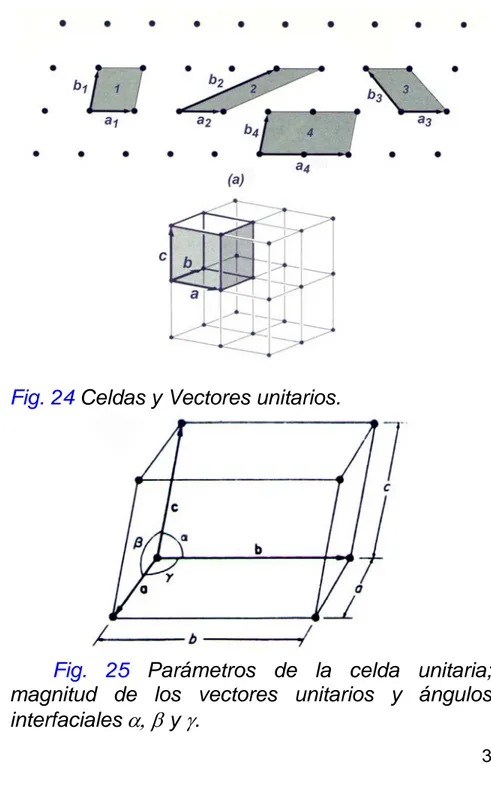
Vectores base ó vectores unitarios: El conjunto de vectores de translación linealmente independientes a b cr r r, , que se pueden usar para definir una red unitaria, la cual contiene todos los elementos de simetría de la red, fig. 24.

Celda unitaria primitiva: Una celda unitaria se dice que es primitiva cuando tiene el volumen mas pequeño ó bien cuando contiene únicamente puntos en cada vértice de la celda, ó un solo punto equivalente, tomando en cuenta que cada punto se comparte entre 8 celdas vecinas.

Por lo tanto una red unitaria puede ser primitiva pero no todas las celdas son primitivas, fig. 24.

Vectores base primitivos. Los vectores base primitivos definen a la celda unitaria primitiva, fig. 24.

Los parámetros de la celda unitaria lo constituyen tanto la magnitud de los vectores como los ángulos interfaciales α, β y γ entre vectores, fig. 25.

En vista de lo anterior, la celda unitaria y la celda unitaria primitiva se pueden definir, para la red cristalina, de muchas formas, fig. 24.

Fig. 24 Celdas y Vectores unitarios.

─

E

,

B

.

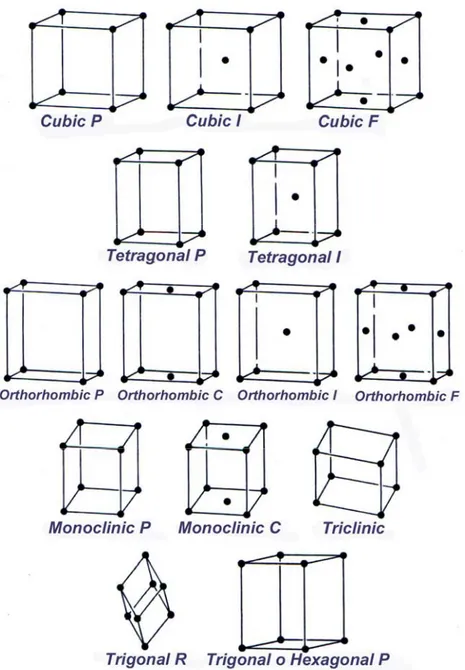
Basados en consideraciones geométricas existen 14 formas de acomodar puntos en las redes cristalinas, conocidas como redes de Bravais. Estas redes se pueden agrupar en 7 sistemas cristalinos en función de la relación directa de la magnitud de los vectores, a, b, c y de los ángulos entre ellos, α, β, γ, fig. 25. Estos sistemas y las redes de Bravais están dados en la tabla I y esquematizados en la fig. 26.

Elementos de simetría: Los cristales contienen diferentes simetrías ó elementos de simetría, los cuales se describen bajo ciertas operaciones. Una operación de simetría sobre un cristal deja al cristal y a su entorno invariante, con respecto a su configuración inicial.

Los elementos de simetría se agrupan en dos categorías:

1) Simetría de grupo puntual, cuando las operaciones se realizan alrededor de un punto ó eje.

2) Simetría de grupo espacial, cuando se realiza una operación por medio de una translación.

Tabla I Los siete sistemas cristalinos

Sistema Elemento

Característico de Simetría

Red de Bravais Características de

la celda Unitaria

Triclínico Ninguno Simple

o 90 c b a ≠ γ ≠ β ≠ α ≠ ≠

Monoclínico Un eje de rotación doble

Simple

Centrada en la base

_α

≠

₌

_β

≠

₌

o

_≠

_γ

90

c

b

a

Ortorrómbico Tres ejes de rotación doble mutuamente perpendiculares

Simple

Centrada en la base Centrada en el cuerpo Centrada en la cara

o

90

c

b

a

=

γ

=

β

=

α

≠

≠

Tetragonal Un eje de rotación cuádruple o un eje de rotación-inversión cuádruple

Simple

Centrada en el cuerpo

_o

90

c

b

a

=

γ

=

β

=

α

≠

=

Cúbico Cuatro ejes de

rotación triple

(diagonales cúbicas)

Simple

Centrada en el cuerpo Centrada en la cara

o

90

c

b

a

=

γ

=

β

=

α

=

=

Hexagonal Una eje de rotación séxtuple Simple

120

o

90

c

b

a

=

γ

=

β

=

α

≠

=

Los cristales exhiben ambos tipos de simetría independientemente y en combinaciones compatibles. Las principales operaciones de simetría son:

1.- Simetría de rotación de orden n: rotación alrededor de un eje a un ángulo 2π/n, n = entero.

2.- Simetría de reflexión: Una mitad del cristal reflejado en un plano de simetría que pasa por algún punto de la red reproduce la otra mitad.

3.- Centro de simetría ó centro de inversión: un punto de la red alrededor del cual la operación rr → −rr, donde rres un vector a cualquier otro punto de la red, deja la estructura sin cambio.

4.- Simetría rotación-inversión: combinación secuencial de las dos operaciones.

Sistema cúbico

En el sistema cúbico existen tres redes de Bravais: cúbico simple (cs), cúbico centrado en el cuerpo (bcc) y cúbico centrado en las caras (fcc).

La red cúbica simple es una celda unitaria primitiva (1 solo punto) con 1 punto en cada vértice el cual es compartido entre 8 celdas vecinas.

La red cúbica centrada en el cuerpo contiene 8 puntos correspondientes a los 8 vértices compartidos entre 8 celdas vecinas y un punto en el centro correspondiendo a un total de (1/8)8 + 1 = 2 puntos en la red.

La red cúbica centrada en las caras contiene 8 puntos de los vértices compartidos por 8 celdas y 6 puntos centrados en las caras, los cuales son compartidos por 2 celdas cada uno, dando un total de 8(1/8) + 6(1/2) = 4 puntos.

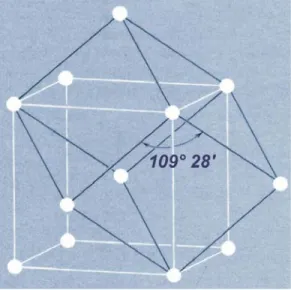
Las dos últimas redes no son por consiguiente primitivas. Una celda primitiva de la red cúbica centrada en el cuerpo es mostrada en la fig. 27a, al igual que sus vectores de translación primitivos, esta corresponde a la red rombohedrica (trigonal) con vectores primitivos:

r

a, = a(x$ $ $+ −y z) 2

r

b, = a(− + +x$ $ $y z)

2

r

c, = a(x$ $ $− +y z) 2

Fig. 27a Vectores primitivos y celda primitiva de la red cúbica centrada en el cuerpo.

Una celda primitiva de la red cúbica centrada en las caras, fig. 27b, es un caso especial de una estructura trigonal en el que α = β = γ = 60o con los vectores primitivos:

r

a, = a(x$ $+y) 2

r

b, = a(y$ $+z) 2

r

c, = a(x$ $+z) 2

Cada lado tiene una magnitud de a

2

Empaquetamiento y número de coordinación, estructuras cristalinas metálicas.

Para la representación de estructuras metálicas los iones ó átomos pueden ser representados por esferas rígidas. El empaquetamiento está relacionado directamente con el número de vecinos más cercanos que rodean a cada átomo, llamado el número de coordinación del cristal. Mientras mayor sea el número de coordinación mayor es el empaquetamiento.

El factor de empaquetamiento es definido como la fracción del espacio ocupado por átomos en una celda; es decir es la razón del volumen del átomo ocupando una celda al volumen de la celda unitaria relativa a la estructura.

La distancia entre vecinos cercanos es la distancia entre centros de dos átomos vecinos mas cercanos (2r).

El radio del átomo es definido como 1/2 de la distancia entre vecinos cercanos en un cristal de un solo elemento (r).

Estructura cúbica simple. En esta estructura hay un átomo en cada vértice de la celda, sí uno elige como centro un átomo en un vértice, se observa que este átomo es rodeado por 6 átomos vecinos y por consiguiente el numero de coordinación es 6. El número de átomos en la celda es 1 ya que 8(1/8) = 1. La distancia entre vecinos cercanos es 2r = a. El volumen ocupado por átomo ν = (4/3)πr3 = (1/6)πa3. El volumen de la celda unitaria V = a3. El factor de empaquetamiento ó densidad de empaquetamiento es:

( )

V

x a

a

= ν = 1 1 6 π = π =

6 0 52 3

3 /

.

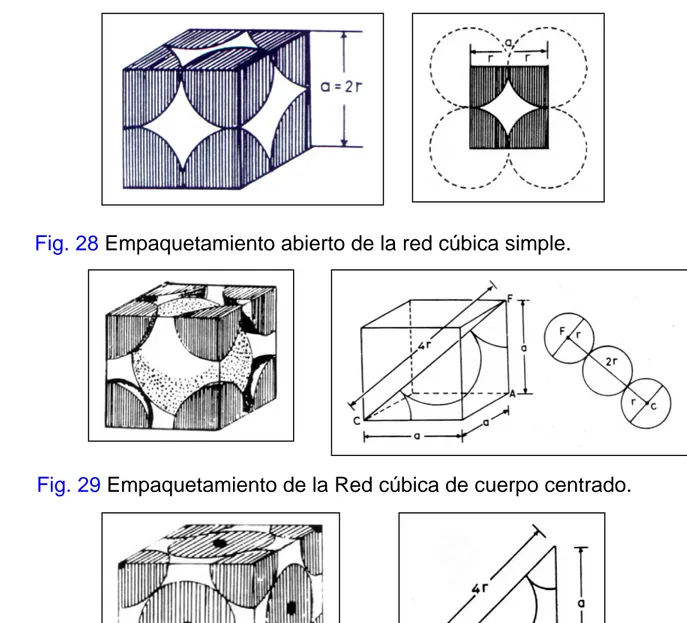
el cual corresponde a un empaquetamiento abierto, fig. 28

Fig. 28 Empaquetamiento abierto de la red cúbica simple.

Fig. 29 Empaquetamiento de la Red cúbica de cuerpo centrado.

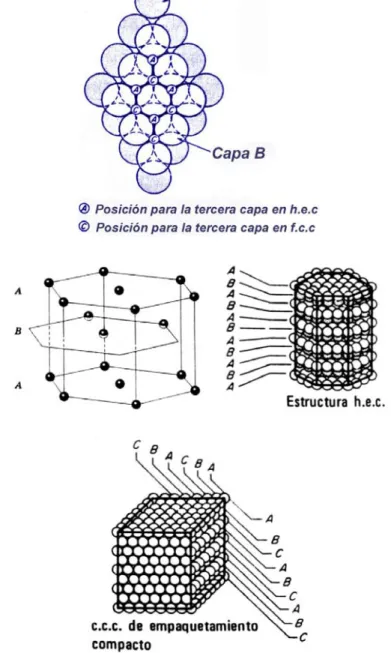
Empaquetamiento cerrado ó compacto. Existen dos formas de arreglar esferas equivalentes en un arreglo regular para minimizar el volumen intersticial, uno conduce a la estructura cúbica de caras centradas, fig. 30 y el otro al sistema hexagonal, el cual es llamado estructura hexagonal de empaquetamiento compacto, hcp. La fracción de volumen llenado por las esferas, PF = 0.74, con un numero de coordinación de 12 en ambas estructuras.

Las esferas pueden ser acomodadas en una capa de empaquetamiento compacto colocando cada esfera en contacto con otras 6, fig. 31. Esta capa será la capa basal de una estructura hcp ó el plano (111) de la estructura fcc, capa (A). La segunda capa (B) es asignada colocando cada esfera en contacto con tres esferas de la capa (A).

La 3a. Capa puede ser acomodada en dos formas: en la estructura fcc las esferas en esta capa son ubicadas sobre los huecos de la 1a. no ocupados por la 2a. capa (C); en la estructura hcp las esferas son ubicadas directamente sobre las esferas de la 1a. Capa, capa (A). De esta forma en fcc la secuencia de capa es ABCABC, mientras que en hcp es ABAB, fig. 31

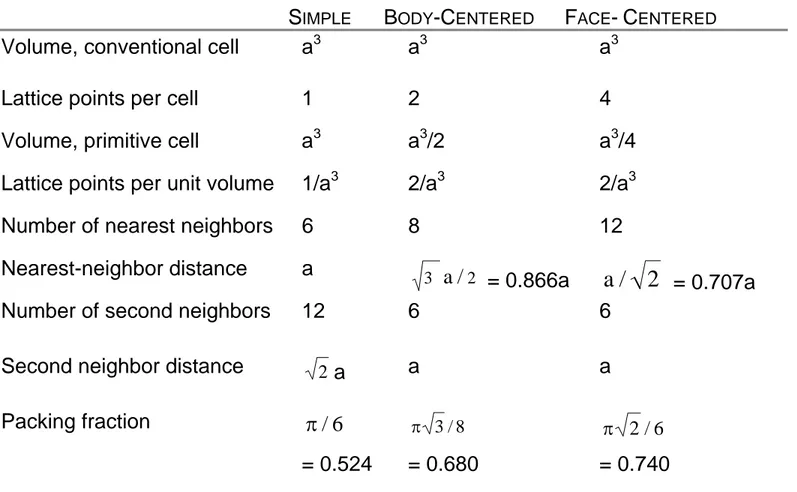
En la tabla II se dan las características de las redes cúbicas:

Tabla II Características de la red cúbica

SIMPLE BODY-CENTERED FACE-CENTERED

Volume, conventional cell a3 a3 a3

Lattice points per cell 1 2 4

Volume, primitive cell a3 a3/2 a3/4

Lattice points per unit volume 1/a3 2/a3 2/a3

Number of nearest neighbors 6 8 12

Nearest-neighbor distance a _{3 a/2}

= 0.866a

a

/

2

Number of second neighbors 12 6 6

Second neighbor distance _{2 a} a a

Packing fraction

π

_/

₆

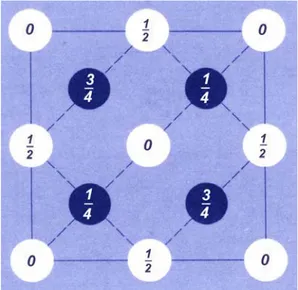
Estructura del diamante. La red espacial del diamante es la fcc con la base compuesta por dos átomos ubicados en las coordenadas (000)y el otro en (1/4 1/4 1/4) asociados con cada punto de la red, el enlace tetraedral es mostrado en la fig. 32, una proyección en un plano bidimensional se da en la fig. 33.

Cada átomo tiene 4 vecinos más cercanos y 12 de segundos vecinos.

El número total de átomos en una celda unitaria es de:

8(1/8) + 6(1/2) + 4 = 8.

La distancia entre vecinos más cercanos es:

2 3

4 r = a.

El volumen ocupado por un átomo es: ν = (4/3)πr3 =

3 8 16

3

× πa .

El factor de empaquetamiento es:

ν π π

V

a

a

= 8× × = =

3

8 16

3

3

3

16 0 34.

Fig. 32 Enlace tetragonal de la estructura del diamante.

Estructura del sulfuro de zinc. La estructura del diamante puede ser visto como dos estructuras fcc desplazadas una de otra por 1/4 de la diagonal del cubo.

La estructura del sulfuro de zinc (zincblenda) resulta cuando los átomos de zinc son colocados en una red fcc y los átomos de azufre en la otra fig. 34.

La red unitaria es una red fcc existiendo 4 moléculas por celda. Por cada átomo, hay cuatro átomos igualmente distantes de clase opuesta acomodados en un tetraedro regular.

Fig. 34 Enlace tetragonal de la estructura del Sulfuro de Zinc.

─

Í

M

,

,

conjunto de planos equidistantes paralelos que pasan a través de los puntos de la red, los cuales se les conoce como planos de la red. Para una red dada, los planos pueden ser elegidos de diferentes modos como se observa en la fig. 35 y el problema central es la designación de este conjunto infinito de planos.

La posición y orientación de un plano en general pueden ser determinadas por tres puntos en el plano, asegurando que estos puntos no sean colineales.

En cada punto cae un eje del cristal. El plano puede ser especificado por medio de la posición de los puntos a lo largo de los ejes en términos de las constantes de red. Sin embargo Miller desarrollo un proceso a partir del cual se especifica el plano por medio de índices (hkl) conocidos como índices de Miller, los cuales están relacionados con la ecuación del plano y el vector normal unitario del plano.

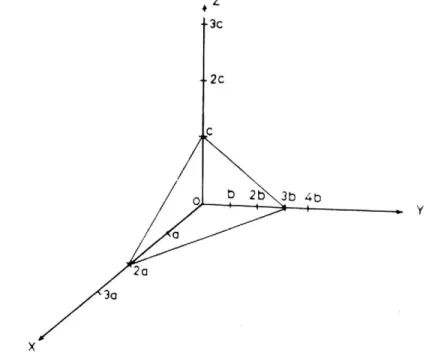
Las etapas en la designación de los índices de Miller son dados con ayuda de la fig. 36:

i) Se determinan las coordenadas de la intersección del plano a lo largo de los 3 ejes cristalográficos a b cr r r, , en función de las constantes de red, de la figura, estas intersecciones son:

x y z 2a 3b c

Fig. 36 Intersección de un plano con los ejes de coordenadas.

ii) Se expresan estas intersecciones en función de múltiplos de las constantes de red a lo largo de los ejes: 2 3 1

iii) Se determina el reciproco de estos números: 1/2 1/3 1

iv) Se reducen estos tres recíprocos al conjunto de números enteros más pequeños y se encierran en un paréntesis:

3 2 6

Índices de Miller: (326)

Los cuales son denotados en general por (hkl).

Características importantes de los índices de Miller.

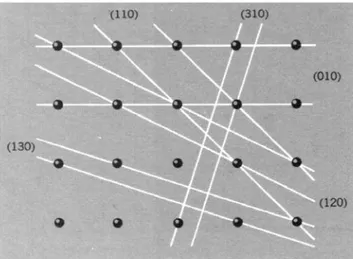
i) Los índices (hkl) pueden denotar un solo plano ó un conjunto de planos paralelos

ii) Los planos paralelos a algún eje de coordenadas tienen una intersección en el infinito y

su correspondiente índice es cero. Fig. 37 Índices de Miller de algunos planos en el

sistema cúbico.

iii) Si los índices de Miller de 2 planos tienen la misma razón (p.E. (844), (422), 211)) entonces los planos son paralelos entre sí.

iv) Si un plano corta a un eje en el lado negativo del origen, el índice correspondiente es negativo, indicándolo por un signo menos arriba del índice (

( )

Los índices de alguno de los planos, en particular en el sistema cúbico son dados en la fig. 37

a) Las caras en el sistema cúbico son denotados por los índices (100), (010), (001), ( 1 00 ), ( 0 1 0 ), y (00 1).

b) Planos equivalentes por simetría son denotados por paréntesis {hkl} por lo que las caras del cubo tendrán los índices {100}.

En la fig. 38 se indica la formación del plano (111) de una estructura fcc partiendo del plano de átomos (100).

Dirección Cristalina.- Los índices [hkl] de una dirección cristalina son el conjunto de enteros que tienen la razón de las componentes de un vector en la dirección deseada referente a los ejes, así el eje

r

a es la dirección [100] el eje −b es la dirección r [ 010r ] etc.

En un sistema cristalino con vectores ortogonales, . el sistema cúbico, la dirección [hkl] es perpendicular al plano (hkl) teniendo los mismos índices; es decir, la dirección de los planos corresponde al vector normal a la superficie del plano, pero en general en sistemas cristalinos no ortogonales esto no sucede. Las direcciones equivalentes se especifican por medio de hkl .

Fig. 38 Formación del plano (111) de una estructura fcc partiendo del plano de átomos (100).

Ecuación del plano y vector normal.- En un sistema ortogonal la ecuación de un plano (hkl) con intersecciones a/h, b/k y c/l es dado a través de la expresión de un vector normal a la superficie Nn) donde n) es el vector unitario, la ecuación del plano es dado por la expresión:

ζ

( , , )

x y z

=

Nn r

) r

⋅

Donde rr es el vector de posición, rr = xx)+yy) +zz), y ζ(x,y,z) es una constante para toda x, y, z, eligiéndose

por lo general igual a 1. Con Nn h a

k b

l c

x y z

ζ = h + + =

ax k by

l

c z 1 (8a)

Para el sistema cúbico con a = b = c:

(

)

ζ = 1 + + =1

a hx ky lz (8b)

El vector unitario normal a la superficie es dado por:

) ) ) )

n h a k b l c

h a k b l c

x y z

= ∇ζ

∇ζ =

+ +

+ +

( / ) ( / ) ( / )

( / )2 ( / )2 ( / )2 (9a)

Para el sistema cúbico: Fig.39 Distancia y ángulo entre planos

) ) ) )

n h k l

h k l

x y z

= + +

+ +

2 2 2 (9b)

Distancia y ángulo entre planos.- La distancia ó separación entre planos (hkl) adyacentes se puede calcular, teniendo cualquier punto reticular de un plano como origen, encontrando la distancia perpendicular existente entre este origen y el plano (hkl), cuyas intersecciones con cada eje son a/h, b/k y c/l. En referencia a la fig. 39 donde α, β y γ son los ángulos que hace el vector normal con cada uno de los ejes:

h/

a

d

c o s

=

α _, cos

/

β = d

acosα = ⋅n a) r etc

d n a

h

n b k

n c l

= ) r⋅ = ) r⋅ = ) r⋅ (10)

Haciendo uso de la expresión para el vector normal unitario ec. (9a).

d

h a k b l c

=

+ +

1

2 2 2

( / ) ( / ) ( / ) (11a)

Para el sistema cúbico: d a

h k l

=

+ +

2 2 2 (11b)

Para el sistema cúbico el ángulo entre direcciones (planos) [h1k1l1] y [h2k2l2] es dado por: cosθ =n) )1⋅n2 donde n)₁ y n)₂ son los vectores normales unitarios característicos de cada plano, dados por la ec. (9b) obteniéndose:

cos

( )( )

θ = + +

+ + + +

h h k k l l

h k l h k l

1 2 1 2 1 2

1 2

1 2

1 2

2 2

2 2

2

─

D

X;

L

B

,

,

E

,

C

V

L

,

.

El estudio de la estructura cristalina se lleva a cabo a través de la difracción de fotones, neutrones y electrones. La difracción depende de la estructura cristalina y de la longitud de onda. En el rango visible de longitud de onda (500 nm) la superposición de ondas dispersadas elásticamente por los átomos individuales de un cristal da lugar a la refracción óptica. Cuando la longitud de onda de la radiación es comparable ó mas pequeña con la constante de red, se puede obtener haces difractados en direcciones muy diferentes a la dirección incidente.

La energía de un fotón de rayos X esta relacionada con su longitud de onda por: E = hν = hc/λ. El estudio de cristales requiere energías del fotón en el rango de 10 a 50 KeV. Los rayos X son generados por la desaceleración de electrones en blancos metálicos y por la excitación de la nube de electrones de los átomos del blanco. El primer proceso da lugar a un amplio espectro continuo; y el segundo a líneas bien definidas. Al ser bombardeado un blanco de cobre por electrones, da lugar a una línea intensa CuKα a 1.5418 Å.

En 1912 von Laue predijo que los átomos de un cristal producirían la difracción de un haz cuyas direcciones e intensidades dependerían de la estructura cristalina y la composición química. Estas predicciones se verificaron poco tiempo después por Friederich y Knipping. La ubicación de los máximos de difracción fue explicada por W. L. Bragg.

Los haces difractados solo se encuentran cuando la reflexión de los planos paralelos interfieren en forma constructiva., fig. 40, es decir con diferencias de fase de 2πn.

Considerando planos paralelos con separación d, la diferencia de trayectoria para reflexiones sucesivas de planos adyacentes es 2dsenθ, donde

θ es el ángulo de incidencia medido a partir del plano. La interferencia constructiva se presenta cuando esta diferencia de trayectoria es igual a un número entero n de longitudes de onda λ:

nλ = 2dsenθ (13) Fig. 40 Condición de difracción, ley de Bragg

La cual es conocida como la ley de Bragg. Esta ley es una consecuencia de la periodicidad de la red. La ley no da referencia respecto al arreglo de átomos en la base asociada con cada punto de la red. La composición de la base determina la intensidad relativa de las diferentes difracciones de orden n de un conjunto dado de planos paralelos. La reflexión de Bragg puede ocurrir únicamente para longitudes de onda

λ ≤ 2d, esta es la razón por la que no es posible utilizar luz visible.

Red recíproca.- Si a b cr r r, , son los vectores primitivos de translación de una red cristalina A B Cr r r, , son los vectores primitivos de la red recíproca, los cuales se pueden definir mediante:

π =

⋅a 2

Ar r Br ⋅br = 2π Cr ⋅cr =2π (14)

Por lo que Ar es perpendicular a br,cr y paralelo al producto: br×cr, pudiéndose definir A de la forma: r ) c b ( R

Ar = r×r donde R es un escalar, el cual debe cumplir con la ec. (14), es decir:

π = ⋅ =

⋅a R(bxc) a 2

Ar r r r r

Con lo que:

) c b ( a 2

R _{r r r}

× ⋅

π =

De tal forma que:

r r r

r r r

A b c

a b c

= ×

⋅ ×

2π

( ) (15a)

De igual manera:

v r r

v r r

B c a

a b c

= ×

⋅ ×

2π

( ) a (b c)

b a 2

C _{r r r}

r r r × ⋅ × π

= _(15b)

Cualquier vector Gr de la forma:

r r r r

G=hA +kB+lC (16)

Cada estructura cristalina tiene asociada 2 redes; la red cristalina y la red recíproca.

Un patrón de difracción de un cristal es un mapa de puntos de la red recíproca. Los vectores en la red cristalina tienen dimensiones de longitud y en la red recíproca tienen dimensiones de (longitud)-1.

Red recíproca de la red cúbica.- La celda primitiva de la red cúbica centrada en las caras tiene sus vectores primitivos dados en la fig. 27b, donde a es la constante de la red cúbica, los vectores primitivos de la red recíproca son dados por:

)

zˆ

yˆ

xˆ

(

a

2

)

zˆ

xˆ

(

)

zˆ

yˆ

(

)

yˆ

xˆ

)(

8

/

a

(

)

zˆ

xˆ

(

)

zˆ

yˆ

)(

4

/

a

(

2

)

c

b

(

a

c

b

2

A

−

+

π

=

=

+

×

+

⋅

+

+

×

+

π

=

×

⋅

×

π

=

_r

_r

_r

r

r

r

Br = π − + +

) zˆ yˆ xˆ ( a 2

Cr = π − + ₍₁₇₎

Fig. 27b Celda primitiva de la red cúbica centrada en las caras.

Fig. 41 Red reciproca de la red cúbica centrada en las caras, correspondiente, a una red cúbica centrada en el cuerpo con separación reticular de 2(2

π

De forma análoga se puede demostrar que la red recíproca de la estructura cúbica centrada en el cuerpo, fig. 27a, es una red cúbica centrada en las caras con dimensión reticular de 2(2π/a), fig.42.

Esfera de Ewald y condiciones de difracción.- Una de las propiedades de la red recíproca es que un vector Gr =h A'r +k B'r +l C'r desde el origen, ubicado en algún punto reticular, a cualquier otro, es normal al plano (hkl), donde h’, k’ y l’ son un múltiplo entero de h, k y l; h’/h = k’/k = l’/l = n. Consideremos el plano (hkl)

de la fig. 43, en el cual cae el vector AC a h

c l

= − +r r al igual que el vector k

b

h a

B A r r

− + = , 0 ) l 'l h ' h ( 2 ) l c h a ( ) C 'l B ' k A ' h ( ) AC (

G⋅ = + + ⋅ − + = + π − + =

r r r r r r

Con Ar ⋅ar =Cr ⋅cr = 2π y h’/h = k’/k = l’/l = n

De igual modo rG ⋅︵B A ︶= 0

Por lo tanto Gr es perpendicular a los dos vectores linealmente independientes AC y BA, que se encuentran en el plano (hkl), por lo que Gr debe ser perpendicular al plano mismo. De esta forma un vector unitario normal al plano puede ser definido por: $ n G G = r (18)

Fig. 43 Plano (hkl)

d a n h

a G h G

a h A k B l C h G

h

h G n G

= r⋅ = r r⋅ = r⋅ + + = =

r r r

$ ( ' ' ' ) '

2π 1 2π 1

Por lo que:

d n 2

G = π (19)

El conjunto de vectores de la red recíproca Gr determinan las posibles reflexiones de rayos X. La condición de refracción de Bragg se puede expresar como una relación entre vectores de propagación de onda y vectores de la red recíproca.

Dibujando el vector de propagación kr = 2πk

λ $

de la onda incidente de rayos X dentro de la red recíproca, trazado en la dirección del haz incidente y terminando en el origen, punto reticular, con el origen de kr , no necesariamente ubicado en un punto reticular, se construye una esfera de radio

kr = 2π/λ, alrededor del punto A, fig. 44.

Consideremos que este esfera intercepta el punto (h’k’l’) de la red reciproca en B, por lo tanto el vector de propagación del haz difractado k'r cae en este punto. Un vector Gr de la red recíproca conecta el origen con el punto (h’k’l’) y es, por lo tanto, normal al plano (hkl) de la red cristalina.

Si el haz incidente

e

y la fase del haz refractado por los planos de la red es k rr r'⋅ , la diferencia de fase es dada por

φ_r =( 'k kr r r− ⋅) r (20)

El cambio en el vector de onda por efecto de la dispersión es Δkr r r= −k k' , o bien kr'= Δkr r+k. En una dispersión elástica la energía del fotón hν se conserva, así que la frecuencia ω’ = ck’ del haz refractado se conserva y es igual a la frecuencia del haz incidente y por lo tanto las magnitudes de kr y k'r son iguales. Cuando se cumple la condición de difracción, el vector Δkr es un vector de la red reciproca y por o tanto

Δkr =Gr , fig. 44. De esta forma kr'=Gr +kr

(kr +Gr) (⋅ +kr Gr) = ⋅ = ⋅k kr r' ' k kr r

r r

k+G2 =k2

O bien:

r r r r r r

k k⋅ + 2k G⋅ + ⋅ =G G k2

y la condición de difracción en forma vectorial es dada por:

2k Gr r⋅ + G2 = 0 (21)

Si Gr es un vector de la red reciproca -Gr lo es también por lo que la ec. 21 puede ser escrita como:

2k Gr r⋅ = G2

2k Gr r⋅ = 2k G senθ = G2, con la ecuación 19:

2ksenθ = G ó bien: 22π 2

λ θ

π

sen = n

d dando la condición de Bragg ec. (13): 2dsenθ = nλ. De acuerdo con esta construcción geométrica, esfera de Ewald, es evidente que la condición de Bragg se satisfacerá para una longitud de onda (constante de propagación k) dada por cada intersección de la superficie de la esfera de radio 2π/λ, trazada alrededor de A, con un punto de la red recíproca. El ángulo apropiado de Bragg, θ, estará dado por el ángulo comprendido entre el vector kr y un plano normal a Gr.

Cuando la condición de Bragg se satisface kv y k'r constituyen un triángulo isósceles con el vector Gr de la red recíproca.

Condiciones de Laue. La condición Δkr =Gr puede expresarse de otra forma para dar las ecuaciones de Laue. Tomando el producto escalar, de ambos lados sucesivamente con a b cr r r, , de la red cristalina se obtienen las tres condiciones de Laue sobre el vector de dispersión:

r r

a⋅Δk = 2πh br⋅Δkr = 2πk cr⋅Δkr = 2πl (22)

Estas ecuaciones tienen un interpretación geométrica. La primera expresión dice que Δkr cae en un cierto cono en la dirección de ar . Así para cada una de las ecuaciones. En tres dimensiones Δkr en una reflexión debe satisfacer las tres ecuaciones y por lo tanto los tres conos se interceptan para formar un haz común.

reflexión (h’k’l’) se representa la relación de la amplitud de radiación que dispersa toda la celda unitaria en función a la que dispersa un electrón de un punto en el origen por medio de:

(

)

_∑

F ₍₂₃₎

Donde fj es el factor de dispersión atómico para el j-esimo átomo de la celda unitaria y φj es la diferencia de fase relacionada con el j-esimo átomo. La suma se obtiene tomando en cuenta todos los átomos de la celda unitaria. Haciendo uso de la ec. 20 esta se puede expresar como:

(

)

_∑

(

)

j

j jexp i k r

f ' l ' k ' h

F r r

Donde rrj es el vector desde el origen hasta el j-esimo átomo de la celda unitaria y se puede escribir como: c z b y a x r j j j

j r r v

r _{= + +}

Por lo que rr_j ⋅Δkr = x_jar⋅Δkr +y_jbr⋅Δkr +z_jcr⋅Δkr y por medio de la ec. 22 se tiene:

(

)

_∑

[

(

)

]

j

j j

j

j exp2 i h'x k'y l'z

f ' l ' k ' h

F ₍₂₄₎

Cuando todos los átomos son idénticos se simplifica la expresión, con fj=f: se tiene ︶

(

)

_∑

[

(

)

]

j j

j k'y l'z

x ' h i 2 exp ' l ' k ' h

S ₍₂₅₎

La amplitud total dispersada esta dada por el producto del factor de dispersión atómica y el factor S, el cual depende de la disposición geométrica de los átomos dentro de la celda unitaria y se conoce como factor geométrico estructural.

La intensidad del haz difractado es proporcional al cuadrado de la magnitud de F, o bien por: F*F, donde F* es el complejo conjugado de F. Con F = α + iβ,

2

2

*

2 _{F F}

F

β + α =

= (26)

Estructura cúbica centrada en el cuerpo.- En esta estructura se tienen dos átomos dentro de la celda unitaria: un átomo del vértice con coordenadas (000) y otro en el centro del cuerpo con coordenadas (1 )

2 1 2

1 2 . Para esta estructura la amplitud de difracción para la dirección de difracción (h’k’l’) es:

[

]

e

1

f

´)

l

´

k

´

h

(

F

=

+

En general la asignación de los átomos que pertenecen a la celda unitaria puede hacerse en cualquier forma arbitraria, siempre que se le asigne a ésta el número correcto de átomos de cada ubicación (vértice, cara ó cuerpo).

Esto se puede comprender físicamente para el caso de la reflexión (100). Para una estructura cúbica simple los haces reflejados de las caras superior e inferior difieren 2π en fase para la dirección de difracción (100).

Mientras que en la estructura cúbica centrada en el cuerpo existe otro plano de átomos (centros de cuerpo), ubicados paralelamente y a la mitad entre los planos de las caras superior e inferior del cubo, fig. 45. La densidad de átomos en este plano intermedio es la misma que la de los planos superior e inferior, y por lo tanto dan origen a haces difractados con la misma intensidad que los producidos por los planos superior e inferior, pero están fuera de fase con estos haces por π.

Los haces difractados, desde el plano superior y el del centro del cuerpo, interfieren en forma destructiva en pares, no produciéndose un haz difractado neto.

Fig. 45 Difracción en planos paralelos (100) y (200)

No obstante, la reflexión (200) se presenta debido a que, en este caso, los planos superior e inferior dan origen a haces que están 4π fuera de fase. Los planos del centro de cuerpo contribuyen con haces que difieren 2π en fase de las reflexiones obtenidas de los planos superior e inferior, presentándose interferencia constructiva y por lo tanto reforzándose. Las otras reflexiones ausentes para la estructura cúbica centrada en el cuerpo (h’+k’+l’ = numero impar) se pueden explicar físicamente en forma análoga.

CELDA PRIMITIVA DE WIGNER-SAITZ.- Otra forma de elegir una celda primitiva de igual volumen es bajo el

siguiente procedimiento:

ii) En el punto medio de estas líneas y perpendicular a ellas, se dibujan nuevas líneas o planos. El volumen más pequeño encerrado de este

modo se le conoce como la celda primitiva de Wigner-Saitz, fig. 46. Todo el espacio puede ser ocupado por estas celdas bajo operaciones de translación, como en el caso de celdas primitivas.

PRIMERA ZONA DE BRILLOUIN.- Una Zona de Brillouin

se define como una celda Wigner-Saitz en la red recíproca.

El conjunto de planos que bisectan perpendicularmente a los vectores de la red recíproca conforman las fronteras de una zona de Brillouin y son de particular importancia en la teoría de propagación de ondas en cristales, porque da una interpretación geométrica de la condición de

difracción 2 k.G = G2 o bien:

2 2 1 2

1

) G ( )

( =

⋅ G

kr r (28)

Se construye un plano normal al vector G en el punto medio, una onda con un vector de propagación k trazado del origen a cualquier punto del plano satisface la condición de difracción. fig. 47.

Un haz de Rayos X incidente en el cristal será difractado si sus vectores de onda tienen la

magnitud y dirección requeridos en la ec. 28, y el haz difractado será en la dirección del vector k - G.

Fig. 47 Interpretación geométrica de la condición de difracción.

Estos planos dividen el espacio de Fourier (espacio recíproco) del cristal en regiones o celdas, fig. 48. La región central, cuadro central de la figura, es una celda primitiva de Wigner Saits de la red recíproca., denominada la primera zona de Brillouin.

La primera zona de Brillouin es el volumen más pequeño completamente encerrado por los planos que bisectan perpendicularmente a los vectores de la red recíproca.

La fig. 49 muestra la construcción de la primera zona de Brillouin en una red bidimensional. En una red lineal, unidimensional, la primera zona de Brillouin se extiende de -π/a a +π/a, siendo estos las fronteras de zona.

En la fig. 50 y fig. 51 se dan la primera zona de Brillouin de la red cúbica de caras centradas y de la red cúbica de cuerpo centrado respectivamente.

Fig. 48 Planos que dividen una red reciproca cuadrada bidimensional en regiones o celdas.

Fig. 50 Red reciproca y primera zona de Brillouin de la red cúbica centrada en las caras, correspondiente, esta última, a una red cúbica centrada en el cuerpo con separación reticular de 2(2

π

─

M

E

La ley de Bragg requiere de ciertos valores de θ y λ. Rayos X monocromáticos de longitud de onda

λ incidiendo sobre un cristal tridimensional en un ángulo arbitrario en general no se refleja.

Para que se satisfaga la ley de Bragg es necesario barrer ya sea en longitud de onda o en ángulo de incidencia.

Los métodos estándar de difracción usados en el análisis de la estructura cristalina se han diseñado expresamente para llevar acabo la variación del ángulo de incidencia o de la longitud de onda del haz incidente de rayos X .

Aquí se verán brevemente tres métodos: Método de Laue

Método de cristal en rotación Método de Polvos.

MÉTODO DE LAUE.- En el método de Laue, fig. 52, un

cristal se encuentra fijo dentro de un haz de rayos X de un espectro amplio de longitudes de onda, fig. 55b. El cristal selecciona y difracta los valores discretos de λ cuyos planos existentes espaciados una distancia d y ángulo de incidencia θ satisfacen

La fuente de rayos X es tal que produce un haz con un amplio rango de longitudes de onda, p. E de 0.2 Å a 2 Å.

Antes de incidir el haz es colimado, Las dimensiones de la muestra cristalina puede ser tan pequeña como de 1mm.

Una película fotográfica plana recibe los haces difractados. El patrón de difracción consiste de una serie de manchas de puntos, fig. 53.

El patrón muestra la simetría del cristal: si un cristal tiene un eje de simetría de orden cuatro paralelo al haz, el patrón de Laue mostrara la misma simetría de orden 4.

El método de Laue es utilizado ampliamente para orientar cristales.

MÉTODO DE CRISTAL EN ROTACION.- En este método,

fig. 54, un monocristal se mantiene en rotación alrededor de un eje fijo, al incidir un haz de rayo X monocromático, fig. 55a.

Fig. 53 Patrón fotográfico de difracción de rayos x en el método de Laue

La variación del ángulo de incidencia θ al ser girado el cristal, da lugar a que diferentes planos atómicos cumplan con la ley de Bragg.

La película fotográfica es montada en un cilindro, concéntrico con el eje de giro del cristal.

Fig. 54 Cámara de difracción en el método del cristal en rotación

Fig. 56 Difractor de doble cristal.

Fig. 55 a) Espectros de emisión de rayos X monocromático y b) continuo.

El haz de R-X monocromático es difractado de un dado plano cristalino cuando, durante el giro, el valor del ángulo de incidencia θ satisface la ecuación de Bragg.

Normalmente el cristal se gira en un rango angular limitado en lugar de girar los 360o, con el fin de reducir la posibilidad de un traslapamiento de reflexiones.

MÉTODO DE POLVOS.- En el método de polvos, fig. 57, un haz de rayos X monocromático incide sobre una

muestra cristalina finamente pulverizada, o bien sobre una muestra policristalina de grano pequeño, la cual es contenida en un tubo capilar.

Fig. 57 Cámara de difracción para el método de polvos

Este método es adecuado ya que no se requieren monocristales. Los haces difractados provienen de los cristalitos individuales que están orientados adecuadamente, cuyos planos hacen un ángulo de incidencia θ con el haz, que satisface la ecuación de Bragg.

Los haces difractados por la muestra generan conos concéntricos con el haz incidente.

Los conos interceptan a la película fotográfica en una serie de anillos concéntricos, fig. 58.

En la actualidad los difractómetros cuentan con contadores en la detección de la radiación difractada, lo cual permite obtener espectros de difracción como el mostrado en la fig. 59.

Fig. 58 Patrón fotográfico de difracción de rayos x en el método de polvos.