CAOS DETERMINISTA Y SU APLICACION EN LAS TELECOMUNICACIONES

(1)

CAOS DETERMINISTA Y SU APLICACIÓN EN LAS

TELECOMUNICACIONES

T E S I S

P R O Y E C T O D E

I N V E S T I G A C I Ó N

SIP 20091457

Q U E P A R A O B T E N E R E L T Í T U L O D E : INGENIERO EN COMUNICACIONES Y ELECTRÓNICA

P R E S E N T A

RONQUILLO ARVIZU REY DAVID

ASESOR:

DR. ALEJANDRO VIVAS HERNÁNDEZ

FECHA: MÉXICO D.F. 22 DE JUNIO DEL 2010

ESCUELA SUPERIOR DE INGENIERÍA

(2)

PROYECTO DE INVESTIGACIÓN SIP 20091457 2/80

Índice Pág.

i. Relación de figuras_………... 3

ii. _{Glosa io………..} 5

iii. Resu e ……… 6

iv. _{I t odu ió ………} 7

v. _{Justifi a ió ……….} 7

vi. Objetivo general………... 7

Capítulo 1 Antecedentes de caos………. 8

1.1 _{De He i Po ai é a Lo e z……….….} 9

1.2 _{Fe ó e os aóti os……….} 10

Capítulo 2 La ruta del caos en aplicacio es o li eales……… 15

2.1 Pa á et os de la apli a ió logísti a……….. 16

2.2 Pu tos fijos at a to es epulso es……… 19

2.3 Duplicidad de período……….. 23

2.4 Co po ta ie to o plejo, i egula o aóti o……….. 27

2.5 Sensibilidad a las condiciones iniciales _{efe to a iposa …} 28 2.6 Diferencia entre _{o po ta ie to aóti o uido………} 31

2.7 Diag a a de ifu a ió ……… 32

Capítulo 3 Caos e siste as t idi e sio ales………. 36

3.1 _{“iste as e dos di e sio es………} 37

3.2 “iste as e t es di e sio es……… 41

3.3 A álisis e el tie po………. 44

3.4 3.4 Secciones de _{Po ai é………} 45

Capítulo 4 Aplicación del caos en las _{tele o u i a io es……….} 49

4.1 Ci uito de Chua………. 50

4.2 “i o iza ió ……….. 56

4.3 Co e tido es de I peda ia……….. 59

4.4 Ventajas y desventajas del uso de los sistemas caóticos en las t_{ele o u i a io es ……….} 63

4.5 Encriptado y desencriptado de una señal por medio del circuito de Chua……….... 64

Conclusiones _………. 71

Aportaciones ………. 72

Referencias _………. 73

Apéndice A. Ci uitos o o po ta ie to aóti o……… 74

(3)

i. Relación de Figuras

Capítulo 1

Figura 1 Una piedra lanzada hacia arriba……… 10

Figura 1.1 Cuando dos cuerpos caen a partir del reposo _……… 11

Figu a . Dos pied as ue ae desde pu tos disti tos de u a o taña………. 12

Figura 1.3 Ilustración de pequeñas variaciones en las posiciones iniciales……… 13

Capítulo 2 Figura 2.1 Máximo valor de ……… 17

Figura 2.2 Solución gráfica de ……….. 19

Figura 2. 3 Valores negativos para 0<r<1……… 19

Figura 2.4 Atractor hacia para r=0.9 ………. 20

Figura 2. 5 Atractor hacia para r=0.9 ……….. 21

Figura 2.6 Atractor para r=1.8……….. 22

Figura 2. 7 r= 2.8 y x=0.09………. 22

Figura 2.8 r= 3.1 x=0.09 Punto fijo repulsor ………. 23

Figura 2.9 r= 3.2 x=0.09 a: Primera iteración, b:y=x,c: Órbitas de período dos……… 25

Figura 2.10 r= 3. x=0.09 Las órbitas oscilan entre 0.5 y 0.76………. 25

Figura 2.11 r= 3.4 x=0.80 ………..………. 26

Figura 2.12 r= 3.4 x=0.80 Función periódica de período cuatro………. 26

Figura 2.13 r= 3.6 x=0.80 a: Primera iteración, b:y=x , c: Órbitas de período cuatro……… 27

Figura 2.14 r= 3.8 x=0.80 Tercera iteración órbitas de período o ho………. 27

Figura 2.15 r= 3.9 x=0.80 Cuarta iteración treinta y dos puntos fijos……… 28

Figura 2.16 r= 3.8 x=0.80 a: Primera iteración, b: y=x ,c: Órbitas de período ocho……… 29

Figura 2.17 Comparación de 2.15 y 2.16 (efecto mariposa)……… 29

Figura 2.18 Comportamiento caótico de la función logística r= 3.8 con condición inicial x=8………. 30

Figura 2.19 Comportamiento caótico de la función logística r= 3.8 Con condición inicial x=0.80000000001……… 30

Figura 2.20 Co pa a ió de la figu a . . ……….. 31

Figura 2.21 Tercera interacción con r=3.8, a:y=x b: Primera iteración, c: Segunda……… 32

Figura 2.22 Diagrama de bifurcación de la ecuación logística_………. 32

Figura 2.23 a: Primera bifurcación ,b: Segunda bifurcación, c: Tercera bifurcación, d: Región caótica………... 33

Figura 2.24 Destino de las órbitas en un solo punto fijo_………. 33

Figura 2.25 r=3.2 y x=0.8 orbita de período 2……… 34

Figura 2.26 Orbita de período 4 r=3.6 x=0.8 (segunda iteración)……… 34

Figura 2.27 Tercera interacción r=3.8 a:y=x ,b: Primera iteración, c: Segunda iteración, d: Tercera iteración, e: Cuarta iteración, f: No se distingue el período de las órbitas……….. 35

(4)

Capítulo 3

Figura 3.1 Gráficas de soluciones superpuestas sobre el campo de pendientes_………... 38

Figura 3.2 Vecto ……….. 39

Figuran 3.3 Campo vectorial y curva solución del sistema_………. 40

Figuran 3.4 Curvas solución del sistema depredador presa_………. 40

Figura 3.5 Gráfica de ecuaciones de Lorenz en espacio tridimensional………. 42

Figura 3.6 Gráfica de ecuaciones de Lo e z ...……… 43

Figura 3.7 Gráfica de ecuaciones de Lorenz _……….. 43

Figura 3.8 Respuesta del sistema en el tiempo_……… 44

Figura 3.9 Gráfica del atractor de Rössler……….. 46

Figura 3.10 Bifurcaciones sucesivas para el modelo de Rössler con diferentes valores del parámetro ……….. 46

Figura 3.11 Sección de Poncairé sobre el atractor de Rössler_……….. 47

Figura 3.12 Superficie S normal a las líneas de flujo_……….. 47

Figura 3.13 Diagrama de bifurcación para el atractor de Rössler………. 48

Capítulo 4 4.2 Diodo de Chua con oscilador _……….. 50

Figura 4.2 Circuito que permite obtener la curva de transferencia……….. 51

Figura 4.3 Circuito equivalente al diodo de Chua ………. 52

Figura 4.4 Orientación de corrientes en el circuito de Chua _……….. 53

Figura 4.5 Esquema de sincronización _……….. 59

Figura 4.6 Convertidor Generalizado de i peda ia……….……… 60

Figura 4.7 Circuito de Chua con dos amplificadores operacionales……….. 64

Figura 4.8 Señal proveniente del circuito de Chua_………. 65

Figura 4.9 Señal proveniente del circuito de Chua………. 65

Figura 4.10 Atractor de Chua……….. 66

Figura 4.11 Diagrama de bloques para la transmisión_……….. 66

Figura 4.12 Señal s(t) de 4 volts de amplitud y 1kHz de frecuencia_……….. 67

Figura 4.13 Señal caotica y señal senoidal ……….. 67

Figura 4.14 Señal encriptada r(t)………. 68

Figura 4.15 Diagrama de bloques para el receptor_……….. 68

Figura 4.16 Circuito completo del diagrama de bloques de transmisor y receptor_……. 69

Figura 4.17 Señal e saje s t o t a señal dese iptada s’ t ………. 70

Figura 4.18 Sincronización en fase_……….. 70

(5)

ii. Glosario.

Aplicaciones iteradas Las aplicaciones iteradas son, probablemente el ejemplo más

simple de un sistema dinámico no lineal.

Atractor Se llama atractor a un conjunto de órbitas, que son atraídas

hacia uno o varios puntos fijos.

Bifurcación En gráficas que representan funciones reiteradas (es decir la

función se aplica otra vez al resultado) a menudo se observan resultados imprevisibles que presentan una increíble sensibilidad a los parámetros iniciales que se utilizan para el estudio del comportamiento caótico de esas funciones no lineales a menudo se utilizan unos diagramas de bifurcación que representan el cambio del resultado según el cambio del parámetro inicial.

Caos determinista Comportamiento aperiódico que se puede reconstruir

conociendo las condiciones iniciales.

Iteración Se construyen eligiendo un número cualquiera como dato de

entrada de una función, utilizando el resultado como nuevo dato de entrada de la misma función, y repitiendo el proceso sucesivamente.

Punto de bifurcación Valor de un parámetro que tiene como consecuencia la

aparición de dos nuevos puntos fijos.

Sistema autónomo En matemáticas, es conocido también como ecuaciones

diferenciales autónomas, es un sistema de ecuaciones diferenciales ordinarias las cuales no dependen de la variable independiente. En circuitos un sistema autónomo es aquél que no necesita de una fuente externa para ser alimentado.

Sistema dinámico Un sistema dinámico es un sistema complejo que presenta un

cambio o evolución de su estado en un tiempo, el comportamiento en dicho estado se puede caracterizar determinando los límites del sistema, los elementos y sus relaciones; de esta forma se pueden elaborar modelos que

buscan representar la estructura del mismo sistema.

Sistema no lineal En matemáticas, los sistemas no lineales representan sistemas

cuyo comportamiento no es expresable como la suma de los comportamientos de sus descriptores. Más formalmente, un sistema físico, matemático o de otro tipo es no lineal cuando las ecuaciones de movimiento, evolución o comportamiento que regulan su comportamiento son no lineales. En particular, el comportamiento de sistemas no lineales no está sujeto al

principio de superposición, como lo es un sistema lineal.

Teoría del caos La rama de los sistemas dinámicos que trabaja con la definición,

(6)

iii. Resumen

El comportamiento irregular o caótico extremadamente sensible a las condiciones iniciales que presentan sistemas no lineales se aplica en las comunicaciones después del artículo publicado por Pecora y Caroll [1], donde se demostró la característica de sincronización. Leon Chua a quien se le considera el padre de los circuitos caóticos construyó un circuito conocido como el circuito de Chua y es uno de los más usados en el encriptado de señales usando una portadora caótica.

iv. Introducción

En el capítulo uno hacemos una recopilación de los primeros matemáticos que dieron pie a lo que es la teoría del caos y damos ejemplos muy sencillos para explicar los tipos de fenómenos caóticos y la dependencia a condiciones iniciales.

En el capítulo dos estudiamos una aplicación lineal en particular, la llamada ecuación logística y explicamos los siguientes términos.

 Atractor

 Repulsor

 Duplicación de período.

 Comportamiento complejo, irregular o caótico

 Sensibilidad a las condiciones iniciales(efecto mariposa)

También definimos los parámetros de la ecuación logística y explicamos la transición de un movimiento regular, periódico a un movimiento complejo irregular o caótico y para finalizar explicamos el diagrama de bifurcación.

En el capítulo tres damos ejemplos de caos en sistemas de dos y tres dimensiones y analizamos algunas características de las ecuaciones diferenciales autónomas además de aplicar las secciones de Poncairé.

En el capítulo cuatro aplicamos el llamado caos determinista en las telecomunicaciones usando una señal caótica proveniente del circuito de Chua y exponemos las ventajas y desventajas de usar encriptamiento caótico en las telecomunicaciones.

(7)

v. Justificación

El campo de la investigación en seguridad en las telecomunicaciones requiere de explorar nuevas teorías, como la teoría del caos, entre otras, para mejorar los procesos de aseguramiento de las comunicaciones y por lo tanto de la información.

Las observaciones realizadas por Pecora y Carrol [1] sobre la sincronización de dos sistemas caóticos, ha generado gran interés en torno a la transmisión segura de información utilizando señales caóticas de banda ancha, sin embargo estos temas se han estado estudiando a nivel maestría o doctorado, la presente tesis pretende sentar las bases para el estudio del caos determinista aplicado a las telecomunicaciones a nivel licenciatura y describir de una manera clara la transición de un movimiento regular periódico a un movimiento complejo o caótico y su aplicación en el encriptamiento de señales usadas en las telecomunicaciones, además de servir como base a nuevos temas de tesis que involucren las más nuevas tecnologías en el encriptamiento usando caos como es el caso del proyecto OCCULT( Optical Chaos Communications Using Laser-diodes Transmitters) [2] o encriptamiento de imágenes usando la ecuación logística[3].

vi. Objetivo general

(8)

CAPÍTULO l

ANTECEDENTES DEL CAOS

[HENRI PONCAIRÉ]

(9)

PROYECTO DE INVESTIGACIÓN SIP 20091457

9/80

1.1 De Henri Poincaré a Lorenz

A finales del siglo XlX Henri Poncairé estudió el problema de la estabilidad del sistema solar, se dio cuenta de que sistemas dinámicos deterministas aparentemente simples podrían presentar un comportamiento dinámico extremadamente complicado por lo que se le considera el precursor de la teoría del caos. El matemático que retomó los estudios

dePoncairé fue el matemático americano George David Birkhoff (1884-1944), quien a su

vez fue profesor en la Universidad de Harvard de Edward Lorenz quien redescubriría la dependencia sensible a las condiciones iniciales.

En 1960, el matemático Edward Lorenz usaba su computadora Royal McBee para desentrañar la maraña matemática que él mismo había creado con sus doce ecuaciones para predecir el tiempo atmosférico en el Massachusetts Institute of Technology. Su pasión por el pronóstico atmosférico le vino durante la 2ª Guerra Mundial. Tras su graduación en Matemática Pura en el Dartmouth College. En 1938 participó en la contienda diagnosticando el tiempo para las fuerzas aéreas. Transcurrida la guerra, optó por dedicar sus esfuerzos matemáticos aplicándolos a la meteorología.

La predicción del tiempo se debía regir por ecuaciones, al igual que las de los planetas, satélites y galaxias, quizá más complicadas pero ecuaciones al fin y al cabo. Para ello escogió 12 funciones, unas establecían el vínculo entre velocidad y viento, otras entre presión y temperatura y así unas cuantas variables más.

Hojeando los rollos y rollos de papel con datos numéricos que salían de su impresora, Lorenz ideó un método para que la computadora señalara cada minuto el paso de un día imprimiendo una hilera de números. En 1961, Lorenz cansado de observar ese vaivén numérico de la impresora intentó ahorrar tiempo partiendo de una sucesión anterior pero al traspasar los dígitos sólo tecleó 3 en vez de los 6 originales, esperando que el comportamiento no cambiara. Los resultados obtenidos trajeron de cabeza a Lorenz pues no eran los esperados y revisó el software y hardware hasta darse cuenta finalmente, que el error lo cometió al truncar el valor inicial de la función cambiando de 0.506127 a 0.506.

(10)

10/80

1.2 Fenómenos Caóticos

Consideremos un fenómeno físico muy simple, la caída de los cuerpos. Una piedra cae al soltarla debido a que experimenta una fuerza, la de gravedad, que está dirigida hacia el centro de la Tierra. Con base en las leyes de Newton se pueden encontrar que la trayectoria que sigue la piedra es una línea recta vertical. Sin embargo, la misma piedra sujeta a la misma fuerza (su peso) también puede moverse a lo largo de otra trayectoria. Por ejemplo, si la lanzamos bajo un ángulo con la horizontal, entonces se moverá a lo largo de la trayectoria que resulta ser una parábola (ver figura 1.1) .

Figura 1.1 Una piedra lanzada hacia arriba, describe una trayectoria parabólica.

Nos podemos hacer la siguiente pregunta: si en los dos casos la misma piedra estuvo sujeta a la misma fuerza, ¿por qué en un caso se movió a lo largo de una línea recta vertical y en el otro a lo largo de una parábola? Como podemos apreciar, a pesar de ser la misma piedra y la misma fuerza, hubo una diferencia.

• En el primer caso se soltó la piedra, lo que significa que en el instante inicial su

velocidad fue nula.

• En el segundo caso se le dio a la piedra, en el instante inicial, una velocidad dirigida

hacia arriba, (ver figura 1.1)

Por lo tanto, en los dos casos hubo condiciones iniciales diferentes y, en consecuencia, las trayectorias seguidas fueron distintas, a pesar de que en ambos casos la piedra estuvo sujeta a la misma fuerza, la gravedad.

(11)

11/80

Bajo las mismas leyes, diferentes condiciones iniciales producen distintas evoluciones en el tiempo.

[image:11.612.147.467.351.573.2]

La cuestión a la que se refirió Poincaré tiene que ver con lo siguiente. Tomemos dos piedras iguales. Soltemos la primera piedra desde cierto punto, digamos el A, sobre el suelo (ver figura 1.2a). Al mismo tiempo soltemos la segunda piedra desde el punto B, que está muy cercano al punto A. Nos damos cuenta de que, no obstante que en ambos casos las velocidades iniciales de las piedras son iguales (cero), sus posiciones iniciales no son iguales ya que las soltamos desde dos puntos distintos, aunque difieren muy poco. Decimos que las condiciones iniciales de ambas piedras no son las mismas, aunque sí muy parecidas. Veamos qué pasa con las posiciones que van ocupando las dos piedras en sus caídas. Si nos fijamos medio segundo después de haber soltado las piedras veríamos que están en las posiciones C y D, respectivamente (figura 1.2b). Nos damos cuenta de que la distancia entre los puntos C y D también es muy pequeña (de hecho es igual a la de los puntos iniciales A y B). En consecuencia, si la diferencia de condiciones iniciales es muy pequeña, entonces al transcurrir el tiempo la diferencia entre las posiciones de las dos piedras sigue siendo muy pequeña. Es decir, en este caso, las trayectorias que siguen son muy cercanas.

Figura 1.2 a) Cuando dos cuerpos caen a partir del reposo y desde posiciones muy cercanas no se separan mucho en sus trayectorias, b)la distancia entre los puntos C y D también es muy pequeña (de hecho es igual a la de los puntos

iniciales A y B)

(12)

12/80

[image:12.612.147.451.168.382.2]

posiciones de ambas piedras será muy grande: una en la cima y la otra abajo. En este caso, nuevamente las condiciones iniciales de las dos piedras son muy parecidas pero ahora sus posiciones, al transcurrir el tiempo, difieren marcadamente. Es decir, con el paso temporal en este caso no se conservan las posiciones muy cercanas unas de otras.

Figura 1.3 Dos piedras que caen desde puntos distintos de una montaña y a partir de posiciones muy cercanas, se separan mucho a lo largo de sus trayectorias.

(13)

13/80

Figura 1.4 Pequeñas variaciones en las posiciones iniciales producen grandes cambios en las trayectorias.

De los dos casos que hemos considerado podemos afirmar que hay dos tipos de situaciones:

1) Condiciones iniciales muy parecidas producen condiciones finales también muy parecidas.

2) Condiciones iniciales muy parecidas producen condiciones finales completamente diferentes.

Ahora bien, para determinar la evolución de un sistema cuando el tiempo transcurre debemos conocer las leyes que lo rigen, así como sus condiciones iniciales. Si fuera posible determinar con toda precisión estas condiciones iniciales entonces podríamos saber en cualquier instante las características que tiene el sistema. A esto se refería Laplace cuando decía que si se le daban las condiciones iniciales del Universo podría determinar el futuro. Sin embargo, en una situación real no podemos afirmar que se puedan determinar con toda precisión las condiciones iniciales. Al medir estas cantidades siempre se cometerán errores, que son inevitables, por lo tanto, lo más que se puede hacer es fijar las condiciones iniciales en forma aproximada. Estas condiciones iniciales diferirán de las verdaderas condiciones iniciales del sistema en muy poco, si los errores cometidos son pequeños. ¿Qué podemos decir acerca de la trayectoria que seguirá el sistema?, ¿Podemos predecirla?

De lo que se ha observado puede ocurrir una de dos posibilidades:

(14)

14/80

trayectorias es muy pequeña y la predicción que se haga será muy parecida a la trayectoria real.

2) Si se está en el caso en que pequeñas diferencias en las condiciones iniciales producen condiciones finales muy distintas, entonces la trayectoria real que siga el sistema se separará muy marcadamente de la trayectoria que podamos predecir. En este caso nuestra predicción está muy lejos de la realidad, por lo que no hay posibilidad de hacer predicción válida alguna, o si la hay el error sería muy grande.

(15)

LA RUTA DEL CAOS EN

APLICACIONES NO

LINEALES

(16)

Los sistemas dinámicos no lineales son modelados por ecuaciones diferenciales autónomas. En 1976 Robert May publicó un artículo sobre la ecuación diferencial no lineal la cual modela el crecimiento de poblaciones.

Este modelo de ecuación diferencial también llamado ecuación diferencial logística permite mostrar con claridad la transición de un movimiento regular o periódico a un movimiento complejo, irregular o caótico [4 ,6-8].

Para explicar los siguientes términos característicos de un sistema dinámico no lineal usamos la ecuación logística.

 Atractor.

 Repulsor.

 Duplicación de período.

 Comportamiento complejo, irregular o caótico.

 Sensibilidad a las condiciones iniciales (efecto mariposa).

 Diagrama de bifurcación.

2.1 Parámetros de la aplicación logística

La aplicación logística surge del estudio de la dinámica de poblaciones hechas por Robert May y el matemático belga Pierre Verhuls.

Esta ecuación está dada por la iteración

representa el porcentaje o fracción de población máxima viva en la generación y

toma valores de . Es decir simboliza la extinción y simboliza el nivel

máximo de población [3,4].

Para conocer el punto máximo de tomamos

=

Derivando obtenemos

e Igualando a ceroresulta Despejando a

(17)

Tomando un valor para menor que por ejemplo y sustituyendo este valor en

Tenemos para r>1

Tomando un valor para mayor que por ejemplo y sustituyendo este valor en

Tenemos para r>1

Como la función va de más a menos sabemos que se trata de un valor máximo para

[image:17.612.173.444.275.495.2]

tal como se muestra en la siguiente figura.

Figura 2.1 Máximo valor de en r=4.

Como x toma valores de entonces podemos conocer el valor máximo de

despejando de

1

Y evaluando el valor máximo de

(18)

Por lo tanto

No interesa analizar a r para valores negativos debido a que r es la tasa de crecimiento de la población.

Por lo tanto r puede tomar valores entre (0,4)

Una vez que ya se tienen definidos los parámetros de población y tasa de crecimiento procederemos a estudiar la dinámica de la ecuación logística para varios intervalos del parámetro

Empezamos solucionando la ecuación analíticamente Si tomamos una población inicial tendremos

(19)

De forma analítica podemos encontrar a los puntos fijos, como ejemplo damos un valor de

y sustituyendo en y tenemos

y

De forma geométrica también podemos encontrar los puntos fijos si graficamos

yen el mismo plano la recta , los puntos donde se interceptan las dos

funciones son las soluciones de la ecuación para , en la figura 2.1 observamos que

las soluciones geométricas son las mismas que de forma analítica [9].

Figura2.2 Solución grafica de para y

2.2 Puntos fijos atractores y repulsares

(20)

Analíticamente evaluamos en en valores de 0<r<1 tendremos valores

negativos por lo tanto para que pueda estar en el intervalo de r debe ser

mayor a uno como se muestra en la siguiente figura.

Figura 2. 3 Valores negativos para 0<r<1[7]

Analizando gráficamente para 0<r<1 con r=0.9 tenemos que las órbitas

convergen hacia el punto fijo por lo tanto tenemos un atractor en el punto fijo

[image:20.612.175.438.433.635.2]

como se muestra en la figura 2.4

(21)

Para r=0.7 (ver figura 2.5) tenemos que las órbitas convergen o son atraídas hacia

el punto fijo por lo tanto es de nuevo un atractor y puede ser llamado atractor

global en el intervalo de 0<r<1 y para cualquier valor de x de 0 a 1 [7,9]

Figura 2. 5 Atractor para r=0.7

Para 1<r<3 también tenemos un atractor global pero hacia el punto fijo (figura 2.6 y

2.7)

Analíticamente podemos calcular el valor de para algunos valores de 1<r<3

r =1.8 Y de x=0.9

=.444444

r =2.8 Y de x=0.09

(22)

[image:22.612.168.446.72.274.2]

PROYECTO DE INVESTIGACIÓN SIP 20091457 22/80 Figura 2.6 Atractor para r=1.8 x

Figura 2.7 Atractor para r= 2.8 y x=0.09

Para valores de 3<r<4 observamos que las órbitas se alejan del punto fijo si

r =3.1 Y

=0.678

[image:22.612.175.439.346.547.2]

(23)

[image:23.612.175.435.68.271.2]

PROYECTO DE INVESTIGACIÓN SIP 20091457 23/80 Figura 2.8 Punto fijo repulsor para con r= 3.1 x=0.09

2.3 Duplicidad de período

Si se itera la función una vez obtendremos una ecuación de cuarto grado,

eso quiere decir que tendríamos 4 puntos fijos como resultado de resolver la ecuación,

gráficamente la recta y=x debe tocar en cuatro ocasiones la función de cuarto grado (ver

figura 2.9)[8].

Resolviendo analíticamente la primera iteración tendremos

f(x)=rx(1-x) función sin iterar

g(x)=f(f(x)) Primera iteración

Después de desarrollar la ecuación tendremos:

(24)

Ecuación que parece complicada, pero como sabemos que los puntos fijos de la ecuación

son también puntos fijos de esta última, resulta que y también son raíces de esta ecuación.

La solución nos permite simplificar, dividiendo por , a una de tercer orden

Dividiendo esta última por resulta

Dividiendo por tenemos

_)/r)x+_)/ ₌₀

Resolviendo la ecuación cuadrática encontramos las siguientes soluciones

Para graficar damos valor a r= 3.2, los cuatro puntos fijos resultado de la primera

iteración son los siguientes [7].

Los puntos fijos son los dos puntos fijos en donde oscilan las órbitas, también son

llamados puntos de bifurcación.

La ecuación de cuarto grado es la de línea punteada y toca la recta y=x en cuatro

(25)

Esos puntos es donde oscilan las órbitas por lo tanto tenemos una función periódica

de período dos (ver figuras 2.9 y 2.10).

Figura2.9 Puntos fijos en común para la primera y segunda iteración con r= 3.2 x=0.09 a: Primera iteración

b: y=x , c: Órbitas de período dos d: Primera iteración

(26)

Analíticamente es cada vez más complicado encontrar los puntos de las demás iteraciones ya que necesitaríamos resolver ecuaciones de octavo y dieciseisavo grado para la segunda y tercera iteración. Por eso graficaremos con ayuda de la computadora para encontrar los puntos fijos de la segunda y tercera iteración.

La función iterada dos veces toca a la recta y=x ocho veces cuatro puntos fijos son

comunes con la función iterada una vez de modo que tenemos cuatro nuevos puntos fijos

en los que oscilan las órbitas, por lo tanto el punto r=3.4 es también un punto de

bifurcación, tenemos una función periódica de período cuatro porque las órbitas oscilan entre los cuatro nuevos puntos fijos ( figura 2.11 y 2.12).

Figura2.11 Función iterada dos veces con r= 3.4 x=0.80 a: Primera iteración b: y=x c: Segunda iteración con ocho puntos fijos

(27)

2.4 Comportamiento complejo, irregular o caótico

Si seguimos iterando la función tendremos funciones periódicas de período cuatro, ocho y dieciséis para la segunda, tercera y cuarta iteración respectivamente. Como ya mencionamos anteriormente las órbitas oscilan entre los puntos fijos por lo que las gráficas muestran a simple vista comportamiento complejo irregular o caótico (figura 2.13

y 2.14)[9,10].

Figura 2.13 r= 3.6 x=0.80 a: Primera iteración b: y=x c: Órbitas de período cuatro d: Segunda iteración con ocho puntos fijos

(28)

2.5Sensibilidad a las condiciones iniciales (efecto mariposa)

La característica de sensibilidad a las condiciones iniciales se aprecia en las iteraciones que dan como resultado ocho o más puntos fijos, cuando cambiamos los valores del parámetro r.

Para entenderlo observemos la figura 2.15 y 2.16 en los que la comparación de las gráficas con r=3.9 y r=3.9009 para la cuarta iteración da como resultado dos gráficas que difieren

demasiado con solo haber alterado en nueve diezmilésimos el valor de r (ver figura 2.17).

A este cambio tan drástico se le conoce como sensibilidades a las condiciones iniciales fue observado como ya se menciono anteriormente por el matemático meteorólogo Eduart Lorenz mientras trataba de predecir el clima, por ahorrar tiempo no tomó en cuenta todos los decimales y los resultados en las gráficas fueron totalmente diferentes[6].

Figura 2.15 r= 3.9 x=0.80 a: y=x b: Cuarta iteración con treinta y dos puntos fijos

(29)

PROYECTO DE INVESTIGACIÓN SIP 20091457 29/80 Figura 2.16 r= 3.9009 x=0.80 a: Primera iteración b: y=x c: Cuarta iteración

con treinta y dos puntos fijos

Figura 2.17 Comparación de 2.15 y 2.16 (efecto mariposa)

Esta característica de sensibilidad a las condiciones también se aprecia en el destino de las órbitas (figuras 2.18, 2.19 y 2.20)

(30)

PROYECTO DE INVESTIGACIÓN SIP 20091457 30/80 Figura 2.18 Comportamiento caótico de la función logística r= 3.8 con condición inicial x=0.8

[image:30.612.153.463.69.298.2]

Y la misma gráfica pero variando las condiciones iniciales de una forma insignificante

(31)

Comparando las gráficas 2.18 y 2.19 tenemos el siguiente resultado que nos permite ver que un pequeño cambio en las condiciones iniciales produce grandes cambios en el resultado como se observa en la siguiente figura [6, 9, 10].

Figura 2.20 Comparación de la figura 2.18 y 2.19

comportamiento caótico de la función logística r= 3.8 x=0.80000000001y x=0.8

2.5 Diferencia entre comportamiento caótico y ruido

Conforme iteramos la función, se duplica el período y las órbitas que oscilan entre los puntos fijos muestran un comportamiento cada vez más complejo al que se le ha dado el nombre de caótico (ver figura 2.21).

(32)

32/80

Figura 2.21 Tercera interacción con r=3.8 a: y=x b: Primera iteración c: Segunda Iteración d: Tercera iteración e: Cuarta iteración f: No se distingue

el período de las órbitas.

2.6 Diagrama de bifurcación

El diagrama de bifurcación (Figura 2.22) muestra de manera resumida el comportamiento de las órbitas que oscilan alrededor de los puntos fijos al variar el parámetro r para todos sus valores posibles, podemos ver de manera clara en donde empieza la primera y segunda bifurcación hasta llegar a la región que es considerada como caótica o compleja

la cual se obtiene de iterar la ecuación n número de veces (figura 2.23) [8-10].

(33)

33/80

Figura 2.23 a: primera bifurcación b: segunda bifurcación c: tercera bifurcación d: región caótica [4-6].

Para valores de r menores a 3 el diagrama de bifurcación muestra un destino de las órbitas que tiende a un solo punto fijo (ver figura 2.24).

Figura 2.24 Destino de las órbitas en un solo punto fijo.

(34)

34/80

Figura 2.25 r=3.2 y x=0.8 órbitas de período 2 (Primera iteración)

En r= 3.6 el diagrama de bifurcación muestra una segunda bifurcación las órbitas oscilan entre 4 puntos fijos ( figura 2.26).

(35)

35/80

[image:35.612.158.457.444.650.2]

Para r mayor a 3.6 el diagrama de bifurcación entra en lo que se conoce como régimen caótico ya que tenemos demasiados puntos fijos sobre los que oscilan las órbitas y es difícil observar su período ( figura 2.27 y 2.28).

Figura 2.27 Tercera interacción con r=3.8 a: y=x b: Primera iteración c: Segunda iteración d: Tercera iteración e: Cuarta iteración f: No se distingue

el período de las órbitas.

(36)

36/80

CAPÍTULO 3

[EDWARD LORENZ]

(37)

37/80

3.1 Sistemas en dos dimensiones

En esta sección veremos algunas características de las ecuaciones diferenciales autónomas ampliamente utilizadas en el modelado de crecimiento de poblaciones, en la predicción del clima, estudios que dieron origen a la teoría del caos [6, 9, 10].

Las ecuaciones diferenciales autónomas son de la forma , el lado derecho de la

ecuación no depende de la variable independiente que por lo general es el tiempo.

El campo de pendientes de una ecuación autónoma se observa en la figura 3.1. Podemos usar la siguiente ecuación que analizamos en el capítulo anterior para ejemplificarlo.

Las pendientes que corresponden a dos puntos diferentes con la misma coordenada (y)

son iguales. Es decir el campo de pendientes para una ecuación autónoma es paralelo a lo largo de cada línea horizontal [9].

Recordando que la derivada de una ecuación es la pendiente de la recta en un punto dado

entonces podemos dar valores a (x, y) para encontrar algunas pendientes.

Si damos valores y=1 y x=2

Tendremos

Podemos ver que tenemos una pendiente negativa y lo mismo para

y=1 y x=3

(38)

38/80

Figura 3.1 Gráficas de soluciones superpuestas sobre el campo de pendientes [9].

En los sistemas de ecuaciones autónomas se usan campos de vectores para tener una representación geométrica.

Como ejemplo usamos el sistema depredador presa modelado por las siguientes

ecuaciones diferenciales[9,10].

Para cada denota un vector

para calcular la derivada de la función vectorial P(t), determinamos las derivadas de cada

(39)

39/80

Y podemos escribirlo como

El lado derecho de la ecuación es una función que asigna a cada punto del plano(R,F) un

vector dado un punto con coordenadas(R,F).

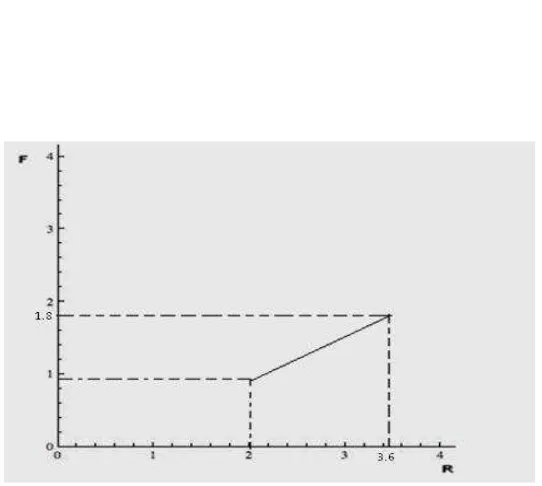
En el plano R, F podemos graficar un primer vector si damos valores (R=2, F=1) y lo

[image:39.612.174.445.295.538.2]

evaluamos en la ecuación anterior (ver figura 3.2).

Figura 3.2 Vector para el punto (2,1)

(40)

40/80

Figura 3.3 a) Campo vectorial, b) Curva solución del sistema

La variación de cada variable o especie con respecto al tiempo se muestra en la siguiente figura.

Figuran 3.4 Variación con respecto al tiempo de R y F.

(41)

41/80

3.2 Sistemas tridimensionales

Una solución de un sistema autónomo con tres variables dependientes es una curva en un espacio de fase tridimensional.

Consideremos el sistema tridimensional conocido como las ecuaciones de Lorenz. Este sistema fue estudiado por Eduart Lorenz en 1963 en un esfuerzo por modelar el clima, es importante porque el campo vectorial está formado por ecuaciones muy simples pero cuyas soluciones conducen a curvas muy complicadas [9,10].El sistema de Lorenz está definido por las siguientes ecuaciones.

Donde son los parámetros y son las variables dependientes. Al estudiar este

sistema Eduart Lorenz dio paso a una revolución científica llamada teoría del caos [10,11].

Lorenz propuso los siguientes valores de los parámetros.

Sustituyendo las ecuaciones quedan de la siguiente manera:

Los lados derechos de la ecuación definen el comportamiento del espacio tridimensional que a signa un vector a cada punto tal como se vio en dos dimensiones en el ejemplo del sistema depredador presa.

Resolviendo por el método numérico de Rudge kuta tenemos los siguientes puntos fijos o

puntos de equilibrio para los cuales el campo vectorial es cero [11].

(42)

42/80

En los sistemas dinámicos el objetivo básico es predecir el futuro de las órbitas y como se comportan alrededor de los puntos fijos. En el ejemplo de Lorenz veremos que las órbitas oscilan alrededor de dos puntos fijos atrayéndose hacia ellos, por eso se le ha dado el nombre de atractor de Lorenz.

Para entender este atractor, enfocaremos la curva solución en un plano coordenado. Geométricamente esto significa que nos olvidemos de una de las coordenadas de la curva solución. En la figura 3.5,3.6 y 3.7 esbozamos la solución que tiene el atractor de Lorenz.

(43)

[image:43.612.165.459.318.519.2]

43/80

Figura 3.6 Gráfica de ecuaciones de Lorenz en dos dimensiones (y,z)

Figura 3.7 Gráfica de ecuaciones de Lorenz en dos dimensiones (x,z)

(44)

44/80

3.3 Análisis en el tiempo

[image:44.612.87.529.256.674.2]

Las gráficas en el tiempo para cada variable se muestran en la figura 3.8, en las que podemos observar un comportamiento aperiódico muy diferente entre cada una de ellas pero al graficarlas juntas en tres dimensiones sin depender del tiempo toman formas como las figuras 3.5, 3.6, 3.7 [9-12], todas estas gráficas presentan sensibilidad a condiciones iniciales.

(45)

45/80

3.4 Secciones de de Poncairé

Existe una forma de estudiar el comportamiento caótico en las ecuaciones de Lorenz basada en el empleo de secciones de Poncairé, para poder visualizar mejor el comportamiento caótico en el Atractor de Lorenz usaremos solo la mitad del Atractor de

[image:45.612.154.470.239.457.2]

Lorenz conocido como el Atractor de Rössler (ver figura 3.9).

Figura 3.9 Gráfica del atractor de Rössler [12]

El sistema de Rössler está dado por el siguiente sistema de ecuaciones

(46)

46/80

[image:46.612.127.498.121.553.2]

En este sistema las bifurcaciones se obtienen al variar el parámetro µ como se observa en la figura siguiente:

Figura 3.10 Bifurcaciones sucesivas para el modelo de Rössler con diferentes valores del parámetro µ [12].

Supongamos que cortamos el atractor de Rössler por medio de una sección de Poncairé tal como se indica en la figura 3.11. En esta gráfica vemos que la sección de Poncairé atraviesa la sección caótica a lo largo de un conjunto de puntos que viene dado

considerando la variable , por:

(47)

47/80

Figura 3.12 a) Superficie S normal a las líneas de flujo, donde se crea el mapa de Poncairé. b) Diagrama de obtenido a partir de los valores que interceptan a [12].

Figura 3.11 Sección de Poncairé sobre el atractor de Rössler[12]

Podemos obtener una imagen simplificada del fenómeno recurriendo a la aplicación

Suponiendo que es un punto fijo de , es decir ,entonces una trayectoria que

comience en retorna a luego de algún tiempo t, y por lo tanto es una órbita cerrada

del sistema (figura 3.11 a). Si representamos estas órbitas cerradas en un diagrama de

retorno tendremos como resultado un sistema dinámico unidimensional el cual

(48)

48/80

[image:48.612.191.463.166.398.2]

En el diagrama de bifurcación ( figura 3.13) o escenario de Feigenbaum podemos ver la transición de movimiento regular o periódico a movimiento caótico, además de la duplicidad de período [12].

(49)

49/80

CAPÍTULO 4

Leon Chua

APLICACIÓN DEL CAOS

EN LAS

(50)

50/80

4.1 Circuito de Chua

Leon Ong Chua nació en China en 1936, es profesor de Ingeniería Eléctrica y Ciencias Computacionales en la Universidad de California desde 1971. Considerado el padre de la teoría de los circuitos no lineales, es el inventor del circuito de Chua.

El circuito es una herramienta didáctica para el estudio de los fenómenos no lineales. Este circuito se caracteriza por ser autónomo, es decir, no necesita alimentación por fuentes de corriente alterna para producir su comportamiento caótico, solo necesita la fuente DC de polarización. El circuito está formado por dos partes principales: la parte formada por un Oscilador amortiguado (condensadores, resistencia e inductancia) y el elemento no lineal denominado diodo de Chua. Este elemento actúa como una fuente de energía de todo el circuito, su función es retroalimentarlo y lo mantiene oscilando.

Como en todos los sistemas caóticos, encontramos en el circuito de Chua, un comportamiento que presenta una fuerte dependencia respecto a las condiciones iniciales (valores de los componentes y voltajes iniciales). También veremos que el sistema de ecuaciones que lo rigen, es no lineal y cumple con un sistema de ecuaciones diferenciales, que se obtiene al aplicar las leyes de Kirchhoff.

El circuito de la figura 4.1a fue presentado por primera vez por Leon Ong Chua y consiste

en un oscilador (condensador y bobina L en paralelo), una resistencia en serie con

el oscilador y un condensador en paralelo con un dispositivo lineal a trazos R, cuya

relación de transferencia ( )se observa en la figura 4.1b [13-15].

(51)

51/80

El circuito más simple que permite obtener esa curva de transferencia se representa en la figura 4.2. Se trata de un circuito alimentado por una fuente de voltaje continuo VCC,

encargada de polarizar los transistores y (a través de las resistencias en región

activa. Cuando la señal de entrada al dispositivo (, proveniente del oscilador,,

proveniente del circuito equivalente al diodo de Chua) es pequeña (| |< ) los diodos

y no superan su voltaje umbral y se comportan como circuitos abiertos. Si es

levemente positiva, aumenta la corriente de base del transistor y el colector exige del

circuito una corriente entrante que es proporcional al voltaje aplicado. Esto equivale a

decir que la corriente es saliente del dispositivo, teniéndose una pendiente negativa

entre el voltaje de entrada y la corriente neta que circula. Cuando > comienza a

conducir el diodo y parte de la corriente que exige el colector del transistor ,

proviene de la corriente que circula por el diodo, disminuyendo de esa forma la corriente

en valor absoluto. Un comportamiento similar que involucra al transistor y al

diodo , se verifica para los valores de negativos.

(52)

52/80

La misma curva de transferencia puede implementarse con un amplificador operacional como se observa en la siguiente figura [13].

Fig. 4.1 Circuito equivalente al diodo de Chua utilizando un Opam en régimen no lineal[14]

Si analizamos el diodo de Chua implementado con un amplificador operacional obtenemos una curva con relación corriente-voltaje a la que llamamos resistencia no lineal que se observa en la ecuación a.

Para obtener la salida de voltaje máxima en el operacional cuando tenemos una entrada máxima de voltaje en la entrada del circuito, tenemos:

Ahora que conocemos Vout que es el voltaje máximo en el operacional, también

conocemos el voltaje máximo Vin.

Mientras que el máximo no es alcanzado, calculamos Vin.

(53)

53/80

Como

Finalmente tenemos:

_---(a)

Una vez que ya conocemos el comportamiento del diodo de Chua lo analizamos junto con el oscilador para obtener las tres ecuaciones que modelan este circuito por medio de las

leyes de Kircchhoff por corrientes como se observa en la siguiente figura.

(54)

PROYECTO DE INVESTIGACIÓN SIP 20091457 54/80 Nodo =0---(A) Nodo =0---(B)

Nodo de referencia

i ---(C)

Posteriormente se pasan a ecuaciones integro-diferenciales.

De Ec. A

=0 Donde O bien --- (D)

De Ec. B

O bien ____________________(E)

De Ec. C

(55)

55/80 Por convenencia

---(F)

Sust. Ecs. D y E en F

Derivando ambos miembros de la igualdad

_{--- (G)}

Finalmente obtenemos el siguiente sistemita de ecuaciones diferenciales autónomas para el circuito de Chua[14].

Donde la corriente por la resistencia de pendiente negativa verifica:

Siendo los módulos de las pendientes en los diferente tramos de linealidad que se

(56)

56/80

4.2 Sincronización

Las primeras ideas de sincronización se remontan al físico Christian Huygens (1629-1695) tenía en una pared de su dormitorio dos relojes de péndulo de su propia invención. En febrero de 1665, convalecía de una gripe en su cuarto, mientras los miraba aburrido, se dio cuenta de que los péndulos de ambos relojes estaban perfectamente sincronizados. Huygens sabía que era prácticamente imposible que ambos péndulos oscilaran exactamente igual por azar. Y eso llamó poderosamente su atención. Es más, era casi imposible que se mantuvieran así durante mucho tiempo. Los observó durante horas y ambos relojes seguían sincronizados. De modo que supuso que, de alguna manera, los relojes estaban interaccionando. Huygens intuyó que eran las vibraciones que se transmitían por la pared donde ambos relojes estaban colgados. Colocó uno de los relojes en el otro extremo de la habitación y, al poco tiempo, ambos se sincronizaron.

El acoplamiento de los relojes a través de la pared generaba la sincronía o sincronización entre ellos.

A partir de esta observación fortuita de Huygens, los científicos han desarrollado toda una rama de la Matemática aplicada y la Física: la teoría de los osciladores acoplados.

Gracias a ella han sido capaces de explicar por qué la Luna, en su órbita alrededor de la Tierra, nos muestra siempre la misma cara (hoy día, el período de rotación de la Luna coincide con su período de traslación alrededor de la Tierra). O entender fenómenos como superconductividad, algo así como electricidad sin resistencia, donde quienes se acoplan son parejas de electrones. O inventar la luz láser, donde trillones de átomos acoplados pulsan en concierto emitiendo fotones con la misma frecuencia y fase.

(57)

57/80

El estudio sistemático moderno, tanto experimental como teórico de este fenómeno, fue iniciado por Edward Appleton, Balthasar Van der Pol y Andronov y Vitt que observaron sincronización en generadores eléctricos. Cobra popularidad hace aproximadamente 20 años, tiempo en el cual se produjeron diversidad de artículos y libros que tratan de una u otra manera sobre la sincronización en sistemas que van desde los biológicos, tales como luciérnagas, grillos, cigarras, hormigas, sistemas ecológicos, diferentes comportamientos en poblaciones humanas, células cardiacas, neuronas en el sistema nervioso y en la relación fisiológica entre el corazón y pulmones, pasando por sistemas químicos (osciladores bioquímicos) y llegando a sistemas artificiales como circuitos electrónicos, etc.

Los grandes trabajos sobre la sincronización del caos se atribuyen a Fujisaka, Picovsky y Afraimovich y a Pecora & Carroll [1] quienes presentaron los primeros ejemplos sobre la sincronización unidireccional de sistemas caóticos acoplados.

Sin embargo, tras el trabajo de Pecora y Carroll, se ha mostrado que dos comportamientos caóticos imprevisibles, que inicialmente evolucionan sobre trayectorias diferentes, pueden fundirse en una única trayectoria común si se acoplan adecuadamente. El desarrollo de los sistemas de comunicaciones utilizando caos, nació a partir de esa idea y se ha afianzado, a través de trabajos fundamentales de un número importante de investigadores.

Los circuitos se presentan como una herramienta de una gran utilidad para estudiar una gran variedad de procesos, actuando como complemento entre el experimento en sí y la simulación numérica por computadora. Entre las ventajas que ofrece la simulación con circuitos se encuentran tanto el alto grado de desarrollo de componentes electrónicos como el bajo costo de los dispositivos. Y son varios los ejemplos de circuitos electrónicos utilizados para el estudio de Caos. El sistema de Lorenz, Rössler y Chua son algunos de ellos que se trataran más adelante.

El significado de sincronización de caos se refiere al proceso en el que se involucran dos (o varios) sistemas caóticos (equivalentes o no equivalentes) ajustando sus propiedades para que tiendan a un comportamiento común (periódico o ruidoso). Este fenómeno de sincronización inicialmente hace que los sistemas evolucionen sobre atractores diferentes para que finalmente puedan lograr empatar, acoplarse y coincidir en una misma trayectoria. Es sorprendente que la sincronización entre dos sistemas caóticos aparece cuando se considera la dependencia de la dinámica caótica en las condiciones iniciales del sistema.

Hay que destacar que hay una gran variedad de esquemas de acoplamiento que conducen al régimen de sincronización. Dependiendo de la configuración particular del acoplamiento, podemos distinguir dos casos principales: acoplamiento unidireccional y

(58)

58/80

Acoplamiento unidireccional.

El sistema global está formado por dos subsistemas acoplados según una configuración de tipo maestro-esclavo. Eso implica que el comportamiento del sistema esclavo depende del comportamiento del sistema maestro, mientras que este último no se ve influido por el comportamiento del sistema esclavo. Como resultado, el sistema esclavo se encuentra forzado a seguir la dinámica (o una función propia de la dinámica) del maestro. Dicho de otro modo, cuando la evolución de uno de los dos sistemas no es alterada por el acoplamiento la configuración resultante es un acoplamiento unidireccional.

Acoplamiento bidireccional.

Aquí ambos subsistemas son acoplados con otro, o cuando los dos subsistemas son conectados de tal forma que sus trayectorias están mutuamente influenciadas por el comportamiento del otro. Esta situación ocurre en fisiología, entre el sistema cardiaco y el respiratorio también se da en láseres con retroalimentación.

Es sorprendente que la sincronización entre dos sistemas caóticos aparece cuando se considera la dependencia de la dinámica caótica en las condiciones iniciales del sistema.

Cuando las condiciones iniciales en los sistemas caóticos, al tener la mas mínima variación en el sistema, provoca que se obtengan resultados y evolucione en un sistema más complejo que al que originalmente se tenía, esto hace que a simple vista sea difícil la sincronización en sistemas caóticos reales, ya que en la práctica no es posible igualar las condiciones iniciales o hacer dos sistemas totalmente idénticos, para poder lograr la sincronización; se pueden crear sistemas muy parecidos pero siempre existirá un margen de error.

(59)

59/80

Fig. 4.5 a) Esquema de sincronización b) Trayectoria del esclavo XS del esclavo sincronizada con la trayectoria del

Maestro XM

La sincronización entre dos sistema, se consigue cuando uno de los sistemas modifica su comportamiento y sigue la trayectoria del otro sistema, o ambos oscilan en una nueva trayectoria común.

4.3 Convertidores de Impedancia.

Los convertidores de impedancia son circuitos muy útiles para obtener el valor de un capacitor o un inductor que no se encuentra de manera comercial, utilizando un arreglo de amplificadores operacionales, resistores y capacitores. Esta clase de circuitos es muy importante al tratar de implementarse en los generadores caóticos, al no tener el valor exacto del inductor o capacitor en cuestión podemos obtener un equivalente con el convertidor de impedancia, recordemos que es útil, ya que el comportamiento caótico depende mucho de las condiciones iniciales de nuestro sistema dadas por los elementos del circuito.

Para poder obtener el valor equivalente del inductor o capacitor, debemos obtener el

valor de la impedancia equivalente Zin. El circuito a analizar consta de dos amplificadores

[image:59.612.146.471.78.310.2]

(60)

[image:60.612.168.445.77.328.2]

60/80

Fig. 4.6 Convertidor Generalizado de Impedancia[17]

Considerando que tenemos amplificadores operacionales ideales y aplicando el criterio de

masa virtual, tenemos que la tensión de entrada es la misma en los puntos V2 y V4.

Analizando la tensión V2 y V4 tenemos que:

(61)

61/80

Despejamos de la ecuación anterior tenemos:

Sustituimos en

Despejamos a V1.

Sustituimos en

(62)

62/80

Aplicando ley de Ohm

Finalmente:

(63)

63/80

4.4

Ventajas y desventajas del uso de los sistemas caóticos en las telecomunicaciones

Los esquemas de comunicaciones digitales convencionales hasta ahora usaban señales senoidales obteniendo buenos resultados además de gozar con una ventaja de fácil implementación, cabe preguntarse ahora ¿por qué cambiar la portadora?.

Las principales ventajas de los sistemas caóticos son: Cuando se usa una portadora senoidal, la potencia transmitida se concentra en una estrecha banda, dando lugar a una elevada densidad espectral de potencia y eso implica una serie de desventajas además de que los criptosistemas tradicionales emplean algoritmos que sólo incrementan la difusión y confusión de la linealidad del criptosistema con un incremento lineal de iteraciones o longitud de clave, en cambio la criptografía caótica presenta mejores propiedades en esta área. El caos ha sido principalmente atractivo para encriptar información debido a que las señales que generan los sistemas caóticos tienen un ancho de banda infinito, y son determinísticas, pues dependen del sistema y su condición inicial.

Las principales desventajas de los sistemas caóticos son: Sensibilidad a las condiciones iniciales, para una sincronización completa debe ser idéntico tanto el transmisor como el receptor.

La propiedad de sincronización se puede aprovechar para la utilización de señales caóticas como portadoras, para ocultar mensajes de baja intensidad. Si el mensaje y la portadora se superponen en el momento de la emisión, el mensaje queda oculto y puede ser transmitido por un canal público con seguridad. En el canal público sólo se verá una señal con el aspecto aleatorio característico del caos determinista. Si esta señal transmitida es capaz de inducir la sincronización de un sistema caótico idéntico al emisor que se encuentre en el lugar de recepción, la señal portadora podrá reproducirse en el sistema receptor. Una vez reproducida la portadora, un procedimiento inverso al utilizado para la superposición podrá ser utilizado para recuperar el mensaje.

(64)

64/80

En nuestros días, los sistemas de mayor difusión y amplio uso para encriptar información se basan en criptografía digital. Dicha masificación se justifica por la facilidad de implementación en arquitecturas digitales y que ofrecen una recuperación perfecta de la información. Sin embargo, recientemente, y ante la vulnerabilidad que han mostrado algunos de estos métodos, se realizan esfuerzos por generar sistemas de criptografía basados en señales análogas, los cuales prometen tener una mayor seguridad, debido a la alta redundancia y a la posibilidad de transmisión por medios diferentes a las redes de datos convencionales. Entre los sistemas de encriptación analógica se destacan los basados en caos.

Los sistemas de encriptación caótica fueron propuestos inicialmente por Pecora y Caroll en 1990 [10], como resultado del descubrimiento de la posibilidad de sincronización de dos sistemas caóticos.

4.5 Encriptado y desencriptado de una señal por medio del circuito de Chua

El circuito de Chua es de gran utilidad producir una señal caótica la cual se usa en la transmisión segura de la información.

[image:64.612.93.518.427.645.2]

El circuito de Chua que usamos se muestra en la figura 4.7, se forma por un diodo de Chua construido por dos amplificadores operacionales TL082CD y un circuito oscilador construido con una resistencia, dos capacitores y una bobina.

Figura 4.7 Circuito de Chua con dos amplificadores operacionales

(65)

65/80

[image:65.612.87.526.120.368.2]

Las señales en el tiempo se muestran en la figura 4.8 y 4.9, el atractor de Chua ya estudiado anteriormente se muestra en la figura 4.10

Figura 4.8 Señal proveniente del circuito de Chua

[image:65.612.86.528.408.651.2]

(66)

66/80

Figura 4.10 Atractor de Chua

El diagrama de bloques del transmisor es mostrado en la figura 4.11, la señal s(t) se

suma a la señal caótica que genera el circuito de Chua y se obtiene la señal r(t). El

buffer es usado para conseguir una señal sin atenuación y el inversor se usa para

[image:66.612.88.529.108.342.2]

que la señal r(t) a transmitir no cambie su fase[18].

(67)

67/80

La señal mensaje s(t) que utilizamos se muestra en la figura 4.12, es una señal senoidal

[image:67.612.88.528.122.346.2]

de 4 volts de amplitud y 1kHz de frecuencia .

Figura 4.12 Señals(t) de 4 volts de amplitud y 1kHz de frecuencia

En la figura 4.13 se observa la comparación de y s(t), en la figura 4.14 se

muestra la señal resultante r(t) del transmisor que es la suma de la señal

caótica y la señal senoidal s(t).

[image:67.612.89.529.448.662.2]

(68)

68/80

Figura 4.14 Señal encriptada r(t)

En la figura 4.15 se muestra el diagrama de bloques del receptor. El receptor consiste en el circuito de un Chua similar al que en el transmisor genera una señal caótica

que perfectamente se acopla con la señal caótica generada en el transmisor. La señal r(t)

del transmisor y la señal caótica generada por el circuito caótico del receptor se

restan y la salida es , y resulta la misma señal mensaje. El buffer de

[image:68.612.86.530.79.301.2]

igual forma que en el transmisor se usa para que no se a tenue la señal.

Figura 4.15 Diagrama de bloques para el receptor

(69)

69/80

El circuito completo del diagrama de bloques de transmisor y receptor se muestra en la figura 4.16, está formado por dos circuitos de Chua de donde provienen dos señales

idénticas , dos buffer Tl071ACD, un sumador, un restador y un inversor.

Figura 4.16 Circuito completo del diagrama de bloques de transmisor y receptor

En la figura 4.17 se muestra la señal de salida del receptor s’(t) en azul y s(t) en rojo, no

[image:69.612.99.530.167.471.2]

(70)

70/80

[image:70.612.87.528.79.321.2]

Figura 4.17 Señal mensaje s(t) (rojo)vs señal desencriptada (azul) s’ t

Figura 4.18Sincronización en fase s'(t) contra s(t)

(71)

71/80 Conclusiones