Código 𝑯𝒖𝒇𝒇𝒎𝒂𝒏
Codificación:
El proceso de asignar secuencias binarias a los símbolos Asignación de secuencias binarias a un alfabeto.
Alfabeto: conjunto de símbolos llamados letras. Código: conjunto de secuencias binarias.
Palabras de código (𝑐𝑜𝑑𝑒𝑤𝑜𝑟𝑑𝑠): miembros del código.
Código de longitud fija: el que usa el mismo número de bits para representar cada símbolo. Para reducir el número de bits (rata) para representar un mensaje se debe usar un código de longitud variable.
Rata del código: número de bits promedio por símbolo. La longitud promedio de un código está dada por
𝑳 = ∑ 𝑷𝒊∗ 𝒍𝒊
𝒒 𝒊=𝟏
En donde 𝑷𝒊 es la probabilidad de ocurrencia de cada símbolo y 𝒍𝒊 es el número de 𝑏𝑖𝑡𝑠 𝑝𝑜𝑟 𝑝𝑎𝑙𝑎𝑏𝑟𝑎.
La longitud promedio no es el único criterio para la escogencia de un buen código. La representación de cada símbolo debe ser no ambigua
El código también debe tener la característica de decodificabilidad única Símbolos Probabilidad Código 1 Código 2 Código 3 Código 4
𝒂𝟏 𝟎. 𝟓 𝟎 𝟎 𝟎 𝟎
𝒂𝟐 . 𝟐𝟓 𝟎 𝟏 𝟏𝟎 𝟎𝟏
𝒂𝟑 𝟎. 𝟏𝟐𝟓 𝟏 𝟎𝟎 𝟏𝟏𝟎 𝟎𝟏𝟏
𝒂𝟒 𝟎. 𝟏𝟐𝟓 𝟏𝟎 𝟏𝟏 𝟏𝟏𝟏 𝟎𝟏𝟏𝟏
Long. media 𝟏. 𝟏𝟐𝟓 𝟏. 𝟐𝟓 𝟏. 𝟕𝟓 𝟏. 𝟖𝟕𝟓
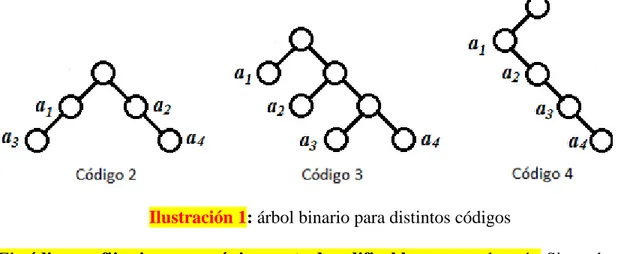
Código prefijo: aquel en el cual ninguna palabra de código es prefijo de ninguna otra palabra de código. Esto se chequea construyendo un árbol binario correspondiente al código.
El árbol binario consta de un nodo raíz y dos tipos adicionales de nodos: los que dan lugar a otros nodos (nodos internos) y los que no (nodos externos u hojas).
El código para cualquier símbolo puede obtenerse atravesando el árbol desde la raíz hasta el nodo externo (o interno) correspondiente a aquel símbolo. Cada rama en la ruta contribuye con un bit al código del símbolo (cero si la rama va hacia la izquierda y uno si va hacia la derecha).
El código prefijo es aquel en el que las palabras de código se asignan solamente a los nodos externos.
Un código que no es prefijo es aquel al que se le asignan algunas palabras de código a los nodos internos.
Ilustración 1: árbol binario para distintos códigos
El código prefijo siempre es únicamente decodificable pero no al revés. Sin embargo un código que sea únicamente decodificable pero que no sea prefijo tiene un equivalente prefijo (equivalente en el sentido de que tiene la misma longitud promedio).
Códigos 𝑯𝒖𝒇𝒇𝒎𝒂𝒏:
Estos códigos son prefijos y son óptimos para un modelo dado de probabilidad. Se basan en dos observaciones:
En un código óptimo, los símbolos que ocurren más frecuentemente tendrán las palabras de código más cortas que los que ocurren menos frecuentemente.
En un código óptimo los dos símbolos que ocurren menos frecuentemente tendrán códigos de la misma longitud.
El procedimiento de 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 se obtiene agregando un requerimiento simple a los dos anteriores:
las palabras de código correspondientes a los dos símbolos menos probables difieren únicamente en el último bit.
Ejemplo: Se tiene una fuente de información que genera cinco símbolos con las probabilidades que se muestran en la tabla 2.
Letra Probabilidad Palabra de código
𝒂𝟐 𝟎. 𝟒 c(𝒂𝟐)
𝒂𝟏 𝟎. 𝟐 𝒄(𝒂𝟏)
𝒂𝟑 𝟎. 𝟐 𝒄(𝒂𝟑)
𝒂𝟒 𝟎. 𝟏 𝒄(𝒂𝟒)
𝒂𝟓 𝟎. 𝟏 𝒄(𝒂𝟓)
Tabla 2: Alfabeto inicial de cinco letras
Para codificar los símbolos de esta fuente según el algoritmo de 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 se deben organizar los símbolos en orden descendiente de probabilidad, generar fuentes reducidas y codificar de acuerdo con las observaciones como se muestra a continuación:
Letra Probabilidad Palabra de código
𝒂𝟐 𝟎. 𝟒 c(𝒂𝟐)
𝒂𝟏 𝟎. 𝟐 𝒄(𝒂𝟏)
𝒂𝟑 𝟎. 𝟐 𝒄(𝒂𝟑)
𝒂𝟒′ 𝟎. 𝟐 𝜶𝟏
𝑪(𝒂𝟒) = 𝜶𝟏∗ 𝟎 𝑪(𝒂𝟓) = 𝜶𝟏∗ 𝟏
Letra Probabilidad Palabra de código
𝒂𝟐 𝟎. 𝟒 c(𝒂𝟐)
𝒂𝟑′ 𝟎. 𝟒 𝜶𝟐
𝒂𝟏 𝟎. 𝟐 𝒄(𝒂𝟏)
Tabla 4 : Alfabeto reducido de tres letras
𝑪(𝒂𝟑) = 𝜶𝟐∗ 𝟎 𝑪(𝒂𝟒′) = 𝜶𝟐∗ 𝟏
Luego
𝜶𝟏= 𝜶𝟐∗ 𝟏 𝑪(𝒂𝟒) = 𝜶𝟐∗ 𝟏𝟎 𝑪(𝒂𝟓) = 𝜶𝟐∗ 𝟏𝟏
𝑪(𝒂𝟑′) = 𝜶𝟑∗ 𝟎 𝑪(𝒂𝟏) = 𝜶𝟑∗ 𝟏 𝜶𝟐= 𝜶𝟑∗ 𝟎
𝐶(𝑎𝟑) = 𝛼𝟑∗ 00 𝑪(𝒂𝟒) = 𝜶𝟑∗ 𝟎𝟏𝟎 𝑪(𝒂𝟓) = 𝜶𝟑∗ 𝟎𝟏𝟏
Letra Probabilidad Palabra de código
𝒂𝟑′′ 𝟎. 𝟔 𝜶𝟑
𝒂𝟐 𝟎. 𝟒 c(𝒂𝟐)
Tabla 5 : Alfabeto reducido de dos letras
𝑪(𝒂𝟑′′) = 𝟎 𝒄(𝒂𝟐)= 𝟏 𝒄(𝒂𝟏)= 𝟎𝟏 𝒄(𝒂𝟑)= 𝟎𝟎𝟎 𝒄(𝒂𝟒)= 𝟎𝟎𝟏𝟎 𝒄(𝒂𝟓)= 𝟎𝟎𝟏𝟏
Letra Probabilidad Palabra de código
𝒂𝟐 𝟎. 𝟒 𝟏
𝒂𝟏 𝟎. 𝟐 𝟎𝟏
𝒂𝟑 𝟎. 𝟐 𝟎𝟎𝟎
𝒂𝟒 𝟎. 𝟏 𝟎𝟎𝟏𝟎
𝒂𝟓 𝟎. 𝟏 𝟎𝟎𝟏𝟏
Tabla 6: Código 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 para el alfabeto original de cinco letras
Redundancia: diferencia entre la longitud media lograda con el código y la entropía
Ilustración 2: Diagrama de árbol para el código 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 del ejemplo
Códigos 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 de mínima varianza
Se construyen colocando las combinaciones de los símbolos menos probables encima de los símbolos que tienen su misma probabilidad.
La ventaja de estos códigos de mínima varianza es que no sobrecargan los búferes de transmisión (es decir se requieren búferes más pequeños para una rata fija de salida).
Longitud de los códigos 𝑯𝒖𝒇𝒇𝒎𝒂𝒏
La longitud promedio del código 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 está entre 𝑯(𝑺) ≤ 𝑳 ≤ 𝑯(𝑺) + 𝟏
Los siguientes programas permiten calcular el código 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 de una fuente dadas las probabilidades de ocurrencia de cada uno de los símbolos:
Function [code,compression]=ℎ𝑢𝑓𝑓𝑚𝑎𝑛5(p); %𝐻𝑈𝐹𝐹𝑀𝐴𝑁5
%𝐻𝑈𝐹𝐹𝑀𝐴𝑁 CODER FOR V5
% Format [CODE, COMPRESSION] =𝐻𝑈𝐹𝐹𝑀𝐴𝑁5(P)
% P is the probability (or number of occurrences) of each alphabet symbol % CODE gives the ℎ𝑢𝑓𝑓𝑚𝑎𝑛 code in a string format of ones and zeros % COMPRESSION gives the compression rate
% 𝐻𝑢𝑓𝑓𝑚𝑎𝑛5 works by first building up a binary tree (eg p = [.5 .2 .15 .15]) % a_1 a_4
% / / % b3 b1 % \ / \ % 0\ 1/ 0\ % b2 a_3 % \
% 0\ % a_2
% Such that the tree always terminates at an alphabet symbol and the % symbols furthest away from the root have the lowest probability. % the branches at each level are labeled 0 and 1.
% for this example CODE would be
% 1 00 010 011
% and the compression rate 1.1111
% Sean Danaher University of Northumbria at Newcastle UK 98/6/4 p=p (:)/sum(p); %normalizes probabilities
c=huff5 (p);
code =char(getcodes(c,length(p)));
compression =ceil(log(length(p))/log(2))/ (sum(code' ~= ' ')*p); %---
function c=huff5(p);
% HUFF5 Creates 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 Tree
% simulates a tree structure using a nested cell structure % P is a vector with the probability (number of occurrences) % of each alphabet symbol
% C is the 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 tree. Note Matlab 5 version
% Sean Danaher 98/6/4 University of North Umbria, Newcastle UK c=cell(length(p),1); % Generate cell structure
for i=1:length(p) % fill cell structure with 1,2,3...n c{i}=i; % (n=number of symbols in alphabet) end
% figure; % cellplot(c); % figure;
% cellplot(num2cell(p));
while size(c)-2 % Repeat till only two branches [p,i]=sort(p); % Sort to ascending probabilities c=c(i); % Reorder tree.
c{2}={c{1},c{2}};c(1)=[]; % join branch 1 to 2 and prune 1 p(2)=p(1)+p(2);p(1)=[]; % Merge Probabilities
% figure; % cellplot(c); % figure;
%--- function y= getcodes(a,n)
% Y=GETCODES (A, N)
% pulls out 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 Codes for V5
% a is the nested cell structure created by huffcode5 % n is the number of symbols
% Sean Danaher 98/6/4 University of North Umbria, Newcastle UK global y
y=cell(n,1); getcodes2(a,[])
%--- function getcodes2(a,dum)
% GETCODES (A, DUM) %getcodes2
% called by getcodes
% uses Recursion to pull out codes
% Sean Danaher 98/6/4 University of North Umbria, Newcastle UK global y
if isa(a,'cell')
getcodes2(a{1},[dum 0]); getcodes2(a{2},[dum 1]); else
y{a}=setstr(48+dum); end
Otro código:
%the name of this m-file is 𝒉𝒖𝒇𝒇𝒎𝒂𝒏𝒄𝒐𝒅𝒆. 𝒎
%x is a data vector with nonnegative integer components %y=𝒉𝒖𝒇𝒇𝒎𝒂𝒏code(x) is the Kraft vector of a 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 %code for x
Function y = 𝒉𝒖𝒇𝒇𝒎𝒂𝒏code(x) F=frequency(x);
k=length (F); M=zeros (k, k+1); M (:, 1)=F'; R=k; while R > 1
t1=find (r1==0); t2=find (r2==0); m1=min(t1); m2=min(t2); if m1 > 2
m1=m1-1; else
end if m2 > 2
m2=m2-1; else
end
v1=r1(2:m1); v2=r2(2:m2);
bottom=[r1(1)+r2(1) v1+1 v2+1 zeros(1,k+2-m1-m2)]; N=zeros(R-1,k+1);
for i=1:k+1; s1=1:j1-1; s2=j1+1:j2-1; s3=j2+1:R; Q=M(:,i)';
Qnew=[Q(s1) Q(s2) Q(s3) bottom(i)]; N(:,i)=Qnew';
end R=R-1; M=N; End R=R-1; M=N; end
z=M(1,2:k+1); y=sort(z);
Al ejecutarlo, tenemos:
𝒉𝒖𝒇𝒇𝒎𝒂𝒏code ([1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 3 4 5 6])
Y usted verá el vector Kraft [1 2 4 4 4 4] impreso en la pantalla.
Esto significa que el código Huffman para el vector de datos [1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 3 4 5 6] es un código (1; 2; 4; 4; 4; 4).
entonces, usted verá el siguiente conjunto de palabras código prefijo para el código Huffman impreso en la pantalla:
0 10 1100 1101 1110 1111 Códigos 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 extendidos
En el caso en que el tamaño del alfabeto sea grande la desviación de la longitud con respecto a la entropía es pequeño, esto no se cumple para tamaños pequeños en donde la desviación es grande.
En este último caso se codifican bloques de símbolos para reducir la rata del código, logrando que la longitud del código de 𝒏 símbolos tenga una rata
𝑯(𝑺) ≤ 𝑳 ≤ 𝑯(𝑺) +𝟏 𝒏
Esto genera un alfabeto de tamaño 𝒒𝒏 siendo 𝒒 el tamaño del alfabeto original y 𝒏 el número
de símbolos concatenados
Ejemplo: considera una fuente que pone letras independientes e idénticamente distribuidas (iid) de un alfabeto 𝑨 = {𝒂𝟏, 𝒂𝟐, 𝒂𝟑} con un modelo de probabilidad 𝑷(𝒂𝟏) = 𝟎. 𝟖,
𝑷(𝒂𝟐) = 𝟎. 𝟎𝟐, 𝑷(𝒂𝟑) = 𝟎. 𝟏𝟖. La entropía para esta fuente es 𝟎. 𝟖𝟏𝟔 𝒃𝒊𝒕/𝒔í𝒎𝒃𝒐𝒍𝒐. Un
código 𝐻𝑢𝑓𝑓𝑚𝑎𝑛 para esta fuente se muestra en la tabla 7. Letra Palabra de código
𝒂𝟏 𝟎
𝒂𝟐 𝟏𝟏
𝒂𝟑 𝟏𝟎
Tabla 7: Código 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 para la fuente del ejemplo
La longitud promedio para este código es de 𝟏. 𝟐 𝒃𝒊𝒕/𝒔í𝒎𝒃𝒐𝒍𝒐. La redundancia para este código es de 𝟎. 𝟑𝟖𝟒 𝒃𝒊𝒕/𝒔í𝒎𝒃𝒐𝒍𝒐, lo cual representa el 𝟒𝟕% de la entropía. Esto significa que se está utilizando un código que requiere un 𝟒𝟕% más de la longitud mínima requerida. Para la fuente descrita en el ejemplo previo, en vez de generar una palabra de código para cada símbolo, generaremos una palabra de código para cada dos símbolos, lo que implica que tomamos los símbolos por pares y que el tamaño del alfabeto extendido es 𝟑𝟐 = 𝟗. El
Letra Probabilidad Código
𝒂𝟏𝒂𝟏 𝟎. 𝟔𝟒 𝟎
𝒂𝟏𝒂𝟐 𝟎. 𝟎𝟏𝟔 𝟏𝟎𝟏𝟎𝟏
𝒂𝟏𝒂𝟑 𝟎. 𝟏𝟒𝟒 𝟏𝟏
𝒂𝟐𝒂𝟏 𝟎. 𝟎𝟏𝟔 𝟏𝟎𝟏𝟎𝟎𝟎 𝒂𝟐𝒂𝟐 𝟎. 𝟎𝟎𝟎𝟒 𝟏𝟎𝟏𝟎𝟎𝟏𝟎𝟏 𝒂𝟐𝒂𝟑 𝟎. 𝟎𝟎𝟑𝟔 𝟏𝟎𝟏𝟎𝟎𝟏𝟏
𝒂𝟑𝒂𝟏 𝟎. 𝟏𝟒𝟒 𝟏𝟎𝟎
𝒂𝟑𝒂𝟐 𝟎. 𝟎𝟎𝟑𝟔 𝟏𝟎𝟏𝟎𝟎𝟏𝟎𝟎 𝒂𝟑𝒂𝟑 𝟎. 𝟎𝟑𝟐𝟒 𝟏𝟎𝟏𝟏
Tabla 8: Modelo de probabilidad y código 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 para la fuente extendida del ejemplo
La longitud promedio de palabra para este código extendido es 𝟏. 𝟕𝟓𝟔 𝒃𝒊𝒕/𝒔𝒊𝒎𝒃𝒐𝒍𝒐. Sin embargo, cada simbolo en el alfabeto extendido corresponde a dos simbolos del alfabeto original. Luego en términos del alfabeto original, la longitud promedio de palabra de código es de 𝟎. 𝟖𝟕𝟓𝟖 𝒃𝒊𝒕/𝒔í𝒎𝒃𝒐𝒍𝒐. La redundancia es de cerca de 𝟎. 𝟎𝟔 𝒃𝒊𝒕/𝒔í𝒎𝒃𝒐𝒍𝒐, lo cual es poco más del 7% de la entropía.
Códigos 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 no binarios. Códigos compactos 𝒓 − 𝒂𝒓𝒊𝒐𝒔
Se muestra que el procedimiento de generación de un código compacto cuando el alfabeto código consta de 𝒓 𝑠í𝑚𝑏𝑜𝑙𝑜𝑠 consiste de las mismas tres etapas.
En este caso resulta el inconveniente que al reducir las fuentes la última no tenga 𝒓 𝑠í𝑚𝑏𝑜𝑙𝑜𝑠 para asignarles palabras de longitud 𝟏 ya que al reducir, la fuente resultante tiene 𝒓 − 𝟏 𝑠í𝑚𝑏𝑜𝑙𝑜𝑠 con respecto a la anterior.
Fuente original Fuentes reducidas Símbolo Probabilidad Palabra 𝑆1 𝑆2 𝑆3
𝑠1 0.22 2 0.22 2 0.23 1 0.4 0
𝑠2 0.15 3 0.15 3 0.22 2 0.23 1
𝑠3 0.12 00 0.12 00 0.15 3 0.22 2
𝑠4 0.10 01 0.10 01 0.12 00 0.15 3
𝑠5 0.10 02 0.10 02 0.10 01
𝑠6 0.08 03 0.08 03 0.10 02
𝑠7 0.06 11 0.07 10 0.08 03
𝑠8 0.05 12 0.06 11
𝑠9 0.05 13 0.05 12
𝑠10 0.04 100 0.05 13
𝑠11 0.03 101
𝑠12 0.00 102
𝑠13 0.00 103
Ejemplo: Se dispone de una fuente 𝑺 de memoria nula de 𝟏𝟑 𝒔í𝒎𝒃𝒐𝒍𝒐𝒔, cuyas probabilidades se representan en la tabla 9. En ella se enumeran los códigos compactos (𝐻𝑢𝑓𝑓𝑚𝑎𝑛) correspondientes a alfabetos de 2 a 13 símbolos
𝑷(𝒔𝒊) 𝒔𝒊 13 12 11 10 9 8 7 6 5 4 3 2
𝟏/𝟒 𝒔𝟏 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎𝟎
𝟏/𝟒 𝒔𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 𝟏 𝟏 𝟏 𝟏 𝟏 𝟏 𝟎𝟏
𝟏/𝟏𝟔 𝒔𝟑 𝟐 𝟐 𝟐 𝟐 𝟐 𝟐 𝟐 𝟐 𝟐 𝟐𝟎 𝟐𝟎𝟎 𝟏𝟎𝟎𝟎
𝟏/𝟏𝟔 𝒔𝟒 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑 𝟑𝟎 𝟐𝟏 𝟐𝟎𝟏 𝟏𝟎𝟎𝟏
𝟏/𝟏𝟔 𝒔𝟓 𝟒 𝟒 𝟒 𝟒 𝟒 𝟒 𝟒 𝟒 𝟑𝟏 𝟐𝟐 𝟐𝟎𝟐 𝟏𝟎𝟏𝟎
𝟏/𝟏𝟔 𝒔𝟔 𝟓 𝟓 𝟓 𝟓 𝟓 𝟓 𝟓 𝟓𝟎 𝟑𝟐 𝟐𝟑 𝟐𝟏𝟎 𝟏𝟎𝟏𝟏
𝟏/𝟏𝟔 𝒔𝟕 𝟔 𝟔 𝟔 𝟔 𝟔 𝟔 𝟔𝟎 𝟓𝟏 𝟑𝟑 𝟑𝟎 𝟐𝟏𝟏 𝟏𝟏𝟎𝟎 𝟏/𝟏𝟔 𝒔𝟖 𝟕 𝟕 𝟕 𝟕 𝟕 𝟕𝟎 𝟔𝟏 𝟓𝟐 𝟑𝟒 𝟑𝟏 𝟐𝟏𝟐 𝟏𝟏𝟎𝟏 𝟏/𝟏𝟔 𝒔𝟗 𝟖 𝟖 𝟖 𝟖 𝟖𝟎 𝟕𝟏 𝟔𝟐 𝟓𝟑 𝟒𝟎 𝟑𝟐 𝟐𝟐𝟎 𝟏𝟏𝟏𝟎
𝟏/𝟔𝟒 𝒔𝟏𝟎 𝟗 𝟗 𝟗 𝟗𝟎 𝟖𝟏 𝟕𝟐 𝟔𝟑 𝟓𝟒 𝟒𝟏 𝟑𝟑𝟎 𝟐𝟐𝟏 𝟏𝟏𝟏𝟏𝟎𝟎
𝟏/𝟔𝟒 𝒔𝟏𝟏 A A 𝑨𝟎 𝟗𝟏 𝟖𝟐 𝟕𝟑 𝟔𝟒 𝟓𝟓𝟎 𝟒𝟐 𝟑𝟑𝟏 𝟐𝟐𝟐𝟎 𝟏𝟏𝟏𝟏𝟎𝟏 𝟏/𝟔𝟒 𝒔𝟏𝟐 𝑩 𝑩𝟎 𝑨𝟏 𝟗𝟐 𝟖𝟑 𝟕𝟒 𝟔𝟓 𝟓𝟓𝟏 𝟒𝟑 𝟑𝟑𝟐 𝟐𝟐𝟐𝟏 𝟏𝟏𝟏𝟏𝟏𝟎 𝟏/𝟔𝟒 𝒔𝟏𝟑 𝑪 𝑩𝟏 𝑨𝟐 𝟗𝟑 𝟖𝟒 𝟕𝟓 𝟔𝟔 𝟓𝟓𝟐 𝟒𝟒 𝟑𝟑𝟑 𝟐𝟐𝟐𝟐 𝟏𝟏𝟏𝟏𝟏𝟏
𝑳̅ 𝟏 𝟑𝟑
𝟑𝟐 𝟔𝟕 𝟔𝟒
𝟏𝟕 𝟏𝟔
𝟗 𝟖
𝟏𝟗 𝟏𝟔
𝟓 𝟒
𝟖𝟕 𝟔𝟒
𝟐𝟑 𝟏𝟔
𝟐𝟓 𝟏𝟔
𝟏𝟑𝟏 𝟔𝟒
𝟐𝟓 𝟖
Tabla 9: Códigos 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 de diferentes longitudes para una fuente de 𝟏𝟑 𝒔í𝒎𝒃𝒐𝒍𝒐𝒔.
Aplicaciones del código 𝑯𝒖𝒇𝒇𝒎𝒂𝒏
o Compresión de imagen sin pérdidas
Ilustración 5: Imágenes a codificar.
Nombre imagen Bits/pixel Tamaño total(bytes) Rata de compresión
Sena 7.01 57504 1.14
Sensin 7.49 61430 1.07
Tierra 4.94 40534 1.62
Omaha 7.12 58374 1.12
Tabla 10: Compresión usando códigos 𝑯𝒖𝒇𝒇𝒎𝒂𝒏 sobre los valores de pixeles
Nombre imagen Bits/pixel Tamaño total(bytes) Rata de compresión
Sena 4.02 32968 1.99
Sensin 4.70 38541 1.70
Tierra 4.13 33880 1.93
Omaha 6.42 52643 1.24
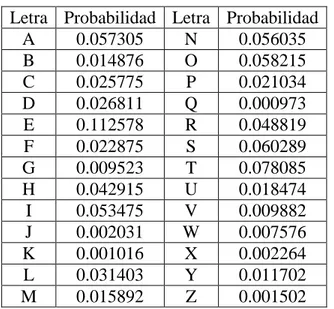
o Compresión de texto
Letra Probabilidad Letra Probabilidad
A 0.057305 N 0.056035
B 0.014876 O 0.058215
C 0.025775 P 0.021034
D 0.026811 Q 0.000973
E 0.112578 R 0.048819
F 0.022875 S 0.060289
G 0.009523 T 0.078085
H 0.042915 U 0.018474
I 0.053475 V 0.009882
J 0.002031 W 0.007576
K 0.001016 X 0.002264
L 0.031403 Y 0.011702
M 0.015892 Z 0.001502
Tabla 12: Probabilidades de ocurrencia de las letras en el alfabeto inglés en el texto de la constitución de los estados unidos.
Letra Probabilidad Letra Probabilidad
A 0.049855 N 0.048039
B 0.016100 O 0.050642
C 0.025835 P 0.015007
D 0.030232 Q 0.001509
E 0.097434 R 0.040492
F 0.019754 S 0.042657
G 0.012053 T 0.061142
H 0.035723 U 0.015794
I 0.048783 V 0.004988
J 0.000394 W 0.012207
K 0.002450 X 0.003413
L 0.025835 Y 0.008466
M 0.016494 Z 0.001050
Tabla 13: probabilidad de ocurrencia de las letras del alfabeto ingles en este capítulo
o Compresión de audio
Nombre archivo
Tamaño original (bytes)
Entropía (bits)
Tamaño estimado de archivo comprimido
Rata de compresión
Mozart 939862 12.8 725420 1.30
Cohn 402442 13.8 349300 1.15
Mir 884020 13.7 759540 1.16
Tabla 14: Codificación Huffman de audio de calidad CD de 16 bits.
Nombre archivo
Tamaño original (bytes)
Entropía (bits)
Tamaño estimado de archivo comprimido
Rata de compresión
Mozart 939862 9.7 569792 1.65
Cohn 402442 10.4 261590 1.54
Mir 884020 10.9 602240 1.47