32
INERCIA ROTACIONAL DE UNA MASA PUNTUAL
OBJETIVO.
Encontrar la inercia rotacional de una masa puntual y verificar si corresponde al valor teórico.
FUNDAMENTO TEORICO
El momento de inercia o inercia rotacional es una magnitud que da cuenta de cómo es la distribución de masas de un cuerpo o un sistema de partículas alrededor de uno de sus puntos. En el movimiento de rotación, este concepto desempeña un papel análogo al de la masa inercial en el caso del movimiento rectilíneo y uniforme.
Representa la resistencia que presenta un cuerpo a cambiar su estado de movimiento rotacional. El momento de inercia (escalar) de una masa puntual rotando alrededor de un eje conocido se define por
𝐼 = 𝑚𝑟2 Donde:
m es la masa del punto y r es la distancia entre la partícula y el eje de rotación (medida perpendicularmente a dicho eje).
Dado un eje arbitrario, para un sistema de partículas se define como la suma de los productos entre las masas de las partículas que componen un sistema, y el cuadrado de la distancia r de cada partícula al eje escogido. Matemáticamente se expresa como:
𝐼 = ∑ 𝑚𝑟2
Para un cuerpo de masa continua (Medio continuo) lo anterior se generaliza como:
𝐼 = lim
∆𝑚𝑖→0
∑ 𝑟𝑖2∆𝑚𝑖 = ∫ 𝑟2𝑑𝑚
En esta expresión, el subíndice V de la integral indica que hay que integrar sobre todo el volumen del cuerpo, generalmente se reescribe dm en términos de la densidad del objeto, es decir.
𝐼 = ∫ 𝜌𝑟2𝑑𝑉
Como se menciono anteriormente, este concepto desempeña en el movimiento de rotación un papel análogo al de masa inercial en el caso del movimiento rectilíneo y uniforme. La masa es la resistencia que presenta un cuerpo a ser acelerado en traslación, mientras que el Momento de Inercia es la resistencia que presenta un cuerpo a ser acelerado en rotación.
Así, por ejemplo, la segunda ley de Newton tiene como equivalente para la rotación:
∑ 𝜏 = 𝐼𝛼
donde
33
I es el momento de inercia del cuerpo con respecto al eje de rotación y a es la aceleración angular.
Teorema de Steiner o Teorema de los ejes paralelos
El teorema de Steiner establece que el momento de inercia con respecto a cualquier eje paralelo a un eje que pasa por el centro de gravedad, es igual al momento de inercia con respecto al eje que pasa por el centro de gravedad mas el producto de la masa por el cuadrado de la distancia entre los dos ejes:
𝐼 = 𝐼𝐶𝑀+ 𝑀𝐷2
donde:
I es el momento de inercia respecto al eje de rotación (que no pasa por el centro de masa); ICM es el momento de inercia para un eje paralelo al anterior y que pasa por el centro de masa;
M es la masa del objeto que rota; y
D es la distancia entre los dos ejes paralelos considerados
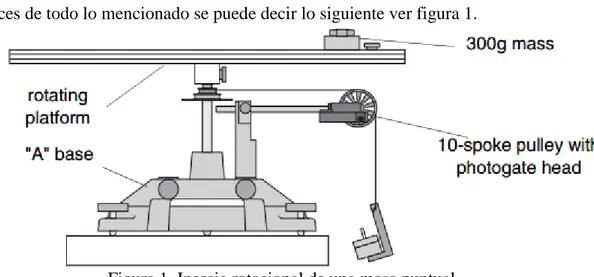
Entonces de todo lo mencionado se puede decir lo siguiente ver figura 1.
Figura 1. Inercia rotacional de una masa puntual.
Entonces se sabe que una masa está dada por 𝐼 = 𝑀𝑅2, donde M es la masa y R es la distancia de la masa desde el eje de rotación
Para encontrar la inercia de rotación experimentalmente se conoce que el torque se aplica al objeto y se mide la aceleración angular resultante. Dado que: 𝜏 = 𝐼𝛼
𝐼 = 𝜏 𝛼
donde α es la aceleración angular que es igual 𝑎
𝑟 y 𝜏 es el momento de torsión, provocad por el peso que cuelga de un hilo que se envuelve alrededor de la base del aparato.
𝜏 = 𝑟𝑇
34
También para esto se realiza dos tipos de análisis, uno tomando el sistema con la masa colgando de bajada y el otro análisis tomando el sistema con la masa colgante de subida
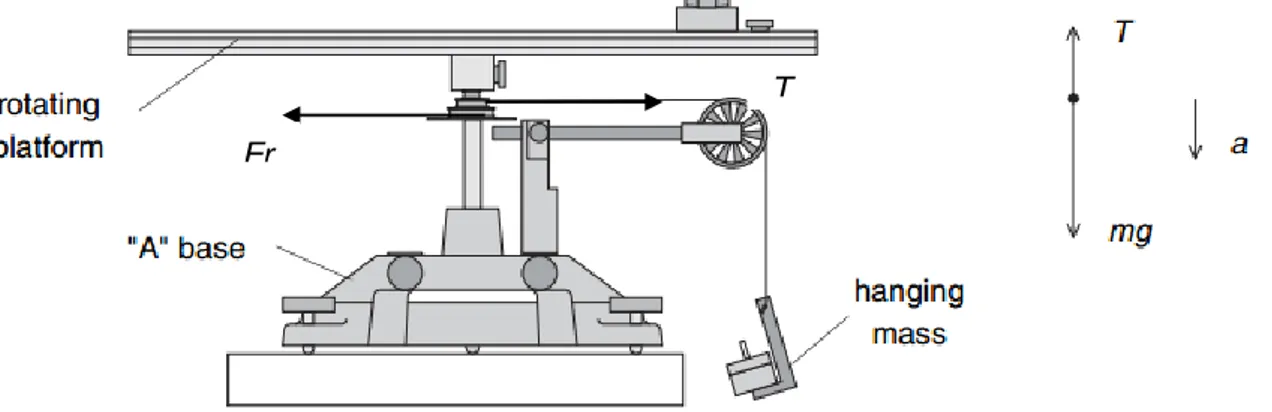
Aplicando la segunda ley de Newton para la masa que cuelga, en el movimiento de bajada (Ver Figura 2)
Figura 2: Aparato de rotación y su diagrama de cuerpo libre de una masa colgante de bajada.
∑ 𝐹 = 𝑚𝑔 − 𝑇 = 𝑚𝑎 ↓
Despejando en función de la tensión obtenemos:
𝑇 = 𝑚𝑔 − 𝑚𝑎 𝑇 = 𝑚(𝑔 − 𝑎 ↓) (1)
Realizando la sumatoria del momento de torsión del sistema se tiene:
∑ 𝜏 = 𝑟𝑇 − 𝜏𝐹𝑟 = 𝐼𝛼
Donde 𝑎 ↓= 𝑟 𝛼
despejando se tiene: 𝛼 =𝑎↓
𝑟
reemplazando se obtiene lo siguiente:
𝑟𝑇 − 𝜏𝐹𝑟 = 𝐼𝑎↓
𝑟 (2)
Reemplazando la ecuación (1) en (2) se obtiene:
𝑟𝑚(𝑔 − 𝑎 ↓) − 𝜏𝐹𝑟 = 𝐼𝑎↓
𝑟 (3)
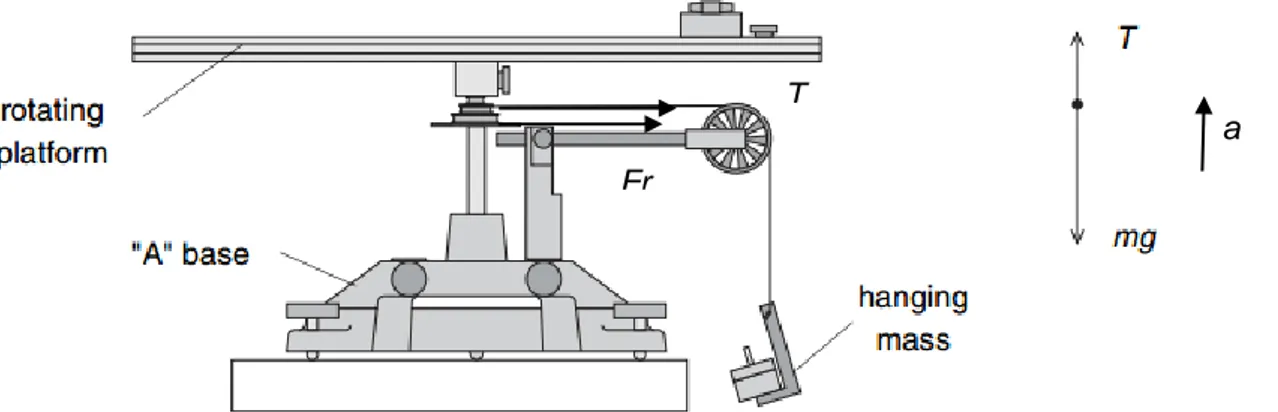
Aplicando la segunda ley de Newton para la masa que cuelga, en el movimiento de subida (Ver Figura 3)
Fr
35
Figura 3 : Aparato de rotación y su diagrama de cuerpo libre de una masa colgante de subida.
∑ 𝐹 = 𝑇 − 𝑚𝑔 = 𝑚𝑎 ↑
Despejando en función de la tensión obtenemos:
𝑇 = 𝑚𝑔 + 𝑚𝑎 𝑇 = 𝑚(𝑔 + 𝑎 ↑) (4)
Realizando la sumatoria del momento de torsión del sistema se tiene:
∑ 𝜏 = 𝑟𝑇 + 𝜏𝐹𝑟 = 𝐼𝛼 Donde 𝑎 ↑= 𝑟 𝛼
despejando se tiene: 𝛼 =𝑎↑
𝑟
reemplazando se obtiene lo siguiente:
𝑟𝑇 + 𝜏𝐹𝑟 = 𝐼𝑎↑
𝑟 (5)
Reemplazando la ecuación (4) en (5) se obtiene:
𝑟𝑚(𝑔 + 𝑎 ↑) + 𝜏𝐹𝑟 = 𝐼𝑎↑
𝑟 (6)
Una vez que se determina las ecuaciones correspondientes se pueden obtener para el cálculo de la inercia de rotación. de la siguiente manera:
𝑟𝑚(𝑔 − 𝑎 ↓) − 𝜏𝐹𝑟 = 𝐼𝑎↓
𝑟 (3)
𝑟𝑚(𝑔 + 𝑎 ↑) + 𝜏𝐹𝑟 = 𝐼𝑎↑
𝑟 (6)
𝑟𝑚(𝑔 − 𝑎 ↓) + 𝑟𝑚(𝑔 + 𝑎 ↑) = 𝐼𝑎↓
𝑟 + 𝐼 𝑎↑
𝑟
Reordenado la expresión obtenida
𝑟2𝑚 (2𝑔 − 𝑎 ↓ + 𝑎 ↑) = 𝐼(𝑎 ↓ +𝑎 ↑)
Entonces el momento de Inercia está definido como:
a Fr
36
𝐼 =
𝑟2𝑚 (2𝑔−𝑎↓+ 𝑎↑) (𝑎↓+𝑎↑) (7)PROCEDIMIENTO
Realice los cálculos para el momento de Inercia teórica presentado en la tabla 1.
Inercia teórica de la masa puntual (gr cm2)
Inercia teórica de la plataforma giratoria. (gr cm2)
Inercia teórica total (gr cm2)
Tabla 1. Datos Teóricos del Momento de Inercia.
Parte 1.
1. Nivele la plataforma giratoria (masa de la plataforma 565,8 gr).
2. Coloque la masa cuadrada (masa puntual 300 gr) a la pista en la plataforma giratoria en cualquier radio que desee.
3. Monte el sistema Fotosensor, Polea a la base y conectar el Fotosensor a una interfaz de un ordenador Science Workshop 7500. Consulte la Figura 2.
4. Coloque un hilo alrededor de la plataforma giratoria (Diámetro de giro 3,03 cm) y que pase por la polea, para que este sujete una masa colgante, la masa no debe exceder los 90gr.
5. Enrolle el hilo alrededor de la plataforma giratoria.
6. deje caer la masa colgante, registre los datos por medio de la Interfaz. Science Workshop 7500 y anote los datos en la tabla 1.
7. Determine la velocidad de cada muestra en la polea mediante la expresión
𝑉 =
𝑠𝑡 ,
donde S es el arco de la medida de la polea en cm.
8. Obtenga el valor de la aceleración de bajada (𝑎 ↓) con un análisis velocidad-tiempoacumulado.
Parte 2.
1. Realice la calibración respectiva del mismo sistema mencionado en el procedimiento de la parte 1.
2. Coloque la misma masa colgante que la parte 1. 3. Deje el hilo desenrollado de la plataforma giratoria.
4. Por medio de una fuerza externa gire la plataforma y este enrollara el hilo con la masa colgante, registre los datos por medio de la Interfaz. Science Workshop 7500. y anote los datos en la tabla 2.
5. Determine la velocidad de cada muestra en la polea mediante la expresión
𝑉 =
𝑠 𝑡 , donde S es el arco de la medida de la polea.6. Obtenga el valor de la aceleración de subida (𝑎 ↑) con un análisis velocidad-
tiempoacumulado. En este caso tenga en cuenta que la aceleración de subida se considerará
37 DATOS
Tabla 2. Sistema con masa colgante de bajada.
masa colgante m (gr) =_________
N° t (s) V (cm/s)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 17 18 19 20
Tabla 3. Sistema con masa colgante de subida.
masa colgante m (gr) =_________
N° t (s) V (cm/s)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15