Optimización Del Ángulo De Transmisión Del Mecanismo Articulado De Cuatro Barras De Una Bicicleta Elíptica

UNIVERSIDAD NACIONAL DE TRUJILLO

FACULTAD DE INGENIERÍA

ESCUELA ACADÉMICO PROFESIONAL

DE INGENIERÍA MECÁNICA

OPTIMIZACIÓN DEL ÁNGULO DE TRANSMISIÓN DEL

MECANISMO ARTICULADO DE CUATRO BARRAS DE UNA

BICICLETA ELÍPTICA

TESIS PARA OBTENER EL TÍTULO PROFESIONAL DE

INGENIERO MECÁNICO

AUTOR:

Br. NOÉ SAMUEL GARCÍA SERNA

ASESOR:

Mg. Ing. LEÓN LESCANO JAVIER EDWARD

TRUJILLO – PERÚ

PRESENTACIÓN

SEÑORES MIEMBROS DEL JURADO:

De conformidad con lo estipulado por el reglamento de grados y títulos de la Escuela Profesional de Ingeniería Mecánica de la Universidad Nacional de Trujillo, presento a su consideración el presente trabajo de Investigación titulado: “OPTIMIZACIÓN DEL ANGULO DE TRANSMISIÓN DEL MECANISMO ARTICULADO DE CUATRO

BARRAS DE UNA BICICLETA ELÍPTICA. “

El presente trabajo se realizó con la finalidad de mejorar la transmisión de la fuerza que ejercemos sobre la bicicleta elíptica. De manera que se determinó el dimensionamiento optimo y se cuantifico la mejora a través del ángulo de transmisión y la ventaja mecánica.

Para su ejecución se emplearon los conocimientos básicos de teoría de máquinas y mecanismos, y los fundamentos de la metodología de la investigación científica.

Trujillo, agosto del 2017

DEDICATORIA

A DIOS por brindarme vida y salud, además de acompañarme en cada paso que he

dado a través de mi vida familiar, social, académica y laboral.

A mis padres, Fernando y Mariela, por su apoyo incondicional a través de mi camino

académico, profesional y familiar. Sobre todo, por confiar en mí y bridarme su amor por, sobre todo.

A mi hermana, Zoila, por demostrarme y enseñarme el valor de luchar por nuestros

ideales a pesar de todas las adversidades, por más fuertes que sean.

A mis Familiares: Nelly Sánchez, Andrés García y a todos aquellos que participaron

AGRADECIMIENTO

Agradezco a DIOS por haber guiado mis pasos desde la niñez, por acompañarme siempre en los momentos más difíciles de mi vida, por guiarme y guardarme de las vicisitudes de la vida.

A mis padres Fernando García Carranza y Mariela Serna Cueva por darme la vida, por brindarme su apoyo y la paciencia que tuvieron para encaminar mis pasos hasta este momento.

A mi querida hermana Zoila, la cual confió en mi para llegar hasta esta instancia, la recuerdo con el mejor de los sentimientos fraternos.

A mis profesores quienes con su profesionalismo y ética puesto de manifiesto en las aulas enrumban a cada uno de los que acudimos a ellos, en busca del saber.

Al Ing. Javier León Lescano, por su apoyo incondicional y sincero para llevar a cabo

ÍNDICE PAGINA

TITULO i

PRESENTACIÓN ii

DEDICATORIA iii

AGRADECIMIENTO iv

ÍNDICE v

LISTA DE FIGURAS viii

LISTA DE TABLAS xi

RESUMEN xii

ABSTRACT xiii

CAPITULO I : INTRODUCCIÓN 1

1.1 Realidad problemática 1

1.2 Enunciado del problema 2

1.3 Hipótesis 2

1.4 Justificación 2

1.5 Objetivos 3

1.5.1 Objetivos generales 3

1.5.2 Objetivos específicos 3

CAPITULO II : FUNDAMENTOS TEÓRICOS 4

2.1 Antecedentes 4

2.2 Marco teórico 5

2.2.1 Ejercicio cardiovascular 5

2.2.2 Bicicleta elíptica 6

2.2.3 Condición Grashof 7

2.2.4 Angulo de transmisión 8

2.2.4.1 Valor extremo del ángulo de transmisión 9

2.2.5 Números complejos como vectores 11

2.2.6 Generación de movimiento de tres posiciones mediante síntesis analítica

11

2.2.6.1 La diada WZ 12

2.2.6.2 La diada US 15

2.2.7 Círculos con punto en el círculo y punto en el centro 15

2.2.8 Regla de Kennedy 18

2.2.9 Ventaja mecánica 19

2.2.11 Análisis de aceleración 22

2.2.12 Soluciones analíticas para el análisis de aceleración 23

2.2.13 Momento de inercia de masa 25

2.2.14 Análisis de fuerzas de una mecanismo de cuatro barras 26

2.3 Definición de términos 29

CAPITULO III: MATERIALES Y MÉTODOS 30

3.1 Material de estudio 30

3.2 Metodología 30

3.2.1 Variables 30

3.2.2 Población 31

3.2.3 Muestra 31

3.2.4 Tipo de estudio 31

3.3 Técnicas de recopilación y procesamiento de la información 31

3.4 Procedimiento 31

CAPITULO IV : RESULTADOS 33

4.1 Datos iniciales del mecanismo 33

4.1.1 Calculo del ángulo ϕ inicial 33

4.1.2 Calculo de γ3 y γ2 ideal 39

4.1.2.1 Iteración de γ3 39

4.1.2.2 Iteración de γ2 44

4.2 Síntesis analítica 49

4.2.1 Síntesis analítica cuando γ3 = -45.5° 49

4.2.2 Síntesis analítica cuando γ2 = -35° 60

4.2.3 Reacciones del eslabón V y U del mecanismo inicial 61

4.3 Angulo de transmisión del mecanismo inicial 77

4.3.1 Iteración de β2 80

4.3.2 Iteración de β3 90

4.4 Calculo de la ventaja mecánica 99

4.4.1 Calculo de ventaja mecánica del mecanismo inicial 99

4.4.2 Calculo de la ventaja mecánica cuando β3 = -160° 102

CAPITULO V : DISCUSIÓN DE RESULTADOS 120

CAPITULO VI: CONCLUSIONES Y RECOMENDACIONES 121

6.1 Conclusiones 121

6.2 Recomendaciones 122

CAPITULO VII : REFERENCIAS BIBLIOGRÁFICAS 123

LISTA DE FIGURAS PAGINA

CAPITULO II : FUNDAMENTOS TEÓRICOS 4

Fig. 2.1 Diversos ejercicios cardiovasculares 5

Fig. 2.2 Musculatura que accionamos en la elíptica 6

Fig. 2.3 Mecanismo Grashof 7

Fig. 2.4 Angulo de transmisión 𝜇 8

Fig. 2.5 Interpretación del ángulo de transmisión a través de velocidades 8

Fig. 2.6 Reacciones en el eslabón de salida 9

Fig. 2.7 Valor extremo de 𝜇1, eslabones colineales y traslapados 10 Fig. 2.8 Valor extremo de 𝜇2, eslabones colineales y no traslapados 10

Fig. 2.9 Síntesis Analítica de tres posiciones 12

Fig. 2.10 Pivotes fijo y móviles del mecanismo 16

Fig. 2.11 Círculos M para valores de β2 (0° < β3 < -360°) para generación

de movimiento

17

Fig. 2.12 Localización de centros instantáneos 18

Fig. 2.13 Diagrama de ventaja mecánica 19

Fig. 2.14 Diagrama del lazo vectorial 20

Fig. 2.15 Diagrama de aceleraciones 22

Fig. 2.16 Lazo vectorial y aceleraciones mecanismo de cuatro barras 23

Fig. 2.17 Momento de inercia del cuerpo rígido respecto de Z 25

Fig. 2.18 Momento de Inercia de un tubo hueco 25

Fig. 2.19 Análisis de fuerzas dinámicas en mecanismo de cuatro barras 27

CAPITULO III: MATERIALES Y MÉTODOS 30

Fig. 3.1 Bloque de variables 30

CAPITULO IV : RESULTADOS 33

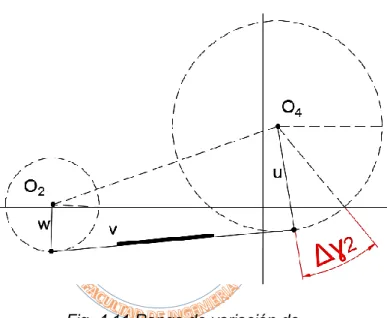
Fig. 4.1 Ubicación del ángulo de transmisión en el mecanismo inicial 34

Fig. 4.2 Configuración para el valor extremo de ϕ - traslapados 35

Fig. 4.3 Configuración para el valor extremo de ϕ – no traslapados 35 Fig. 4.4 Configuración para el valor de ϕ en el punto prescrito P1 36

Fig. 4.5 Configuración para el valor de ϕ en el punto prescrito P2 37

Fig. 4.6 Configuración para el valor de ϕ en el punto prescrito P3 38

Fig. 4.7 Rango de la variación de

𝛾

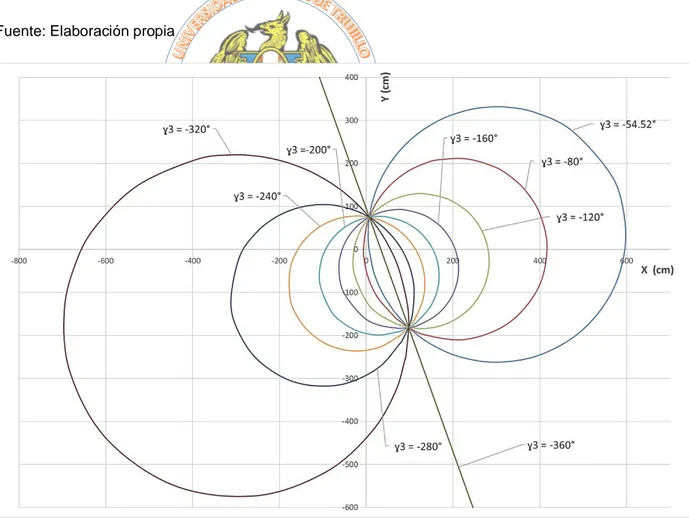
Fig. 4.8 Ubicaciones posibles de O4, según iteración de 𝛾3 39

Fig. 4.10 Comportamiento de γ3 vs ϕ 42

Fig. 4.11 Rango de variación de 𝛾2 44

Fig. 4.12 Ubicaciones posibles de O4, según iteración de 𝛾2 45

Fig. 4.13 Círculos con punto en el centro para valores γ3 (0° < γ2 < -360°) 45

Fig. 4.14 Comportamiento de γ2 vs ϕ 47

Fig. 4.15 Vectores que forman el lazo en la diada WZ en el punto P2 50

Fig. 4.16 Vectores que forman el lazo en la diada WZ en el punto P3 50

Fig. 4.17 Vectores que forman el lazo en la diada US en el punto P2 53

Fig. 4.18 Vectores que forman el lazo en la diada US en el punto P3 53

Fig. 4.19 Configuración para valor extremo de ϕ – traslapados (𝛾3= -45.5°) 58

Fig. 4.20 Configuración para valor extremo ϕ –no traslapados (𝛾3= -45.5°) 58

Fig. 4.21 Configuración para valor de ϕ en punto P3, P2, P3 (

𝛾

Fig. 4.22 Velocidades del mecanismo inicial en P1 62

Fig. 4.23 Diagrama de velocidad de punto A y B (método gráfico) 64

Fig. 4.24 Aceleraciones del mecanismo inicial en P1 66

Fig. 4.25 Diagrama de Aceleraciones de puntos A y B (método gráfico) 68

Fig. 4.26 Aceleraciones de puntos G2, G3, G4. 68

Fig. 4.27 Diagrama de aceleraciones de puntosA y G3 (método gráfico) 70

Fig. 4.28 Tubería para la construcción del mecanismo 71

Fig. 4.29 Diagrama de fuerzas del eslabón 2 72

Fig. 4.30 Vectores de posición en eslabón 2 72

Fig. 4.31 Diagrama de fuerzas del eslabón 3 73

Fig. 4.32 Vectores de posición en eslabón 3 73

Fig. 4.33 Diagrama de fuerzas del eslabón 4 74

Fig. 4.34 Vectores de posición en eslabón 4 74

Fig. 4.35 Puntos críticos de aplicación de fuerza hacia eslabón de salida. 77 Fig. 4.36 Angulo 𝜇1 en la posición prescrita P1 del mecanismo inicial 78

Fig. 4.37 Angulo 𝜇2 en la posición prescrita P2 del mecanismo inicial 78

Fig. 4.38 Angulo 𝜇3 en la posición prescrita P3 del mecanismo inicial 79

Fig. 4.39 Angulo 𝜇4 en una de la posición P4 79

Fig. 4.40 Ubicación de 𝛽2 a iterar 80

Fig. 4.41 Posiciones del punto O2, según la iteración de 𝛽2 80

Fig. 4.42-4.61 Ángulos 𝜇1, 𝜇2 ,𝜇3 ,𝜇4, cuando 𝛽2= -60°,-70°,-80°,-90°,-100° 83

Fig. 4.62 Ubicación de 𝛽3 a iterar 90

Fig. 4.64-4.83 Ángulos 𝜇1,𝜇2,𝜇3,𝜇4 cuando 𝛽3= -160°,-170°,-180°,-190°,-200° 93

Fig. 4.84 Ubicación de fuerza de entrada y salida del mecanismo inicial 100

Fig. 4.85 Dimensiones necesarias para el cálculo de G3 103

Fig. 4.86 Velocidades del mecanismo en P1 cuando 𝛽3 = -160° 103

Fig. 4.87 Diagrama de velocidad de punto A y B (mediante método gráfico) 105

Fig. 4.88 Aceleración del punto A y B 106

Fig. 4.89 Diagrama de aceleraciones de punto A y B (método gráfico) 108

Fig. 4.90 Aceleraciones de centros de gravedad de eslabones 109

Fig. 4.91 Diagrama aceleraciones centros de gravedad (método gráfico) 110

Fig. 4.92 Distancias usadas en el Teorema de ejes paralelos 112

Fig. 4.93 Diagrama de fuerzas del eslabón 2 113

Fig. 4.94 Vectores de posición en eslabón 2 113

Fig. 4.95 Diagrama de fuerzas del eslabón 3 113

Fig. 4.96 Vectores de posición en eslabón 3 114

Fig. 4.97 Diagrama de fuerzas del eslabón 3 114

Fig. 4.98 Vectores de posición en eslabón 4 115

Fig. 4.99 Ubicación de fuerza entrada y salida mecanismo modif. 𝛽3=-160 117

ANEXOS 125

Figura A. Síntesis Analítica del mecanismo inicial 125

Figura B. Síntesis Analítica del mecanismo modificado 126

Figura C. Calculo de ventaja mecánica del mecanismo inicial en punto P1 127

Figura D. Cálculo de ventaja mecánica del mecanismo optimizado pto. P1 128

Figura E. Dimensiones del mecanismo inicial de 4 barras 129

Figura F. Mecanismo optimizado por ángulo transmisión y ventaja mec. 129

Figura G. Distancia G del eslabón 1 130

Figura H. Distancia W del eslabón 2 131

Figura I. Distancia V del eslabón 3 132

Figura J. Distancia Z del eslabón 3 133

Figura K. Distancia S del eslabón 3 134

LISTA DE TABLAS PAGINA

CAPITULO III: MATERIALES Y MÉTODOS 30

Tabla 3.1 Tabla de materiales 30

CAPITULO IV : RESULTADOS 33

Tabla 4.1 Medidas de eslabones iniciales 33

Tabla 4.2 Iteración de γ3 para ubicación de O4 41

Tabla 4.3 Valores extremos de ϕ para la iteración de γ3 43

Tabla 4.4 Iteración de γ2 para ubicación de O4 46

Tabla 4.5 Valores extremos de ϕ para la iteración de γ2 48

Tabla 4.6 Valores hallados de la síntesis analítica, con γ3 = -45.5° 57

Tabla 4.7 Valores hallados de la síntesis analítica, con γ2 = -35° 60

Tabla 4.8 Comparación de reacciones interiores en el eslabón U 76

Tabla 4.9 Coordenadas del O2, según la iteración de β2 81

Tabla 4.10 Coord. de O2, según iteración β2 y restricciones establecidas 82

Tabla 4.11 Ángulos de transmisión, donde se cumplen las restricciones(β2) 88

Tabla 4.12 Ángulos de transmisión de puntos interés, según iteración β2 89

Tabla 4.13 Ángulos transmisión de posibilidades (β2) que optimizan μinicial 89

Tabla 4.14 Coordenadas del O2, según la iteración de β3 91

Tabla 4.15 Coord. de O2, según iteración de β3 y restricciones establecidas 92

Tabla 4.16 Angulo de transmisión, donde se cumplen las restricciones (β3) 98

Tabla 4.17 Angulo de transmisión para punto de interés, según iteración β3 98

Tabla 4.18 Ángulos transmisión de posibilidades (β3) que optimizan μinicial 99

Tabla 4.19 Dimensiones para hallar G3 102

Tabla 4.20 Ventaja mecánica en los puntos críticos 119

RESUMEN

El presente trabajo titulado “Optimización del ángulo de transmisión del mecanismo articulado de cuatro barras de una bicicleta elíptica”, se desarrolló usando el método

de Generación de movimiento de tres posiciones mediante síntesis an alítica, además del proceso iterativo de los ángulos de giro de la manivela (β) y balancín(γ). Se consideró inicialmente el mecanismo con tres puntos prescritos (ubicación por donde pasa el pie del deportista), los cuales son: P1(0,0); P2(-15.12,-9); P3

(-29.128,-4). Lo cual definió posiciones de puntos fijos y longitud de los eslabones. Además, se analiza el ángulo de transmisión y ventaja mecánica, los cuales serán el parámetro de optimización. [1]

Optimizamos el ángulo de transmisión modificando los puntos fijos O2 y O4, bajo el

criterio: Circulo con punto en el centro, donde describe el espacio de las soluciones posibles. El método de Círculos con punto en el centro para O4, nos determinó dos

regiones para la variación de Ɣ2 , quees el ángulo de giro del eslabón balancín al

pasar por P2 (con Ɣ3 = -54.52°) y Ɣ3,es el ángulo de giro del eslabón balancín al

pasar por el punto P3 (conƔ2 = -29.63°), dentro de cada región hay un punto que

mejora el ángulo ϕ, ya que inicialmente el rango de este ángulo era de 48.31° hasta

90°, y se obtuvo que el punto ideal sería O4 (6.45,52.73) lo cual conlleva a un rango

de ángulo ϕ desde 64.3° hasta 90°. Se aplica el mismo procedimiento para los valores de β2 y β3 (modificación de O2), donde la posición optima es (-51.9; 9.49).

Desarrollamos un programa en Excel que realiza el proceso de síntesis analítica y análisis dinámico, la iteración con los valores de β y Ɣ nos conduce a distintos comportamientos del ángulo de transmisión. Se eligen valores óptimos del ángulo de transmisión y se determinan las dimensiones del mecanismo mejorado.

El ángulo de transmisión para las posiciones críticas y puntos prescritos del mecanismo inicial era 𝛍1= 2.68°, 𝛍2= 83.27°, 𝛍3= 7.81°, 𝛍4= 72.7°, y el valor de la

ventaja mecánica en tales posiciones era mAp1 = 0.578, mAp2= 1.02, mAp3= 0.57,

mAp4= 1.14. Pero luego de la elección de β3=-160°, el ángulo de transmisión para

el mecanismo optimizado es:1= 21.81°, 𝛍2=66.16°, 𝛍3= 3.09°, 𝛍4= 84.67° y la ventaja

mecánica es: mAp1 = 0.75, mAp2= 1.41, mAp3= 0.74, mAp4= 1.1. Entonces el

ABSTRACT

The present qualified work "Optimization of the transmission angle at the articulated mechanism of four bars in elliptical bicycle", was developed using the method of Generation of movement at three positions with analytical synthesis, also the iterative process at the angles of rotation of the crank (β) and rocker (γ).

We considered the mechanism with three prescribed points (location where the athlete's foot passes), which are: P1 (0,0); P2 (-15.12, -9); P3 (-29,128, -4). This

defined positions at fixed points and length of the links. Also, we analyze the angle of transmission and mechanical advantage, which will be the optimization parameter. [1]

We optimize the transmission angle by modifying points O2 and O4, using the theory:

Circle with point in the center, where it describes the space of the possible solutions. The method circle with center point for O4, determined two regions for the variation

of Ɣ2 it is angle of rotation when rocker pass by P2 (with Ɣ3 = -54.52 °) and Ɣ3, is

angleof rotation when rocker pass by P3 (with Ɣ2 = -29.63 °), within each region

have a point that optimize the angle ɸ, because initially the range of this angle was

48.31 ° to 90°, and we calculated that the ideal point is O4 (6.45,52.73) with a range

of angle ɸ from 64.3 ° to 90 °. The same procedure is applied for the values of β2

and β3 for the modification of O2, where the optimal position is (-51.9; 9.49).

We developed an Excel program that calculated the analytical synthesis and dynamic

analysis, iteration with the values of β and Ɣ gets different behavior of the angle of

transmission. We chose optimal values of the angle of transmission and determined

dimensions of the improved mechanism.

The transmission angle for critical positions and prescribed points of the initial

mechanism : μ1 = 2.68 °, μ2 = 83.27 °, μ3 = 7.81 °, μ4 = 72.7 °, and the value of the

mechanical advantage at this positions: mAp1 = 0.578, mAp2 = 1.02, mAp3 = 0.57, mAp4 =

1.14. But after the choice β3 = -160 °, the transmission angle for the optimized

mechanism: μ1 = 21.81 °, μ2 = 66.16 °, μ3 = 3.09 °, μ4 = 84.67 ° and the mechanical

advantage : mAp1 = 0.75 , mAp2 = 1.41, mAp3 = 0.74, mAp4 = 1.1.

Then the final sizing of the mechanism is (Link 1 = 72.64cm, Link 2 = 14.4cm, Link 3 =

67.38cm, Link 4 = 36.17cm, Link Z = 38.37cm, Link S = 36.38cm), we could be concluded

CAPITULO I

INTRODUCCIÓN

1.1 Realidad Problemática

El aumento de las enfermedades cardiovasculares es alarmante según OMS: Las ECV son la principal causa de muerte en todo el mundo. Se calcula que en 2012 murieron por esta causa 17,5 millones de personas, lo cual representa un 31% de todas las muertes registradas en el mundo. De estas muertes, 7,4 millones se debieron a cardiopatías coronarias, y 6,7 millones, a los AVC (accidente vascular cerebral) [2]. En Perú las enfermedades cardiovasculares causan el 15.5% de las muertes totales, por las malas costumbres al comer, por el consumo de tabaco, inactividad física. [3]

El ejercicio aeróbico, se basa en el desarrollo de actividades con menor intensidad que las realizadas en el ejercicio anaeróbico, pero durante periodos de tiempo más largos (andar, correr, nadar y montar en bicicleta), con el objetivo de conseguir mayor

resistencia.

[4]

La máquina ha sido diseñada para aunar una serie de movimientos en uno solo repetido de forma cíclica. Se trata de los movimientos propios del step, el running y el esquí. Nos brinda una serie de beneficios: es la máquina más completa para el trabajo cardiovascular, trabaja la musculatura tren del inferior, con bajo impacto articular. [5] Estas bicicletas tienen un sistema que se basa en la inercia del volante, esto hace que el movimiento sea fluido y, con una selección de la longitud de zancada adecuada se tiene una máquina estable. [6]

Aumentar la resistencia en la elíptica durante tus rutinas te hará más fuerte, pero es importante no exagerar. Es recomendable trabajar en un nivel de resistencia de 7 en una escala de 10, o lo suficiente para ejercitarte y poder tener una conversación a la vez. Si es demasiado fuerte, se sentirá más como castigo, y es mejor bajar la escala en

lugar de perder la motivación para tus rutinas.

[7]

1.2 Enunciado del Problema

¿Cuál es el dimensionamiento del mecanismo articulado de cuatro barras para una bicicleta elíptica, que optimiza el ángulo de transmisión en las posiciones críticas?

1.3 Hipótesis

Usando la síntesis analítica de movimiento y la teoría de círculo con punto en el centro es posible determinar el dimensionamiento correspondiente al mecanismo articulado de cuatro barras para una bicicleta elíptica que optimiza el ángulo de transmisión y la ventaja mecánica para las posiciones críticas.

1.4 Justificación

El trabajo presentado permite mejorar el desempeño motriz de las personas que se inician en el uso de la bicicleta elíptica, mejorando la actividad física, y realizar un ejercicio más continuo y con mayor confort. La investigación realizada colaborara con uno de los métodos de optimización desde el punto de vista del ángulo de transmisión y ventaja mecánica. Se aplican teorías de diseño de mecanismos. Además, ofrece una visión del comportamiento de las reacciones que actúan en los eslabones para cada una de las posiciones estudiadas.

 En lo teórico: Este trabajo no tendrá resultados que lleven a establecer un conocimiento

nuevo, si no que se aplican los conocimientos ya existentes en solución de problemas prácticos de ingeniería.

 En el procedimiento: El trabajo realizado determina ángulos de transmisión que

mejoran el mecanismo y se cuantifica esa mejora a través de la ventaja mecánica

 En lo económico: Es posible construir o modificar mecanismos de cuatro barras con

configuraciones similares a la bicicleta elíptica, mejorándolos a través de la medición del ángulo de transmisión y optimizando su ventaja mecánica.

 En lo social: Mejorar el desempeño de la bicicleta elíptica ayudara a los atletas que

1.5 Objetivos

1.5.1 Objetivos Generales

Determinar las dimensiones correspondientes al mecanismo articulado de cuatro barras para una bicicleta elíptica y optimizar el ángulo de transmisión para las posiciones críticas.

1.5.2 Objetivos Específicos

1. Determinar en el mecanismo inicial el rango de ángulos entre los eslabones V y U (ϕ), el valor de γ3 (ángulo de giro del eslabón balancín cuando pasa por el punto P3)

y γ2 (ángulo de giro del eslabón balancín cuando pasa por el punto P2) que mejoran

ϕ (ángulo que forma el eslabón balancín con el acoplador), usando la teoría de

circulo con punto en el centro.

2. Usando la síntesis analítica determinar el dimensionamiento según la mejora de γ3

y γ2, comparar las reacciones en los eslabones V y U del mecanismo inicial y del

mejorado según γ3 = -45.5°

3. Hallar los rangos de β2 (ángulo de giro del eslabón manivela cuando pasa por P2)

y β3 (ángulo de giro del eslabón manivela cuando pasa por P3) obtenidos a partir

de la teoría circulo con punto en el centro, que optimizan el ángulo de transmisión

μ del mecanismo inicial en las posiciones críticas.

CAPITULO II

FUNDAMENTOS TEÓRICOS

2.1 Antecedentes

A continuación, se presenta un breve resumen de las investigaciones realizadas que sirvieron de base, bien sea por su contenido o su metodología, para el desarrollo del presente proyecto:

 Eder Stevens Herrera Chavez (2013), en su tesis “Síntesis de un mecanismo

articulado de cuatro barras para una bicicleta elíptica con una zancada de 32 cm”

En este estudio, logra determinar la geometría de una bicicleta elíptica bajo parámetros iniciales como longitud de zancada y posición prescritas por las que pasara el pie del deportista. Finalmente obtiene los resultados y comprueba los cálculos con el programa Solidworks.

 Pinito Linares, Heriberto Augusto (2007), en su tesis “Diseño óptimo de

mecanismo de cuatro barras para generación de movimiento con restricciones de

montaje y ángulo de transmisión” asegura:

Este trabajo averigua la manera de usar una diada estándar encontrando soluciones óptimas para la generación de movimiento teniendo restricciones de montaje asociadas a los pivotes fijos. Usa la estrategia de optimización multiobjeto, ya que los valores de ángulo de transmisión son diversos, también uso la “suma ponderada de funciones” donde considera 5 posiciones prescritas.

 Pablo Roberto Herrera Lascano (2013), en su tesis “Diseño y construcción de una

máquina de gimnasio para realizar rutinas de ejercicios con fuerza relativa” afirma

lo siguiente:

2.2 Marco teórico

2.2.1 Ejercicio cardiovascular

Los ejercicios cardiovasculares, también conocidos como ejercicios aeróbicos, son los ejercicios de baja o media intensidad que dependen más de la capacidad de oxigenación que de la fuerza física y son los que más nos ayudan a quemar calorías. Los mejores ejercicios de cardio son: el baile, la natación, correr, montar en bicicleta, la maquina elíptica y el patinaje; como se muestra en le Fig.2.1 [8]

A las principiantes, se les recomienda partir con ejercicio cardiovascular de bajo impacto como andar en bicicleta estacionaria, ejercitarse en la máquina elíptica, en que trabaja toda la musculatura del cuerpo, o el trote suave en terreno plano. Si parten con 30 minutos quemarán hasta 130 calorías, aproximadamente. Deben realizarlo 2 o 3 veces a la semana. Ya en una segunda etapa, tanto en la bicicleta como en la elíptica, pueden subir la carga, aumentando la dificultad, o pueden trotar desde una velocidad moderada a carrera, utilizando en algunos tramos inclinación. Si se ejercitan unos 45 minutos quemarán hasta 220 calorías, aproximadamente. Como mínimo deben ejercitarse 3 veces a la semana. [9]

Figura 2.1 Diversos ejercicios cardiovasculares

Fuente: Adelgazar más rápido. (2011). Ejercicios cardiovasculares. [Figura]. Recuperado de:

Unas de los factores que podemos adoptar para iniciar actividades físicas es: Comienza con un ejercicio que sea muy pequeño. La mejor forma para hacer del ejercicio un hábito es comenzando con algo que sea tan fácil que lo puedas hacer aun cuando no tienes una gran motivación, “comienza con algo que sea tan fácil no puedas decir que no”. [10]

2.2.2 Bicicleta elíptica

La bicicleta elíptica es una máquina diseñada para ejercitar simultáneamente los músculos del cuerpo, suavemente y sin esfuerzo, eso inicialmente ya que puede subirse la carga paulatinamente después de crear el habito en el deportista. Esta bicicleta es una mejor alternativa que la bicicleta convencional. Una bicicleta elíptica cuenta con dos pedales fijados a dos mangos que llegan hasta la altura del hombro. Los pedales realizan el movimiento en forma ovalada mientras que los mangos se mueven de atrás para adelante, como si se estuviera remando. [11] En la Fig. 2.2 se muestra la actividad de la musculatura que trabaja en la bicicleta elíptica: los muslos, los glúteos, las pantorrillas, los brazos, los hombros, los pectorales, La bicicleta elíptica obliga a mantener la espalda recta, fortalece la cintura abdominal, incluyendo los oblicuos. [11]

Fig. 2.2 Musculatura que accionamos en la elíptica

Fuente: Esensa Pilates. (2013). Beneficios de la bicicleta elíptica. [Figura]. Recuperado de:

Un ejercicio de bajo impacto significa que la máquina elíptica requiere poca fuerza para trabajar la misma rutina que otras máquinas ofrecen. Esto se debe a que tus pies nunca dejan los pedales. Esto hace que la bicicleta de ejercicio elíptica ofrezca un ejercicio que es seguro para tus articulaciones y huesos. Además, este equipo tiene menos riesgo de lesión que las cintas caminadoras, correr o trotar. Estas bicicletas incluso son seguras para los ancianos y las personas con lesiones o problemas en las articulaciones como la artritis. También es beneficiosa para las personas que son obesas o que no están acostumbradas a hacer rutinas cansadoras. [12]

2.2.3 La condición de Grashof:

La condición de Grashof es una relación muy simple que predice el comportamiento de rotación o rotabilidad de las inversiones de un eslabonamiento de cuatro barras basado solo en las longitudes de los eslabones. Sea: S = longitud del eslabón más corto; L = longitud del eslabón más largo; P = longitud de un eslabón restante; Q = longitud de otro eslabón restante.

Luego si:

S + L ≤ P + Q (2.1)

En un eslabonamiento es de Grashof por lo menos un eslabón será capaz de realizar una revolución completa con respecto al plano de bancada (Ver Fig.2.3). Esta se llama cadena cinemática de clase I. Si la desigualdad no es cierta, entonces el eslabonamiento no es Grashof y ningún eslabón será capaz de realizar una revolución completa con respecto a cualquier otro eslabón. Esta es una cadena cinemática de clase II. [13, p.43]

Fig. 2.3 Mecanismo Grashof

2.2.4 Ángulo de transmisión

En general, se considera como el valor absoluto del ángulo agudo del par de ángulos formado en la intersección de dos eslabones y varia continuamente de un valor mínimo a un valor máximo conforme el eslabonamiento pasa por su intervalo en movimiento. Es una medida de la calidad de transmisión de fuerza y velocidad en la junta. La Fig.2.4 muestra la ubicación del ángulo de transmisión. [13, p.80]

Fig. 2.4 Angulo de transmisión 𝜇

Fuente: Adaptado de Norton Robert. Angulo de Transmisión. Diseño de maquinaria. (2005).

También se define el ángulo de transmisión (μ) como el menor ángulo (agudo) entre la dirección del vector de diferencia de velocidad del eslabón flotante y la dirección de la velocidad absoluta del eslabón de salida, ambas tomadas en el punto de conexión. (Ver Fig. 2.5) [14, p.125]

Fig. 2.5 Interpretación del ángulo de transmisión a través de las velocidades

Fuente: Adaptado de Erdman A. y Sandor G. Análisis de desplazamiento y velocidad.

La figura 2.6 muestra un par de torsión T2 aplicado al eslabón 2. Incluso antes de que

ocurra cualquier movimiento, esto provoca una fuerza colineal estática F34 a ser aplicada

por el eslabón 3 al 4 en el punto D. Sus componentes radiales y tangenciales Fr

34 y Ft34

se descomponen en forma paralela y perpendicular al eslabón 4, respectivamente. En el caso ideal, sería conveniente que toda la fuerza F34 fuera empleada para producir el

par de torsión de salida T4 en el eslabón 4. Sin embargo, sólo la componente tangencial

crea un par de torsión en el eslabón 4. La componente radial Fr34 sólo produce tensión

o compresión en el eslabón 4. Esta componente radial sólo incrementa la fricción en el pivote y no contribuye al par de torsión de salida. Por consiguiente, el valor óptimo del ángulo de transmisión es de 90°. [13, p.80]

Fig. 2.6 Reacciones en el eslabón de salida

Fuente: Adaptado de Norton Robert. Angulo de Transmisión. Diseño de maquinaria. (2005).

2.2.4.1 Valores extremos del ángulo de transmisión:

Según la geometría del mecanismo, el valor mínimo del ángulo de transmisión µmin

ocurrirá cuando los eslabones 1 y 2 se encuentran colineales y traslapados, como se muestra en la Fig. 2.7 o cuando los eslabones 1 y 2 son colineales y no traslapados, como se muestra en la Fig. 2.8. Los valores del ángulo de transmisión en estas posiciones son fáciles de calcular con la ley de cosenos. [13, p.165]

a = eslabón 2; b = eslabón 3; c = eslabón 4; d = eslabón 1

Para el caso de traslape la ley de cosenos da: (Ver fig. 2.7)

µ1 = cos -1

[

𝑏2+ 𝑐2−(𝑑−𝑎)2

y en el caso extendido, la ley de cosenos da: (Ver fig. 2.8)

µ2 = π - cos -1[

𝑏2+ 𝑐2−(𝑑+𝑎)2

2𝑏𝑐 ]

(2.3)

Fig. 2.7 Valor extremo de 𝜇1, eslabones colineales y traslapados

Fuente: Adaptado de Norton Robert. Ángulos de Transmisión. Diseño de maquinaria. (2005)

Fig. 2.8 Valor extremo de 𝜇2, eslabones colineales y no traslapados

Fuente: Adaptado de Norton Robert. Ángulos de Transmisión. Diseño de maquinaria. (2005).

El ángulo de transmisión mínimo µmin en un mecanismo de Grashof de

2.2.5 Números complejos como vectores

Existen muchas maneras de representar vectores, pueden definirse en coordenadas polares por su magnitud y ángulo o en coordenadas cartesianas como componentes x

y y.

Forma polar Forma cartesiana

𝑅@∡θ 𝑟 cos 𝜃 î + 𝑟 𝑠𝑒𝑛 𝜃 ĵ (2.4)

𝑟𝑒𝑗𝜃 _{𝑟 cos 𝜃 + 𝑗 𝑟 𝑠𝑒𝑛 𝜃 (2.5)}

La ecuación (2.4) utiliza vectores unitarios para representar las direcciones de los componentes vectoriales x y y en la forma cartesiana. La ecuación (2.5) utiliza notación de numero complejo donde el componente en la dirección X se llama parte real y el componente en la dirección Y se llama parte imaginaria. Una ventaja de utilizar esta notación de número complejo para representar vectores planos se deriva de la identidad de Euler

𝑒±𝑗𝜃 _{= cos 𝜃 ± 𝑗 sen 𝜃 (2.6)}

Se utilizará esta notación de número complejo de vectores para desarrollar y derivar las ecuaciones de posición, velocidad y aceleración de mecanismos. [13, p.153]

2.2.6 Generación de movimiento de tres posiciones mediante síntesis analítica

La figura 2.9 muestra un mecanismo de cuatro barras en una posición general, con un punto del acoplador localizado en el primer punto de precisión P1. También se muestran

la segunda y tercera posición de precisión (P2 y P3). Éstas deben ser alcanzadas por la

rotación del balancín de entrada, eslabón 2, a través β2 y β3. Se puede observar también

que los ángulos del eslabón acoplador 3 en cada uno de los puntos de precisión están definidos por los ángulos de los vectores de posición Z1, Z2 y Z3. El eslabón 4 describe

ángulos γ2, γ3 para alcanzar las posiciones P2 y P3 respectivamente.

El procedimiento de síntesis analítica de movimiento de tres posiciones es el siguiente: se sitúa el sistema de coordenadas XY global en el primer punto de precisión P1. Se

definen las otras dos posiciones de precisión en el plano con respecto a este sistema global, como se muestra en la figura 2.9. Los vectores de diferencia de posición P21

trazados de P1 a P2 y P31, trazado de P1 a P3 tienen ángulos δ2 y δ3, respectivamente.

Fig. 2.9 Síntesis Analítica de tres posiciones

Fuente: Adaptado de Norton Robert. Síntesis analítica de tres posiciones. Diseño de

maquinaria. (2005).

2.2.6.1 La díada WZ

Define la mitad izquierda del mecanismo. Los vectores Z1 y S1 están insertados en el

acoplador rígido, y ambos girarán el mismo ángulo α2 de la posición 1 a la 2 y el ángulo

α3 de la posición 1 a la 3. La longitud de pasador a pasador y el ángulo del eslabón 3

(vector V1) está definida en función de los vectores Z1 y S1.

Se escriben dos ecuaciones de lazo vectorial, una alrededor del lazo que incluye las posiciones P1 y P2, y la segunda alrededor del lazo que incluye las posiciones P1 y P3

(véase la figura 2.9). Se procede en el sentido de las manecillas del reloj alrededor del primer lazo para el movimiento de la posición 1 a la 2, al comenzar con W2 y luego se

S3

S2 S1

ψ

δ3

P2

P3

U3

U2

U1

𝜭 β3 β2

W2

W3

W1

σ

γ

γ

B1

B2

B3

A3

A2

A1

Z2

Z1

Z3

α

α

ϕ

P31

Y

X P1

G1

V1

❶ ❷

❸

escribe la segunda ecuación de lazo vectorial para el movimiento de la posición 1 a la 3 al comenzar con W3.

𝑊₂+ 𝑍₂− 𝑃₂₁− 𝑍₁− 𝑊₁ = 0

(2.7)

𝑊₃+ 𝑍₃− 𝑃₃₁− 𝑍₁− 𝑊₁ = 0

Sustituyendo por su equivalente compleja y simplificando tenemos:

𝑤𝑒𝑗𝜃_(𝑒𝑗𝛽2− 1) + 𝑧𝑒𝑗∅(𝑒𝑗𝛼2− 1) = 𝑃₂₁𝑒𝑗𝛿2

(2.8)

𝑤𝑒𝑗𝜃_(𝑒𝑗𝛽3− 1) + 𝑧𝑒𝑗∅(𝑒𝑗𝛼3− 1) = 𝑃₃₁𝑒𝑗𝛿3

Este conjunto de cuatro ecuaciones puede resolverse para cuatro incógnitas. La ecuación escalar puede revelarse al sustituir la identidad de Euler (Ec. 2.6) y separar los términos real e imaginario:

Parte real:

[𝑤 cos 𝜃](cos 𝛽2− 1)

− [𝑤 sen 𝜃] sen 𝛽2+ [𝑧 cos ∅](cos 𝛼2− 1)

− [𝑧 sen ∅] sen 𝛼2= 𝑃21cos 𝛿2

(2.9)

[𝑤 cos 𝜃](cos 𝛽₃− 1)

− [𝑤 sen 𝜃] sen 𝛽₃+ [𝑧 cos ∅](cos 𝛼₃− 1) − [𝑧 sen ∅] sen 𝛼₃= 𝑃₃₁cos 𝛿₃

(2.10)

Parte imaginaria

[𝑤 sen 𝜃](cos 𝛽2− 1)

+ [𝑤 cos 𝜃] sen 𝛽2+ [𝑧 sen ∅](cos 𝛼2− 1)

+ [𝑧 cos ∅] sen 𝛼2= 𝑃21sen 𝛿2

(2.11)

[𝑤 sen 𝜃](cos 𝛽3− 1)

+ [𝑤 cos 𝜃] sen 𝛽₃+ [𝑧 sen ∅](cos 𝛼₃− 1) + [𝑧 cos ∅] sen 𝛼₃= 𝑃₃₁sen 𝛿₃

(2.12)

Hay doce variables en las ecuaciones (2.9, 2.10, 2.11, 2.12): w, θ, β2, β3, z, ϕ, α2, α3,

enunciado del problema: α2, α3, P21, P31, δ2 y δ3. De los seis restantes, w, θ, β2, β3, z, ϕ,

se deben elegir dos como elecciones libres para determinar las otras cuatro. Una estrategia es suponer valores para los dos ángulos β2 y β3. Esto deja a las magnitudes

y ángulos de los vectores W y Z pendientes de ser encontrados (w, Ѳ, z, ϕ). Para

simplificar la solución usaremos: 𝑊1𝑥 = 𝑤 cos 𝜃 ; 𝑊1𝑦 = 𝑤 sen 𝜃 ;

𝑍1𝑥= 𝑧 cos ∅ ; 𝑍1𝑦 = 𝑧 sen ∅. [13, p.198]

Al sustituir en las ecuaciones tenemos:

𝑊_1𝑥(cos 𝛽2− 1) − 𝑊1𝑦sen 𝛽2+ 𝑍1𝑥(cos 𝛼2− 1) − 𝑍1𝑦sen 𝛼2= 𝑃21cos 𝛿2 (2.13)

𝑊_1𝑥(cos 𝛽3− 1) − 𝑊1𝑦sen 𝛽3+ 𝑍1𝑥(cos 𝛼3− 1) − 𝑍1𝑦sen 𝛼3= 𝑃31cos 𝛿3 (2.14)

𝑊_1𝑦(cos 𝛽2− 1) + 𝑊1𝑥sen 𝛽2+ 𝑍1𝑦(cos 𝛼2− 1) − 𝑍1𝑥sen 𝛼2= 𝑃21sen 𝛿2 (2.15)

𝑊_1𝑦(cos 𝛽3− 1) + 𝑊1𝑥sen 𝛽3+ 𝑍1𝑦(cos 𝛼3− 1) − 𝑍1𝑥sen 𝛼3= 𝑃31sen 𝛿3 (2.16)

Simplificaremos la notación, usando:

𝐴 = cos 𝛽₂− 1 𝐵 = 𝑠𝑒𝑛 𝛽₂ 𝐶 = cos 𝛼₂− 1

(2.17)

𝐷 = sen 𝛼₂ 𝐸 = 𝑃₂₁cos 𝛿₂ 𝐹 = cos 𝛽₃− 1

𝐺 = 𝑠𝑒𝑛 𝛽₃ 𝐻 = cos 𝛼₃− 1 𝐾 = sen 𝛼₃

𝐿 = 𝑃₃₁cos 𝛿₃ 𝑀 = 𝑃₂₁sen 𝛿₂ 𝑁 = 𝑃₃₁sen 𝛿₃

Al sustituir convenientemente las ecuaciones (2.17) en las (2.13,2.14,2.15,2.16) para simplificar:

𝐴𝑊1𝑥− 𝐵𝑊1𝑦+ 𝐶𝑍1𝑥− 𝐷𝑍1𝑦 = 𝐸 (2.19)

𝐹𝑊1𝑥− 𝐺𝑊1𝑦+ 𝐻𝑍1𝑥− 𝐾𝑍1𝑦 = 𝐿 (2.20)

𝐵𝑊1𝑦+ 𝐴𝑊1𝑦+ 𝐷𝑍1𝑥+ 𝐶𝑍1𝑦 = 𝑀 (2.21)

𝐺𝑊_1𝑥+ 𝐹𝑊_1𝑦+ 𝐾𝑍_1𝑥+ 𝐻𝑍_1𝑦 = 𝑁 (2.22)

El sistema puede expresarse en forma de matriz estándar:

[

𝐴 −𝐵 𝐶 −𝐷 𝐹

𝐵 𝐺

−𝐺 𝐴 𝐹

𝐻 𝐷 𝐾

−𝐾 𝐶 𝐻

] x [

𝑊1𝑥

𝑊_1𝑦 𝑍_1𝑥 𝑍1𝑦]

= [ 𝐸 𝐿 𝑀 𝑁

] (2.23)

2.2.6.2 La diada US

Se debe repetir el proceso anterior para el lado derecho del mecanismo. La figura 2.9 también muestra las tres posiciones de la díada US y los ángulos σ, γ2, γ 3, ψ, α2 y α3,

los cuales definen las rotaciones de los vectores para las tres posiciones. La derivación de la solución para la díada derecha, US, es idéntica a la realizada para la díada izquierda WZ. Se supondrán valores para los ángulos γ2 y γ3. Finalmente se obtiene:

𝐴 = cos 𝛾2− 1 𝐵 = 𝑠𝑒𝑛 𝛾2 𝐶 = cos 𝛼2− 1

(2.24)

𝐷 = sen 𝛼2 𝐸 = 𝑃21cos 𝛿2 𝐹 = cos 𝛾3− 1

𝐺 = 𝑠𝑒𝑛 𝛾3 𝐻 = cos 𝛼3− 1 𝐾 = sen 𝛼3

𝐿 = 𝑃31cos 𝛿3 𝑀 = 𝑃21sen 𝛿2 𝑁 = 𝑃31sen 𝛿3

𝐴𝑈_1𝑥− 𝐵𝑈_1𝑦+ 𝐶𝑆_1𝑥− 𝐷𝑆_1𝑦= 𝐸 (2.25)

𝐹𝑈_1𝑥− 𝐺𝑈_1𝑦+ 𝐻𝑆_1𝑥− 𝐾𝑆_1𝑦 = 𝐿 (2.26)

𝐵𝑈_1𝑦+ 𝐴𝑈_1𝑦+ 𝐷𝑆_1𝑥+ 𝐶𝑆_1𝑦 = 𝑀 (2.27)

𝐺𝑈_1𝑥+ 𝐹𝑈_1𝑦+ 𝐾𝑆_1𝑥+ 𝐻𝑆_1𝑦 = 𝑁 (2.28)

También es evidente que existe una infinidad de soluciones a este problema de síntesis de tres posiciones. Por lo tanto, hay que verificar la función de la solución sintetizada con éste o cualquier otro método. [13, p.200]

2.2.7 Círculos con punto en el círculo y punto en el centro

Las incógnitas angulares se considerarán como candidatos de parámetro de los cuales dependerán las posiciones de los pivotes fijo y móviles de las diadas de la solución. Si se escoge un valor arbitrario para un parámetro angular no prescrito al tiempo que se permite que el otro parámetro angular varié a través de todos los valores posibles, los lugares geométricos resultantes de los pivotes fijos m y pivotes móviles k1

correspondientes son pares de círculos.

Veamos la figura 2.10 con las posiciones prescritas P1, P2 y P3; si 𝛅2, 𝛅3, 𝛂2 y 𝛂3 están

prescritos, entonces la tarea es generación de movimiento y existen dos opciones libres. Si se escoge arbitrariamente un valor numérico de 𝛃2, entonces los puntos m y k1

0 y 2𝛑. El lugar geométrico de los pivotes tierra se denomina círculo con punto en el centro o circulo M; el lugar geométrico de los pivotes móviles se denomina círculo con punto circular, o circulo K1. [14, p.560]

Fig. 2.10 Pivotes fijo “m” y móviles “k” del mecanismo

Fuente: Adaptado Erdman A. y Sandor G. Círculos de los puntos centrales y puntos

circulares. Diseño de mecanismos. (1998).

Los vectores de la diada m, k1, P1 se definen en la fig. 2.10. Las ecuaciones de cierre

de circuito para la diada en tres posiciones separadas por distancias finitas son las siguientes:

Primera posición R + W + Z = 0 (2.29)

Segunda posición R + Wei𝛃

2 + Zei𝛂2 = 𝛅2 (2.30)

Tercera posición R + Wei𝛃_{3 + Ze}i𝛂_{3 = 𝛅3} (2.31)

La posición desconocida del pivote móvil k1 está definida por el vector –Z con respecto

a P1, el origen del sistema de coordenadas fijo (Ver fig. 2.10), que coincide con la

posición inicial dada P1 del punto trazador del plano móvil. El pivote fijo m aún

desconocido, se localiza con el vector R. Podemos formular problemas de síntesis especificando 𝛅2 y 𝛅3, más los parámetros angulares apropiados. Los vectores R y –Z

se pueden obtener de las ecuaciones 2.29 – 2.31 (usando la regla de Cramer). Con ei𝛂j

R =

|

0 1 1

𝛿₂ 𝛽₂ 𝛼₂ 𝛿₃ 𝛽₃ 𝛼₃|

|

1 1 1

1 𝛽₂ 𝛼₂ 1 𝛽₃ 𝛼₃|

R = 𝛿2( 𝛽3− 𝛼3)− 𝛿3 (𝛽2− 𝛼2 )

𝛼₂− 𝛼₃− 𝛽₃− 𝛽₂+ 𝛽₂𝛼₃− 𝛼₂𝛽₃

(2.32)

Y

-Z =

|

1 1 0

1 𝛽₂ 𝛿₂ 1 𝛽₃ 𝛿₃|

|

1 1 −1

1 𝛽₂ −𝛼₂ 1 𝛽₃ −𝛼₃|

-Z = −𝛿2( 𝛽3− 1)+ 𝛿3 (𝛽2− 1 )

𝛽₂− 𝛽₃+ 𝛼₃− 𝛼₂− 𝛽₂𝛼₃+ 𝛼₂𝛽₃

(2.33)

La figura 2.11 muestra los circulos con punto en centro cuando el valor de β2 =

0°;10°;25°;30°;60°;90°;120°;150°;180°;210°;240°;270°;300°; mientras 0° < 𝛽3 < 360°

Fig. 2.11 Círculos M para valores de 𝛽2 (0° <𝛽3 <360°) para generación de movimiento

Fuente: Erdman A. y Sandor G. Círculos de los puntos centrales y puntos circulares. Diseño

de mecanismos. (1998).

Para la obtención de cada una de estas circunferencias se realiza la síntesis analítica donde se establece un valor de β2 cte. y se

itera el valor de β3 de 0° a 360°,

entonces las ubicaciones de los puntos fijos se plasman en el plano cartesiano, obteniendo un circulo. Se realiza el mismo procedimiento para otros valores arbitrarios de β2, obteniéndose la

Si todos los parámetros del miembro derecho de las ecuaciones 2.32 y 2.33 están fijos excepto algún parámetro angular 𝛉 que adopta todos los posibles valores, entonces las ecuaciones para R y –Z se pueden expresar como funciones de R(𝛉) y –Z(𝛉); donde 𝛉

puede ser 𝛂2, 𝛂3, 𝛃2, 𝛃3. Si utilizamos transformaciones bilineales se puede demostrar

que los lugares geométricos de R(𝛉) y –Z(𝛉) realmente son círculos M y K1 [14, p.563]

El método grafico (el que usamos en este estudio) ubica el lugar geométrico de las soluciones posibles. Se ha demostrado que si se mantiene una de las elecciones libres (por ejemplo, β2), y luego se resuelven las ecuaciones 2.19-2.22 y 2.23 mientras se itera

la otra elección libre β3 a través de todos los valores posibles de 0 a 2π, se generará un

círculo. Si se hace lo mismo para el vector Z, al mantener α2 constante a un valor

arbitrario e iterando α3 de 0 a 2π, se generará otro círculo. Este círculo es el lugar

geométrico de todas las ubicaciones posibles de la raíz del vector Z para el valor elegido de α2. [14, p.563]

2.2.8 Regla de Kennedy

Se define: “Tres cuerpos cualesquiera en movimiento plano tendrán exactamente tres centros instantáneos, y quedarán en la misma línea recta”. Observe que esta regla no

requiere que los tres cuerpos estén conectados de algún modo. La figura 2.12 muestra la construcción para localizar el centro instantáneo I1,3 e I2,4.[13, p.238]

Fig. 2.12 Localización de centros instantáneos

Fuente: Adaptado de Norton Robert. Centros Instantáneos de Velocidad. Diseño de

2.2.9 Ventaja mecánica

La ventaja mecánica (mA) se define como:

𝑚_𝐴= 𝐹𝑠𝑎𝑙

𝐹_𝑒𝑛𝑡

(2.34)

Si se supone que se aplican las fuerzas de entrada y salida con los radios rent y rsal,

perpendiculares a sus vectores de fuerza respectivos, sabiendo que F = T/r

𝑚

=(

𝑇𝑒𝑛𝑡

) (

𝑟𝑒𝑛𝑡

𝑟𝑠𝑎𝑙

)

(2.35)

Para un sistema conservador Pent = Psal, además teniendo claro que P = T* ω, tenemos

𝑚

=(

𝜔𝑠𝑎𝑙

) (

𝑟𝑒𝑛𝑡

𝑟𝑠𝑎𝑙

)

(2.36)

Observamos la Fig. 2.13

𝑚

=(

𝑂2𝐴𝑠𝑒𝑛𝜈

) (

𝑟𝑒𝑛𝑡

𝑟𝑠𝑎𝑙

)

(2.37)

La ecuación 2.37 muestra que con cualquier elección de rent y rsal, la ventaja mecánica

responde a los cambios de los ángulos ν y μ de manera opuesta a la de la relación de

velocidad angular. [13, p.247]

Fig. 2.13 Diagrama de ventaja mecánica

Fuente: Adaptado de Norton Robert. Relación velocidad angular. Diseño de maquinaria.

2.2.10 Soluciones analíticas para el análisis de velocidad

De acuerdo con la fig.2.14 La ecuación de lazo vectorial será:

R2 + R3 – R4 – R1 = 0 _(2.38)

Se sustituyen los vectores por la notación de numero complejo y se denotan sus longitudes escalares como a, b, c, d como se muestra en la figura 2.14.

𝑎𝑒

₊

𝑏𝑒

_-

𝑐𝑒

_-

𝑑𝑒

Para obtener una expresión para la velocidad, se diferencia la ecuación 2.39 con respecto al tiempo.

𝑗𝑎𝑒

𝑑𝑡

+

𝑗𝑏𝑒

𝑑𝑡

-

𝑗𝑐𝑒

𝑑𝑡 = 0

(2.40)

Pero,

𝑑𝜃2

𝑑𝑡 = ω2 ;

𝑑𝜃3

𝑑𝑡 = ω3 ;

𝑑𝜃4

𝑑𝑡 = ω4

(2.41)

Entonces:

𝑗𝑎𝜔₂𝑒𝑗𝜃_{2 + 𝑗𝑏𝜔}

3𝑒𝑗𝜃3 - 𝑗𝑐𝜔4𝑒𝑗𝜃4 = 0 (2.42)

Fig. 2.14 Diagrama del lazo vectorial

Fuente: Norton Robert. Lazo vectorial de mecanismo de cuatro barras y diagrama de

La ecuación 2.42 es, en realidad, la velocidad relativa

VA + VBA − VB = 0 (2.43)

En primer lugar, se sustituye la identidad de Euler en cada término de la ecuación 2.42:

𝑗𝑎𝜔2(𝑐𝑜𝑠𝜃2+ 𝑗𝑠𝑒𝑛𝜃2) + 𝑗𝑏𝜔3(𝑐𝑜𝑠𝜃3+ 𝑗𝑠𝑒𝑛𝜃3) - 𝑗𝑐𝜔4(𝑐𝑜𝑠𝜃4+ 𝑗𝑠𝑒𝑛𝜃4) = 0 (2.44)

Acomodando:

𝑎𝜔₂(−𝑠𝑒𝑛𝜃₂+ 𝑗𝑐𝑜𝑠𝜃₂) + 𝑏𝜔₃(−𝑠𝑒𝑛𝜃₃+ 𝑗𝑠𝑒𝑛𝜃₃) - 𝑐𝜔₄(−𝑠𝑒𝑛𝜃₄+ 𝑗𝑠𝑒𝑛𝜃₄) = 0 (2.45)

Ahora es posible separar esta ecuación vectorial en sus dos componentes reuniendo todos los términos reales e imaginarios por separado:

Parte real:

−𝑎𝜔2𝑠𝑒𝑛𝜃2- 𝑏𝜔3𝑠𝑒𝑛𝜃3 + 𝑐𝜔4𝑠𝑒𝑛𝜃4 = 0 (2.46)

Parte imaginaria:

𝑎𝜔₂𝑐𝑜𝑠𝜃₂+ 𝑏𝜔₃𝑐𝑜𝑠𝜃₃ - 𝑐𝜔₄𝑐𝑜𝑠𝜃₄ = 0 (2.47)

Resolviendo simultáneamente ambas ecuaciones:

ω3 =

aω2

b

sen(θ4−θ2)

sen(θ3−θ4)

(2.48)

ω4 =

aω2

c

sen(θ2−θ3)

sen(θ4−θ3)

(2.49)

Una vez que se resuelven para ω3 y ω4, entonces se puede resolver para la velocidad

lineal al sustituir la identidad de Euler en las ecuaciones 2.43 [13, p.258]

VA = 𝑗𝑎𝜔2(𝑐𝑜𝑠𝜃2+ 𝑗𝑠𝑒𝑛𝜃2) = 𝑎𝜔2(−𝑠𝑒𝑛𝜃2+ 𝑗𝑐𝑜𝑠𝜃2) (2.50)

VBA = 𝑗𝑏𝜔3(𝑐𝑜𝑠𝜃3+ 𝑗𝑠𝑒𝑛𝜃3) = 𝑏𝜔3(−𝑠𝑒𝑛𝜃3+ 𝑗𝑐𝑜𝑠𝜃3) (2.51)

2.2.11 Análisis de aceleración

La aceleración se define como la tasa de cambio de velocidad con respecto al tiempo.

α = dω

dt A =

dV dt

(2.53)

La figura 2.15 muestra un sistema en el que el pivote A ya no está inmóvil. Tiene una aceleración lineal AA conocida como parte del carro trasladante, eslabón 3. Ahora debe

encontrarse la aceleración absoluta AP con la ecuación de diferencia de aceleración

cuya solución gráfica se muestra en la figura 2.15: [13, p.289]

AP = AA + APA (2.54)

At_{P + A} P n _{= (A}

A t _{+ A}

A n_{) + (A}

PA t _{+ A}

PA

n _{) (2.55)}

Donde:

APA = p(-senθ + jcosθ) - pω2(cosθ + jsenθ) (2.56)

Fig. 2.15 Diagrama de aceleraciones

2.2.12 Soluciones analíticas para el análisis de la aceleración

La aceleración angular de entrada α2 puede variar con el tiempo. La ecuación de lazo

vectorial será:

R2 + R3 – R4 – R1 = 0 (2.57)

Se sustituyen los vectores por la notación de número complejo y se denotan las longitudes escalares como a, b, c, d, como se muestra en la figura 2.16.

𝑎𝑒𝑗𝜃2 ₊ 𝑏𝑒𝑗𝜃3 _-𝑐𝑒𝑗𝜃4 _- 𝑑𝑒𝑗𝜃1 _{= 0} (2.58)

Luego derivaremos la ecuación 2.58, descomponemos y acomodando tenemos:

(𝑎𝛼₂𝑗𝑒𝑗𝜃2− 𝑎𝜔₂2𝑒𝑗𝜃2 _{) + (} 𝑏𝛼₃𝑗𝑒𝑗𝜃3 − 𝑏𝜔₃2𝑒𝑗𝜃3_{) -} ( 𝑐𝛼₄𝑗𝑒𝑗𝜃4− 𝑐𝜔₄2𝑒𝑗𝜃4 )_{= 0} (2.59)

De lo que podemos deducir:

AA + ABA − AB = 0 (2.60)

Donde:

AA = At_A + An_A = (𝑎𝛼2𝑗𝑒𝑗𝜃2− 𝑎𝜔22𝑒𝑗𝜃2 ) (2.61)

ABA = At_BA + An_BA = ( 𝑏𝛼3𝑗𝑒𝑗𝜃3 − 𝑏𝜔32𝑒𝑗𝜃3) (2.62)

AB = AtB + AnB = ( 𝑐𝛼4𝑗𝑒𝑗𝜃4− 𝑐𝜔42𝑒𝑗𝜃4 ) (2.63)

Fig. 2.16 Lazo vectorial y aceleraciones mecanismo de cuatro barras

Primero se sustituye la identidad de Euler en cada término de la ecuación 2.59

[𝑎𝛼2𝑗(𝑐𝑜𝑠𝜃2+ 𝑗𝑠𝑒𝑛𝜃2) − 𝑎𝜔22(𝑐𝑜𝑠𝜃2+ 𝑗𝑠𝑒𝑛𝜃2)] + [𝑏𝛼3𝑗(𝑐𝑜𝑠𝜃3+ 𝑗𝑠𝑒𝑛𝜃3) −

𝑏𝜔₃2_{(𝑐𝑜𝑠𝜃}

3+ 𝑗𝑠𝑒𝑛𝜃3)] - [( 𝑐𝛼4𝑗(𝑐𝑜𝑠𝜃4+ 𝑗𝑠𝑒𝑛𝜃4) − 𝑐𝜔42(𝑐𝑜𝑠𝜃4+ 𝑗𝑠𝑒𝑛𝜃4) )]= 0

(2.64)

Si multiplicamos por j y acomodamos, obtenemos una expresión que separamos en:

parte real

−𝑎𝛼₂𝑠𝑒𝑛𝜃₂− 𝑎𝜔₂2_{𝑐𝑜𝑠𝜃}

2 - 𝑏𝛼3𝑠𝑒𝑛𝜃3− 𝑏𝜔32𝑐𝑜𝑠𝜃3 + 𝑐𝛼4𝑠𝑒𝑛𝜃4+ 𝑐𝜔42𝑐𝑜𝑠𝜃4= 0 (2.65)

Parte imaginaria

𝑎𝛼₂𝑐𝑜𝑠𝜃₂− 𝑎𝜔₂2_{𝑠𝑒𝑛𝜃}

2 + 𝑏𝛼3𝑐𝑜𝑠𝜃3− 𝑏𝜔32𝑠𝑒𝑛𝜃3 - 𝑐𝛼4𝑐𝑜𝑠𝜃4+ 𝑐𝜔42𝑠𝑒𝑛𝜃4= 0 (2.66)

Las ecuaciones 2.65 y 2.66 se resuelven simultáneamente para obtener:

α3 =

CD−AF

AE−BD (2.67)

α4 =

CE−BF

AE−BD (2.68)

donde:

A = 𝑐. 𝑠𝑒𝑛𝜃₄ B = 𝑏. 𝑠𝑒𝑛𝜃₃

C = 𝑎𝛼2𝑠𝑒𝑛𝜃2+ 𝑎𝜔22𝑐𝑜𝑠𝜃2 + 𝑏𝜔32𝑐𝑜𝑠𝜃3− 𝑐𝜔42𝑐𝑜𝑠𝜃4

D = 𝑐. 𝑐𝑜𝑠𝜃₄ E = 𝑏. 𝑐𝑜𝑠𝜃₃

F = 𝑎𝛼2𝑐𝑜𝑠𝜃2− 𝑎𝜔22𝑠𝑒𝑛𝜃2 - 𝑏𝜔32𝑠𝑒𝑛𝜃3 + 𝑐𝜔42𝑠𝑒𝑛𝜃4

(2.69)

Una vez resuelto para α3 y α4, es posible entonces resolver para las aceleraciones

lineales al sustituir la identidad de Euler en las ecuaciones 2.61, 2.62, 2.63. [13, p.296]

AA = 𝑎𝛼2(−𝑠𝑒𝑛𝜃2+ 𝑗𝑐𝑜𝑠𝜃2) − 𝑎𝜔22(𝑐𝑜𝑠𝜃2+ 𝑗𝑠𝑒𝑛𝜃2)

(2.70)

ABA = 𝑏𝛼3(−𝑠𝑒𝑛𝜃3+ 𝑗𝑐𝑜𝑠𝜃3) − 𝑏𝜔32(𝑐𝑜𝑠𝜃3+ 𝑗𝑠𝑒𝑛𝜃3) (2.71)

2.2.13 Momento de inercia de masa

El momento de inercia de masa de un cuerpo es una propiedad que mide la resistencia del cuerpo a una aceleración angular, es un indicador de la cantidad de par de torsión que se requerirá para acelerar el cuerpo rotacionalmente. El momento de inercia de masa se define como la integral del “segundo momento” con respecto a un eje de todos

los elementos de masa dm que componen el cuerpo

I= ∫(r2)dm (2.73)

Fig. 2.17 Momento de inercia del cuerpo rígido respecto de Z

Fuente: Hibbeler R.C. Momento de inercia de masa. Ingeniería Mecánica Estática. (1999).

En la fig. 2.17 el brazo de momento “r” es la distancia perpendicular desde el eje hasta el elemento arbitrario dm. Puesto que la fórmula 2.73 involucra “r”, el valor de I es único

para cada eje. Sin embargo, el eje que generalmente se elige para el análisis atraviesa el CG. El momento de inercia calculado con respecto a este eje se definirá como IG.

[15, p.504]. Ejemplo:

I = 𝑀₄(𝑅_𝑒𝑥𝑡2 + 𝑅_𝑖𝑛𝑡2 ) + 𝑀𝐿₁₂2

Fig. 2.18 Momento de Inercia de un tubo hueco

Fuente: Wikilibros. (25/10/2016). Física/Dinámica de rotación/ Rotación de un sólido. [Figura].

Recuperado:https://es.wikibooks.org/wiki/F%C3%ADsica/Din%C3%A1mica_de_rotaci%C3%B3

2.2.14 Análisis de fuerzas de un mecanismo de cuatro barras

La figura 2.19 muestra un mecanismo de cuatro barras, todas las longitudes de los eslabones, las posiciones de los eslabones, las ubicaciones de los centros de gravedad de los eslabones, las aceleraciones de los centros de gravedad y las velocidades y aceleraciones angulares de los eslabones se determinaron previamente con un análisis cinemático. Este mecanismo tiene tres eslabones móviles. La ecuación de la segunda ley de Newton proporciona tres ecuaciones para cualquier eslabón o cuerpo rígido en movimiento. Se espera tener nueve ecuaciones con nueve incógnitas en este problema.

La figura 2.19 muestra también los diagramas de cuerpo libre de todos los eslabones, con todas las fuerzas mostradas. Obsérvese que se muestra una fuerza externa Fp que

actúa en el punto P del eslabón 3. También se muestra el par de torsión externo T4 que

actúa sobre el eslabón 4. Los parámetros cinemáticos del mecanismo se definen con respecto a un sistema global XY cuyo origen está en el pivote motriz O2 y cuyo eje X

pasa por el pivote fijo O4 del eslabón 4. También se requieren la masa (m) de cada

eslabón, la ubicación de su CG y su momento de inercia de masa (IG) con respecto a

ese CG.

El CG de cada eslabón inicialmente se define dentro de cada eslabón con respecto a un sistema de ejes local rotatorio y móvil insertado en el eslabón porque su CG es una propiedad física invariable. El origen de este sistema de ejes x’, y’ está en una junta de pasador y el eje x’ es la línea de centros del eslabón.

La posición del CG dentro del eslabón se define por un vector de posición en este sistema. La ubicación instantánea del CG se determina fácilmente en cada posición dinámica del eslabón, al sumar el ángulo del vector de posición interno del CG al ángulo actual en el CGS del eslabón. Primero se escriben las ecuaciones 2.73 para cada eslabón móvil. [13, p.499].

F12x + F32x = m2aG2x

(2.74)

F12y + F32y = m2aG2y (2.75)

Fig. 2.19 Análisis de fuerzas dinámicas en mecanismo de cuatro barras

Fuente: Adaptado de Norton Robert. Análisis de fuerzas de mecanismo de cuatro barras.

Diseño de maquinaria. (2005)

Para el eslabón 3, con sustitución de la fuerza de reacción –F32 en lugar de F23, tenemos:

F43x - F32x + FPx = m3aG3x (2.77)

F43y - F32y + FPy = m3aG3y (2.78)

Para el eslabón 4, al sustituir la fuerza de reacción –F43 en lugar de F34, obtenemos:

F14x – F43x = m4aG4x (2.80)

F14y – F43y = m4aG4y

(2.81)

( R14x F14y – R14y F14x ) - (R34x F43y – R34y F43x) + T4 = IG4α4

(2.82)

Obsérvese de nuevo que T12, el par de torsión fuente, solo aparece en la ecuación para

el eslabón 2. El eslabón 3, en este caso, tiene una fuerza externa Fp. El eslabón 4, no

tiene ninguna fuerza externa que actué sobre el (aunque podría tenerla), pero si un par externo T4. Existen nueve incógnitas en estas nueve ecuaciones, F12x, F12y, F32x, F32y,

F43x, F43y, F14x, F14y y T12, que pueden resolverse simultáneamente. [13, p.499]

[ 𝟏_𝟎

−𝐑𝟏𝟐𝐲

𝟎 𝟎 𝟎 𝟎 𝟎 𝟎

𝟎 𝟏 𝐑_𝟏𝟐𝐱

𝟎 𝟎 𝟎 𝟎 𝟎 𝟎

𝟏 𝟎 −𝐑_𝟑𝟐𝐲

−𝟏 𝟎 𝐑_𝟐𝟑𝐲

𝟎 𝟎 𝟎

𝟎 𝟏 𝐑_𝟑𝟐𝐱

𝟎 −𝟏 −𝐑_𝟐𝟑𝐱

𝟎 𝟎 𝟎

𝟎 𝟎 𝟎 𝟏 𝟎 −𝐑_𝟒𝟑𝐲

−𝟏 𝟎 𝐑_𝟑𝟒𝐲

𝟎 𝟎 𝟎 𝟎

𝟎 𝟎 𝟎 𝟎

𝟎 𝟎 𝟎 𝟏

𝟎 𝟎 𝟎 𝟎

𝟏 𝟎 𝟎 𝟎

𝐑_𝟒𝟑𝐱 𝟎 𝟎 𝟎

𝟎 𝟏 𝟎 𝟎

−𝟏 −𝐑_𝟑𝟒𝐱

𝟎 −𝐑𝟏𝟒𝐲

𝟏

𝐑_𝟏𝟒𝐱 𝟎𝟎 ]

x

[ 𝐅𝟏𝟐𝐱

𝐅_𝟏𝟐𝐲 𝐅_𝟑𝟐𝐱 𝐅_𝟑𝟐𝐲 𝐅_𝟒𝟑𝐱 𝐅_𝟒𝟑𝐲 𝐅_𝟏𝟒𝐱 𝐅_𝟏𝟒𝐲 𝐓_𝟏𝟐]

=

[

𝐦_𝟐𝐚_𝐆𝟐𝐱 𝐦𝟐𝐚𝐆𝟐𝐲

𝐈𝐆𝟐𝛂𝟐

𝐦𝟑𝐚𝐆𝟑𝐱− 𝐅𝐏𝐱

𝐦_𝟑𝐚_𝐆𝟑𝐲− 𝐅_𝐏𝐲 𝐈𝐆𝟑𝛂𝟑− 𝐑𝐏𝐱𝐅𝐏𝐲+ 𝐑𝐏𝐲𝐅𝐏𝐱

𝐦𝟒𝐚𝐆𝟒𝐱

𝐦_𝟒𝐚_𝐆𝟒𝐲

𝐈_𝐆𝟒𝛂_𝟒− 𝐓_𝟒 ]

2.3 Definición de términos

 Sistema coordenado global (GCS)

El sistema global a menudo se considera como unido a la Tierra, aunque muy bien podría estar unido a otro plano fijo arbitrario, tal como el armazón de un automóvil. Si la meta fuera analizar el movimiento de la pluma de limpiaparabrisas, posiblemente no se incluiría el movimiento bruto del automóvil en el análisis. El sistema de coordenadas global unido al carro sería útil, y sería un sistema de coordenadas absoluto. [13, p.144]

 Sistema coordenado local

Los sistemas de coordenadas locales generalmente se unen a un eslabón en algún punto de interés. Éste podría ser: junta de pasador, un centro de gravedad o una línea de centros de un eslabón. Estos sistemas de coordenadas locales pueden ser rotatorios o no rotatorios, según como se desee [13, p.145]

 Punto prescrito

Los puntos o posiciones prescritas por ubicaciones sucesivas del eslabón de salida (acoplador o balancín) en el plano, en general se conocen como puntos de precisión o posiciones de precisión. El número de puntos de precisión que pueden sintetizarse está limitado por el número de ecuaciones disponibles para su solución. [13, p.186]

 Síntesis cualitativa:

Significa la creación de soluciones potenciales en ausencia de un algoritmo bien definido que configure la solución. La mayoría de los problemas de diseño reales tendrán más variables desconocidas que ecuaciones para describir el comportamiento del sistema, no se puede simplemente resolver las ecuaciones para obtener una solución. [13, p.75]

 Síntesis cuantitativa o síntesis analítica

CAPITULO III

MATERIALES Y MÉTODOS

3.1. Material de estudio

En la tabla 3.1 se muestran los recursos usados en el proyecto

Tabla 3. 2 Tabla de materiales

Recursos Cantidad

Laptop Toshiba satellite 01

Impresora HP 01

Bibliografia impresa 04

Pizarra 01

Plumones 03

Hojas Bond 50

Software

Solidworks 01

Microsoft office Excel 01

Microsoft office Word 01

AutoCAD 01

Fuente: Elaboración propia

3.2. Metodología

3.2.1Variables

Fig. 3.1 Bloque de variables

Fuente: Elaboración propia ENTRADA

P1 ; P2 ; P3 ;O2 ; O4 ;

𝜎 ; 𝜃 ; W ; V; U ; α2 ;

α3 ; β2 ; β3 γ2 ; γ3 ;

𝜔2

SÍNTESIS ANALÍTICA, ANÁLISIS CINEMÁTICO Y

DINÁMICO

F12 ; F32 :F43 ; F14 ;VA ; VB ;

VBA ;AA ;AB ; ABA; AG2 ; AG3 ;

AG4

SALIDA

W’,V’,Z’,S’,U’, O’2

; O’4 ; mA-ptoscriticos;

Variables Independientes:

- Puntos prescritos (P1, P2, P3).

- Masa del deportista.

- Velocidad angular constante que el sujeto imprime a la volante.

- Datos del mecanismo inicial

Variables dependientes:

- Dimensiones de eslabones.

- Ventaja mecánica en los puntos críticos.

- Angulo de transmisión en las posiciones críticas.

- Reacciones en los eslabones.

- Velocidades y aceleración de los eslabones y centros de gravedad.

3.2.2 Población

Mecanismos de cuatro Barras.

3 .2 .3 Muestra

Mecanismo de cuatro barras para una bicicleta elíptica

3 .2 .4 Tipo de estudio

Aplicativo – Descriptivo.

3 .3 Técnicas de recopilación y procesamiento de la información

- Observación y medición de espacios disponibles.

- Análisis bibliográfico del diseño mecánico en el desarrollo de mecanismos.

- Inspección visual de bicicletas en el mercado local.

- Revisión de revistas deportivas

3 .4 P ro c ed imie n to

1. Determinamos el rango del ángulo ϕ entre los eslabones V y U del mecanismo

inicial. Aplicamos la teoría de circulo con punto en el centro estableciendo valores arbitrarios de γ2, visualizamos así las posibles ubicaciones de O4. Luego

graficamos los valores de γ3 (con γ2 = -29.63) vs ϕ donde ubicaremos el punto

Procedemos de la misma manera estableciendo valores arbitrarios de γ3. Lo cual

nos conlleva a dos posibilidades de mejora una por parte de γ2 y otra de γ3

2. Hacemos la síntesis analítica para tres puntos prescritos, de las dos posibilidades que indican según γ2 y γ3. Lo cual nos describe el

dimensionamiento completo de cada una de las opciones. Se elige la opción que mejor el ángulo ϕ.

Realizamosel análisis de velocidades, aceleraciones y fuerzas dinámicas para el mecanismo inicial y para el mecanismo que mejora el ángulo ϕ, lo cual nos

describe las reacciones internas.

3. Calculamos el valor del ángulo de transmisión μ del mecanismo inicial, aplicamos la teoría de circulo con punto en el centro para los valores de β2 y β3

lo cual nos describe un rango de ángulos que mejoran el valor de μ inicial, entonces aplicamos restricciones adecuadas para cada rango.

4. Determinamos la ventaja mecánica del mecanismo inicial, y de los mecanismos determinados en los 2 rangos restringidos según la iteración de 𝛃2 y 𝛃3.

Comparamos las ventajas mecánicas para los puntos críticos y determinamos la mejor opción. Finalmente, detallamos el dimensionamiento completo del mecanismo optimizado (previamente se realizó la síntesis analítica). Se procede entonces a graficar y simular en Solidworks.