Optimización estocástica
-Fundamentos de cálculo
estocástico-Prof. John F. Moreno T.
Universidad Externado de Colombia.
Maestría en Gestión y Evaluación de Proyectos de Inversión
Índice
1. Definición de proceso estocástico 1
1.1. Martingalas . . . 4
2. Caminatas aleatorias 4
3. Movimiento Browniano 7
3.1. Algunos procesos asociados al movimiento Browniano . . . 10
4. Integral estocástica 12
5. Fórmula de Itô 14
5.1. Fórmula de Itô para el movimiento Browniano . . . 15
5.2. Fórmula de Itô para procesos de Itô . . . 16
1.
Definición de proceso estocástico
La teoría de procesos estocásticos estudia la estructura de familias de variables aleatorias y su aplicación en diversas
disciplinas. A continuación se presenta la definición y resultados básicos relacionados con los procesos estocásticos.
Definición 1.1: Proceso estocástico
Una colección de variables aleatorias{Xt}t∈I, definidas sobre un mismo espacio de probabilidad (Ω,F,P) recibe
el nombre deproceso estocásticooproceso aleatorio.
1. Xtdescribe el número de defectos en un objeto manufacturado en volument.
2. La cantidad de aguaYtde una represa observada hasta un instantet.
3. La utilidadMten pesos obtenida por un jugador después detrondas de un juego.
4. El precioStde un activo en el instantetcont∈[0,T].
5. El flujo de cajaFCtde un proyecto en el añot.
6. Rt que denota la rentabilidad de una inversión en el instantet.
Los elementos principales que distinguen a un proceso{Xt}son:
El conjuntoI, en el cual toma valores el parámetrot, se denominaconjunto de índicesoconjunto de parámetros.
Este conjunto puede ser discreto (como en el ejemplo del flujo de caja en el añot,FCt, en dondet∈ {0,1,2, ...}) y
en este caso se dice que el proceso es unasucesión aleatoriaoproceso de parámetro discreto. Si el conjuntoIes
continuo (un intervalo), se dice que el proceso es unafunción aleatoriaoproceso de parámetro continuo(como en
el ejemplo del proceso de precioStdondet∈[0,T]).
Elespacio de estados, que se denotara comoS, es el conjunto que contiene los posibles valores de cada variable
Xt del proceso{Xt}t∈I. Si S es numerable, nos referimos al procesoXt comoproceso de estado discreto, por el
contrario, siSno es numerable nos referimos al procesoXt comoproceso de estado continuo.
Ejemplo 1. Consideremos de nuevo el proceso estocástico{FCt}t=0,1,2,..., que describe el flujo de caja de un proyecto en
el año t. Se puede ver que este es un proceso estocástico de parámetro discreto y espacio de estados continuo S= (−∞,∞).
En general, un proceso estocástico{Xt}t∈I, depende deωyt, es decir,{Xt(ω); ω∈Ω,t∈I}. Si se considera unω∈Ω
fijo, el procesoXt(ω)es una función del tiempoty su representación gráfica se denominatrayectoria del proceso. Por
otro lado, si se considera untfijoXt(ω)es una variable aleatoria cuyo valor depende delω.
Ejemplo 2. Considere un proceso estocástico{St}t=0,1,2,3que describe el comportamiento del precio de un activo durante tres periodos de tiempo. Supongamos que entre dos instantes consecutivos t−1y t la variable aleatoria Stes tal que:
St=
uSt−1 con probabilidad1/2
dSt−1 con probabilidad1/2
donde u y d son factores constantes de crecimiento y decrecimiento del precio respectivamente y los resultados son
independientes entre periodos.
Lo anterior es análogo a considerar que el precio del activo puede subir (u) o bajar (d) entre periodos consecutivos como
resultado del lanzamiento de una moneda, por ejemplo, si el resultado es cara (C) el precio sube y si es sello(S)el precio
baja. De esta forma los posibles resultados en el modelo de tres periodos es:
Ω={(C,C,C),(C,C,S),(C,S,C),(C,S,S),(S,C,C),(S,C,S),(S,S,C),(S,S,S)}
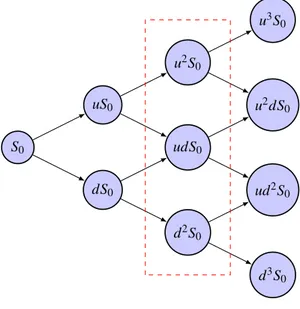
Para unω∈Ωfijo, por ejemploω ={(C,S,C)}, la trayectoria correspondiente es la descrita por linea punteada en la
figura 1.
Por otro lado para t=2, por ejemplo, el proceso St representa los posibles valores de la variable aleatoria S2, como se
muestra en la figura 2.
S0
dS0 uS0
d2S0 udS0 u2S0
d3S0 ud2S0 u2dS0 u3S0
Figura 1: Trayectoria del proceso de precio discreto.
S0
dS0 uS0
d2S0 udS0 u2S0
d3S0 ud2S0 u2dS0 u3S0
Figura 2: Variable aleatoria ent=2.
Las relaciones de dependencia entre las variablesXt que conforman un proceso estocástico son especificadas dando la
distribución de probabilidad conjunta de cada familia finita de variables del proceso. Con frecuencia estas distribuciones
conjuntas pueden ser especificadas en términos de otras distribuciones asociadas al proceso. Algunos ejemplos de procesos
estocásticos que resultan de interés son: las caminatas aleatorias y el movimiento Browniano, los cuales se describen en
1.1.
Martingalas
Un proceso estocásticoXtdefinido sobre(Ω,Ft,P)se diceadaptadoa la filtraciónFt, si su valor entes conocido dada
la información hasta dicho instante,Ft. También se dice que el proceso esFt-medible.
Por otro lado, si un proceso estocásticoXtes tal que su valor entes conocido con la información disponible hasta algún
instante anteriors, entonces se dice que el procesoXtespredecible. En este caso se dice queXtesFs-medible cons<t.
Definición 1.2: Proceso Martingala
Un proceso estocásticoXt definido sobre(Ω,Ft,P)talqueE[Xt]<∞para todot, se dice:
Martingalasi para todos<t, se tiene que:
E[Xt|Fs] =Xs (1)
es decir, el valor esperado del proceso en el futuro dada la información disponible hasta hoy es precisamente
el valor del proceso hoy.
Supermartingalasi para todos<t, se tiene que:
E[Xt|Fs]<Xs (2)
es decir, el valor esperado del proceso en el futuro dada la información disponible hasta hoy es menor que
el valor del proceso hoy.
Submartingalasi para todos<t, se tiene que:
E[Xt|Fs]>Xs (3)
es decir, el valor esperado del proceso en el futuro dada la información disponible hasta hoy es mayor que
el valor del proceso hoy.
2.
Caminatas aleatorias
Lascaminatas aleatoriasson procesos estocásticos que permiten describir la posición(Xt)de una partícula en
determi-nados instantes de tiempo(t)a partir de su posición inicial(X0), de forma queXt+1=Xt+ϕt, es decir, la posición de
la partícula en el instantet+1 esta determinada por su posición ent y la variable aleatoriaϕt que describe la ley de
probabilidad para el siguiente paso.
Un primer ejemplo sencillo de este tipo de procesos son lascaminatas aleatorias binomiales{Xn}n=0,1,2,.., cuya
Definición 2.1: Caminatas aleatorias
Considere las variables aleatorias discretas independientesZj, tales queP[Zj=u] =pyP[Zj=d] =1−p. Se
define la caminata aleatoria binomial{Xn}como:
X0=0 ; Xn= n
∑
j=1
Zj (4)
Sobre este proceso se puede ver que:
1.
E[Xn] =E
"
n
∑
j=1 Zj
#
=
n
∑
j=1 E[Zj] =
n
∑
j=1
[up+ (1−p)d] =n[up+ (1−p)d]
2.
V[Xn] =E[Xn2]−(E[Xn])2=n[u2p+d2(1−p)] + (2−n)n[up+ (1−p)d]2
Un caso particular de este proceso es la denominada caminata aleatoria simétrica, que se tiene al considerar que las
variablesZjson tales queP[Zj=1] =1/2 yP[Zj=−1] =1/2. En este caso:
E[Xn] =0 ; V[Xn] =n
La figura 3 muestra cinco posibles trayectorias de una caminata aleatoria simétrica conn=100.
Figura 3: Trayectorias de una caminata aleatoria simétrica.
En términos más generales, lascaminatas aleatorias simétricaspueden definirse como un proceso estocástico{Xn}n=0,1,2,.. en el cual:
X0=0 ; Xn= n
∑
j=1 Zj
E[Xn] =0 ; V[Xn] =nk2
Ademas, dado que cada una de las variablesZjes de tipo Bernulli con probabilidad de éxito constante (1/2) y se asumen
independientes entre ellas, entoncesXnsigue una distribución binomial con parámetrosnyp, es decir,Xn∼Bin(n,p). La
figura 4 muestra el histograma para los valores finales de 5000 trayectorias simuladas de una caminata aleatoria de 100
pasos, conk=1.
Figura 4: Histograma de los valores después de 100 pasos de una caminata aleatoria simétrica conk=1.
Se puede ver claramente de la figura que la distribución es la de una binomial con los para metros indicados, y además se
hace clara la tendencia del procesos a la distribución normal a medida que el número de pasos aumenta y la probabilidad
es 1/2.
Otra propiedad interesante de las caminatas aleatorias simétricas es que estas son martingalas.
E[Xn+1|Fn] =E[Xn+1−Xn+Xn|Fn]
=E[Xn+1−Xn|Fn] +E[Xn|Fn]
=E[Xn+1−Xn] +Xn
=E[Zn+1] +Xn=Xn
Ejercicio
Considere una caminata en la cualP[Zj=1] =1/3,P[Zj=0] =1/3 yP[Zj=−1] =1/3]. Determine el valor
Ejercicio
Muestre que en general la condición de martingala, submartingala o supermartingala de una caminata aleatoria
depende de los posibles valores de las variablesZjy de la probabilidad de los mismos.
3.
Movimiento Browniano
El movimiento Browniano es elmovimiento aleatorio que se observa en las partículas que se hallan en un medio fluido
(líquido o gas), como resultado de choques contra las moléculas de dicho fluido. Este fenómeno de transporte recibe
su nombre en honor al biólogo y botánico escocés Robert Brown, quien en 1827, mientras observaba a través de un
microscopio partículas atrapadas en las cavidades internas de un grano de polen en el agua, señaló que las partículas se
movían a través del líquido; pero no fue capaz de determinar los mecanismos que provocaron este movimiento. En 1905,
Albert Einstein publicó un artículo donde explicó con todo detalle cómo el movimiento que Brown había observado era el
resultado del polen siendo movido por moléculas de agua individuales. Esta explicación sirvió como prueba convincente
de que existen los átomos y moléculas, y fue verificado experimentalmente por Jean Perrin en 1908.
La caracterización matemática completa de este tipo de procesos estocásticos se debe al matemático norteamericano
Norbert Wiener, razón por la cual en muchos casos se denomina como movimiento Browniano al proceso fisico y proceso
de Wiener a su representación matemática. En estas notas estos dos términos se utilizaran de forma indistinta.
Definición 3.1: Movimiento Browniano estándar
Un proceso estocástico{Wt}t≥0es unmovimiento Browniano estándarsi cumple:
1. Wt parat≥0, es una función continua ent, es decir, las trayectorias del proceso son continuas.
2. W0=0.
3. Paras<t, los incrementos(Wt−Ws)siguen una distribución normal de media 0 y varianza(t−s).
(Wt−Ws)∼N(0,t−s) (5)
4. Para 0≤u≤v≤s≤t, se tiene que(Wt−Ws)es independiente de(Wv−Wu). Otra forma de expresar esto
es considerando que(Wt−Ws)es independiente de la información disponible hasta el instantes(Fs).
A partir de la definición de movimiento Browniano podemos ver que:
1. Wt−W0=Wt∼N(0,t).
2. Paras<tse tiene que:
donde la igualdad es en distribución, es decir(Wt−WS)tiene la misma distribución de(Wt−s), luego el movimiento
Browniano tiene incrementos estacionarios.
3. El movimiento Browniano es un proceso gaussiano con función de autocovarianza dada porCov(Wt,Ws) =m´ın{s,t},
e inversamente, todo proceso gaussiano con función de autocovarianza dada por m´ın{s,t}, es un movimiento
Brow-niano.
4. El movimiento Browniano tiene variación cuadrática finita; en particular, siWt es un movimiento browniano
están-dar se tiene que su variación cuadrática en el intervalo[0,T]es igual aT. Esto quiere decir que el valor esperado
de las variaciones al cuadrado del movimiento Browniano en un intervalo de tiempo finito, son finitas, e iguales a
la longitud del intervalo de tiempo.
Lo anterior se tiene dado que:
E[(Wti−Wti−1)
2] =V[(W
ti−Wti−1)] =ti−ti−1 (7)
y adicionalmente:
V[(Wti−Wti−1)
2] =E
[(Wti−Wti−1)
2−(t
i−ti−1)]2
=E
(Wti−Wti−1)
4−2(t
i−ti−1)(Wti−Wti−1)
2+ (t
i−ti−1)2
=E[(Wti−Wti−1)
4]−2(t
i−ti−1)E[(Wti−Wti−1)
2] + (t
i−ti−1)2
=E[(Wti−Wti−1)
4]−(t
i−ti−1)2
Para calcular el valor esperadoE[(Wti−Wti−1)
4], consideramos la función generadora de momentos de(W
ti−Wti−1),
la cual está dada porm(W
ti−Wti−1)(u) =e
u2(t
i−ti−1)/2. Por propiedades de la generadora de momentos, se tiene que:
d4m(W
ti−Wti−1)(u)
du4 |u=0=E[(Wti−Wti−1)
4] =3(t
i−ti−1)2 (8)
y entoncesV[(Wti−Wti−1)2] =2(ti−ti
−1)2.
Se puede ver entonces que:
a) E[(Wti−Wti−1)
2] =t i−ti−1
b) V[(Wti−Wti−1)
2] =2(t
i−ti−1)2
Si denotamos pordWt≡Wti−Wti−1ydt≡ti−ti−1, lo que se denomina notación diferencial, entonces tenemos que:
a) E[dWt2] =dt
lo que muestra que la varianza dedWt2tiende mas rápidamente a cero que su valor esperado sidtriende a cero. Lo anterior permite desarrollar la siguiente regla de multiplicación de diferenciales.
· dWt dt
dWt dt 0
dt 0 0
(9)
5. Dado que(Wti−Wti−1)∼N(0,ti−ti−1)y si consideramos una variable aleatoriaZ∼N(0,1), tenemos que:
(Wti−Wti−1)=d√ti−ti−1Z
de donde,
Wti
d
=Wti−1+
√
ti−ti−1Z
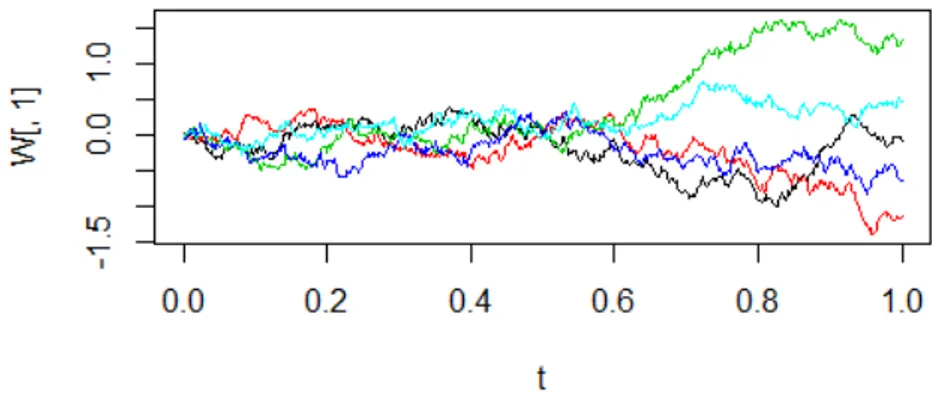
Expresión que se puede utilizar para simular trayectorias del movimiento Browniano dado queW0=0. La figura 5
muestra 5 posibles trayectorias del movimiento Browniano estándar.
Figura 5: Trayectorias simuladas del movimiento Browniano
6. El movimiento Browniano es martingala. Esto dado que paras<t.
E[Wt|Fs] =E[Wt−Ws+XS|Fs]
=E[Wt−Ws|Fs] +E[Ws|Fs]
=E[Wt−Ws] +Ws
3.1.
Algunos procesos asociados al movimiento Browniano
1. Movimiento browniano con deriva.SeaXt el proceso definido como:
Xt=µt+σWt conµ,σconstantes, (10)
denominadomovimiento browniano con derivaµ. En este caso lo que se tiene es un proceso cuyas trayectorias se
ubican alrededor de la recta µt, mientras que el valor deσ determina el peso de las fluctuaciones respecto a esta
recta, las cuales están descritas porWt.
Es importante mencionar que este fue el proceso estocástico utilizado por Louis Bachelier en sus tesis doctoral para
describir el precio de los activos en la bolsa de París en el año 1900, y que se utiliza también de forma habitual para
describir el comportamiento de flujos de caja futuros, con tasa proyectada de crecimientoµy volatilidadσ.
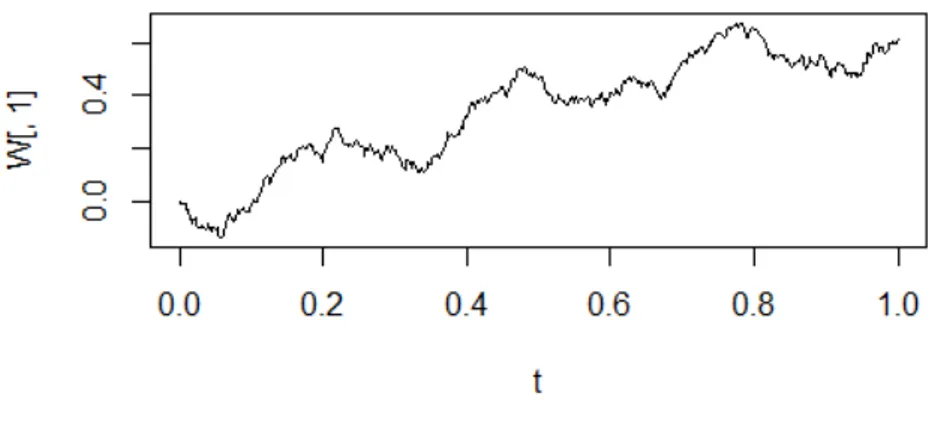
Para este proceso se puede verificar fácilmente queE[Xt] =µt,V[Xt] =σ2tyCov(Xt,Xs) =σ2m´ın{s,t}. La figura 6 muestra una posible trayectoria de este proceso.
Figura 6: Trayectoria simulada de un movimiento Browniano con tendencia conµ=1 yσ=0,3
2. Movimiento Browniano geométrico (económico).SeaXtel proceso definido como:
Xt=eµt+σWt conµ∈R,σ≥0,t≥0. (11)
este se denominamovimiento browniano geométricoo económico, por ser el tipo de proceso más utilizado en la
modelación del precio de activos, como se mostrará más adelante.
Figura 7: Trayectoria simulada de un movimiento Browniano geométrico conµ=0,25 yσ=0,5
Ejercicio
Determine el valor esperado y la varianza del movimiento Browniano Geométrico.
En diversas situaciones es de interés trabajar conmovimientos Brownianos correlacionados. Por ejemplo, las utilidades
de un proyecto son función de ingreso It y de los costosCt. Si se asume que el ingreso sigue un proceso Browniano
geométrico, mientras que los costos siguen un proceso Browniano aritmético, es posible que los movimientos Brownianos
estándar de cada proceso estén correlacionados.
ConsideremosWt1yWt2dos movimientos Brownianos independientes, y un númeroρtal que−1≤ρ≤1 entonces, para
todo instante 0≤t≤T, el proceso definido como:
Zt:=ρWt1+
q
(1−ρ2)Wt2 (12)
tiene las siguientes propiedades:
1.
E[Zt] =E[ρWt1+
q
(1−ρ2)Wt2]
=ρE[Wt1] +
q
(1−ρ2)E[Wt2]
=ρ(0) +
q
(1−ρ2)(0) =0
(13)
2.
V[Zt] =V[ρWt1+
q
(1−ρ2)Wt2]
=ρ2V[Wt1] +
q
(1−ρ2)
2
V[Wt2]
=ρ2(t) + (1−ρ2)(t) =t
3. Si consideramos los incrementos del procesoZt, es decir,Zt+u−Zt, se tiene que: Zt+u−Zt= [ρWt1+u+
q
(1−ρ2)Wt2+u]−[ρWt1+
q
(1−ρ2)Wt2]
=ρ[Wt1+u−Wt1] +
q
(1−ρ2)[Wt2+u−Wt2]
(15)
y por las propiedades ya establecidas de los incrementos del movimiento browniano se tiene que:
E[Zt+u−Zt] =0
V= [Zt+u−Zt] =ρ2u+ (1−ρ2)u=u
De donde se concluye queZtes un movimiento Browniano estándar.
4. Al considerar la correlación entreZtyWt1, se tiene que:
Corr(Zt,Wt1) =
Cov(Zt,Wt1)
p
V[Zt]
p
V[Wt1]
=Cov(ρW
1
t +
p
(1−ρ2)Wt2,Wt1)
p
V[Zt]pV[Wt1]
=Cov(ρW
1
t ,Wt1) +Cov(
p
(1−ρ2)Wt2,Wt1)
p
V[Zt]
p
V[W1 t ]
=ρCov(W
1 t ,Wt1) +
p
(1−ρ2)Cov(Wt2,Wt1)
p
V[Zt]
p
V[W1 t ]
=ρV[W
1 t ] +
p
(1−ρ2)(0)
p
V[Zt]
p
V[Wt1]
=√ρt t√t =ρ
(16)
Se tiene entonces que la correlación entreZtyWt1es precisamenteρ. Este resultado será de gran utilidad al momento de simular movimientos brownianos correlacionados.
4.
Integral estocástica
En esta sección se presenta la definición de integral estocástica o Integral de Itô, que es una integral de la forma:
IT =
Z T
0
∆tdWt (17)
donde∆t es algún tipo de proceso adaptado (de valor conocido ent si se tiene la información hastatgenerada porWt), y
Definición 4.1: Integral de Itô
Dado un proceso estocástico∆t adaptado a la filtración generada porWt, y un movimiento Browniano estándar
Wt, se define:
IT =
Z T
0 ∆t
dWt:=l´ım n→∞
n−1
∑
j=0
∆tj(Wtj+1−Wtj) (18)
Ejemplo 3. Consideremos la integral
Z T
0
W tdW t (19)
Se tiene que:
Z T
0
WtdWt=l´ım n→∞
n−1
∑
i=0
Wti(Wti+1−Wti
| {z }
∗
) (20)
y se verifica fácilmente que la expresión marcada con (*) se satisface que:
Wti(Wti+1−Wti) = 1 2[W
2 ti+1−W
2
ti −(Wti+1−Wti)
2] (21)
luego,
Z T
0
WtdWt=l´ım n→∞
n−1
∑
i=0
1 2[W
2 ti+1−W
2
ti −(Wti+1−Wti)
2]
=1 2[W
2
T−W02]−
1 2nl´ım→∞
n−1
∑
i=0
(Wti+1−Wti)
2=1
2W
2
T−
1 2T
donde el segundo término corresponde a la variación cuadrática del browniano. En conclusión:
Z T
0
W tdW t=W
2 T
2 −
T
2
La integral de Itô cumple con las siguientes propiedades:
1. Siαyβ son constantes yXtyYt son procesos adaptados, entonces:
Z t
0
[αXs+βYs]dWs=α
Z t
0
XsdWs+β
Z t
0
YsdWs (22)
2. El valor esperado deIT es cero.
3. La varianza deIT =
RT
0 ∆tdWtes igual a
RT
4. La integralIT sigue una distribución normal tal que:
IT ∼N
0,
Z T
0 ∆2tdt
(23)
5. La integral estocástica es martingala, es decir, paras<t
E[It|Fs] =Is (24)
6. (Integración por partes) En general, si el integrando en IT es una función g continua y diferenciable, con g0acotada
y continua, se tiene que:
IT=
Z T
0
g(t)dWt d
=g(T)WT−
Z T
0
g0(t)Wtdt (25)
Ejercicio
Suponga queWtes un movimiento Browniano estándar, y considere el proceso estocásticoGtdefinido como sigue.
En el instantet=0 se lanza una moneda, si el resultado es caraG0=2, y si el resultado es selloG0=3. En el
instantet=√2, se lanza un dado yG√
2es igual al resultado de lanzar el dado. Si 0<t< √
2, se defineGt=G0,
y sit>√2 se defineGt=G√2.
1. Trace una posible trayectoria del procesoGt.
2. Determine la media y la varianza de:
Z 5 0
GtdWt
Nota
Se acostumbra utilizar la notación diferencialdItpara representar la integral estocástica
Rt
0∆sdWs, y esta notación
debe ser interpretada solamente en este contexto.
5.
Fórmula de Itô
Laformula de Itôes un resultado conseguido por el matemático Japones Kyoshi Itô (1915-2008), y permite establecer expresiones para la aplicación de funciones sobre el movimiento Browniano, y de forma más general sobre procesos de
5.1.
Fórmula de Itô para el movimiento Browniano
1. Si f∈C2(R), yWt es un movimiento browniano estándar, entonces:
f(Wt) =f(W0) +
Z t
0
f0(Ws)dWs+1 2
Z t
0
f00(Ws)ds (26)
y en notación diferencial
d f(Wt) =f0(Wt)dWt+
1 2f
00(
Wt)dt (27)
Ejemplo 4. Considere la función f(x) =xm, para m≥2, luego:
f0(x) =mxm−1 ; f00(x) =m(m−1)xm−2
entonces,
d f(Wt) =d(Wtm) =mWtm−1dWt+
1
2m(m−1)W
m−2
t dt
o
Wtm=W0m+m
Z t
0
Wsm−1dWs+
1
2m(m−1)
Z t
0
Wsm−2ds
Para el caso m=2se tiene que:
Wt2=2
Z t
0
WsdWs+
Z t 0 ds luego, Z t 0
WsdWs= Wt2
2 −
t
2
2. Si f∈C1([0,∞)])×C2(R), yWtes un movimiento browniano, entonces:
f(t,Wt) = f(0,W0) +
Z t
0 ∂
∂tf(s,Ws)ds+
Z t
0 ∂
∂xf(s,Ws)dWs+ 1 2
Z t
0 ∂2
∂x2f(s,Ws)ds (28)
o en notación diferencial:
d f(t,Wt) = ∂
∂t f(t,Wt)dt+ ∂
∂xf(t,Wt)dWt+ 1 2
∂2
Ejemplo 5. Si f(t,x) =tx2, entonces:
∂f
∂t =x
2 ; ∂f
∂x =2tx ; ∂2f ∂x2 =2t
f(t,Wt) =tWt2=
Z t
0
Ws2ds+
Z t
0
2sWsdWs+
1 2 Z t 0 2sds = Z t 0
Ws2ds+2
Z t
0
sWsdWs+ t2
2
d[tWt2] =Wt2dt+2tWtdWt+tdt= (t+Wt2)dt+ (2tWt)dWt
Del resultado en forma integral podemos despejar:
Z t
0
sWsdWs=
1 2
tWt2−t 2
2 −
Z t
0 Ws2ds
(30)
Ejercicio
Determinar la difrencial estocástica del procesoXt=eµt+σWt, dondeµyσ se asumen constantes.Es decir,
hallar una expresión paraX dt.
Nota
Las expresiones diferenciales consideradas en los resultados anteriores sonecuaciones diferenciales
esto-cásticasasociadas al movimiento browniano.
5.2.
Fórmula de Itô para procesos de Itô
A continuación se presenta la fórmula de Itô aplicada a procesos estocásticos más generales. A este tipo de procesos se
les denominaprocesos de Itô, y se definen como:
Definición 5.1: Procesos de Itô
Un proceso estocástico{Xt}t≥0se dice unproceso de Itôsi se puede expresar en la forma:
Xt=X0+
Z t
0
a(s,Xs)ds
| {z }
Riemann
+
Z t
0
b(s,Xs)dWs
| {z }
Itô
(31)
o, en notación diferencial:
dXt=a(t,Xt)dt
| {z }
Tendencia
+b(t,Xt)dWt
| {z }
Difusión
(32)
dXtdXt=b2(t,Xt)dt, por la regla de multiplicación de diferenciales.
La aplicación de la fórmula de Itô, para este tipo de procesos, establece que:
1. Dado queXtes un proceso de Itô, para el cualdXt=a(t,Xt)dt+b(t,Xt)dWt, y f ∈C2(R), entonces:
d(f(Xt)) =f0(Xt)dXt+
1 2f
00(X
t)(dXt)2 (33)
2. Si f(t,x)∈C1([0,∞))×C2(
R), entonces:
d(f(t,Xt)) =
∂f(t,Xt) ∂t dt+
∂f(t,Xt) ∂x dXt+
1 2
∂2f(t,Xt) ∂x2 (dXt)
2 (34)
3. Si f(t,x,y)∈C1([0,∞))×C2(R)×C2(R), entonces:
d(f(t,Xt,Yt)) =
∂f(t,Xt,Yt) ∂t dt+
∂f(t,Xt,Yt) ∂x dXt+
∂f(t,Xt,Yt) ∂y dYt+
1 2
∂2f(t,Xt) ∂x2 (dXt)
2+∂2f(t,Xt) ∂y2 (dYt)
2+2∂2f(t,Xt)
∂x∂y (dXt)(dYt)
(35)
Ejemplo 6. Determinar el proceso de Itô que satisface la ecuación diferencial estocástica:
dXt=
1
2Xtdt+XtdWt Xt>0
Utilizando la fórmula de Itô para la función f(x) =ln(x), se tiene que:
d[ln(Xt)] =
1
XtdXt−
1 2
1
X2 t
(dXt)2
= 1
Xt
1
2Xtdt+XtdWt
−1
2 1
Xt2(X 2 tdt)
=
dt
2 +dWt
−dt
2
=dWt
Lo anterior implica queln(Xt)−ln(X0) =eWt−W0, luego Xt=X0eWt.
Ejemplo 7. Consideremos el proceso de Itô,
Xt=
Z t
0
µ(s)−1
2σ
2(s)
ds+
Z t
0
σ(s)dWs
o, en notación diferencial,
dXt= (µ(t)−1
2σ
y sea, f(x) =S0ex, donde S0es constante. Se tiene que f(Xt) =St, es decir,
f(Xt) =S0e
Rt
0(µ(s)−1
2σ2(s))ds+
Rt
0σ(s)dWs=St
y por la aplicación de la fórmula de Itô se tiene que:
d f(Xt) =dSt=S0eXtdXt+
1 2S0e
Xt(dX
t)2
=S0eXt((µ(t)−1 2σ
2(t))dt+
σ(t)dWt) +
1 2S0e
Xt(σ2(t)dt)
=S0eXt(µ(t)dt+σ(t)dWt)
=St(µ(t)dt+σ(t)dWt)
de donde tenemos que: