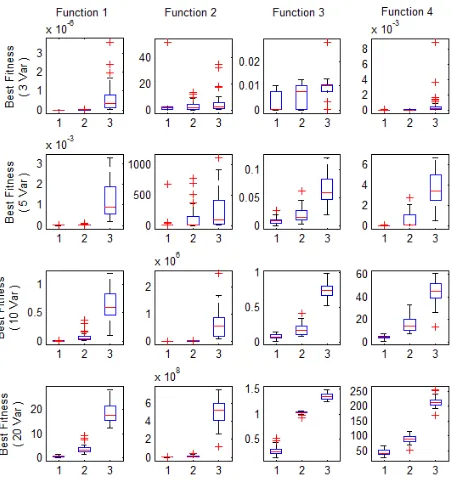
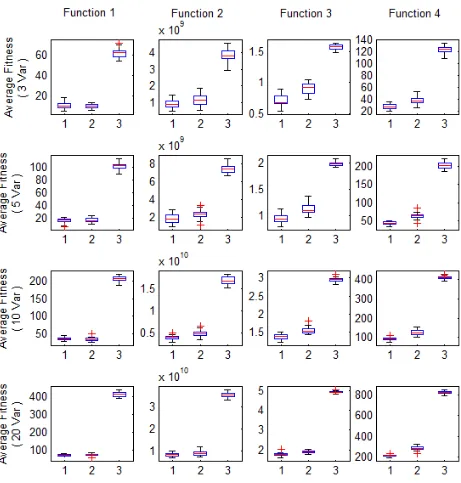
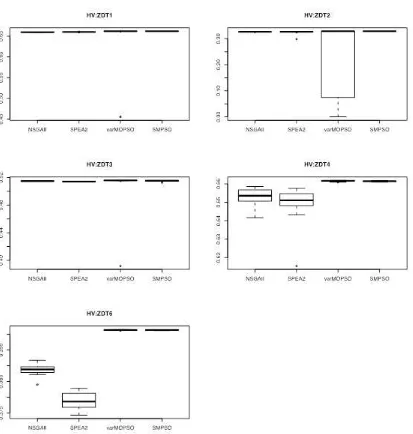
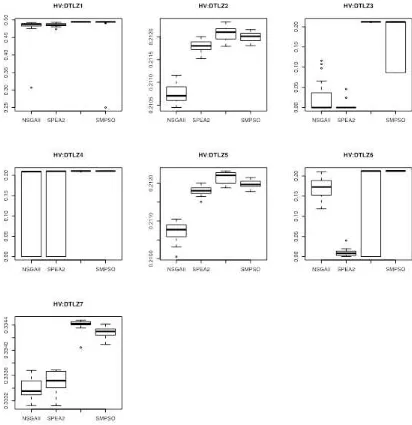
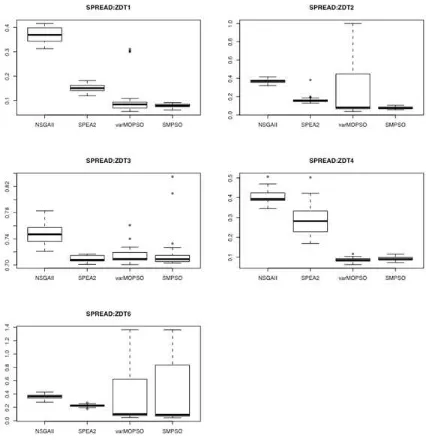
Optimización multi-objetivo . Aplicaciones a problemas del mundo real
Texto completo
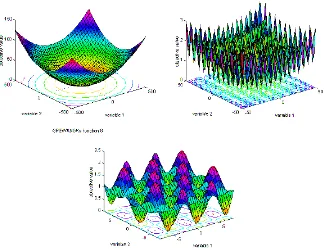
Figure
Documento similar
Volviendo a la jurisprudencia del Tribunal de Justicia, conviene recor- dar que, con el tiempo, este órgano se vio en la necesidad de determinar si los actos de los Estados
Las características del trabajo con grupos que se debería llevar a cabo en los Servicios Sociales de Atención Primaria (SSAP), en términos de variabilidad o estabilidad
de su infinito amor.. imperio sobre las nubes, que.. desgracias vencidas, se vu elven las calamidades risueñas.. Publicad sus maravillas, sus inumerables beneficios ,
A partir de aquí se procederá sistemáticamente a un análisis racional de su esencia, lo cual se efectúa desde la filosofía crítica kantiana —que tiende a la separa- ción-
o esperar la resolución expresa" (artículo 94 de la Ley de procedimiento administrativo). Luego si opta por esperar la resolución expresa, todo queda supeditado a que se
en una especie de «era pospartidos». Según este punto de vista, la cuestión de la estabilidad electoral de los sistemas de partidos de Europa occidental se convierte en
Sabemos que, normalmente, las cookies deben ser almacenadas y enviadas de vuelta al servidor sin modificar; sin embargo existe la posibilidad de que un atacante
Figura 5.9 Comparaci´ on del ranking la mejor soluci´ on encontrada hasta cada iteraci´ on, entre el algoritmo de b´ usqueda y su respectiva b´ usqueda aleatoria, para cada funci´