TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES

TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES

La técnica del desarrollo de fracciones parciales es establecida para cuidar todos los casos sistemáticamente.

Hay 4 clases de problemas, dependiendo del denominador D(s): Caso 1: C(s) tiene polos reales de 1er orden.

Caso 2: C(s) tiene polos reales repetidos de primer orden.

Caso 3: C(s) tiene un par de polos complejos conjugados (un factor cuadrático en el denominador). Caso 4: C(s) tiene pares repetidos de polos complejos conjugados (un factor cuadrático repetido en el denominador).

CASO 1: POLOS REALES DE 1ER ORDEN.

La posición de estos polos reales deC(s) en el plano s se muestra en la figura 1. Los polos pueden ser positivos ceros o negativos y ellos están situados en el eje real en el plano s. En este ejemplo

s₁

es positivo,

s₀

es cero,

s₂

es negativo. Para los polos mostrados en la figura 1, la transformada F(s) y sus fracciones parciales son:

𝐶(𝑠) =𝑁(𝑠) 𝐷(𝑠)=

𝑁(𝑠) 𝑠 (𝑠 − 𝑠1) (𝑠 + 𝑠2)

𝐶(𝑠) = 𝐴0 𝑠 +

𝐴₁ 𝑠 − 𝑠₁+

𝐴₂

𝑠 + 𝑠₂

X x x

Figura 1. Localización de los polos reales en el plano s

Hay tantas fracciones como hay factores en el denominador de C(s), ya que

s₀

=0, el factor

s-s₀

es escrito simplemente como s. la transformada inversa para C(s) es: 𝑐(𝑡) = 𝐴₀+ 𝐴₁𝑒𝑠1𝑡+ 𝐴

2𝑒−𝑠2𝑡

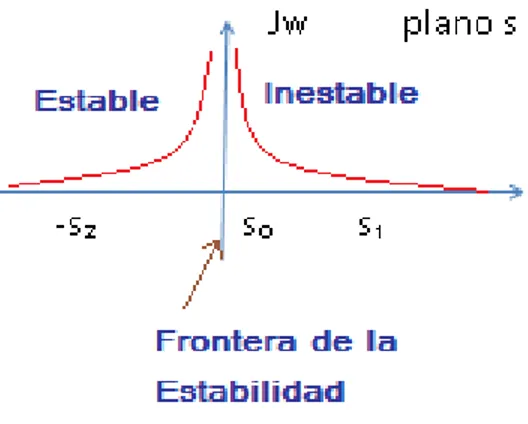
Jw plano s

El polo

s₁

es positivo, por lo tanto el término 𝑨𝟏𝒆𝒔𝟏𝒕 es un incremento exponencial y el

sistema es inestable. El polo

s₂

es negativo, y el término 𝑨𝟐𝒆−𝒔𝟐𝒕 es una caída exponencial con

valor final de cero. Por lo tanto, para que un sistema sea estable, todos los polos reales que contribuyen a complementar la solución deben estar en la mitad izquierda del plano s.(ver figura 1A)

Figura 1A. Comportamiento de los polos: positivo y negativo.

Para evaluar un típico coeficiente 𝐴𝑘 , multiplicando ambos lados de la ecuación por el

factor (𝑠 − 𝑠𝑘) . El resultado es:

(𝑠 − 𝑠_𝑘) 𝐶(𝑠) = (𝑠 − 𝑠_𝑘)𝑁(𝑠) 𝐷(𝑠)= 𝐴1

𝑠 − 𝑠𝑘

𝑠 − 𝑠₁+ 𝐴2 𝑠 − 𝑠𝑘

𝑠 − 𝑠₂+ ⋯ + 𝐴𝑘+ ⋯ + 𝐴𝑣 𝑠 − 𝑠𝑘

𝑠 − 𝑠_𝑣 La multiplicación del factor 𝑠 − 𝑠𝑘 sobre el lado izquierdo del a ecuación. Y el mismo factor

D(s) deberá dividirse fuera. Si 𝑠 = 𝑠𝑘, todos los términos en el lado derecho de la ecuación son

cero excepto 𝐴𝑘. Así, una regla general para evaluar las constantes para polos reales de orden

simple es:

𝐴

𝑘

[(𝑠 − 𝑠

𝑘

)

𝑁(𝑠)

𝐷(𝑠)

]

𝑠=𝑠𝑘

= [

𝑁(𝑠)

𝐷

′

_(𝑠)

]

𝑠=𝑠𝑘

Donde D’(s) es 𝑑𝐷(𝑠)_𝑑𝑠 = _{(𝑠−𝑠𝑘)}𝐷(𝑠) . Los coeficientes 𝐴𝑘 son llamados los residuos de C(s) de los

polos correspondientes. Para el caso de: 𝐶(𝑠) = 𝑠 + 2

𝑠(𝑠 + 1)(𝑠 + 3)= 𝐴₀

𝑠 + 𝐴₁ (𝑠 + 1)+

𝐴₂ (𝑠 + 3)

Las constantes son:

𝐴₀ = [𝑠 𝐶(𝑠)]_𝑠=0= [ 𝑠 + 2

𝐴₁= [(𝑠 + 1)𝐶(𝑠)]_𝑠=−1= [ 𝑠 + 2

𝑠(𝑠 + 3)]𝑠=−1= − 1 2

𝐴₂= [(𝑠 + 3)𝐶(𝑠)]_𝑠=−3= [ 𝑠 + 2

𝑠(𝑠 + 1)]𝑠=−3= − 1 6

La solución de c(t) es: 𝒄(𝒕) =𝟐

𝟑− 𝒆−𝒕

𝟐 − 𝒆−𝟑𝒕

𝟔

CASO 2: POLOS REALES DE ORDEN MÚLTIPLE.

La posición de los polos reales de F(s), algunos de los cuales son repetidos, se muestra en la figura 2. El símbolo ]𝑟 es proyectado para indicar un polo de orden r.

X x 0

Figura 2. Localización de polos reales en el plano s.

Todos los polos reales están situados sobre el eje real del plano s. para los polos mostrados en la figura 2, la transformada de C(s) y sus fracciones parciales son:

𝐶(𝑠) =𝑁(𝑠) 𝐷(𝑠)=

𝑁(𝑠) (𝑠 − 𝑠₁)3_{(𝑠 + 𝑠}

2)

𝐶(𝑠) = 𝐴13 (𝑠 − 𝑠₁)3+

𝐴₁₂ (𝑠 − 𝑠₁)2+

𝐴₁₁ 𝑠 − 𝑠₁+

𝐴₂

𝑠 + 𝑠₂ El orden de D(s) en este caso es cuatro, y hay cuatro fracciones. Note que el polo múltiplo

s

, el cual es de orden 3, tiene resultados en tres fracciones en el lado derecho de la ecuación C(s). Para designar las constantes en las fracciones parciales, un solo subíndice es usado para un polo de primer orden. Para polos de orden múltiplo, una notación de doble subíndice es usada. El primer subíndice designa el polo, y el segundo subíndice designa el orden del polo en la fracción parcial. Los constantes asociados con los denominadores de primer orden en el desarrollo de las

s₁ ]3 s₁

fracciones parciales son denominados residuos; por lo tanto únicamente las constantes 𝐴11 𝑦 𝐴2

son residuos de la ecuación C(s). La transformada inversa de C(s) es:

𝑐(𝑡) = 𝐴₁₃𝑡2

2 𝑒𝑠1𝑡 + 𝐴12𝑡𝑒𝑠1𝑡+ 𝐴11𝑒𝑠1𝑡+ 𝐴2𝑒𝑠2𝑡 Como calcular las constantes del orden múltiplo:

Para la transformada general con raíces reales repetidas: 𝐶(𝑠) =𝑁(𝑠)

𝐷(𝑠)=

𝑁(𝑠)

(𝑠 − 𝑠_𝑞)𝑟 (𝑠 + 𝑠₁) …

𝐶(𝑠) = 𝐴𝑞𝑟 (𝑠 − 𝑠𝑞)𝑟+

𝐴_{𝑞(𝑟−1)}

(𝑠 − 𝑠_𝑞)(𝑟−1)+ ⋯ +

𝐴_{𝑞(𝑟−𝑘)}

(𝑠 − 𝑠_𝑞)(𝑟−𝑘)+ ⋯ +

𝐴_𝑞1 𝑠 − 𝑠𝑞+

𝐴1

𝑠 − 𝑠1+ ⋯

La constante 𝐴𝑞𝑟 puede evaluarse simplemente, multiplicando ambos lados de la ecuación C(s)

por (𝑠 − 𝑠𝑞)𝑟 obtendremos:

(𝑠 − 𝑠_𝑞)𝑟_{𝐶(𝑠) = (𝑠 − 𝑠} 𝑞)𝑟

𝑁(𝑠) 𝐷(𝑠)=

𝑁(𝑠) (𝑠 − 𝑠1) …

= 𝐴_𝑞𝑟+ 𝐴_{𝑞(𝑟−1)}(𝑠 − 𝑠_𝑞) + ⋯ + 𝐴_𝑞1(𝑠 − 𝑠_𝑞)𝑟−1_{+ 𝐴} 1

(𝑠 − 𝑠_𝑞)𝑟

𝑠 − 𝑠₁ + ⋯ Nótese que el factor (𝑠 − 𝑠𝑞) es dividido fuera de la parte izquierda de la ecuación

Para 𝑠 = 𝑠𝑞 todos los términos en el lado derecho de la ecuación son ceros excepto para 𝐴𝑞𝑟 :

𝐴_𝑞𝑟= [ (𝑠 − 𝑠_𝑞)𝑟𝑁(𝑠)

𝐷(𝑠) ]𝑠=𝑠𝑞

La evaluación de 𝐴𝑞(𝑟−1) no puede realizarse en una manera similar. Multiplicando ambos

lados de la ecuación C(s) por (𝑠 − 𝑠𝑞)(𝑟−𝑘) y haciendo 𝑠 = 𝑠𝑞 resultando en ambos lados su

estado infinito, lo cual hace que 𝐴𝑞(𝑟−1) sea indeterminable.

Si el término 𝐴𝑞𝑟 queda eliminado en la ecuación (𝑠 − 𝑠𝑞)𝑟𝐶(𝑠), 𝐴𝑞(𝑟−1) puede

evaluarse. Así puede realizarse por diferenciación de la ecuación (𝑠 − 𝑠𝑞)𝑟𝐶(𝑠) con respecto a

s

:

𝑑

𝑑𝑠[ (𝑠 − 𝑠𝑞)𝑟 𝑁(𝑠)

𝐷(𝑠)] = 𝐴𝑞(𝑟−1)+ 2𝐴𝑞(𝑟−2)(𝑠 − 𝑠𝑞) + ⋯ Haciendo 𝑠 = 𝑠𝑞 :

𝑑

Repitiendo la derivación obtenemos el coeficiente 𝐴𝑞(𝑟−𝑧)

𝐴_{𝑞(𝑟−𝑧)}=1 2

𝑑2

𝑑𝑠2[ (𝑠 − 𝑠𝑞)𝑟

𝑁(𝑠)

𝐷(𝑠)]𝑠=𝑠𝑞 Este proceso puede repetirse hasta que cada constante sea determinada. Una fórmula general para descubrir esos coeficientes asociados con el polo real repetido de orden

r

, es:

𝐴_{𝑞(𝑟−𝑘)}= 1 𝑘!

𝑑𝑘

𝑑𝑠𝑘[ (𝑠 − 𝑠𝑞)𝑟

𝑁(𝑠)

𝐷(𝑠)]𝑠=𝑠𝑞

Para el caso de: 𝐶(𝑠) = 1

(𝑠 + 2)3_{(𝑠 + 3)}=

𝐴13

(𝑠 + 2)3+

𝐴12

(𝑠 + 2)2+

𝐴11

𝑠 + 2+ 𝐴2

𝑠 + 3

Las constantes son:

𝐴₁₃= [ (𝑠 + 2)3_𝐶(𝑠)]

𝑠=−2= [

1

𝑠 + 3]_𝑠=−2 = 1

𝐴₁₂= 𝑑

𝑑𝑠[ (𝑠 + 2)3𝐶(𝑠)]𝑠=−2= 𝑑 𝑑𝑠[

1

𝑠 + 3]_𝑠=−2= [ −(1)1 (𝑠 + 3)2]

𝑠=−2

= −1

𝐴

11

=

1

2!

𝑑

2

𝑑𝑠

2

[(𝑠 + 2)

3

𝐶(𝑠)]

𝑠=−2

=

1

2

𝑑

2

𝑑𝑠

2

[

1

𝑠 + 3

]

𝑠=−2

=

1

2

𝑑

𝑑𝑠

[

−(1)1

(𝑠 + 3)

2

]

𝑠=−2

=

𝐴

₁₁

=

1₂

[

+1(2)(𝑠+3)_(𝑠+3)4

]

𝑠=−2

=

1 2

[

2 1

]

=1

𝐴

₂

= [(𝑠 + 3)𝐶(𝑠)]

_𝑠=−3

= [

1

(𝑠 + 2)

3

]

𝑠=−3

= −1

Y la solución como una función de tiempo es

c (t) =

𝑡

2

CASO N° 3. POLOS COMPLEJOS CONJUGADOS.

La posición de los polos complejos de F(s) en el plano s se muestra en la figura 3.

Los polos complejos siempre son presentados en pares complejos conjugados; su

parte real puede ser positivo o negativo. Para los polos mostrados en la figura 3 la

transformada F(s) y sus fracciones parciales son:

𝐶(𝑠) =

𝑁(𝑠)

𝐷(𝑠)

=

𝑁(𝑠)

(𝑠

2

_{+ 2𝛿𝑤}

𝑛

𝑠 + 𝑤

𝑛2

)(𝑠 − 𝑠

3

)

=

𝐴

1

(𝑠 − 𝑠

₁

)

+

𝐴

2

(𝑠 − 𝑠

₂

)

+

𝐴

3

(𝑠 − 𝑠

₃

)

=

𝐴1

(𝑠+𝛿𝑤_𝑛−𝑗𝑤_𝑛√1−𝑠2₎

+

𝐴₂

(𝑠+𝛿𝑤_𝑛−𝑗𝑤_𝑛√1−𝑠2₎

+

𝐴₃

(𝑠−𝑠₃)

La transformada inversa de C(s) es:

f(t)=

𝐴

₁

𝑒

(−𝛿𝑤𝑛+𝑗𝑤𝑛√1−𝛿2)

+ 𝐴

2

𝑒

(−𝛿𝑤𝑛+𝑗𝑤𝑛√1−𝛿2)

+ 𝐴

1

𝑒

(𝑠3𝑡)

Entonces los polos

𝑆

₁

y

𝑆

₂

son complejos conjugados y entonces f(t) es una cantidad

real, los coefiientes

𝐴

1

y

𝐴

2

tienen también que ser complejos conjugados. La ecuación

puede escribirse con los primeros términos combinados para una más usual forma

senosoidal amortiguada:

𝑐(𝑡) = 2|𝐴

1

|𝑒

−𝛿𝑤𝑛𝑡

𝑠𝑒𝑛 (𝑤

𝑛

√1 − 𝛿

2

𝑡 + ∅) + 𝐴

3

𝑒

𝑠3𝑡

𝑐(𝑡) = 2|𝐴

1

|𝑒

𝜎𝑡

𝑠𝑒𝑛(𝑤

𝑑

𝑡 + ∅) + 𝐴

3

𝑒

𝑠3𝑡

Donde el ángulo:

∅ = 𝑎𝑛𝑔𝑢𝑙𝑜 𝑑𝑒 𝐴

₁

+ 90.

Los valores de

𝐴

₁

𝑦 𝐴

₃

, del mismo modo que se fundamenta en la manera previamente

mostrada, son:

𝐴

₁

= ⟦(𝑠 − 𝑠

₁

)𝐶(𝑠)⟧

_𝑠=𝑠1

𝐴

2

= ⟦(𝑠 − 𝑠

3

)𝐶(𝑠)⟧

𝑠=𝑠3

Así como

𝑠

1

es complejo, la constante

𝐴

1

es también compleja. Recuérdese que

𝐴

3

está

asociada con el polo complejo con la parte imaginaria positiva.

En la figura 3, los polos complejos tienen una parte real negativa,

𝜎 = −𝛿𝑤

_𝑛

,

donde la

razón de amortiguamiento

𝛿

es positiva. Para este caso la correspondiente respuesta

transitoria es conocida como una sinusoidal de amortiguada y se muestra en la figura 4.

Si las raíces complejas son en la mitad derecha del plano s, la razón del

amortiguamiento es negativa. El ángulo n para este caso es medido para el eje real positivo

y está dado por:

cos 𝑛 = |𝛿|

Para el caso de:

𝐶(𝑠) =

1

(𝑠2_{+6𝑠+25)(𝑠+2)}

=

𝐴1

𝑠+3−𝑗4

+

𝐴2

𝑠+3+𝑗4

+

𝐴3

𝑠+2

Las constantes son:

Su valor final es cero. El ángulo ∅ mostrado en la figura 4, es medido del eje real negativo y se relaciona a la razón de amortiguamiento por : Cos 𝑛 = 𝛿

Si el polo complejo tiene una parte real positiva, la respuesta con respecto al tiempo se incrementa exponencialmente con el tiempo y el sistema es inestable.

𝐴

₁

⟦(𝑠 + 3 − 𝑗4)

1

(𝑠+6𝑠+25)(𝑠+2)

⟧

_{𝑠=−3+𝑗4}

=

⟦

1

(𝑠+3+𝑗4)(𝑠+2)

⟧

_{𝑠=−3+𝑗4}

=

1

(−3+𝑗4+3+𝑗4)(−3+𝑗4+2)

=

1

(𝑗8)(−1+𝑗4)

=

1

(8 ∡900_{)(4.123 ∡−75.96}0₎

=

1

(32.984 ∡900₊₍₁₈₀0_−75.960₎

=

0.0303

−194.04°

∅ = −194.04° + 90

0

_{= −104.04°}

𝐴

₃

⟦(𝑠 + 2)

_{(𝑠2+6𝑠+25)(𝑠+2)}1

⟧

𝑠=−2

=

⟦

1

(𝑠2_{+6𝑠+25)(𝑠+2)}

⟧

𝑠=−2

= 0.059

La solución es:

c(t)=0.06

𝑒

−3𝑡

𝑠𝑒𝑛 (4𝑡 − 104.04°) + 0.059𝑒

−2𝑡

Este ejemplo es usado para ilustrar las técnicas en fracciones parciales de expansión.

C(s)

c(t) 0≤t

1

(𝑠 + 𝑐)[(𝑠 + 𝑎)

2

_{+ 𝑏}

2

_]

𝑒

−𝑐𝑡

(𝑐 − 𝑎)

2

_{+ 𝑏}

2

+

𝑒

−𝑎𝑡

_{𝑠𝑒𝑛(𝑏𝑡 − ∅)}

𝑏√(𝑐 − 𝑎)

2

_{+ 𝑏}

2

∅ = 𝑡𝑎𝑛

−1

𝑏

𝑐 − 𝑎

El ángulo de fase en el término sinusoidal amortiguada es:

∅ = 𝑡𝑎𝑛

−1 𝑏

𝑐−𝑎

= ∅ = 𝑡𝑎𝑛

−1 42−3

= 104°

Esto es importante para hacer notar que:

𝑡𝑎𝑛

−1 4

−1

≠

𝑡𝑎𝑛

−1 4−1

Para obtener el valor correcto para el ángulo de

∅

, es útil trazar un esquema, como

el mostrado e la figura 5. Esto evita ambigüedades y confirma que

∅

es evaluado

Figura 5. Calculo del ángulo θ.

POLOS IMAGINARIOS.

La posición de los polos imaginarios de C(s) en el plano s se muestra en la figura 6.

Como la parte real de los polos es cero, los polos se proyectan sobre los ejes imaginarios.

Esta situación es un caso especial de polos complejos, u,gr, la razón de amortiguamiento

𝛿 = 0

. Para los polos mostrados en la figura 4-5, la transformada f(s) y sus fracciones

parciales son:

𝐶(𝑠) =

𝑁(𝑠) 𝐷(𝑠)

=

𝑁(𝑠) (𝑠2_+𝑤

𝑛2)(𝑠−𝑠3)

=

𝐴1

𝑠−𝑠1

+

𝐴2

𝑠−𝑠2

+

𝐴3

𝑠−𝑠3

La cuadrática puede factor izarse en término de los polos

𝑠

1

y

𝑠

2

;

asi:

𝑠

2

_{+ 𝑤}

𝑛2

= (𝑠 − 𝑗𝑤

𝑛

)(𝑠 + 𝑗𝑤

𝑛

)

=(

𝑠 − 𝑠

1

)

(

𝑠 + 𝑠

2

)

La transformada inversa de la ecuación (4-57) es:

c(t)=

𝐴

₁

𝑒

𝑗𝑤𝑛𝑡

₊

𝐴

2

𝑒

−𝑗𝑤𝑛𝑡

+

𝐴

3

𝑒

𝑠3𝑡

como c(t)es una cantidad real, los coeficientes A

₁

y A

₂

son complejos conjugados.

Los terminos de la ecuación pueden combinarse para una forma mas usual.

c(t)=2

|𝐴

₁

|

sen (

𝑤

_𝑛

𝑡 + ∅) + 𝐴

₃

𝑒

𝑠3𝑡

Ya que no hay términos de amortiguamiento multiplicando la senoide, esos términos

representan un valor de estado estable. El ángulo

∅

es:

∅

=angulo de

𝐴

₁

+90°

Los valores de

𝐴

₁

𝑦 𝐴

₂

, establecidos de la manera convencional son:

𝐴

1

= [(𝑠 − 𝑠

1

)C(s)]

𝑠=𝑠1

𝐴

₂

= [(𝑠 + 𝑠

₂

)C(s)]

_{𝑠=−𝑠2}

Para el caso donde

𝐶(𝑠) =

100

(𝑠

2

_{+ 25)(𝑠 + 2)}

=

𝐴

₁

(𝑠 − 𝑗5)

+

𝐴

₂

(𝑠 + 𝑗5)

+

𝐴

₂

(𝑠 + 2)

Los valores de los coeficientes son

𝐴

₁

= [(𝑠 − 𝑗5)𝐶(𝑠)]

_𝑠=𝑗5

=

[

_{(𝑠+𝑗5)(𝑠+2)}100

]

_𝑠=𝑗5

=

_{(𝑗5+𝑗5)(𝑗5+2)}100

=

_{(𝑗10)(𝑗5+2)}100

=

100

(10∡90°)(5.385∡68.2°)

=

100

53.85∡(90°+68.2°)

=

1.86 ∡ − 158.2°

𝐴

3

= [(𝑠 + 2)𝐶(𝑠)]

𝑠=−2

=

[

_(𝑠2100₊₂₅₎

]

𝑠=−2

=

100 (−22₊₂₅₎

=

100

(29)

= 3.45

𝜙 = −158.2° + 90° = −68.2°

La solución es:

c(t)= 3.72 sen (5t-68.2°)+3.45

𝑒

−2𝑡

CASO 4: POLOS COMPLEJOS DE ORDEN MÚLTIPLE.

C(s)=

𝑁(𝑠) (𝑠2_{+2𝛿𝑤𝑛𝑠+𝑤𝑛}2₎𝑟_𝑄

1(𝑠)

=

𝐴_𝑟

(𝑠+𝛿𝑤_𝑛+𝑗𝑤_𝑛√1−𝛿2₎𝑟

+

𝐴𝑟´

(𝑠+𝛿𝑤_𝑛+𝑗𝑤_𝑛√1−𝛿2₎𝑟

+

𝐴_𝑟−1

(𝑠+𝛿𝑤_𝑛+𝑗𝑤_𝑛√1−𝛿2₎𝑟−1

+

𝐴_𝑟−1´

(𝑠+𝛿𝑤_𝑛+𝑗𝑤_𝑛√1−𝛿2₎𝑟−1

+ …

𝐴1

(𝑠+𝛿𝑤_𝑛+𝑗𝑤_𝑛√1−𝛿2₎

+

𝐴₁𝑟

(𝑠+𝛿𝑤_𝑛+𝑗𝑤_𝑛√1−𝛿2₎

+ …

Las constantes son evaluadas en la misma manera como para raíces reales repetidas, la

transformada inversa es de la forma:

c(t)= 2

|𝐴

_𝑟

|

𝑡

𝑟−1

(𝑟−1)!

𝑒

−𝛿𝑤𝑛𝑡

sen(

𝑤

𝑛

√1 − 𝛿

2

𝑡

+

∅

𝑟

) +

2

|𝐴

_𝑟−1

|

𝑡

𝑟−2

(𝑟−2)!

𝑒

−𝛿𝑤𝑛𝑡

_sen(

𝑤