CAPÍTULO IV
RESULTADOS
MODELO 2: INVESTIGACIÓN DE
TIPO CORRELACIONAL
4.1. Descripción
Tabla 1
Inteligencia emocional y logros de aprendizaje de los niños de la institución educativa Perú
Inteligencia emocional
Logros de aprendizaje
Total Inicio Proceso Logrado
n % n % n % n %
Bajo 0 0% 0 0% 0 0% 0 0%
Medio 29 19% 27 18% 38 25% 94 63%
Alto 0 0% 10 7% 46 31% 56 37%
Total 29 19% 37 25% 84 56% 150 100%
Chi-cuadrado de Pearson = 29.863 g.l. = 2 ***p < .001 Correlación de Spearman = .741***
Fuente: Cuestionario dirigido a niños (Anexo 1)
Como se muestra en la tabla 1, la inteligencia emocional está relacionado
directamente con los logros de aprendizaje de los niños del segundo ciclo
según la correlación de Spearman de 0.741, representando ésta una aceptable
asociación de las variables y siendo altamente significativo. Además, según la
prueba de la independencia (Chi-cuadrado: ***p < .001) altamente significativo,
se acepta la relación entre la inteligencia emocional y los logros de aprendizaje
de los niños de la institución educativa Perú.
Figura 1. Inteligencia emocional y logros de aprendizaje de los niños de la institución educativa Perú
0% 0% 0% 19% 18% 25% 0% 7% 31% Logr o s d e ap re n d izaje In ic io Pr o ce so Logr ad o
Como se observa en la figura 1; los niños con inteligencia emocional de nivel
medio, el 19% presentan un inicio en su logro de aprendizaje, el 18% se
encuentra en proceso de su logro de aprendizaje y el 25% ha logrado su
aprendizaje. Así mismo, los niños con inteligencia interpersonal de nivel alto, el
7% se encuentra en proceso de su logro de aprendizaje y el 31% ha logrado su
aprendizaje.
Tabla 2
Inteligencia intrapersonal y logros de aprendizaje de los niños de la institución educativa Perú
Inteligencia intrapersonal
Logros de aprendizaje
Total Inicio Proceso Logrado
n % n % n % n %
Bajo 0 0% 0 0% 0 0% 0 0%
Medio 29 19% 27 18% 38 25% 94 63%
Alto 0 0% 10 7% 46 31% 56 37%
Total 29 19% 37 25% 84 56% 150 100%
Chi-cuadrado de Pearson = 29.863 g.l. = 2 ***p < .001 Correlación de Spearman = .742***
Fuente: Cuestionario dirigido a niños (Anexo 1)
Como se muestra en la tabla 2, la inteligencia intrapersonal está relacionado
directamente con los logros de aprendizaje de los niños del segundo ciclo
según la correlación de Spearman de 0.742, representando ésta una buena
asociación de las variables y siendo altamente significativo. Además, según la
prueba de la independencia (Chi-cuadrado: ***p < .001) altamente significativo,
se acepta la relación entre la inteligencia intrapersonal y los logros de
Figura 2. Inteligencia intrapersonal y logros de aprendizaje de los niños de la institución educativa Perú
Como se observa en la figura 2; los niños con inteligencia intrapersonal de nivel
medio, el 19% presenta un inicio en su logro de aprendizaje, el 18% se
encuentra en proceso de su logro de aprendizaje y el 25% ha logrado su
aprendizaje. Así, los niños con inteligencia intrapersonal de nivel alto, el 7% se
encuentra en proceso de su logro de aprendizaje y el 31% ha logrado su
aprendizaje.
Tabla 3
Inteligencia interpersonal y logros de aprendizaje de los niños de la institución educativa Perú
Inteligencia interpersonal
Logros de aprendizaje
Total Inicio Proceso Logrado
n % n % n % n %
Bajo 10 7% 10 7% 9 6% 29 19%
Medio 19 13% 27 18% 39 26% 85 57%
Alto 0 0% 0 0% 36 24% 36 24%
Total 29 19% 37 25% 84 56% 150 100% Chi-cuadrado de Pearson = 39.780 g.l. = 4 ***p < .001
Correlación de Spearman = .651***
Fuente: Cuestionario dirigido a niños (Anexo 1)
0% 0% 0% 19% 18% 25% 0% 7% 31% Logr o s d e ap re n d izaje In ic io Pr o ce so Logr ad o
Como se muestra en la tabla 3, la inteligencia intrapersonal está relacionado
directamente con los logros de aprendizaje de los niños del segundo ciclo
según la correlación de Spearman de 0.651, representando ésta una aceptable
asociación de las variables y siendo altamente significativo. Además, según la
prueba de la independencia (Chi-cuadrado: ***p < .001) altamente significativo,
se acepta la relación entre la inteligencia interpersonal y los logros de
aprendizaje de de los niños de la institución educativa Perú.
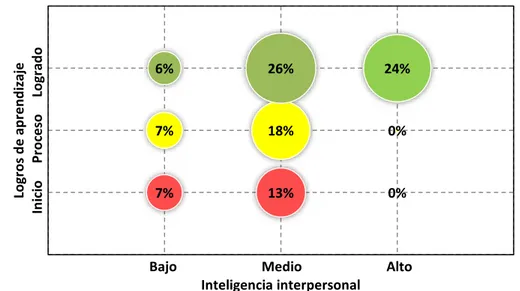
Figura 3. Inteligencia interpersonal y logros de aprendizaje de los niños de la institución educativa Perú
Como se observa en la figura 3; los niños con inteligencia interpersonal de nivel
bajo, el 7% presentan un inicio en su logro de aprendizaje, el 7% se encuentra
en proceso de su logro de aprendizaje y el 6% ha logrado su aprendizaje. Los
niños con inteligencia interpersonal de nivel medio, el 13% presenta un inicio
en su logro de aprendizaje, el 18% se encuentra en proceso de su logro de
aprendizaje y el 26% ha logrado su aprendizaje. Así mismo, los niños con
inteligencia interpersonal de nivel alto que han logrado su aprendizaje,
representan el 26% de la población total.
7% 7% 6% 13% 18% 26% 0% 0% 24% Logr o s d e ap re n d izaje In ic io Pr o ce so Logr ad o
CAPÍTULO III
METODOLOGÍA DE LA INVESTIGACIÓN
3.1. Formulación de hipótesis
3.1.1. Hipótesis general. (No mencionar las hipótesis estadísticas; nulas ni alternas), solo las hipótesis de investigación
3.1.2. Hipótesis específicas. (No mencionar las hipótesis estadísticas; nulas ni alternas), solo las hipótesis de investigación
3.2 Tipo de investigación 3.3 Método de investigación 3.4 Diseño de la investigación 3.5 Población
- población objetiva. Ejemplo: Red educativa “XXX”. - población accesible. Ejemplo; 3 instituciones educativas
3.6 Muestra. Extraer muestras significativas de la población accesible
Las unidades de análisis deben ser las mismas para las aplicaciones de los instrumentos (no pueden ser muestras de estudiantes y docentes a la vez para una investigación correlacional). Aplicar a la misma unidad muestral
Tabla 1.Distribución porcentual de características. (Mencionar las características de las unidades muéstrales en caso se utilice en la investigación)
Sujetos
Sexo
Estudiantes VARONES
MUJERES
GRADO ACADÉMICO
EDAD
OTROS
TOTAL
3.6. Proceso de inclusión y exclusión
Describir las características por las que son seleccionados o excluidos los sujetos de la muestra.
3.6 Técnicas e Instrumentos de acopio de datos
II. Normas de aplicación y corrección: el tiempo de duración de la aplicación del instrumento, forma de aplicación y otras características propias del instrumento.
III. Confiabilidad y validez de la escala. Los instrumentos estandarizados y validados en nuestra realidad ya no debe pasa por validación de experto (opinión técnica de especialistas); pero si pasa por el proceso estadístico; en función a las diversas técnicas para el proceso (ítem test total, r de finn, test retes, por mitades y otros). En casos que los instrumentos estandarizados hayan sido elaborados para sujetos que presentan otras características; se debe realizar el proceso de adaptación a la edad, condición socio económica, grado de estudio, etc. Con la opinión técnica de un experto temático.
3.7 Técnica de procesamiento de datos
Solo mencionar los que se van a aplicar durante el tratamiento de datos:
- Estadísticos descriptivos
(Describir a grandes rasgos) ....- también empleamos la desviación estándar que es el promedio de desviación de las puntuaciones con respecto a la media. Cuanto mayor es la dispersión de los datos alrededor de la media, mayor es la desviación estándar. (no incluir formulas; solo mencionar el estadístico utilizado)
- Estadísticos inferenciales
CAPÍTULO IV
PRESENTACIÓN Y ANÁLISIS DE RESULTADOS
4.1 Análisis de los datos (paramétricos o no paramétricos) Ejem.
- Cuando las variables son cualitativas de escala ordinal; (ejemplo. tipo Likert) y se totaliza las puntuaciones, hacer uso del ρ Spearman.
- Cuando las variables son cuantitativas (Eje. Rendimiento académico y coeficiente intelectual), hacer uso de la r de Pearson.
- Cuando una escala es ordinal y otra de intervalo; evaluar la normalidad de los datos:
n>= 30; evaluar con la técnica de Kolmogorov Smirnov n< 30 ; Evaluar con Shapiro Wilk
Distribución normal: ρ > 0,05 (paramétricos)
Ejemplo de estudio para dos variables con escala de intervalo
Variable Valores Instrumento
Razonamiento
Lógico 00, 01, 02, 03, 04,….. 20 Prueba
Rendimiento
Académico 00, 01, 02, 03, 04,….. 20 Prueba
Análisis descriptivos. Estadísticos
Tabla 26.
Estadísticos de las variables de estudio de los estudiantes de la Institución
Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03
Comas-Lima
Estadísti Variab.
𝑋̅ S2 m
e mo
RAZ LOG. 14,3 3,12 13,5 13
REN. ACAD 15 2,02 13 13
FUENTE. Instrumentos de observación - Investigadores
En la tabla 26, se aprecian los resultados estadísticos de las variables de estudio, observándose que la media del rendimiento académico es mayor que 0,7 puntos frente al razonamiento lógico, así mismo las puntuaciones del rendimiento académico presentan menor grado de dispersión frente al razonamiento lógico en 1,1 puntos, …
Prueba de hipotes
Hipótesis general.
El Razonamiento Lógico y el Rendimiento Académico se relacionan
significativamente en los estudiantes de la Institución Educativa Pública de
Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: Existe relación significativa alta entre el razonamiento lógico y el rendimiento
académico en los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: r ≠ 0
H1: No eexiste relación significativa alta entre el razonamiento lógico y el
rendimiento académico en los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: r = 0
Tabla 26.
Coeficiente de correlación Pearson entre las variables de Razonamiento Lógico y El Rendimiento académico de los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima
Nº Casos Estadístico
Pearson p-valor
180 .8782 .000
Fuente: Elaboración propia
Se puede afirmar que existe evidencia para concluir que existe una relación positiva y significativa alta y el p – valor= .000 < .05, entre las variables de Razonamiento Lógico y El Rendimiento académico en la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima,
Figura 1.Relación entre el pensamiento lógico y el rendimiento académico.
4.2.2 Hipótesis específica
Primera Hipótesis
H0: El nivel del razonamiento serial no se relaciona con el rendimiento académico en
los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: r = 0
H1: El nivel del razonamiento serial se relaciona con el rendimiento académico en los
estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima
Segunda Hipótesis
H0: El nivel del razonamiento secuencial no se relaciona con el rendimiento
académico en los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: r = 0
H1: El nivel del razonamiento secuencial se relaciona con el rendimiento académico
en los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: r ≠ 0
Tercera Hipótesis
H0: El nivel del razonamiento heurístico no se relaciona con el rendimiento
académico en los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: r = 0
H1: El nivel del razonamiento heurístico se relaciona con el rendimiento académico
en los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: r ≠ 0
Tabla 17.
Coeficiente de correlación de Pearson entre las variables de Razonamiento Lógico y El Rendimiento académico de los estudiantes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima
Razonamiento lógico (Dimensiones)
Rendimiento Académico
Estadístico Pearson. p-valor
Serial 0.7131 0.000
Secuencial 0.8548 0.000
Heuristico 0.8593 0.000
Fuente: Autores. Nivel de significancia: .05
El índice de correlación entre las variables de escala de intervalo cuyo valor siempre está comprendido entre -1 y 1. Los valores próximos a 1, en valor absoluto, indican una fuerte relación entre las dos variables. Los valores próximos a cero indican que hay poca o ninguna relación entre las dos variables.
Se puede afirmar que existe evidencia para concluir que existe una relación positiva y significativa y que el p–valor= .000 < .05, entre las dimensiones del Razonamiento lógico y el Rendimiento Académico de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima, rechazándose la hipótesis nula y aceptando la hipótesis alterna en todas las dimensiones planteadas a un nivel de confianza del 95%.
FORMATO: INVESTIGACIÓN
DE TIPO CORRELACIONAL
Ejemplo de estudio para dos variables con escala ordinal
Ejemplo.
Variable Valores Instrumento
Desempeño docente
Muy alta, alto, medio, bajo, muy
bajo Cuestionario
Actitud docente
Nunca, algunas veces, casi
siempre, siempre Cuestionario
Análisis descriptivos. Estadísticos
Tabla 26.
Descripción del desempeño docente de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima
Variable
Índices
Muy alta Alto Medio Bajo Muy bajo
fi %fi fi %fi fi %fi fi %fi fi %fi
Desempeño docente
10 18,5 15 27,7 8 14,81 9 16,6 12 22,2
FUENTE. Instrumentos de observación - Investigadores
En la tabla 26, se aprecian los resultados de frecuencias y porcentuales de los índices de estudio, observándose que el 27,7% afirman tener alto grado de desempeño de los docentes encuestados y el 14,81% un nivel de desempeño medio, …(describir los resultados más significativos)
Tabla 27.
Descripción de la actitud del docente de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima
Variable
Índices
Muy alta Alto Medio Bajo Muy bajo
Actitud docente
10 18,5 15 27,7 8 14,81 9 16,6 12 22,2
FUENTE. Instrumentos de observación - Investigadores
En la tabla 26, se aprecian los resultados de frecuencias y porcentuales de los índices de estudio, observándose que el 27,7% afirman tener alto grado de actitud de los docentes encuestados y el 14,81% un nivel de actitud medio, …(describir los resultados más significativos)
Prueba de hipotes
Para probar esta hipótesis, se procedió a utilizar el coeficiente de correlación de
Spearman, dado que este estadístico es apropiado para ver relaciones entre
variables de escala ordinal, el que es nuestro caso.
Hipótesis general.
El desempeño docente y la actitud docente se relacionan significativamente en los docentes de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: Existe relación significativa entre el desempeño docente y la actitud docente en la
Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: ρ ≠ 0
H1: No Existe relación significativa entre el desempeño docente y la actitud docente
en la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: ρ = 0
Correlación de Spearman entre las variables de desempeño docente y la
actitud en la Institución Educativa Pública de Educación Secundaria “El
Amauta” de la UGEL.03 Comas-Lima
Nº Casos Estadístico
Spearman p-valor
180 .782 .000
Fuente: Elaboración propia
Se puede afirmar que existe evidencia para concluir que existe una relación positiva y significativa alta y el p – valor= .000 < .05, entre las variables de desempeño y la actitud docente en la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima, aceptándose la hipótesis alterna y rechazándose la hipótesis nula.
4.2.2 Hipótesis específica
Primera Hipótesis
H0: El nivel D1……….. no se relaciona con el rendimiento la actitud docente en
de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: ρ = 0
H1: El nivel D1……….. se relaciona con el rendimiento la actitud docente en de
la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: ρ ≠ 0
H0: El nivel D2……….. no se relaciona con el rendimiento la actitud docente en
de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima.
Ho: ρ = 0
H1: El nivel D2……….. se relaciona con el rendimiento la actitud docente en de
la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima..
Ho: ρ ≠ 0
Para probar esta hipótesis específica, se procedió a utilizar el coeficiente de Spearman, dado que este estadístico es apropiado para ver relaciones entre variables de escala ordinal, el que es nuestro caso.
Tabla 17.
Coeficiente de correlación de Spearman entre las variables de estudio por
dimensiones de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima
Desempeño docente (Dimensiones)
Actitud docente
Estadístico Spearman. p-valor
D1 0.6131 0.000
D2 0.9548 0.000
….. 0.3593 0.0600
Fuente: Autores. Nivel de significancia: .05
una fuerte relación entre las dos variables. Los valores próximos a cero indican que hay poca o ninguna relación entre las dos variables.
Se puede afirmar que existe evidencia para concluir que existe una relación positiva y significativa y que el p–valor= .000 < .05, entre las dimensiones del desempeño y actitud docente de la Institución Educativa Pública de Educación Secundaria “El Amauta” de la UGEL.03 Comas-Lima, rechazándose la hipótesis nula y aceptando la hipótesis alterna en todas las dimensiones planteadas a un nivel de confianza del 95%.
ANEXO Nº 0xx
DOCENTES EN GENERAL
DOCEN TES
RELACIONES
INTERPERSONALES TOTAL AUTOREALIZACIÓN TOTAL ESTABILIDAD TOTAL T.S SEX
O C TOTAL
Agota miento Realiza ción Desper sonaliz acion Total IMPLICANC IA COHESI ÓN APO
YO AUTONOMIA ORGANIZACIÓN PRE SION CLARI DAD CON TROL INNOVACI ÓN COMODIFDA D
1 21 25 22 68 25 24 19 68 23 19 24 24 90 30 M N 226 12 16 9 37
2 16 21 22 59 19 17 18 54 20 18 18 21 77 27 M N 190 13 21 7 41
3 18 19 18 55 17 16 20 53 15 19 16 18 68 2 F C 176 12 13 10 35
4 16 24 20 60 20 17 18 55 20 18 18 17 73 26 M N 188 21 16 8 45
5 23 27 24 74 23 22 19 64 26 22 23 23 94 23 M N 232 11 18 6 35
6 12 11 13 36 12 16 13 41 14 11 13 15 53 6 M C 130 23 21 12 56
7 17 20 21 58 21 23 21 65 23 23 25 22 93 6 F C 216 9 22 6 37
8 16 21 22 59 24 22 20 66 20 18 19 21 78 6 F C 203 15 20 8 43
9 18 23 23 64 22 24 18 64 22 21 20 22 85 23 M N 213 16 20 9 45
10 17 20 18 55 20 16 20 56 18 18 18 18 72 21 M C 183 18 16 10 44
11 13 14 12 39 14 12 11 37 13 13 14 12 52 18 M N 128 21 22 20 63
12 18 23 23 64 19 19 17 55 20 16 19 18 73 14 M N 192 15 16 10 41
13 18 20 19 57 20 22 17 59 23 20 19 21 83 4 F N 199 11 23 7 41
14 19 20 20 59 19 19 21 59 21 22 16 24 83 18 M N 201 12 16 9 37
15 17 17 16 50 18 19 17 54 20 17 19 20 76 17 F C 180 19 19 9 47
16 21 24 21 66 24 26 18 68 24 21 22 22 89 1 M N 223 11 21 6 38
17 14 19 19 52 17 18 18 53 17 19 18 20 74 14 F N 179 11 22 8 41
18 21 21 23 65 20 26 21 67 25 22 21 24 92 15 M N 224 18 19 9 46
19 20 22 17 59 21 23 23 67 22 23 21 24 90 26 M N 216 10 19 6 35
20 16 17 15 48 18 11 17 46 13 17 15 17 62 16 M N 156 16 23 8 47
21 16 19 16 51 16 17 19 52 20 19 17 18 74 16 F N 177 11 18 6 35
22 15 19 17 51 16 19 19 54 19 17 17 20 73 18 M N 178 15 22 7 44
23 12 14 13 39 11 14 12 37 12 13 14 16 55 21 M N 131 23 21 13 57
24 20 23 18 61 21 21 17 59 19 18 20 23 80 16 M C 200 12 24 5 41
25 18 23 19 60 19 20 21 60 21 18 19 22 80 23 F N 200 11 22 7 40
26 17 19 18 54 18 21 18 57 18 18 20 21 77 28 M N 188 14 19 6 39
27 17 19 17 53 18 22 18 58 17 21 18 20 76 7 M C 187 16 17 7 40
28 20 20 24 64 22 22 19 63 24 17 23 23 87 5 F N 214 10 22 7 39
29 18 21 16 55 19 21 21 61 20 20 18 21 79 9 M N 195 12 23 7 42
30 16 20 18 54 15 26 19 60 19 19 19 19 76 15 M C 190 14 16 8 38
31 17 24 18 59 23 24 19 66 22 18 19 22 81 4 M N 206 9 21 9 39
32 19 19 20 58 21 19 16 56 20 20 18 21 79 20 M N 193 14 21 9 44
33 14 20 17 51 17 16 18 51 17 20 17 16 70 16 M N 172 22 20 9 51
34 18 22 21 61 20 23 18 61 24 20 21 21 86 14 M C 208 14 19 5 38
35 20 22 22 64 16 23 18 57 25 19 24 21 89 1 M N 210 14 21 5 40
36 15 18 18 51 17 17 19 53 18 20 18 19 75 15 F N 179 12 18 5 35
37 16 20 21 57 18 20 16 54 22 20 20 17 79 7 M N 190 17 20 10 47
38 20 22 22 64 23 18 21 62 20 21 22 22 85 17 M N 211 13 22 8 43
39 22 20 22 64 23 24 17 64 27 21 22 22 92 12 M C 220 11 22 7 40
40 19 20 20 59 22 23 21 66 26 21 23 23 93 8 M N 218 11 20 7 38
41 19 26 21 66 21 21 18 60 20 17 19 20 76 20 M N 202 14 21 9 44
42 17 21 24 62 21 20 21 62 23 21 17 18 79 15 M N 203 15 22 9 46
44 22 24 21 67 22 23 22 67 27 26 25 18 96 15 F N 230 11 20 6 37
45 20 19 20 59 19 19 16 54 18 19 18 23 78 17 M N 191 11 22 7 40
46 14 17 18 49 18 14 18 50 16 19 15 16 66 13 M C 165 12 18 7 37
47 20 25 22 67 25 23 18 66 26 23 23 22 94 10 M N 227 10 24 6 40
48 15 22 19 56 20 21 18 59 22 18 21 22 83 14 F N 198 13 16 6 35
49 20 21 18 59 21 20 19 60 19 21 19 21 80 15 M N 199 14 18 7 39
50 17 22 22 61 19 22 18 59 23 22 19 23 87 14 M N 207 11 19 5 35
51 18 19 17 54 18 19 20 57 18 21 18 18 75 7 M N 186 11 18 7 36
52 19 19 21 59 18 24 19 61 23 18 19 24 84 23 F N 204 12 22 8 42
53 12 14 13 39 16 12 14 42 12 15 16 13 56 12 M C 137 24 23 12 59
54 23 22 23 68 22 24 20 66 26 21 24 22 93 1 M C 227 10 23 5 38
55 17 20 22 59 22 22 17 61 23 18 18 17 76 6 M C 196 11 20 8 39
56 20 24 19 63 19 26 20 65 22 20 24 22 88 8 M N 216 16 23 8 47
57 16 16 21 53 21 18 19 58 21 22 20 19 82 18 F N 193 12 18 8 38
58 13 11 14 38 12 14 12 38 13 15 12 22 62 15 F N 138 25 20 12 57
59 17 18 22 57 24 20 19 63 23 18 21 18 80 9 F C 200 13 17 9 39
desv 2,71 3,29 2,98 7,99 3,10 3,73 2,42 7,80 3,82 2,62 3,08 2,79 10,52 7,2 25,34 3,96 2,52 2,45 6,31 prom 17,63 20,27 19,37 57,27 19,44 20,17 18,34 57,95 20,47 19,15 19,34 20,17 79,14 14 194,36 13,98 19,98 8,00 41,97
C-B1 -0,71 C1-B1 -0,65 C2-B1 -0,71 C3-B1 -0,70
C-B2 0,09 C1-B2 0,02 C2-B2 0,02 C3-B2 0,09
C-B3 -0,67 C1-B3 -0,57 C2-B3 -0,60 C3-B3 -0,67
CAPÍTULO IV
RESULTADOS
MODELO: INVESTIGACIÓN DE TIPO
CUASIEXPERIMENTAL
4.1. Descripción.
Tabla 1
Rendimiento matemático de los estudiantes del 6° grado de primaria del grupo de control y experimental según pretest y postest.
Estadístico
Grupo Test U de
Mann-Whitneya
Control (n=32) Experimental (n=28)
Pretest
Media 5.16 6.43 Z = 2.405
p = .016
Desv. típ. 2.03 2.04
Postest
Media 5.84 15.00 Z = 6.682
p < .001
Desv. típ. 1.85 1.36
Nota.
a Las notas no se aproximación a la distribución normal (K-S = .193; g.l. = 120; 𝑝 < .001)
El rendimiento matemático de los estudiantes del 6° grado de primaria es
diferente al 95% de confiabilidad de acuerdo a la prueba no paramétrica U de
Mann-Whitney, tanto para el grupo de control y experimental según el pretest,
presentando ligera ventaja los estudiantes del grupo experimental respecto a
los estudiantes del grupo de control.
Así mismo, el rendimiento matemático de los estudiantes del 6° grado de
primaria es diferente al 95% de confiabilidad de acuerdo a la prueba no
paramétrica U de Mann-Whitney, tanto para el grupo de control y experimental
según el postest, por lo que, los estudiantes del grupo experimental obtuvieron
mejores resultados en sus notas de matemática (Promedio = 15.00) después
de la aplicación de la técnica de trabajo cooperativo stad (student teams –
achievement divisions) respecto a los estudiantes del grupo de control
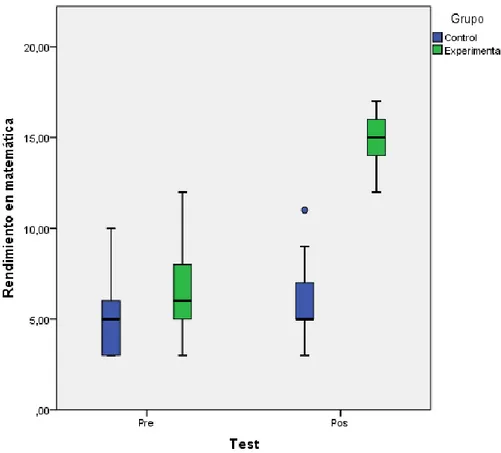
Figura 1. Rendimiento matemático de los estudiantes del 6° grado de primaria del grupo de control y experimental según pre test y pos test.
De la figura 1, se observa que las notas iniciales del rendimiento matemático
(pre test) son diferentes en los estudiantes del 6° grado de primaria del grupo
control y experimental, apreciándose una ligera ventaja para el grupo
experimental. Así mismo, se observa una diferencia significativa en las notas
del rendimiento matemático finales (pos test) entre los estudiantes del grupo de
control y experimental, siendo éstos últimos los que obtuvieron mayores notas
de rendimiento matemático. Además, en ambos casos, se observa una
Tabla 2
Rendimiento matemático: comunicación matemática de los estudiantes del 6° grado de primaria del grupo de control y experimental según pre test y pos test.
Estadístico
Grupo Test U de
Mann-Whitney Control (n=32) Experimental (n=28)
Pretest
Media 5.91 7.32 Z = -1.920
p = .055
Desv. típ. 2.93 2.79
Postest
Media 7.06 14.71 Z = -6.701
p < .001
Desv. típ. 2.66 2.02
Nota.
a Las notas no se aproximación a la distribución normal (K-S = .203; g.l. = 120; 𝑝 < .001)
El rendimiento matemático en comunicación matemática de los estudiantes del
6° grado de primaria es similar al 95% de confiabilidad de acuerdo a la prueba
no paramétrica U de Mann-Whitney, tanto para el grupo de control y
experimental según el pre test, significando así, que las condiciones iniciales de
los grupos son similares.
Así mismo, el rendimiento matemático en comunicación matemática de los
estudiantes del 6° grado de primaria es diferente al 95% de confiabilidad de
acuerdo a la prueba no paramétrica U de Mann-Whitney, tanto para el grupo de
control y experimental según el postest, por lo que, los estudiantes del grupo
experimental obtuvieron mejores resultados en sus notas de matemática
(Promedio = 14.71) después de la aplicación de la técnica de trabajo
cooperativo stad (student teams – achievement divisions) respecto a los
Figura 2. Rendimiento matemático en comunicación matemática de los estudiantes del 6° grado de primaria del grupo de control y experimental según pretest y postest.
De la figura 2, se observa que las notas iniciales del rendimiento matemático
(pretest) son de similar amplitud en los estudiantes del 6° grado de primaria del
grupo control y experimental, apreciándose una ligera ventaja no significativa
para el grupo experimental. Así mismo, se observa una diferencia significativa
en las notas del rendimiento matemático finales en comunicación matemática
(postest) entre los estudiantes del grupo de control y experimental, siendo
éstos últimos los que obtuvieron mayores notas de rendimiento matemático en
comunicación matemática. Además, en ambos casos, se observa una ligera
Tabla 3
Rendimiento matemático: aplicación de algoritmos de los estudiantes del 6° grado de primaria del grupo de control y experimental según pretest y postest.
Estadístico
Grupo Test U de
Mann-Whitney Control (n=32) Experimental (n=28)
Pretest
Media 5.00 5.93 Z = 2.021
p = .043
Desv. típ. 2.13 1.86
Postest
Media 5.47 15.50 Z = 6.641
p < .001
Desv. típ. 2.11 2.82
Nota.
a Las notas no se aproximación a la distribución normal (K-S = .260; g.l. = 120; 𝑝 < .001)
El rendimiento matemático en aplicación de algoritmos de los estudiantes del 6°
grado de primaria es diferente al 95% de confiabilidad de acuerdo a la prueba
no paramétrica U de Mann-Whitney, tanto para el grupo de control y
experimental según el pretest, presentando ligera ventaja los estudiantes del
grupo experimental respecto a los estudiantes del grupo de control.
Así mismo, el rendimiento matemático en aplicación de algoritmos de los
estudiantes del 6° grado de primaria es diferente al 95% de confiabilidad de
acuerdo a la prueba no paramétrica U de Mann-Whitney, tanto para el grupo de
control y experimental según el postest, por lo que, los estudiantes del grupo
experimental obtuvieron mejores resultados en sus notas de matemática
(Promedio = 15.50) después de la aplicación de la técnica de trabajo
cooperativo stad (student teams – achievement divisions) respecto a los
Figura 3. Rendimiento matemático en aplicación de algoritmos de los estudiantes del 6° grado de primaria del grupo de control y experimental según pretest y postest.
De la figura 3, se observa que las notas iniciales del rendimiento matemático en
aplicación de algoritmos (pretest) son diferentes en los estudiantes del 6° grado
de primaria del grupo control y experimental, apreciándose una ligera ventaja
para el grupo experimental. Así mismo, se observa una diferencia significativa
en las notas del rendimiento matemático finales en la aplicación de algoritmos
(postest) entre los estudiantes del grupo de control y experimental, siendo
éstos últimos los que obtuvieron mayores notas de rendimiento matemático en
la aplicación de algoritmos. Además, en ambos casos, se observa una
Tabla 4
Rendimiento matemático: resolución de problemas de los estudiantes del 6° grado de primaria del grupo de control y experimental según pretest y postest.
Estadístico
Grupo Test U de
Mann-Whitney Control (n=32) Experimental (n=28)
Pretest
Media 4.94 6.57 Z = 2.156
p = .031
Desv. típ. 2.34 3.02
Postest
Media 5.53 15.00 Z = 6.712
p < .001
Desv. típ. 2.42 2.97
Nota.
a Las notas no se aproximación a la distribución normal (K-S = .243; g.l. = 120; 𝑝 < .001)
El rendimiento matemático en resolución de problemas de los estudiantes del
6° grado de primaria es diferente al 95% de confiabilidad de acuerdo a la
prueba no paramétrica U de Mann-Whitney, tanto para el grupo de control y
experimental según el pretest, presentando ligera ventaja los estudiantes del
grupo experimental respecto a los estudiantes del grupo de control.
Así mismo, el rendimiento matemático en resolución de problemas de los
estudiantes del 6° grado de primaria es diferente al 95% de confiabilidad de
acuerdo a la prueba no paramétrica U de Mann-Whitney, tanto para el grupo de
control y experimental según el postest, por lo que, los estudiantes del grupo
experimental obtuvieron mejores resultados en sus notas de matemática
(Promedio = 15.00) después de la aplicación de la técnica de trabajo
cooperativo stad (student teams – achievement divisions) respecto a los
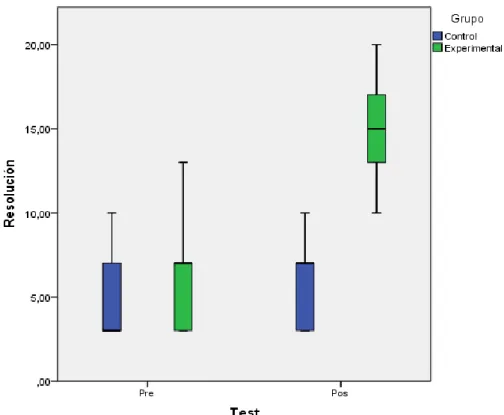
Figura 4. Rendimiento matemático en resolución de problemas de los estudiantes del 6° grado de primaria del grupo de control y experimental según pretest y postest.
De la figura 4, se observa que las notas iniciales del rendimiento matemático
(pretest) son diferentes en los estudiantes del 6° grado de primaria del grupo
control y experimental, apreciándose una ligera ventaja para el grupo
experimental. Así mismo, se observa una diferencia significativa en las notas
del rendimiento matemático finales en la resolución de problemas (postest)
entre los estudiantes del grupo de control y experimental, siendo éstos últimos
los que obtuvieron mayores notas de rendimiento matemático en la resolución
de problemas. Además, en ambos casos, se observa una mínima disminución
de la variabilidad de las notas en el postest respecto al pretest.
CAPÍTULO IV
RESULTADOS
MODELO : INVESTIGACIÓN DE TIPO
CUASIEXPERIMENTAL
4.1. Descripción.
Tabla 1
Rendimiento académico de las matemáticas en alumnos del quinto grado de educación secundaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo
T Student
Control (n=30) Experimental (n=27)
Pretest
[5 - 10] 70.0% 66.7%
t = 0.405
p = .992
[11-15] 23.3% 18.5%
[16-20] 6.7% 14.8%
Postest
[5 - 10] 83.3% 0.0%
t = 6.682
p < .001
[11-15] 13.3% 11.1%
[16-20] 3.3% 88.9%
El rendimiento académico de las matemáticas en alumnos de quinto grado de
educación primaria del grupo control y experimental presentan condiciones
iniciales similares (T Student: 𝑝 = .992) en los puntajes obtenidos del pretest.
Por otro lado, los puntajes del rendimiento académico de las matemáticas del
postest en los alumnos del grupo experimental presentan diferencias
significativas con los puntajes obtenidos del grupo control (T Student: ∗∗∗ 𝑝 <
.001), además, de presentar mayores puntajes obtenidos.
De la figura 1, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) son similares en los alumnos del grupo control y
experimental. Así mismo, se observa una diferencia significativa en los puntajes
finales (postest) entre los alumnos del grupo de control y experimental, siendo
éstos últimos los que obtuvieron mayores puntajes de rendimiento académico
en las matemáticas. Además, en ambos casos, se observa una disminución de
la variabilidad de las puntuaciones en el postest respecto al pretest.
Tabla 2
Dimensión 1 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo
T Student
Control (n=30) Experimental (n=27)
Pretest
[5 - 10] 53.3% 37.0%
t = 0.405
p = .992
[11-15] 30.0% 29.7%
[16-20] 16.7% 33.3%
Postest
[5 - 10] 53.3% 3.7%
t = 6.682
p < .001
[11-15] 40.0% 7.4%
[16-20] 6.7% 88.9%
El rendimiento académico de las matemáticas en la dimensión 1 en alumnos de
quinto grado de educación primaria del grupo control y experimental presentan
condiciones iniciales similares (𝑝 = .231) en los puntajes obtenidos del pretest.
Por otro lado, los puntajes del rendimiento académico de las matemáticas en la
dimensión 1 del postest en los alumnos del grupo experimental presentan
diferencias significativas con los puntajes obtenidos del grupo control (∗∗∗ 𝑝 <
Figura 2. Dimensión 1 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
De la figura 2, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) de la dimensión 1 son similares en los alumnos
del grupo control y experimental. Así mismo, se observa una diferencia
significativa en los puntajes finales (postest) entre los alumnos del grupo de
control y experimental, siendo éstos últimos los que obtuvieron mayores
puntajes de rendimiento académico en las matemáticas de la dimensión 1.
Además, en ambos casos, se observa una disminución de la variabilidad de las
puntuaciones en el postest respecto al pretest.
Pu
n
taje
s
en
la
d
ime
n
si
Tabla 3
Dimensión 2 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo
T Student
Control (n=30) Experimental (n=27)
Pretest
[5 - 10] 63.3% 77.8% t = 0.405
p = .992
[11-15] 16.7% 14.8%
[16-20] 20.0% 7.4%
Postest
[5 - 10] 70.0% 3.7% t = 6.682
p < .001
[11-15] 16.7% 51.9%
[16-20] 13.3% 44.4%
El rendimiento académico de las matemáticas en la dimensión Dimensión 2 en
alumnos de quinto grado de educación primaria del grupo control y
experimental presentan condiciones iniciales similares (𝑝 = .173) en los
puntajes obtenidos del pretest. Por otro lado, los puntajes del rendimiento
académico de las matemáticas en la dimensión 2 del postest en los alumnos
del grupo experimental presentan diferencias significativas con los puntajes
obtenidos del grupo control (∗∗∗ 𝑝 < .001), además, de presentar mayores
Figura 3. Dimensión 2 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
De la figura 3, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) en la dimensión 2 son similares en los alumnos
del grupo control y experimental. Así mismo, se observa una diferencia
significativa en los puntajes finales (postest) entre los alumnos del grupo de
control y experimental, siendo éstos últimos los que obtuvieron mayores
puntajes de rendimiento académico en las matemáticas en la dimensión 2.
Además, en ambos casos, se observa una disminución de la variabilidad de las
puntuaciones en el postest respecto al pretest.
Tabla 4
Dimensión 3 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo
T Student
Control (n=30) Experimental (n=27)
Pretest
[5 - 10] 73.3% 74.1%
t = 0.405
p = .992
[11-15] 23.4% 7.4%
[16-20] 3.3% 18.5%
Postest
[5 - 10] 86.6% 3.7%
t = 6.682
p < .001
[11-15] 6.7% 7.4%
[16-20] 6.7% 88.9%
El rendimiento académico de las matemáticas en la dimensión Dimensión 3 en
alumnos de quinto grado de educación primaria del grupo control y
experimental presentan condiciones iniciales similares (𝑝 = .674) en los
Por otro lado, los puntajes del rendimiento académico de las matemáticas en la
dimensión Dimensión 3 del postest en los alumnos del grupo experimental
presentan diferencias significativas con los puntajes obtenidos del grupo control
(∗∗∗ 𝑝 < .001), además, de presentar mayores puntajes obtenidos.
Figura 4. Dimensión 3 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
De la figura 4, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) en la dimensión Dimensión 3 son similares en los
alumnos del grupo control y experimental. Así mismo, se observa una
diferencia significativa en los puntajes finales (postest) entre los alumnos del
grupo de control y experimental, siendo éstos últimos los que obtuvieron
mayores puntajes de rendimiento académico en las matemáticas en la
dimensión Dimensión 3. Además, en ambos casos, se observa una disminución
de la variabilidad de las puntuaciones en el postest respecto al pretest.
Pu
n
taje
s
en
la
d
imen
si
CAPÍTULO IV
RESULTADOS
MODELO 1: INVESTIGACIÓN DE
TIPO CUASIEXPERIMENTAL
4.1. Descripción.
Tabla 1
Rendimiento académico de las matemáticas en alumnos del quinto grado de educación secundaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo Test U de
Mann-Whitney
Control (n=30) Experimental (n=27)
Pretest
Bajo 70.0% 66.7%
Z = 0.405
p = .992
Medio 23.3% 18.5%
Alto 6.7% 14.8%
Postest
Bajo 83.3% 0.0%
Z = 6.682
p < .001
Medio 13.3% 11.1%
Alto 3.3% 88.9%
El rendimiento académico de las matemáticas en alumnos de quinto grado de educación primaria del grupo control y experimental presentan condiciones
iniciales similares (U-Mann-Whitney: 𝑝 = .992) en los puntajes obtenidos del
pretest.
Por otro lado, los puntajes del rendimiento académico de las matemáticas del postest en los alumnos del grupo experimental presentan diferencias
significativas con los puntajes obtenidos del grupo control (U-Mann-Whitney: ∗∗
Figura 1. Rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
De la figura 1, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) son similares en los alumnos del grupo control y
experimental. Así mismo, se observa una diferencia significativa en los puntajes
finales (postest) entre los alumnos del grupo de control y experimental, siendo
éstos últimos los que obtuvieron mayores puntajes de rendimiento académico
en las matemáticas. Además, en ambos casos, se observa una disminución de
Tabla 2
Dimensión 1 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo Test U de
Mann-Whitney
Control (n=30) Experimental (n=27)
Pretest
Bajo 53.3% 37.0%
Z = 0.405
p = .992
Medio 30.0% 29.7%
Alto 16.7% 33.3%
Postest
Bajo 53.3% 3.7%
Z = 6.682
p < .001
Medio 40.0% 7.4%
Alto 6.7% 88.9%
El rendimiento académico de las matemáticas en la dimensión 1 en alumnos de
quinto grado de educación primaria del grupo control y experimental presentan
condiciones iniciales similares (𝑝 = .231) en los puntajes obtenidos del pretest.
Por otro lado, los puntajes del rendimiento académico de las matemáticas en la
dimensión 1 del postest en los alumnos del grupo experimental presentan
diferencias significativas con los puntajes obtenidos del grupo control (∗∗∗ 𝑝 <
Figura 2. Dimensión 1 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
De la figura 2, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) de la dimensión 1 son similares en los alumnos
del grupo control y experimental. Así mismo, se observa una diferencia
significativa en los puntajes finales (postest) entre los alumnos del grupo de
control y experimental, siendo éstos últimos los que obtuvieron mayores
puntajes de rendimiento académico en las matemáticas de la dimensión 1.
Además, en ambos casos, se observa una disminución de la variabilidad de las
puntuaciones en el postest respecto al pretest.
Pu
n
taje
s
en
la
d
imen
si
Tabla 3
Dimensión 2 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo Test U de
Mann-Whitney
Control (n=30) Experimental (n=27)
Pretest
Bajo 63.3% 77.8% Z = 0.405
p = .992
Medio 16.7% 14.8%
Alto 20.0% 7.4%
Postest
Bajo 70.0% 3.7% Z = 6.682
p < .001
Medio 16.7% 51.9%
Alto 13.3% 44.4%
El rendimiento académico de las matemáticas en la dimensión Dimensión 2 en
alumnos de quinto grado de educación primaria del grupo control y
experimental presentan condiciones iniciales similares (𝑝 = .173) en los
puntajes obtenidos del pretest.
Por otro lado, los puntajes del rendimiento académico de las matemáticas en la
dimensión 2 del postest en los alumnos del grupo experimental presentan
diferencias significativas con los puntajes obtenidos del grupo control (∗∗∗ 𝑝 <
Figura 3. Dimensión 2 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
De la figura 3, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) en la dimensión 2 son similares en los alumnos
del grupo control y experimental. Así mismo, se observa una diferencia
significativa en los puntajes finales (postest) entre los alumnos del grupo de
control y experimental, siendo éstos últimos los que obtuvieron mayores
puntajes de rendimiento académico en las matemáticas en la dimensión 2.
Además, en ambos casos, se observa una disminución de la variabilidad de las
puntuaciones en el postest respecto al pretest.
Pu
n
taje
s
en
la
d
imen
si
Tabla 4
Dimensión 3 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
Nivel
Grupo Test U de
Mann-Whitney
Control (n=30) Experimental (n=27)
Pretest
Bajo 73.3% 74.1%
Z = 0.405
p = .992
Medio 23.4% 7.4%
Alto 3.3% 18.5%
Postest
Bajo 86.6% 3.7%
Z = 6.682
p < .001
Medio 6.7% 7.4%
Alto 6.7% 88.9%
El rendimiento académico de las matemáticas en la dimensión Dimensión 3 en
alumnos de quinto grado de educación primaria del grupo control y
experimental presentan condiciones iniciales similares (𝑝 = .674) en los
puntajes obtenidos del pretest.
Por otro lado, los puntajes del rendimiento académico de las matemáticas en la
dimensión Dimensión 3 del postest en los alumnos del grupo experimental
presentan diferencias significativas con los puntajes obtenidos del grupo control
Figura 4. Dimensión 3 en el rendimiento académico de las matemáticas en alumnos del quinto grado de educación primaria del grupo de control y experimental según pretest y postest.
De la figura 4, se observa que los puntajes iniciales del rendimiento académico
de las matemáticas (pretest) en la dimensión Dimensión 3 son similares en los
alumnos del grupo control y experimental. Así mismo, se observa una
diferencia significativa en los puntajes finales (postest) entre los alumnos del
grupo de control y experimental, siendo éstos últimos los que obtuvieron
mayores puntajes de rendimiento académico en las matemáticas en la
dimensión Dimensión 3. Además, en ambos casos, se observa una disminución
de la variabilidad de las puntuaciones en el postest respecto al pretest.
Pu
n
taje
s
en
la
d
imen
si
CAPÍTULO IV
RESULTADOS
4.1. Descripción.
Tabla 1
Rendimiento académico de las matemáticas en alumnos del quinto grado “C” de educación secundaria pretest
Puntuación Frecuencia Porcentaje Porcentaje
acumulado
[2 - 5] 4 13,8 13,8
[6 - 9] 10 34,5 48,3
[10 -13] 11 37,9 86,2
[14-17] 4 13,8 100
Total 29 100
FUENTE: Archivos investigador; 2012
Figura 1. Rendimiento académico de las matemáticas en alumnos del quinto grado según pretest.
En la tabla y figura se observan los resultados de las calificaciones del
rendimiento académico de las matemáticas en alumnos de quinto grado de
obtuvieron calificaciones por debajo de 09, y el 51,7% de los estudiantes tienen
calificaciones entre 10 a 17 puntos, lo que indica que los estudiantes requieren
de la intervención de laguna estrategia para mejorar el rendimiento académico.
Tabla 2
Rendimiento académico de las matemáticas en alumnos del quinto grado “C” de educación secundaria pos test
Puntuaci ón
Frecuencia Porcentaje Porcentaje
acumulado
[9 - 11] 2 6,9 6,9
[12-14] 10 34,5 41,4
[15-17] 12 41,4 82,8
[18-20] 5 17,2 100
Total 29 100
FUENTE: Archivos investigador; 2012
Figura 2. Rendimiento académico de las matemáticas en alumnos del quinto grado según post test.
En la tabla y figura se observan los resultados de las calificaciones del
educación secundaria; apreciándose que el 6.9% de los estudiantes obtuvieron
calificaciones por debajo de 11, y el 93,1% de los estudiantes tienen
calificaciones entre 12 a 20 puntos, lo que indica que los estudiantes mejoraron
su rendimiento académico después de las estrategias aplicadas.
Figura 3. Rendimiento académico de las matemáticas en alumnos del quinto grado de educación secundaria según el pretest y postest.
En la figura 3, se observa en diagrama de cajas de las puntuaciones del pre
test del rendimiento académico de las matemáticas, en comparación de las
puntuaciones del post test; observándose que existe diferencia significativa
entre las comparaciones de las diferencias cuartílicas, por lo tanto podemos
concluir que el rendimiento académico del post test es consecuencia de la
Toma de decisión.
Tabla 3
Estadísticos del rendimiento académico de las matemáticas en alumnos del quinto grado “C” de educación secundaria pretest y postest.
Instrumentos 𝑋̅ S2 mo me T Student
Pre test 9,55 11,67 12 10 t = 7.819
Post test 15,03 5,18 14 15 p = .000
El rendimiento académico de las matemáticas en alumnos de quinto grado de
educación secundaria del grupo de estudio muestra una diferencia de 5.483
puntos con respecto a la media, así mismo los calificativos del pre test presenta
mayor dispersión frente a los resultados del post test, finalmente. Con respecto
a la prueba de hipótesis; para el efecto se analizó con la prueba t para
muestras relacionadas donde (T Student: 𝑝 = .000), concluyendo que se
acepta la hipótesis alterna y se rechaza la hipótesis nula a un nivel de