Análisis de Corrientes de Eddy en Tanques de Transformadores de Potencia con la Técnica de Elemento Finito-Edición Única

BIBLIOTECAS DEL TECNOLÓGICO DE MONTERREY

PUBLICACIÓN DE TRABAJOS DE GRADO

Las Bibliotecas del Sistema Tecnológico de Monterrey son depositarias de los trabajos recepcionales y de

grado que generan sus egresados. De esta manera, con el objeto de preservarlos y salvaguardarlos como

parte del acervo bibliográfico del Tecnológico de Monterrey se ha generado una copia de las tesis en

versión electrónica del tradicional formato impreso, con base en la Ley Federal del Derecho de Autor

(LFDA).

Es importante señalar que las tesis no se divulgan ni están a disposición pública con fines de

comercialización o lucro y que su control y organización únicamente se realiza en los Campus de origen.

Cabe mencionar, que la Colección de

Documentos Tec,

donde se encuentran las tesis, tesinas y

disertaciones doctorales, únicamente pueden ser consultables en pantalla por la comunidad del

Tecnológico de Monterrey a través de Biblioteca Digital, cuyo acceso requiere cuenta y clave de acceso,

para asegurar el uso restringido de dicha comunidad.

Análisis de Corrientes de Eddy en Tanques de Transformadores

de Potencia con la Técnica de Elemento Finito-Edición Única

Title

Análisis de Corrientes de Eddy en Tanques de

Transformadores de Potencia con la Técnica de Elemento

Finito-Edición Única

Authors

Miguel Gaspar Sánchez

Affiliation

Tecnológico de Monterrey, Campus Monterrey

Issue Date

1996-05-01

Item type

Tesis

Rights

Open Access

Downloaded

19-Jan-2017 01:26:02

INSTITUTO TECNOLÓGICO Y DE ESTUDIOS

SUPERIORES DE MONTERREY

CAMPUS MONTERREY

DIVISIÓN DE GRADUADOS E INVESTIGACIÓN

PROGRAMA DE GRADUADOS EN INGENIERÍA

ANÁLISIS DE CORRIENTES DE EDDY EN TANQUES

DE TRANSFORMADORES DE POTENCIA CON LA

TÉCNICA DE ELEMENTO FINITO

T E S I S

PRESENTADA COMO REQUISITO PARCIAL

PARA OBTENER EL GRADO ACADÉMICO DE

MAESTRO EN CIENCIAS

ESPECIALIDAD EN INGENIERÍA ELÉCTRICA

INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE 

MONTERREY 

CAMPUS MONTERREY 

D I V I S I Ó N D E G R A D U A D O S E I N V E S T I G A C I Ó N P R O G R A M A D E G R A D U A D O S E N I N G E N I E R Í A

ANÁLISIS DE CORRIENTES DE EDDY EN TANQUES DE 

TRANSFORMADORES DE POTENCIA CON LA TÉCNICA DE 

ELEMENTO FINITO 

TESIS 

P R E S E N T A D A C O M O R E Q U I S I T O P A R C I A L P A R A O B T E N E R E L G R A D O A C A D É M I C O D E

MAESTRO EN CIENCIAS 

ESPECIALIDAD EN INGENIERÍA ELÉCTRICA 

ING.  M I G U E L  G A S P A R  S Á N C H E Z 

INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE 

MONTERREY 

CAMPUS MONTERREY 

D I V I S I Ó N D E G R A D U A D O S E I N V E S T I G A C I Ó N P R O G R A M A D E G R A D U A D O S E N I N G E N I E R Í A

ANÁLISIS DE CORRIENTES DE EDDY EN TANQUES DE 

TRANSFORMADORES DE POTENCIA CON LA TÉCNICA DE 

ELEMENTO FINITO 

TESIS 

P R E S E N T A D A C O M O R E Q U I S I T O P A R C I A L P A R A O B T E N E R E L G R A D O A C A D É M I C O D E

MAESTRO EN CIENCIAS 

ESPECIALIDAD EN INGENIERÍA ELÉCTRICA 

ING.  M I G U E L GASPAR  S Á N C H E Z 

INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE 

MONTERREY 

CAMPUS MONTERREY 

D I V I S I Ó N D E G R A D U A D O S E I N V E S T I G A C I Ó N P R O G R A M A D E G R A D U A D O S E N I N G E N I E R Í A

L o s miembros del comité de tesis recomendamos que la presente tesis del Ing. Miguel Gaspar Sánchez sea aceptada como requisito parcial para obtener el grado académico de

Maestro en Ciencias especialidad en:

INGENIERÍA ELÉCTRICA 

Comité de tesis: 

A G R A D E C I M I E N T O S . 

Agradezco a todas las personas que de una  manera u otra han contribuido en la elaboración  de esta Tesis, de manera espacial al Dr. Federico  Viramontes V. por su valiosa asesoría y  enseńanza. 

Al  M . C . Efraín Gutiérrez V. por sus siempre  oportunas aportaciones, y al Centro de  Manufactura por darme la oportunidad de  aprovechar sus recursos. 

DEDICATORIA

A mi padre:

Abraham Gaspar C. 

y a la memoria de mi madre:

Bonifacia Sánchez L. 

Por el ejemplo que me han dado y todo lo que me han enseńado.

A mis hermanos:

Maribel, Delia, Argelia,  Abraham y Agustín. 

ÍNDICE 

P R E F A C I O 

C A P Í T U L O 1  I N T R O D U C C I Ó N 

1.0 Introducción. 1

1.1 Descripción global del trabajo. 3

C A P Í T U L O 2 DEFINICIÓN DEL  P R O B L E M A 

2.0 Justificación. 5

2.1 Objetivo. 6

2.2 Descripción global del problema. 6

C A P Í T U L O 3  F U N D A M E N T A C I Ó N TEÓRICA 

3.0 Fundamentación teórica. 8

3.1 Ecuaciones de Maxwell en forma integral. 11

3.2 El teorema del vector de Poyting. 12

índice 

C A P Í T U L O 4 ANÁLISIS  D E  C A M P O S  E L E C T R O M A G N É T I C O S  U S A N D O  L O S  P A Q U E T E S  E M A S , ARDES Y XL. 

4.0 Procedimiento de modelación con elementos finitos. 22

4.1 Modelación. 23

4.1.1 Geometría. 25 4.1.2 Propiedades de los materiales. 25

4.1.3 Elementos y mallas. 25 4.1.4 Condiciones de frontera. 27 4.1.5 Análisis en dos dimensiones. 28

4.1.6 Excitaciones. 30

4.2 Análisis. 31

4.2.1 Campos, potenciales y grados de libertad. 33

4.2.2 Funciones de forma. 34

4.3 Despliegue de resultados. 34

C A P Í T U L O 5  S I M U L A C I O N E S  E F E C T U A D A S 

5.0 Introducción. 36

5.1 Solución analítica para el modelo con corriente directa. 37

5.1.1 Intensidad de campo magnético. 38 5.1.2 Flujo magnético y densidad de flujo magnético. 39

5.1.3 Potencial magnético A. 40 5.1.4 Energía almacenada. 42 5.1.5 Valores calculados. 43

5.2 Simulación del modelo de corriente directa con la técnica de 

elementos finitos. 44

5.2.1 Comparación de resultados. 45

5.3 Simulación en corriente directa con inserto. 47

índice 

5.5 Simulaciones realizadas de la tapa de lado de baja tensión de 

un transformador de potencia trifásico. 55 5.5.1 Resultados del modelo sin inserto e inyección de

corriente en las tres fases. 56 5.5.2 Resultados del modelo con insertos rectangulares

e inyección de corriente en las tres fases. 58 5.5.3 Resultados del modelo sin inserto e inyección de

corriente en las tres fases aumentando en área de

la placa. 62 5.5.4 Resultados del modelo con insertos rectangulares

entre fases e inyección de corriente en las tres fases

aumentando el área de la placa. 64 5.5.5 Resultados del modelo con insertos rectangulares

entre fases e inyección de corriente solo en una fase. 66

C A P Í T U L O 6  P R U E B A S EXPERIMENTALES 

6.0 Introducción. 68

6.1 Objetivo. 69

6.2 Diseńo del experimento. 69

6.3 Resultados esperados. 71

6.4 Resultados obtenidos. 76

6.4.1 Instrumentación. 76 6.4.2 Circuito implementado. 76 6.4.3 Resultados obtenidos en la placa sin inserto. 79

6.4.4 Estimación de la potencia con convección. 80 6.5.5 Resultados obtenidos en la placa con inserto. 81

6.5 Comentarios. 82

6.5.1 Flujo magnético. 82 6.5.2 Potencia producida por las corrientes de Eddy. 84

C A P Í T U L O 7 CONCLUSIONES Y  R E C O M E N D A C I O N E S 

7.0. Conclusiones y recomendaciones. 85

LISTA  D E  T A B L A S  Tabla 4.1 Resumen de condiciones de frontera utilizadas

en el análisis electromagnético. 28

Tabla 5.1 Intensidad de campo magnético y densidad de flujo

magnético en dos trayectorias diferentes. 44

Tabla 5.2 Resultados calculados y obtenidos en las simulaciones. 47

Tabla 5.3 Comparación de resultados de los modelos en corriente directa. 49

Tabla 5.4 Comparación de resultados de los modelos en corriente alterna. 50

Tabla 5.5 Potencias disipadas en diversas regiones del modelo de la placa. 56

Tabla 5.6 Flujos magnéticos en diversas regiones del modelo de la placa. 56

Tabla 5.7 Potencias disipadas en diferentes regiones del modelo con

insertos rectangulares entre fases. 58

Tabla 5.8 Flujos magnéticos en diversas zonas del modelo de la placa con

insertos rectangulares entre fases. 62

Tabla 5.9 Potencias disipadas en diferentes zonas del modelo de la placa. 63

Tabla 5.10 Flujos magnéticos en diversas regiones del modelo de la placa. 64

Tabla 5.11 Potencias disipadas en diferentes zonas del modelo de la placa. 64

Índice 

Tabla 5.13 Potencias disipadas en diferentes regiones de la placa y densidad

flujo máxima cuando el modelo es excitado en una fase. 66

Tabla 6.1 Comparación de resultados de los modelos en

corriente alterna (I=3000A). 72

Tabla 6.2 Comparación de resultados de los modelos en

corriente alterna (I=2000A). 72

Tabla 6.3 Comparación de resultados de los modelos en

corriente alterna (I= 1000A). 72

Tabla 6.4 Voltajes inducidos en las bobinas (I=1000 A, N=1000 vtas,

f=60 Hz.) 73

Tabla 6.5 Voltaje inducido en la bobina (I= 1000 A, N=1000 vtas). 79

Tabla 6.6 Temperaturas medidas en la placa sin inserto (I=1000 A). 80

Tabla 6.7 Voltaje inducido en la bobina (I=1000 A, N=1000 vtas.) 81

Tabla 6.8 Temperaturas medidas en la placa con inserto (I=1000 A). 82

LISTA DE FIGURAS 

Figura 3.1 Pared cilindrica que es atravesada por un conductor

en el eje z. 15

Figura 3.2 Sección transversal y longitudinal de la estructura

metálica. 16

Figura 3.3 Modelo para las condiciones de frontera. 20

Figura 4.1 Condiciones de frontera para un análisis en dos dimensiones. 28

Figura 4.2 Condiciones de frontera para la mitad del modelo en

dos dimensiones. 29

Figura 4.3 Condiciones de frontera para un cuarta parte del modelo

en dos dimensiones. 29

Figura 4.4 Árbol para la selección del método de solución. 33

Figura 5.1 Dimensiones del modelo simulado en corriente directa. 37

Figura 5.2 Potencial magnético A. 40

Figura 5.3 Trayectorias para el cálculo de la Intensidad de campo

magnético H. 43

Figura 5.4 Modelo utilizado para la simulación en corriente directa. 44

Figura 5.5 Densidad de flujo del modelo en C.D., placa sin inserto. 46

Indice 

Figura 5.7 Densidad de flujo del modelo en C.D., placa con inserto. 48

Figura 5.8 Densidad de potencia del modelo en C.A., placa sin inserto. 51

Figura 5.9 Densidad de potencia del modelo en C.A., placa con inserto. 52

Figura 5.10 Densidad de corriente, placa sin inserto, C.A. 53

Figura 5.11 Modelo analizado de la tapa de lado de baja tensión

de un transformador. 55

Figura 5.12 Diferentes zonas en la que se calcula la potencia y

los flujos magnéticos del modelo de la placa. 56

Figura 5.13 Densidad de potencia, placa con inyección de corriente

en las tres fases, sin inserto. 57

Figura 5.14 Placa con insertos rectangulares entre fases. 58

Figura 5.15 Densidad de potencia, placa con inyección de corriente

en las tres fases, con inserto. 59

Figura 5.16 Disposición de los conductores. 60

Figura 5.17 Encadenamiento de flujo de los conductores. 60

Figura 5.18 Diferentes zonas en las que se calcula el flujo magnético

en la placa con insertos rectangulares entre fases. 62

Figura 5.19 Diferentes zonas en las que se calcula la potencia

disipada en la placa. 63

Figura 5.20 Diferentes zonas en las que se calcula el flujo magnético

en la placa. 64

Figura 5.21 Diferentes zonas en las que se calcula la potencia

disipada en la placa. 65

Figura 5.22 Diferentes zonas en las que se calcula el flujo magnético

en la placa. 65

Figura 5.23 Regiones donde son calculadas las potencias en la placa

con insertos rectangulares excitando una fase. 66

Figura 6.1 Dimensiones y propiedades de los materiales del modelo

Índice 

Figura 6.2 Placa con inserto antimagnético. 70

Figura 6.3 Posición de bobinas para las pruebas experimentales. 70

Figura 6.4 Densidad de potencia en la dona sin inserto. 75

Figura 6.5 Densidad de potencia en la dona con inserto. 76

Figura 6.6 Circuito utilizado para las pruebas. 77

Figura 6.7 Disposición de los instrumentos. 77

Figura 6.8 Formas de onda de voltaje y corriente suministradas

en la prueba 78

Figura 6.9 Contenido armónico de la corriente de excitación 78

Figura 6.10 Placa sin inserto. 79

Figura 6.11 Lugares donde se midió la temperatura. 80

Figura 6.12 Arreglo utilizado para la medición de voltajes y

temperaturas para la placa con inserto antimagnético. 81

PREFACIO 

Para diseńar aparatos electromagnéticos, como son transformadores eléctricos, se necesita estudiar con detalle la distribución de los campos elecromagnéticos, tanto en los circuitos magnéticos como en la estructura del transformador. En este trabajo de tesis se presenta el efecto que producen los campos electromagnéticos variantes en el tiempo en la tapa de lado de bajo voltaje de un transformador de potencia.

Hace unas décadas el estudio de problemas de campos electromagnéticos, mecánica de fluidos, transmisión de calor, se resolvieron analíticamente, encontrando las ecuaciones diferenciales parciales que permiten analizar dichos problemas, las soluciones de estos problemas se extrapolaban para aplicarlos en forma directa a un particular diseńo, con esto se lograban resultados satisfactorios que permitieron fabricar aparatos que cumplían con sus especificaciones.

CAPÍTULO 1 

1.0 Introducción. 

Los proyectos de investigación y desarrollo tecnológico relacionados con el ahorro y uso racional de energía eléctrica han tenido gran auge en los últimos ańos, con el motivo de ubicarse dentro del marco de un esfuerzo por lograr una mayor eficiencia. El uso eficiente de energía ha estado presente prácticamente en la mayoría de empresas de fabricación de equipo eléctrico, considerando que las mejoras en los equipos y procesos relacionados con la generación, transmisión y distribución de energía eléctrica inciden en manera directa o indirecta en una mayor eficiencia energética.

Capítulo 1  Introducción 

Recientemente se han realizado estudios de la distribución de corrientes de Eddy y pérdidas en transformadores de potencia [2], En dichos estudios se consideran estructuras del transformador complicadas. Se estudian distintos casos de la pared del tanque con corasas magnéticas usadas comúnmente con el fin de disminuir las corrientes inducidas en la pared del tanque, también, se estudia la relación de las corrientes de Eddy en distintos materiales. Sin embrago, las formulaciones usadas convencionalmente para calcular pérdidas de Eddy en transformadores tienden ha ser específicas a una configuración particular de diseńo físico para determinadas condiciones de operación, por ejemplo en [3] se centran en el estudio de la distribución de corrientes de Eddy en elementos pasivos del transformador y bobinas, en [4] se describe en forma detallada el cálculo de pérdidas por corrientes de Eddy así como también las pérdidas por histéresis en laminaciones considerando el efecto de saturación.

Ańos de experiencia y grandes bases de datos, acoplados con técnicas de interpolación, permiten al diseńador predecir con exactitud las pérdidas en el transformador. Sin embargo, alguna modificación en la configuración física del transformador puede resultar en que los procedimientos utilizados, basados en fórmulas empíricas, pueden generar respuestas que diferieren significantemente de los resultados de las pruebas. Algunos otros procedimientos utilizados para estimar las pérdidas son caracterizados por su contribución a el cálculo de pérdidas en componentes individuales que ayudan ha entender el comportamiento del fenómeno, tales como la distribución de corrientes de Eddy en estructuras cilindricas construidas de material magnético, de espesor infinito pero de longitud finita, cuando la excitación de corriente es mediante un conductor centrado en dicha estructura cilíndrica[5]. 

Capítulo 1  Introducción 

Modelos recientes [8] muestran técnicas de elementos finitos aplicadas a modelos en tres dimensiones, con el objeto de tener una mejor precisión en los resultados obtenidos, de esta forma se representa físicamente el transformador y se calculan las pérdidas en las partes más importantes. Por otro lado, la experiencia y los métodos para predecir las pérdidas por corrientes de Eddy demuestran que la mayor distribución de las pérdidas se llevan acabo en el tanque, en las orillas del núcleo y el armazón que sostiene el núcleo [9] [10]. 

1.1 Descripción global del trabajo. 

El objetivo de este trabajo consiste en aplicar el método de elementos finitos para estudiar problemas con corrientes de Eddy en tapas de transformadores, se enfoca principalmente en analizar el comportamiento de los campos electromagnéticos que varían en el tiempo.

El trabajo se dividió en siete capítulos, como sigue:

En el primer capítulo, se presenta una introducción del trabajo realizado.

El segundo capítulo, está dedicado a la definición del problema su justificación y se define el objetivo principal de este trabajo.

El tercer capítulo, comprende la fundamentación teórica, se presenta el desarrollo analítico de un modelo simplificado que representa una placa circular que es atravesada en el centro por un conductor por el que circula una corriente que variante en el tiempo, en éste desarrollo, se obtuvo una ecuación diferencial parcial de segundo orden que rige el comportamiento del modelo.

Capítulo 1  Introducción 

E n el capítulo cinco, se presentan las simulaciones realizadas, las cuales comprenden desde la simplificación del problema en corriente directa en una sola fase hasta la simulación de una placa con dimensiones reales de un transformador de potencia trifásico. En la simulación con corriente directa se comparan algunos resultados obtenidos analíticamente con los resultados obtenidos mediante las simulaciones.

E n el capítulo seis, se muestran los resultados de las pruebas experimentales realizadas con el fin de validar los resultados obtenidos con las simulaciones, se estima la potencia que consume una placa circular y se comparan los resultados con los de las simulaciones.

CAPÍTULO 2 

DEFINICIÓN  D E L  P R O B L E M A  2.0 Justificación. 

El problema de las pérdidas en equipo eléctrico es importante, especialmente con las unidades de gran capacidad. Estas no solo reducen la eficiencia de los transformadores, también, producen sobrecalentamientos locales que afectan el funcionamiento y acortan la vida útil del equipo [2], de ahí la necesidad de predecir como se distribuyen las pérdidas producidas por las corrientes de Eddy.

Capítulo 2  Definición del problema 

2.1 Objetivo. 

Evaluación de pérdidas producidas por corrientes de Eddy en la tapa de baja tensión de un transformador de potencia, considerando insertos antimagnéticos comúnmente empleados para la disminución de pérdidas.

2.2 Descripción global del problema. 

U n o de los objetivos de este trabajo es aplicar la técnica de elementos finitos para resolver problemas relacionados con el estudio de campos magnéticos variantes en el tiempo. Lo anterior con el propósito de analizar las corrientes parásitas que se inducen en las estructuras de los aparatos eléctricos, que como ya se ha mencionado producen efectos no deseables, como son la pérdida de energía por efecto Joule, tal es el caso de los transformadores eléctricos en donde se tienen corrientes de Eddy que circulan por el núcleo y tanque, originando calentamientos con su consecuente pérdida de energía.

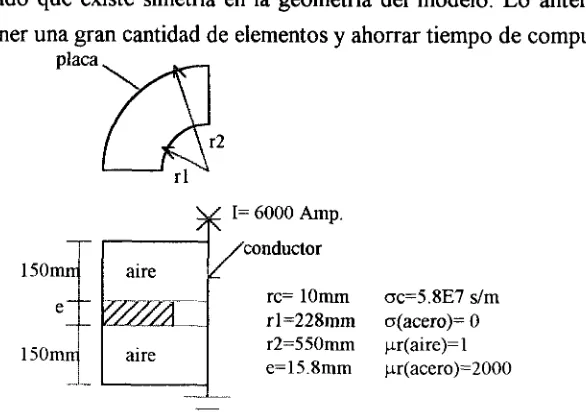
Este trabajo se centra en el estudio de corrientes de Eddy en la tapa de un transformador de potencia y la utilización de insertos de acero no magnético en las boquillas de baja tensión cuando las corrientes en ellas son de 6000 Ampares rms, desfasados 120° eléctricos entre si. Se estudian diversos casos, que van desde modelos simplificados en tres dimensiones del sistema, en los que consideran solo una fase y en corriente directa hasta modelos en tres dimensiones que simulan la tapa completa del transformador, con excitación trifásica senoidal. Esto con el objeto de entender el comportamiento de las variables del sistema.

Para la modelación del problema de campos electromagnéticos se usaron tres productos computacionales, los cuáles utilizan la técnica de elemento finito. Dichos productos son de la compańía MacNeal-Schwendler Corp. El paquete Aries es un pre y postprocesador utilizado para la modelación de la geometría del sistema y preparación de la malla con las condiciones de frontera. El paquete MSC/EMAS (ElectroMagnetic Analysis System) que es un procesador, su principal propósito es analizar campos electromagnéticos con la técnica

Capitulo 2  Definición del problema 

CAPÍTULO 3 

F U N D A M E N T A C I Ó N  T E Ó R I C A 

3.0 Fundamentación teórica. 

Las corrientes de Eddy se producen por la variación con respecto al tiempo del campo magnético que pasa por la estructura metálica de cualquier aparato electromagnético. Estas corrientes son indeseables porque producen pérdidas por efecto Joule. En los diseńos de dispositivos electromagnéticos se buscan maneras de disminuir sus efectos.

Desafortunadamente, no existe un método analítico sencillo para calcular las pérdidas por corrientes de Eddy, dado que este fenómeno se tiene que estudiar mediante las ecuaciones diferenciales de Maxwell, considerando la geometría por donde circulan las corrientes y las características de los materiales que integran la estructura.

Capitulo 3  Fundamentación teórica 

Los dos conceptos básicos en que se fundamenta la teoría electromagnética, son el campo eléctrico producido por un campo magnético variante en el tiempo y el campo magnético producido por un campo eléctrico también cambiante. El primero de estos conceptos es el resultado del trabajo experimental de Michael Faraday. La formulación de estos fenómenos se debe a James Clerk Maxwell [11]. 

E n términos de campo eléctrico, se puede decir que un campo magnético que varía con el tiempo produce una fuerza electromotriz (fem) que puede producir una corriente en un circuito cerrado adecuado. Matemáticamente lo anterior se puede expresar mediante la siguiente ecuación:

L a ecuación (3.1) se conoce como ley de Faraday e implica una trayectoria cerrada. El flujo magnético es el flujo que cruza a través de cualquier superficie cuyo perímetro sea una trayectoria cerrada y dO/dt es la razón de cambio de dicho flujo con respecto al tiempo.

El signo menos indica que la fem tiene una dirección tal, que produce una corriente, cuyo flujo, si se suma al original, reduciría la magnitud de la fem. Este enunciado que establece que el voltaje inducido actúa para producir un flujo opuesto es conocido como la ley de Lenz

El método de elementos finitos para analizar campos electromagnéticos, está basada en la teoría electromagnética que se expresa con las ecuaciones de Maxwell las cuales se resumen a continuación.

En su forma puntual las ecuaciones de Maxwell se pueden expresar.

V (ec. 3.1)

V xE = ­

V x H =

dD

Capitulo 3  Fundamentación teórica 

El rotacional de un campo vectorial es una propiedad importante. Se interpreta como la razón de cambio espacial en dirección transversal al campo. También se considera como una medida de la intensidad de la fuente vectorial del campo en ese punto. Las ecuaciones (3.2) y (3.3) son dos de las ecuaciones de Maxwell para campos variantes con el tiempo.

La divergencia es otra propiedad importante de un campo vectorial. Expresa la densidad de la fuente escalar (un campo escalar) para cualquier punto, se interpreta como el flujo neto por unidad de volumen que diverge o sale de un vecindario infinitesimal de ese punto. En el caso de un campo eléctrico, la divergencia de D nos da la carga neta por unidad de volumen en un punto, indicando que se tiene una carga neta positiva o negativa.

En el caso de un campo magnético, donde no existen cargas magnéticas, las lineas de flujo deben formar trayectorias cerradas. En cambio en un campo eléctrico, este puede iniciarse en una carga eléctrica positiva y terminar en una carga eléctrica negativa. También la divergencia de un campo se interpreta como la razón de cambio espacial en dirección del campo.

Las ecuaciones 3.4 y 3.5 expresan el concepto de divergencia y se aplican tanto para campos no variantes y variantes en el tiempo.

VD = p (ec. 3.4)

V B = 0 (ec. 3.5)

Donde:

H  = Intensidad de campo magnético. = Densidad de corriente.

= Densidad de flujo eléctrico. = Intensidad de campo eléctrico.

J  D 

E

B 

P 

= Densidad de flujo magnético = densidad de carga eléctrica.

t 

_= tiempo. 

Capítulo 3  Fundamentación teórica 

La ecuación (3.4) establece que la densidad de carga es una fuente de las lineas de flujo eléctrico. Obsérvese que no se puede decir que todo el flujo eléctrico comienza y termina en una carga porque la parte importante de la ley de Faraday (3.1) muestra que E, y también D, 

pueden tener circulación si está presente un campo magnético variante. Por ello las líneas de flujo eléctrico pueden formar trayectorias cerradas. Sin embrago, sigue siendo cierto que cada coulomb de carga debe tener un coulomb de flujo eléctrico saliendo de él. La ecuación (3.5) muestra que se ignora de "cargas magnéticas o polos".

Estas cuatro ecuaciones son la base de toda la teoría electromagnética, son ecuaciones diferenciales parciales que relacionan el campo eléctrico y el magnético, y con sus fuentes, cargas y densidades de corriente. Las ecuaciones que relacionan a D con E, a J con E, son las siguientes:

D= e H

B = / / H

J = o-E

(ec. 3.6)

(ec. 3.7)

(ec. 3.8)

3.1 Ecuaciones de Maxwell en forma integral 

La forma integral de las ecuaciones de Maxwell permiten reconocer generalmente, las leyes experimentales de las cuales fueron obtenidas mediante un proceso de generalización. Los experimentos deben tratar con cantidades físicas macroscópicas y sus resultados tienen que ser expresados en términos relaciones integrales. Integrando (3.2)sobre una superficie y aplicando el teorema de Stokes, se obtiene la ley de Faraday.

BB 

JEdL = -j^-dS (ec. 3.9)

§HdL = I + j — (ec. 3.10)

Capüulo 3  Fundamentación teórica 

Las leyes de Gauss para los campos eléctricos y magnéticos se obtienen integrando las

ecuaciones ( 3 . 4 ) y ( 3 . 5 ) sobre un volumen y utilizando del teorema de la divergencia:

ÍD-dS = f pdv (ec. 3 . 1 1 )

Js Jvo\ 

JBdS = 0 (ec. 3 . 1 2 )

Las ecuaciones integrales ( 3 . 9 , 3 . 1 0 , 3 . 1 1 y 3 . 1 2 ) permiten encontrar las condiciones en la

frontera de B,D,H y E.

3.2 El teorema del vector de Poynting. 

La energía puede transportarse a través del espacio vacío y dentro de un conductor de cierta conductividad mediante las ondas electromagnéticas. El flujo de potencia que cruza a una superficie cerrada, es tal que se obtiene por la integración en la superficie de la densidad del flujo de potencia por el vector P = E x H, conocido como vector de Poynting [12]. 

P = ExR \*?- \ ó V m

W 

\m

Tomando la divergencia del producto cruz de E y H, para ambos lados de la ecuación

(2.13) tenemos.

V E x H = ( V x E ) - H - ( Vx H ) E (ec. 3 . 1 4 ) Mediante identidades trigonométricas, y substituyendo para V x E y V x H de las ecuaciones de Maxwell descritas anteriormente, podemos re escribir la ecuación (3.14) como:

O T} O

V - E x H = H - J E - — E (ec. 3.15)

dt dt 

Capitulo 3  Fundamentación teórica 

d(K­B\ 1

Á

2

 J

dx  (ec. 3.16)

D e igual manera se desarrolla la expresión para la segunda parte de la expresión (3.14), para lo cual se utiliza la ecuación D = e E (ec. 3.6)

d_  dx 

ÍE­D^l _

 dD 

Substituyendo las expresiones (3.16) y (3.17) en la expresión (3.15) se obtiene:

V - ( E x H ) =

dx 

H B E D

+ 

Finalmente, integrando a través de un volumen, resulta

f

V-(ExH

)rfv =  ­ — f 

Jvol Jvol 

H B E D

+ 

Jvol 

P o r el teorema de la divergencia también se puede representar la expresión (3.19) como:

í

V(ExH

)żv=

  f

( E x H > f c

Jvol Js  (ec. 3.20)

La ecuación (3.20) representa la integral del teorema de Poynting y su representación completa es la siguiente:

j3

­<f(E xH)ífc = — f  Jí żżI Jvol 

H B E D

Capítulo 3  Fundamentación teórica 

Así, tenemos que para un material isotrópico (si \i y e son constantes), la ecuación

siguiente será válida:

La ecuación (3.22) determina que el flujo de potencia a través de cualquier superficie cerrada S es igual a la razón de disminución de energía con respecto al tiempo en el campo electromagnético en el volumen que encierra la superficie S, menos las pérdidas debidas al calentamiento dentro del volumen.

El término ( l / 2 u H2_{) y ( l / 2 e E}2_{) son densidades de energía asociadas con las componentes}

de campo eléctrico y magnético, representan la energía total almacenada en dichos campos, las derivadas parciales con respecto al tiempo provocan que ese término sea la razón de cambio con respeto al tiempo de la energía almacenada dentro de este volumen, o sea, la potencia instantánea que hará que la energía almacenada dentro de este volumen aumente. La suma de las expresiones a la derecha debe ser, por lo tanto, la potencia total que fluye

hacia el volumen, en consecuencia, la potencia total que fluye fuera del volumen es

D o n d e la integral de la ecuación (3.22) es sobre la superficie que rodea el volumen.

Q u e se interpreta como una densidad de potencia instantánea medida en Watts por metro cuadrado ( W / m2_{) , la dirección del vector de Poynting P indica la dirección del flujo de}

potencia instantáneo en el punto, puesto que está dado por el producto cruz de E y H, la dirección del flujo de potencia en cualquier punto, es normal a ambos vectores.

(ec. 3.22)

Capitulo 3  Fundamentación teórica 

3.3 Cálculo de pérdidas en un núcleo cilindrico 

Las corrientes de Eddy son producidas en la estructura metálica de cualquier aparato electromecánico, por campos magnéticos que varían con el tiempo, debido a la inducción electromagnética.

Para explicar el fenómeno que producen estas corrientes, en la Fig. 3.1, se muestra el caso de un conductor que tiene excitación senoidal y atraviesa una pared metálica. Este es el caso típico en el bote que sostiene el aislador de una terminal de un transformador de potencia. Para simplificar el análisis, se supone despreciable el efecto de las orillas de la pared.

N . W . McLachlan [13] y W. Stevenson [14], tratan un caso muy parecido al mostrado en la Fig. 3.1, solo que es aplicado para determinar el efecto piel que aparece con la distribución no uniforme de la densidad de corriente en un conductor, mediante la obtención de la expresión de la densidad de corriente en función de la distancia del centro del conductor. A continuación se indica como se aplican las mismas expresiones matemáticas para el caso de la Fig. 3.1. En la Fig. 3.2 se muestra una sección transversal de la estructura, enfatizando la trayectoria cerrada donde se aplica la ley de Faraday.

Pored metálica

Capítulo 3  Fundamentación teórica 

Fig. 3.2 Sección transversal y longitudinal de la estructura metálica 

Para el desarrollo matemático se tienen las siguientes consideraciones:

i) El Conductor es excitado por una corriente senoidal, lo que origina que se produzca un flujo magnético variante en el tiempo dentro de la pared cilindrica.

ii) El material (aire) que se encuentra entre el conductor y la pared metálica se considera que tienen una permeabilidad magnética ur = 1.

iii) La pared metálica presenta pérdidas por corrientes parásitas debido a la inducción magnética. Esto implica que su conductividad a * 0.

Capítulo 3  Fundamentación teórica 

v) Se han despreciado los ciclos de histéresis y la característica no lineal dentro de la estructura ferromagnética.

En la fomulación matemática se debe considerar lo siguiente:

D e acuerdo a la ley de Ampere,

|_ J Iencerrada  2nx 

Debido a que la corriente ^ ^ ^ ^ varía senoidalmente, los valores instantáneos están

dados por,

jj _ ^encerrada  2nx 

Ax = Re [V2 = R e *yp2, ^

enCerra<_^a _^ 

2nx 

El símbolo R e significa la parte real de, como las partes reales son siempre iguales, el

símbolo R e se puede omitir, dividiendo entre ­Jl queda:

/ ejw_'

Ex = tjnssrrada (ec.3.24)

2 nx

D o n d e la corriente encerrada por la circunferencia de radio x, donde rj < x < r2, es

X 

I_encerrada=\2_^xJ

xdx-I

Lncerrada=ˇ2_^X_^

XdX­\

2_^XJ

xdX-I (eC. 3.25)

Capítulo 3  Fundamentación teórica 

Sustituyendo la ecuación (3.25) en la ecuación (3.24), se tiene

2nxYíx e

JW_{' = ¡27txJ}

x e'

wt _dx-\lnxJ

x e

JW_{' dx - Ie}JW_{' (ec. 3.26)}

o o 

Utilizando el teorema fundamental del cálculo y derivando con respecto a x, obtenemos

2nH eJW_{' +2xx e}Jvl _{= 2xxJ}

x e

Jwt _{(ec. 3.27)}

dx

finalmente

- TL + _{— =} J_{* (ec. 3.28)}

dx x

La ecuación 3.28 contiene tanto a Hx como Jx como variables dependientes de x.

Encontrando otra relación entre Hx y Jx, se puede eliminar Hx y obtener una ecuación

diferencial que tenga como variable dependiente de x solo a Jx. Tal ecuación puede ser

encontrada mediante la aplicación de la ley de voltajes de Kirchhoff, para el voltaje que cae alrededor de la malla definida por los puntos a1 _{b' b a, mostrada en la Figura 3.2. En dicha}

malla se tiene un diferencial de flujo que induce un voltaje.

dé

^7 = vi n d (ec.3.29)

dt

Considerando que p es la resistividad1 _{del conductor y tomando la trayectoria a'-b' y b-a.}

El voltaje inducido (vˇn tj) será

1 _{El producto de la densidad de corriente J, resistividad p, y la longitud Al, es la caída de voltaje en la} 

sección transversal de área A 

I = J A 

pkl 

y R = t­~ 

A 

De ahí que la caída de voltaje en el área A para la longitud A/, será 

pAl 

Capítulo 3  Fundamentación teórica 

dx pM­y[2Jx e

iw,

pá¡ = vl _ind. 

L a suma equivalente de los voltajes alrededor de la malla, acorde a la ley de Kirchhoff.

resulta:

42^e

_dx

dx (ec. 3 . 3 0 )

El flujo que encadena la malla a'b'b a con espesor dx en la pared metálica, es función del

tiempo t y de la distancia x. La ecuación para el flujo instantáneo se encuentra mediante el

producto de la densidad instantánea de flujo y el área, es decir

<ˇ>=y/2Bx e

Jwt _{A/Í& =  V2 / / H}

X e^túdx

D o n d e :

d<ˇ> 

dt  = jWyÍ2MRx e

J_{"'Mdx = v}

md (ec. 3 . 3 1 )

Sustituyendo el voltaje inducido en la ecuación 3 . 3 0 , se obtiene

e

JW_{'pAIdx =}

jw4l

dx

(ec. 3 . 3 2 )

L a intensidad de campo magnético HX, se obtiene despejándola de la ecuación anterior

HV

P  d J_{* _ JP}  d J

x 

Jwju dx juw dx  (ec. 3 . 3 3 )

Sustituyendo la ecuación 3 . 3 3 en la ecuación 3 . 2 8 , se obtiene la ecuación diferencial que

simula el comportamiento de la corriente de Eddy en la zona de la pared metálica.

jpd2_J

x jp dJx

Capítulo 3  Fundamentación teórica 

(ec. 3.34)

dx1 _{xdx p}

La ecuación 3.34, es una ecuación diferencial de segundo orden relacionando el valor rms de la densidad de corriente y la distancia desde el centro del conductor.

Jx representa el fasor de la densidad de corriente, en términos de la distancia radial del centro del conductor. Es una función compleja, de ahí que, la distancia x deberá de considerarse como una componente real de la variable compleja.

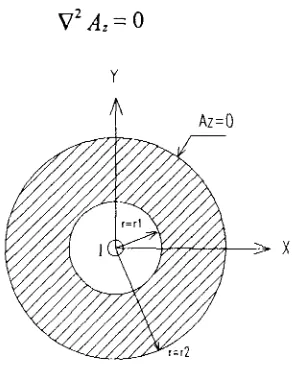
Para un tubo (ver Fig. 3.3) de radio b > 0, una solución parcial de la ecuación 3.34 es

Para determinar las constantes A y B, son necesarias dos ecuaciones. Estas constantes son obtenidas usando las condiciones de frontera e n r = a y r = b.

Para r = b, en el radio interior del tubo no se tiene una fuerza electromotriz inducida por el campo magnético de modo tal que:

Fig. 3.3 Modelo para las condiciones de frontera 

J = AJ0(kri

y2_{) + BK} 0(kri

m₎

dJ 

Capítulo 3  Fundamentación teórica 

Para r = a, en el radio exterior J0 esta dada por:

T0 = AJ0(kri

3l2_{) + BK} 0(kri

1_'2₎

CAPÍTULO 4 

ANÁLISIS DE CAMPOS ELECTROMAGNÉTICOS USANDO LOS 

PAQUETES EMAS, ARIES Y XL. 

4.0 Procedimiento de modelación con elementos finitos. 

El método de elementos finitos se implementa con algoritmos computacionales que mediante el uso de métodos numéricos e interfaces gráficas, simulan los comportamientos de fenómenos mecánicos, térmicos, electromagnéticos, etc. La modelación con elementos finitos en algunas ocasiones es un proceso repetitivo en el cual se comparan los resultados de varios diseńos de prototipos, ó también se comparan los resultados de los modelos con datos experimentales.

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Fase 1: Modelación.

Esta fase es considerada como el pre-procesamiento de la técnica de elementos finitos. Se crea la parte geométrica, se definen las condiciones de frontera, excitaciones y tipo de análisis, se crea el modelo con elementos finitos que divide la pieza en elementos y nodos, también se genera un código que será utilizado en el procesamiento de información. Para realizar lo anterior se utiliza el paquete ARTES.

Fase 2: Análisis.

El análisis es la fase del procesamiento, en esta etapa, se "corre" un programa de análisis para calcular las variables desconocidas, el análisis se realiza con el paquete E M A S , el cual t o m a un código que contiene toda la información del modelo. Este código es previamente generado en la etapa de modelación. El producto E M A S puede realizar análisis estáticos, con excitación senoidal, transitorios, estáticos no lineales, transitorios no lineales y con valores característicos reales y complejos.

Fase 3. Despliegue de resultados.

Está es la fase del post-procesamiento, en esta etapa se despliegan gráficamente los resultados con la ayuda del paquete XL.

4.1 Modelación. 

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

U n modelo válido deberá satisfacer dos requerimientos: El primero, es la precisión de la solución del problema matemático que representa el proceso físico. El segundo, debe ser la precisión del comportamiento físico deseado. El primer criterio es relativamente fácil de comprobar, el segundo criterio puede ser difícil de comprobar en problemas con soluciones n o conocidas.

El proceso de modelación involucra importantes atributos en forma predescrita. Esta forma es llamada interfese de usuario (user interface), el paquete ARTES es en nuestro caso la interfase, toma la información y la "traduce" para que el procesador E M A S genere y resuelva las ecuaciones algebraicas simultáneas.

Los modelos de campos electromagnéticos son definidos por los siguientes atributos principalmente, que deberán de especificarse mediante la construcción de un modelo de elementos finitos:

* Geometría

* Propiedad de los materiales * Elementos y mallas.

* Restricciones y condiciones de frontera * Excitaciones

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

4.1.1 Geometría 

Es la localización física y tamańo de los objetos dentro del volumen, y el espacio entre ellos, para esto se utiliza como ya se ha mencionado el paquete ARTES, que es una interfase, donde se crea la geometría del sistema que se desea modelar.

En esta etapa, se crean superficies, geometrías tridimensionales y geometrías sólidas. Mediante la realización de operaciones geométricas y la adición de detalles tales como perforaciones, perfiles, etc. Es posible obtener geometrías de cualquier complejidad.

4.1.2 Propiedades de materiales 

En la etapa de modelación es necesario especificar las propiedades de los materiales que están relacionados con el análisis. En el caso de los fenómenos electromagnéticos, las propiedades de los materiales son suministradas en tres cantidades específicas: permitividad e, conductividad a , y permeabilidad \i, estas tres propiedades pueden ser anisotrópicas

(dependientes de la dirección) o isotrópicas (independientes de la dirección).

La geometría, las propiedades de los materiales y las excitaciones aplicadas pueden ser expresadas en el sistema M K S , CGS, ó en el sistema Ingles, sin embargo lo más recomendable es utilizar el sistema internacional de unidades.

4.1.3 Elementos y mallas 

Los nodos son conectados por elementos finitos, los elementos tienen cuatro funciones en el modelo:

Geometría: Los elementos incorporan las propiedades de la geometría del modelo, incluyendo la posición y tamańo de los objetos, fronteras y espacio entre ellos.

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Propiedades de los materiales. Propiedades uniformes de los materiales son asociadas con el volumen ocupado por cada elemento.

Ecuaciones de Maxwell. Los elementos se relacionan en la iteración de los grados de libertad en los nodos para asegurar que estos representan la solución de las ecuaciones de Maxwell.

Existe una distinción entre nodos y grid points. Los nodos son características topológicas de los elementos que representan localizaciones donde los grid points pueden ser conectados, ellos no contienen información geométrica por si solos, los elementos adquieren información geométrica cuando los nodos son conectados a grid points a una localización física especifica. El hecho de establecer grid points en el volumen de un modelo y conectarlos a los elementos es llamado mallar. El proceso de malleo también se realiza mediante el paquete ARIES, donde típicamente se definen curvas, superficies y figuras sólidas que definen la forma y posición de los objetos en el modelo, esas figuras después son divididas en elementos finitos, una vez que la malla ha sido establecida, es posible realizar algún análisis.

Sistemas de coordenadas. 

El sistema de coordenadas en el paquete E M A S , sirve a un amplio número de funciones, las cuales se muestran a continuación:

Sistema de coordenadas para localización: Localización de grid points en el espacio.

Sistema de coordenadas para el potencial: El sistema de coordenadas en el cual los componentes de A serán calculados, en principio este sistema de coordenadas puede ser diferente para cada grid point del modelo. El sistema de coordenadas para el potencial es también usado para especificar relaciones de las restricciones.

Capitulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Sistema de coordenadas para materiales: Es el sistema en el cual las propiedades de un material anisotrópico son especificadas.

C o m o se puede observar para un grid point determinado se pueden tener tres diferentes sistemas de coordenadas asociados a él: Sistema de localización, un sistema para el potencial y uno para la excitación, tales sistemas de coordenadas se definen automáticamente.

Un sistema de coordenadas es siempre definido tomando encuenta el sistema de coordenadas básico, éste sistema tiene su origen en (0,0,0). Todos los otros sistemas de coordenadas son definidos en términos del sistema de coordenadas básico.

4.1.4 Condiciones de frontera 

Las condiciones de frontera representan el comportamiento fuera del volumen del modelo. Con tal propósito se aplican condiciones de frontera en las superficies del modelo, c o m o ya se ha mencionado con anterioridad, los valores discretos de A y v|/ en los nodos son llamados grados de libertad, los cuales se dividen en tres clases:

a) Grados de libertad de potencial magnético vectorial A tangente a la frontera b) Grados de libertad de potencial magnético vectorial A normal a la frontera c) Grados de libertad de potencial eléctrico escalar vy

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Condición de frontera Potencial (A y v|/)

B es confinada

Afang

0

B es normal

Anormal

0

B es infinito (baja frecuencia) OB (Open B . C.) E es confinado (baja frecuencia) Natural

E es normal (baja frecuencia) v|/ = constante

Etanj

0 (pared conductora)

Afa™ =

0,

 W

= 0

Tabla

4.1.5. Análisis en dos dimensiones y axisímétrico: 

Análisis en dos dimensiones.

En los análisis en dos dimensiones, una línea de flujo puede ser trazada siguiendo la superficie equipotencial del potencial magnético A. La condición de frontera de Dirchlet 

puede ser usada para representar una línea de flujo que pasa por donde el potencial magnético A es igual a cero. En contraste, si una línea de flujo cruza una superficie con ángulo recto, a esa superfice se tendrá la condición de Neumann. La condición de Neumann también es conocida como la condición de frontera natural. La Fig. 4.1 ilustra la aplicación de las condiciones de frontera de Dirichlet a un modelo completo.

B es confinado 

Modelos en

1

 dimensiones 

Al­0 

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Para modelos que tienen simetría se puede aplicar la condición de frontera natural (Neuman), como lo ilustran las Figuras 4.2 y 4.3. para la mitad y una cuarta parte del modelo mostrado en la Figura 4.1 

Ay =

 0 

Condición de frontera, natural 

B es normal 

B es confinada 

Ay =

 0 

Figura 4.2 Condiciones de frontera para la mitad  del modelo en dos dimensiones. 

Az =

 0 

B es confinada 

Az=0 

Condición de frontera natural 

Bes normal 

Capitulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Análisis Axisimétrico.

En el análisis axisimétrico, las líneas de flujo están determinadas por las superficies en las cuales el producto de radio y potencial magnético es constante.

4.1.6 Excitaciones 

Las excitaciones son producidas por agentes externos, no contenidas en el modelo, es decir no son producidas por algún efecto en el modelo, por ejemplo, si una excitación representa a una corriente que es aplicada a un punto, el modelo responde calculando como resultado los campos magnéticos. La energía requerida para mantener la corriente (la entrada de energía), es automáticamente suministrada por fuera del modelo. E n el paquete ARTES, las excitaciones son de distintas formas para diversos tipos de análisis, también se puede representar magnetización permanente ó bien campos en las fronteras, de cualquier forma, las excitaciones son reducidas matemáticamente a corrientes equivalentes aplicadas a un especifico potencial magnético vectorial A y a y (DOF's). En el caso especial de análisis electrostático, las excitaciones representan cargas eléctricas (las excitaciones son independientes de los campos que ellos producen).

Si es aplicada una excitación a algún punto, el "mundo exterior" suministrará la energía, corriente ó carga necesaria para mantener la excitación, como una analogía con circuitos eléctricos la fuente de voltaje suministrará la corriente necesaria para mantener el voltaje, bajo este criterio, todas las excitaciones en MSC/EMAS son excitaciones ideales.

El paquete ARTES permite suministrar excitaciones en las siguientes formas:

Densidad de corriente Punto de corriente Línea de corriente Punto de carga.

Magnetización remanente. Superficie con valor de H Superficie con valor de D

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

En todos los casos, las excitaciones son representadas como puntos de corrientes (puntos de cargas en electrostática).

4.2 Análisis 

El paquete E M A S (ElectroMagnetic Analysis System) es un programa computacional que tiene como propósito principal analizar el comportamiento de campos electromagnéticos usando el método de elementos finitos, y con las limitaciones que son determinados por los elementos finitos, el programa es capaz de modelar todos los aspectos del comportamiento del campo electromagnético que son descritas por las ecuaciones diferenciales de Maxwell, puede ser usado en el diseńo de un gran rango de equipos eléctricos, incluyendo solenoides, generadores, hornos de inducción, antenas y dispositivos de microondas.

E n el análisis de elementos finitos con el paquete E M A S , las ecuaciones de Maxwell son reducidas a una sola ecuación matricial de la forma:

Esta ecuación tiene la misma forma que en otros sistemas conocidos, tal es el caso de sistemas mecánicos ó el empleado en el análisis de circuitos, los cuatro grados de libertad (DOFs) por nodo {«} representan los tres componentes del potencial magnético vectorial A y el potencial magnético escalar v|/. Si consideramos que N es el número de grados de libertad en el modelo, las matrices tendrán la dimensión de NxN, y las columnas de los vectores {«} y {P} cada uno tendrá N renglones, uno por cada grado de libertad.

El paquete E M A S resuelve esta ecuación matricial usando varias técnicas matemáticas para los potenciales desconocidos.

(ec. 4.1)

Capitulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

D o n d e A, es el vector magnético potencial convencional, y \\i es la integral en el tiempo del potencial electrostático convencional. Una vez que las variables son determinadas, varios campos pueden ser conocidos (energías, corrientes, etc.)

La matriz [M\ es la que representa las propiedades dieléctricas de los materiales del modelo, mientras las matrices [B] y [K] representan la conductividad eléctrica y permeabilidad magnética de los materiales respectivamente. El vector {u} representa los valores desconocidos, es decir los grados de libertad de A y \|/, mientras que el vector {P} representa las excitaciones. Así pues la ecuación (4.1) representa las ecuaciones de Maxwell en su forma general, como resultado un amplio rango de problemas de distintas aplicaciones pueden ser resueltos, tales como problemas de tipo electrostático, corriente circulante, magnetostático, corrientes de Eddy, guías de ondas, entre otras pueden ser obtenidas mediante esta ecuación.

L a forma de la ecuación matricial, como se ha mencionado establece una analogía con otros sistemas familiares, por ejemplo, la misma ecuación obedece a circuitos eléctricos pasivos, en este caso, {M} representa capacitancia, {B} representa resistencia y {k}

representa inductancia, {«} representa voltajes en los nodos, mientras que el vector {P}

representa corrientes inyectadas.

L o s métodos numéricos usados para resolver la ecuación (4.1), son especificados por

secuencias de solución. Cada secuencia representa una particular técnica matemática, de tal forma que una aplicación en particular puede ser analizada usando varias técnicas, tales c o m o respuesta a la frecuencia, análisis transitorio y otros, en la Figura 4.4 se muestra un diagrama para la selección del método de solución.

La matriz de la ecuación (4.1), puede ser resuelta por el paquete E M A S en una variedad de formas, bajo un número de diferentes suposiciones.

Existen tres formas de análisis estático en los cuales los campos no varían con el tiempo:

Electrostático Magnetostático

Capitulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Figura 4.4. Árbol para la selección del método de solución 

En el análisis de respuesta a la frecuencia (AC), se asume que todas las excitaciones y

soluciones varían con el tiempo acorde a

 e(

K

El análisis de respuesta transitorio asume

arbitrariamente dependencia del tiempo de excitaciones y soluciones.

4.2.1 Campos, potenciales

y

 grados de libertad. 

El campo eléctrico E y el campo magnético B son las primeras cantidades desconocidas

de interés en análisis de campos electromagnéticos. Ambos campos están relacionados

mediante las ecuaciones de Maxwell. La solución de las variables en el paquete EMAS es

mediante el potencial magnético vectorial A, y el potencial magnético escalar v|/. En términos

de esas funciones de potencial, el campo eléctrico y magnético están dados por:

E = ­Vy/­A 

Capítulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

Los potenciales magnéticos A's y el potencial escalar if/ no son determinados en todos los puntos a través del volumen del modelo, solo son determinados en algunos nodos. Los valores discretos de A y \j/ en los puntos de nodos son llamados grados de libertad, (DOF's 

del inglés degrees of freedom) los grados de libertad varían con el tiempo acorde con las ecuaciones de Maxwell. Existen cuatro grados de libertad en cada nodo en E M A S : tres componentes del potencial vectorial, y un componente del potencial escalar, dando solución a estos campos, otras cantidades pueden obtenerse por interpolación y diferenciación, los nodos son colocados a través del modelo para llevar a cabo la precisión deseada sin introducir muchos grados de libertad.

4.2.2 Funciones de forma. 

L o s valores del potencial son interpolados con elementos usando funciones de forma. En elementos de primer orden con solo nodos en las esquinas, los potenciales varían linealmente a través de los lados de los elementos. La interpolación dentro de elementos de primer orden es ligeramente mas complicada, pero aún envuelve polinomios de orden bajo. Cuando elementos de segundo orden contienen nodos a la mitad entre nodos de esquinas, los potenciales varían cuadraticamente a lo largo de los lados de los elementos

4.3 Despliegue de resultados 

El paquete M S C / X L es un pre y postprocesador gráfico diseńado para el uso en conjunto con el paquete E M A S , en este caso se uso únicamente como una interfase gráfica a colores, esta adaptada especialmente para el análisis de campos electromagnéticos, de forma tal que es posible ver gráficamente excitaciones, campos electromagnéticos, el flujo de potencia a través del vector de Pointyng, entre otras.

Capitulo 4  Análisis de campos electromagnéticos usando  los paquetes Aries, Ernas y XL. 

a) Gráficas en forma de contornos. Una gráfica de contornos muestra las cantidades de los resultados en bandas de colores o lineas. Los contornos son líneas o regiones coloreadas representando valores constantes. Los resultados son especificados en una barra de colores.

b) Gráficas en forma de vector. Esta opción permite desplegar los vectores en tres dimensiones de distintos campos. Este tipo de gráficas puede desplegar los vectores tanto en los nodos como en los centros de los elementos. Existe una barra de colores donde se muestran los rangos de las magnitudes y la dirección es mostrada por la flecha del vector.

c) Gráficas X-Y

Los cálculos que pueden obtenerse son los siguientes:

• Calcula resultados total y promedio en los elementos y nodos

• Calcula cantidades eléctricas, tales como inductancia y capacitancia.

• . Calcula otras cantidades importantes como, coeficientes de reflexión y otros campos del modelo.

Una explicación más completa relacionada con este capítulo se encuentra en los manuales de usuario de los paquetes ARJES[15], E M A S [16] y XL [17], así como en la guía para modelación con el paquete E M A S [18]. 

CAPÍTULO 5 

SIMULACIONES  E F E C T U A D A S . 

5.0 Introducción 

Capítulo 5  Simulaciones efectuadas 

La formulación matemática para resolver el problema con corriente alterna es más complicada por las corrientes circulantes en el material magnético y es similar al caso que se presenta en la fundamentación teórica del capítulo 3, para el análisis matemático se considero que la placa tiene longitud infinita, para este caso se tiene una longitud finita esto es especialmente importante para placas cuyo espesor es pequeńo.

5,1 Solución analítica para el modelo con corriente directa 

El modelo empleado es el que se muestra en la Fig. 5.1. Como se puede apreciar es un modelo tridimensional el cual consiste en un anillo de acero A-036, al cual se le hace pasar una corriente directa de 6000 A a través de un conductor colocado en el centro del anillo, las propiedades y dimensiones del material ferromagnético se presentan en la misma figura. Las dimensiones de la placa utilizada (espesor y diámetro interior) son las correspondientes a las dimensiones reales de un transformador de potencia, de esta manera éste modelo, representa el modelo simplificado del paso de un cable a través de la tapa del transformador.

az 

re 

U­0­4*E­7HAn 

_\ÍI

 _(aire) = 1 

ax 

f I­6000Amp. 

Capitulo 5  Simulaciones efectuadas 

A continuación se muestra el desarrollo analítico para conocer la intensidad de campo magnético, la densidad y el flujo magnético en el modelo.

5.1.1 Intensidad de campo magnético 

Para obtener la intensidad de campo magnético H, se aplica la ley de Ampere, que

establece que la integral de línea sobre cualquier trayectoria cerrada es igual a la corriente total encerrada por dicha trayectoria. Matemáticamente lo anterior se puede expresar mediante la siguiente ecuación.

Para este caso, el hecho de que H y di son tangentes, permite sustituir el producto punto de la ley de Ampere con el producto de magnitudes escalares. La integral que resulta se reduce a encontrar la longitud de la porción de la trayectoria con respecto a la cual H es paralela.

T o m a n do una trayectoria circular de radio r sobre el plano xy para la cual H mantiene su magnitud constante, se obtiene la expresión para la intensidad de campo magnético

encerrada  (ec. 5.1)

Finalmente tenemos

H = encerrada a (ec. 5.2)

Capítulo 5  Simulaciones efectuadas 

5.1.2 Flujo magnético y densidad de flujo magnético 

La ecuación que relaciona a la densidad de flujo magnético B con la intensidad de campo magnético en el espacio libre es

B = MoH (ec. 5.3)

D o n d e B se mide en Teslas (T). La constante \1q (permeabilidad en el espacio libre) no es adimensional y tiene valor específico para el espacio libre, dado en Henrys por metro (H/m)

//0 = 4 ^ x l 0 "

7 _{H / m}

El flujo magnético se representará por 0,y se define como el número de lineas de flujo magnético que pasan a través de cualquier superficie, se obtiene a partir de

& = ¡B*ds (ec. 5.4)

El flujo magnético contenido en la placa circular (mostrada en la Fig. 5.1) de espesor e

es el flujo magnético que cruza a cualquier plano radial extendiéndose desde r = r¡ hasta

r = r2, y desde z = 0 hasta z = e esta dado por

a¿»drdz aż  (ec. 5.5)

o

Finalmente considerando que u = Uo Hr tenemos la ecuación para calcular el flujo en la

placa.

Mi encerrada ^ J^A

Capítulo 5  Simulaciones efectuadas 

5.1.3 Potencial magnético A 

El cálculo del potencial magnético en función del radio en la placa se puede obtener haciendo uso de la ecuación de poisson, el procedimiento es como sigue

V2 A

z = -M o J (ec. 5.7)

Considerando que la corriente fluye en dirección  az y fuera del conductor, J = 0 V2_A

z=0

5> X

Fig. 5.2 Potencial magnético A. 

D a d o que la corriente en este problema está enteramente en la dirección de z como lo muestra la Fig. 5.2, A tiene solamente componente z. Por lo tanto

\_d_ r dr

(

£áL)

±*l4L

£LdL

dr d</>2 _d z

2

Por condiciones de simetría, se tiene que  Az es función únicamente del radio r, 

entonces

1 _{^ ^ 1 = 0}