Matemáticas aplicadas para
administración, economía
MATEMÁTICAS
APLICADAS PARA
ADMINISTRACIÓN,
ECONOMÍA Y
CIENCIAS SOCIALES
Cuarta edición
Frank S. Budnick
University of Rhode Island
Traducción
José Julián Díaz Díaz
Efrén Alatorre Miguel
Traductores profesionales
Revisión técnica
Raúl Gómez Castillo
Profesor de Física y Matemáticas
Instituto Tecnológico y de Estudios Superiores de Monterrey, CEM
MÉXICO • AUCKLAND • BOGOTÁ • BUENOS AIRES • CARACAS • GUATEMALA
LISBOA • LONDRES • MADRID • MILÁN • MONTREAL• NUEVA DELHI • NUEVA YORK
Director Higher Education:
Miguel Ángel Toledo Castellanos
Director editorial:
Ricardo A. del Bosque Alayón
Editor sponsor:
Pablo Eduardo Roig Vázquez
Editora de desarrollo:
Diana Karen Montaño González
Supervisor de producción:
Zeferino García García
Matemáticas aplicadas para administración, economía y ciencias sociales
Cuarta edición
Prohibida la reproducción total o parcial de esta obra,
por cualquier medio, sin la autorización escrita del editor.
DERECHOS RESERVADOS © 2007 respecto a la cuarta edición en español por
McGRAW-HILL/INTERAMERICANA EDITORES, S.A. DE C.V.
A Subsidiary of
The McGraw-Hill
Companies, Inc.
Edificio Punta Santa Fe
Prolongación Paseo de la Reforma 1015, Torre A
Piso 17, Colonia Desarrollo Santa Fe,
Delegación Álvaro Obregón
C.P. 01376, México, D. F.
Miembro de la Cámara Nacional de la Industria Editorial Mexicana, Reg. Núm. 736.
ISBN 970-10-5698-1
(ISBN 970-10-4679-X edición anterior)
Traducido de la cuarta edición de: APPLIED MATHEMATICS FOR BUSINESS, ECONOMICS, AND
THE SOCIAL SCIENCES
Copyright © MCMXCIII by The McGraw-Hill Companies, Inc. All rights reserved.
Previous editions © 1979, 1983, and 1988.
0-07-008902-7
1234567890 09875432106
ACERCA DEL AUTOR
A mi esposa, Deb,
2.3 Forma de pendiente-intercepción
56
Según un punto de vista ventajoso y diferente
56
Interpretación de la pendiente y la intercepción de
y
57
2.4 Determinación de la ecuación de una línea recta
61
Pendiente e intercepción
61
Pendiente y un punto
61
Dos puntos
64
2.5 Ecuaciones lineales con más de dos variables
69
Sistemas de coordenadas tridimensionales
69
Ecuaciones con tres variables
71
Ecuaciones con más de tres variables
73
2.6 Aplicaciones adicionales
76
Términos y conceptos clave
80
Fórmulas importantes
80
Ejercicios adicionales
80
Evaluación del capítulo
86
CAPÍTULO
3
SISTEMAS DE ECUACIONES LINEALES
88
3.1 Sistemas de ecuaciones con dos variables
90
Sistemas de ecuaciones
90
Análisis gráfico
91
Soluciones gráficas
92
El procedimiento de eliminación
93
Sistemas de (
m
2),
m
> 2
97
3.2 Método de eliminación de Gauss
101
La idea general
101
El método
103
3.3 Sistemas con
n
variables,
n
≥
3
109
Análisis gráfico para sistemas con tres variables
109
Procedimiento de eliminación de Gauss para sistemas de (3
3)
110
Menos de tres ecuaciones
115
Sistemas con
n
variables,
n
> 3
117
3.4 Aplicaciones selectas
118
Problema de mezcla de productos
120
Modelo de mezcla
121
Modelo de cartera
122
3.5 Notas finales
126
Términos y conceptos clave
127
Ejercicios adicionales
127
Evaluación del capítulo
130
Ejercicios por computadora
131
CONTENIDO
xiii
CAPÍTULO
4
FUNCIONES MATEMÁTICAS
140
4.1 Funciones
142
Definición de funciones
142
La naturaleza y la notación de las funciones
143
Consideraciones de dominio y rango
147
Dominio y rango restringidos
150
Funciones de varias variables
151
4.2 Tipos de funciones
158
Funciones constantes
158
Funciones lineales
159
Funciones cuadráticas
160
Funciones cúbicas
161
Función polinomial
162
Funciones racionales
162
Combinación de funciones
163
Funciones compuestas
163
4.3 Representación gráfica de las funciones
169
Representación gráfica de funciones en dos dimensiones
169
Prueba de la línea recta vertical
174
Términos y conceptos clave
177
Fórmulas importantes
177
Ejercicios adicionales
177
Evaluación del capítulo
180
CAPÍTULO
5
FUNCIONES LINEALES: APLICACIONES
182
5.1 Funciones lineales
184
Forma general y suposiciones
184
Funciones lineales del costo
186
Funciones lineales del ingreso
188
Funciones lineales de la utilidad
188
5.2 Otros ejemplos de funciones lineales
192
5.3 Modelos basados en el punto de equilibrio
206
Suposiciones
206
Análisis del punto de equilibrio
206
Términos y conceptos clave
218
Fórmulas importantes
219
Ejercicios adicionales
219
Evaluación del capítulo
223
CAPÍTULO
6
FUNCIONES CUADRÁTICAS Y POLINOMIALES
226
6.1 Funciones cuadráticas y sus características
228
Forma matemática
228
Representación gráfica
229
6.2 Funciones cuadráticas: aplicaciones
240
6.3 Funciones polinomiales y racionales
249
Funciones polinomiales
249
Funciones racionales
254
Términos y conceptos clave
256
Fórmulas importantes
256
Ejercicios adicionales
257
Evaluación del capítulo
261
Minicaso: Guerras del comercio minorista
263
CAPÍTULO
7
FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
264
7.1 Características de las funciones exponenciales
266
Características de las funciones exponenciales
267
Funciones exponenciales de base
e
272
Conversión a funciones de base
e
275
7.2 Aplicaciones de las funciones exponenciales
277
7.3 Logaritmos y funciones logarítmicas
288
Logaritmos
288
Propiedades de los logaritmos
290
Solución de ecuaciones logarítmicas y exponenciales
291
Funciones logarítmicas
296
Términos y conceptos clave
304
Fórmulas importantes
305
Ejercicios adicionales
305
Evaluación del capítulo
310
Minicaso: ¿Hora del fallecimiento?
311
MATEMÁTICAS FINITAS
CAPÍTULO
8
MATEMÁTICAS DE LAS FINANZAS
312
8.1 Interés y su cálculo
314
Interés simple
314
Interés compuesto
316
El poder del crecimiento capitalizado
317
8.2 Cálculos de pagos simples
320
Monto compuesto
320
CONTENIDO
xv
Otras aplicaciones de la fórmula del monto compuesto
326
Tasas efectivas de interés
329
8.3 Anualidades y su valor futuro
332
La suma de una anualidad
332
Determinación del importe de una anualidad
335
8.4 Anualidades y su valor presente
338
El valor presente de una anualidad
338
Determinación del importe de una anualidad
341
Hipotecas
342
La ventaja del pago quincenal de la hipoteca
345
8.5 Análisis costo-beneficio
347
Flujo de efectivo descontado
347
Extensiones del análisis del flujo de efectivo descontado
350
Términos y conceptos clave
352
Fórmulas importantes
353
Ejercicios adicionales
354
Evaluación del capítulo
358
Minicaso: Corporación XYZ
360
CAPÍTULO
9
ÁLGEBRA MATRICIAL
362
9.1 Introducción a las matrices
364
¿Qué es una matriz?
364
Propósito del estudio del álgebra matricial
365
9.2 Tipos especiales de matrices
366
Vectores
366
Matrices cuadradas
367
Transpuesta de una matriz
368
9.3 Operaciones matriciales
370
Adición y sustracción de matrices
370
Multiplicación escalar
372
El producto interno
373
Multiplicación de matrices
374
Representación de una ecuación
379
Representación de sistemas de ecuaciones
380
9.4 El determinante
383
El determinante de una matriz de orden (1
1)
384
El determinante de una matriz de orden (2
2)
384
El determinante de una matriz de orden (3
3)
384
El método de cofactores
386
Propiedades de los determinantes
391
Regla de Cramer
393
9.5 La inversa de una matriz
396
Obtención de la inversa usando cofactores (opcional)
401
La inversa y los sistemas de ecuaciones
403
9.6 Aplicaciones selectas
406
Sugerencias para la solución de aplicaciones matriciales
407
Términos y conceptos clave
423
Ejercicios adicionales
424
Evaluación del capítulo
430
Ejercicios por computadora
431
Minicaso: Planeación de recursos humanos
435
CAPÍTULO
10
PROGRAMACIÓN LINEAL: INTRODUCCIÓN
436
10.1 Programación lineal
438
Introducción
438
Un escenario
439
Restricciones estructurales y restricciones de no negatividad
440
10.2 Soluciones gráficas
440
Gráficas de las desigualdades lineales
441
Sistemas de desigualdades lineales
444
Región de soluciones factibles
447
Incorporación de la función objetivo
448
Soluciones del punto vértice
451
Soluciones óptimas alternativas
453
Sin solución factible
456
Soluciones no acotadas
456
10.3 Aplicaciones de la programación lineal
459
Modelos de la mezcla dietética
459
Modelos de transporte
461
Modelos del presupuesto de capital
463
Modelos de mezcla
465
Términos y conceptos clave
473
Ejercicios adicionales
474
Evaluación del capítulo
478
Minicaso: Programación de controladores de tráfico aéreo
479
CAPÍTULO
11
MÉTODO SIMPLEX Y MÉTODOS DE SOLUCIÓN
POR COMPUTADORA
482
11.1 Preliminares del método simplex
484
Panorama del método simplex
484
Requerimientos del método simplex
485
Soluciones factibles básicas
489
11.2 El método simplex
498
Solución por enumeración
499
CONTENIDO
xvii
Incorporación de la función objetivo
503
Resumen del procedimiento simplex
510
Problemas de maximización con restricciones mixtas
512
Problemas de minimización
515
11.3 Fenómenos especiales
519
Soluciones óptimas alternativas
519
Carencia de solución factible
521
Soluciones no acotadas
523
Cuadros condensados
524
11.4 Métodos de solución por computadora
526
Ilustración de un paquete de programación lineal
526
Precios sombra
529
Análisis de la sensibilidad
530
11.5 El problema dual
533
Formulación del problema dual
534
Soluciones al problema primal y dual
536
Epílogo
538
Términos y conceptos clave
539
Ejercicios adicionales
540
Evaluación del capítulo
545
Minicaso: Concesión de contratos
546
CAPÍTULO
12
MODELOS DE TRANSPORTE Y ASIGNACIÓN
548
12.1 El modelo de transporte
550
Forma general y suposiciones
550
12.2 Métodos de solución para el modelo de transporte
554
Soluciones iniciales (de arranque)
555
El algoritmo del cruce de arroyo
558
Métodos de solución por computadora
565
12.3 El modelo de asignación y los métodos de solución
570
Forma general y suposiciones
571
Métodos de solución
573
El método húngaro
574
Resumen del método húngaro
577
Términos y conceptos clave
580
Ejercicios adicionales
580
Evaluación del capítulo
583
Minicaso: Distribución del almacenamiento
585
CAPÍTULO
13
INTRODUCCIÓN A LA TEORÍA DE LA PROBABILIDAD
586
13.1 Introducción a los conjuntos y operaciones con conjuntos
589
Conjuntos
589
Representacións del diagrama de Venn
592
Operaciones con conjuntos
593
13.2 Permutaciones y combinaciones
598
Permutaciones
600
Combinaciones
603
13.3 Conceptos básicos de la probabilidad
609
Experimentos, resultados y eventos
609
Probabilidades
615
Algunas reglas adicionales de la probabilidad
617
13.4 Determinación de independencia y dependencia estadística
626
Independencia estadística
626
Dependencia estadística
630
Términos y conceptos clave
638
Fórmulas importantes
638
Ejercicios adicionales
639
Evaluación del capítulo
645
Minicaso: El problema del cumpleaños
646
CAPÍTULO
14
DISTRIBUCIONES DE PROBABILIDAD
648
14.1 Variables aleatorias y distribuciones de probabilidad
650
Variables aleatorias
650
Distribuciones de las frecuencias
651
Distribuciones de la probabilidad
653
Histogramas
655
14.2 Medidas de la tendencia central y variación
660
La media
660
La mediana
662
La moda
662
Media de una distribución de probabilidad discreta
663
La desviación estándar
664
14.3 Distribución de la probabilidad binomial
669
Procesos de Bernoulli
669
Distribución binomial
670
Media y desviación estándar de la distribución binomial
675
14.4 Distribución de la probabilidad normal
678
Distribución de la probabilidad normal
678
CONTENIDO
xix
EL CÁLCULO
CAPÍTULO
15
DIFERENCIACIÓN
698
15.1 Límites
700
Límites de las funciones
701
15.2 Propiedades de los límites y continuidad
708
Algunas propiedades de los límites
708
Límites e infinito
712
Continuidad
716
15.3 Razón de cambio promedio
720
Razón de cambio promedio y pendiente
720
15.4 La derivada
728
Razón de cambio instantánea
728
Aproximación del límite para encontrar la derivada
733
15.5 Diferenciación
738
Reglas de la diferenciación
738
15.6 Reglas adicionales de la diferenciación
744
Regla de la cadena
746
15.7 Interpretación de la razón de cambio instantánea
749
15.8 Derivadas de orden superior
753
La segunda derivada
753
Tercera derivada y derivadas de orden superior
755
Términos y conceptos clave
757
Fórmulas importantes
757
Ejercicios adicionales
758
Evaluación del capítulo
763
Apéndice: Demostración de algunas reglas de la diferenciación
763
CAPÍTULO
16
OPTIMIZACIÓN: METODOLOGÍA
768
16.1 Derivadas: interpretaciones adicionales
770
La primera derivada
770
Concavidad y puntos de inflexión
774
Concavidad desde una perspectiva diferente
778
16.2 Identificación de los máximos y mínimos
781
Extremos relativos
781
Puntos críticos
782
Prueba de la primera derivada
785
Prueba de la segunda derivada
788
Cuando falla la prueba de la segunda derivada
793
16.3 Trazado de curvas
797
Puntos de datos clave
798
16.4 Consideraciones del dominio restringido
803
Cuando el dominio está restringido
803
Términos y conceptos clave
806
Ejercicios adicionales
807
Evaluación del capítulo
808
CAPÍTULO
17
OPTIMIZACIÓN: APLICACIONES
810
17.1 Aplicaciones del ingreso, costo y utilidad
813
Aplicaciones del ingreso
813
Aplicaciones del costo
816
Aplicaciones de la utilidad
820
Aproximación marginal para la maximización de la utilidad
823
17.2 Aplicaciones adicionales
834
Ejercicios adicionales
855
Evaluación del capítulo
862
Minicaso: El modelo de la cantidad económica de pedido
863
CAPÍTULO
18
CÁLCULO INTEGRAL: UNA INTRODUCCIÓN
866
18.1 Antiderivadas
868
El concepto de la antiderivada
868
Funciones de ingreso y costo
871
18.2 Reglas de la integración
873
Integración
874
Reglas de la integración
875
18.3 Reglas adicionales de integración
879
18.4 Otras técnicas de integración (opcional)
886
Integración por partes
886
Integración por fracciones parciales
890
Tablas de integrales
895
18.5 Ecuaciones diferenciales
898
Clasificación de las ecuaciones diferenciales ordinarias
899
Soluciones de las ecuaciones diferenciales ordinarias
899
Extensión de las ecuaciones diferenciales
904
CONTENIDO
xxi
CAPÍTULO
19
CÁLCULO INTEGRAL: APLICACIONES
910
19.1 Integrales definidas
912
La integral definida
912
Evaluación de las integrales definidas
915
Propiedades de las integrales definidas
918
19.2 Integrales definidas y áreas
923
Áreas entre una función y el eje de las
x
923
Obtención de áreas entre curvas
927
19.3 Métodos de aproximación
935
Regla de los rectángulos
935
Regla de los trapecios
937
Regla de Simpson
938
19.4 Aplicaciones del cálculo integral
943
19.5 Cálculo integral y probabilidad (opcional)
957
Términos y conceptos clave
960
Fórmulas importantes
960
Ejercicios adicionales
961
Evaluación del capítulo
965
Minicaso: El dilema de la seguridad social: un problema de solvencia
967
CAPÍTULO
20
OPTIMIZACIÓN: FUNCIONES DE VARIAS VARIABLES
968
20.1 Representación gráfica de funciones de dos variables
970
Representación gráfica
970
Trazado de funciones de dos variables
971
20.2 Derivadas parciales
975
Derivadas de funciones de dos variables
975
Interpretación de las derivadas parciales
980
Derivadas de segundo orden
984
20.3 Optimización de las funciones de dos variables
987
Puntos críticos
987
Cómo distinguir los puntos críticos
992
20.4 Aplicaciones de la optimización de dos variables
1002
20.5 Optimización de
n
variables (opcional)
1014
Condición necesaria para los extremos relativos
1015
Condiciones suficientes
1015
20.6 Optimización sujeta a restricciones (opcional)
1019
Método del multiplicador de Lagrange (restricción de la igualdad)
1019
Condición suficiente
1021
Caso de restricción de una sola igualdad con
n
variables
1023
Interpretación de
1026
Términos y conceptos clave
1027
Fórmulas importantes
1028
Ejercicios adicionales
1028
Evaluación del capítulo
1031
Minicaso: Modelo de inventario de pedidos retrasados
1032
TABLAS DE INTERÉS COMPUESTO
T-1
A
PÉNDICEA
REVISIÓN DE ÁLGEBRA (OPCIONAL)
A-1
Evaluación preliminar de álgebra
A-1
Repuestas a la evaluación preliminar de álgebra
A-2
A.1 El sistema de los números reales
A-2
Números reales
A-2
Valor absoluto
A-3
A.2 Polinomios
A-4
Exponentes enteros positivos
A-4
Expresiones polinomiales
A-6
Adición y sustracción de polinomios
A-7
Multiplicación de polinomios
A-8
División de polinomios
A-9
A.3 Factorización
A-11
Factores monomiales
A-11
Polinomios cuadráticos
A-12
Otras formas especiales
A-14
A.4 Fracciones
A-15
Adición y sustracción de fracciones
A-15
Multiplicación y división
A-17
A.5 Exponentes y radicales
A-19
Exponentes fraccionarios
A-19
Radicales
A-19
APÉNDICE
B
NOTACIÓN DE SUMATORIA
A-23
RESPUESTAS SELECTAS
Ejercicios de seguimiento y evaluaciones del capítulo
R-1
P
REFACIOxxiii
CAPÍTULO
1
ALGUNOS CONOCIMIENTOS PRELIMINARES
2
1.1 Ecuaciones de primer grado con una variable
4
Las ecuaciones y sus propiedades
4
Solución de ecuaciones de primer grado con una variable
6
1.2 Ecuaciones de segundo grado con una variable
8
Solución de ecuaciones cuadráticas
8
1.3 Las desigualdades y su solución
11
Desigualdades
11
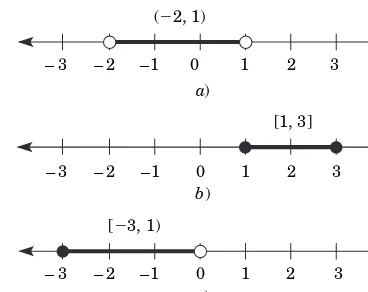
Notación de intervalo
13
Solución de desigualdades
14
Desigualdades de segundo grado
17
1.4 Relaciones de valor absoluto
20
Algunas propiedades de los valores absolutos
21
Solución de ecuaciones y desigualdades que implican valores absolutos
22
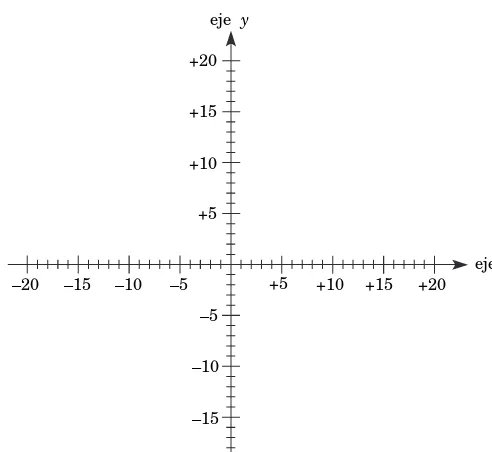
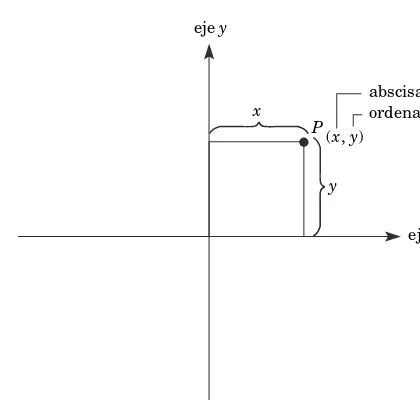
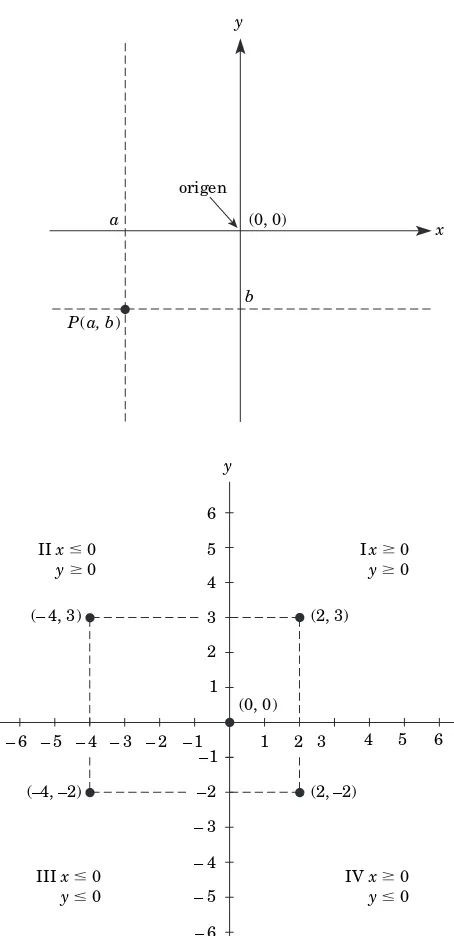
1.5 Sistemas de coordenadas rectangulares
25
El plano cartesiano
25
Fórmula del punto medio
28
Fórmula de la distancia
29
Términos y conceptos clave
31
Ejercicios adicionales
32
Evaluación del capítulo
33
ECUACIONES Y FUNCIONES
CAPÍTULO
2
ECUACIONES LINEALES
34
2.1 Ecuaciones lineales
36
Forma general
36
Representación mediante el uso de las ecuaciones lineales
37
Ecuaciones lineales con
n
variables
40
2.2 Características gráficas
45
Representación gráfica de ecuaciones con dos variables
45
Intercepciones
47
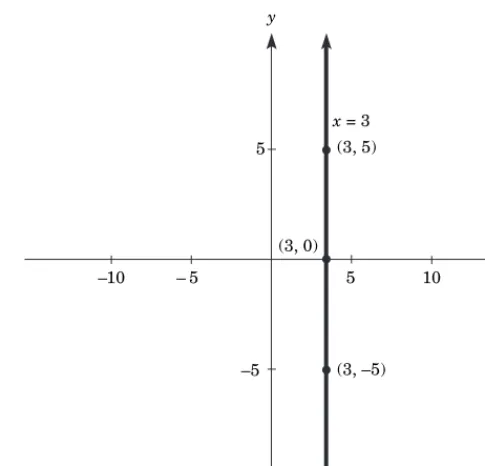
La ecuación
x
=
k
48
La ecuación
y
=
k
48
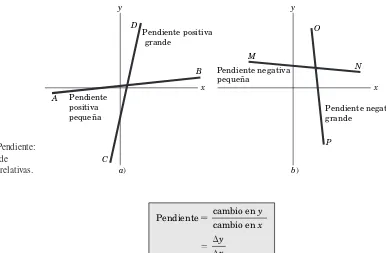
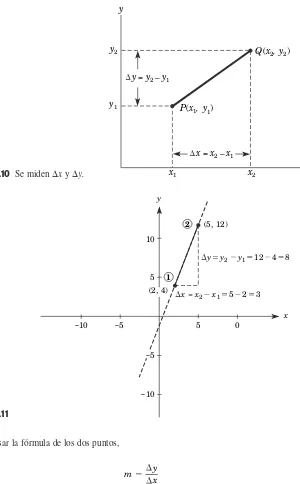
Pendiente
50
Características específicas
❑
Una mayor orientación hacia el uso de la COMPUTADORA COMO UNA
HERRA-MIENTA para el análisis matemático.
❑
A lo largo del libro se utilizan REGRESIONES DE ÁLGEBRA para ayudar al
estu-diante a recordar las reglas y los conceptos esenciales. La regresión consiste
gene-ralmente en volver a presentar una regla o un concepto haciendo referencia a
secciones de revisión de álgebra apropiadas en el texto.
❑
NOTAS PARA EL ESTUDIANTE que ofrecen discernimientos acerca de un
con-cepto matemático o una aplicación.
❑
“PUNTOS PARA PENSAR Y ANALIZAR” que permiten a los estudiantes hacer
una pausa por un momento para reconsiderar un concepto o ejemplo desde una
perspectiva diferente. Su propósito es reforzar y ampliar la comprensión del
alum-no al inducir al pensamiento crítico.
Características pedagógicas
❑
Los PROBLEMAS CON BASE EN LA COMPUTADORA, identificados en el
conjunto de ejercicio con un ícono brindan al alumno y al profesor una oportunidad
para resolver problemas de mayor escala.
❑
Los MINICASOS permiten que los estudiantes analicen e interpreten una
aplica-ción más compleja y realista. Pueden ser la base para estimular el análisis en clase.
* Capítulo opcional
Algunas estructuras sugeridas para el curso A Combinación de matemáticas finitas y cálculo en dos niveles
Primer nivel
Segundo nivel
B Combinación de matemáticas finitas y cálculo en un nivel
1 2 3 4 5 6 7* 8* 9* 10* 13*
15 16 17 18 19* 20*
1 2 3 4 5 6 7* 9 15 16 17 18 19*
C Énfasis en el cálculo en un nivel
1 2 4 5 6 7* 15 16 17 18 19* 20*
D Énfasis en las matemáticas finitas en un nivel
PREFACIO
xxv
❑
Una gran variedad de otros elementos de ayuda para el aprendizaje, incluyendo
objetivos del capítulo, numerosos ejemplos resueltos, un caudal de ejercicios,
eva-luaciones de los capítulos, listas de términos y conceptos clave, y listas resumidas
de fórmulas importantes.
Nuevas características y cambios
Los principales cambios en la cuarta edición tienen lugar en la organización. Primero, se
ha organizado el libro en tres subsecciones principales:
I.
Ecuaciones y funciones
II.
Matemáticas finitas
III.
Cálculo
Otros cambios importantes incluyen los siguientes:
Capítulo 1:
Algunos conocimientos preliminares
es un nuevo capítulo que analiza
algu-nos conceptos fundamentales (más allá de la revisión de los principios algebraicos básicos
en el apéndice A) los cuales son un requerimiento previo para el material que sigue.
Se ha movido el material sobre ecuaciones lineales y sistemas de ecuaciones de modo que
preceda el análisis de las funciones matemáticas.
Se ha consolidado el material acerca de las funciones matemáticas en cuatro capítulos al
principio del libro de texto. El capítulo 4 introduce el concepto y la notación de las
Funciones matemáticas
. El capítulo 5 se enfoca en las
Funciones lineales:
aplicacio-nes
. El capítulo 6 estudia las
Funciones cuadráticas y polinomiales
con aplicaciones. El
capítulo 7 presenta
Funciones exponenciales y logarítmicas
con aplicaciones.
Se ha reorganizado ligeramente el tratamiento de la programación lineal en los capítulos
10 y 11. En tanto que las aplicaciones se presentaban primero en la edición anterior, el
capítulo 10 se enfoca primero en los métodos de solución gráfica, seguidos por
aplicacio-nes seleccionadas. Se ha cambiado la sección que estudia los métodos de solución por
com-putadoras al final del capítulo 11, el cual presenta el método simplex.
Se ha eliminado en esta edición el material sobre programación entera y programación de
objetivo. A pesar de que hay extensiones interesantes de la programación lineal, se
deter-minó que estos temas son de poca importancia relativa.
En el análisis del cálculo, se ha dividido en dos capítulos separados el material sobre
optimi-zación (como en la segunda edición). El capítulo 16 presenta la metodología de la
optimiza-ción y el capítulo 17 está dedicado exclusivamente a las aplicaciones de la optimizaoptimiza-ción. El
motivo principal por el que se separaron estos temas es que se presenta demasiado material
para un solo capítulo. La pedagogía es hacer que los estudiantes aprendan la metodología
matemática en el capítulo 16, seguida de las aplicaciones seleccionadas del capítulo 17.
El material sobre optimización de funciones de varias variables se ha cambiado al último
capítulo en el libro de texto. Este tema es opcional para muchas escuelas y su nueva
ubi-cación es compatible con textos que compiten con éste.
Otras modificaciones importantes incluyen:
Se ha eliminado el capítulo 11 de la tercera edición (Aplicaciones seleccionadas de
proba-bilidad), aunque se han transferido algunas aplicaciones al capítulo sobre álgebra matricial.
Se ha aumentado significativamente el número de Ejercicios de práctica con el fin de dar
más oportunidades para el refuerzo de nuevos conceptos.
Además de estos cambios, el autor ha incorporado una cantidad considerable de
aplicacio-nes (ya sea como ejemplos o ejercicios) que contienen “datos de la vida real”. Asimismo,
el autor hace un intento significativo por hacer que los estudiantes estén conscientes de la
naturaleza que tiene la
estimación
al aplicar las matemáticas. Es decir, la aplicación del
análisis matemático en el “mundo real” implica la aproximación de relaciones entre
varia-bles. Es importante que los estudiantes entiendan las fuerzas y debilidades del análisis
matemático.
El libro contiene un gran número de aplicaciones distintas. Se pretende que los
profe-sores cubran tantas aplicaciones en estos capítulos como consideren conveniente para sus
alumnos.
Se considera que algunos ejercicios del libro de texto son de mayor nivel de dificultad
que la mayoría de los demás. Estos ejercicios están precedidos por un asterisco (*).
Reconocimientos
Deseo expresar mi sincero agradecimiento a las personas que han contribuido ya sea
direc-ta o indirecdirec-tamente en este proyecto. Quiero agradecer a: Thomas Arbutiski, Community
College of Allegheny County; Helen B. Chun, Community College of Allegheny County;
Benjamin Eichorn, Rider College; Joseph Fadyn, Southern College of Technology; Odene
Forsythe, Westark Community College; Gary Grimes, Mount Hood Community College;
Anne Hughes, St. John’s University; Harry Hutchins, Southern Illinois University; Harlan
Koca, Washburn University of Topeka; Joyce Longman, Villanova University; Daniel J.
Madden, University of Arizona; Victor McGee, Dartmouth College; Michael Mogavero,
Alfred University; Dean Morrow, Robert Morris College; Richard Semmler, Northern
Virginia Community College; Richard Witt, University of Wisconsin, Eau Claire; y
Cathleen Zucco, Le Moyne College, por sus muchos comentarios útiles durante el
desa-rrollo del manuscrito. Expreso un agradecimiento especial a Thomas Arbutiski por sus
revisiones y sugerencias concienzudas y extremadamente detalladas.
También deseo agradecer a varias personas de McGraw-Hill con quienes trabajé
direc-tamente. Estas personas incluyen a Michael Johnson, Margery Luhrs y David Damstra.
Doy gracias también a Karen Minette por coordinar el paquete de complementos y a Leon
Bolognese por su trabajo en el diseño del libro.
De igual manera estoy agradecido por los esfuerzos de Shaochi Xu quien colaboró en
el desarrollo de los conjuntos de soluciones para los ejercicios. Doy un especial
agradeci-miento a mis 520 alumnos de QBA que sirvieron como “conejillos de indias” por
permi-tirme probar en clase algunas partes del manuscrito. Del mismo modo, querría hacer
patente mi reconocimiento por las útiles sugerencias de Sandra Quinn, Kathy Bowser y la
finada Elizabeth Flaherty, así como sus esfuerzos en el desarrollo del
Instructor’s Resource
Manual
y el
Student’s Solutions Manual.
Por último, quiero dar gracias a mi esposa, Deb, por su apoyo a lo largo de esta
exte-nuante experiencia, al igual que por las otras vivencias que hemos compartido juntos.
Introducción
Las matemáticas son una parte integral de la educación de estudiantes de administración,
economía y ciencias sociales. Existe un creciente deseo de mejorar el nivel de sofisticación
cuantitativa que tienen los graduados en estos tipos de programas. El objetivo no es
con-vertir a estos estudiantes en matemáticos, sino hacer que se sientan tan cómodos como sea
posible en un entorno en el que cada vez se utilizan más el análisis cuantitativo y la
com-putadora. Los estudiantes descubren que deben integrar las matemáticas, el análisis
esta-dístico y la computadora en cursos tanto obligatorios como optativos de sus programas.
Además, las organizaciones ahora usan con mayor eficiencia las herramientas cuantitativas
y la computadora. Quienes toman decisiones estarán mejor preparados para operar en este
tipo de entorno si están familiarizados con las clases de análisis cuantitativo y la
tecnolo-gía de cómputo que se emplean con mayor frecuencia. Dicha familiaridad puede ayudarles
a ser mejores “críticos” y “usuarios” de estas herramientas y quizás tomen mejores
deci-siones.
Matemáticas aplicadas para administración, economía y ciencias sociales
, cuarta
edi-ción, aún presenta de manera informal y no intimidante los principios matemáticos,
técni-cas y aplicaciones más útiles para los estudiantes de negocios, economía, administración y
las ciencias naturales y sociales. Diseñado principalmente como un curso de dos niveles de
matemáticas aplicadas (es posible adaptar con facilidad el libro para un curso de un solo
periodo escolar), trata en forma integral los temas seleccionados de matemáticas finitas y
cálculo. Su uso es apropiado tanto en escuelas con cursos de dos años como en escuelas
con cursos de cuatro años, al igual que como nivel “fundamental” para los programas
uni-versitarios que tienen como un requerimiento previo contar con conocimientos de
mate-máticas. Las maestrías en administración de empresas y administración pública son
programas universitarios que normalmente exigen este tipo de requerimiento.
Características
Se han conservado las siguientes características de la edición anterior:
❑
Un nivel de presentación que desarrolla y refuerza con cuidado los temas.
❑
Un estilo que apela a la
intuición
de los estudiantes y da mucho
refuerzo visual
.
❑
Una
aplicación orientada
que motiva a los estudiantes y da un sentido de
propósi-to para el estudio de las matemáticas.
❑
Un planteamiento que desarrolla primero el concepto matemático y luego lo
refuer-za con aplicaciones.
❑
Un planteamiento que minimiza el uso de demostraciones matemáticas rigurosas.
Algunos
conocimientos
preliminares
1.1
ECUACIONES DE PRIMER GRADO CON UNA VARIABLE
1.2 ECUACIONES DE SEGUNDO GRADO CON UNA VARIABLE
1.3 LAS DESIGUALDADES Y SU SOLUCIÓN
1.4 RELACIONES DE VALOR ABSOLUTO
1.5 SISTEMAS DE COORDENADAS RECTANGULARES
Términos y conceptos clave
Ejercicios adicionales
◗
Estudiar las ecuaciones y los métodos de solución.
◗
Presentar las propiedades de las desigualdades y los métodos
de solución.
◗
Ilustrar las relaciones del valor absoluto.
◗
Introducir las propiedades de los sistemas de coordenadas
rectangulares.
Este capítulo presenta un análisis de conceptos algebraicos selectos. Para estudiar de
mane-ra exitosa el material de este libro de texto, es un requerimiento previo entender estos
con-ceptos, así como los conceptos fundamentales que se revisan en el apéndice A.
Ecuaciones de primer grado con una variable
En este libro continuamente se trabaja con ecuaciones. Es esencial en absoluto comprender
el significado de las ecuaciones y sus propiedades.
Las ecuaciones y sus propiedades
Una
ecuación
indica la igualdad de dos expresiones algebraicas. Las expresiones
algebrai-cas pueden escribirse en términos de una o más
variables
. Los siguientes son algunos
ejem-plos de ecuaciones.
En las ecuaciones (1) y (3), las variables son
x
y
w
, respectivamente. En la ecuación (2) hay
tres variables,
r
,
s
y
t
. Se utiliza el término
variable
porque se pueden sustituir las letras con
distintos valores numéricos.
La
solución
de una ecuación consta de esos valores numéricos, los cuales, al ser
sus-tituidos por las variables, hacen válida una ecuación. Los valores numéricos que hacen
vá-lida una ecuación se conocen como
raíces
de una ecuación. Se dice que las raíces son los
valores de la(s) variable(s) que
satisface(n) la ecuación
. En la ecuación (1), la sustitución
del número 0 por la variable
x
da como resultado
10 22
lo cual no es cierto. El valor
x
= 0 no es una raíz de la ecuación. Sin embargo, al sustituir
el número 4 por la variable
x
se obtiene
3(4) 10225(4)
o
22Se considera que el valor
x
= 4 es una raíz de la ecuación.
Se pueden distinguir tres tipos de ecuaciones. Una
identidad
es una ecuación que es
válida para cualquier valor numérico asignado a las variables. Un ejemplo de una identidad
es la ecuación
2
6x1212x24 2
3x 10 22 5x
2r 5s 8t
3 100
w2 5w 16
(1)
(2)
(3)
1.1 Ecuaciones de primer grado con una variable
5
Otro ejemplo es
5(xy) 5x5y
En cada una de estas ecuaciones, cualquier valor que se asigne a las variables hará que
am-bos lados sean iguales.
Una
ecuación condicional
es válida únicamente para un número limitado de valores
de las variables. Por ejemplo, la ecuación
x3 5
es verdadera sólo cuando
x
es igual a 2.
Un
enunciado falso
, o
contradicción
, es una ecuación que nunca es verdadera. Esto
significa que no hay valor alguno que se pueda asignar a las variables para que los dos
la-dos de la ecuación sean iguales. Un ejemplo es la ecuación
xx5
Se indica que los dos lados
no son iguales
al usar el símbolo
; para este ejemplo,
xx5
La
solución de una ecuación
se refiere al proceso de encontrar las raíces de una
ecua-ción, si es que existe alguna. Con el fin de resolver ecuaciones, por lo general se
manipu-lan o se reordenan. Las reglas siguientes indican las operaciones permitidas.
Reglas seleccionadas para el manejo de ecuaciones
I
Se pueden sumar o sustraer expresiones con valores reales que son
iguales de ambos lados de una ecuación.
II
Es posible multiplicar o dividir ambos lados de una ecuación por
cualquier constante diferente a cero.
III
Se pueden multiplicar ambos lados de una ecuación por una cantidad que
implique variables.
IV
Es posible elevar al cuadrado ambos lados de una ecuación.
V
Se pueden dividir ambos lados de una ecuación por una expresión que
incluya variables siempre que la expresión no sea igual a 0
.
El
grado de un polinomio
se define como el grado del término elevado a la mayor
po-tencia en un polinomio. Si se puede escribir una ecuación en la forma
Expresión polinomial0
el grado de la expresión polinomial es el
grado de la ecuación
. Por tanto, la ecuación
2
x
4
0 es una ecuación de primer grado. La ecuación 4
r
2r
10
0 es una
ecua-ción de segundo grado. La ecuaecua-ción
n
43
n
29
0 es una ecuación de cuarto grado.
Solución de ecuaciones de primer grado con una variable
El procedimiento que se emplea para resolver ecuaciones depende de la naturaleza de la
ecuación. Considérense primero ecuaciones de primer grado que implican una variable.
Los siguientes son algunos ejemplos de estas ecuaciones.
3x2x5
5x412x
Es relativamente fácil resolver ecuaciones de esta forma. Al usar las reglas de manejo
apropiadas, el planteamiento consiste sólo en aislar la variable en un lado de la ecuación y
todas las constantes al otro lado de la ecuación.
Resuelva las dos ecuaciones de primer grado que se presentaron antes.
SOLUCIÓN
Para la ecuación 3x2x– 5, se suma 2xen ambos lados de la ecuación para obtener
o
Nuestra conclusión: el único valor de xque satisface esta ecuación es 5. Para la ecuación 5x4 12 x, se puede sumar 4 y x a ambos lados
o
Dividir ambos lados entre 4 (o al multiplicarlos por 1–4) dan la raíz de la ecuación:
x4
Nuestra conclusión: el único valor de xque satisface la ecuación es 4.
5x 4 4 ( x) 12 x 4 ( x)
5x x 12 4
x 16 XAMPLE
3x(2x)2x5(2x)
x 5
1 4
1.1 Ecuaciones de primer grado con una variable
7
Para resolver la ecuación
se puede sustraer 2xde ambos lados, lo que da como resultado
o
Este resultado es un enunciado falso, o contradicción, que señala que la ecuación original no tiene raíces.
Para resolver la ecuación
se multiplican ambos lados de la ecuación por 2, lo que da como resultado
Ambos lados de la ecuación son idénticosy esto sugiere que es posible asignar cualquier valor a x para satisfacer la ecuación. Si se trata de aislar xen el lado izquierdo de la ecuación, al sustraer 2xen ambos lados se tiene como resultado
Esto es una identidad, que también señala que se puede asignar cualquier valor a la variable x. ❑
6 6
XAMPLE
2(x3)2x6 2x62x6 XAMPLE
x32x6 2
1 4
XAMPLE
510
1 4
XAMPLE
2x52x102x2x
1 4
XAMPLE
2x5102x
Resuelva las siguientes ecuaciones de primer grado:
Respuesta: a) 3, b) cualquier número real,c) no hay valores.
a) 4x 10 8 2x b) x 5 ( 2x 10)
2
c) 3x 3 3x 5
Ejemplo 3
Ejemplo 2
Ejercicio de práctica
Sección 1.1 Ejercicios de seguimiento
Resuelva las siguientes ecuaciones de primer grado.
Ecuaciones de segundo grado con una variable
Una ecuación de segundo grado que implica la variable
x
tiene la forma generalizada
ax2bxc0
donde
a
,
b
y
c
son constantes, con la condición adicional de que a
0. Normalmente se
dice que las ecuaciones de segundo grado son
ecuaciones cuadráticas
. Si
a
es igual a
ce-ro, el término
x
2desaparece y la ecuación deja de ser de segundo grado. Éstos son algunos
ejemplos de ecuaciones de segundo grado
Solución de ecuaciones cuadráticas
Una ecuación cuadrática (excluyendo una identidad) puede tener
raíces no reales
,
una raíz
real
o
dos raíces reales
. Es posible utilizar diferentes procedimientos para determinar las
raíces de una ecuación cuadrática. Se analizarán dos de estos procedimientos. En cualquier
caso, el primer paso consiste en volver a escribir la ecuación en la forma
ax
2bx
c
0.
Método de factorización.
Si se puede factorizar el lado izquierdo de la ecuación
cuadrá-tica, será muy fácil identificar las raíces. Considérese la ecuación cuadrática
2 2 2 2 2 2
x24x0
XAMPLE
2
2
2
6x22x10
3x212
2x215x9
2
2
XAMPLE
2
1. x52x8 2. 182x83x
3. 2x46x 4. 5x12 163x
5. 2(x8)3(x4) 6. 5(3x)3(5x)
7. 162t4t12 8. 8y106y20
9. 35t3t5 10. 10y2 6y4
11. 3t104t6 12. 3(2t8)4(2t)
£Î° £{° Ý È® x ÓÝ® Ó ä
È x Ó Ç
£x° Ì Î
Ó Ì Î { n Ì Î Ó £È° Î Ý Ó Ý Î Ó £Ç° Û
Ó Î x
Û Ó £n° { Ý Î Ý Ó £° Ì Î®ÉÓ { ÎÌ®É{ Óä° ÎÝ Ó® Ý Î®ÉÓ
Ó£° ÓÞ £® ÎÞ £® x Þ ÓÓ° Î£Ó Ý® £È Ó
Óΰ ÎÝ Ó® {Ó Ý® Ý ÓÝ £® Ó{° ÎÝ £ Ó Ý {® ÎÝ
Ý Ý
1.2 Ecuaciones de segundo grado con una variable
9
Se puede factorizar el lado izquierdo de la ecuación, lo que da como resultado
La forma factorizada de la ecuación sugiere que el producto de los dos términos es igual
a 0. El producto equivaldrá a 0 si cualquiera de los dos factores es igual a 0. Para esta
ecuación, el primer factor equivale a 0 cuando
x
0 y el segundo factor es igual a 0
cuan-do
x
4. Por tanto, las dos raíces son 0 y 4.
Determine las raíces de la ecuación
SOLUCIÓN
Se puede factorizar el lado izquierdo de la ecuación obteniendo como resultado
Al establecer cada factor igual a 0, se descubre que hay una raíz para la ecuación y ésta ocurre
cuan-do x 3. ❑
Fórmula cuadrática.
Cuando no se puede factorizar la ecuación cuadrática o si no es
po-sible identificar los factores, puede aplicarse la
fórmula cuadrática
para identificar todas
las raíces de una ecuación de la forma
(1.1)
Dados los valores para
a
,
b
y
c
, la fórmula cuadrática es
(1.2)
Los ejemplos siguientes ilustran el uso de la fórmula.
Dada la ecuación cuadrática x2 2x48 0, los coeficientes son a1, b 2 y c= 48. Al sustituir estos coeficientes en la fórmula cuadrática, las raíces de la ecuación se calculan así
2
2
XAMPLE
2
x(2)√(2)
24(1)(48)
2(1)
2√4192
2
2√196
2
214 2 16 2 12 2 XAMPLE 2 2 2
x b √b2 4ac
2a
2
2
ax2bxc0
2 XAMPLE 2 2 16 2 12 2 XAMPLE 2 2 2 2 2 2 2 XAMPLE 2
(x3)(x3)0
2 2 2 2 2 XAMPLE
x26x90
2
2
2
2
2
x(x4)0
XAMPLE
2
Ejemplo 4
Ejemplo 5
CAPÍTULO 1 Algunos conocimientos preliminares
10
Al usar el signo más, se obtiene
Al utilizar el signo menos, se tiene
Por consiguiente, 8 y 6 son los dos valores reales de xque satisfacen la ecuación cuadrática.
Encontrar las raíces de la ecuación x22x1 0, a1, b= 2 y c1. Al sustituir los valores en la fórmula da como resultado
Puesto que el radicando equivale a cero, al aplicar el signo se obtiene la misma raíz, 1.
Encontrar las raíces de la ecuación x2x10, a1, b 1 y c10. La sustitución en la fórmula cuadrática da
Ya que no hay raíz cuadrada real de –39, se concluye que no hay valores de xque satisfagan la
ecua-ción cuadrática. ❑
XAMPLE
2
x(1)√(1)
24(1)(10)
2(1)
1√140
2
1√39
2 2 2 2 2 2 2 2 2 XAMPLE 2 2 16 2 12 2 XAMPLE 2
x(2)√(2)
24(1)(1)
2(1)
2√44
2
20
2
1
x 2 14
2
12
2 6
x 2 14
2
16
2 8
Ejemplo 6
Ejemplo 7
Resuelva las siguientes ecuaciones de primer grado:
a
)
x
23
x
2
0
b
) 3
x
22
x
5
0
c
)
x
210
x
25
0
Respuesta:a) x 1, 2, b) no hay valores, c) x 5.
Ejercicio de práctica
1.3 Las desigualdades y su solución
11
La expresión debajo del radical de la fórmula cuadrática,
b
24
ac
, recibe el nombre
de
discriminante.
Obsérvense las generalizaciones siguientes con respecto del
discrimi-nante y las raíces para ecuaciones de segundo grado.
Interpretaciones del discriminante
Para una ecuación cuadrática de la forma
ax
2bx
c
0.
I
Si b
24ac
0, hay dos raíces reales.
II
Si b
24ac
0, hay una raíz real
.
III
Si b
24ac
0, no hay raíces reales.
Sección 1.2 Ejercicios de seguimiento
Resuelva las siguientes ecuaciones cuadráticas utilizando la factorización.
Las desigualdades y su solución
Esta sección estudia las
desigualdades
, la
notación de intervalo
y la
solución de
desigual-dades
.
Desigualdades
Las
desigualdades
expresan la condición de que dos cantidades no son iguales. Una
mane-ra de expresar esta condición es mediante el uso de los
símbolos de desigualdad
< y >. La
tabla siguiente ilustra el uso y la interpretación de estos símbolos:
1. x2 x 12 0 2. x2 36 0
3. x2 2x 1 0 4. x2 3x 10 0
5. x2 3x 4 0 6. t2 2t 8 0
7. 2t2 9t 4 0 8. 5r2 2r 3 0
9. 6y2 9y 6 0 10. x2 10x 25 0
11. r2 16 0 12. 3t2 9t 6 0
13. x2 2x 15 0 14. 2x2 x 1 0
15. 4y2 18y 10 0 16. x2 10x 21 0
Resuelva las siguientes ecuaciones cuadráticas usando la fórmula cuadrática.
17. x2 8x 12 0 18. x2 12x 36 0
19. r2 2r 1 0 20. t2 2t 1 0
21. x2 x 20 0 22. x2 3x 5 0
23. x2 3x 10 0 24. 9x2 3x 2
25. 2x2 2 2x 26. 3r2 14r 8
27. x2 2x 2 28. 4t2 3t 1
29. y2 2 2y 30. x2 4x 5 0
31. x2 2x 5 32. 2x2 32 0
–10
–1 < 3
–9 –8 –7 –6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 6 < 7
–6 < –3
Estas desigualdades son
desigualdades estrictas
, puesto que los elementos que se
compa-ran nunca son iguales entre sí. El caso
a
) ilustra una
desigualdad absoluta
, la cual siempre
es verdadera. Una
desigualdad condicional
sólo es verdadera en ciertas situaciones. La
desigualdad del caso
b
) es verdadera cuando la variable
x
tiene un valor mayor que 100. Si
x
150, la desigualdad es verdadera; si
x
25, la desigualdad no es verdadera. El caso
c
) ilustra lo que se denomina una
doble desigualdad
.
Un uso de las desigualdades es facilitar la comparación de números. La figura 1.1 ilustra
la
recta de los números reales
.
Dados dos números reales a
y b, si a
< b, significa que a
cae
a la izquierda de b
en la recta de los números reales
. En la figura 1.1 se presentan
ejem-plos de desigualdades.
Desigualdad
Interpretación
a) 3 5 “3 es menor que 5”
b) x100 “el valor de xes mayor que 100”
c) 0 y10 “el valor de yes mayor que cero y menor que 10”
Desigualdad
Interpretación
a) x3 15 “la cantidad (x3) es mayor que oigual a 15” b) y x “el valor de yes menor que oigual al valor de x”
a
es menor que
b
.
b
es mayor que
a
.
a
b
b
a
b
a
0
a
b
0
a
cae a la izquierda de
b
en la recta de los números reales.
b
cae a la derecha de
a
en la recta de los números reales.
Figura 1.1 (6 es izquierda de 3) (1 es izquierda de 3) (6 es izquierda de 7)