Sobre las Matrices de Pascal

Texto completo

(1)Sobre las Matrices de Pascal. Hugo Alejandro Villanueva Dı́az. Universidad Distrital Francisco José de Caldas Facultad de Ciencias y Educación Bogotá, Colombia 2015.

(2)

(3) Sobre las Matrices de Pascal. Hugo Alejandro Villanueva Dı́az. Trabajo de grado presentado como requisito para optar al tı́tulo de: Matemático. Directora: MSc Verónica Cifuentes Vargas. Semillero de Investigación: ITENU. Universidad Distrital Francisco José de Caldas Facultad de Ciencias y Eduación Bogotá, Colombia 2015.

(4)

(5) Nota de aceptación:. Firma del Director. Firma del Jurado. Bogotá D.C, Octubre de 2015.

(6)

(7) A mi novia amada Mircia, tu compañı́a es un regalo bendito del Eterno, con el cual he podido conocer la maravillosa gracia de amar..

(8)

(9) Agradecimientos Agradezco primero que todo a mi Padre Eterno; en su infinito amor y gracia, siempre dispone lo mejor para mi vida y me ayuda crecer en todo aspecto personal, a Él sea la gloria siempre. A mi madre por su continuo sacrificio y ánimo durante todo este tiempo, a mi padre por su incondicionalidad y apoyo abnegado durante el proceso. A mi novia que con su cariño y compañı́a me ha demostrado su gran valor. A mi amigo y casi hermano Pedro Fernandez por el tiempo compartido y su confianza; a mis amigos Edwin Castillo y Juan Pablo Mojica, personas con las cuales compartı́ excelentes momentos durante la carrera. Dirijo mi gratitud en especial, a la profesora Verónica Cifuentes, por su dirección, consejo y paciencia en el emprendimiento este proyecto..

(10)

(11) xi. Introducción. El artı́culo Pascal Matrices muestra cuatro demostraciones interesantes con distintos enfoques para determinar la representación del triángulo de Pascal como matrices simétricas, triangulares inferiores y triangulares superiores, (la primera como producto de las dos últimas). Cada demostración se trabajará en un capitulo distinto. La primera de ellas se puede apreciar esta representación como un producto de matrices con coeficientes binomiales en sus entradas. La segunda ofrece una deducción de este tipo de matrices, mediante el estudio de un grafo encolado, contando sus caminos. La tercera muestra una recursión utilizando la eliminación de Gauss para obtener las tres matrices. La última, sin duda, la más especial de las cuatro; mediante matrices infinitas y criterios de convergencia demuestra la igualdad del producto. Este trabajo manejará los preliminares en cada capı́tulo, ya que cada demostración abarca ramas distintas de las matemáticas..

(12) xii. Planteamiento del problema El triángulo de Pascal es sin duda una de las construcciones de la matemática que de forma sutil, desarrolla complejos y estructurados resultados en las matemáticas. Dentro de sus fascinantes propiedades internas y sus interesantes aplicaciones se hace necesario mirar esta representación de coeficientes binomiales,vista de una forma matricial para observar que ventajas se puede obtener en el entorno de este enfoque. De acuerdo con el trabajo de (Edelman y Strang, 2004) existen ciertas formas que permiten llegar a la representación matricial del triángulo de Pascal y del mismo modo partiendo de una de ellas, fundamentar una aproximación a la teorı́a de representaciones del grupo de Möbius, aprovechando la forma y recursos matemáticos que ofrecen las construcciones de este tipo de matrices. Teniendo en cuenta este trabajo y la elaboración de las construcciones de dichas formas para llegar a la representación del triángulo de Pascal de manera matricial, surge un interrogante propicio para el desarrollo del trabajo presente: ¿Cuáles son los conceptos de la teorı́a matemática que son necesarios para llevar a cabo la reconstrucción argumentativa del trabajo de Edelman y Strang sobre la representación del triángulo de Pascal en forma matricial?.

(13) xiii. Justificación El triángulo de Pascal se presenta como una forma especial de organizar y representar los coeficientes binomiales en diferentes situaciones, entre ellas, al expandir un binomio a cualquier potencia entera positiva n, al realizar estudios de probabilidad mediante la distribución binomial, al desarrollar la derivada de un producto de dos o más funciones, entre otros. Esta organización de dichos coeficientes se torna más interesante cuando se ve como una matriz. Observar el triángulo de Pascal en un contexto matricial, puede ser de ayuda, para optimizar el uso de las propiedades ya conocidas del famoso triángulo y a su vez descubrir propiedades ocultas en este. Dentro de los estudios de (Edelman y Strang, 2004) en el cual se basa este trabajo, se aprecia una prueba efectiva de la anterior afirmación; en las cuatro demostraciones para la obtención de esta clase de matrices, la cuarta muestra una interesante conexión entre la representación de los grupos de Möbius y las matrices en las cuales este trabajo centra su atención: al mirar un binomio con potencia entera positiva (x + y)n a manera de funcional, las matrices asociadas a estos son de tipo Pascal. Al reflexionar sobre esto, inmediatamente se piensa en el hecho de un desarrollo sorpresivo de la teorı́a matemática donde el triángulo de Pascal es aplicado utilizando dicho enfoque matricial. Adicionalmente se concibe la emocionante posibilidad de conectar otras ramas de las matemáticas insospechadas con este interesante artilugio matricial de coeficientes binomiales..

(14) xiv. Objetivos Objetivo General Describir de manera detallada la generación de las matrices de Pascal mediante cuatro métodos: multiplicación matricial utilizando coeficientes binomiales, el conteo de caminos de un grafo dirigido, la recursión de Pascal y la observación de los coeficientes de (x + y)n con un significado funcional. Objetivos Especı́ficos. Presentar los argumentos inmersos en el artı́culo [6] de las cuatro demostraciones de la obtención de la matrices de Pascal. Explicar los elementos del álgebra lineal y la teorı́a de grafos que se utilizaron en la construcción de las matrices de pascal. Ilustrar la teorı́a con variados ejemplos..

(15) Contenido Introducción Planteamiento del problema. XI. XII. Justificación. XIII. Objetivos. XIV. 1. Matrices de Pascal mediante multiplicación de matrices 1.1. Conceptos previos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.2. Multiplicación de matrices de Pascal . . . . . . . . . . . . . . . . . . . . . .. 2 2 6. 2. Contando caminos de un grafo dirigido 2.1. Grafos dirigidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.2. El conteo de caminos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 9 9 13. 3. La recursión de Pascal 3.1. Eliminación gaussiana . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.2. Matrices de eliminación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.3. Matrices de Pascal, como producto de matrices bloque. . . . . . . . . . . . .. 19 19 21 25. 4. Igualdad de Funciones 4.1. Serie geométrica y matrices infinitas . . . . . . . . . . . . . . . . . . . . . . . 4.2. El producto de las matrices infinitas de Pascal . . . . . . . . . . . . . . . . .. 27 27 32. 5. Conclusiones. 37. A. Triángulo de Pascal A.1. Una breve historia del triángulo . . . . . . . . . . . . . . . . . . . . . . . . . A.2. Aplicaciones del triángulo . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 38 38 43. Bibliografı́a. 46.

(16) 1. Matrices de Pascal mediante multiplicación de matrices Al realizar el producto de una matriz triangular inferior con coeficientes binomiales como entradas ubicadas apropiadamente, con su transpuesta (que es una matriz triangular superior); se obtiene una matriz simétrica que de igual forma a las anteriores, contiene coeficientes binomiales como entradas. Para exponer este resultado, a continuación se considerará de manera previa ciertos conceptos teóricos que son necesarios para obtener los resultados de este capı́tulo. En primera instancia se consideraran los conceptos binomiales y su arreglo como triángulo de Pascal, posteriormente se tomará en cuenta la definición de matriz y la forma de organizar los coeficientes binomiales en estas. Por último aplicando el producto de matrices y utilizando el teorema del binomio se procederá a realizar la demostración de esta primera parte.. 1.1.. Conceptos previos. En [12] se define Definición 1.1 (Coeficientes Binomiales). Sean n y r enteros no negativos. El coeficiente ( ) ( ) n! binomial nr es definido por nr = r!(n−r)! si n ≤ r, y es 0 de otra manera. ( ) Definición 1.2 (Triángulo de Pascal). Los distintos coeficientes nr , donde 0 ≤ r ≤ n pueden arreglarse en forma de un triángulo, llamado triángulo de Pascal como sigue: (0). (3) (4 ) 0. 0. (1). 0. (1 ). (2). 0. (2). 1. (2 ). 0. (3). 1. (3 ). 2. (3). (4). 1. (4). 2. (4 ). 3. 1. 2. 3. (4) 4. Triángulo de Pascal Aplicando la definición 1.1 al desarrollar los coeficientes binomiales en componentes del triángulo, se genera:.

(17) 1.1 Conceptos previos. 3 1 1 1. 2. 1 1. 1 1. 3 4. 3 6. 1 4. 1. Desarrollo por coeficientes binomiales Teorema 1.1 (Teorema del Binomio). Sean x, y cualesquiera números reales y n cualquier entero negativo. Entonces n ( ) ∑ n n−r r n (x + y) = x y r r=0 Una interesante demostración de este teorema se puede encontrar en [12], en la página 37. Definición 1.3 (Término constante). En un binomio de la forma (1 + x)n , se llama término constante, al coeficiente binomial que acompaña a la expresión x0 Ahora los postulados del álgebra lineal, en referencia a [9] Definición 1.4. Una matriz (m + 1) × (n + 1) es un arreglo rectangular de números . a00 a10 .. .. ··· ···. a01 a11 .. .. a0(n+1) a1(n+1) .. .. .         a(m+1)0 a(m+1)1 · · · a(m+1)(n+1) Las ”lı́neas”horizontales se llaman filas y las ”lı́neas”verticales se llaman columnas. Una matriz m × n tiene m + 1 filas y n + 1 columnas. La i−ésima fila de la matriz dadas es [ ] ai0 ai1 · · · ai(n+1) y la j−ésima columna es . a0j a1j .. .. .         a(m+1)j Los números aij se llaman componentes o entradas de la matriz..

(18) 4. 1 Matrices de Pascal mediante multiplicación de matrices. Teniendo en cuenta el concepto de matriz, hay ciertos aspectos que se deben considerar para el desarrollo del trabajo presente: cuando la matriz tiene igual número de filas y de columnas es decir m = n, la matriz se denomina cuadrada. En las matrices cuadradas, las entradas de la forma aii se les conoce como diagonal principal. Conociendo que es una matriz cuadrada, a continuación se definirán tres casos particulares de estas matrices. Definición 1.5. Una matriz cuadrada en la cual todas las componentes que están por encima de la diagonal principal son ceros, se llama matriz triangular inferior.  a00 0  a10 a11      .. .. . .  .  . . an0 an1 · · · a(n+1)(n+1) . Una matriz cuadrada en la cual todas las componentes que están por debajo de la diagonal principal son ceros, se llama matriz triangular superior.   a00 a01 · · · a0(n+1)  a11 · · · a1(n+1)      .. . .   . . 0. a(n+1)(n+1). Definición 1.6. La transpuesta de una matriz (m + 1 × n + 1) A = aij es la matriz AT , AT = bij con orden (n + 1 × m + 1) donde bij = aji . Una matriz cuadrada A, tal que A = AT , se dice que es simétrica. Definición 1.7. [Matrices de Pascal] Son matrices1 simétricas, triangulares inferiores o triangulares superiores que contienen los coeficientes del triángulo de Pascal en una forma. 1. Como las componentes de las matrices aquı́ trabajadas son coeficientes binomiales, en las matrices triangulares inferiores las posiciones de sus entradas, también determinaran su expresión como número combinado () es decir: ji = aij.

(19) 1.1 Conceptos previos. 5. matrices n × n Sn , Ln y Un como sigue: (j ) (n−1)  ··· ··· 0 (1+j ) (n0 )  ··· · · ·  1 1 .. .. ..  ... . . .  (i+n−1)  (i+j )  ··· ···  i i .. .. ..  .. . . . .  (n−1+j ) (2(n−1)) ··· ··· n−1 n−1 n−1 n−1   (0) 0 (1)   (01)   (0) 1) ) ( (   2 2 2   0 1 2   . . . ..   .. . . . . . Ln =  ( )  ( ) ( ) ( )   i i i i   0 · · · 1 2 j   . .. .. .. .. ..   . .  ( . ) ( . ) ( . ) . ( . ) ( ) n−1 n−1 n−1 n−1 n−1 ··· · · · n−1 0 1 2 j ( ) ( ) ( ) (j ) (n−1) 0 1 2 · · · · · · 0 ) (0j ) (n−1  0 (01) (02)  · · · · · ·   1 1 1 1 ( ) ( ) ( )  2 j n−1    ··· 2 ··· 2 2   . .. ..  ..  . .. . .  Un =  ( ) ( )  j n−1    · · · j j   ..   .. . .  (n−1) 0 n−1. conveniente. Estas truncaciones producen ( 1)  (0 ) 0 (20)  (1 )  1 1  .. ..  . .  Sn =  (i) (i+1)  i i  .. ..  . . (n−1) ( n ). Definición 1.8. Sea A = aij una matriz (m + 1) × (n + 1) y sea B = bij una matriz (n + 1) × (r + 1). El producto AB se define como la matriz (m + 1) × (r + 1), AB = cij , donde el elemento cij de la matriz AB se define como cij = ai0 b0j + ai1 b1j + ... + ai(n−1) b(n−1)j para i = 0, 1, ..., m y j = 0, 1, ..., r. Este producto está definido si y solo si el número de columnas de la matriz A es igual al número de de filas de la matriz B.          . a00 a10 .. .. a01 a11 .. .. ··· ···. a0(n−1) a1(n−1) .. .. ai0 .. .. ai1 .. .. ···. ai(n−1) .. .. a(m−1)1 a(m−1)1 · · · a(m−1)(n−1).          .     . b00 b10 .. .. b01 b11 .. .. ··· ···. b0j b1j .. .. ··· ···. b1(r−1) b2(r−1) .. .. b(n−1)0 b(n−1)1 · · · b(n−1)j · · · b(n−1)(r−1).    = .

(20) 6. 1 Matrices de Pascal mediante multiplicación de matrices          . c00 c10 .. .. c01 c11 .. .. ··· ···. c0j c1j .. .. ··· ···. c0(r−1) c1(r−1) .. .. ci0 .. .. ci1 .. .. ···. cij .. .. ···. ci(r−1) .. ..          . c(m−1)1 c(m−1)2 · · · c(m−1)j · · · c(m−1)(r−1). 1.2.. Multiplicación de matrices de Pascal. Si se observa las definiciones 1.7 y 1.1, en el caso particular cuando n = 4 se generan las siguientes matrices. (0) (01)  S4 = (12)  2 (3 ) 3. (1) (02) (13) (24). (2) (03) (14) (25). 3. 3.  1  1 S4 =  1 1. (0)  (0) (1) (2) (3) 0 0 0 (04) (10) (1)   0 (01) (02) 0 0    0 1 (15) L4 = (02) (12) (2) (12)  U4 =  0 0 0     2 (26) (03) (13) (23) (3) 0 0 0 3 0 1 2 3 1 2 3 4. .  1 1 1   3 4 1  L4 =  6 10 1 10 20 1. 0 1 2 3. 0 0 1 3.   0 1   0 0  U4 =  0 0 1 0. 1 1 0 0. 1 2 1 0. (3) (03) (13)   (23) 3. . 1  3  3 1. Es notable en este ejemplo, que la matriz U4 es la transpuesta de L4 y S4 = L4 U4 , lo que permite generalizar este resultado para cualquier n por medio del siguiente teorema: Teorema 1.2 (Multiplicación de matrices de Pascal). Sea Ln una matriz de Pascal y sea Un = LTn , entonces: Ln Un = Sn Demostración. Sin pérdida de generalidad, tomando la i−ésima fila de la matriz Ln y la j−ésima columna de la matriz Un , como lo especifica la definición 1.7 y aplicando la multiplicación de matrices, se llega a la equivalencia: ( ) j 0) (  j    n−1 ( )( ) [( ) ( ) ( ) ] ( i ) (1j ) ∑ i j i i i  ··· j  (1-1) 0 1 2  2.  = k  .  k=0 k ( . ) j j. Se mostrará que la igualdad 1-1 se puede apreciar como entrada de 1.7, ya que es la entrada de la matriz Sn respecto a su posición en la fila i y columna j y tiene como coeficiente.

(21) 1.2 Multiplicación de matrices de Pascal. 7. ( ) binomial i+j . i Realizando la expansión de la suma en 1-1: n−1 ( )( ) ∑ i j k=0. k. k. ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) i j i j i j i j i j = + + +···+ +···+ 0 0 1 1 2 2 j j n−1 n−1. Puesto que para k > j y k > i, los coeficientes binomiales son 0, la igualdad 1-1 queda reducida a la siguiente expresión: mı́n(i,j) (. ∑ k=0. i k. )( ) ( ) j i+j = k i. (1-2). Por lo tanto el teorema se demostrará, probando 1-2. Para tal efecto se partirá de la siguiente identidad polinomial: (1 + x−1 )i (1 + x)j = = = = = =. (1 + x1 )i (1 + x)j )i (1 + x)j ( x+1 x ( x1 (1 + x))i (1 + x)j ( x1 )i (1 + x)i (1 + x)j x−i (1 + x)i (1 + x)j x−i (1 + x)i+j. Luego (1 + x−1 )i (1 + x)j = x−i (1 + x)i+j. (1-3). Empleando el teorema del binomio en el lado izquierdo de 1-3, se obtiene: (∑ ( ) ) (∑ ( ) ) i j i j i−l l i−k −k (1 + x−1 )i (1 + x)j = 1 x 1 x l (∑k=0 (k) ) (∑ (l=0 ) l) i j i j −k = x x k=0 l=0 ∑i ∑kj ( i ) −k (j ) l l = x l x (ki )(j ) l−k ∑k=0 ∑l=0 i j = k=0 l=0 k l x El término constante del lado izquierdo de la identidad se da cuando l −k = 0, esto es cuando k = l por ende el coeficiente binomial serı́a mı́n(i,j) ( )( ) i ( )( ) ∑ ∑ i j k−k i j x = k k k k k=0 k=0. Análogamente expandiendo la parte derecha de 1-3: ∑i+j (i+j ) i+j−r r 1 x x−i (1 + x)i+j = x−i r=0 ∑i+j (i+j ) rr −i = r=0 ( r )x x ∑i+j i+j xr−i = r=0 r. (1-4).

(22) 8. 1 Matrices de Pascal mediante multiplicación de matrices. El término constante de la expansión del binomio anterior, se tiene si r − i = 0 lo que implica que r = i, en consecuencia el término constante del lado derecho de 1-3 es: ( ) ( ) i + j i−i i+j x = (1-5) i i Al igualar 1-4 con 1-5, se ha demostrado con éxito 1-2. En conclusión Ln Un = Sn.

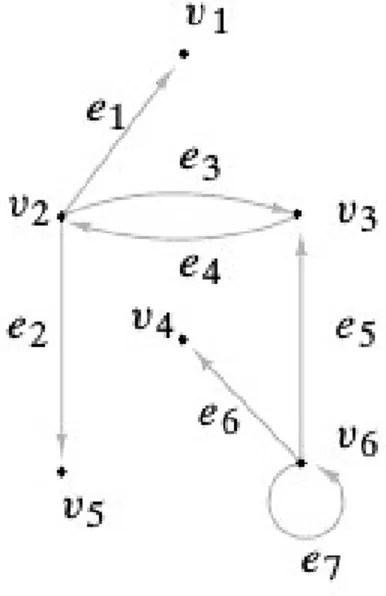
(23) 2. Contando caminos de un grafo dirigido La siguiente demostración es un ejemplo interesante donde se puede apreciar una elegante aplicación del triángulo de Pascal en la teorı́a de grafos. Dicho ejemplo en forma especı́fica mostrará el conteo de caminos de un grafo dirigido para deducir la expresión S = LU . EL fundamento de ello será la famosa identidad de Pascal, la cual entablara la asociación entre las matrices de Pascal y este grafo.. 2.1.. Grafos dirigidos. En la teorı́a acorde en [11], se encuentra: Definición 2.1. Un grafo G = (V, E) se trata de un conjunto V de vértices y un conjunto E de aristas de tal forma que cada arista e ∈ E esta relacionada con un par ordenado de vértices. Si existe una arista única e que se relaciona con el par ordenado (u, w) de vértices, se denota como la arista que va de v a w, como e = (u, w). En el caso que una arista e en un grafo que se relaciona con el par de vértices v y w se dice que es incidente sobre v y w, y cuando v y w son incidentes sobre e se dice que son vértices adyacentes..

(24) 10. 2 Contando caminos de un grafo dirigido. Figura 2-1.: Grafo dirigido Definición 2.2. Sean v0 y vn vértices en una gráfica. Una trayectoria o camino de longitud n es una sucesión alternante de n + 1 vértices y n aristas que comienza en el vértice v0 y termina en el vértice vn , v0 , e1 , v1 , e2 , v2 . . . , vn−1 , en , vn , de tal modo que la arista ei es incidente sobre los vértices vi−1 y vi para i = 1, . . . , n. Definición 2.3 (Principio de la multiplicación). Si una actividad se puede ejecutar en t pasos sucesivos y el paso 1 se puede realizar de n1 maneras, el paso 2 se puede realizar de n2 maneras, . . ., y el paso t de nt formas, entonces el número de actividades posibles diferentes es de n1 · n2 · · · nt . Definición 2.4 (Permutación). Una permutación de n elementos diferentes x1 , . . . , xn es un ordenamiento de los n elementos x1 , . . . , xn . Teorema 2.1. Existen n! permutaciones de n elementos. Demostración. Haciendo uso del principio de la multiplicación. Una permutación de n elementos se construye en n pasos sucesivos; se elige el primer elemento; se el segundo elemento, ası́ en lo sucesivo hasta el último elemento. El primer elemento se puede seleccionar de n maneras. Una vez elegido, el segundo elemento se puede seleccionar n − 1 maneras. Una vez elegido, el tercer elemento se puede selecciona den − 2 maneras, y ası́ sucesivamente. Por el principio de la multiplicación, existen n(n − 1)(n − 2) · · · 2 · 1 = n! permutaciones de n elementos..

(25) 2.1 Grafos dirigidos. 11. Definición 2.5. Una permutación r de n elementos distintos x1 , . . . , xn es un ordenamiento de r elementos de [x1 , . . . , xn ] . El número de permutaciones r de un conjunto de n elementos diferentes se denota P (n, r). Teorema 2.2. El número de permutaciones r de un conjunto de n objetos diferentes es P (n, r) = n(n − 1)(n − 2) · · · (n − r + 1),. r≤n. Demostración. Se debe contar el número de maneras de ordenar r elementos seleccionados de un conjunto de n elementos. El primer elemento se puede elegir de n maneras. Ya elegido el primer elemento, el segundo elemento se puede seleccionar de (n − 1) formas. Al continuar con la elección de elementos hasta haber elegido el elemento r − 1, se pasa al elemento r que se puede seleccionar de n − r + 1 formas. Por el principio de multiplicación, el número de permutaciones r de un conjunto de n objetos distintos es n(n − 1)(n − 2) · · · (n − r + 1). Corolario 2.1. El número de permutaciones P (n, r) se puede expresar de la forma n! (n − r)! Demostración. Por el teorema anterior P (n, r) = n(n − 1)(n − 2) · · · (n − r + 1) lo que serı́a igual a P (n, r) =. n(n − 1) · · · (n − r + 1)(n − r) · · · 2 · 1 n! = (n − r) · · · 2 · 1 (n − r)!. Definición 2.6. Dado un conjunto X = {x1 , . . . , xn } Una combinación r de X es una selección no ordenada de r elementos de X, dicho de otro modo, un subconjunto de X con r elementos. El número de combinaciones r de un conjunto de n elementos distintos se denota por ( ) C(n, r) o nr . Teorema 2.3. El número de combinaciones de r de un conjunto de n objetos distintos es ( ) n! n P (n, r) = r ≤ n. C(n, r) = = r r! (n − r)!r!.

(26) 12. 2 Contando caminos de un grafo dirigido. Demostración. Contando el número de permutaciones r de un conjunto de n elementos de dos maneras. La primera usa la fórmula P (n, r). La segunda cuenta el número de permutaciones de un conjunto de n elementos implica C(n, r). Al construir r permutaciones de un conjunto X de n elementos en dos pasos sucesivos: primero, se elige una combinación r de X es decir, un subconjunto no ordenado de r elementos; segundo, se ordena. EL principio de multiplicación dice que el número de permutaciones r es el producto del número de combinaciones r por el número de ordenamientos de r elementos; es decir, P (n, r) = C(n, r)r!. Por lo tanto, P (n, r) n! = r! (n − r)!r! El extremo derecho de la igualdad anterior se justifica mediante el corolario 2.1. C(n, r) =. Teorema 2.4. [Identidad de Pascal] Sea n y r enteros positivos, donde r ≤ n. Entonces ( ) ( ) ( ) n n−1 n−1 = + . r r−1 r Demostración. Se comprobará que el lado derecho de la ecuación es igual al lado izquierdo de esta: (n−1) (n−1) (n−1)! (n−1)! + r = (r−1)!(n−r)! + r!(n−r−1)! r−1 r(n−1)! (n−r)(n−1)! = r(r−1)!(n−r)! + r!(n−r)(n−r−1)! r(n−1)! + (n−r)(n−1)! = r!(n−r)! r!(n−r)! (n−1)![r+(n−r)] = r!(n−r)! (n−1)!n = r!(n−r)! n! = r!(n−r)! (n ) = r . Lema 2.1. Sea n y r enteros positivos, donde r ≤ n. Entonces: ( ) ( ) n n = . r n−r Demostración. En efecto dado que: ( n ) n−r. Por lo que queda demostrado el lema.. n! = (n−r)!(n−(n−r))! n! = (n−r)!r! n! = r!(n−r)! (n ) = r ..

(27) 2.2 El conteo de caminos. 13 b3. b2. b1. b0. 2.2.. a0. a1 a2 a3 Figura 2-2.: Grafo dirigido. El conteo de caminos. La figura 2-2 muestra un grafo dirigido que tiene como propósito contar el número de rutas posibles, entre un punto ai con i ≥ 0 del costado inferior del grafo hasta un punto bj con j ≥ 0 en el costado izquierdo de este. Como el grafo es dirigido solo es permitido escoger trayectorias donde sus aristas se dirigen hacia la izquierda o hacia arriba. b3. b2. b1. b0. a0. a1 a2 a3 Figura 2-3.: Sección del grafo.. La figura 2-3 permite deducir que la longitud de cualquiera de los caminos en el grafo entre vértices ai y bj estará dada por la expresión i + j por las condiciones de dirección del grafo, mientras se avanza en este, solo existe la posibilidad de tomar i aristas hacia la izquierda y j aristas hacia arriba. La diferencia entre cada camino consiste en el orden de decisión acerca del tipo de arista que se tome. Igualmente la figura indica que el número de trayectorias posibles entre ai y bj será establecido.

(28) 14. 2 Contando caminos de un grafo dirigido. al considerar los dos casos que existen al comienzo de cada camino en el punto ai ; es decir las rutas que empiezan con la arista incidente al vértice ai hacia la izquierda y las rutas generadas por la arista incidente en el mismo vértice hacia arriba. Por consiguiente el total de caminos posibles entre los vértices ai y bj será la suma de todos los caminos establecidos por estos dos casos. El número de trayectorias hacia bj , que empiezan por la arista ai , es igual al número de trayectos existentes entre ai−1 y bj . De manera análoga las rutas que inician hacia arriba de ai , son el total de caminos que hay desde ai a bj−1 ; todo esto por iniciar el conteo en un nivel menos hacia la izquierda de ai y un nivel más hacia arriba de ai respectivamente. En el caso del número de trayectorias que empiezan por la izquierda de ai , si se nota con l a las aristas que van hacia la izquierda y con u las que van hacia arriba. Un trayecto entre ai−1 y bj serı́a: lll . . . }l uuu | {z | {z. . . u} . i−1. j. Lo que indica que la longitud de los caminos de este caso es i − 1 + j, luego el número de todos los recorridos de la situación presente, es la cantidad de posibilidades de escoger las i − 1 aristas hacia la izquierda durante el recorrido. Por esta razón el total de estos trayectos es: ( ) i−1+j (2-1) i−1 De forma similar para el número de trayectorias entre ai y bj−1 : . . . }l . uuu | {z | {z. . . u} lll j−1. i. El total de caminos será: ( ) i+j−1 i. (2-2). Es evidente que solo existe un camino entre cualquier punto ai y b0 . Igualmente para la trayectoria entre a0 y bj . Por otra parte contando los caminos entre ai y aj , considerando los trayectos hacia la izquierda y hacia arriba como lo indica 2-1 y 2-2 a 0 b1 a 1 b1 a 2 b1 a 3 b1. = = = = .. .. 1 (1) (1) + (20) (21) + (31) (32) + 3 2.

(29) 2.2 El conteo de caminos. 15. a 0 b2 a 1 b2 a 2 b2 a 3 b2. = = = = .. .. 1 (2) (2) + (03) (13) + (14) (24) + 3 2. a 0 b3 a 1 b3 a 2 b3 a 3 b3. = = = = .. .. 1 (3) (3) + (40) (14) + (15) (25) + 3 2. a0 bj a1 bj a2 bj a3 bj. = = = = .. .. 1 (j ) (1+j−1) + 0 ) 1 (1+j (2+j−1 ) + 1 2 (2+j ) (3+j−1) + 2 3. Siguiendo la recursión se puede concluir que: ( ) ( ) i−1+j i+j−1 ai bj = + i−1 i Ahora por la identidad de Pascal el resultado anterior se reduce a: ( ) i+j a i bj = i Lo que muestra que el número de caminos desde ai y bj , expresa las entradas de la matriz S de la definición 1.7 ai bj = Sij ai bj = Si−1,j + Si,j−1 . Por consiguiente está es la manera en la cual, las matrices de Pascal están asociadas al grafo estudiado en el apartado presente. Adicionalmente, si se corta el grafo con una linea de 45◦ de inclinación como lo indica la figura 2-4, esta implanta unos nuevos vértices (k, k) en la diagonal del grafo. El propósito ahora será contar los caminos que hay entre ai a (k, k), del mismo modo los trayectos desde (k, k) a bj . De manera similar al caso anterior de la figura 2-2, el número de caminos que hay desde ai a (k, k), será determinado por los caminos que inician con la arista incidente hacia la izquierda de ai y los caminos que comiencen de su arista hacia arriba. Por lo tanto se tendrá que contar los caminos que existen de ai−1 a (k, k) y los trayectos de ai a (k − 1, k − 1) respectivamente..

(30) 16. 2 Contando caminos de un grafo dirigido b3. b2. b1. b0. a0. a1 a2 a3 Figura 2-4.: Grafo cortado. Para los caminos que existentes entre ai−1 y (k, k), tenemos que sus longitudes estará determinada por (i − 1) − k hacia la izquierda y k hacia arriba, por lo tanto la longitud cualquiera de sus trayectos es de: k + ((i − 1) − k) = i − 1. Consecuentemente el total de caminos de la situación presente, será el número de formas de escoger las (i − 1) − k aristas hacia la izquierda en un trayecto de longitud i − 1, lo que es igual a: ( ) i−1 (i − 1) − k Pero por lema 2.1, la expresión anterior se simplificarı́a a: ) ( i−1 (2-3) k Igualmente para los caminos que hay de ai a (k − 1, k − 1): ( ) i i − (k − 1) ( ) i k−1. (2-4). Es fácil ver que existe solo un camino de ai a (0, 0) y solo un camino desde ai a (i, i), si se usa un planteamiento similar al anterior el total del los caminos entre ai a bj será igual a la suma de 2-3 y 2-4: ( ) ( ) i−1 i ai (k, k) = + k k−1.

(31) 2.2 El conteo de caminos. 17. De nuevo por identidad de pascal la igualdad anterior se simplifica a: ( ) i ai (k, k) = . k Por lo tanto el número de recorridos que hay entre los vértices corresponden a las entradas de la matriz L de la definición 1.7 del capitulo previo, dicho de otro modo: ai (k, k) = Lik ai (k, k) = Li−1,k + Li,k−1 . En el conteo de trayectorias desde (k, k) a bj se tiene la particularidad que hay k aristas hacia la izquierda y j − k hacia arriba, por lo tanto, debido a la simetrı́a con el problema anterior, se puede inferir que la longitud de los caminos es dada por j, luego los trayectos que empiezan a izquierda y hacia arriba de (k, k) se plantean respectivamente por las expresiones: ) ( j (2-5) k−1 ( ) j−1 (2-6) k Luego el total de trayectos serı́a: ( j ) (j−1) (k, k)bj = k−1 + k (j ) (k, k)bj = k Esta expresión implica que el número caminos entre ambos vértices, representan las entradas de la matriz U de la definición 1.7 (k, k)bj = Ukj (k, k)bj = Uk−1,j + Uk,j−1 . Finalmente, se debe tomar en cuenta que para cada camino de ai a (k, k), existen Ukj posibilidades para terminar la trayectoria en bj . En otras palabras la expresión Lik Ukj , cuenta el número de caminos que hay desde ai a bj a través del vértice (k, k). Luego la suma sobre k cuenta todas los trayectorias entre los vértices del grafo 2-2, en otras palabras: ∑mı́n(i,j) Si j = Lik Ukj k=0 ( i )( j ) ∑mı́n(i,j) = k=0 k k Lo cual proporciona otra demostración para el teorema 1.2. Ejemplo 2.1. Contar el número de caminos que hay desde el vértice a2 hasta el vértice b2 De acuerdo con el conteo de caminos, esta situación estarı́a representada por la expresión.

(32) 18. 2 Contando caminos de un grafo dirigido ( )( ) ( )( ) ( )( ) S2,2 = 20 20 + 21 21 + 22 22 = 1·1+2·2+1·1 = 1+4+1 = 6. Por tanto hay 6 caminos entre ambos vértices, lo que corresponde a la entrada de la matriz () de Pascal S2,2 = 42 = 6..

(33) 3. La recursión de Pascal El siguiente método de demostración está basado en la reconstrucción de las matrices Pascal mediante la eliminación gaussiana, generando matrices bloque. De manera similar el producto de estas nuevas matrices, también cumplirán el postulado de S = LU en sus respectivos bloques.. 3.1.. Eliminación gaussiana. Como parte del trabajo es necesario definir las condiciones para aplicar el método de eliminación gaussiana. Si se tiene un sistema de ecuaciones lineales de la forma: a00 x0 a10 x0 .. .. + +. a01 x1 s11 x1 .. .. + · · · + a0(n−1) xm−1 = + · · · + s1(n−1) xm−1 = .. .. t0 t1 .. .. a(n−1)0 x0 + a(n−1)1 x1 + · · · + a(n−1) x(m−1) = tn−1 Al considerar el caso cuando el sistema es homogéneo es decir ti = 0 para i = 0, 1, 2, . . . , n−1, entonces la representación matricial del sistema o matriz aumentada será: .  a00 a01 · · · a0(n−1)  a10 a11 · · · a1(n−1)    A= .  .. ..  ..  . . an0 an1 · · · a(n−1)(n−1) De este modo, trabajando con la matriz aumentada se facilitará las operaciones necesarias para el método de eliminación gaussiana 1 . Esta reducción se ejecuta por medio de las operaciones elementales de filas, las cuales son: 1. Multiplicación de una fila de A por un escalar c no nulo. 2. Remplazo de la r− ésima fila de A por la fila i más c veces la fila ju, donde c es cualquier escalar y r ̸= s. 3. Intercambio de dos filas de A 1. En lo común el método es una herramienta para hallar las soluciones de los sistemas de ecuaciones lineales.En lo menester del trabajo solo se utilizará para obtener las matrices de Pascal en bloque..

(34) 20. 3 La recursión de Pascal. Ası́ una operación elemental de filas es un tipo de función que relaciona a una matriz m × n, A, a una matriz m × n, e(A). Se puede notar las operaciones elementales e de forma precisa en los tres casos del siguiente modo: 1. e(A)ij = Aij si i ̸= r, e(A)rj = cArj . 2. e(A)ij = Aij si i ̸= r, e(A)rj = Arj + cAsj . 3. e(A)ij = Aij si i ̸= r y i ̸= s, e(A)rj = Asj , e(A)sj = Arj . Grossman resume el método eliminación: Se reduce por renglón la matriz de coeficientes a la forma escalonada por renglones, se despeja el valor de la última incógnita y después se usa sustitución hacia atrás para las demás incógnitas. [9] Continuando, se debe enunciar dos teoremas que afianzaran los resultados de la demostración mediante matrices de Pascal en bloques, las pruebas de estos teoremas pueden ser revisadas en [10] en las páginas 7 y 8. Estos teoremas son necesarios ya que permiten crear una noción de relación en equivalencia entre matrices y aplicar la teorı́a en estos casos de bloque a un nivel particular. Teorema 3.1. A cada operación elemental de filas e corresponde una operación elemental de filas e1 , del mismo tipo de e, tal que e1 (e(A)) = e(e1 (A)) = A para todo A. Es decir, existe la operación inversa de una operación elemental de filas y es una peración elemental de las filas del mismo tipo. Definición 3.1. Si A y B son matrices m × n, se dice que B es equivalente por filas a A si B se obtiene por una sucesión finita de operaciones fundamentales de filas. Teorema 3.2. Si A y B son matrices equivalentes por filas, los sistemas homogéneos de ecuaciones lineales correspondientes tienen exactamente las mismas soluciones, Definición 3.2. Una matriz m × n, R, se llama reducida por filas si: 1. El primer elemento no nulo de cada fila no nula de R es igual a 1. 2. Cada columna de R que tiene el primer elemento no nulo de 0 En la demostración no se utilizará el método de eliminación gaussiana de forma completa, las operaciones fundamentales serán realizadas en las matrices de Pascal hasta cuando sea 1 la primera entrada de de la primera fila y de la primera columna y los demás elementos de ellas sean 0. Teorema 3.3. Si A es una matriz (n + 1 × n + 1) y B una matriz (n + 1 × n + 1) entonces (AB)T = B T AT.

(35) 3.2 Matrices de eliminación. 21. Demostración. Se define las entradas de AT = cij B T = dij , donde cij = aji y dij = bji . ∑ Entonces la componente (i, j) de B T AT es n+1 k=0 dik ckj . Sean las entradas de AB = eij y de T (AB) = fij , donde fij = eji . Por tanto, f( ij) = eij =. n+1 ∑. aik bkj =. k=0. n+1 ∑ k=0. ckj cik =. n+1 ∑. dik ckj .. k=0. Está última expresión es la componente (i, j) de B T AT , luego (AB)T = B T AT .. 3.2.. Matrices de eliminación. De acuerdo con [2] se define la matrices de eliminación. Estas matrices son fundamentales para el desarrollo de la tercera demostración. Definición 3.3. Se definen las matrices (n + 1 × n + 1) Gn y En mediante: { 1 si j ≤ i Gn (i, j) := 0 si j > i En (i, i) = 1 para i = 0, 1, . . . , n En (i + 1, i) = −1 para i = 0, 1, . . . , n − 1 En (i, j) = 0 si j > i ó j < i − 1 Ejemplo 3.1. Un ejemplo especı́fico  1 0 0  1 1 0 G4 =  1 1 1 1 1 1. para las matrices de la definición 3.3, serı́a G3 y E3 :    0 1 0 0 0    0 1 0 0   −1 E =    4 0 1 0   0 −1 1 0 0 −1 1. La relación entre las matrices de la definición 3.3 puede ser contemplada en el siguiente lema: Lema 3.1. La matriz En es la inversa de Gn . Demostración. Para realizar esta demostración se comprobará que Gn En = I, por tal motivo se considerara los siguientes casos al ejecutar el producto de matrices: i > j. i < j. i=j.

(36) 22. 3 La recursión de Pascal. Es fácil ver que las filas de la matriz Gn tienen valor 1 hasta la entrada (i, i) y en las demás entradas cero, es decir: [. ] [ ] G00 G01 . . . Gii Gi(i+1) . . . Gn = 1 1 . . . 1 0 . . . 0. Para las columnas de la matriz En todas sus entradas son cero, con excepción de (j, j) y (j + 1, j) que son entradas con valor 1 y −1 respectivamente: . E0j E1j .. .. . . 0 0 .. .. .                      Ejj  =  1      E   −1    (j+1)j    .   .   ..   ..  0 Enj Ası́, cuando i > j y al aplicar el producto de matrices se obtiene: . 0 0 .. .. .          [ ]  = 1·0+1·0+. . .+1·1+1·−1+. . .+0·0 = 0. Gn En (i, j) = 1 1 . . . 1 0 . . . 0  1    −1     .   ..  0 Luego: Gn En (i, j) = 0, si i > j. (3-1). Por otro lado si i < j . 0 0 .. .. .          [ ]  Gn En (i, j) = 1 1 . . . 1 0 . . . 0  1   = 1·0+1·0+. . .+0·1+0·−1+. . .+0·0 = 0.  −1     .  .  .  0 Entonces: Gn En (i, j) = 0, si i < j. (3-2).

(37) 3.2 Matrices de eliminación. 23. Con respecto al caso i = j se da que: . 0 0 .. .. .          [ ]  Gn En (i, j) = 1 1 . . . 1 0 . . . 0  1   = 1·0+1·0+. . .+1·1+0·−1+. . .+0·0 = 1.  −1     .   ..  0 Por lo tanto: Gn En (i, j) = 1, si i = j. (3-3). Las igualdades 3-1,3-2 y 3-3, muestran que Gn En = I, lo que confirma que Gn = En−1 . Definición 3.4. Las matriz (n + 1) × (n + 1) de Pascal en bloque se define como: [. 1 0 Ln := 0 Ln−1. ]. Ejemplo 3.2. Un caso particular para estas matrices  1 0 [ ]  1 0 0 1 L4 = = 0 L3 0 1 0 1. en bloque serı́a L4 :  0 0  0 0  1 0 2 1. El siguiente lema, dará a conocer la correspondencia de las matrices en bloque, con las anteriores que se han definido en el capı́tulo presente: Lema 3.2. Para las matrices Gn y Ln se cumple: Gn Ln = Ln para n ≥ 1. Demostración. Para n = 1 se tiene que Ln = In , por lo tanto Gn = Ln . Si n > 1, con la definición de producto entre matrices y las entradas de la matriz Ln , se tendrı́a que llegar a la expresión: Gn Ln (i, j) =. ) i ( ∑ k−1 k=1. j−1. ) ( ) i−1 ( ∑ k i = = = Ln (i, j), j−1 j k=j−1. (3-4).

(38) 24. 3 La recursión de Pascal. De la ecuación 3-4 se encuentra la expresión: ) ( ) i−1 ( ∑ k i = j−1 j k=j−1. (3-5). La cual será demostrada por inducción matemática sobre i. Para k = j − 1 se observa que: ) ( ) j−1 ( ∑ j−1 j =1= j−1 j k=j−1 Si se supone que la igualdad 3-5 se cumple para cierto i = l: ) ( ) l−1 ( ∑ k l = j−1 j k=j−1 Debido a la hipótesis de inducción y por teorema 2.4 se deduce que: ( ) ( ) ( ) l l l+1 + = j j−1 j . Lo cual demuestra 3-5 Para j = 0 se obtiene que Gn Ln (i, j) = 1 = Ln , luego Gn Ln = Ln (i, j). Teorema 3.4. Para las matrices Ln y En se cumple el siguiente resultado: En Ln = Ln Demostración. En efecto, por el lema 3.2 se tiene: Gn Ln = Ln . Multiplicando ambos extremos de la igualdad por En y haciendo uso del lema 3.3, se llega a la igualdad deseada. Ejemplo 3.3. Para las matrices E4 y L4 , usando tado:   1 0 1 0 0 0   1 0 0  1 1  −1 E4 L4 =   1 0  1 2  0 −1 1 3 0 0 −1 1. el teorema 3.4 su producto da como resul   1 0 0 0 0 0    0 0 0 1 0 0  = L4 = 1 0 0 1 1 0 0 1 2 1 3 1. Las entradas de la matriz Ln (i, j) = Lik − Li−1,k , son el resultado de aplicar la eliminación Gaussiana hasta el n − 1 paso, restando la fila i − 1 a la fila i. Produciendo ası́ la matriz bloque Ln−1 ..

(39) 3.3 Matrices de Pascal, como producto de matrices bloque.. 25. Lema 3.3. Las entradas del producto de matrices En y Sn , son asignadas mediante la identidad de pascal: En Sn (i, j) = Sij − Si−1 j Demostración. Usando la definición de producto de matrices:. En Sn (i, j) =. = = =.  (j )  ( 0 )  1+j   1   ..   .  [ ]  (i−1+j )   0, 0, · · · , −1, 1, · · · , 0   (i−1)   i+j   i   .   ..  (n−1+j ) n−1 ( ) (i+j ) − i−1+j + (i+j )i−1 (i−1+j )i − i−1 i Sij − Si−1,j. Finalmente las condiciones están dispuestas para proceder con la tercera demostración.. 3.3.. Matrices de Pascal, como producto de matrices bloque.. Para mostrar que Sn = Ln Un de acuerdo a los preceptos de este capı́tulo, se dará uso de la inducción matemática. Para tal efecto se considera el caso cuando n = 1. De este modo, por la definición 3.4 y por teorema 3.4 se tiene que: [ (E1 L1 )(U1 E1T ). = = = =. ][ ] 1 0 1 0 0 L0 0 U0 [ ][ ][ ] 1 0 1 0 1 −1 −1 1 0 1 0 1 [ ] 1 0 0 1 E1 S1 E1T. Por lo tanto la expresión para k = 1, es verdadera. Asumiendo que la igualdad es válida para k = k − 1, en concordancia Lk−1 Uk−1 = Sk−1 . Por este motivo se puede afirmar lo siguiente:.

(40) 26. 3 La recursión de Pascal [. (Ek Lk )(Uk EkT ). 1 0 = 0 Lk−1. ][. ] [ ] 1 0 1 0 = 0 Uk−1 0 Sk−1. (3-6). Se espera que el último término de la igualdad 3-6, coincida con Ek Sk EkT , para concluir que Lk Un = Sk , por ello, al emplear el lema 3.3 y un razonamiento similar al de este teorema, es posible examinar las entradas de la matriz Ek Sk EkT . Ek Sk (i, j) = Sij − Si−1,j Ek Sk EnT = (Sij − Si−1,j ) − (Si,j−1 − Si−1,j−1 ) Por tanto, al hacer uso de los teoremas 2.4 y 3.3: Ek Sk EkT (i, j) = = = =. (Sij − Si−1,j ) − (Si,j−1 − Si−1,j−1 ) Sij − Si−1,j − Si,j−1 + Si−1,j−1 Si,j − Sij + Si−1,j−1 Si−1,j−1. Por el análisis previo se deduce que: [. Ek Sk EkT. 1 0 = 0 Sk−1. ]. Por esta razón, se puede inferir que (Ek Lk )(Uk EkT ) = Ek Sk EkT , luego por principio de inducción matemática se demuestra que Ln Un = Sn , suministrando una nueva demostración para el teorema 1.2. Ejemplo 3.4. Multiplicar las matrices de Pascal en bloque L4     1 0 0 0 1 0 0 0 1     0 1 0 0 0 1 1 1 0 L4 U4 =   = 0 1 1 0 0 0 1 2 0 0 1 2 1 0 0 0 1 0. y U4 0 1 1 1. 0 1 2 3.  0  1  3 6.

(41) 4. Igualdad de Funciones Sin duda, la más fascinante demostración del teorema 1.2 hasta aquı́ mostrada. Esta demostración combina elementos como la serie geométrica, para mostrar que el principal teorema se cumple para matrices de orden infinito. Como ha sido costumbre en el trabajo, se empezará por definir las herramientas que son necesarias para desarrollar esta última demostración. Para la prueba se trabajará las entradas del producto de matrices, con un andamiaje de series convergentes que son derivables en cualquier orden.. 4.1.. Serie geométrica y matrices infinitas. Sea (fn ) una sucesión de funciones, donde fn : A ⊆ R → R, se define como la serie de como la sucesión de sumas parciales: ∞ ∑. ∑ n. fn. fn = (f1 , f1 + f2 , f1 + f2 + f3 , . . .). n=0. En primera instancia se nombran los conceptos fundamentales para dar desarrollo a la demostración, en lo referido al tema en [3] y [14], se dispone: Definición 4.1 (Serie uniformemente convergente). Si se toma una serie de funciones ∑∞ ∑∞ n=0 fn , como una sucesión de sumas parciales Sn = n=0 xn , en un conjunto A ⊆ R Se dice que Sn , converge uniformemente en A, hacia la función f, si y sólo si: ∀ε > 0, ∃N ∈ N tal que si n ≥ N entonces |Sn − f (x)| < ε, ∀x ∈ A. Definición 4.2. Una sucesión de funciones (fn ) con fn : A ⊆ R → R, se dice que (fn ) es uniformemente de Cauchy 1 si. ∀ε > 0 ∃N ∈ N tal que, si n, m > N entonces |fn − fm | < ε (∀x ∈ A.) Teorema 4.1. Si fn es diferenciable en [a, b] para todo n ∈ N. Si la sucesión de funciones derivadas converge uniformemente en A ⊆ R a una función g, y existe un valor c ∈ [a, b] en el cual fn (c) es convergente, entonces la sucesión fn converge uniformemente a una función f derivable, además f ′ = g. 1. Al igual que ocurre con las sucesiones de números reales, una sucesión es uniformemente de Cauchy si y sólo si es uniformemente convergente..

(42) 28. 4 Igualdad de Funciones. Demostración. El objetivo de la prueba se centra en comprobar que (fn ) es uniformemente de Cauchy. Sea ε > 0. Por definición 4.2 e hipótesis se establece la siguiente desigualdad. |fn (x) − fm (x)| ≤ |(fn − fm )(x) − (fn − fm )(c)| + |(fn − fm )(c)| . Debido al teorema del valor medio del cálculo diferencial, existe un valor z ∈ A que satisface |(fn − fm )(x) − (fn − fm )(c)| = |(fn − fm )′ (z)| |x − c| ≤ |(fn − fm )′ (z)| |b − a| . Por hipótesis la sucesión (fn′ ) es uniformemente de Cauchy, por lo tanto existe N1 ∈ N tal que ε |(fn − fm )′ (y)| ≤ 2(b − a) para n, m > N1 . Asimismo (fn (c)) es convergente, por tanto es de Cauchy luego existe N2 ∈ N de manera que |(fn − fm )(c)| ≤. ε 2. para n, m > N2 . En su totalidad, si n, m > máx {N1 , N2 } entonces ε ε + = ε. 2 2 Es ası́ que fn es uniformemente de Cauchy y ası́ existe el lı́mite uniforme que es f. Ahora se probará que f es diferenciable y f ′ = g. Se considera la siguiente desigualdad, sea x, y ∈ A: |fn (x) − fm (x)| ≤ |(fn − fm )(x) − (fn − fm )(c)| + |(fn − fm )(c)| ≤. fm (y)−fm (x) y−x. − g(x). ≤. fm (y)−fm (x) n (x) − fn (y)−f y−x y−x n (x) + fn (y)−f − fn′ (x) + y−x. |fn′ (x) − g(x)|. (4-1). Sea ε > 0, una vez más por el teorema del valor medio del cálculo diferencial, existe un valor z ∈ A, para el cual se cumple fm (y) − fm (x) fn (y) − fn (x) ′ (z) − fn′ (z)| −→ 0 ≤ |fm − n,m→∞ y−x y−x de este modo, por la convergencia de (fn ) f (y) − fm (x) fn (y) − fn (x) − −→ 0 n→∞ y−x y−x de donde f (y) − fm (x) fn (y) − fn (x) ε < − y−x y−x 3 para algún n suficientemente grande..

(43) 4.1 Serie geométrica y matrices infinitas. 29. Por hipótesis la sucesión (fn′ ) converge uniformemente a g, luego para un n suficientemente grande ε |fn′ (x) − g(x)| < . 3. Ahora es necesario elegir el n suficientemente grande para que se cumplan las dos consideraciones anteriores. Por hipótesis, fn es diferenciable y ası́, existe δ > 0 tal que fn (y) − fn (x) − fn′ (x) y−x si |x − y| < δ. Por tanto, reemplazando las 3 estimaciones anteriores en la desigualdad 4-1 se concluye fn (y) − fn (x) ε ε ε − g(x) < + + = ε y−x 3 3 3 para |x − y| < δ. Ası́ f es diferenciable y f ′ = g. ∑ Teorema 4.2. Sea fn diferenciable [a, b] para todo n ∈ N. Si la serie n fn′ es uniformemente ∑ ∑ convergente a g, y si existe c ∈ [a, b] tal que n fn (c) es convergente, entonces n fn es convergente, su convergencia f es derivable y además f ′ = g, es decir ( )′ ∑ ∑ fn = fn′ . n. n. Demostración. Debido a que fn es diferenciable, entonces también lo son las funciones f1 + . . . + fn que conforman la sucesión de sumas parciales. Por hipótesis, la sucesión (f1 + . . . + fn )′ = f1′ + . . . + fn′ converge uniformemente a g y existe c para el cual, la sucesión f1 (c) + . . . + fn (c) es convergente. Por teorema 4.1, la sucesión f1 + . . . + fn converge uniformemente a una función derivable f , cuya derivada es f ′ = g. Definición 4.3 (Serie de potencias). Sea a ∈ R, se denomina serie de potencias centrada en a, a toda serie de la forma ∞ ∑ n=0. Donde cn ∈ R.. cn (x − a)n = c0 + c1 (x − a) + c2 (x − a)2 + · · · + cn (x − a)n + · · · ..

(44) 30. 4 Igualdad de Funciones. Definición 4.4 (Serie absolutamente convergente). Una serie convergente si: ∞ ∑ |fn | < ∞. ∑∞ n=0. fn se dice absolutamente. n=0. ∑ Definición 4.5 (Criterio de la raı́z en series de potencias). Para todo x la serie n cn (x−a)n verifica: √ Si lı́m sup n |cn (x − a)n | < 1 entonces la serie es absolutamente convergente. n→∞. √ Si lı́m sup n |cn (x − a)n | > 1 entonces la serie no es convergente. n→∞. √ Si lı́m sup n |cn (x − a)n | = 1 entonces la serie puede ser convergente o no y hay que n→∞. estudiar el caso por separado. Debido a que lı́m sup n→∞. √ n. |cn (x − a)n | = |x − a| lı́m sup. √ n. n→∞. |cn |. se puede definir ( )−1 √ n r = lı́m sup |cn | n→∞. (r = 0 si el lı́m sup = +∞ y r = +∞ si lı́m sup = 0), ası́ l anterior se puede expresar como √ si |x − a| < r entonces la serie n |cn (x − a)n | es absolutamente convergente. √ si |x − a| > r entonces la serie n |cn (x − a)n | no es convergente. si |x − a| = r, lo que es igual para x = a ± r, entonces la serie puede ser convergente o no y se estudia el caso por aparte. El valor r se llama radio de convergencia de la serie. Este determina el intervalo (a − r, a + r) en el cual la serie está definida. Si x pertenece a este intervalo, la serie es absolutamente convergente. Definición 4.6 (Serie geométrica). Si x es un número real, se define como serie geométrica2 , a la serie de potencias a la expresión: ∞ ∑. xn = 1 + x + x2 + · · · + xn + · · · =. n=0. 1 si |x| < 1. 1−x. La cual es convergente si |x| < 1. 2. Para mayor información de series y convergencia, remitirse a [1], pag 469..

(45) 4.1 Serie geométrica y matrices infinitas. 31. Teorema 4.3 (Criterio M de Weiertrass). Si |fn (x)| ≤ cn , para todo n y para todo x ∈ A, ∑ ∑ adicionalmente cn es convergente, entonces fn es absoluta y uniformemente convergente en A. ∑ Demostración. La serie cn es absolutamente convergente, luego todos sus términos son positivos y de esta manera se cumple la condición de Cauchy: dado ε > 0 existe N ∈ N tal ∑ ∑m que m k=n |Ck | < ε para n, m > ε. En consecuencia k=n |Ck | < ε para todo x ∈ A ∑ Corolario 4.1. Si n cn (x − a)n es una serie con radio de convergencia r > 0, entonces la serie es absoluta y uniformemente convergente en [a − s, a + s] Demostración. Por el criterio M se puede establecer la convergencia uniforme de la serie. ∑ Dada una serie n cn (x − a)n con radio de convergencia r > 0, si 0 < s < r, para cada x ∈ [a − s, a + s], se da que |cn (x − a)n | ≤ |cn | sn . Por el criterio M anterior y haciendo uso ∑ ∑ del criterio de la raı́z, la serie n |cn | sn es convergente, entonces n cn (x − a)n es absoluta y uniformemente convergente en [a − s, a + s] . ∑ Lema 4.1. Si n cn (x − a)n converge a una función f (x) con x ∈ (a − r, a + r), entonces f es indefinidamente diferenciable en este intervalo. ∑ ∑ n−1 Demostración. Sea g(x) = ∞ la serie que resulta al derivar la serie n cn (x− n=1 ncn (x−a) a)n término a término por teorema 4.2. Ambas series tienen el mismo radio de convergencia, teniendo en cuenta que √ √ rg−1 = lı́m sup n n |cn | = lı́m sup n |cn | = r−1 . n. n. Luego g es lı́mite uniforme de la sucesión de sumas parciales derivadas. Haciendo uso del teorema 4.1, se tiene que f es derivable y f ′ = g. El mismo argumento sirve para comprobar ∑ n−2 que f ′′ (x) = ∞ , y en lo sucesivo. n=2 n(n − 1)cn (x − a) Definición 4.7 (Funciones analı́ticas). Se dice que f : A ⊂ R → R es analı́tica en a ∈ A si f es suma de una serie de potencias en un entorno a. En correspondencia con la teorı́a hallada en [5] se permite definir: Definición 4.8 (Matrices Infinitas). Una matriz infinita es un arreglo rectangular A = (aij ) (i, j = 0, 1, 2, . . . , ∞) de números reales o complejos, con adición y multiplicación definida por: A + B = (aij + bij ), λA = (λaij ), AB = Donde λ es número escalar.. ∑∞ k=0. aik bkj ,.

(46) 32. 4 Igualdad de Funciones. Definición 4.9 (Matrices de Pascal infinitas). pleando la definición 4.8, se determina:    1 0 1 1 1 1 · 1 1 1 2 3 4 ·       S := 1 3 6 10 · L := 1 2    1 3 1 4 10 20 · · · · · · · ·. 4.2.. De forma similar a la definición 1.7 y em-. 0 0 1 3 ·.   1 ·   · 0   · U := 0   0 · · ·. 0 0 0 1 ·. 1 1 0 0 ·. 1 2 1 0 ·. 1 3 3 1 ·.  · ·   ·  · ·. El producto de las matrices infinitas de Pascal. Está última demostración, parte de la consideración del vector infinito v = (1, x, x2 , x3 ...). Al ejecutar el producto de este vector con la matriz infinita S, se obtiene:      1 1 1 1 · 1 1 + x + x2 + x3 + · · · 1 2 3 4 ·  x   1 + 2x + 3x2 + 4x3 + · · ·          2   Sv = 1 3 6 10 · x  =  1 + 3x + 6x2 + 10x3 + · · ·       1 4 10 20 · x3   1 + 4x + 10x2 + 20x3 + · · ·  · · · · · · · La primera fila del vector Sv produce la serie geométrica, la cual, por teorema 4.2 se puede derivar término a termino generando una nueva serie convergente y en consecuencia del lema 4.1 esta se puede derivar indefinidamente. Bajo estos postulados, derivando indefinidamente en ambos lados la serie geométrica 1 + x + x2 + x3 + · · · 1 + 2x + 3x2 + 4x3 + · · · 2 + 6x + 122 + 20x3 + · · · 6 + 24x + 60x2 + 120x3 + · · ·. = = = = .. .. 1/(1 − x) 1/(1 − x)2 2/(1 − x)3 6/(1 − x)4. lo cual es igual a 1 + x + x2 + x3 + · · · 1 + 2x + 3x2 + 4x3 + · · · 2(1 + 3x + 62 + 10x3 + · · · ) 6(1 + 4x + 10x2 + 20x3 + · · · ) ası́. = = = = .. .. 1/(1 − x) 1/(1 − x)2 2(1/(1 − x)3 ) 6(1/(1 − x)4 ). (4-2).

(47) 4.2 El producto de las matrices infinitas de Pascal. 1 + x + x2 + x3 + · · · 1 + 2x + 3x2 + 4x3 + · · · 1 + 3x + 62 + 10x3 + · · · 1 + 4x + 10x2 + 20x3 + · · ·. 33. = = = = .. .. 1/(1 − x) 1/(1 − x)2 1/(1 − x)3 1/(1 − x)4. De esta manera se obtiene la convergencia de cada una de las fila de Sv, luego   1/(1 − x) 1/(1 − x)2      Sv = 1/(1 − x)3    1/(1 − x)4  · Ahora el propósito será comprobar que LU v = Sv. Para tal efecto se ejecuta el producto de la matriz infinita U con el vector v      1 1 1 1 · 1 1 + x + x2 + x3 + · · · 0 1 2 3 ·  x   x + 2x2 + 3x3 + 4x4 + · · ·            U v = 0 0 1 3 · x2  =  x2 + 3x3 + 6x4 + 10x5 + · · ·     3  3  0 0 0 1 · x   x + 4x4 + 10x5 + 20x6 + · · ·  · · · · · · · tomando las igualdades 4-2 como referencia, se puede afirmar que 1 + x + x2 + x3 + · · · x + 2x2 + 3x3 + 4x4 + · · · x2 + 3x3 + 6x5 + 10x6 + · · · x3 + 4x4 + 10x5 + 20x6 + · · ·. = = = = .. .. 1/(1 − x) x/(1 − x)2 x2 /(1 − x)3 x3 /(1 − x)4. por lo tanto  1/(1 − x)  x/(1 − x)2      U v = x2 /(1 − x)3    3 x /(1 − x)4  · . 1 x Al factorizar 1−x y haciendo a = 1−x , entonces las componentes de U v corresponderán a las potencias de a, luego el vector U v se expresarı́a de la forma.

(48) 34. 4 Igualdad de Funciones   1 a  1   2 Uv = a  1 − x  3 a  ·. Ahora al multiplicar por izquierda, la matriz L infinita al vector U v, se da      1 1 0 0 0 · 1  1 1 0 0 ·  a   1+a        2 1   1  2 = L(U v) = 1−x a 1 2 1 0 · 1 + 2a + a    1−x      3    1 3 3 1 · a  1 + 3a + 3a2 + a3  · · · · · · . Dado que en la multiplicación con L no produce sumas infinitas, la convergencia no presenta problema. Ejecutando esta multiplicación es claro que la matriz L produce el teorema del binomio en las componentes del vector resultante del reciente producto, luego   (1 + a)0 (1 + a)1     1  L(U v) = 1−x (1 + a)2    (1 + a)3  · La n−ésima fila de L multiplicado por U v está dada por ( )n ( )n 1 1 x 1 1 1 n (1 + a) = 1+ = = 1−x 1−x 1−x 1−x 1−x (1 − x)n+1 por lo tanto  1/(1 − x) 1/(1 − x)2     3 L(U v) = 1/(1 − x)    1/(1 − x)4  · . Consecuentemente Sv = LU v. Se utilizará este hecho, para comprobar que en las matrices infinitas de pascal se satisface S = LU. Dado que la serie geométrica es convergente para los |x| < 1, para x = 0 la serie converge ya que 0 pertenece al radio de convergencia de esta. Es ası́ que haciendo x = 0 en el vector infinito v = (1, x, x2 , x3 , . . .) se obtiene el vector coordenado v0 v0 = (1, 0, 0, 0, . . .).

(49) 4.2 El producto de las matrices infinitas de Pascal. 35. Si se efectúa el producto Sv0 es claro que es igual a LU v0 , el resultado proporciona la columna fila tanto de la matriz infinita S y el producto de matrices del mismo orden U L, como se aprecia a continuación; dado que Sv = LU v entonces    1 1 1 1 · 1     2 3 4 · 0 1    3 6 10 · 0 = 1    4 10 20 · 0 1 · · · · · ·.  1 1   Sv0 = 1  1 ·. 0 1 2 3 ·. 0 0 1 3 ·. 0 0 0 1 ·.  1 ·   · 0  · 0  · 0 · ·. 1 1 0 0 ·. 1 2 1 0 ·. 1 3 3 1 ·.     1 · 1      · 0 1     · 0 = LU v0 = 1     1 · 0 · · ·. Si se puede construir los otros vectores coordenados a partir del vector v, se podrá concluir que todas las columnas de S y LU coinciden. La manera para llegar al vector coordenado v1 = (0, 1, 0, 0, . . .), es diferenciar v en x = 0 utilizando de nuevo la convergencia de la serie geométrica en valores cercanos a 0. Introduciendo v∆ = (1, ∆, ∆2 , ∆3 , . . .) y formando una combinación lineal entre v∆ y v0 , se establece ( ) ( ) v∆ − v0 v∆ − v0 S = LU ∆ ∆ ( v −v0 ) Analizando ∆∆ , en forma general, este vector es: (. v∆ − v0 ∆. ) =. (1, ∆, ∆2 , ∆3 , . . .) − (1, 0, 0, 0, . . .) (0, ∆, ∆2 ∆3 , . . .) = = (0, 1, ∆, ∆2 , . . .) ∆ ∆.  1  ( ) 1 v∆ − v0  S = 1  ∆ 1 ·.    1 1 1 · 0   2 3 4 ·  1      3 6 10 ·  ∆  =     4 10 20 · ∆2  · · · · ·. 1 + ∆ + ∆2 + · · · 2 + 3∆ + 4∆2 + · · · 3 + 6∆ + 10∆2 + · · · 4 + 10∆ + 20∆2 + · · ·.  ) (  v∆ − v0   = LU ∆ . Si ∆ → 0, entonces  1  ( ) 1 v∆ − v0  S = 1  ∆ 1 ·.    0 1 1 1 ·   2 3 4 ·  1     3 6 10 · 0 =     4 10 20 · 0 · · · · ·. 1 2 3 4.  ) (  v∆ − v0   = LU ∆ . El producto de v1 con S y LU, produce respectivamente, sus segundas columnas.Puesto que el vector resultante de la combinación lineal (0, 1, ∆, ∆2 , . . .), al multiplicarse con las matrices de Pascal infinitas, genera series de potencias, por corolario 4.1, cada serie converge.

(50) 36. 4 Igualdad de Funciones. uniformemente y adicionalmente son analı́ticas. Partiendo de esto se puede decir que cada serie se puede derivar indefinidamente, verificándose las condiciones del lema 4.1. De este modo cada derivada es legı́tima. Las derivadas de orden superior del vector (0, 1, ∆, ∆2 , . . .), ( ) proporcionan los otros vectores coordenados, es decir, derivando v∆∆−v0  1  )′ 1 ( v∆ − v0  = 1 S  ∆ 1 ·.    0 1 1 1 ·    2 3 4 ·  0      3 6 10 ·  1  =     4 10 20 · 2∆ · · · · ·. 1 + 2∆ + · · · 3 + 8∆ + · · · 6 + 20∆ + · · · 10 + 40∆ + · · ·. de manera que, si ∆ → 0 se tiene     1 1 1 1 · 0     ( )′ 1 2 3 4 · 0  v∆ − v0     S = 1 3 6 10 · 1 =      ∆ 1 4 10 20 · 0 · · · · · ·. 1 3 6 10.  ( )′  v∆ − v0   = LU ∆ .  )′ (  v∆ − v0   = LU ∆ . De dicho modo, se llega v2 y se comprueba la igualdad de la tercera fila para S y LU. Derivando indefinidamente se llegarı́a los vectores v3 , v4 , . . . vn , . . . y haciendo uso de la convergencia uniforme se concluye que las columnas de S y LU son idénticas. Al trabajar con matrices infinitas, S = LU es confirmado para todos los ordenes n al mismo tiempo. Ası́ se otorgarı́a la última demostración al teorema 1.2..

(51) 5. Conclusiones De acuerdo con el estudio anterior, el producto de dos matrices tiene distintas perspectivas que inducen a tomar distintos rumbos para llegar a una meta en común. Está claro que aunque el concepto de multiplicación de matrices triangulares es algo propio del álgebra lineal, sin embargo las interpretaciones que otras ramas de las matemáticas le dan a algo de apariencia simple, motivan a generar conceptos más trascendentales. La factorización de la matriz de Pascal simétrica, más allá de apreciarla como la sumatoria de una multiplicación componente a componente, si se observa detenidamente, se llega a descripciones de fenómenos matemáticos interesantes..

(52) A. Triángulo de Pascal A.1.. Una breve historia del triángulo. Comúnmente se denomina al matemático francés Blaise Pascal (1623-1662), como el padre intelectual del afamado triángulo. Sin embargo este se conocı́a hace mucho tiempo. Los orı́genes del trı́angulo aritmético pueden considerarse desde los griegos con su trabajo en número poligonales, en el siglo VI antes de Cristo. Se llaman de este modo, porque son números enteros y pueden representarse mediante figuras geométricas planas o espaciales; estableciendo puntos en los vértices en la figura poligonal representada. Un ejemplo de esto, son los números triangulares 1, 3, 6, 10, 15, ...,, que se representan mediante puntos en el plano que forman triángulos. Hay documentos del año 1261 en los que se muestran que la organización del triángulo aritmético era usado por los chinos con seis lineas en desarrollo. En 1303, se encontró otro documento con ocho lineas de profundidad y con la misma disposición que utilizarı́a Pascal más tarde; se cree que los chinos utilizaban estás representaciones de coeficientes binomiales, para el cálculo de raı́ces cuadradas y cúbicas.. Figura A-1.: Triángulo aritmético de Zhu Shijiei, 1303.

(53) A.1 Una breve historia del triángulo. 39. En una edición de 1407 de la Arithmetica de Jordano, se encuentra un triángulo similar. Jordanus de Nemore, fue un matemático alemán que tuvo ciertos conocimientos de los coeficientes badinomiales; de acuerdo a la obra citada se presentaba los siguientes resultados: ∑ (n) ∑ (n) n =2 , 2r = 3r . r r r r Además su desarrollo del triángulo aritmético:. Figura A-2.: Triángulo de Jordanus, 1407 Un matemático alemán protestante llamado Miguel Stifel, (1486-1567), quien se cree fue el que introdujo los sı́mbolos + y − ası́ como las letras para dentar las cantidades desconocidas también hizo su aporte al triángulo aritmético. En 1544 en su publicación de Nuremberg y su trabajo Arithmetica integra, adicionalmente a su idea de los logaritmos, también se observa un triángulo con números figurados el cual servı́a para el cálculo de raı́ces..

(54) 40. A Triángulo de Pascal. Figura A-3.: Triángulo de Stifel, 1544 Poco después el sabio, filósofo y matemático Jerónimo Cardano, utilizaba el triángulo para determinar el número total de maneras de tomar dos o más objetos de un conjunto de n elementos, dicho de otro modo es la primera vez en la historia que se utiliza el triángulo con objeto del cálculo combinatorio.. Figura A-4.: Triángulo de Cardano, 1570 A mitad del siglo XVI el algebrista alemán Johannes Scheubel, hacia referencia del triángulo aritmético con el propósito del calculo de raı́ces en su obra De numeris, se puede apreciar en la gráfica su versión..

(55) A.1 Una breve historia del triángulo. 41. Figura A-5.: Triángulo de Scheubel,1545 Nicolo fontana (1499-1557), matemático nacido en Italia, más conocido por Tartaglia, reconoce un triángulo en forma de tanla en su tratado, General trattato di numero e misure,tiempo después habla de un segundo triángulo utilizado para el calculo binomial, en el caso especı́fico de calcular el número total de formas que podı́an caer n dados en un tablero.. Figura A-6.: Triángulo de Tartaglia para toma de medidas, 1523. Figura A-7.: Triángulo de Tartaglia para toma de medidas, 1523 Finalmente ya llegando a Pascal se dice que este se pudo inspirar, en un triángulo usado por el flamenco Stevin,1548-1620, que, como Stifel, lo usaba para el cálculo de raı́ces. Es.

(56) 42. A Triángulo de Pascal. posible que Pascal también le era familia la tabla que se en encuentra dentro del tratado sobre el álgebra de Hérigone, Cursus mathematicus, el cual era destinado para la deducción de coeficientes binomiales en el desarrollo de potencias del binomio (a + b)n . Es probable que Pascal también tomara como fundamento la Table des variétés d’un chant de 12 notes prises en 36 que Mersenne introduce en su Harmonicorum Libri XII, en el año de 1636.. Figura A-8.: Tabla de Marin Mersenne, 1636 Pascal comienza con la investigación del triángulo en el año de 1654. En toda la historia, fue el primero en estudiarlo sistemáticamente de tal modo que imprimió una memoria completa de este, llamada Tratado del triángulo aritmético. Esta obra presentaba tratados que mostraban las aplicaciones del triángulo, los números figurados u órdenes numéricos, las combinaciones, problemas sobre sumas de potencias y productos de números consecutivos. En realidad lo que hace que a Pascal se le adjudique el crédito de autor intelectual de la construcción y el contenido del triángulo, es su investigación a profundidad que no fue concebida por sus predecesores; Pascal utiliza el razonamiento por recurrencia y emplea la disposición del trı́angulo para distintas aplicaciones de la aritmética como los que incluı́a su tratado. Adicionalmente hace uso de el trı́angulo para el estudio de problemas de una rama matemática de su invención, la probabilidad, investigando sobre el problema de los repartos..

(57) A.2 Aplicaciones del triángulo. 43. Figura A-9.: Triángulo aritmético original de Pascal. A.2.. Aplicaciones del triángulo. Pascal en el trabajo Diversos usos del triángulo aritmético cuyo generador es la unidad, muestra cuatro aplicaciones: los órdenes numéricos, las combinaciones, determinación de los repartos y la potencia de los binomios (a + b) o (a − b). La forma que utilizó Pascal para desarrollar su triángulo le sirve también para representar los órdenes numéricos. De este modo la primera fila estará formada por la unidad; los elementos de la segunda fila, se obtienen sumando los que le preceden en la misma fila hasta el mismo, de manera consecutiva, 1 1 1 1 1 1... 1 2 3 4 5 6... Deduciendo ası́ la sucesión natural o de números de segundo orden aritmético. Con un proceso similar, se obtiene la tercera fila del triángulo que es la sucesión de tercer orden o los números triangulares. 1 3 6 10 15 21... En esta fila cada elemento se reconoce pomo el n−ésimo elemento de la serie: Tn =. n ∑ i=1. i=. n(n + 1) 2. De igual forma, a partir de los números anteriores, se forma el cuarto orden o de los números piramidales, los cuales están ubicados en la cuarta fila del triángulo de Pascal:.