LIBRO DE ECUACIONES DIFERENCIALES

Universidad de Antioquia, Depto. de Matematicas

ECUACIONES

DIFERENCIALES

con aplicaciones en Maple

Jaime Escobar A.

1_{Profesor Titular de la Universidad de Antioquia, Magister en}

Universidad de Antioquia, Depto. de Matematicas

´INDICE GENERAL

1. INTRODUCCION 1

1.1. CAMPO DE DIRECCIONES . . . 5

1.2. ECUACI ´ON DE CONTINUIDAD . . . 6

2. M´ETODOS DE SOLUCI ´ON 7 2.1. VARIABLES SEPARABLES . . . 7

2.2. ECUACIONES HOMOG ´ENEAS . . . 10

2.3. E.D. CON COEFICIENTES LINEALES . . . 14

2.4. ECUACIONES EXACTAS . . . 15

2.5. FACTORES DE INTEGRACI ´ON . . . 21

2.6. E.D. LINEAL DE PRIMER ORDEN . . . 26

2.7. ECUACION DIFERENCIAL DE BERNOULLI . . . . 32

2.8. E.D. NO LINEALES DE PRIMER ORDEN . . . 34

2.9. OTRAS SUSTITUCIONES . . . 43

2.10. ANEXO CON EL PAQUETE Maple . . . 46

3. APLICACIONES DE LAS E.D. DE PRIMER ORDEN 49 3.1. APLICACIONES GEOM´ETRICAS . . . 49

3.1.1. Trayectorias Isogonales y Ortogonales . . . 49

3.1.2. Problemas de Persecuci´on: . . . 51

3.1.3. Aplicaciones a la geometr´ıa anal´ıtica . . . 54

3.2. CRECIMIENTO Y DESCOMPOSICI ´ON . . . 55

3.2.1. Desintegraci´on radioactiva . . . 56

Universidad de Antioquia, Depto. de Matematicas

3.2.2. Ley de enfriamiento de Newton . . . 57

3.2.3. Ley de absorci´on de Lambert . . . 57

3.2.4. Crecimiento de Cultivos de Bacterias o Crecimientos poblacionales . . . 58

3.3. PROBLEMAS DE DILUCI ´ON . . . 59

3.4. VACIADO DE TANQUES . . . 68

3.5. APLICACIONES A LA FISICA . . . 73

4. TEORIA DE LAS E.D.O. LINEALES 81 4.1. INTRODUCCION . . . 81

4.2. DIMENSI ´ON DEL ESP. VECT. SOL. DE UNA E.D.O. . . 90

4.3. M´ETODO DE REDUCCI ´ON DE ORDEN . . . 97

4.4. E.D.O. LINEALES CON COEFICIENTES CONSTANTES . 101 4.5. E.D. LIN. DE ORDEN MAYOR QUE DOS CON COEF. CONST. . . 105

4.6. OPERADOR ANULADOR . . . 107

4.7. M´ETODO DE LOS COEFICIENTES INDETERMINADOS . 110 4.8. VARIACI ´ON DE PAR ´AMETROS . . . 113

4.8.1. GENERALIZACI ´ON DEL M´ETODO DE VARIACI ´ON DE PAR ´AMETROS . . . 122

4.9. OPERADORES . . . 125

4.10. M´ETODO DE LOS OPERADORES INVERSOS . . . 127

4.11. E.D.O. DE EULER - CAUCHY . . . 139

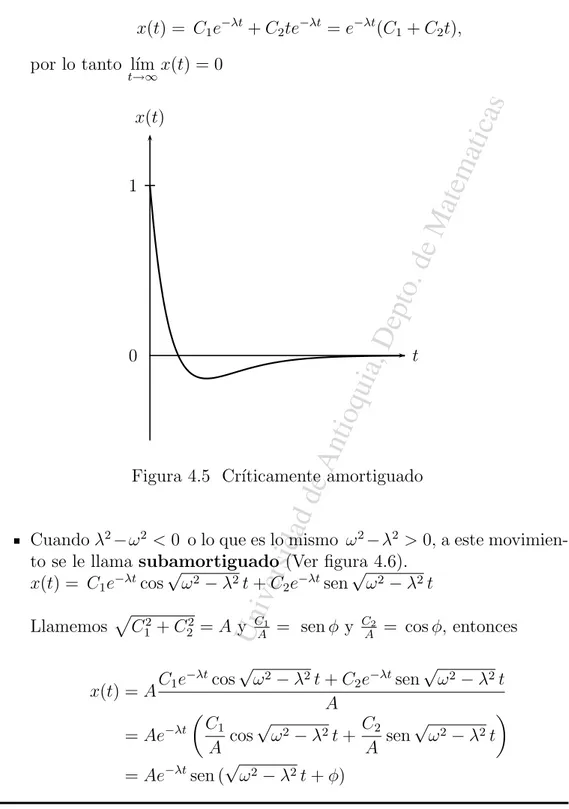
4.12. APLIC. DE LA E.D. SEGUNDO ORDEN: OSCILADORES . 142 4.12.1. MOVIMIENTO ARM ´ONICO SIMPLE . . . 142

4.12.2. MOVIMIENTO AMORTIGUADO . . . 145

4.12.3. MOVIMIENTO FORZADO. . . 148

4.13. ANEXO CON EL PAQUETE Maple . . . 163

5. SOLUCIONES POR SERIES 169 5.1. INTRODUCCION . . . 169

5.2. SOLUCION EN PUNTOS ORDINARIOS . . . 172

5.3. SOLUCIONES EN TORNO A PUNTOS SINGULARES REGULARES . 182 5.3.1. CASO II: r1−r2 = entero positivo . . . 188

5.3.2. FUNCI ´ON GAMMA: Γ(x) . . . 191

5.3.3. CASO III: r1 =r2 . . . 195

5.3.4. ECUACI ´ON DE BESSEL DE ORDEN p: . . . 199

5.3.5. PUNTO EN EL INFINITO . . . 206

5.4. ANEXO CON EL PAQUETE Maple . . . 213

Universidad de Antioquia, Depto. de Matematicas

6. TRANSFORMADA DE LAPLACE 215

6.1. INTRODUCCION . . . 215

6.2. TRANSFORMADA INVERSA DE LAPLACE . . . 219

6.3. TEOREMAS SOBRE LA TRANSFORMADA DE LAPLACE 222 6.4. APLICACIONES DE LA TRANSFORMADA A LAS E.D.₂₃₈ 6.5. IMPULSO UNITARIO O DELTA DE DIRAC . . . 243

6.6. ANEXO CON EL PAQUETE Maple . . . 246

7. SISTEMAS LINEALES DE E.D. DE PRIMER ORDEN 251 7.1. CONJUNTOS FUNDAMENTALES Y SISTEMAS HOMO-G´ENEOS . . . 254

7.2. M´ETODO DE LOS VALORES Y VECTORES PROPIOS . . 255

7.3. E.D. NO HOMOG´ENEA Y VARIACI ´ON DE PAR ´AMETROS 274 7.4. TRANSFORMADA DE LAPLACE PARA SISTEMAS . . . . 278

7.5. ANEXO CON EL PAQUETE Maple . . . 281

8. INTRODUCCION A LA TEORIA DE ESTABILIDAD 283 8.1. SISTEMAS AUT ´ONOMOS, EL PLANO DE FASE . . 283

8.2. TIPOS DE PUNTOS CRITICOS, ESTABILIDAD. . . 287

8.2.1. TIPOS DE PUNTOS CRITICOS. . . 288

8.3. PUNTOS CRITICOS Y CRITERIOS DE ESTABILIDAD . . 297

8.4. CRITERIO DE ESTABILIDAD: METODO DE LIAPUNOV . 310 8.5. LINEALIZACION DE SISTEMAS NO LINEALES . . . 319

8.6. CICLOS LIMITES: TEOREMA DE POINCARE-BENDIXSON339 8.7. ANEXO CON EL PAQUETE Maple . . . 348

A. F´ormulas 353 A.1. F´ormulas Aritm´eticas . . . 353

A.2. F´ormulas Geom´etricas . . . 354

A.3. Trigonometr´ıa . . . 356

A.4. Tabla de Integrales . . . 357

B. Existencia y Unicidad de soluciones 361 B.1. PRELIMINARES . . . 361

B.2. TEOREMA LOCAL DE EXISTENCIA Y UNICIDAD, CASO UNIDI-MENSIONAL . . . 363

B.3. TEOREMAS LOCAL Y GLOBAL PARA SISTEMAS DE E. D. LINEALES370

C. EXPONENCIAL DE OPERADORES 375

Universidad de Antioquia, Depto. de Matematicas

D. FRACCIONES PARCIALES 379

D.1. Factores lineales no repetidos. . . 379

D.2. Factores Lineales Repetidos. . . 380

D.3. Factores Cuadr´aticos. . . 382

D.4. Factores Cuadr´aticos Repetidos. . . 383

Universidad de Antioquia, Depto. de Matematicas

CAP´ITULO 1

INTRODUCCION

Definici´on 1.1 . Si una ecuaci´on contiene las derivadas o las diferenciales de una o m´as variables dependientes con respecto a una o m´as variables independientes, se dice que es una ecuaci´on diferencial (E.D.).

Si la ecuaci´on contiene derivadas ordinarias de una o m´as variables dependi-entes con respecto a una sola variable independiente entonces la ecuaci´on se dice que es una ecuaci´on diferencial ordinaria (E.D.O.).

Ejemplo 1.3dy_dx+ 4y= 5

Ejemplo 2.(x2_{−y)dx+ 5 seny dy= 0} Ejemplo 3.udu_dx +v_dxdv =x

Si la ecuaci´on contiene derivadas parciales de una o m´as variables depen-dientes con respecto a una o m´as variables independepen-dientes, se dice que es una ecuaci´on en derivadas parciales.

Ejemplo 4. ∂u_∂y =₋∂v_∂x

Ejemplo 5. ∂2u

∂x∂y =y−x

Definici´on 1.2 (Orden). La derivada o la diferencial de m´as alto orden determina el orden de la E.D.

Universidad de Antioquia, Depto. de Matematicas

Ejemplo 6. d_dx3y3 +x2

d2_y

dx2 +x

dy

dx = lnx, es de orden 3.

Ejemplo 7.xdy₋ydx = 0 =_{⇒ dx}dy = _xy, la cual es de orden 1.

Definici´on 1.3 (E.D.O. lineal) Una E.D. es lineal si tiene la forma:

an(x)d

n_y

dxn +an₋1(x)d

n₋1_y

dxn₋1 +. . .+a1(x)dxdy +a0(x)y=g(x)

Es decir, la variable dependienteyy todas sus derivadas tienen exponente uno y cada coeficiente a0(x), a1(x), . . . , an(x), g(x), depende solo de x. Si no

se cumple lo anterior se dice que la E.D. no es lineal.

Ejemplo 8.x2d3_y

dx3 + cosx

d2_y

dx2 + senx

dy dx +x

2_y=ex _{es lineal de orden 3.}

Ejemplo 9. senxd_dx3y3 +xy2 = 0 no es lineal.

Ejemplo 10.y2d2_y

dx2 +y

dy

dx+xy=xno es lineal.

Definici´on 1.4 . Se dice que una funci´on f con dominio en un intervalo I

es soluci´on a una E.D. en el intervalo I, si la funci´on satisface la E.D. en el intervalo I.

Ejemplo 11.x=yln(cy) es soluci´on de y0_{(x+y) = y}

En efecto, derivando impl´ıcitamente: 1 = dy_dxln(cy) +y1 cyc

dy dx

1 = dy_dx(ln(cy) + 1), luego dy_dx = _ln(cy)+11 Sustituyendo en la ecuaci´on diferencial:

yln(cy) +y

ln (cy) + 1 =

y(ln (cy) + 1) ln (cy) + 1 =y, luego y=y

por tanto x=yln (cy) es soluci´on.

Universidad de Antioquia, Depto. de Matematicas

Una E.D. acompa˜nada de unas condiciones iniciales se le llama un blema de valor inicial (P.V.I.). Con frecuencia es importante saber si un pro-blema de valor inicial tiene soluci´on y tambi´en deseamos saber si esta soluci´on es ´unica, aunque no podamos conseguir expl´ıcitamente la soluci´on. El si-guiente teorema nos responde las inquietudes que acabamos de plantear.Este teorema lo enunciamos y demostramos con m´as profundidad en el Ap´endice al final del texto.

Teorema 1.1 (Picard)

Sea R una regi´on rectangular en el plano XY definida por

a _≤ x _≤ b, c _≤ y _≤ d que contiene al punto (x0, y0) en su interior.

Si f(x, y)y ∂f_∂y son continuas en R, entonces existe un intervalo I con cen-tro en x0 y una ´unica funci´on y(x)definida enI que satisface el problema

de valor inicial y0 _{=f(x, y), y(x}

0) = y0 .

Ejemplo 12. Para la E.D. y0 _{= x}2 _+y2_{, se tiene que f(x, y) = x}2_+y2

y ∂f_∂y = 2y son continuas en todo el plano XY, por lo tanto por cualquier punto (x0, y0) del plano XY pasa una y solo una soluci´on de la E.D.

anteri-or. Es importante anotar que para esta E.D. es imposible hallar una soluci´on expl´ıcita; s´olo con m´etodos num´ericos se puede hallar la soluci´on.

Ejercicio 1. Demostrar que y=c1cos 5x es soluci´on de y00+ 25y = 0. Ejercicio 2. Demostrar que y = e−x2Rx

0 e t2

dt +c1e−x

2

es soluci´on de

y0_{+ 2xy= 1.}

Ejercicio 3. Demostrar que y=xR₀x sent

t dt es soluci´on de

xy0 _=y+xsenx.

Ejercicio 4.Demostrar que y=e−x

2 es soluci´on de 2y0+y= 0, tambi´en y = 0 es soluci´on.

Nota: si todas las soluciones de la E.D.F(x, y, y0_{, . . . , y}(n)_{) = 0 en un}

in-tervalo I pueden obtenerse de G(x, y, C1, . . . , Cn) mediante valores

apropia-dos deCi, entonces aGse le llamala soluci´on general; una soluci´on que no

contenga los par´ametrosCise le llamala soluci´on particular; una soluci´on

que no pueda obtenerse a partir de la soluci´on general se le llama soluci´on singular.

Veremos m´as adelante que la soluci´on general a una E.D. lineal de orden n

Universidad de Antioquia, Depto. de Matematicas

tiene n par´ametros. En las E.D. no lineales a veces no es posible obtener expl´ıcitamente una soluci´on general.

Ejemplo 13.y=Cx4 _{es soluci´on general de xy}0_{−4y= 0.}

Con C = 1 entonces la soluci´on particular es y =x4_.

Tambi´en

f(x) =

x4 _x≥0

−x4 _{x <0}

es una soluci´on singular, porque no se puede obtener a partir de la soluci´on general.

Ejercicio 5. Siy0_−xy12 = 0, demostrar

a). y= (x2

4 +C)

2 _{es soluci´on general.}

b). Si C= 0 mostrar que y= x₁₆4 es soluci´on particular. c). Explicar porqu´ey = 0 es soluci´on singular.

Ejercicio 6. Siy0 _=y2_{−1, demostrar}

a). y= 1+Ce2x

1−Ce2x es soluci´on general.

b). Explicar porqu´ey =₋1 es soluci´on singular.

Ejercicio 7. Si xy0 _{+ 1 = e}y_{, comprobar que e}−y _{−Cx = 1 es soluci´on}

general.

Ejercicio 8.Si 2xy dx+ (x2_{+ 2y)dy = 0, comprobar que x}2_y+y2 _=C 1

es soluci´on general.

Ejercicio 9. Si (x2_+y2_{)dx+ (x}2_{−xy)dy= 0, comprobar que}

C1(x+y)2 =xe

y

x, es soluci´on general.

Ejercicio 10. Sixy0_{+ 1 =e}y_{, comprobar que e−}y

−Cx= 1 es soluci´on general.

Universidad de Antioquia, Depto. de Matematicas

1.1.

CAMPO DE DIRECCIONES

Dada la E.D. y0 _{=f(x, y) y sabiendo que la primera derivada representa}

una direcci´on en el plano XY, podemos por lo tanto asociar a cada punto (x, y) una direcci´on. A este conjunto de direcciones lo llamamos el campo de direcciones o campo pendiente de la E.D. y0 _{= f(x, y). Este campo de}

di-recciones nos permite inferir propiedades cualitativas de las soluciones, como por ejemplo si son asint´oticas a una recta, si son cerradas o abiertas, etc.. Con el paquete Maple haremos un ejemplo.

Ejemplo 14. Hallar el campo de direcciones de la E.D. y0 _{= −2x}2 _+y2 _y

cuatro curvas soluci´on de la E.D. que pasan por los puntos (0,2),(0,0),(0,1),

(0,₋1) respectivamente.

> with(DEtools):

DEplot (diff(y(x),x)=-2*x^2+y(x)^2,y(x),x=-2..2,color=black, {[0,2],[0,0],[0,1],[0,-1]},y=-2..2,linecolor=black);

y(x) 2

1

0

-1

-2 x

2 1

0 -1

-2

Figura 1.1

Universidad de Antioquia, Depto. de Matematicas

1.2.

ECUACI ´

ON DE CONTINUIDAD

Para finalizar este Cap´ıtulo, es importante hacer un corto comentario so-bre la ecuaci´on de continuidad; con ella se construyen modelos de fen´omenos en diferentes ´areas del conocimiento que dependen del tiempo, dando como resultado una o varias Ecuaciones Diferenciales. La ecuaci´on de continuidad nos dice que la tasa de acumulaci´on de una variable x en un recipiente (el cual puede ser un tanque, un ´organo humano, una persona, una ciudad, un banco, una universidad, un sistema ecol´ogico, etc.) es igual a su tasa de en-trada menos su tasa de salida; tanto la tasa de enen-trada como la tasa de salida pueden ser constantes o variables.

Si la variable esx y la tasa de entrada esE(t) y la tasa de salida es S(t) entonces la tasa de acumulaci´on es

dx

dt =E(t)−S(t).

Ejemplo 15. La concentraci´on de glucosa en la sangre aumenta por ingesta de comidas ricas en azucares, si se suministra glucosa a una raz´on constante

R (en mg/minuto). Al mismo tiempo, la glucosa se transforma y se elimina a una tasa proporcional a la concentraci´on presente de glucosa. Si C(t) re-presenta la concentraci´on de glucosa en un instante t, entonces E(t) = R y

S(t) = kC(t), entonces por la ecuaci´on de continuidad, la Ecuaci´on Diferen-cial que rige este fen´omeno es

dC(t)

dt =E(t)−S(t) =R−kC(t).

Universidad de Antioquia, Depto. de Matematicas

CAP´ITULO 2

M´

ETODOS DE SOLUCI ´

ON

2.1.

VARIABLES SEPARABLES

Definici´on 2.1 . Se dice que una E.D. de la forma: dy

dx =

g(x)

h(y) es separable o de variables separables.

La anterior ecuaci´on se puede escribir comoh(y)dy=g(x)dxe

integran-do: _Z

h(y)dy= Z

g(x)dx+C,

obteni´endose as´ı una familia uniparam´etrica de soluciones.

Nota: la constante o par´ametro C, a veces es conveniente escribirla de otra manera, por ejemplo, m´ultiplos de constantes o logaritmos de constantes o exponenciales de constantes o si aparece la suma de varias constantes re-unirlas en una sola constante.

Ejemplo 1. dy_dx =e3x+2y

Soluci´on:

dy

dx =e

3x+2y _=e3x_e2y

Universidad de Antioquia, Depto. de Matematicas

dy e2y =e

3x_dx

e integrando

−1₂e−2y+C = e

3x

3 la soluci´on general es

e3x

3 +

e−2y

2 =C

Ejemplo 2. dy_dx =xy3_{(1 +x}2₎−1

2, con y(0) = 1

Soluci´on: separando variables

y−3dy= 2x

2√1 +x2dx

= 1 2

d(1 +x2₎

√ 1 +x2

haciendo u = 1 +x

2

du = 2xdx

obtenemos

= 1 2

du

√

u

e integrando y−

2

−2 = 1 2

(1 +x2₎1 2

1 2

+C

soluci´on general

−₂1_y2 =

√

1 +x2_+C.

Cuando x= 0, y = 1

− 1 2_×1 =

√

1 + 02_+C

Universidad de Antioquia, Depto. de Matematicas

luego C = −₂3

La soluci´on particular es

−1 2y2 =

√

1 +x2₋ 3

2

Resolver los siguientes ejercicios por el m´etodo de separaci´on de variables:

Ejercicio 1. (4y+yx2_)dy−(2x+xy2_{)dx= 0}

(Rta. 2 +y2 _{=C(4 +x}2₎₎

Ejercicio 2. y0_+y2_{senx= 0}

(Rta. y =₋ 1 cosx+c)

Ejercicio 3. 3ex_{tany dx+ (2}

−ex_{) sec}2_{y dy = 0}

(Rta. (2₋ex₎3 _=Ctany)

Ejercicio 4. y0_{senx=ylny, si y} π 2

=e

(Rta. lny= cscx₋cotx)

Ejercicio 5. dy

dx =

xy+ 3x₋y₋3

xy₋2x+ 4y₋8 (Rta. (y+3_x+4)5 _=Cey₋x₎

Ejercicio 6. x2_y0 _{=y−xy, si y(−1) =−1}

(Rta. ln_|y_|=₋1

x−ln|x| −1)

Ejercicio 7. Hallar la soluci´on general de la E.D. dy_{dx −}y2 _{=−9 y luego}

hallar en cada caso una soluci´on particular que pase por: a) (0,0), b) (0,3), c) 1₃,1

(Rta. a) y_y+3−3 =₋e6x_{, b) y = 3, c)} y₋3 y+3 =−

1 2e−

2_e6x₎

Ejercicio 8. Se suministran bacterias como alimento a una poblaci´on de protozoarios a una raz´on constante µ. Se ha observado que las bacterias son devoradas a una tasa proporcional al cuadrado de su cantidad. Si c(t) es la cantidad de bacterias en el instante t, hallar la E.D.; determinar c(t) en funci´on de c(0); ¿cu´al es la concentraci´on de equilibrio de las bacterias, es decir, cuando c0_{(t) = 0 ?}

(Rta.:õ+

√

kc(t)

√_µ

−√kc(t) =

√_µ+√_kc(0) √_µ

−√kc(0)e

2√kµt _{; concentraci´on de equilibrio c=}pµ k)

Universidad de Antioquia, Depto. de Matematicas

Ejercicio 9.Resolver por variables separables: axdy_dx+ 2y =xydy_dx en

y=a y x= 2a. (Rta.: yx2 ₌ 4a3

e e

y a)

2.2.

ECUACIONES HOMOG´

ENEAS

Definici´on 2.2 :f(x, y)es homog´enea de gradonsi existe un realn tal que para todo t: f(tx, ty) =tn_{f(x, y).}

Ejemplo 3.f(x, y) = x2_+xy+y2 _{es homog´enea de grado dos.}

Definici´on 2.3 .Si una ecuaci´on en la forma diferencial :

M(x, y)dx+N(x, y)dy = 0

tiene la propiedad que M(tx, ty) = tn_{M(x, y) y N(tx, ty) = t}n_{N(x, y),}

en-tonces decimos que es de coeficientes homog´eneos o que es una E.D. ho-mog´enea.

Siempre que se tenga una E.D. homog´enea podr´a ser reducida por medio de una sustituci´on adecuada a una ecuaci´on en variables separables.

M´etodo de soluci´on: dada la ecuaci´on

M(x, y)dx+N(x, y)dy = 0

donde M(x, y) y N(x, y) son funciones homog´eneas del mismo grado; me-diante la sustituci´on y = ux ´o x = yv (donde u ´o v son nuevas variables dependientes), puede transformarse en una ecuaci´on en variables separables.

Nota: si la estructura algebraica de N es m´as sencilla que la de M, en-tonces es conveniente usar las sustituci´on y =ux.

Si la estructura algebraica deM es m´as sencilla que la de N, es conveniente usar la sustituci´on x=vy.

Ejemplo 4.Resolver por el m´etodo de las homog´eneas, la siguiente E.D.: (x+yeyx)dx−xe

y

x dy= 0, con y(1) = 0.

Universidad de Antioquia, Depto. de Matematicas

Soluci´on:

(x+yeyx)dx−xe y

xdy = 0 donde

homog´enea de grado 1

z }| {

M(x, y) = x+yeyx y

homog´enea de grado 1 z }| {

N(x, y) =₋xeyx

ComoN es m´as sencilla queM, hacemos la sustituci´on:y=ux, por tanto

dy =u dx+x du

Sustituyendo en la E.D.

(x+uxeuxx )dx−xe ux

x (u dx+x du) = 0

o sea que

x dx₋x2eudu= 0

luego x dx = x2_eu_{du, separando variables y considerando x}

6

= 0, obte-nemos,

dx

x =e

u

du _⇒lnx=eu+C

Por lo tanto la soluci´on general es

lnx=eyx +C

Para hallar la soluci´on particular que pasa por el punto y(1) = 0, susti-tuimos en la soluci´on general y obtenemos:

ln 1 =e01 +C ⇒ 0 = 1 +C de donde C =−1

Por lo tanto,

lnx=exy −1

es la soluci´on particular

Ejemplo 5. (x2_y2_{−1)dy+ 2xy}3_{dx = 0 (ayuda: hacer y =z}α _{y calcular}

α para convertirla en homog´enea) Soluci´on:

No es homog´enea; hagamos y=zα _{y hallemos αde tal manera que la E.D.O.}

se vuelva homog´enea:

dy=αzα−1_dz

Universidad de Antioquia, Depto. de Matematicas

α(x2z3α−1₋zα−1)dz+ 2xz3αdx= 0 (2.1) suma de exponentes en los t´erminos: 2+3α₋1, α₋1 y 1+3αrespectivamente. An´alisis de exponentes para que se cumpla la homogeneidad:

1 + 3α= 2 + 3α₋1 =α₋1, se concluye α=₋1

Sustituyo en la E.D. (2.1): (₋1)(x2_z−2_−1)z−2_{dz+ 2xz}−3_{dx= 0}

(₋x2z−4+z−2)dz+ 2xz−3dx= 0 Es homog´enea de orden ₋2.

La sustituci´on m´as sencilla esx=uz _⇒dx=u dz+z du.

(₋u2z2z−4+z−2)dz + 2uzz−3(u dz+z du) = 0

(₋u2z−2+z−2+ 2u2z−2)dz+ (2uz−1)du= 0

(u2z−2+z−2)dz+ 2uz−1du= 0

z−2(u2+ 1)dz+ 2uz−1du = 0

z−2_dz

z−1 +

2u

u2_{+ 1}du= 0

dz

z +

2u

u2_{+ 1}du= 0

Integrando: ln_|z_|+ ln(u2_{+ 1) = lnC}

ln_|z(u2+ 1)_|= lnC _⇒z(u2+ 1) =C

reemplazou= x

z y tenemos, tomandoz 6= 0

Universidad de Antioquia, Depto. de Matematicas

x2

z +z =C

Comoy =z−1 _{o sea que z =y}−1_{, entonces} x2

y−1 +y−1 =C

luego

x2_y2_{+ 1 =Cy,}

es la soluci´on general.

Resolver los siguientes ejercicios por el m´etodo de las homog´eneas, ´o con-vertirla en homog´enea y resolverla seg´un el caso:

Ejercicio 1. y+xcot_xy dx₋x dy = 0. (Rta.: C =xcosy_x)

Ejercicio 2. (x+py2_−xy)dy

dx =y , con y(1) = 1.

(Rta.: ln2_|y_|= 4(y−_yx))

Ejercicio 3. x₋ycos y_x dx+xcos y_xdy= 0. (Rta.: ln_|x_|+ seny_x =C)

Ejercicio 4. (x2_−2y2_{)dx+xy dy = 0.}

(Rta.: x4 _=C(x2_−y2₎₎

Ejercicio 5. xy0 _{=y+ 2xe}−y x .

(Rta.: lnx= 1₂eyx+c)

Ejercicio 6. (x+y3_{)dx+ (3y}5_−3y2_{x)dy= 0, (Ayuda: hacer x=z}α_).

(Rta.: ln_|C(x2_+y6_{)|= 2 arctan}y3

x)

Ejercicio 7. 2(x2_y+p_{1 +x}4_y2_)dx+x3_{dy= 0, (Ayuda: hacery =z}α_).

(Rta.: x4_{(1 + 2Cy) =C}2₎

Ejercicio 8. ycosx dx+ (2y₋ senx)dy= 0, (Ayuda: hacer u= senx). (Rta.: y2 _=Ce−senyx)

Ejercicio 9. y(ln y_x+ 1)dx₋xlny_xdy= 0. (Rta.: ln_|x_{| −} 1₂ln2_|xy_|=C)

Universidad de Antioquia, Depto. de Matematicas

Ejercicio 10. dy_dx = cos(y_x) + y_x. (Rta.: sec(_xy) + tan(y_x) =Cx)

Ejercicio 11. Hallar la soluci´on particular de la E.D.

yx2dx₋(x3+y3)dy= 0,

donde y(0) = 1 (Rta.: ln_|y_|= 1

3( x y)

3₎

Ejercicio 12. Hallar la soluci´on particular de la E.D.

xy2dy₋(x3+y3)dx= 0,

donde y(1) = 0 (Rta.: ln_|x_|= 1₃(y_x)3₎

Ejercicio 13. (y+√xy)dx₋2xdy = 0 (Rta.: x(py_x−1)4 _{=C, si x >0, y >0 yx(}py

x + 1)

4 _{=C , si x <0, y <0)}

Ejercicio 14. Hallar la soluci´on particular de la E.D.

y(lny₋lnx₋1)dx+xdy= 0,

donde y(e) = 1 (Rta.: xln_|y_x|=₋e)

2.3.

E.D. DE COEFICIENTES LINEALES:

(

ax

+

by

+

c

)

dx

+ (

αx

+

βy

+

γ

)

dy

= 0

Se presentan dos casos:

1. Si (h, k) es el punto de intersecci´on entre las rectas:

ax+by+c= 0 y αx+βy+γ = 0

entonces se hace la sustituci´on: x=u+h y y=v+k y se consigue la ecuaci´on homog´enea:

(au+bv)du+ (αu+βv)dv= 0

Universidad de Antioquia, Depto. de Matematicas

2. Si las dos rectas no se intersectan (o sea son paralelas), entonces

αx+βy =n(ax+by)

y por tanto se hace la sustituci´on z = ax +by, lo cual quiere decir que αx+βy = nz, esta sustituci´on convierte la E.D. en una E.D. de variables separables.

Ejercicios:resolver por el m´etodo anterior:

1. (x₋y+ 1)dx+ (x+ 2y₋5)dy= 0

(Rta.: (x₋1)2_{+ 2(y−2)}2 _=Ce√2 arctan√x−1

2(y−2))

2. dy_dx = 2y_2x−₋x+5_y−4

(Rta.: (x+y+ 1)3 _{=C(y−x+ 3))} 3. (x₋2y+ 4)dx+ (2x₋y+ 2)dy= 0

(Rta.: (x+y₋2)3 _=C2_{(x−y+ 2))} 4. (x+y+ 1)2_{dx+ (x+y−1)}2_{dy = 0}

(Rta.: 4x=₋1₂(x+y)2_{+ 2(x+y)−ln|x+y|+C)} 5. (x+y+ 1)dx+ (2x+ 2y₋1)dy = 0

(Rta.: 4₋x₋2y= 3 ln_|2₋x₋y_|+C)

6. (x+y₋2)dx+ (x₋y+ 4)dy= 0

(Rta.: C = 2(x+ 1)(y₋3) + (x+ 1)2_−(y−3)2₎ 7. (x₋y₋5)dx₋(x+y₋1)dy= 0

(Rta.: (x+y₋1)2 _−2(x−3)2 _=C) 8. (2x+y)dx₋(4x+ 2y₋1)dy= 0

(Rta.: x= 2₅(2x+y)_{− 25}4 ₋ln_|5(2x+y)₋2_|+C)

2.4.

ECUACIONES EXACTAS

Siz =f(x, y), entonces

dz = ∂f

∂xdx+

∂f

∂y dy

Universidad de Antioquia, Depto. de Matematicas

es la diferencial total de f; pero si z = c = f(x, y) (familia de curvas uni-param´etricas en el plano XY ), entonces

dz = 0 = ∂f

∂xdx+

∂f

∂y dy

.

Definici´on 2.4 .La forma diferencial M(x, y)dx+N(x, y)dy es una dife-rencial exacta en una regi´on R del plano XY si corresponde a la diferencial total de alguna funci´on f(x, y).

La ecuaci´on M(x, y)dx +N(x, y)dy = 0, es exacta si es la diferencial total de alguna funci´on f(x, y) = c.

Teorema 2.1 (Criterio para E.D. exactas) .

Si M(x, y) y N(x, y) son continuas y tienen derivadas parciales de primer orden continuas en una regi´on R del plano XY, entonces la condici´on nece-saria y suficiente para que la forma diferencial

M(x, y)dx+N(x, y)dy

sea una diferencial exacta es que

∂M

∂y =

∂N ∂x.

Demostraci´on:ComoM(x, y)dx+N(x, y)dyes una diferencial exacta, entonces existe una funci´on f(x, y) tal que:

M(x, y)dx+N(x, y)dy = ∂f

∂xdx+

∂f

∂y dy=d f(x, y)

luego

M(x, y) = ∂f

∂x

y

N(x, y) = ∂f

∂y

Universidad de Antioquia, Depto. de Matematicas

por tanto,

∂M

∂y =

∂2_f

∂y∂x =

∂2_f

∂x∂y =

∂N ∂x.

La igualdad entre las derivadas cruzadas se produce porque M y N son continuas con derivadas de primer orden continuas.

M´etodo. Dada la ecuaci´onM(x, y)dx+N(x, y)dy= 0, hallar una funci´on

f(x, y) =C tal que

∂f

∂x =M y

∂f

∂y =N

i) Comprobar que es exacta, es decir, verificar que ∂M_∂y = ∂N_∂x.

ii) Suponer que ∂f_∂x =M(x, y) y luego integrar con respecto a xdejando a

y constante:

f(x, y) = Z

M(x, y)dx+g(y) (2.2)

iii) Derivar con respecto ay la ecuaci´on (2.2)

∂f

∂y =

∂ ∂y

Z

M(x, y)dx+g0(y) =N(x, y)

despejar

g0(y) = N(x, y)₋ ∂

∂y

Z

M(x, y)dx (2.3)

Esta expresi´on es independiente de x, en efecto:

∂ ∂x

N(x, y)₋ ∂

∂y

Z

M(x, y)dx

= ∂N

∂x −

∂ ∂x

∂ ∂y

Z

M(x, y)dx

= ∂N

∂x −

∂ ∂y

∂ ∂x

Z

M(x, y)dx= ∂N

∂x −

∂

∂yM(x, y) = 0

iv) Integrar la expresi´on (2.3) con respecto ayy sustituir en (2.2) e igualar a C.

Universidad de Antioquia, Depto. de Matematicas

Nota: en ii) se pudo haber comenzado por ∂f_∂y =N(x, y).

Ejemplo 6.Resolver la siguiente E.D.: (2xy2_+yex_{)dx+ (2x}2_y+ex

−1)dy= 0 Soluci´on:

paso i)

∂M

∂y = 4xy+e

x

∂N

∂x = 4xy+e

x

   

  

de donde ∂M

∂y =

∂N ∂x

paso ii)

f(x, y) = Z

N(x, y)dy+h(x) = Z

(2x2y+ex₋1)dy+h(x) = x2y2+yex

−y+h(x)

paso iii)

∂f

∂x =M = 2xy

2_+yex

∂f

∂x = 2xy

2_+yex_+h0_(x)⇒h0_{(x) = 0}

paso iv)h(x) =C

paso v) sustituyo h(x) en el paso ii):

x2y2+yex₋y+C1 = C

x2y2 +yex₋y = C2 Soluci´on general Ejemplo 7.Hallar el valor deb para que sea exacta la E.D.:

(xy2+bx2y)dx+ (x+y)x2dy = 0.

Soluci´on:

∂M

∂y = 2xy+bx

2

∂N

∂x = 3x

2_{+ 2xy}

⇒b= 3

Universidad de Antioquia, Depto. de Matematicas

∂f

∂x = xy

2_{+ 3x}2_{y (2.4)}

∂f

∂y = x

3_+x2_{y (2.5)}

integramos (2,4) : f(x, y) = Z

(xy2+ 3x2y)dx+g(y)

f(x, y) = y2x

2

2 +x

3_{y+g(y) (2.6)}

derivamos (2,6) con respecto ay ∂f

∂y = yx

2_+x3 _+g0_{(y) (2.7)}

igualamos (2,5) y (2,7)

x3+x2y = yx2+x3 +g0(y)

K = g(y)

reemplazamosg(y) en (2,6)

f(x, y) = y2x2

2 +x

3_{y+K =C} 1

= y

2_x2

2 +x

3_y=C

que es la soluci´on general.

Ejercicio 1. Resolver la siguiente E.D. por el m´etodo de las exactas : (tanx₋ senxseny)dx+ cosxcosy dy = 0.

(Rta.: f(x, y) = cosxseny₋ln_|cosx_|=C)

Ejercicio 2. Resolver la siguiente E.D. por el m´etodo de las exactas: (y2cosx₋3x2y₋2x)dx+ (2ysenx₋x3+ lny)dy= 0, cony(0) =e.

(Rta.: f(x, y) =y2_senx−x3_y−x2_{+y(lny−1) = 0)}

Ejercicio 3.Determinar la funci´onM(x, y) de tal manera que la siguiente E.D.O sea exacta:

M(x, y)dx+

xex_{y+ 2xy+} 1

x

dy= 0

Universidad de Antioquia, Depto. de Matematicas

x2 +g(x))

Ejercicio 4. Determinar la funci´on N(x, y) para que la siguiente E.D. sea exacta:

y12x− 1

2 + x

x2_+y

dx+N(x, y)dy = 0

(Rta.: N(x, y) =x12y− 1 2 + 1

2(x

2_+y)−1_+g(y))

Ejercicio 5. Resolver por el m´etodo de las exactas la siguiente E.D.: (2xy2+yex_{)dx+ (2x}2_y+ex

−1)dy= 0 (Rta.: f(x, y) =y(x2_y+ex_{−1) =C)}

Ejercicio 6. Resolver por el m´etodo de las exactas la siguiente E.D.: (2x₋ysenxy₋5y4)dx₋(20xy3+xsenxy)dy= 0

(Rta.: f(x, y) =x2_{+ cos(xy)−5y}4_x=C)

Ejercicio 7. Resolver por el m´etodo de las exactas la siguiente E.D.: ( senxy+xycosxy)dx+ (x2cosxy)dy = 0

(Rta.: f(x, y) =xsen (xy) = C)

Ejercicio 8. Resolver por el m´etodo de las exactas la siguiente E.D.: (yexy_{+ 4y}3_{)dx+ (xe}xy_{+ 12xy}2

−2y)dy = 0, cony(0) = 2 (Rta.: f(x, y) =exy _{+ 4xy}3 _−y2 ₌₋₃₎

Ejercicio 9. Resolver por el m´etodo de las exactas la siguiente E.D.: (1₋ senxtany)dx+ cosxsec2y dy= 0

(Rta.: f(x, y) = cosxtany+x=C)

Universidad de Antioquia, Depto. de Matematicas

2.5.

FACTORES DE INTEGRACI ´

ON

Definici´on 2.5 (Factor Integrante F.I.) . Sea la E.D.

M(x, y)dx+N(x, y)dy= 0.

Si µ(x, y) es tal que

µ(x, y)M(x, y)dx+µ(x, y)N(x, y)dy= 0

es una E.D. exacta, entonces decimos que µ(x, y) es un factor integrante (F.I.).

Ejemplos de algunas formas diferenciales que son exactas. Ejemplo: x dx+y dy es la diferencial de 1₂(x2_+y2_{) ya qued} 1

2(x2+y2)

=

x dx+y dy.

An´alogamente: para x dy+y dx =d(xy).

Pero py dx+qx dy no es exacta, la expresi´on µ(x, y) = xp₋1_yq₋1 _{es un}

factor integrante.

Paray dx₋x dy, las expresiones:

µ= 1

y2 ; µ=

1

x2; µ=

1

xy; µ=

1

x2_+y2 ; µ=

1

ax2_+bxy+cy2

son factores integrantes.

Teorema 2.2 (Teorema del Factor Integrante) :

Sea M(x, y)dx+N(x, y)dy= 0una E.D. yµ(x, y)un factor integrante, con

M,N yµcontinuas y con primeras derivadas parciales continuas , entonces

µ

∂M

∂y −

∂N ∂x

=Ndµ

dx =−M

dµ dy

Demostraci´on:Siµes tal queµM dx+µN dy = 0 es exacta yµ, M, N

tienen primeras derivadas parciales continuas, entonces:

Universidad de Antioquia, Depto. de Matematicas

∂

∂y (µM) = ∂

∂x(µN)

o sea que

µ∂M

∂y +M

∂µ

∂y =µ

∂N

∂x +N

∂µ ∂x luego µ ∂M ∂y − ∂N ∂x

=N∂µ

∂x −M

∂µ

∂y =N

∂µ ∂x − M N ∂µ ∂y

como dy_dx =₋M_N, entonces:

µ ∂M ∂y − ∂N ∂x =N ∂µ ∂x + dy dx ∂µ ∂y

=Ndµ

dx =−M

dµ dy

ya que siµ=µ(x, y) y y=y(x) entonces:

dµ= ∂µ

∂x dx+

∂µ

∂y dy

y por tanto

dµ dx = ∂µ ∂x + ∂µ ∂y dy dx Nota. 1. Si ∂M ∂y− ∂N ∂x

N =f(x),

entonces µf(x) = dµ_dx y por tanto f(x)dx= dµ_µ, luego µ=keRf(x)dx_{; tomando k = 1 se tiene µ=e}R

f(x)dx_.

2. Similarmente, si

∂M ∂y−

∂N ∂x

−M =g(y),entonces µ=e R

g(y)dy_.

Ejemplo 8. (2xy2_{−2y)dx+ (3x}2_{y−4x)dy = 0.}

Soluci´on:

M(x, y) = 2xy2₋2y_⇒ ∂M

∂y = 4xy−2

N(x, y) = 3x2y₋4x_⇒ ∂N

∂x = 6xy−4

Universidad de Antioquia, Depto. de Matematicas

luego

∂M

∂y −

∂N

∂x =−2xy+ 2

por tanto

∂M ∂y −

∂N ∂x

−M =

−2xy+ 2 −2xy2_{+ 2y} =

2(₋xy+ 1) 2y(₋xy+ 1) luego

g(y) = 1

y ⇒F.I.=µ(y) =e

R ₁

ydy =eln|y| =y

multiplico la E.D. original pory: (2xy3_−2y2_{)dx+ (3x}2_y2_{−4xy)dy= 0}

el nuevoM(x, y) = 2xy3_−2y2 _{y el nuevoN(x, y) = 3x}2_y2_−4xy Paso 1.

∂M

∂y = 6xy

2

−4y

y

∂N

∂x = 6xy

2

−4y

luego es exacta.

Paso 2.

f(x, y) = Z

(2xy3₋2y2)dx+g(y) =x2y3₋2xy2+g(y)

Paso 3. Derivando con respecto a y:

N = 3x2y2₋4xy= ∂f

∂y = 3x

2_y2

−4xy+g0(y) luego g0_{(y) = 0}

Paso 4. g(y) = k

Paso 5. Reemplazo en el paso 2.

f(x, y) = x2y3₋2xy2+k=c

luego x2_y3_−2xy2 _=k

1 que es la soluci´on general.

Universidad de Antioquia, Depto. de Matematicas

Ejemplo 9.x dy₋y dx= (6x2_−5xy+y2_)dx

Soluci´on:

comod(y

x) =

x dy₋y dx x2

entonces dividimos a ambos lados de la E.D. por x2_{, luego}

x dy₋y dx

x2 =

6x2_−5xy+y2

x2

dx

luego

d(y

x) =

6₋5(y

x) + ( y x)

2_dx,

hagamos u= y_{x ⇒}du= (6₋5u+u2_)dx

luego du

6₋5u+u2 =dx⇒

du

(u₋3)(u₋2) =dx pero por fracciones parciales 1

(u₋3)(u₋2) =

A

u₋3 +

B

u₋2

o sea queA= 1 y B =₋1, por tanto Z

du

(u₋3)(u₋2) = Z

dx_⇒

Z

du u₋3−

Z

du

u₋2 = ln|u−3|−ln|u−2|+lnc=x luego

c(u−3)

(u₋2) =e

x_{, six}

6

= 0 _⇒c(y−3x)

(y₋2x) =e

x

Obs´ervese quex= 0 es tambi´en soluci´on y es singular porque no se desprende de la soluci´on general.

En los siguientes ejercicios, hallar el factor integrante y resolver por el m´etodo de las exactas:

Ejercicio 1. (cos(2y)₋ senx)dx₋2 tanxsen (2y)dy= 0. (Rta.: senxcos(2y) + 1₂cos2_x=C)

Ejercicio 2. (3xy3_{+ 4y)dx+ (3x}2_y2_{+ 2x)dy= 0.}

(Rta.: f(x, y) =x3_y3_{+ 2x}2_y=C)

Universidad de Antioquia, Depto. de Matematicas

Ejercicio 3. 2xylny dx+ (x2_+y2p_y2_{+ 1)dy= 0.}

(Rta.: f(x, y) =x2_lny+ 1

3(y2+ 1)

3 2 =C)

Ejercicio 4. (2wz2_{−2z)dw+ (3w}2_{z−4w)dz = 0.}

(Rta.: w2_z3_−2z2_w=C)

Ejercicio 5. ex_{dx+ (e}x_{coty+ 2ycscy)dy = 0}

(Rta.: f(x, y) =ex_seny+y2 _=C)

Ejercicio 6. x dy+y dx= (x3_{+ 3x}2_{y+ 3xy}2_+y3_)(dx+dy).

(Rta.: xy = 1

4(x+y) 4_+C)

Ejercicio 7. x dy₋y dx= (2x2_{+ 3y}2₎3_{(2xdx+ 3ydy).}

(Rta.: q2₃tan−1₍q3 2

y x) =

1

3(2x2+ 3y2)3+C) Ejercicio 8. y dx+ (2x₋yey_{)dy= 0.}

(Rta.: y2_x−y2_ey _{+ 2ye}y

−2ey _=C)

Ejercicio 9. (xy₋1)dx+ (x2_{−xy)dy= 0.}

(Rta.: f(x, y) =xy₋ln_|x_{| −} y₂2 =C)

Ejercicio 10. ydx+ (x2_{y−x)dy= 0.}

(Rta.: f(x, y) =₋y_x +y₂2 =C)

Ejercicio 11. (2xy₋e−2x_{)dx+xdy= 0.}

(Rta.: f(x, y) =ye2x_−ln|x|=C)

Ejercicio 12. ydx+ (2xy₋e−2y_{)dy = 0.}

(Rta.: f(x, y) =xe2y_−ln|y|=C)

Ejercicio 13. (x+y)dx+xlnxdy= 0. (Rta.: f(x, y) =x+ylnx=C)

Ejercicio 14. Hallar la soluci´on particular que pasa por el punto

y(1) =₋2, de la E.D.

dy

dx =−

3x2_y+y2

2x3_{+ 3xy}

Universidad de Antioquia, Depto. de Matematicas

Ejercicio 15. x dx+y dy= 3px2 _+y2 _y2_dy.

(Rta.: px2_+y2 _=y3_+C)

Ejercicio 16. 4y dx+x dy=xy2_dx.

(Rta.: _yx14 − _3x13 =C)

Ejercicio 17. Si

My−Nx

yN ₋xM =R(xy),

entonces µ=F.I.=eRtR(s)ds_{, donde t=xy}

Ejercicio 18. Bajo que condiciones M dx+N dy = 0 tendr´a un F.I.=

µ(x+y)

Ejercicio 19. Si M dx+ N dy = 0 es homog´enea, entonces µ(x, y) =

1 xM+yN

2.6.

E.D. LINEAL DE PRIMER ORDEN

Definici´on 2.6 . Una E.D. de la forma:

a1(x)

dy

dx +a0(x)y=h(x),

donde a1(x)6= 0, en I y a1(x), a0(x), h(x)son continuas en I, se le llama

E.D. lineal en y de primer orden.

Dividiendo por a1(x), se obtiene la llamada ecuaci´on en forma can´onica

´o forma estandar:

dy

dx +p(x)y=Q(x),

donde p(x) = a0(x)

a1(x)

y Q(x) = h(x)

a1(x)

.

Universidad de Antioquia, Depto. de Matematicas

Teorema 2.3 (Teorema de la E.D. lineal de primer orden) : La soluci´on general de la E.D. lineal en y, de primer orden:

y0+p(x)y=Q(x) es :

yeRp(x)dx₌

Z

eRp(x)dx_Q(x)dx+C.

Demostraci´on:

dy

dx +p(x)y = Q(x) (2.8)

⇒ p(x)y dx+dy =Q(x)dx

o sea que (p(x)y₋Q(x))dx+dy = 0, como ∂M

∂y =p(x) y ∂N

∂x = 0, entonces ∂M

∂y − ∂N

∂x

N =p(x)

y por tanto µ=eRp(x)dx_{=F.I.; multiplicando (2.8) por elF.I.:}

eRp(x)dxdy

dx+p(x)ye

R

p(x)dx_=Q(x)eR p(x)dx

o sea d dx(ye

R

p(x)dx_{) = Q(x)e}R

p(x)dx _{e integrando con respecto ax se tiene:}

yeRp(x)dx = Z

Q(x)eRp(x)dxdx+C

Obs´ervese que la expresi´on anterior es lo mismo que:

y F.I.= Z

Q(x)F.I. dx+C

Ejemplo 10.Hallar la soluci´on general de la E.D.:(6₋2µν)dν dµ +ν

2 _{= 0}

Soluci´on:

dν

dµ =−

ν2

6₋2µν dµ

dν =−

6

ν2 +

2µ ν

Universidad de Antioquia, Depto. de Matematicas

dµ

dν −

2µ

ν =−

6

ν2

que es lineal en µcon

p(ν) = ₋2

ν, Q(ν) = −

6

ν2

F.I.=eRp(ν)dν =eR−2νdν =e−2 ln|ν|=eln|ν|−

2

=ν−2 = 1

ν2

La soluci´on general es 1

ν2µ=

Z 1

ν2(−

6

ν2)dν+C

1

ν2µ=−6

Z

ν−4dν+C =₋6ν−

3

−3 +C

µ ν2 =

2

ν3 +C ⇒µ=

2

ν +Cν

2

que es la soluci´on general.

Ejemplo 11.Hallar una soluci´on continua de la E.D.: dy_dx+ 2xy=f(x)

dondef(x) =

x , 0_≤x <1 0, x_≥1 y y(0) = 2

Soluci´on:

F.I.:eR2xdx=ex2 _⇒ex2y= Z

ex2f(x)dx+C

a). si 0_≤x <1 :ex2

y=R ex2

x dx+C

ex2

y = 1₂R ex2

2x dx+C

ex2

y = 1₂ex2

+C, soluci´on general

Universidad de Antioquia, Depto. de Matematicas

y(0) = 2_⇒e02

2 = 1₂e02

+C

2 = 1₂ +C _⇒C = 3₂

y= 1

2 +Ce−

x2 _⇒y= 1 2 +

3 2e−

x2_{, soluci´on particular}

b). si x_≥1 :F.I.y =R F.I.0dx+C

ex2_{y= 0 +C ⇒y =Ce}−x2

Soluci´on: f(x) = ₁

2 + 3 2e−

x2 _{0≤x <1}

Ce−x2 _x≥1

Busquemos C, de tal manera que la funci´onf(x) sea continua en x= 1. Por tanto

l´ım

x_→1(

1 2 +

3 2e

−x2

) =f(1) =y(1) 1

2 + 3 2e

−1 _=Ce−1

⇒C =

1 2 +

3 2e−

1

e−1 =

1 2e+

3 2

Ejemplo 12.Con un cambio de variable adecuado transformar la E.D.:

y0 +xsen 2y=xe−x2cos2y

en una E.D. lineal de primer orden y luego resolverla. Soluci´on. Lo trabajamos mediante cambios de variable. Dividiendo por cos2_y:

1 cos2_y

dy

dx+

x(2 senycosy)

cos2_y =xe− x2

sec2ydy

dx + 2xtany=xe

−x2

hagamos el siguiente cambio de variable: t= tany, por lo tanto

dt dx = sec

2_ydy

dx.

Universidad de Antioquia, Depto. de Matematicas

dt

dx + 2xt=xe

−x2

, es lineal en t con

p(x) = 2x, Q(x) = xe−x2

F.I.=eR2x dx =ex2

Resolvi´endola

t F.I.= Z

F.I.Q(x)dx+C

tex2 ₌

Z

ex2_(xe−x2_)dx+C

⇒tany ex2 ₌ x2

2 +C

Ejercicio 1. Hallar una soluci´on continua de la E.D.:

(1 +x2₎dy

dx + 2xy=f(x)

dondef(x) =

x , 0_≤x <1

−x , x_≥1 con y(0) = 0.

(Rta.: y(x) = ( _x2

2(1+x2₎, si 0≤x <1

− x2

2(1+x2₎+ _1+x12, si x≥1

)

Ejercicio 2. Hallar la soluci´on de la E.D.: dy_dx = _y−y_x con y(5) = 2 (Rta.: xy= y₂2 + 8)

Ejercicio 3. Resolver paraϕ(x) la ecuaci´on R₀1ϕ(αx)dα=nϕ(x) (Ayuda: con un cambio de variable adecuado transforme la ecuaci´on en una E.D. lineal de primer orden.)

(Rta.: ϕ(x) = Cx(1−n n ))

Ejercicio 4. Hallar la soluci´on de la E.D.: y0 _{−2xy = cosx−2xsenx}

Universidad de Antioquia, Depto. de Matematicas

(Rta.: y = senx)

Ejercicio 5.Hallar la soluci´on de la E.D.: 2√x y0_−y=−sen√_x−cos√_x

donde y es acotada cuando x_{→ ∞}. (Rta.: y = cos√x)

Ejercicio 6. Resolver la E.D.: (x+ 2)2 dy

dx = 5−8y−4xy.

(Rta.: y(2 +x)4 ₌ 5

3(2 +x)3+C)

Ejercicio 7. Resolver la E.D.: y₋xdy_dx = dy_dxy2_ey_.

(Rta.: x y =e

y_+C)

Ejercicio 8.El suministro de glucosa al torrente sangu´ıneo es una t´ecni-ca importante para detectar la diabetes en una persona. Para estudiar este proceso, definimos G(t) como la cantidad de glucosa presente en la sangre de un paciente en el tiempo t. Suponga que la glucosa se suministra al sis-tema sangu´ıneo a una tasa constante k_min.gr. . Al mismo tiempo la glucosa se transforma y se separa de la sangre a una tasa proporcional a la cantidad de glucosa presente. Construir la E.D. y resolverla. Hallar G(t) cuando t _{→ ∞}.

Ejercicio 9. Hallar la soluci´on general en t´erminos def(x), de la E.D.:

dy dx + 2

f0_(x)

f(x) y=f

0_(x)

(Rta.: y = 1₃f(x) + C [f(x)]2)

Ejercicio 10. Hallar la soluci´on general de la E.D. (x+ 1)y0+ (2x₋1)y=e−2x

(Rta.: y =₋1 3e−

2x_+Ce−2x_{(x+ 1)}3₎

Ejercicio 11. Hallar la soluci´on particular de la E.D.

y0+y= 2xe−x_+x2_{si y(0) = 5}

(Rta.: y=x2_e−x_+x2_{−2x+ 2 + 3e}−x₎

Universidad de Antioquia, Depto. de Matematicas

Ejercicio 12. Hallar la soluci´on particular de la E.D. (1₋2xy2)dy =y3dx

si y(0) = 1

(Rta.: xy2 _{= lny)}

2.7.

ECUACION DIFERENCIAL DE

BERNOULLI

Definici´on 2.7 . Una E.D. de la forma _dxdy +p(x)y = Q(x)yn _{con n 6= 0}

y n ₆= 1, se le llama una E.D. de Bernoulli. Obs´ervese que es una E.D. no lineal.

La sustituci´on w=y1−n _{convierte la E.D. de Bernoulli en una E.D. lineal en}

w de primer orden:

dw

dx + (1−n)p(x)w= (1−n)Q(x).

Ejemplo 13. xy(1 +xy2₎dy

dx = 1 cony(1) = 0.

Soluci´on:

dy dx =

1

xy(1+xy2₎ ⇒ dx_dy =xy(1 +xy2) = xy+x2y3 dx

dy −xy = x

2_y3 _(2.9)

tiene la forma de Bernoulli con variable dependiente x, con n = 2 Hagamos w=x1−2 _=x−1 _⇒x=w−1

dx

dy =−w

−2dw

dy

sustituimos en (2.9): ₋w−2dw

dy −yw−

1 _=y3_w−2

multiplicamos por ₋w−2_: dw

dy +yw=−y

3_{, lineal en wde primer orden.}

luego p(y) =y; Q(y) = ₋y3

F.I.=eRP(y)dy _=eR

y dy _=ey₂2

w F.I.= Z

F.I. Q(y)dy+C

Universidad de Antioquia, Depto. de Matematicas

2.7. ECUACION DIFERENCIAL DE BERNOULLI

w ey 2 2 =

Z

ey 2

2 (−y3)dy+C

hagamos: u= y₂2 _⇒du=y dy, y2 _{= 2u}

w ey 2 2 =−

Z

y3ey 2

2 dy+C =−2

Z

ueu _du+C

e integrando por partes, obtenemos: w ey22 =−2u eu+ 2eu+C

x−1ey 2

2 =−y2e

y2

2 + 2e

y2

2 +C ⇒ 1

x =−y

2_{+ 2 +Ce}−y22

Como y(1) = 0 entonces C =₋1, por lo tanto la soluci´on particular es: 1

x =−y

2_{+ 2}

−e−y 2 2

Resolver las E.D. de los siguientes ejercicios:

Ejercicio 1. 2dy_dx = y_{x− y}x2 con y(1) = 1.

(Rta.: y3 _=−3x2_{+ 4x}3₂₎ Ejercicio 2. y0 ₌ 3x2

x3_+y+1.

(Rta.: x3 _{=−y−2 +Ce}y₎ Ejercicio 3. tx2dx

dt +x

3 _=tcost.

(Rta.: x3_t3 _{= 3(3(t}2_{−2) cost+t(t}2_{−6) sent) +C)} Ejercicio 4. y0 ₌ x

x2_y+y3.

(Rta.: x2_+y2_{+ 1 =Ce}y2

)

Ejercicio 5. xy0_+y=x4_y3_.

(Rta.: y−2 _=−x4_+cx2₎

Ejercicio 6. xy2_y0_+y3 ₌ cosx x .

(Rta.: x3_y3 _{= 3xsenx+ 3 cosx+C)}

Universidad de Antioquia, Depto. de Matematicas

Ejercicio 7. x2_y0_−y3 _{+ 2xy= 0.}

(Rta.: y−2 ₌ 2

5x +Cx 4₎

Ejercicio 8. Hallar la soluci´on particular de la E.D.

dx

dy −

2

yx=

√_y(x y2)

3 2

tal que y(1) = 1 (Rta.: y3 _=x)

Ejercicio 9. Hallar y(x) en funci´on def(x) si

dy

dx +f(x)y =f(x)y

2

(Rta.: y= 1 (1−CeRf(x)dx₎)

2.8.

E.D. NO LINEALES DE PRIMER

OR-DEN

Sea

(y0)n+a1(x, y)(y0)n−1+a2(x, y)(y0)n−2+. . .+an₋1(x, y)y0+an(x, y) = 0,

dondeai(x, y) parai= 1. . . nson funciones reales y continuas en una regi´on

R del plano XY. Casos:

i) Se puede despejary0_.

ii) Se puede despejary. iii) Se puede despejarx.

Caso i). Si hacemos p= _dxdy =y0_{, entonces}

pn_+a

1(x, y)pn−1+a2(x, y)pn−2+. . .+an−1(x, y)p+an(x, y) = 0.

Universidad de Antioquia, Depto. de Matematicas

2.8. E.D. NO LINEALES DE PRIMER ORDEN

En caso que sea posible que la ecuaci´on anterior se pueda factorizar en factores lineales de p, se obtiene lo siguiente:

(p₋f1(x, y))(p−f2(x, y)). . .(p−fn(x, y)) = 0,

donde fi(x, y) parai= 1, . . . , nson funciones reales e integrables en una

re-gi´on R del plano XY.

Si cada factor tiene una soluci´on ϕi(x, y, c) = 0, para i= 1, . . . , n.

entonces la soluci´on general es Qn_i=1ϕi(x, y, c) = 0.

Ejemplo 14.(y0 _{− senx)((y}0₎2_{+ (2x−lnx)y}0 _{−2xlnx) = 0.}

Soluci´on:

(p₋ senx)(p2+ (2x₋lnx)p₋2xlnx) = 0

(p₋ senx)(p+ 2x)(p₋lnx) = 0

Para el factor p₋ senx= 0_{⇒ dx}dy ₋ senx= 0_⇒dy = senx dx_⇒ y =₋cosx+C

φ1(x, y, C) = 0 =y+ cosx−C

Para el factor p+ 2x= 0 _{⇒ dx}dy =₋2x_⇒dy=₋2x dx

⇒y=₋x2 +C _⇒φ2(x, y, C) = 0 =y+x2−C

Para el factor p₋lnx= 0 _⇒ dy_dx = lnx_⇒dy= lnx dx

y=

Z

lnx dx+C,

e integrando por partes:

y=

Z

lnx dx+C =xlnx₋

Z

x1

xdx=xlnx−x+C φ3(x, y, C) = 0 =y−xlnx+x−C

La soluci´on general es: Q3_i=1φi(x, y, C) = 0

(y+ cosx₋C)(y+x2 ₋C)(y₋xlnx+x₋C) = 0

Universidad de Antioquia, Depto. de Matematicas

Ejercicio 1. p(p2_−2xp−3x2_{) = 0.}

(Rta.: (y₋c)(2y₋3x2_+c)(2y+x2_{+c) = 0)}

Ejercicio 2. 6µ2dν dµ

2

−13µνdν dµ −5ν

2 _{= 0.}

(Rta.: (νµ13 −c)(νµ− 5

2 −c) = 0)

Ejercicio 3. (y0₎3_−y(y0₎2_−x2_y0_+x2_{y = 0.}

(Rta.: (x₋ln_|y_|+c)(y+x2

2 −c)(y− x2

2 −c) = 0) Ejercicio 4. n2_p2_−x2n_{= 0, con n 6= 0 y} dy

dx =p=y0.

(Rta.: (y+ xn+1

n(n+1) −c)(y− xn+1

n(n+1) −c) = 0) Ejercicio 5. x2_(y0₎2_{+ 2xyy}0_+y2 _=xy

Ejercicio 6. Denotando por P cualquier punto sobre una curva C y T

el punto de intersecci´on de la tangente con el ejeY. Hallar la ecuaci´on deC

si P T =k.

(Rta.:(y+c)2 ₌h√_k2_−x2_+kln

√

k2_−x2_−k

x

i2

, con _|x_{| ≤}k, k >0.)

Caso ii). Son ecuaciones de la forma F(x, y, p) = 0 y de la cual puede despejarse y, es decir: y=f(x, p), donde xy p se consideran como variables independientes, la diferencial total es:

dy= ∂f

∂xdx+

∂f

∂p dp

luego

dy

dx =p=

∂f ∂x + ∂f ∂p dp dx

o sea que

0 =

∂f

∂x −p

+∂f

∂p dp

dx =g(x, p, p

0_{), donde p}0 ₌ dp

dx

y por tanto

∂f

∂x −p

dx+ ∂f

∂p dp= 0

Universidad de Antioquia, Depto. de Matematicas

2.8. E.D. NO LINEALES DE PRIMER ORDEN

es una E.D. de primer orden en xyp. Generalmente (teniendo buena suerte)

g(x, p, p0) = 0

se puede factorizar, quedando as´ı: g(x, p, p0_{) = h(x, p, p}0_{)φ(x, p) = 0.}

a) Con el factor h(x, p, p0_{) = 0 se obtiene una soluci´on h}

1(x, p, c) = 0,

se elimina p entre h1(x, p, c) = 0 y F(x, y, p) = 0 y se obtiene la soluci´on

general.

b) Con φ(x, p) = 0 se obtiene una soluci´on singular, al eliminar p entre

φ(x, p) = 0 y F(x, y, p) = 0.

Ejemplo 15.y=f(x, p) = (px+x2_{) lnx+ (px+x}2₎2₋x2

2, dondep= dy dx

Soluci´on: dy_dx =p= ∂f_∂x +∂f_∂pdxdp si x₆= 0

p= (p+2x) lnx+(px+x2)1

x+2(px+x

2_)(p+2x)

−x+[xlnx+2(px+x2)x]dp

dx

p= (p+ 2x) lnx+p+x+ 2x(p+x)(p+ 2x)₋x+ [xlnx+ 2x2_(p+x)]dp dx

0 = (p+ 2x) lnx+ 2x(p+x)(p+ 2x) + [xlnx+ 2x2_(p+x)]dp dx

0 = (p+ 2x)[lnx+ 2x(p+x)] +x[lnx+ 2x(p+x)]dp_dx

0 = [lnx+ 2x(p+x)]p+ 2x+xdp_dx

0 =h(x, p),Φ(x, p, p0₎

1) Con el factor Φ(x, p, p0_{) = p+ 2x+x}dp dx = 0

⇒x_dxdp +p=₋2xx_⇒=06 _dxdp +_xp =₋2 (dividimos porx) E.D.lineal en p, P(x) = _x1, Q(x) =₋2

F.I.=eRP(x)dx_=eR 1

xdx=eln|x|=x

p F.I.=R F.I.Q(x)dx+C

Universidad de Antioquia, Depto. de Matematicas

px=R x(₋2)dx+C =₋2x₂2 +C =₋x2_+C

p=₋x+C

x (dividimos por x)

luego sustituimos en la E.D. original:

y= (px+x2) lnx+ (px+x2)2₋ x

2

2

y= (₋x2+C+x2) lnx+ (₋x2+C+x2)2₋ x

2

2 soluci´on general

y=Clnx+C2₋ x

2

2 2)h(x, p) = lnx+ 2x(p+x) = 0

0 = lnx+ 2xp+ 2x2

2xp=₋lnx₋2x2

luego p=₋lnx_2x−2x2 _⇒px=₋lnx+2x₂ 2 sustituyo en la E.D. original:

y= (px+x2) lnx+ (px+x2)2₋ x

2

2

y =

−lnx+ 2x

2

2 +x

2

lnx+

−lnx+ 2x

2

2 +x

2

2

− x

2

2

y =

−lnx₋2x2_{+ 2x}2

2

lnx+

−lnx₋2x2_{+ 2x}2

2

2

− x

2

2

y=₋ln

2

x

2 + ln2x

4 −

x2

2 luego la soluci´on singular es

y=₋ln

2_x

4 −

x2

Universidad de Antioquia, Depto. de Matematicas

2.8. E.D. NO LINEALES DE PRIMER ORDEN

Resolver por el m´etodo anterior los siguientes ejercicios, dondep= dy_dx:

Ejercicio 1. xp2_{−2yp+ 3x= 0.}

(Rta.: 2cy =c2_x2_{+ 3, y}2 _{= 3x}2₎

Ejercicio 2. y=pxlnx+p2_x2_.

(Rta.: y=clnx+c2_{, y =−}1 4ln

2_x)

Ejercicio 3. y= 5xp+ 5x2_+p2_.

(Rta.: y=cx₋x2 _+c2_{, 4y+ 5x}2 _{= 0)} Ejercicio 4. p2_x4 _=y+px.

(Rta.: y=c2_−cx−1_{, y=−} 1 4x2)

Ejercicio 5. 2y= 8xp+ 4x2_{+ 3p}2_.

(Rta.: 2y= 3(c₋x)2_{+ 8(c−x)x+ 4x}2_{, y=−}2x2

3 ) Ejercicio 6. y=xp₋1

3p 3_.

(Rta.: y=cx₋ 1 3c

3_{, y =±}2 3x

3 2)

Caso iii). Si en la ecuaci´on F(x, y, p) = 0, se puede despejar x=g(y, p) con y y p como variables independientes; hacemos dy_dx =p, o sea que dx_dy = 1_p y como

dx= ∂g

∂ydy+

∂g

∂pdp

luego

dx

dy =

1

p =

∂g

∂y +

∂g ∂p

dp dy

por tanto

∂g

∂y −

1

p

+∂g

∂p dp

dy = 0 =h(y, p, p

0₎

donde p0 ₌ dp dy.

Ejemplo 16.cos2_β dβ dα

3

−2α_dαdβ + 2 tanβ = 0 Soluci´on: con p= dβ_dα, se tiene: