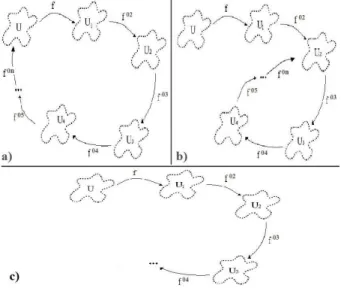
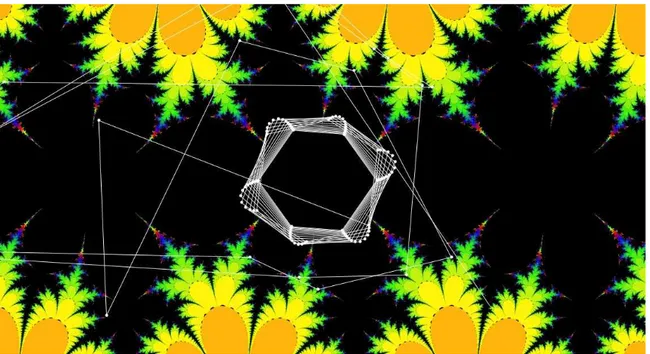
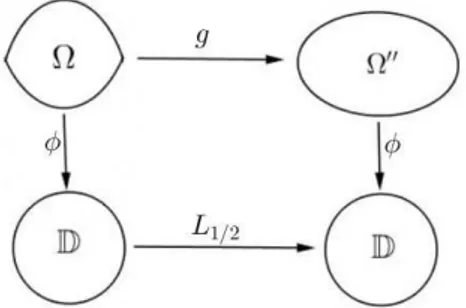
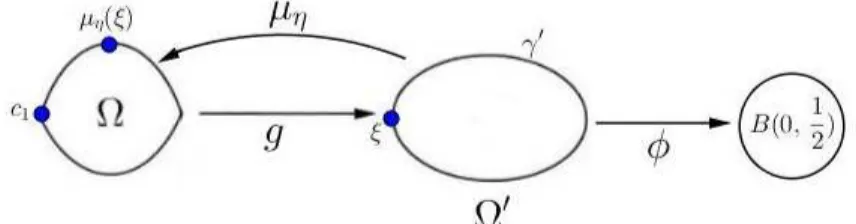
Un estudio de la dinámica de e2πiθsen(z)

Las lecturas de francobordo/calado se toman para establecer la posición de la flotación y determinar a su vez el desplazamiento del buque en el momento de realizar la prueba

Volviendo a la jurisprudencia del Tribunal de Justicia, conviene recor- dar que, con el tiempo, este órgano se vio en la necesidad de determinar si los actos de los Estados

Un método de estudio aparte de ser una herramienta muy útil al momento de estudiar también nos ayuda a agilizar nuestra mente y tener una buena memoria para futuro?. Palabras

Para ello, trabajaremos con una colección de cartas redactadas desde allí, impresa en Évora en 1598 y otros documentos jesuitas: el Sumario de las cosas de Japón (1583),

Entre nosotros anda un escritor de cosas de filología, paisano de Costa, que no deja de tener ingenio y garbo; pero cuyas obras tienen de todo menos de ciencia, y aun

[r]

SVP, EXECUTIVE CREATIVE DIRECTOR JACK MORTON

Social Media, Email Marketing, Workflows, Smart CTA’s, Video Marketing. Blog, Social Media, SEO, SEM, Mobile Marketing,