UNIVERSIDAD AUTONOMA METROPOLITANA UNIDAD IZTAPALAPA
T E O R Í A Y D E S A R R O L L O D E G R A F I C A C I ~ N P O R C O M P U T A D O R A
INTRODUCCI~N CAPITULO I. CAPITULO IL CAPITULO III.
TRANSFORMACIONES EN DOS DIMENSIONES. TRANSFORMACIONES Y PROYECCIONES EN
TRES
DIMENSIONES. CUR VAS PLANAS.
DIRIGIDO POR:
I '
z
1-4
8.3
CONTENIDO
PANORAMA GENERAL DE LOS EDITORES GRÁFICOS
Simulación tndlmensional 1
DlbuJando en dos dimensiones ... ?
Reducción de tres a dos dimensiones ... 3
DlbuJando en tres dimensiones ... 4
El punto de visión en un espacio tndlmensional
...
5. . ...
. .
. .. . .
CREACIóN DE DIBUJOS Modelos gráficos ... 5Construcclon de objetos ... 7
Modelos esquematlcos ... 7
.I
, .
Modelo de superficie ... ..S PROCESAMIENTO DE IMÁGENES Y V I S U A L I Z A C I ~ N Tecnología de procesamiento de imágenes....
.9TECNOLOGÍA DE PROCESAMIENTO DE IMÁGENES Aplicaciones y fuentes de las lmagenes 1 O Reconstrucclon de lmagenes 1 O Restauración de lmagenes 11 Mejorar la imagen ... 1 1 . I ... .I . I ... . , ... Hardware necesario para el procesamiento de imágenes ... 12
TECNOLOGÍA DE VISUALIZACIóN CIENTÍFICA Simulaclon 12 Reconstrucción de volúmenes ... 13
.,
... Voxels. ... 13Modelo de superficie ... 13
Reconstrucción directa de volúmenes ... 14
Aplicaciones ... 14
Publlcldad electrónica ... 15
Animación y gráficas ... 15
Sistema de informaclon geográfica ... ..:. ... 15
Recursos de la tierra ... 16
Medicina ... 16
Ingeniería Química ... 16
Medidas de desempeño y requerimientos ... 17
Bibliotecas gráficas ... 18
QUIEN NECESITA DE GRÁFICAS POR COMPUTADORA
Los sistemas gráficos ... 21
La pantalla ... 21
Pixeles y puntos de fósforo ... 22
Converslon y refrescado 22 Cálculos para l a s gráficas ... 3’ 3 El ambiente de ventanas ... 23
El ratón ... 24
La apllcaclon ... 24
Disposltlvos perlfencos ... 25
Scanner ... 26
Video ... ~6
Impresoras ... 26
Gráficas en una red ... 27
Tecnología Raster . . . 28
Espacio 2-D y posiciones de los pixeles ... 28
Espacio 3-D y posiciones de los pixeles ... 29
Pantallas de sistemas multlblts 30 True color ... 30
. . ...
. . .
Interacción del software y del hardware ... 24. .
. . .
. . ...CAPITULO 1
TRANSFORMACIONES EN DOS DIMENSIONES Introducción ... 32Representaclon de puntos 32 Transformaciones de puntos
...
33Transformaciones de líneas rectas ... 36
Transformaciones de puntos medios ... 37
Transformaciones de líneas paralelas ... 38
Transformaciones de líneas intersectadas ... 39
Rotación ... 42
Reflexión ... 44
Escala: ampllaclon y reducción ... 47
Comblnacron de transformaciones ... 49
Transformaciones de un cuadrado unitario ... 52
Transformaciones de cuerpos sólidos ... 5 5 Translación y coordenadas homogéneas ... j 6 Rotación alrededor de un punto arbitrario ... 57
Reflexión a través de una línea arbitraria ... 58
CAPITULO
2
TRANSFORbIACIONES Y PROYECCIONES EN TRES DIMENSIONES
Introducclon 64 Escalamiento en tres dimensiones ... 65
Cizallamiento en tres dimensiones ... 68
Rotaclon en tres dimensiones 69
Reflexión tridimensional ... 76 Translaclon trldlmensional ... 78 Transformaciones multiples 79
..
.... .
...
. . . .
. .
...
Rotaciones alrededor de un eje paralelo a un eje coordenado ... 82 Rotación alrededor de un eje arbitrario en el espacio ... 88 Reflexión alrededor de un plano arbitrario ... 95
Geometría perspectiva y ann 100
Proyecciones axonometrlcas ... 111
Transformaciones en perspectiva
...
134 Técnicas para la generación de vistas en p e q e c t i v a ... 149 Desvaneclmlento de puntos 160Fotografia y la transformación en perspectiva ... 166 Comparación de proyecciones con objeto fijo
y con centro de proyecclon f i ~ o ... 169 Reconstrucción cle imágenes tridimensionales ... 175
C I
... Proyecciones ortográficas ... 103
Proyecciones oblicuas ... 124
. .
. .
...
. . .
CAPITULO 3
CURVAS
PLANASIntroducción ... 183 Representac . 011 de curvas ... 183 Curvas ncj
F
lrametrizadas ... 185Curvas pan metncas 187
Representa :ión paramétrica de una elipse ... 198 Representa :ión paramétrica de una parábola ... 203
. .
. .
...
Representa :ión paramétrica de un circulo ... 193
Representadón paramétrica de una hipérbola ... 207 Procedimiento para utilizar secciones cónicas ... 212
. .
PANORAMA GENERAL
DE LOS EDITORES GRÁFICOS.
El presente capitulo mostrará los componentes esenciales d e los gráficos por computadora, se mostraran conceptos sobre dibujo en dos y
tres dimensiones.
La base para la generación de dibujos por computadora es la geometría. Los dibujos gráficos son compuestos de elementos geométricos, tal como puntos, líneas, círculos, arcos, triángulos y
rectángulos, también conocidos como "Primitivas".
Esencialmente la generación de los dibujos es por la conexión de los puntos con líneas. Estas primitivas sirven como la base de
construcciones de objetos más complejos.
También por computadora, proporciona primitivas más complejas, como polilíneas, polimarcas.
La diferencia fundamental entre objetos gráficos en dos y tres dimensiones, es que los objetos en dos dimensiones son planos y los de tres dimensiones tienen volumen; hay que notar que los objetos en tres dimensiones son creados de primitivas de dos dimensiones; también hay que notar que los dibujos en tres dimensiones, son simulados, dibujando el objeto tridimensional en una superficie bidimensional.
SIMULACIóN TRIDIMENSIONAL.
Uno puede crear la apariencia d e tres dimensiones sobre una gráfica, simulando los objetos de dos dimensiones, este efecto crea la
apariencia de una escena en tres dimensiones, pero usando varias figuras en dos dimensiones que hacen la apariencia de frente y atrás del objetos en tres dimensiones.
Escena Polígonos
Fig. 1. Los polígonos requeridos para simular formas en tres dimensiones con formas de dos dimensiones
Estos objetos no pueden ser rotados, en el espacio tridimensional, porque son planos, los dibujos son datos en dos dimensiones que solo crean la ilusión de tres dimensiones. Se necesita crear una nueva escena si se quiere ver los objetos en una nueva posición.
DIBUJANDO EN DOS DIMENSIONES.
El dibujo en dos dimensiones se describe por dos ejes: un eje que recorre horizontalmente, llamado el eje X, otro eje corre verticalmente, llamado eje Y. Estos ejes forman un sistema de coordenadas que
empiezan con un origen (0,O). Cada pixel tiene una dirección en el sistema de coordenadas, en una intersección de X,Y. Un punto coordenado de un pixel puede ser identificado por la distancia a los ejes X, y Y.
Las líneas dibujadas sobre la cuadricula del sistema coordinado son llamados vectores. Un vector se dibuja, especificando los dos puntos extremos de este.
Similarmente se puede dibujar un rectángulo especificando las cuatro esquinas o vértices.
Fig. 3. Dibujando un rectángulo.
REDUCCIóN DE TRES A DOS DIMENSIONES.
En gráficos en tres dimensiones la computadora calcula la
geometría de objetos en tres dimensiones. Una imagen es descrita en un espacio de tres dimensiones en términos de ancho, alto y largo; sin embargo, porque la superficie de desplegado es plano, el resultado final debe ser en dos dimensiones.
Un objeto puede ser red,Jcido a dos dimensiones antes de dibujarse. Esto es a partir de una secuencia de pasos que ocurre en un tiempo, un objeto es dibujado y manipulado para después redibujarse.
Cuando se usan rotaciones
e n
un objeto a una nueva orientación 0escalas a nuevos tamaños, la computadora calcula las nuevas posiciones y orientaciones de las primitivas d e las figuras en tres dimensiones y son trasladadas en un espacio de la pan:alla en dos dimensiones y que pueden ser desplegados en la pantalla. El proceso de reducción de tres dimensiones a dos, para dibujar es llamado proyecciiin.
DIBUJANDO EN TRES DIMENSIONES.
Los gráficos en tres dimensior:es son mucho más complejos que la de dos dimensiones por diversas razones. Primero, la computadora debe hacer más cálculos en la creaciór; de gráficos en tres dimensiones.
También se tiene que ver que existe L n paso extra involucrado en el dibujo de gráficos en tres dimensiones, Dor que el último paso debe ser
proyectado sobre la superficie de dc S dimensiones. Adicionalmente, con
las gráficas en tres dimensiones t,ene que dibujarse el volumen de espacio, una figura en tres dimension ?S puede tener mucho lados y puede moverse hacia adelante, atrás en el espacio.
Para entender el espacio en tres dimensiones hay que pensar en los ejes X y Y formando un plano, viendo el final como una caja rectangular. El eje
2
es conectado a este plant) en una esquina y corriendo perpendicularmente a el plano, representa el largo de la caja. El espacio tridimensional es definido por estos tres ejes, llamados la vistads
volumen, puede ser considerado un espacio infinito en todas direcciones.Y
X
Punto de Visión Vista de volumen
Fig. 4. La vista de volumen: el espacio en tres dimensiones creado por los ejes X,Y,Z.
La vista de volumen se considera un espacio en tres dimensiones, que el usuario puede ver como un cuarto con la puerta abierta. Pero en realidad, el usuario puede figurarse dentro del cuarto y ver las imágenes desde cualquier lugar.
Esta capacidad es algunas veces descrita con analogía a una cámara (y a veces es llamada cámara sintética).
Cada escena vista en un monitor es vista desde un ángulo. Aparte de las coordenadas de vista de volumen, existe un sistema de
coordenadas adicional que puede ser orientado en cualquier lugar de la vista de volumen. El sistema coordinado de la cámara sintética, es una definición matemática que crea la ilusión de tres dimensiones. Por que los
sistemas gráficos conocidos de la geometría de tres dimensiones de una escena, como si existieran en el espacio del mundo real, los sistemas gráficos son hechos para producir imágenes de los objetos en la escena de todos los ángulos. La ventaja de es aprovechar que los objetos en la escena pueden ser calculados y puestos en un lugar, en posiciones con
respecto a otro. El punto de visión puede recorrer la escena al rededor.
CREACIóN
DE
DIBUJOS.
Existen varios caminos para crear dibujos por computadora,
dependiendo del efecto deseado. Los dibujos sofisticados requieren de un tiempo de proceso de la computadora.
MODELOS GRÁFICOS.
Un modelo gráfico es un objeto que típicamente aproxima un objeto
del mundo real con propiedades tales como figuras, tamaño, orientación y color. Hay dos tipos de modelos generales en gráficos en tres
dimensiones. El modelo de esquema de alambrey el modelo de superficie.
El modelo a escoger depende de las necesidades del usuario, en cualquier caso el modelo de esquema de alambre es el más apropiado.
Fig. 5. Modelo de estructura de alambre en tres dimensiones.
Sin embargo, si se quiere simular un objeto con más realismo es posible usar un modelo de superficie con colores complejos, iluminación y sombreado. Note que el modelo de superficie es conocido también como
modelo sólido.
Fig. 6. Modelo de superficie en tres dimensiones con iluminación.
Hay un conocimiento geométrico en ambos modelos de alambre y superficie, por que los objetos gráficos son manipulados por geometría. La diferencia entre los modelos, es que el modelo de superficie puede hacer: opacar el color del sólido, la luz, la sombra y ocultar líneas.
La distinción entre construcción de objetos en esquema de alambre
y superficie, es que los objetos en alambre s m creados por vectores. Juntos estos vectores forman las aristas de un gbjeto de superficie. En un esquema de alambre también puede ser creado de polilíneas. En contraste los modelos de superficie son ccnstruidos por poligonos que crean la superficie d e un cspacio cerrado.
CREACIóN DE MODELOS ESQUEMÁT’COS
(O
DE ALAMBRE).En el dibujo de este modelo s . ; necesita conocer la longitud de los vectores y donde se unen. Podern;>s describir esta información en dos lista que pueden ser almacenadAs en una base de datos. Una lista contiene
los
vértices del modelo, y anotar las aristas del modelo. La listad e vértices describe la geumetrra del modelo, cuando cada esquina es
localizada en el espacio tr:dimensional. La lista de aristas describe la conectividad, com9 cada v c c t x es conectado a otros vectores por sus vértices en común.
5
1 2
a b
List2 de Vertices Lista de Aristas Vert ces x , y , z Arista Vertice 1 Vertice 2
1
o,o,o
1 1 22
2
33 2,0,2 3 3 4
4 o,o,2 4 4 1
5 1,3,1 5 5 4
6 5 3
7 5 2
8 5 1
CREACIóN DEL MODELO DE SUPERFICIE.
Para crear un modelo de superficie para el mismo ejemplo, se necesitan 5 polígonos. Los datos del dibujo consisten de las caras de los
poligonos del modelo. Cada cara del polígono es definido por todos los
vértices. En el dibujo del modelo de superficie, la aplicación necesita
conocer como las caras del objeto están y que vértices están por cara.
5
Lista de Caras Vertices
A 1 2 3 B 2 3 5 C 3 4 5
D
1 4 1 E 1 2 3 4La tecnología d e imágenes complementa las gráficas por computadora. Para trabajar con imágenes es necesario interrelacionar varias tecnologías de la ciencia computacional; además de las gráficas por computadora diseñadas para procesar o generar imágenes.
La reconstrucción de imágenes se utiliza principalmente en medicina, donde los usuarios pueden elaborar imágenes de calidad a partir de rayos-x. La visualización trata de acelerar el proceso de análisis de datos científicos a través de su representación gráfica. También hay reconstrucción de volúmenes a partir de ciertos datos
.
TECNOLOGíA DE PROCESAMIENTO DE IMÁGENES
En muchas aplicaciones el procesamiento de imágenes y las gráficas por computadora son tecnologías que se acompañan.
Generalmente el termino gráficas se refiere a imágenes generadas por una computadora. Mientras que procesamiento de imágenes se refiere a fotos obtenidas de fuentes externas ( datos digitales o imágenes físicas que deben ser convertidos a datos digitales que representen una imagen en la pantalla de la computadora ). Por ejemplo fotografías tomadas por naves espaciales robots, datos d e censores remotos ( satélites, imágenes aéreas )
,
tomografía axial computarizada, imágenes de resonancia magnética y ultrasonido.En el procesamiento de imágenes hay que modificar datos visuales, para mejorar o clarificar imágenes y así lograr un análisis más profundo, un ejemplo de lo anterior son los datos que mandan las naves espaciales.
Los datos de imágenes son colecciones de valores, la relación bit-
pixel representa uno de muchos valores que al ser combinados
correctamente forman una imagen en la pantalla. Por ejemplo una imagen geométrica se define por sus vértices y puede ser manipulada al hacer transformaciones únicamente sobre esos vértices; por otro lado una imagen similar digitalizada es representada por una gran cantidad de pixeles.
El volumen de los datos que describen imágenes escaneadas es mucho más grande que los datos necesarios para que una computadora genere una imagen similar. por esto mismo, el procesamiento de
imágenes digitalizadas requiere gran poder de computo ( aceleradores gráficos ).
APLICACIONES Y FIJENTES DE LAS IMÁGENES
Cualquier imagen puede ser digitalizada en datos binarios y después mostrada m un monitor; este tipo de imágenes se utiliza en publicidad
,
planeac; i n urbana, manufactura de mapas. Cada vez más los equipos de censores remotos, producen directamente datos digitales y las aplicaciones doride se utilizan estas imágenes son por ejemplo: el estudio de la radiacion y el calor provenientes de la tierra o el océano, los cambios en regiones sismicas, el estudio de la capa de ozono, vigilancia militar, etcétera.En el campo de la medicina, los rayos-x son la fuente más común de imágenes, la tomografía axial computarizada (TAC ) produce imágenes de dos dimensiones que mepresentan rebanadas de cierto tejido u órgano; las imágenes de resonansia magnética son otro ejemplo donde después de aplicar radiación eiec ':romagnética se pueden detectar células anormales en imágenes s e c c i ó n ~ ~ l e s d e musculos, tejidos y huesos. Los médicos pueden así analizar
los
órganos internos sin necesidad de hacer unacirugía exploratoria y m caso de ser necesario la cirugía será más precisa y con mayores probab'lidades de éxito.
RECONSTRUCCI~N D E IMÁGENES
La reconstrucc ón de imágenes se realiza principalmente en el campo medico. Los dzltos de la imagen son reunidos al emitir radiación a través de un objeto y proyectar los rayos hacia un detector. Las
proyecciones reunida:; forman un patrón bidimensional que puede ser reconstruido en una re5anada seccional.
J
t
Fuente
t
.dDetectores Rebanadas
J
de datos
RESTAURACIóN DE IMÁGENES
Estas técnicas reparan imágenes degradadas o dañadas, hasta tener una aproximación d e la apariencia ideal de la imagen. La degradación es inevitable mientras las imágenes son capturadas y
transferidas al medio electrónico o impreso. Mayor degradación ocurre cuando la cámara no esta enfocada, si el objeto se esta moviendo, si la actividad atmosférica causa distorsión. Una de las técnicas más comunes es el filtrado.
MEJORAR LA IMAGEN
Las técnicas de mejoramiento de imágenes no necesariamente reflejan el ideal original de la imagen. Usualmente lo que se desea es modificar una imagen y que Ciertas caracteristicas sean más prominentes, que el color sea más notorio. En medicina se utiliza para que el medico pueda analizar la estructura VaSCular, muscular o esquelética más fácilmente y así detectar anormalidades. Otra técnica es crear grandes contrastes en la imagen para eliminar características que no es
importante analizar
HARDWARE NECESARIO PARA EL PROCESAMIENTO DE IMÁGENES
Ya que las imágenes no están predefinidas en términos de primitivas geométricas que pueden ser transformadas aisladamente; mostrar y
manipular imágenes exige grandes capacidades de computo y mucha rapidez.
Las computadoras utilizadas para estas tareas han sido las "Super computadoras" y estaciones de trabajo dedicadas al procesamiento de
imágenes. Actualmente la tendencia es utilizar estaciones de trabajo con capacidades de multiproceso, alta resolución y alta calidad en el manejo de grandes volúmenes de datos.
TEC NOLO GSA DE VISUA ,L I Z A C I ~ N
Se utilizan gráficas y otras imágenes para ayudar a los científicos a analizar datos complejos.
Los científicos reúnen datos de investigación. De exploraciones espaciales, experimentos de laboratorio, censores de movimientos
sismicos, muestras oceánicas, de suelos, etcétera. El analizar estas
grandes cantidades de datos es una tarea muy laboriosa, todos esos datos no tienen un significado claro. La visualización comunica
eficientemente las ideas y resume el significado de patrones repetitivos en datos numéricos; así el usuario puede eliminar rápidamente de las
consideraciones, los datos de poca importancia y concentrarse en los
datos que presentan información concreta y relevante.
SIMULACIóN
Es una visualización científica usada en ambientes de prueba y entrenamiento, por ejemplo, animación de movimientos mecánicos, flujo de fluidos, simulación de reacciones químicas, simulación de vuelos.
tiempo y dinero; la simulación computarizada permite seleccionar
opciones de diseño y examinar los resultados; finalmente será necesario construir un modelo y probarlo pero se habrán eliminado muchos pasos intermedios. Esto es de gran importancia en costo, calidad, tiempo de
mercado y cornpetitividad.
RECONSTRUCCIÓN DE VOLúMENES
Es un cpmpo nuevo que introduce modelos y gráficas en ( 3-D ) para visualizar datos volumétricos de investigaciones científicas, que pueden ser obtenido.; al combinar rebanadas bidimensionales y construir
volúmenes 3D
VOXELS
En reconstrucción de volúmenes, un volumen 3-D es una estructura compuesta de el1:mentos de volumen (voxels) ; los voxels son análogos a
los pixeles. Para mostrar los voxels 3-D que son visibles, deben ser mapeados a los pixeles correspondientes. En forma deben ser mapeados a los pixeles correspondientes. En forma similar a la proyección de
gráficas 3-0 en sL,perficies 2-D.
La superficie de un volumen 3-D es reconstruida de las rebanadas 2- D existentes. Primero se detectan las orillas (aristas)
,
para definir la estructura; después se definen superficies tridimensionales y contornos basados en aristas de diversas formas; después las superficies pueden ser descritas en términos de primitivas geométricas.RECONSTRUCCIóN DIRECTA DE VOLúMENES
Este método crea un volumen 3-0 sólido en lugar de una superficie que define un volumen. Los voxels son tratados como células ocupadas o
desocupadas. Aquellas que son parte de la imagen están ocupadas y son visibles las otras no son mostradas.
Con este método es posible cortar el volumen en cualquier ángulo y
ver su composición interna, es útil en medicina, también se usa para analizar regiones sísmicas.
AI volumen se le pueden añadir apariencias por ejemplo (colores) para representar datos de otras variables y serían imágenes gráficas de cuarta o hasta quinta dimensión.
APLICACIONES
Las sofisticadas bibliotecas gráficas, gráficas interactivas,
procesamiento d e imágenes y las herramientas de visualización; permiten
PUBLICIDAD ELECTR~NICA
La publicidad electrónica se utiliza en muchas industrias, en
empresas de publicidad, periódicos, revistas, industrias de alta tecnología aerospacial, automotriz, de manufacturas y
telecomunicaciones.
El diseño asistido por computadora ( ECAD ) se usa en muchas industrias; el diseño electrónico automatizado ( EDA ) se usa en el diseño de chips y placas de circuitos. Los ambientes EDA y ECAD se basan principalmente en primitivas de dos dimensiones ( 2-0 vectores, 2-D polígonos y texto ). El realizar diseños por computadora permiten probar la viabilidad antes de que el diseño sea implementado.
Las industrias de arquitectura, ingeniería y construcción ( AEC )
utiliza los sistemas gráficos para el diseño de interiores, estructuras
comerciales, edificios, redes de telecomunicación, autopistas, vías, aeropuertos, presas, etcétera.
Las aplicaciones AEC necesitan sofisticadas bibliotecas gráficas y bases de datos con gran capacidad de almacenamiento; la mayoría de las aplicaciones AEC usan primitivas 2-0, pero al bajar el costo del software y de los sistemas gráficos. Los sistemas tridimensionales se están usando cada vez más, el usuario puede tener vistas de la estructura interior y
exterior desde muchos ángulos.
Aplicaciones mecánicas CAD simplifica el proceso mecánico de diseño, el diseñador puede construir eficientemente nuevos productos a partir de modelos establecidos y proponer nuevas dimensiones y
características.
A N I M A C I ~ N Y GRÁFICAS
Se utiliza en publicidad, arte comercial y no comercial, tecnología de video, caricaturas y simulación científica. Para las caricaturas primero se crean todos los dibujos y después se pasan en cierto orden rápidamente, en la pantalla de la computadora. Por el contrario los modelos de simulación ( de vuelo ) requieren mucho poder de computo, ninguno de los movimientos son precalculados.
Incluyen bases de datos; combinan datos de censos, información demográfica y geográfica, por ejemplo encontrar el mejor lugar para
ubicar un hospital de emergencia. Básicamente utilizan bibliotecas Z-D,
pero los ambientes 3-D se están incrementando; también se utilizan en investigaciones culturales, arqueológicas.
RECURSOS DE LA TIERRA
El estudio de recurso naturales e interpretación de datos sísmicos y geológicos son los más comunes. Datos de mapas combinados con la
información de bases de datos le dan al usuario la posibilidad de analizar grandes cantidades de datos. Muchas aplicaciones requieren del
procesamiento de imágenes y datos gráficos. Se utiliza en estudios ambientales, por ejemplo el calentamiento terrestre debido al exceso de bióxido de carbono y otros contaminantes y variables.
MEDICINA
Un radiologista puede usar gráficas por computadora para modelar una irradiación; sobreponer el modelo del rayo sobre el modelo del volumen del tumor y analizar donde debería dar el rayo y con que intensidad.
Un centro medico plantea tratar el cáncer con aceleradores de protones que utilizan radiación para destruir un tumor sin dañar el tejido que lo rodea. El doctor utilizaría el sistema gráfico para posicionar el
ángulo del rayo y aplicar la dosis apropiada basada en la simulación y en el tratamiento.
INGENIERÍA QUíMICA
Los químicos analizan las reacciones de las moléculas a varias sustancias y con equipos de alta calidad ( software y hardware ) pueden modelar estar reacciones. Con técnicas de animación el químico puede efectuar enlaces moleculares y con cambios de color en el modelo molecular simular las reacciones. Debido a los archivos de datos que se utilizan y a las transformaciones que hay que hacer sobre las
animaciones, la modelación molecular es el campo que requiere el
software más sofisticado y el hardware más rápido. Una aplicación típica en esta área es la cristalografía ( cristalización, formas y estructuras de cristales normalmente usados en investigación farmacéutica )
,
también en genética, en modelación molecular y en diseño de drogas.Es importante que las aplicaciones descansen sobre un hardware adecuado a sus demandas. El análisis de datos científicos en modelos volumétricos necesitan nivel de procesamiento de alto nivel, así como excelente software de visualización.
Requerimientos de software de las aplicaciones.
Requerimientos de Software Aplicación
Reconstrucción devolumen
Procesamiento deimágenes Transparencias 3D
S m h e a d o en 3D
Sóldos en 3D
Eskucturas en 3D
Sóiidos en 2D
Estructuras en 2D
Pohgonos en perspecha
Texto
A
11
lnnnnnnn
: F G H I J K L h . Gráficas denegocios E. Mapas geográficos I. hnimacih 3D
B. Diseño electrónico F. Recursos dela t i m a J. Modelacihmoleculm
C. Animación en 2D G. Arsuitectvta en 3D K. Imioenesmédicas
D. CAD 2D H. CAD mécanico L. Visualizacitm cienflfica
Requerimientos de hardware de las aplicaciones.
S opcte sofisticado de hscdware
T
Aceleración aha
Aceleración baja
I
No aceleradaA.'Gráficas de negocios B. Diseño electrónico C. Animación en 2D D. CAD 2D
r
I
I
1
A B C D E F G H I ' J ~ K L E. Mapas geográficos I. Animación 3D
F. Remsos dela t i m a J. Modelaciónmolemlx
G. Arwiteciuca en 3D K. ImBames mCdicas H. CAD mécanico L. Visualización c i d c a
Es importante analizar las capacidades del CPU y el acelerador, pues si uno de los componentes es lento y no puede manejar la cantidad de datos que van siendo generados, se forma un cuello de botella y el sistema completo se vuelve lento.
BIBLIOTECAS GRÁFICAS
Una biblioteca gráfica es la herramienta que el desarrollador de aplicaciones utiliza para hacer software para el usuario. Una API (
Interface del programador de aplicaciones ) es una colección de rutinas que dibujan elementos geométricos llamados ( primitivas )
,
que se utilizan para construir dibujos, así el desarrollador no tiene que escribir código de bajo nivel ( decirle a la computadora como dibujar primitivas simples ) ypuede concentrarse en construir software de alta calidad.
La biblioteca de gráficos trabaja muy de cerca con el hardware, calcula el tamaño y la posición de las primitivas, algunas bibliotecas trabajan exclusivamente con 2-D ó 3-0 y otras con ambas; algunas bibliotecas están diseñadas para trabajar con determinado tipo de
hardware. Ya que la aplicación terminada no requiere de todas las
herramientas que el desarrollador necesito para crearla, va acompañada de un sub conjunto de la biblioteca ( biblioteca de tiempo de corrida )
,
la cual habilita al usuario a utilizar las rutinas de dibujo.Las transformaciones de imágenes requieren actualizaciones a 10s
datos que describen a la imagen. Los deben permanecer intactos en alguna parte del sistema, hasta que la actualización ocurre, los datos son
bibliotecas gráficas también guardan copias de actualizaciones intermedias.
A las bibliotecas gráficas que guardan una copia de los datos de la imagen se les conoce como bibliotecas de retención a las otras se les
conoce como bibliotecas de modo inmediato.
Modo Inmediato
Aplicación
Modo Retención
Aplicación
A
r 1
Biblioteca Gráfica
I
Hardware de Desplegado
Hardware de Desplegado
I I
En las bibliotecas de retención se encuentran la lista de aristas para un modelo de estructura o la lista de caras para un modelo de volumen, así como características de la imagen. Son convenientes cuando se interactua con la base de datos de la aplicación y no se quiere accesarla cada vez que el usuario hace un cambio a la imagen.
Cuando los cambios a los datos de la imagen son tan extensos que una forma es completamente diferente de otra, es necesario accesar la base de datos para actualizar u obtener nuevos datos.
Algunas librerías tienen los dos sistemas, el de retención seria adecuado para el diseño industrial y mecánico y análisis de programas. El sistema inmediato seria adecuado para aplicaciones de animación.
LA BIBLIOTECA GRÁFICA GKS
Se usa en aplicaciones 2-D. Relaciona primitivas con atributos de la imagen en segmentos que pueden ser escalados, rotados y trasladados; pueden formar un objeto completo. Cuando hay que trasladar un objeto de una parte de la pantalla a otra, cada segmento debe ser trasladado
individualmente. Se puede controlar la visibilidad, prioridad,
detectabilidad, brillo. Los segmentos no pueden ser editados. La GKS
puede operar en modo de retención y en inmediato al mismo tiempo.
LA BIBLIOTECA GRÁFICA PHIGS
Da numerosos servicios a aplicaciones 2-D y 3-D
,
incluso entrada y archivo de datos, organiza los datos en estructuras jerárquicas que contienen primitivas y atributos que describen la imagen. Estasestructuras pueden ser agrupadas, compartidas. Una vez que la estructura esta definida se le puede tratar como una unidad y ser
referenciada para múltiples apariciones. Reduciendo la cantidad de datos necesarios para dibujar una imagen.
Las estructuras PHIGS son almacenadas en una base de datos llamada estructura central de almacenamiento
CSS.
Las sub estructuras heredan las características de sus ancestros. PHIGS se utiliza en programas de simulación, modelación molecular y en aplicaciones dediseño asistido (CAD). Las estructuras pueden ser editadas y modificadas interactivamente.
QUIEN NECESITA DE GRÁFICAS POR COMPUTADORA
Las gráficas por computadora eran accesibles solo a algunos individuos con muchos recursos, ahora cada vez es más accesible para muchos usuarios. Las gráficas por computadora ayudan a los usuarios en
los campos técnicos, científicos y creativos a representar información por vasta que esta sea.
Se utilizan por ejemplo para acelerar la fase d e diseño del desarrollo de un producto. El uso de las gráficas por computadora es muy amplio, pero ayudan a comunicar ideas visualmente. El usuario provee las ideas y la información y la computadora usa estos datos para construir una representación visual las gráficas por computadora son magnificas para el trabajo de diseño y simulaciones, por ejemplo el usuario puede mover el objeto a distintas posiciones, rotarlo, moverlo desde distintos ángulos.
Las gráficas por computadora nos dan la magia de probar nuestras ideas y tratar nuevas soluciones antes de moldearlas en acero.
La televisión es un medio común para las gráficas por computadora, por ejemplo la gran variedad de caricaturas, los logotipos que vuelan por la pantalla; las gráficas por computadora se emplean para elaborar
Los científicos generan grandes volúmenes de datos por medio de investigaciones climáticas y atmosféricas, exploración geológica y
astrofísica, etc.; pero los datos no son claros si permanecen en forma numérica, si estos datos son visualizados el análisis se simplifica
muchisimo.
Las gráficas por computadora y el procesamiento de imágenes nos permiten visitar lugares distintos, muy pequeños, muy calientes, muy fríos
o inaccesibles a los humanos.
Para acabar pronto las gráficas por computadora son más que bellas imágenes y mucho más que un campo elitista para quienes pueden pagar su costo.
Los programas gráficos van desde elaboradas caricaturas, hasta modelados para médicos e investigación farmacéutica. Las gráficas por computadora en todas sus formas están teniendo un papel preponderante en la forma de ver nuestro ambiente y en como hacer negocios en el
mundo moderno.
LOS SISTEMAS GRÁFICOS
Estos sistemas se componen de hardware y programas gráficos que juntos producen imágenes; el hardware representa el potencial del
sistema, el software representa la orquestación de ese potencial.
El hardware lo constituyen dispositivos como los siguientes : monitor de alta resolución con memoria especial de pantalla, para que pueda reproducir imágenes complejas, teclado, ratón, uno o más procesadores, dispositivos de almacenamiento (discos), etcétera.
Las estaciones de trabajo gráficas tienden a ser considerablemente más poderosas que las PCs. Muchos programas gráficos son muy sofisticados y requieren hardware poderoso para correr eficientemente. Mientras más rápidos y especializados sean los componentes de la computadora, las gráficas de la computadora serán desplegadas más rápidamente.
LA PANTALLA
El monitor es como una televisión que muestra imágenes gráficas, la mayoría de estas pantallas son tubos de rayos catódicos CRTs. Dentro del CRT un cañón de electrones emite un rayo controlado de estos electrones y al impactarse por dentro con la superficie de la pantalla, su capa de fósforo se ilumina.
Los monitores de color muestran imágenes con la combinación de tres colores primarios; rojo, verde y azul. El método de combinación es el mismo con el que se combina la luz de colores, es el método RGB de coloración. Porciones de los tres colores primarios se añaden para conseguir el color indicado.
PIXELES Y PUNTOS DE FóSFORO
La capa de fósforo de la pantalla se compone de pequeños puntos, cada uno de estos puntos es una triada de fósforo que emite luz roja, verde y azul.
Debido a que las triadas son muy pequeñas y cercanas entre si los ojos del observador ven el resultado correcto. Las triadas de fósforo se agrupan y a estos elementos visibles de dibujo se les conoce como pixeles. El resultado final es una imagen compuesta de patrones de puntos en un enrejado rectangular llamado ( raster )
.
Las estaciones de trabajo gráficas normalmente tienen mejor resolución que los monitores de televisión, por lo tanto los pixeles son más pequeños y más numerosos que los de una pantalla normal.La resolución es el numero de pixeles a lo ancho y a lo alto de la pantalla y hay muchas combinaciones posibles.
CONVERSIóN Y REFRESCADO
Determinar el color, monocromo o escala de grises de cada uno de
los pixeles involucra un proceso llamado ( scan conversion )
.
La imagen a dibujar en la pantalla debe de ser mapeada para determinar la posición delos pixeles en la pantalla. El rayo de electrones se desliza por la superficie de la pantalla a lo largo de cada línea de pixeles, el valor ( en memoria ) de cada pixel es transformado a un valor análogo ( voltaje ) y así determinar la intensidad del rayo de electrones.
Ya que el fósforo brilla muy brevemente, la pantalla debe de ser refrescada, para esto el rayo de electrones barre secuencialmente todas
En el método entrelazado el rayo recorre cada una de las líneas y
después regresa a la parte superior de la pantalla. El método no entrelazado ( el preferido para sistemas gráficos ) recorre todas las líneas de pixeles, de una sola vez, este método requiere de una razón de
escaneo de aproximadamente 60 ciclos por segundo.
CÁLCULOS PARA LAS GRÁFICAS
Los procesadores de las computadoras son maquinas que
interpretan y transforman las ideas almacenadas a algún tipo de acción. El hardware de un sistema gráfico puede incluir muchos procesadores
que desarrollan distintas actividades. Estos procesadores deben manejar todos los datos que representan las imágenes que transformaran y mostraran.
EL CPU desarrolla actividades de calculo de todo tipo, maneja las entradas del usuario desde el teclado u otros dispositivos, así como la
salida a la pantalla o a la impresora, las actividades relacionadas a la comunicación, un buen sistema gráfico debe incluir por lo general un segundo procesador llamado acelerador gráfico.
El acelerador gráfico permite mejorar la velocidad con que se dibuja la imagen y libera al CPU y al software de la pesada tarea de dibujar
imágenes. En general el acelerador actúa como esclavo del CPU, procesa
los datos que el CPU le pasa ( usualmente realiza las conversiones que transforman los datos de la imagen a pixeles de la pantalla )
.
Hay varios niveles de aceleración gráfica, depende del grado de sofisticacióndeseada en el desempeño del sistema.
EL AMBIENTE DE VENTANAS
La mayoría de las estaciones gráficas d e trabajo cuentan con tecnología de ventanas; las ventanas operan como dispositivos separados, cada ventana puede correr su propio programa gráfico y
pueden correr simultáneamente, se pueden cerrar ventanas que no están
en uso, para liberar recursos del sistema, otras ventanas que no se usan frecuentemente pueden permanecer en forma de icono. Es sistema de ventanas maneja en coordinación con el sistema operativo los múltiples
programas que pueden correr en un sistema gráfico, por ejemplo un programa de diseño, calendario, correo electrónico, un programa de
publicidad, etcétera.
EL RATÓN
AI tener varias ventanas es importante poder apuntar a varios lugares de la pantalla y seleccionar Breas de trabajo; el ratón es el apuntador más común, una bolita rodante le da información de movimiento y dirección a la computadora, tiene dos o tres botones.
El ratón manda mensajes a un controlador ( device driver ) código de software que maneja interacción entre el hardware y el software, a la flecha que representa el ratón se le llama cursor; el apuntar y hacer click con el ratón puede significar distintas acciones, dependiendo de la
aplicación.
El sistema de ventanas es la interface de la computadora con el usuario, debe de ser intuitivo y fácil de usar. Usualmente con menús, barras de deslizamiento y botones el usuario manipula aspectos de la imagen rápida y fácilmente.
LA APLICACIóN
Una aplicación es un paquete de software diseñado para cumplir con ciertos requerimientos del usuario, además de almacenar y recuperar información rápidamente, debe de tener la habilidad de corregir o
modificar material existente.
Toda la información que debe de ser accesada cuando la aplicación se utiliza constituye la base de datos de la aplicación. Datos para controlar las ventanas, las llamadas a rutinas de dibujo de primitivas, algunas representaciones de imágenes y sus atributos se guardan en la base de datos así como sus actualizaciones.
INTERACCI~N DEL SOFTWARE Y DEL HARDWARE
El usuario se comunica con el software de la aplicación vía el hardware de entrada ( el teclado, el ratón, etc. ) estas entradas son interpretadas por la aplicación y la biblioteca gráfica, la cual utiliza al procesador para hacer los cálculos
imagen y guarda todos los datos que
de tamaño, color y orientación de la representan a esta imagen.
c3
DiscosSistema de ventanas
de tiempo de corrida
t
Hardware de desplegado y / o Acelerador griiico
Sistema
Gráticas >. de
Muchos de estos procesos ocurren simultáneamente y describen simplificada mente, en forma general como ocurren las cosas.
DISPOSITIVOS PERIFÉRICOS
Las cajas de botones, activan funciones especificas disparadas al apretar cierto botón (rotaciones o movimientos predefinidos, por ejemplo ).
La tableta gráfica, primariamente se utilizo en ambientes de diseño,
Pluma
SCANNER
Convierte imágenes impresas a información digital, el scanner dirige el rayo de luz a la imagen y la cantidad de luz reflejada por las
partes del documento es medida por una foto celda. Los datos resultantes son una imagen electrónica del documento.
ViDEO
La tecnologia de multimedia hace posible capturar señales de video para mostrarlas en un monitor ( se usa en publicidad y teleconferencias )
.
Las imágenes de video que serán transferidas a el sistema gráfico sontransformadas por un hardware especial, de señal analógica a una señal digital; son almacenadas en memoria y posteriormente pueden ser mostradas. Las películas suelen ser usadas para producir imágenes de alta calidad en el sistema gráfico.
IMPRESORAS
Las impresoras de matriz de puntos a color utilizan cintas con los colores ( cían, magenta y amarillo ) son los colores opuestos a los colores
rojo, verde y azul, son sus complementos. AI añadir en partes iguales los
colores CMA
,
el color resultante es el negro; la combinación de loscolores RGB por el contrario da blanco. Por lo tanto para obtener el color deseado en la impresión, se realiza una substracción de colores.
para poder imprimir esas imágenes.
Las impresoras láser reproducen las imágenes desde su memoria, utilizan los llamados toners de impresión y el rayo láser recorre el papel calentándolo con distintas intensidades para producir la imagen, que es por mucho de mejor resolución que las de matriz de puntos.
Los ploters son sofisticados dispositivos de impresión que tienen sus propio microprocesador el cual traslada las rutinas de dibujo a
movimientos d e la pluma del ploter, las impresiones resultantes son muy precisas. Se utilizan principalmente en diseño mecánico y arquitectura; los ploters de inyección de tinta a color producen imágenes de alta calidad. Los ploters también utilizan un enrejado para determinar la
posición de la imagen.
GRÁFICAS EN UNA RED
El sistema de archivos de red permite que múltiples usuarios de la misma red puedan intercambiar datos y recursos como software, espacio en disco y dispositivos de impresión. Aplicaciones con requerimientos intensivos pueden ser manejadas por un servidor; mientras que las estaciones de trabajo y las PCs que actúan como clientes del servidor hacen uso de alguno recursos del servidor y mejoran su propio
desempeño.
Estaciones de Trabaio
El arreglo clientelservidor es útil en grupos de trabajo donde la misma aplicación gráfica es utilizada por muchos miembros del grupo. Las maquinas cliente pueden obtener datos, memoria y programas de
aplicación, del servidor simultáneamente.
TECNOLOGíA RASTER
Esta tecnología permite simular efectos de color, luz y sombra en objetos que parecen reales, esto se logra gracias a un controlador de video. La memoria de pantalla ( frame buffer ) contiene todos los valores de los pixeles de la imagen a desplegar en la pantalla.
La memoria de pantalla del sistema gráfico ( frame buffer ) contiene el estado o valor de los pixeles de el enrejado ( raster ) en cualquier momento. Y pasa esta información al rayo de electrones quien
rápidamente mapea y refresca la pantalla; cuando el dibujo cambia, la memoria de pantalla es actualizada y el rayo de electrones ilumina los pixeles del nuevo patrón de dibujo. La información de los pixeles es almacenada en bits de la computadora que pueden ser encendidos o
apagados.
Un monitor monocromático es el dispositivo más simple, puede tener combinaciones de negrolverde ó negrolámbar en lugar de negrolblanco.
AI arreglo de valores de los pixeles del dibujo, en la memoria de pantalla, se le llama mapa de bits.
ESPACIO 2-D Y DIRECCIONES DE PIXELES
La coordenada en X es siempre el primer numero en la dirección del pixel y la coordenada Y es el segundo número. Teniendo identificada la dirección de un pixel, el sistema gráfico puede iluminarlo. En la mayoría de las computadoras la numeración del enrejado comienza de arriba a abajo para la coordenada Y, ya que el barrido del rayo de electrones comienza por a línea superior de pixeles.
ESPACIO 3-D Y DIRECCIONES DE PIXELES
El espacio tridimensional es artificialmente creado con geometría; el volumen es representado con un tercer eje (
2
). Los dibujos que aparentan estar en tres dimensiones también pueden ser rotados en tres dimensiones y vistos desde distintos ángulos.Y
3
PANTALLAS DE SISTEMAS MULTlBlTS
Los monitores de color y de escala de grises, tienen asignados para cada pixel varios bits. el numero de colores que la pantalla puede reproducir depende del numero de bits por pixel; normalmente hay 8 ó 24
bits por pixel, pero los sistemas más sofisticados pueden tener hasta 100
bits por cada pixel.
TRUE COLOR
También llamado RGB color puede combinar más colores de los que el ojo puede distinguir. El modelo para este sistema es un cubo de tres dimensiones ( tres primitivas de color )
.
Seis colores son los principales más el blanco, el negro y una escala de grises. Cada uno de los seis colores puede mezclarse directamente con el blanco o el negro cambiando así la brillantes.Las combinaciones posibles son 256 x 256 x 256
Si se tuviera un sistema de tres bits por pixel los posibles colores serian los siguientes 2 x 2 x 2 = 8
Composició en bits
n Color del pixel
1
Azu I 1 O
O
Verde O 1 O Rojo O O 1 Negro O O O Blanco 1 1 O Amarillo O 1 1 Magenta 1O
1 Cian 1 IAI combinar un color con su complemento se obtiene gris o blanco; con un mayor numero de bits por pixel los posibles colores aumentan en forma exponencial. Si se tuvieran seis bits por pixel serian 26 = 64
colores, el
ojo
puede detectar más de 64 colores; por lo tanto con este sistema no se obtendrían gráficos de apariencia real. Entonces el sistema debe de tener por lo menos 8 bits por pixel 28 = 256 colores, ya que n se acostumbran números impares.CAPITULO 1
TRANSFORMACIONES EN
DOS DIMENSIONES
INTRODUCCI~N
Para comenzar nuestro estudio de graficación por computadora es necesario saber algunos puntos en las matemáticas fundamentales, primero, considerar la representación de puntos y líneas. Los puntos y
líneas bajo un algoritmo apropiado son usados para representar objetos o desplegar información gráficamente.
La habilidad de transformar estos puntos y lineas es básica en graficación por computadora.
Cuando nosotros visualizamos un objeto, podemos hacerlo más agradable si
lo
hacemos a escala, rotándolo, transladándolo, distorsionándolo o proyectándolo en perspectiva. Todas estas transformaciones pueden ser realizadas usando técnicas matemáticas que se discuten a continuación.REPRESENTACIóN DE PUNTOS
Un punto es representado en dos dimensiones por sus coordenadas. Estos dos valores son especificados como los elementos de un matriz de 1 -renglón, 2-columnas
(1
x2):En tres dimensiones como una matriz de 1-renglón, 3-columnas (1 x3):
Alternativamente, se puede representar un punto con una matriz de 2-renglones, 1-columna (Zxl), aunque es menos usado.
En tres dimensiones (3x1):
TRANSFORMACIONES DE PUNTOS
Considerando los resultados de la multiplicación d e una matriz
(X y) que contiene las coordenadas de un punto P y en general una matriz
de transformación de 2x2:
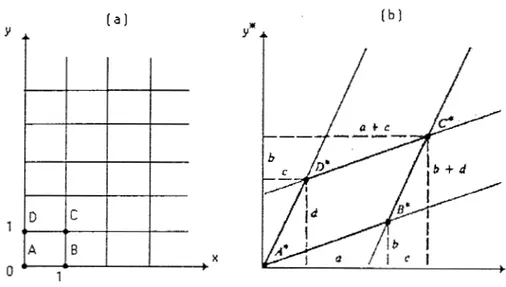
Esta notación matemática muestra que las coordenadas iniciales X
y Y son transformadas a x * y y * , donde x * = (ax
+
cy) y y* = (bx+
dy).Con este interesante resultado, podemos empezar por considerar los casos especiales.
Considerando el caso donde a = d = I y c = b = O. La matriz transformación es reducida a la matriz identidad. de este modo,
Y sucede que no cambian los valores del punto P. Como vemos la matriz identidad equivale en álgebra ordinaria a multiplicar por I un
número.
Ahora, considerando d = I , b = c =
O,
Como X* = ax, produce un cambio en la componentex del punto P lo que indicaría una escala en ese vector de posición. (El efecto de esta
figura es considerado en la fig. 1 a)
Si consideramos ahora, b = c = O,
CAPITULO 1
Esto produce una escala en ambas coordenadas X y y de la posición original del vector P. (ver fig. I b). Si a #d, entonces las escalas no son iguales para los dos coordenadas. Si a = d > 1, entonces ocurre un alargamiento en la escala en las coordenadas de P. Si O < U = d c 1,
entonces ocurre una compresión en las coordenadas de P.
Si a ylo d son negativos, ocurre una reflexión a través del plano X O
del plano y. Por ejemplo, considerando b = c = O, d = I y a = -I. tenemos una reflexión a través del plano y: (ver fig. I c)
(X)(T)=(x Y)(
o
I)
=(-x Y ) = ( x * Y*)
-1
o
Y una reflexión a través del plano x, si b = c = U, a = I y d = - I , (ver fig. d)
Si a = d < O, entonces ocurre una reflexión a través del origen.
Similarmente, cuando a = d = I, c= U , la transformación producida es sólo
un cambio de posición en la coordenada y, (como se muestra en la fig. 1 e).
1
Y. Y"2
1 P c"PL
r P
Y, Y"
1
'1
3
7
1
o
fig. l. Transformación de puntos
CAPITULO 1
TRANSFORMACIONES DE LíNEAS RECTAS
Una línea puede ser definida por la posición de sus dos vectores como la especificación de el principio y el final de sus puntos. La posición y la orientación de
la
línea junto con sus dos puntos puede ser cambiada por medio de operaciones realizadas a sus vectores.Una línea en dos dimensiones esta unida por dos puntos A y
B
en el plano (ver fig, 2). La posición de los vectores A y B son los puntos ( A ) = (O 1) y ( B ) = (2 3 ) , respectivamente. Ahora considerando la matriz transformación :Fig. 2 Transformación de líneas rectas
Nosotros podemos producir un efecto al transformar la posición de
los vectores de A y
B
usando(T),
al obtener como resultadolos
vectores A * y B*.( B ) ( T ) = ( 2 3 f 3 1 2J = ( I l 7 ) = ( B * )
De este modo, los resultado para A * son X * = 3 y y * = 1. Similarmente B* es un nuevo punto con coordenadas X * = 11 y y* = 7. La
línea
A B
puede representarse por la matriz de 2x2:Ahora si multiplicamos por la matriz transformación, podemos producir L* :
Donde los componentes de
L*
representan los vectores ( A * ) y(B
*I
La transformación de A en A * y
B
en B* son mostradas en la fig. 2,donde se ve que la línea aumento y cambio su orientación.
TRANSFORMACIóN DE PUNTOS MEDIOS
En la matriz de transformación de 2x2 (T) =
(i
:)
transforma lalínea recta y = x
+
I , entre los puntos A yB,
dentro de otra línea recta y =(3/4)x
- Y 4 ,
entre A*B*. De hecho, una matriz 2x2 transforma cualquier línea recta en una segunda línea recta. Los puntos sobre la segunda línea recta tienen una correspondencia uno a uno con los puntos sobre la primera línea recta.Teniendo ( A ) = (x1 yl) (B)= (x2 Y : ) Y (T) =
(;
3
y transformándola llegamos a que el punto medio de la línea transformada A*B* es:
[
(xl;x:) y 1 + p (XI+ X:) y1+y2( X * " y * - ) = a +C _.__
b
+d-1
2
22
y el punto medio de la línea AB es :
Comparando las dos ecuaciones, tenemos que el punto medio de la línea A B se transforma hacia el punto medio de la línea A*B*. Entonces, aseguremos que existe una correspondencia uno a uno entre los puntos sobre la línea A B y
A*B*.
CAPITULO 1
Por ejemplo:
Considerar la línea AB donde ( A ) = (O 1) y
(B)
= (2;),
con latransformación (T) =
(;
3 .Transformando AB:
El punto medio de A
*
B*
es:(.x*-
y * m ) p 2E)
2 = ( 7 4)El punto medio de AB es:
(x-
.,=(y
E )
2=('
2)Transformando este punto medio nos queda:
1 2
(X" y-)(T) =(I
,1
= ( 7 4 ) = ( x * - y * - )Para aplicaciones gráficas en computadora, estos resultados
demuestran que cualquier línea recta puede ser transformada en cualquier otra línea recta en cualquier posición por una simple
transformación y redibujando la linea entre los puntos finales.
TRANSFORMACIóN DE LíNEAS PARALELAS
Cuando una matriz de 2x2 es usada para transformar un par de lineas paralelas, el resultado es un segundo par de líneas paralelas. Para ver esto, consideramos una línea entre ( A ) = (xI y,) y
(B)
= (x2 y * ) y una línea paralela a A B entreE
yF.
para demostrara que estas líneas y cualquier transformación de ellas son paralelas, se deben examinar las pendientes de AB,EF,
A*B*
yE*F*.
Entonces, son paralelas las pendientes de AB yEF:
TEORÍA Y DESARROLLO DE GRAFICACIÓN POR COMPUTADORA 3 8
m=-
x2 - XI
y2 - y1
Transformando A B y usando la matriz transformación de 2 x 2
tenemos:
por tanto la pendiente para A *B* es : b
+
dm a + c m m =”-donde m, a,
b,
c y d son los mismos paraEF
y AB. Por lo tanto m * es la misma paraE*
F*
y A*B*.
Así líneas paralelas permanecen paralelas después de la transformación.Estos pasos transforman paralelogramos en otros paralelogramos cuando se operan sobre una matriz de transformación general de 2x2. Este simple resultado demuestra el poder de usar una multiplicación de matriz para producir efectos gráficos.
TRANSFORMACIóN DE LíNEAS INTERSECTADAS
Cuando una matriz de 2x2 es utilizada para transformar un par de líneas intersectantes, el resultado es también un par de líneas
intersectantes.
CAPITULO 1
Fig. 3 Transformación de líneas intersectadas.
Las líneas de la fig. 3 tienen como ecuaciones:
Reformulando estas ecuaciones en notación de matriz:
(x y)(-"'
-:)
= (b, b,) = (bl b2) ó bien@(Íbo
=(B)
1
Si existe una solución para estas ecuaciones, entonces las líneas se intersectan. Si no, entonces son paralelas. Puede obtenerse una solución por medio de utilizar la matriz inversa:
donde:
Ejemplo:
Consideraremos las líneas de la figura anterior A B y
EF
con puntos(A) = (-I -1) ,
(B)
= (3 51'3) ,(E)
= (-I /2 3/2) y(F)
= (3 -2)La ecuación de la línea A B es -(2/3)x + y = -(1/3) y la de
EF
es x+y = 1. En notación de matriz quedan representadas por:Usando la matriz inversa, la intersección de estas líneas es:
Ahora consideraremos la transformación de estas líneas usando
El resultado es:
Con punto de intersección en (xi* yi*) = (1 1)
Transformando el punto de intersección de la línea no transformada:
El cual es idéntico al punto de intersección de las líneas transformadas.
CAPITULO 1
Examinando el ejemplo y las figuras 2 y 3 vemos que (T) lleva una rotación, una reflexión y una escala.
ROTACIÓN
Para realizar la rotación de una figura dada un ángulo B cualquiera se tomarán las siguientes consideraciones. El vector de posición P se rota un ángulo B hasta
P*
(ver fig. 4).Los vectores de posición para P y
P*
son:P
= (x y) = (rcosb rsengS)P* = (x
* *
y ) = (reos($+@ rsen(++@)Fig. 4 Rotación de un vector de posición.
Utilizando las fórmulas para los ángulos
P*
puede escribirse comoP*
= (r(c0sqkosB- sen+sen8) r(cosq5senB+
sen4 cos@)tenemos que x = rcosq5 y y = rsenb
por IO tanto:
P*
= (x* y*) = (xcosBysen6 XsenBtycost))Así las componentes del punto transformado son:
x* = xcos@- ysen6
y* = xsen6
+
ycosoen forma de matriz
(X*)=
(4Q)
= (x* y*)Así tenemos que la matriz de transformación para una rotación general alrededor del origen para un ángulo arbitrario es:
(7')
= ('Os @ sen@)-sen@ cos 6
Las rotaciones alrededor del origen en sentido contrario a las manecillas del reloj las consideraremos positivas.
El determinante de la matriz general de rotación es
[TI
=
cos28+
sen26 = IEn general, transformaciones con determinante igual a +I nos indican rotaciones puras.
Un resultado m i s , es que la inversa de la matriz general de rotación
(T) es su transpuesta. p)T = ( ~ ) - l ya que computacionalmente es mas fácil
determinar la transpuesta de una matriz, este es un resultado importante. en general, la inversa de una matriz de rotación pura es su transpuesta.
Cuando se da esta situación se dice que las matrices son ortogonales.
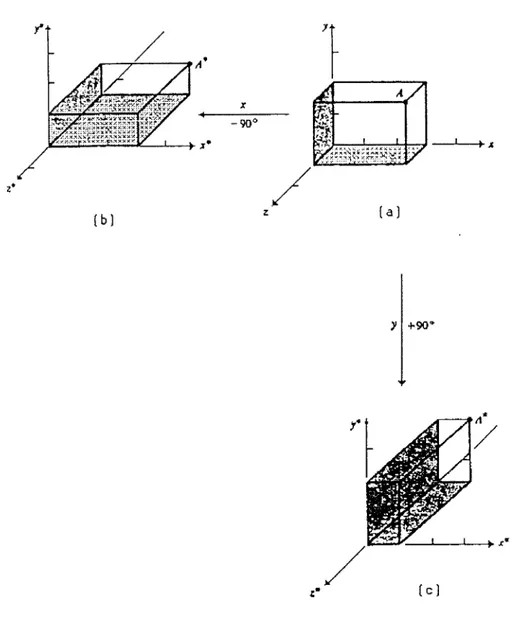
Por ejemplo para rotar una figura 90" grados alrededor del origen en el sentido contrario a las manecillas del reloj se utiliza la matriz de transformación.
o 1
Para rotar una figura 180" grados se utiliza
-,7
-1