TRANSFORMADA DE LAPLACE
YOEL GUTIÉRREZ
UNEXPO-PUERTO ORDAZ
1
INTRODUCCIÓN
Los métodos de la transformada de Laplace tienen un papel fundamental en el enfoque al análisis y diseño en los sistemas de ingeniería. Usando estos métodos, podemos resolver problemas prácticos importantes que no pueden ser tratados usando los méto-dos clásicos, y podemos obtener una alternativa más sistemática para la investigación de ecuaciones diferenciales.
El propósito de usar una transformación es crear un nuevo dominio en el cual sea más fácil manipular el problema a ser investigado. Una vez obtenidos los resultados en el nuevo dominio, pueden ser transformados inversamente para dar los resultados deseados en el dominio original.
La transformada de Laplace es una ejemplo de una clase llamada transformada integral. Una transformada integralT toma una función f(t) de una variablet (a la cual nos referiremos como tiempo) y la transforma en un función F(s) de otra variable s (llamada frecuencia).
f(t) F(s)
Dominio t
[image:1.612.142.467.463.669.2](Dominio de tiempo) (Dominio de frecuencia)Dominio s T
Figura 1
T(t) =
Z
I
f(t)N(s; t)dt =F(s);
2
De…nición y notación
De…nición 2.1 La transformada de Laplace de una función f de valores reales o complejos y de variable real t 0 es una función F de…nida mediante la expresión
F(s) = L[f(t)] =
Z 1
0
f(t)e stdt; (1)
siempre que la integral converja.
Observaciones
1. La variable s es compleja. Por simplicidad, trataremos, la mayoría de las veces as como real.
2. e st es llamado el núcleo de la transformación.
3. El símbolo L denota el operador transformada de Laplace; cuando opera en una funciónf(t) la transforma en una funciónF(s).
4. Con frecuencia ocurre en la práctica que existe un número real s0 tal que la
integral (1) converge si s > s0, pero no converge si s s0. El conjunto de
valores realess, tal ques > s0, recibe el nombre de rango de convergencia o de
existencia deL[f(t)]. Puede ocurrir que la integral en (1) no exista para ningún valor de s.
5. Cuando tomamos la transformada de Laplace, el comportamiento de f(t) para valores negativos det es ignorado o suprimido. Esto signi…ca queF(s)contiene información sobre el comportamiento def(t)sólo part 0, así que la transfor-mada de Laplace no es una herramienta conveniente para investigar problemas en los que sean relevantes los valores de f(t) para t < 0. en la mayoría de las aplicaciones a la ingeniería esto no causa ningún problema, ya que estamos interesados en sistemas físicos para los cuales las funciones con las que estamos tratando varían con el tiempo t. Un atributo de los sistemas físicos realizables es que no son anticipantes en el sentido de que no hay una salida (o respuesta) hasta que se aplica una entrada (o excitación).
6. Si el comportamiento de f(t) para t < 0 es de interés entonces necesitamos la transformada de Laplace bilateral o de dos lados de la función f(t)
de…nida por
LB[f(t)] = Z 1
1
f(t)e stdt:
La transformada de Laplace de…nida por con límite inferior cero es algunas veces llamada la transformada de Laplace unilateral o de un lado de la función f(t). Nos ocuparemos solamente de estas últimas transformadas y nos referiremos a ellas simplemente como la transformada de Laplace de la función
3
Existencia de la transformada de Laplace
Para poder establecer ciertas condiciones sobre f(t) de manera que garantice la ex-istencia deL[f(t)], introduciremos los conceptos de, continuidad parcial y orden ex-ponencial.
De…nición 3.1 Una función f(t) discontinua en un punto t0, tiene una
discon-tinuidad de salto en ese punto si
lim
t !t0+
f(t) = f(t0+) y lim
t !t0
f(t) =f(t0 )
existen.
De…nición 3.2 Una funciónf(t)es parcialmente continuaen el intervalo [0;1) si f(0+) existe y, para cada b > 0; f(t) es continua en (0; b) excepto, posiblemente, en un número …nito de punto de(0; b) en los cuales f(t) tiene una discontinuidad de salto.
De…nición 3.3 Una función f(t) es de orden exponencial si existen constantes reales , M >0 y T 0 tales que
jf(t)j M e t
siempre que t T.
Lo que nos dice esta de…nición es que una funciónf(t)es de orden exponencial si no crece más rápido que una función exponencial de la formaM e t. Afortunadamente la mayoría de las funciones de signi…cado práctico satisfacen este requerimiento, y por tanto son de orden exponencial.
La elección de ; en la de…nición de orden exponencial, no es única. Por esta razón, de…nimos el orden exponencial def(x)como el mínimo del conjunto de valores posibles de :
Teorema 3.1 (Existencia de la transformada de Laplace) Si la función f(t) es parcialmente continua en [0;1) y de orden exponencial , entonces la transfor-mada de Laplace existe existe para s > .
Prueba. Por la de…nición de la transformada de aplace obtenemos que
L[f(t)] =
Z 1
0
f(t)e stdt
=
Z T
0
f(t)e stdt+
Z 1
T
Es inmediato que R0Tf(t)e stdt eiste, porque se puede escribir como una suma de integrales sobre intervalos en quef(t)e st es continua. Ahora, como f(t) es de orden exponencial ;entonces
jf(t)j M e t; t T;
por lo tanto,
Z 1
T
f(t)e stdt
Z 1
T
f(t)e st dt
M
Z 1
T
e (s )tdt
= Me
(s )t
s
1
T
= Me
(s )T
s
Cuando s > : Como RT1e (s )tdt existe, R1 T f(t)e
stdt converge para s > : La
existencia de R0T f(t)e stdt y RT1f(t)e stdt implica que
L[f(t)] =
Z 1
0
f(t)e stdt
existe cuando s > :
Las condiciones dadas en la hipótesis del teorema anterior son su…cientes para garantizar la existencia de la transformada de Laplace de una función.
4
Linealidad y primer teorema de traslación
Teorema 4.1 (Linealidad) Si L[f(t)] existe para Re(s) > y L[g(t)] existe para Re(s)> , entonces también existe L[af(t) +bg(t)]para Re(s)>maxf ; g, y
L[af(t) +bg(t)] = aL[f(t)] +bL[g(t)];
donde a y b son constantes arbitrarias.
La demostración de este teorema se sigue directamente de la linealidad de las integrales.
Teorema 4.2 (Primer teorma de traslación) Si f(t) es una función que tiene una transformada de Laplace F(s) con s > , entonces la función f(t)eat también
tiene una transformada de Laplace dada por
L[f(t)eat] =F(s a); s > +a;
Prueba. La prueba se sigue directamente de la de…nicón de la transformada de Laplace.
L[f(t)eat] =
Z 1
0
f(t)eate stdt=
Z 1
0
f(t)e (s a)tdt:
Como Z 1
0
f(t)e stdt =F(s); s > ;
entonces Z 1
0
f(t)e (s a)tdt=F(s a); s a > :
Por lo tanto
L[f(t)eat] =F(s a); s > a+ :
Otra manera de escribir el resultado del teorema anterior es
L[f(t)eat] = L[f(t)]js !s a = F(s)js !s a;
donde s !s a implica que reemplazamoss en F(s)por s a:
5
La transformada inversa
En la práctica es de mucha importancia la capacidad de recuperar f(t) a partir de su transformada de LaplaceF(s). Así, es natural hablar de la transformada inversa de Laplace de una función F(s), esto es, de una función f(t) tal que L[f(t)] = F(s). Escribimos f(t) = L 1[F(s)]: Aunque es claro que siempre que
exista una transformada de Laplace, ésta es única, no se puede a…rmar lo mismo respecto a la transformada inversa de Laplace. Por ejemplo, para las funciones
f(t) =sent; t 0 y g(t) = 1; t= 0
sent; t >0 ;
es inmediato que
L[f(t)] =L[g(t)] = 1 s2+ 1;
luego L 1[s21+1] no es única. Nótese que estas dos funciones son patcialmente
continuas en[0;1);de orden exponencial y die…eren sólo en t= 0:
Para garantizar la unicidad de la transformada inversa, restringiremos nuestra atención a las funciones que son continuas en[0;1).
Observaciones
1. El símbolo L 1 se llama operador de la transformada inversa de Laplace.
2. La propiedad de linealidad para la transformada de Laplace establece que si a
y b son constantes cualesquiera,
L[af(t) +bg(t)] =aL[f(t)] +bL[g(t)] = aF(s) +bG(s):
Entonces se sigue que
L 1[aF(s) +bG(s)] =af(t) +bg(t) =aL 1[F(s)] +bL 1[G(s)];
así que el operador inverso de la transformada de Laplace L 1 también es un operador lineal.
3. Uno de los métodos más importantes para buscar la transformada inversa de Laplace es el método de la fracciones parciales (ver Apéndice B) .
4. En el primer teorema de traslación vimos que para un escalar a,
L[f(t)] =F(s) ! L[eatf(t)] =F(s a):
Expresado en forma inversa, el primer teorema de traslación se convierte en
L 1[F(s)] = f(t) !L 1[F(s a)] =eatf(t) = eatL 1[F(s)]:
5. Para encontrar la transformada de Laplace inversa F(s) de una función hace-mos uso de una tabla de transformadas (ver apéndice A). Algunas veces es posible escribir la transformada inversa directamente a partir de la tabla, pero es más frecuente que sea necesario primero hacer manipulaciones algebraicas sobre F(s):
Teorema 5.2 Si f(t) es parcialmente continua en [0;1) y de orden exponencial, entonces
l{m
s !1F(s) = 0 (2)
Prueba. Como f(t) es de orden exponencial, existe 2R; M1 >0 y T 0 tal que
jf(t)j M1e t; t T: (3)
Como f(t) parcialmente continua en [0;1); es parcialmente continua en (0; T): Por lo tanto existe M2 tal que
Sea M3 el real positivo más pequeño que toma e t en [0; T]; entonces
jf(t)j M2
M2
M3
e t; 0< t < T: (5)
Así, para M =maxnM1;MM23
o
; de (3) y (5) se cumple que
jf(t)j M e t; t >0:
Entonces
jF(s)j =
Z 1
0
f(t)e stdt
Z 1
0
jf(t)je stdt M
Z 1
0
e te stdt
= M
se
( s)t 1
0
= M
s ; s > :
Esto es
jF(s)j M
s ; s > :
Es inmediato que, cuando s ! 1, se cumple que jF(s)j ! 0; por lo tanto, F(s) !0:
La condición (2) limita a las funciones que pueden ser transformadas de Laplace de una función parcialmente continua en[0;1)y de orden exponencial. Por ejemplo, para
F(s) = s s+ 1
se cumple que l{m
s !1F(s) = 1; luego no puede ser la transformada de laplace de una funciónque satisfaga las condiciones anteriores.
El recíproco del teorema anterior no se cumple, en efecto,
f(t) = p1 t
no es parcialmente continua en[0;1);pero
l{m
s !1L[f(t)] =l{m r
s = 0:
s !1
6
Derivada de la transformada de Laplace
Teorema 6.1 (Derivada de la transformada de Laplace) Sif(t)es parcialmente continua en [0;1), de orden exponencial y L[f(t)] = F(s), entonces para n = 1;2; : : :,
dn
dsnF(s) = ( 1) n
Del mismo modo, si L 1[F(s)] =f(t), entonces
L 1[d
n
snF(s)] = ( 1)
ntnf(t):
Prueba. Por de…nición de la transformada de Laplace
L[f(t)] = F(s) =
Z 1
0
f(t)e stdt;
por lo tanto
dnF(s)
dsn =
dn
dsn Z 1
0
f(t)e stdt: (6)
Como f(t) es parcialmente continua en [0;1), de orden exponencial ; la integral considerada en (6) es convergente para s > ; por lo tanto, en (6) podemos inter-cambiar las operaciones de derivación e integración. Así
dnF(s)
dsn =
Z 1
0
@n
@sn f(t)e st dt
=
Z 1
0
f(t) @
n
@sn e st dt
=
Z 1
0
f(t)( 1)ntne stdt
= ( 1)n
Z 1
0
tnf(t)e stdt
= ( 1)nL[tnf(t)]; s > ;
que es lo queriamos demostrar.
Del teorema anterior se desprende que
L[tnf(t)] = ( 1)n d
n
dsnF(s); s > : (7)
Ejemplo 6.1 Compruebe que L[tn] = n!
sn+1; n= 1;2; :::; s >0:
Solución. Como
L[1] = 1
s; s >0;
entonces, para s >0;
L[tn] = L[tn:1]
= ( 1)n d
n
dsnL[1]
= ( 1)n d
n
dsn
1 s
= ( 1)n ( 1)n n! sn+1
= n!
Esto es
L[tn] = n!
sn+1; n = 1;2; :::; s >0: (8)
De la expresión (8) obtenemos que
L 1 n!
sn+1 =t
n; n= 1;2; ::: (9)
Si n= 1;en el teorema de la derivada de la transformada de Laplace, obtenemos
d
dsF(s) = L[tf(t)];
y en su forma inversa
L 1 dsd F(s) = tf(t) = tL 1[F(s)]: (10)
Por lo tanto
L 1[F(s)] = 1 tL
1 d
dsF(s) : (11)
Las ecuaciones (9), (10) y (11) son útiles para hallar la transformada inversa de algunas funciones.
De…nición 6.1 Se de…ne la función gamma como
(x) =
Z 1
0
tx 1e tdt; x >0: (12)
Observaciones
1. De (12) podemos demostrar la relación de recurrencia
(x+ 1) =x (x) (13)
2. Cuando x= 1;aplicando la de…nición de la función gamma, obtenemos
(1) =
Z 1
0
e tdt = e t 10 = 1;
y usando (13)
(2) = 1 (1) = 1 = 1!; (3) = 2 (2) = 2:1 = 2!;
(4) = 3 (3) = 3:2:1 = 3!; (5) = 4 (4) = 4:3:2:1 = 4!:
Así, cuando n es un entero no negativo
3. La función gamma suele denominarse función factorial generalizada.
Ejemplo 6.2 Compruebe que si > 1 y t >0; entonces
L[t ] = ( + 1)
s +1 : (15)
Solución. Aplicando la de…nición de la transformada de Laplace y usando la susti-tución u=st; para s >0; es inmediato que
L[t ] =
Z 1
0
t e stdt
=
Z 1
0
u
s e
u1
sdu
= 1
s +1
Z 1
0
u( +1) 1e udu
= ( + 1)
s +1 ; + 1 >0
Del ejemplo anterior, obtenemos que
1. Su forma inversa de (15) es
L 1 ( + 1)
s +1 =t : (16)
2. Si en (15) sustituimos por n, un entero no negativo, entonces por (14), es inmediato que
L[tn] = (n+ 1) sn+1 =
n! sn+1;
que es la misma relación obtenida a partir del teorema de la derivada de la transformada de Laplace.
7
Integral de la transformada de Laplace
Teorema 7.1 (Integral de la transformada de Laplace) Sif(t)es parcialmente continua en[0;1), de orden exponencial ,L[f(t)] = F(s)ylimt !0+ f(tt) existe,
en-tonces Z
1
s
F(x)dx=L f(t)
Prueba. Supongamos que
H(s) =L f(t)
t : (18)
Aplicando el teorema de la derivada de la transformada de Laplace obtenemos
d
dsH(s) =L[ th(t)] =L t f(t)
t = L[f(t)] = F(s):
En consecuencia
H(s) =
Z s
a
F(x)dx=
Z a
s
F(x)dx;
para algún a. Como
l{m
x !1H(s) = 0; entonces a=1: Con lo que obtenemos
H(s) =
Z 1
s
F(x)dx: (19)
De regla (18) y (19), tenemos lo que queriamos demostrar. Se tiene que si limt !0+ f(tt) existe, entonces
Z 1
s
F(x)dx =L f(t)
t s > ;
lo que se puede escribir como Z 1
0
f(t) t e
stdt= Z 1
s
F(x)dx: (20)
Haciendo ques!0+;(20) se puede escribir como Z 1
0
f(t) t dt =
Z 1
0
F(x)dx: (21)
Esta fórmula se suele utilisar a veces para evaluar integrales que son di…ciles de manejar por los métodos usuales.
8
Ecuaciones diferenciales ordinarias lineales
Teorema 8.1 (Transformadas de las derivadas de una función) Sif(t)es una función continua en [0;1) y de orden exponencial , y su derivada es parcialmente continua en [0;1), entonces
L[f0(t)] =sF(s) f(0) s > : (22)
Prueba. Integrando por partes se tiene que
L[f0(t)] =
Z 1
0
e stf0(t)dt = e stf(t) 1
0 +s
Z 1
0
e stf(t)dt;
esto es
L[f0(t)] = l{m
t !1e
stf(t) f(0) +s
L[f(t)]: (23)
Nótese que como f(t) es de orden exponencial , entonces
jf(t)j M e t; t T; M >0:
Por lo tanto
je stf(t)j e stM e t=M e( s)t !0 si t ! 1: (24)
Así, de (23) y (24) obtenemos que
L[f0(t)] =sF(s) f(0) s > :
Mediante la aplicación sucesiva de la regla (22) se obtienen reglas para hallar las transformadas de Laplace de derivadas de orden superior, por ejemplo
L[f00(t)] = sL[f0(t)] f0(0) =s2F(s) sf(0) f0(0)
y
L[f(3)(t)] = sL[f00(t)] f00(0) =s3F(s) s2f(0) sf0(0) f00(0):
En general, se obtiene el siguiente resultado
Teorema 8.2 Si f(t), f0(t), : : :, f(n 1)(t) son funciones continua en [0;
1) y de orden exponencial , y f(n)(t) es parcialmente continua en [0:1), entonces
L[f(n)(t)] =snF(s) sn 1f(0) sn 2f0(0) : : : sf(n 2)(0) f(n 1)(0):
Estamos ahora en posición de usar el método de la transformada de Laplace para resolver ecuaciones diferenciales ordinarias lineales con coe…cientes constantes. Para ilustrar esto, consideremos la EDO lineal de segundo orden
ad
2y
dt2 +b
dy
sujeta a las condiciones inicialesy(0) =t0, y0(0) =t1.
Al tomar la transformada de Laplace de cada término en (25) obtenemos
aL d
2y
dt2 +bL
dy
dt +cL[y] =L[f(t)]
a[s2Y(s) sy(0) y0(0)] +b[sY(s) y(0)] +cY(s) =F(s)
[as2+bs+c]Y(s) =F(s) +at1+ [as+b]t0
así que
Y(s) = F(s) +at1 + [as+b]t0
as2+bs+c (26)
:Por último, aplicamos la transformada inversa de Laplace a ambos miembros de la ecuación (26) para obtener la solución
y=L 1[Y(s)]:
Observaciones
1. Una ventaja distintiva al usar la transformada de Laplace es que nos permite reemplazar la operación de diferenciación por una operación algebraica. Con-secuentemente, al tomar la transformada de Laplace de cada término de una EDO, ésta es convertida en una ecuación algebraica en la variables.
2. El método la transformada de Laplace produce la solución completa de la EDO lineal con las condiciones iniciales automáticamente incluidas. Esto contrasta con el tratamiento del tema clásico en donde la solución general consiste de dos componentes, la función complementaria y la solución particular, con las condiciones iniciales que determinan las constantes indeterminadas asociadas con la función complementaria.
3. Debe notarse que el denominador del lado derecho de (26) es el lado izquierdo de (25) reemplazando el operador dtd con s. El denominador igualado a cero también corresponde a la ecuación auxiliar o ecuación característica usada en el tratamiento clásico.
4. El método también puede ser aplicado a EDO lineales de orden superior.
9
Ecuaciones integrodiferenciales e integrales
Consideremos un circuito electrico en serie que consiste de una resistencia R, una inductancia L y una capacitancia C, sujeto a un voltaje aplicado E. Por la segunda ley de Kirchho¤, la cargaq, está dada por
Ld
2q
dt2 +R
dq dt +
1
Como i= dqdt; la ecuación (27) se puede escribir como
Ldi
dt +Ri+ 1 C
Z t
0
i(r)dr=E: (28)
Si el circuito es del tipo RC, la ecuación (28) se reduce a
Ri+ 1 C
Z t
0
i(r)dr =E: (29)
La ecuación (28) se llamaecuación integrodiferencialy la (36) se llamaecuación integral. Para resolver directamente tales ecuaciones, es conveniente poder obtener las transformada de Laplace de integrales tales comoR0tf(r)dr:
Es inmediato que
g(t) =
Z t
0
f(r)dr
es una solución del PVI
dg
dt =f(t); g(0) = 0:
Tomando transformada de Laplace en cada miembro de la ecuación diferencial obtenemos
L dg
dt = L[f(t)]
sG(s) g(0) = F(s)
sL[g(t)] = F(s);
llegando al resultado
L Z t
0
f(r)dr = 1
sF(s) = 1
sL[f(t)]: (30)
La fórmula (30) es llamadatransformada de Laplace de la intergral de una función, su forma inversa es
L 1 1sF(s) =
Z t
0
f(r)dr: (31)
10
Convolución
De…nición 10.1 Dadas dos funciones f(t) yg(t) parcialmente continuas en(0;1],
la convolución de f(t) y g(t), se denota por (f g)(t) y se de…ne como
(f g)(t) =
Z t
0
f( )g(t )d (32)
La inetegral en el lado derecho de (32) se llama la integral de convolución. Otros nombres alternativos son laintegral de superposición, integral de Duhamel, integral envolventey la integral de faltung.
La convolución satisface la propiedad conmutativa
(f g)(t) = (g f)(t): (33)
El resultado (33) se prueba fácilmente, ya que haciendo la Sustitución x = t
obtenemos
(f g)(t) =
Z t
0
f( )g(t )d
=
Z 0
t
f(t x)g(x) ( dx)
=
Z t
0
g(x)f(t x)dx
= (g f)(t):
Otras propiedades básicas de la convolución son las siguientes:
1. c(f g) =cf g =f cg c constante
2. f (g h) = (f g) h
3. f (g+h) = (f g) + (f h),
Teorema 10.1 Sif(t)yg(t)son dos funciones parcialmente continuas en[0;1), de orden exponencial y tienen transformadas de LaplaceF(s)y G(s)respectivamente, entonces
L Z t
0
f( )g(t )d =L[(f g)(t)] = F(s)G(s) (34)
o, en la forma inversa más usual,
L 1[F(s)G(s)] = (f g)(t): (35)
Prueba. Por de…nición
F(s)G(s) =L[f(t)]L[g(t)] =
Z 1
0
e sxf(x)dx
Z 1
0
donde hemos usado, en las integrales, las variables …cticiasx e y, en lugar de t, para evitar confusiones. Ahora, esto puede ser expresado mediante la integral doble como
F(s)G(s) =
Z 1
0
Z 1
0
e s(x+y)f(x)g(y)dxdy=
Z Z
R
e s(x+y)f(x)g(y)dxdy;
donde R es el primer cuadrante en el plano (x; y). Haciendo la sustitución
x+y=t y = ;
la integral doble se transforma en
F(s)G(s) =
Z Z
R1
e stf(t )g( )dtd ;
donde R1 es la región semi-in…nita en el plano ( ; t) acotada por la recta = 0 y
=t. Esto puede escribirse como
F(s)G(s) =
Z 1
0
e st
Z t
0
f(t )g( )d dt=
Z 1
0
e st(g f)(t)dt=L[(g f)(t)]
y como la convolución es conmutativa, podemos escribir
F(s)G(s) =L[(f g)(t)];
lo cual concluye la demostración.
Nótese que si en (34) g(t) = 1;entonces
L Z t
0
f( )g(t )d =L
Z t
0
f( )d =L[f(t)]L[1] = 1 sF(s);
Por lo tanto, obtenemos la propiedad
L Z t
0
f( )d = 1
sF(s) (36)
Así, transformada de Laplace de la integral de una función, es un caso particular de la convolución de dos funciones.
11
Función escalón unitario
De…nición 11.1 La función escalón unitario U(t), se de…ne como
U(t) =
(
0 t <0
1 t 0
La función escalón unitario también se suele denotar como H(t) y se suele llamar función de Heaviside. Se ilustra grá…camente en la Figura 1(a).
0 0
1 1
a
u(t) u(t-a)
[image:17.612.103.514.207.391.2](a) (b)
Figura 2
Una función que representa un escalón unitario en t = a puede ser de…nida por una traslación horizontal de duracióna (ver Figura 1 (b)). Ésta está de…nida por
U(t a) =
(
0 t < a
1 t a
0 0 a
(a) (b)
a
f(t) f(t)u(t-a)
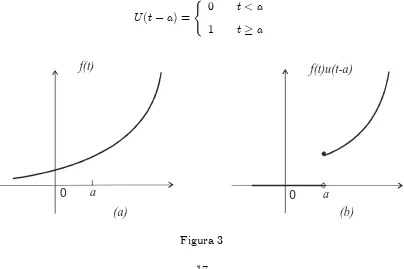
[image:17.612.104.508.441.710.2]La función producto f(t)U(t a)se de…ne como
f(t)U(t a) =
(
0 t <0
f(t) t 0
así la función U(t a) puede ser interpretada como un mecanismo para encender la funciónf(t)ent =a. Ésto se muestra en la Figura 3 . De esta manera, la función escalón unitario se puede utilizar para escribir en forma compacta funciones de…nidas por tramo. Para ello podemos usar las operaciones deencendido y apagado.
Alternativamente, una función discontinua también puede construida en forma compacta usando la función sombrero de copa, de…nida como
U(t a) U(t b) =
8 > < > :
0; t < a 1; a t < b
0; t b
:
En este sentido, la función sombrero de copaU(t a) U(t b)puede ser interpre-tado como un mecanismo para encender una función en el intervalo[a; b)y apagarla en los intervalos ( 1; a)y [b;1). En efecto
f(t) [U(t a) U(t b)] =
8 > < > :
0; t < a
f(t); a t < b
0; t b
Escribir una función discontinua en términos de funciones escalón unitario, será de mucha utilidad para aplicar la transformada de Laplace en la resolución de EDO lineales que involucran funciones discontinuas. En función de ésto, enunciamos a continuación el siguiente teorema
Teorema 11.1 (Transformada de Laplace de U(t a):) Para a 0 se cumple que
L[U(t a)] = e
as
s ; s >0; (37)
y en su forma inversa
L 1[e
as
s ] =U(t a): (38)
Prueba. Ésto es consecuencia inmediata de la de…nición de la transformada de Laplace, en efecto
L[U(t a)] =
Z 1
0
U(t a)e stdt
=
Z a
0
0:e stdt+
Z 1
a
e stdt
= e
st
s
1
a
= e
as
Por lo tanto,
L[U(t a)] = e
as
s ; a 0; s >0;
que es lo que queriamos demostrar.
En particular si a = 0 en (37), entonces
L[U(t)] = 1
s; s >0;
y en su forma inversa
L 1 1s =U(t) = 1; t 0:
El siguiente teorema algunas veces es conocido como teorema de Heaviside o de retraso.
Teorema 11.2 (Segundo teorema de traslación) siL[f(t)] =F(s)entonces para una constante no negativa a
L[f(t a)U(t a)] = e asF(s); (39)
y en su forma inversa
L 1 e asF(s) =f(t a)U(t a) =L 1[F(s)]t!t aU(t a) (40) Prueba. Por de…nición
L[f(t a)U(t a)] =
Z 1
0
f(t a)U(t a)e stdt =
Z 1
a
f(t a)e stdt:
Haciendo la sustitución T =t a
L[f(t a)U(t a)] =
Z 1
0
f(T)e s(T+a)dT =e as
Z 1
0
f(T)e sTdT:
Como
F(s) = L[f(t)] =
Z 1
0
f(T)e sTdT;
se sigue que
L[f(t a)U(t a)] = e asF(s):
Se cuenta con otra alternativa del segundo teorema de traslación. Con la sustitu-ción u=t a, obtenemos que
L[f(t)U(t a)] =
Z 1
0
f(t)U(t a)e stdt
=
Z 1
a
f(t)e stdt
=
Z 1
0
f(u+a)e s(u+a)du
= e sa
Z 1
0
esto es
L[f(t)U(t a)] =e asL[f(t+a)]: (41)
Observaciones
1. La forma usual del segundo teorema de traslación es su forma inversa (40), para el caso directo usualmente se usa la forma (41).
2. Es importante distinguir entre las dos funcionesf(t)U(t a)yf(t a)U(t a). Como vimos antes f(t)U(t a) simplemente indica que la función f(t) está encendida en el tiempo t=a, así que
f(t)U(t a) = 0 t < a
f(t) t a
Por otro lado, f(t a)U(t a) representa una traslación a la derecha (ya que
a 0) de la funciónf(t) a unidades, así que
f(t a)U(t a) =
(
0 t < a
f(t a) t a
puede interpretarse como la representación de la función f(t) retrasada en el tiempo por a unidades. Así, cuando consideramos su transformada de Laplace
e asF(s), dondeF(s)denota la trasformada de Laplace def(t), la componente
e as puede ser interpretada como el operador retraso en la transformadaF(s). Esto indicará que la respuesta del sistema caracterizada porF(s)será retrasada en el tiempo a unidades. Como muchos sistemas prácticos importantes tienen alguna forma de retraso inherente a su comportamiento, es claro que el resultado de este teorema es muy útil.
3. En la práctica, la importancia del segundo teorema de traslación radica en determinar transformadas inversas, ya que, en muchos sistemas prácticos los ingenieros están interesados en conocer como in‡uyen los retrasos en la respuesta del sistema.
12
Funciones periódicas
Ya hemos determinado la transformada de Laplace de funciones periódicas tales como
Teorema 12.1 Si f(t)es continua por tramos en[0;1),de orden exponencial y per-iódica con periodo T, esto es f(t+nT) = f(t) para todo entero n, entonces
L[f(t)] = 1 1 e sT
Z T
0
e stf(t)dt: (42)
Prueba. La transformada de Laplace de f(t)existe y puede ser expresada como una serie de integrales sobre periodos sucesivos; esto es,
L[f(t)] =
Z 1
0
f(t)e stdt =
1 X
r=0
Z (1+r)T
rT
f(t)e stdt:
Si hacemos la sustituciónt=v+rT, entonces
L[f(t)] =
1 X
r=0
Z T
0
f(v+rT)e s(v+rT)dv:
Como f(t) es periódica con periodo T,
f(v+rT) = f(v) r= 0;1;2; : : : ;
así que
L[f(t)] =
1 X
r=0
Z T
0
f(v)e sve srtdv =
1 X
r=0
e srt
! Z T
0
f(v)e svdv:
La serieP1r=0e srt es una progresión geométrica in…nita cuyo primer término es 1 y razón común e sT. Su suma está dada por 1
1 e sT, así que
L[f(t)] = 1 1 e sT
Z T
0
f(v)e svdv:
Como, dentro de la integral,v es una variable nula, la podemos reemplazar portpara obtener el resultado deseado.
El teorema anterior puede ser expresado en términos de la función escalón unitario como sigue
Teorema 12.2 Si f(t); de…nida para todo t positivo, es una función periódica con perior T; entonces
L[f(t)] = 1
1 e sTL[f1(t)];
donde
13
La función delta de Dirac
Con frecuencia, sobre los sistemas mecánicos actúan funciones fuerza (o bien sobre los circuitos eléctricos) de gran magnitud sólo durante un lapso muy breve; por ejemplo, en un ala de aeroplano que se encuentra oscilando, puede caer un rayo, se puede dar un golpe brusco a una masa en un resorte con un martillo, o una bola de béisbol, podría mandarse volando golpeándola violentamente con un bate. Estas funciones son conocidas como fuerzas impulsivas. Matemáticamente, tales funciones de fuerza son representadas por la función delta de Dirac, que es una función cuyo valor total está concentrado en un punto. Para desarrollar una formulación matemática de esta función y comprender su interpretación física, consideremos La función de pulso
(t) de…nida por
(t) =
8 > > < > > :
0 t < t0 a
A
2a t0 a t < t0+a
0 t t0+a;
; a >0; t0 0; A >0;
e ilustrada en la Figura 4 (a). Como la altura del pulso es A
2a y su duración (o ancho) es2a; el área debajo del pulso es A; esto es
Z 1
1
(t)dt=
Z t0+a
t0 a
A 2adt =
A 2at
t0+a
t0 a
=A:
0 t 0
0
t -a0 t +a0 t
A/2a
Φ(t) A (t-t )δ 0
[image:22.612.117.496.368.601.2](a) (b)
Figura 4
si ahora consideramos el proceso límite en el que la duración del pulso se apróxima a cero, de tal manera que el área bajo el pulso siga siendoA, entonces obtenemos una formulación para la función impulso de magnitud A que ocurre en el tiempot =t0:
A (t t0) = lim
Es importante recalcar que la magnitud de la función,impulso está medida por su área. La función impulso cuya magnitud es unitaria es llamada función impulso unitario o función delta de Dirac. El impulso unitario que ocurre en el tiempo
t =t0, es el caso límite del pulso (t) de la Figura 4 (a) con el valor de A igual a la
unidad. Se denota por (t t0)y se puede caracterizar mediante las dos propiedades
siguientes:
1. (t t0) =
(
1 t =t0
0 t6=t0
2. R11 (t t0)dt = 1.
Igualmente, una función impulso de magnitud A que ocurre en el tiempo t = t0
es denotada por A (t t0) y puede ser representada como el diagrama de la Figura
4 (b)
Observaciones
1. La función delta de Dirac no es una función en el sentido usual, pero es un ejemplo de una clase de las llamadas funciones generalizadas, que pueden ser analizadas usando la teoría del cálulo generalizado. Sin embargo, sus propiedades, son tales que, usadas con cuidado pueden conducir a resultados que tienen signi…cado físico o práctico y que en muchos casos no se pueden obtener por ningún otro método. En este contexto, provee a los ingenieros de una herramienta matemática importante.
2. Es posible, bajo condiciones adecuadas, multiplicar una función ordinaria por la función delta de Dirac. Así
(t t0)f(t) = f(t) (t t0) = f(t0) (t t0) (43)
siempre que la funciónf(t) sea continua en t=t0.
3. La expresión (43) y la propiedad (2) de la función delta de Dirac establecen que sif(t) es continua ent=t0 entonces
Z 1
1
f(t) (t t0)dt=f(t0)
Z 1
1
(t t0)dt=f(t0): (44)
Esta propiedad importante de la función delta de Dirac es de signi…cado prac-tico y es llamada propiedad de …ltrado, porque provee un método que per-mite aislar, o separar, el valor de una función en cualquier punto particular. Por razones teóricas es conveniente usar límites in…nitos en (44) aunque en realidad pueden ser sustituidos por límites …nitos. Esto es cierto ya que para
t0 , donde y son constantes
Z
13.0.1 La transformada de Laplace de la función delta de dirac
La transformada de Laplace de la función del de Dirac se puede deducir fácilmente de la propiedad (44). Como (t t0) = 0 para t6=t0, si hacemos f(t) =e st en (44),
vemos que parat0 0,
L[ (t t0)] =
Z 1
1
e st (t t0)dt =e t0s:
Así, para t0 0
L[ (t t0)] =e t0s: (45)
o, en términos de la transformada inversa,
L 1[e t0s] = (t t
0): (46)
En particular, si t0 = 0, entonces
L[ (t)] = 1;
0 en su forma inversa
L 1[1] = (t):
Luego, para cada constantea
L 1[a] =a (t):
13.0.2 Funciones generalizadas equivalentes
De…nición 13.1 Una función de prueba (t) es una función continua que tiene derivadas continuas de todos los ordenes y que es cero fuera de un intervalo …nito.
Una clase de función de prueba adoptada por R. R. Gabel y R. A. Roberts, es
(t) =
(
e d
2
d2 t2;
jtj< d
0; jtj d ;
donde d es una constante.
Para una función generalizadag(t)se evalúa la integral
G( ) =
Z 1
1
(t)g(t)dt:
Esta integral asigna el númeroG( ) a cada función (t);así que G( ) es una genera-lización del concepto de función: es unfuncional linealen el espacio de las funciones prueba (t): Por ejemplo, sig(t) = (t) entonces
G( ) =
Z 1
1
(t) (t)dt = (0);
así, que en este caso particular, para cada función de prueba (t); se asigna el valor
De…nición 13.2 Dos funciones generalizadasg1(t) yg2(t)son equivalentes si y sólo
si Z 1
1
(t)g1(t)dt =
Z 1
1
(t)g2(t)dt
para toda función de prueba (t) para la cual las integrales existan.
Si las funciones generalizadasg1(t)yg2(t)son equivalentes, escibiremos queg1(t) =
g2(t):
Usando el consepto de una función de prueba (t), la función delta de dirac (t)
puede de…nirse en la forma generalizada Z 1
1
(t) (t)dt= (0):
Interpretada como una integral usual, ésta no tiene signi…cado. La integral y la función (t)están simplemente de…nidas por el número (0):En este sentido podemos tratar a (t) como si fuera una función ordinaria, excepto que nunca hablaremos del valor de (t); más bien, hablamos del valor de las integrales que involucran a (t):
13.0.3 Relaciones entres la funciones ecalón unitario y delta de Dirac De las de…niciones de u(t)y (t) se puede argumentar que
U(t) =
Z t
1
(t)dt; (47)
ya que el intervalo de integración contiene al cero si t >0 pero no si t < 0. Inversa-mente, (47) puede escribirse como
(t) = d
dtU(t) =U
0(t); (48)
que expresa el hecho de que u0(t) es cero en todas partes excepto en t = 0, cuando ocurre el salto en u(t).
Mientras este argumento puede bastar en la práctica, ya que estamos tratando con funciones generalizadas, una demostración más formal requiere de la propiedad de equivalencia. Podemos ahora con…rmar (48), comproando que
Z 1
1
(t) (t)dt=
Z 1
1
(t)U0(t)dt; (49)
para cualquier función de prueba (t): Es inmediato que Z 1
1
Por otra parte, integrando por partes el lado dereco de (49), tenemos Z 1
1
(t)U0(t)dt = (t)U(t)j11
Z 1
1
0
(t)U(t)dt
= 0
Z 1
0
0 (t)dt
= (t)j10 ;
esto es Z 1
1
(t)U0(t)dt = (0): (51)
Con (50) y (51) tenemos que la equivalencia de (t) y U0(t) está probada.
Igualmente se puede comprobar que
(t t0) =
d
dtU(t t0) =U
0(t t
0): (52)
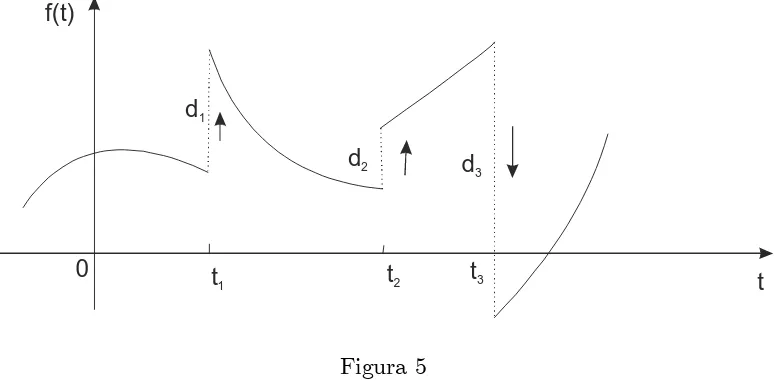
Los resultados (48) y (52) pueden usarse para obtener laderivada gene-ralizada de funciones continuas por partes que tienen saltos de discontinuidad d1; d2; : : : ; dn en los tiempos t1; t2; : : : ; tn respectivamente, como se muestra en la Figura 5.
d1
d2 d 3
t1 t2 t3
f(t)
0
[image:26.612.114.501.393.584.2]t
Figura 5
Escribiendo a f(t) en términos de funciones escalón unitario. derivando con la regla del producto y, usando (48) y (52) obtenemos el resultado
f0(t) =g0(t) +
n X
i=1
donde g0(t) denota la derivada usual de f(t) donde ésta existe. La magnitud di de un salto de una funciónf(t) en el punto ti, es la diferencia entre los límites laterales derecho e izquierdo def(t) enti;esto es
di =f(ti+) f(ti ):
Se sigue que un salto hacia arriba, como d1 yd2 en la Figura 5, es positivo, mientras
que el salto hacia abajo, como d3 es negativo.
El resultado (53) nos dice que la derivada de una función continua por partes con saltos de discontinuidad es la derivada común donde ésta existe más la suma de las funciones delta de Dirac, en las discontinuidades, multiplicadas por las magnitudes de los saltos respectivos. En sistemas prácticos, el uso de las derivadas no se recomienda, ya que la introducción de funciones delta de dirac signi…ca que las derivadas incre-mentan los niveles de ruido en la recepción de salida. En contraste, las integrales tienen un efecto suavizante en las señales, por la que son usadas ampliamente.
La derivada 0(t) de la función delta de Dirac es una función generalizada, y usando la propiedad de equivalencia se demuestra fácilmente que
Z 1
1
f(t) 0(t)dt = f0(0)
o, en forma más general Z 1
1
f(t) 0(t t0)dt = f
0
(t0); t0 0;
siempre y cuando f sea continua en t =t0:Igualmente la n-ésima derivada satisface
Z 1
1
f(t) (n)(t t0)dt = ( 1)nf
(n)
(t0):
suponinendo que f(n)(t) es continua ent =t0:
Usando la de…nición de la transformada de Laplace se sigue que
L[ (n)(t t0)] =
Z 1
0
e st (n)(t t0)dt
= ( 1)n d
n
dtne st
t=t0
= ( 1)n( 1)nsne st t=t
0
= sne st0:
En particular, si t0 = 0;entonces
L[ (n)(t)] =sn:
En su forma inversa
L 1[sne st0] = (n)(t t
14
Ejercicios
De…nición de transformada de Laplace, linealidad y primer teorema de traslación
1. Usar la de…nición de transformada de Laplace para obtener las transformadas def(t) cuando
(a) f(t) = cosh(2t)
(b) f(t) = t2
(c) f(t) = 1 + 2t
(d) f(t) = te 3t
Establezca la región de convergencia en cada caso.
2. Hallar, aplicando la de…nición, la transformada de Laplace de cada función
(a) f(t) = 0; 0 t 2
t 1; t >2
(b) f(t) = e
t; 0 t 5
2; t >5 ;
3. Hallar la trasformada de Laplace de cada función, estableciendo la región de convergencia
(a) f(t) = etcosh(3t)
(b) f(t) = 4 2t+ cos(3t)
(c) f(t) = t(e2t e 3t)
(d) f(t) = t(e3t 1)2
(e) f(t) = 2e 3tcos 2t
La transformada inversa
4. Hallar la trasformada inversa de cada función
(a) F(s) = (s+3)(1s+7)
(b) F(s) = 5s
(s 2)2
(c) F(s) = s2s(s+3)1
(d) F(s) = s22s4s3+9
(f) F(s) = s(s 1)(s2s+1+1)(s 2)
(g) F(s) = (s+2)(2s2+4s2s3+9s+3)
Derivada e integral de la transformada de Laplace
5. Hallar la transformada de Laplace de cada función
(a) f(t) = e 2tte t
(b) f(t) = te tsen(2t);
(c) f(t) = e
1 2t 3
p t ;
(d) f(t) = ett
1=5
;
(e) f(t) = e tpt
6. Hallar la transformada inversa de Laplace de cada función
(a) F(s) = s22(ss+1)13
(b) F(s) = 3s
(s2+1)2
(c) F(s) = s+1
(s2+2s+3)2;
(d) F(s) = lnss+31;
(e) F(s) = lnss22+1+4
(f) F(s) = arctagss+23;
7. Evaluar las siguientes integrales
(a) R01 e tsent (2t)dt
(b) R01 sent(5t)dt
Ecuaciones diferenciales ordinarias lineales
8. Resolver cada PVI aplicando el método de la transformada de Laplace
(a) dydt + 3y=e 2t; y(0) = 2
(b) dydt + 2y=e3t; y(0) = 1;
(c) y00 4y0+ 4y= 6e 2t; y(0) = 2; y(0) = 8;
(d) y0+ 2y=t; y(0) = 1;
(f) x00+ 4x0 + 5x= 3e 2t; x(0) = 4; x0
(0) = 7;
(g) x00+ 8x0 + 16x= 16sen(4t); x(0) = 12; x0(0) = 1;
9. Aplique la transformada de Laplace para resolver cada sistema de ecuaciones diferenciales sujeta a condiciones iniciales
(a) dx
dt = x+y dy
dt = 2x
; x(0) = 0; y(0) = 1
(b) (
d2x
dt2 +x y= 0
d2y
dt2 +y x= 0
; x(0) = 0; x0(0) = 2; y(0) = 0; y0(0) = 1
(c) dx
dt + 3x+ dy dt = 1 dx
dt x+ dy
dt y =e
t , x(0) =y(0) = 0
Ecuaciones integrodiferenciales e integrales
10. Evalúe la transformada de Laplace en cada caso, sin evaluar la integral
(a) LhtR0te udui
(b) Lhe 2tRt
0 ue
2usenudui
(c) LhR0t(u+e u)dui
(d) LhtR0txe xdxi
(e) LhR0txsenxdxi
11. Determine la transformada inversa de cada función, aplicando la fórmula (31)
(a) s(s21+1)
(b) s31s
12. Resuelva la ecuación integrodiferencial, usando el método de la transformada de Laplace
y0(t) = 1 sent
Z t
0
y(r)dr; y(0) = 0
Aplicaciones
14. Aplique la transformada de Laplace para determinar la carga, q(t); en el ca-pacitor de un circuito en serie LC, cuandoq(0) = 0, i(0) = 0 y E(t) =E0e kt;
k >0:
15. Una pesa de 4 kg. estira 2 m: un resorte. dicha pesa parte del reposo a 18 m
s arriba de la posición de equilibrio y el movimiento se produce en un medio que presenta una fuerza de amortiguamiento numéricamente igual a 78 por la velocidad instantánea. Encuentre la ecuación del movimiento con la transformada de Laplace.
16. Deduzca el sistema de ecuaciones diferenciales que describe el mivimiento verti-cal de los resortes acoplados del la Figura 1. Emplee la transformada de Laplace para resolver el sistema cuandok1 = 1; k2 = 1; k3 = 1; m1 =m2 = 1; x1(0) = 0;
x01(0) = 1; x2(0) = 0 y x
0
2(0) = 1:
k1
k2
k3
x1
x2
x =01
x =02
Funciónes escalón unitario y periódicas
17. Si f(t) =t2;representa grá…camente las siguientes funciones
(a) f(t); t2R
(b) f(t); t 0
(c) f(t 2)
(d) f(t 2)U(t 2)
18. Escribir en términos de funciones escalón unitario cada una de las siguientes funciones, y hallar su transformada de Laplace
(a) f(t) =
8 < :
t; 0 t <2 1; 2 t <4
(b) f(t) =
8 < :
2t; 0 t <3
t+ 4; 3 t <5
9; t 5
(c) f(t) =
8 < :
2t; 0 t <3
t+ 4; 3 t <5
9; t 5
(d) f(t) =
8 > > < > > :
t; t <1
1; 1 t <3
t+ 1; 3 t <5
2; t 5
(e) f(t) = sent; 0 t <2
0; t 2
19. Hallar la transformada inversa de Laplace de cada función
(a) F(s) = s(ss+12+1)e s
(b) F(s) = s2s++1s+1e s
(c) F(s) = ss4+11e3 4s
(d) F(s) = 2ss2 1+8se+193s;
20. Resuelva cada PVI aplicando el método de la transformada de Laplace
(a) y00+y= 3sen(2t) [1 U(t 2 )]; y(0) = 1; y0(0) = 2
(b) x00+x0 +x=g(t); x(0) = 1; x0(0) = 0;donde
g(t) =
8 < :
t; 0 t <1
2 t; 1 t <2
0; t 2
:
21. Aplique la transformada de Laplace para hallar la cargaq(t)en el capacitor de un circuito en serie RC, cuandoq(0) = 0c:; R= 2;5 ; ; C = 0;08 f: y
E(t) =
8 < :
0; t <1
E0; 1 t <2
0; t 2
:
22. Hallae la transformada de Laplace de la función
f(t) =t
Z t
0
23. Obtenga la solución del PVI
dx
dt +x=f(t); x(0) = 0;
donde
f(t) = t; 0 t 1
0; t >1 :
24. Obtenga la solución del PVI
d2x
dt2 +
dx
dt +x=g(t); x(0) = 1; x 0
(0) = 0;
donde
g(t) =
8 < :
t; 0 t <1
2 t; 1< x < 2
0; t 2
:
25. Veri…que que la función
f(t) = 0; 0 t < 2
sent; t 2
puede expresarse en la formaf(t) = cos(t 2)U(t 2): Luego resuelva el PVI
d2x
dt2 + 3
dx
dt + 2x=f(t); x(0) = 1; x 0
(0) = 1:
26. Exprese la función
f(t) = 3; 0 t <4
2t 5; t 4
en términos de las funciones escalón unitario. Obtenga la respuesta del oscilador armónico
d2x
dt2 +x=f(t)
para tal función de fuerza, dado quex(0) = 1 y x0(0) = 0
27. Hallar la transformada de Laplace de cada función periódica f(t), de periodo
T:
(a) f(t) = 1; 0 t < a
1; a t <2a ; T = 2a
28. Una función periódicaf(t);con periodo de 4 unidades, está de…nida dentro del intervalo[0;4) por
f(t) = 3t; 0 t <2 6; 2 t <4 :
Dibuja una grá…ca de la función para0 t <12y obtenga su transformada de Laplace.
Convolución
29. Resuelva cada ecuación integral o integrodiferencial, usando el método de la transformada de Laplace
(a) x(t) =R0tcos(2t 2u)x(u)du+e3t; (b) y00+y0 4y 4Rt
0 y(u)du = 6e
t 4t 6; y(0) =y0
(0) = 0
(c) f(t) + 2R0tf(u) cos(t u)du= 4e t+sen(t); (d) f(t) = 2t+ 4R0tsen(u)f(t u)du;
30. Hallar la transformada inversa de Laplace de cada función;aplicando el método de la convolución.
(a) F(s) = s2(s1 1)
(b) F(s) = s(s31)
(c) F(s) = (s 3)(1s+2)
(d) F(s) = s
(s2+1)2
31. Mediante la ecuación
Ldi
dt +Ri+ 1 C
Z t
0
i(u)du=E(t);
determine la corriente i(t) en un circuito LRC, cuando L = 0;005h:; R = 1 ; C = 0;02f:; E = 100V: y i(0) = 0:
La función delta de Dirac
32. Hallar la transformada inversa de Laplace de cada función
(a) F(s) = (s+2)(2s2+1s+3)
(b) F(s) = ss22+41
(c) F(s) = s2s+22+2s+5
(e) F(s) = ss32+1+1
33. Aplicar el método de la transformada de Laplace para resolver cada PVI
(a) y0+y= (t 1); y(0) = 2
(b) y00+ 16y= (t 2 ); y(0) = 0; y0(0) = 1
(c) y00+y= (t 2 ) + (t 4 ); y(0) = 1; y0(0) = 0
(d) y00+y=et (t 2 ); y(0) = 0; y0
(0) = 0
(e) y00 2y0 = 1 + (t 2); y(0) = 0; y0(0) = 1;
34. Obtenga la derivada generalizada de las sisguientes funciones continuas por partes
(a) f(t) =
8 < :
3t2; 0 t <4
2t 3; 4 t <6
5; t 6
(b) f(t) =
8 < :
t; 0 t <1
2t 1; 1 t <2
0; t 2
(c) f(t) =
8 < :
2t+ 5; 0 t <2
9 3t; 2 t <4
t2 t; t 4
35. Rsuelva oarat 0 la ecuación diferencial
d2x
dt2 + 7
dx
dt + 10x= 2u(t) + 3 d dtu(t);
sujeta a las condiciones inicialesx(0) = 0; x0(0) = 2y donde u(t) = e 2tU(t):