y0 =f (t;y); y(t0) =y0
Solución numérica en el intervalo[t0;T]:
[t;y] =ode45(g;[t0;T];y0)
g =inline(0funci on0;0t0;0y0)
t= [t0 t1 t2 :::T]; tj+1 =tj +hj
y= [y(t0) y(t1) :::y(T)] 0funci on0 es la funciónf
Ejemplo:
y0 =yt; y(1) =2; t 2[1;3]
[t;y] =ode45(inline(0y t0;0t0;0y0);[1;3];2)
Si escribimos
ode45(g;[t0;t1];y0);
Ecuaciones diferenciales: resolución numérica
Ejercicio 1. Resolvemos la la ecuación y0 =2ty en el intervalo[ 2;2]:
Teclear:
1 [t;y] =ode45(inline(02 y t0;0t0;0y0);[ 2;2];2) 2 [t;y] =ode45(inline(02 y t0;0t0;0y0);[ 2;2];2); 3 ode45(inline(02 y t0;0t0;0y0);[ 2;2];2)
Ejercicio 2. Vamos a dibujar varias soluciones de la ecuación y0 =2ty en
el intervalo [ 2;2]y en distintos colores.
1 Creamos un archivo nombre.m y lo guardamos. 2 Tecleamos en el archivo los siguientes comandos:
hold on
axis([ 2;2; 20;20])
f =inline(02 y t0;0t0;0y0) [t1;y1] =ode45(f;[ 2;2];10); [t2;y2] =ode45(f;[ 2;2]; 10);
Repetimos los mismos pasos para las condiciones iniciales 15; 15;20
plot(t1;y1;0r0); plot(t2;y2;0b0), etc.
3 Ejecutamos en la terminal de Matlab el archivo escribiendo el nombre
Ecuaciones diferenciales: resolución numérica
hold on axis([-2,2,-20,20]) f=inline(’2*y*t’,’t’,’y’) [t1,y1]=ode45(f,[-2,2],10); [t2,y2]=ode45(f,[-2,2],-10); [t3,y3]=ode45(f,[-2,2],0); [t4,y4]=ode45(f,[-2,2],15); [t5,y5]=ode45(f,[-2,2],-15); plot(t1,y1,’r’) plot(t2,y2,’b’) plot(t3,y3,’g’) plot(t4,y4,’y’) plot(t5,y5,’c’)Ecuaciones diferenciales: resolución numérica
Ejercicio 3. Ejecutar [t;y] =ode45(inline(02 y t0;0t0;0y0);[ 2;2];10) y
ver que el paso h no es …jo. Para comprobarlo, podemos hacer lo siguiente:
1 Calculamos el número de …las det:[m;n] =size(t), donde mes el
número de …las.
2 Calcular algunos valores de h tecleando, por ejemplo, t(2) t(1),
t(3) t(2);t(m) t(m 1), y cualquiert(j) t(j 1)conj m:
[t,y]=ode45(inline(’2*t*y’,’t’,’y’),[-2,2],10) [m,n]=size(t)
Ecuaciones diferenciales: resolución numérica
Ejercicio 3. Ejecutar [t;y] =ode45(inline(02 y t0;0t0;0y0);[ 2;2];10) y
ver que el paso h no es …jo. Para comprobarlo, podemos hacer lo siguiente:
1 Calculamos el número de …las det:[m;n] =size(t), donde mes el
número de …las.
2 Calcular algunos valores de h tecleando, por ejemplo, t(2) t(1),
t(3) t(2);t(m) t(m 1), y cualquiert(j) t(j 1)conj m:
Solución
[t,y]=ode45(inline(’2*t*y’,’t’,’y’),[-2,2],10) [m,n]=size(t)
Ecuación dependiente de un parámetro
y0=at2y; y(0) =2; t 2[0;10]
a=3
[t;y] =ode45(@(t;y) a t^2 y;[0;10];2)
Ecuaciones diferenciales: resolución numérica
Ejercicio 4. Dada la ecuación y0 =at2y en el intervalo [0;1.5]con la
condición inicial y(0) =2:
1 Resolver la ecuación paraa=4: 2 Dibujar el grá…co de la solución.
Solución
a=4
f=@(t,y) a*t^2*y
Ejercicio 4. Dada la ecuación y0 =at2y en el intervalo [0;1.5]con la condición inicial y(0) =2:
1 Resolver la ecuación paraa=4: 2 Dibujar el grá…co de la solución.
Solución
a=4
f=@(t,y) a*t^2*y
Ecuaciones diferenciales: resolución numérica
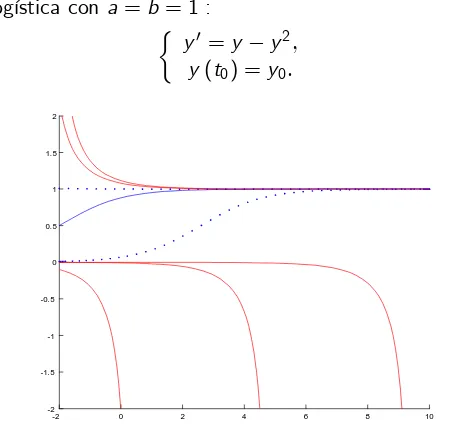
Ecuación logística con a=b =1:
y0 =y y2;
y(t0) =y0:
-2 0 2 4 6 8 10
[image:10.363.62.288.37.249.2]-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
y0 =y y2;
y(t0) =y0:
Ejercicio 5. Obtener un grá…co con distintos tipos de soluciones de la
ecuación logística en el intervalo [ 2;10]. Realizar los siguientes pasos:
1 Fijar los ejes [ 2;10] [ 2;2]:
2 Hallar las soluciones para y( 2) =1,y( 2) =0 y dibujarlas en color
negro.
3 Hallar las soluciones para y( 2) =2,y( 2) =5 y dibujarlas en color
rojo.
4 Hallar las soluciones para y( 2) =0.01,y( 2) =0.5 y dibujarlas en
color azul.
5 Hallar las soluciones para y( 2) = 0.01,y( 2) = 0.5 y
dibujarlas en color verde.
Ecuaciones diferenciales: resolución numérica
hold on axis([-2,10,-2,2]) f=inline(’y-y^2’,’t’,’y’) [t1,y1]=ode45(f,[-2,10],1); [t2,y2]=ode45(f,[-2,10],0); [t3,y3]=ode45(f,[-2,10],2); [t4,y4]=ode45(f,[-2,10],5); [t6,y6]=ode45(f,[-2,10],0.5); [t5,y5]=ode45(f,[-2,10],0.01); [t7,y7]=ode45(f,[-2,10],-0.01); [t8,y8]=ode45(f,[-2,10],-0.5); plot(t1,y1,’k’), plot(t2,y2,’k’) plot(t3,y3,’r’), plot(t4,y4,’r’) plot(t5,y5,’b’), plot(t6,y6,’b’) plot(t7,y7,’g’), plot(t8,y8,’g’)title(’Soluciones de la ecuación logística’)
-2 0 2 4 6 8 10 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
Las funciones permite crear programas. Su sintaxis es:
function argumentos_salida=nombre_funci on(argumentos_entrada)
seguida de las instrucciones necesarias.
Cuando haymás de un argumento de salida, éstos deben irentre
corchetes y separados por comas.
Es conveniente utilizar las primeras líneas del …chero para insertar un comentario (iniciándolas con ’%’). Así, dicha de…nición será visible mediante la instrucción
help nombre de la función
La función puede …nalizarse en cualquier punto utilizando la instrucciónreturn.
Las funciones se guardan en un archivo con extensión ".m". Si tenemos el …chero Nombre.m,para ejecutarlos escribiremos:
Programación: funciones
Ejemplo 1. Crear una función que calcule el valor de la hipotenusa de un
triángulo rectángulo a partir de sus dos catetos. Las variables de entrada serán los valores de los dos catetos, mientras que la variable de salida será el valor de la hipotenusa.
% La función hipotenusa calcula el valor de la hipotenusa de un triángulo dado el valor de sus dos catetos
function hip = hipotenusa (cateto1, cateto2) hip = sqrt(cateto1*cateto1+cateto2*cateto2);
>> z=hipotenusa(5,12) z =
Ejemplo 1. Crear una función que calcule el valor de la hipotenusa de un triángulo rectángulo a partir de sus dos catetos. Las variables de entrada serán los valores de los dos catetos, mientras que la variable de salida será el valor de la hipotenusa.
% La función hipotenusa calcula el valor de la hipotenusa de un triángulo dado el valor de sus dos catetos
function hip = hipotenusa (cateto1, cateto2) hip = sqrt(cateto1*cateto1+cateto2*cateto2);
>> z=hipotenusa(5,12) z =
Programación: funciones
Ejemplo 2. Vamos a repetir el mismo programa anterior pero con dos
variables de salida. Además de la hipotenusa hemos de calcular también la suma de los dos catetos.
%La funciónhipotenusa calcula el valor de la hipotenusa de un triángulo dado el valor de sus dos catetos, así como la suma de los dos catetos function [hip,suma] = hipotenusa2 (cateto1, cateto2)
hip = sqrt(cateto1*cateto1+cateto2*cateto2); suma=cateto1+cateto2;
[h,s]=hipotenusa2(5,12) h =
13 s =
17
hipotenusa2(5,12) ans =
Programación: funciones
Ejemplo 2. Vamos a repetir el mismo programa anterior pero con dos
variables de salida. Además de la hipotenusa hemos de calcular también la suma de los dos catetos.
%La funciónhipotenusa calcula el valor de la hipotenusa de un triángulo dado el valor de sus dos catetos, así como la suma de los dos catetos function [hip,suma] = hipotenusa2 (cateto1, cateto2)
hip = sqrt(cateto1*cateto1+cateto2*cateto2); suma=cateto1+cateto2;
[h,s]=hipotenusa2(5,12) h =
13 s =
17
Programación: funciones
Ejemplo 2. Vamos a repetir el mismo programa anterior pero con dos
variables de salida. Además de la hipotenusa hemos de calcular también la suma de los dos catetos.
%La funciónhipotenusa calcula el valor de la hipotenusa de un triángulo dado el valor de sus dos catetos, así como la suma de los dos catetos function [hip,suma] = hipotenusa2 (cateto1, cateto2)
hip = sqrt(cateto1*cateto1+cateto2*cateto2); suma=cateto1+cateto2;
[h,s]=hipotenusa2(5,12) h =
13 s =
17
hipotenusa2(5,12) ans =
Programación: funciones
Ejercicio 6. Construir una función que calcule, dado el valor del radio r, el
área del círculo y la longitud de la circunferencia correspondientes. La función tendrá una variable de entrada y dos de salida.
Escribir unos comentarios explicativos al principio del archivo.
Programación: funciones
Ejercicio 6. Construir una función que calcule, dado el valor del radio r, el
área del círculo y la longitud de la circunferencia correspondientes. La función tendrá una variable de entrada y dos de salida.
Escribir unos comentarios explicativos al principio del archivo.
Solución
function [area,long]=circulo(r) area=pi*r^2;
if condición
Instrucciones que deben ejecutarse si la condición es cierta.
else
Instrucciones a ejecutar si no se veri…ca la condición anterior
end
Si no hay instrucciones que ejecutar si la condición no se cumple:
if condición
Instrucciones que deben ejecutarse
Programación: estructuras condicionales
Si se encadenan varios bloques alternativos, la sintaxis queda como:
if condición_1
Instrucciones a ejecutar cuando se veri…ca la condición 1
elseif condición_2
Instrucciones a ejecutar cuando no se veri…ca la condición 1 y sí la condición_2
. . .
else
Instrucciones a ejecutar cuando no se veri…can las condiciones anteriores
Podemos imponer más de una condición, o condiciones complejas, utilizando los operadores relacionales combinados con operadores lógicos
Símbolo
lógico Símbolo relacional
< Menor ~A Negación lógica
o complementario
<= Menor o igual A&B Intersección\
> Mayor AjB Unión[
>= Mayor o igual xor(A;B)
Unión exclusiva (sólo uno ha de ser cierto)
x ==y Igualdad any([A1;A2; :::;An])
Unión de varios elementos
x ~ =y Desigualdad all([A1;A2; :::;An])
Programación: estructuras condicionales
Ejemplo 1.
Vamos a escribir un programa que devuelva el valor de la hipotenusa dados dos catetos si el valor absoluto de alguno de los dos es inferior a uno. En caso de no cumplirse la condición el valor devuelto será cero.
%Devuelve el valor de la hipotenusa si alguno de los dos catetos es menor %que uno en valor absoluto.
%En caso contrario devuelve el valor cero function H=HipCond(x,y)
if abs(x)<1 jabs(y)<1 H=sqrt(x^2+y^2); else
Ejemplo 2. Escribir un programa que devuelva el valor de la hipotenusa dados dos catetos si el valor absoluto de los dos es inferior a uno, el valor del perímetro del triángulo si alguno de los dos catetos es igual a uno, o cero si no se cumple ninguna de las dos condiciones.
%Devuelve el valor de la hipotenusa si los dos catetos son menores que uno en valor absoluto,
%el valor del perímetro del triángulo si algún cateto es igual a uno, %o cero si no se cumple ninguna de las dos condiciones
function H=HipCond2(x,y) if abs(x)<1 & abs(y)<1
H=sqrt(x^2+y^2); elseif abs(x)==1jabs(y)==1
Hip=sqrt(x^2+y^2); H=Hip+x+y;
Programación: estructuras condicionales
Ejercicio 7. Escribir un programa que dibuje la solución del problema de
Cauchy
dy dt =y
2 1; y(t0) =y 0;
para una condición inicial dada en el intervalo [t0;T]. Indicaciones:
1 Las variables de entrada son la condición inicialy0, el tiempo inicialt0
y el tiempo …nal T:
2 Las variables de salida son los vectores t e y.
3 Hallar la solución del problema usando el comandoode45:
4 Si la condición inicial es 1 o 1, dibujar la solución en color negro. 5 Si la condición inicial es mayor que 1 o menor que 1, dibujar la
solución en rojo.
6 Si la condición inicial está entre 1 y 1, dibujar la solución en verde. 7 Usar el comando hold on.
8 Establecer los ejes [t0;T] [ 4;5]:
9 Ejecutar el programa en el intervalo [0;5]con las condiciones iniciales
function [t,y]=MatlabPractica2Ej4(y0,t0,T) [t,y]=ode45(inline(’y^2-1’,’t’,’y’),[t0,T],y0); axis([t0 T-4 5])
hold on
if y0==1 jy0==-1 plot(t,y,’k’)
elseif y0>1 jy0<-1 plot(t,y,’r’)
else
Programación: estructuras condicionales
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5