Presentada en la Facultad de Ciencias de la Universidad Sacional Autónoma de México

T e s i s D o c t g r a l

I

I I

I

1

I

1

I

l-

I

1

I

I

I

I

I

1 I

Esta t e s i s e s t á dedicada a mis _{tres tesoros: Ursula )largarita,}

h a Eugenia y Pablo Gian-Carlo, y a T í , por su amor y confianza.

Quiero agradecer a todo mi “Equipo de Apoyo” su ayuda oportuna e incondicional.

Doy las gracias al

ET.

Fernando del

Río

por

su

valiosa orientación

y por permitirme asumir toda l a responsabilidad del trabajo.

Deseo también hacer patente mi agradecimiento a todas aquellas personas que me ayudaron con sus oFiniones a d e f i n i r y estructurar l a

I

!

E l potencial de pozo cua6radu en :‘.a teoría de perturbaciones para e l estado líquido

Contenido:

Indice

I.

Introducción

11.

Formuiación perturbativa

Desarrollo en s e r i e de Taylor ordinaria Desarrollo funcional

111. E l sistema de referencia de pozo cuadrado

(PC)

Teoría a l f a Teoría b l i p

Coeficientes v i r i a l e s

Parámetros efeczivos y diámetros de colisión y de enlace.

iV.

Representación del

PC

La f.&..ci4z

& 2i;triYUci& rz*;al 61)c(r]

Los valores

Resultados de esauema ITDA de o~cí%\ _ j ~ -

Resultados de l a representación con

iá

I L y l a

IC

La energía l i b r e Fpc

Aplicación a illl sistema Lennard-Jones

(U)

como prueba de

l a

TPPC.

La función de distribución radial

g(r)

La energía l i b r e de Helnholt: E l factor de compresibilidad

E l equilibrio líquido-xrauor Los parjmerros efectivos d y

R

Cimuicintes en la teoría

V.

VI.

Diicusión g e n e r a l y conclusiones ;~:isdecimiencos

.+Endice

A

B

i

bi

i

ogr:i

fí

a

1:; Lgur3s -

~

,

.

.. ,. .. .~ , ,

t

i

, .

- , 3.

I I?;;'RO:OWCCIO.ú -

1

Los líquidos son da \<tal i~iiporran,:ia en l a naturaleza y sin edc!rir _~-

go, ocupan una parte smarnente pequeha del enorme intervalo de tenneraturs

:-

presiones que existen en e l imiverso.

Fn

l a Física Fstadística se quiere en- tender porcyié las fases flu?. son estables en ciertos interíalos de densihd

y temperatura y relacionar 1; _{Estabilidad, estructura} y propiedades tennodins- micas de éstos con e l tamaño y f o n a de l a s partículas que forman a l sistema

y con l a naturaleza de l a s fuerzas entre e l l a s .

cultades especiales que ocasionaron su retraso respecto a l entendimiento de

los estados sólido y gaseoso y no ha sido sino hasta hace unos 15 años, _{que se}

ha

dado un desarrollo sistemático en l a comprensión y cálculo de propiedades de fluidos densos.

Este,estudio ha ofrecido aifi -

Entre l a s distintas teoríaq que se han usado para estudiar a l o s

líquido<-, l a t e o r í a de perturbaciones ha jugado un papel importante.

F

n

e l l a , se u t i l i z a l a información de un fluido nodelo bien conocido, que se espera ccn - tenga e l comportamiento que se considera esencial en e l sistema a estudiar y cuyo Hamiltonian0 se usa corno referencia para representar e l " n i l t o n i m g 621

. /

en computadora (71-22 ) y de cfilculos teóricos para densidades haias e inter-

medias (23-26) y es independiente de l a temperatura. Además su ecuación dc -

estado para l a presión e s a n a l í t i c a (27).

En ese esquema pertiirbativo las fuerzas repulsivas y :itrrictivns

se tratan de manera diferente: l a s fuerzas repulsivas contribuyen. ;i OTC!~?II cero representadas por e l sistema de reierencia de

EE,

mientra- q:~e 1::s [_ .:y

?as a t r x t i v a s , que se consideran a l mismo nivel que l a fomú o 5i1.yiciad :I.: las repulsivas -como perturbaciones scbr? el sistema de

referencia-.

contriiy-

yen

a

primer orden.

-

Aunque l a teoría de perturbaciones referida a ED ha tenido éxito en l a predicción de l a s propiedades de líquidos simples 3 a l t a s densidades

(cerca del punto t r i p l e ) , en l a región de densidad baja

e

intermedia, en i n que e l efecto de l a temperatura es irrrportante, dicha teoría no puede predec.ir correctamente las propiedades de un fluido r e a l . Esta deficiencia se manifies-

tl prscticmente en l a dificultad de predecir correctamente Fropiedades en las que interviene una fase gaseosa. como p o r eiemplo en e l equilibrio líqxi- do-vapor. Aunque hay maneras de calcular l a s propiedades de l o s gases con l a

aproxiniación necesaria (desarrollos v i r i a l e s ) , se ve uno

en

la necesidad de

usar d i s t i n t a s teorías en regiones de d i s t i n t a dens'idad cuando un fluido ninnL

f i e s t a una continuidad entre su fase vapor y l í q u i d a , continuidad quc ijiiisl6-

ramos se r e f l e j a r a en e l planteamiento teórico. Además

la

teoría de pcrtui,ln ~~ ciones referida a ED no p e n i t ? establecer una relacion con otros aspectos teóricos importantes de l a f í s i c a de líquidos, como l o es e l principio de c s -

I

I '

i

En e l c a p í t u l o

IV

se d i s c u t e l a representación del sistema de r-c - i e r e n -

c i a de pozo cuadrado usando 2

s a r i o en cada caso y l o s

res=

.,:dos a l o s que conducen e s t a s aproximaciones.

Lntas aproximaciones, e l manejo de datos nece

-

En

e l c a p í t u l o irse presenta l a prueba de e s t a t e o r í a aplicándola 3 un

sistema Lerlnard Jones (12-6) y se analiLan sus predicciones para l a función de

d i s t r i b u c i h r a d i a l , l a energía l i b r e de Helmholtz, e l f a c t o r de compresibili-

dad y e l e q u i l i b r i o líquido-vapor, comparándolas con resultados de s i m l a c i o -

nes en computadora

y/o

resultados de o t r a s t e o r € a s .

Finalmente, en

e l

capítulo VI se presenta una discusión de l a s caracte-

r í s t i c a s relevantes de e s t a t e o r í a y l a s conclusiones más importantes de e s t e

la propi 1 _{I C} Da_.i l a dificiiltad para representar analíticamen

de un líquido, usualmente se recurre a l método de perturbaciones en e l CLIC .;e aprovecha e l conocimiento de al.* flTido modelo que se usa como cistern de re -

ferenciz, sobre e1 cual se hace un desarrollo en serie de Taylor de l a finciOn de partición configuracional del sistema cuyas propiedades termodinámicas y

e s

- tructurales

se

desean re3resentar.

I

Considérese un fluido uniforme

e

isotropic0 formado por S molécu-

las

en

un volunen V que interaccionan con un potencial esféricamente simétrico

y aditivo entre pares u(r), de manera que l a energía potencial del sistema es

1

y su fimciíín de particinn configuracional en e l conjimto canónico es

Q

=:

J

. ..

J T

$(rij)

8;

N

i¿j

en

donde

i l l

- 4

con

r;i=

\ri-

';I

,

& =

(}i-i)-'

,

siendo k l a constante de Boltzirann y T 1;i tempera'tura del sist;ma.

1

En

estas condiciones, 13 fimción de distribución radial del sistt.ii:i C'S

9

.

I La. enerzía l i b r e de Heldiolt: -juede escribirse como

i

, ,

.

. . .

, . . ,.*-*.

.--"

...-. ., , . ,,,, , ., ,, , ,

en

donde Fid

es

l a energía l i b r e del gas ideal.

hacer un desarrrllo en peifurbaciones de e s t a función, aquí

se

Droponen dos

formas: h c i o n c i l

.

Entre l a s alternativas para

una se?.ie de potencias con varios p a r h e t r o s perturbativos y m a s e r i e

Desarrollo-en sc:rie de Taylcr ordinaria.

Sean $j,

j=i,

...,N p a r h e t r o s perturbativos en t é n i n o s de

_los

cuales e l desarrollo en s e r i e de Taylor para F con respecto a un sistema de referencia a r b i t r a r i o , cuyo potencial de interacción entre pares es u

(r)

cc

rrespondiente a

z.=

₁

O

,

toma la-forma 3

n

vr

F - T

t

Z8.G

-k

1

b';&

r:

,l

+..*

J J j,.i

o

bl

j=i

donde Fo reprecenta.la energía l i b r e del sistema de referencia v

son lcs t e i i n o i

cienes, evaluados en e l sistema de referencia.

?rirne!rr,;'=egiindlo ::Órdenes sucesivos de l a s e r i e en perturba

_-

Desarrollo funcional.

Considéresuna funcional del potencial entre pares

f

[u(.)]

arbi -

t r a r i a , en términos de l a cual e l desarrollo fmcional de F referido al siste:nn de referencia e s t á dado por (19):

f5f

r=f,+

j q

t

2!

2-

(

s l q y +

3!

( P f )

O

+...

r

en donde

. .. . .i

.

~.

I11

FL SICTE;\LL\

DE

FEFERJ3'CI:l

DE

POZO CU.i\I)RLUX)

(PC)

E l sistema de referencia se selecciona tomando er ccer.ta do.; ,-:ite _. r i o s básicos:

esencial en e l sistema a estudiar y que sus propiedades sean conocidas.

que dicho sistema incorpore

el

comportamiento que .jc cons:aera

En la< aplicaciones de l a teoría de perturbaciones a

los

liapido

shples, tradicionalmente se ha partido de considerar a las fuerzas atractivas como una perturbación. En estas aplicaciones e l sistema de referencia está en tonces formado por partículas que interactúan con l a parte repulsiva del poten cial, y l a perturbación se introduce mediante un desarrollo en serie de Taylor

del

tipo 3.1

,

con un solo parámetro perturbativo

iy

definido por

- -

De

esta manera l a contribución a primer orden es proporcional al

En,m

segundo paso se calculan las propiedades del s i s t e m con po- tencial urep

,

usando de

nuevo

un desarrollo en perturbaciones, en e i que :d!o - 10 e l sistema de referencia es un sistema de esferas duras (ED)

Este se,mdo desarrollo puede i1aserse de cuilquierci de 1:1+ ?,>< !I;:!-

n e r x presentadas en e l capítulo

iI

í 5 , 1 2

> .

esferas duras se determina

orden en este segmdo desarrollo se anule.

En

amlas,

el dii-:tro

& I:!.: ir.ponierdo l a c o d i c i ó n de que e l ??mi:1? :i ?I'!:YT

COTO se ve de esta

breve

descripción, 13s fuerzas reyti:siv:i.;

:..

atractivas se tratan de manera d i s t i n t a :

cero, representadas p o r e l sistt.r!n Cc ED, mientras que las iuericis ; I t T : i i t : \ :I5

7

I

I I 1

I

'

j

/

j

'

1 1

I

I I

. g

TO.

contribuyena primer orden, como tambiÉ'n l o hace

la

forma ("suavidad") de

+ep.

E l resultado de e s t a ciobli. perturbación es

en donde l o s términos de seamdo orden contienen tanto la contribución de las

fueTZ3S atractivas

(

<

uQ-T>fap

-

<UaTrbrep

cuanto l a de l a suavidad de

i a parte repulsiva.

2 2

La teoría de perturbaciones con base en un sistema de referen-

cia de ED ha tenido éxito en l a predicción de las propiedades de líquidos sim-

ples (e.g. argón) a altas densidades, esto e s , cerca del punto t r i p l e , porque

a tales densidades, l a estructura del fluido está determinada en su mayor

parte por las fuerzas repulsivas. Sin embargo, a densiciades bajas y moderadas,

lac

esferas duras no representan adecuadamente l a estructura de un fluido r e a l ,

y a que d e>;& U = ~ ~ ~ ; U C ~ L L C ~ 7

.-.,

-,--

1; ---+.--- L C ~ ~ + < - n o CAL..- ~ L ,u~~ m~-Cop+,, ~

____

Y ~ ~ n n + g h l ~ ~ ~ ~°2F nn ?llPde

ser explicado mediante un potencial de referencia puraTente repulsivo.

hecho, la teoría de perturbaciones de esferas duras no predice correctamente

e l segundo coeficiente virial, sino sólanente

De

su límite a altas temperaturas.

En

este trabajo se ha seleccionado un s i s t e m de referencia

que pemite tratar a l a s fuerins a t ~ a c t i v a s al mismo nivel que las repulsivas

y 7.-diante e l mismo procedimiento. Est- s i s t e m tiene un potencial de inter- x c i ó n entre pares de pozo cuadrdu

[TC)

,

definido por t r e s p a r , h t r o s :

d i k e t r o d:, su profundidad

E

su

y

SLI a l c ~ n c : 7 , erL la forma

r:;

,l

Con este s i s t e m d 2 -e ~e:~er.cia s e considerará como perturi.:i-

ción, l a diferencia entre l a fornil p.1r;ii u;ax de l a interacción real y la Lie1

p o x (ver Fic. 1 ) .

.__I_.--

__

-La teoría dr perturbaciones con un sistema de referencia de pc requiere que, dado un potenc id intermolecular

u(r]

,

se proporcione

un

cri terio p x i l a deteninación óp1 h a de d, € y

R.

pmfixr,di&d fiel poro

_(-E

) i g u c l a l mínimo de u(r) (localizado en r=h] y 10s

px,unetros d y

R

se determinan imponiendo l a condición de que 13s téminos de priiner orden en 135 perturbacicies se anulen.

-

i

En este trabajo se f i j a l a

I

Teoría alfil. -

,

En

e l desarrollo en s e r i e dado

por

[37 y [43 se introdcen

dos parámetros de suavidad

M,

y

repulsiva y atractiva de u ( r ) , a través de un potencial modificado

asociados respectivamente, a _las regiones

de manera que

b]

pueda escribirse como

Como se muestra en l a Fig. 1 , los pránetros de suavidad

u,

yc$producen ma variación continua de

vCr)

en i i s dos rezionec:

va (r> an), respectivamente. cuando d,=q=

U,

d,=

d

;z,=

2

, ~ m t e

2:d

y

wz

R

,

de mcnera que V(r)=

~bp~(r);

y cuando

&,=

d2=f

,

v(r)=u(r).

repulsiva ( r < b ) y atracti- y por consi-

k Con estos ~ai.ánztrcs, los dos téminos a primer orden en la

12.

en donde

La ecuación _[iza] s j l o conciene i n f o m c i ó r . .ace:.::i (je tr!

parte repulsiva de l a interacción

( ~ 5 % ; .

La condición F, = O _conduce ;i la

que coincide con l a definición del d i á w t r o de esfera dura de Barker y Henderson ( 5 ) .

La expresión

[12b]

involucra Únicamente a

l a

región atractiva

de

u(r)

(r>h) y produce con

Fz=O,

un alcance efectivo de pozo cuadrado

[is]

R,(T)=

R , t

(e

Ambos

parámetros d, y

R,

son funciones monotónicas de T, doblemexte acotadas:

con

Para c a l c u l a r e s ' o s t é m i n o s e s necesario conocer los valores

I

de ypc(r)

y

Ypc =

$$

en con acto (r=d, para

F

(FR*

para FZx )

,

para una razó

) y en e l .ilcance

I1

I , = R d / d , dada.

La

e x i s t e n c i a d e l téirnino cruzado F depende de l a rr,aiern

. . 12.

Las condiciones

F,

= F2 O: que permiten d e f i n i r a d, como

12

.

La foma adoptada [,A41 produce F = O[.\iof

.

de

representar . : ,. ( r ) [la]

[14] y a

R,

como

[lS]

conducen además,

a

que

F

= F + 20. orden

PC

20

De

[17] y t S 1 e s de esperarse, que con e s t a seleción de los

I parámetros e f e c t i v o s d, y Its ~ los t.6iminos de

rorrerri5r

de S ~ I - E & ir&n

sean muy pequeños, de modo que, s i s e desprecian éstos y l o s términos de orden superior

PC F = F

a primer orden.

Teoría b l i p .

_ _

Considérese a?!o;.a el dcr;,iri-ollo funcional [ S I escogiendo a

fL'(r)l

como l a función de i.ix.e

que puede separaice en dos regiones, una asociada a l a parte r e p u l s i v a de u(r)

( r i b )

y 1.1 otra asociada

a

su parte atractiva

(r3

h),

en l a fonna siguiente

c>

Esta expr:s ;Ón se reduce a l a propuesta por Keeks e t a l ( 12 )

para un sistema de r c f c r e i c i a do esferas duras.

A _5enejanza dr: :a teoría a l f n , l a segunda condici

Y

n para i n obtención de db y I'b irrpuzsta eii e s t e plantcmLtrito es

docir

( J F )

'=

0

,

es

FC

-

.~. -- __ . .. .. . .

La expresión [24a] corresponde a l límite de baja densidad d e l

I

I

diámetro de e s f e r a dura de Weeks e t a l . , y es una función continua de T , acota

da e n t r e

a&,

(T)=IOii

y

dL, (T)=O.

6) -

I - I

Anslogamente, _{(T) es una función continua de} T acotada

entre

Con l a condición

($y)

4, e l Último térmirio del segundo ordcli

I:

9dI

Af,=Oy como de[22] u f F u f

,

s e tiene en C9a-J que

hf;

=

O

.

LOS t é r -

gpc (123) y g1 c ~4 ( 1 2 3 4 ) . Sin exbargo, auncpe l a s correlaciones de t r e s y

C w t r o psrtfcula: C,OP importantes, su contribución, comparada con l a dz gpc(l?)

es bastant;: :)ec!ucña. Además, cmo l o s p a r h c t r o c efectivos db y Rb derivados

en e s t a t e o r i a ,

:or]

funcimes no s ó l o de T como en e l caso a l f a , sino taini'oién

de 12 densld-td, coni0 s e ver5, los resultados que produce

a

primer orden, en e l

ad

l a energía l i b r e d r l sisteinci de i n t e r é s se reduce a l a de los pozos [?On],

son aún m e i x e s que 13s de l a a l f a a seguido orden.

P C

2 -

Coeficientes v i r i a l e s ,

Para un E u i d o poco denso l a s e r i e v i r i a l en p o t e n c i a de l a dens idad

es una adecuada representación del factor de compresibilidad.

Usando l a relación

puede determinarse l a contribución a los coeficientes v i r i a l e s términos de l o s desarrollos perturbativos aquí discutidos.

los términos de orden cero, primero y se-gmdo

[

1 2 3

,

[

171 y 1183

,

contri - buyen a l segundo coeficiente v i r i a l

P I

(T) del sistema estudiado. Pero l a con-

dicion b,

=Ft

=U, elimina l a contribucion a B 2 [ij de l o s tenninos &primer orden.

Bi(T), de los

Ea

l a teoría alfa,

.

E l término de orden cero es

B F

(T)

,

B~~

(7-)=-$vd3

[e

pe

₍

/ - I 3 )

+ I 3 ]

I

271 2

Por l o que respecta a l z teoría b l i p , se demostrará a continua - c i h que a primer orden, e Lla contiene exactanente a S2(T).

partiendo de _{l a} defini'ciór d-1 segimdo coeficiente virial

Esto puede verse

con f ( u ) &da por

[

?1;~1

.

2

Ai

agreTar y restar en e l integrando e l término

[

f(Lpc(r)) + i]se tiierte

I

l a desviación entre e l coeficiente

Viriai

e~cacto

y

e l aproximado por la

teoría, con ' f(r) [21bI

.

como

corres~onde a l límite de baja densidad

\23a, b]

,

en este caso

B2

(T)

=

f32C(T)

y

la.

teoría b l i p es exacta a primer orden

en

l a densidad.

l e asegura predicciones precisas de las propiedades del vapor d i l u j d o : y

-5 una caracterís'tica que no está incorporada en las teorZas de perturbaciones

que usan un sistema de referencia de

E-

n i en l a teoría a l f a usando PC, aLinque en ésta se obtiene un Segundo coeficiente virial cualitativamente correcto,

ya

B

p)

de un sistema r e a l .

Esta ,.:liz,q,:iLLisLi..

que

B t

PC (T) tiene esencialmente e l mismo coiiiportaíniento con l a temperatura que

2

Los téminos de segundo crden diferentes de cero en e l desarro -

110 b l i p con pozos cuadrados

A F ~

I9bJ y

h

Fj

1

9c] contribuyen, respectiva- mnte, a l tercero y cuarto coeficientes v i r i a l e s , por i o cual, en esta teoría a primer orden, los coeficientes v i r i a l e s B (T)

,,

B,,

(T)

,

. . .

no estarán dados exactamente. No obstante, aquí también estos coeficientes B;(T), i 7 2

,

apro - ximados por B (T)

,

tendrán un comportamiento con l a temperatura cualitativa - niente correcta.

3

Parámtros

--

sfectivos y diámetros de colisión y de enlace.

I

10s parhetros efectivos d y R derivados en las teorías a l f a y b l i p pueden jdcntificarse con cantidudes que tienen una interpretación fT5-i -

ca dentro del m i c o de l a teoría cinéticn.

D.

Ayala

expresarse come l a distancia media de iri&iino acercamiento entre dos partículas

Como se mostró por

F.

del Río y (28) el diámetro de Barker y [lenderson que coincide con

L141

,

puede

en colisió!i:

en

donde p(s)

es

la distribucijn de distancias de rriáximo acercamiento s < b ,

&+emina& por la energía cinética

De

modo que 4s) puede escribirse en l a

forma

y entonces

d,=

4 ~ 7

.

E l alcance Rapemite una i n t e r p r e t a c i h similar: Como l a dis- I

tancia promedio de máxima separación entre dos partículas ligadas (es decir, pares de partículas cuya energía t o t a l en e l centro de masa e s t á entre O y -E)

y

en este caso l a distribución de energías

cinéticas

(normalizada entre

O

y e )

de modo que, l a distribución de distancias de máxima separación p(A) es en-

deecpués d? >ma i n t e u a c i ó n parcial

<

17 queda eqresado como

<I

>

=

R,

4

(ep'-

i)-'JO'[e

-pure)

-

11

d l

R m

qui. es i8éntica a i a expresión para

R,

cinta por

r1S-j

.

RMes cl pTomedio de las Listanciar; de máxima separación entre pares de partí- culas ligadas, I?,=<)>, que puede llanarse diámetro de enlace.

T-

I

.I

19.

i<

Tmhi6n l o s ténnnos de segundo orden

en

l a teorfa alfa

5,

y

F,,

dados por

1

177 y I 1 8 1

,

rrbspectivamente, pueden escribirse en términos des>..!.

como

p

~

]

~

~

w

~

s d s

su promedio en c m a n t e s

<

s'>,

=

<

s'>

-

¿

s 7 2

=

<

( 5

-

¿ S

>

)

>*

es entonces r

y mide l a desviación cuadrática media de las distancias de máximo acercamiento s drededor de SU valor medio d,

.

En

forma

semejante

...

da l a fluctuación wadrática media de

1

.

Estas fluctuaciones

[2Ql

y [29] son las expresiones que apare-

C l n entre

{I

en [ 1 7 1 y 1183

,

respectivavente, de modo que

F

y

F Z 2

pueden

e:;cribirce como I1

Esto s u g i e r e clue l c s momentos de orden superior de s y

1

est&

21.

* .

Por

o t r a p a r t e ,

l a

adema& representación de l o s coeficientes

viriales,

asegura e l tratamiento correcto d e l f l u i d o

a

bajas densidades, me-

diante e l mismo formali-mo usado para e l f l u i d o denso.

con l a t e o r í a <e perturbaciones referida a ED, que t i e n e é x i t o s ó l o en l a

Esto iiitimo contrasta

oión de alta densidad.

re,

IV _{REFECENT.4CION}

E

L

Pc

Aci como la teoria b l i p

a

l e r . orden necesita e l conocimiento de

la f,mción ypc

,

2133

,

para l a determinación de sus parámetros efectivos

d b

- a través de

la

solucióri del sistema de ecuaciones acopladas [?3 a.b.1

ver Fig. 2 - l a teorfa alfa requiere

los

valores de esta función y de su:

+

+

derivadas en r = d-

,

R

(en e l calculo de C(r)

,

1191

) para l a obt.e:,rii"c de sus terminos de 2 0 . orden Fll y FZ2 r - 1 7 1 ~ [IS]

,

respectivamente.

Y R t

Por

consiguiente, para l a aplicación de estas teorias ?' aCin para

p e r l a s a prueba, deben conocerse varias propiedades de

los

poz' 5 .

propiedades son SU funci6n y (r) o su funci6n de distribución radial

r)

y su energfa l i b r e Fpc, como funciones de

p * ,

T*

y

A

= R/d.

embargo, a primer orden, tanto en. l a teorla a l f a como en e l limite de baja densidad de l a b l i p , l a determinación de los parhetros efectivos del f l u i do en estudio es independiente de l a estructura del PC, necesitándose única

PC *

mente una bu2na representaci6n de

F

Estas PC

S i n RPC (

-

-

.~ . ~.

Estas funciones gpc y

FPC

han sido estudiadas para pozos de

alcances particulares, especialmente

A

= 1.5

,

en ciertos estados termodiná

micos mediante distintos procedimientos, l o s cuales pueden separarse en 3

grupos :

perturbativos referidos

a

ED y simulaciones en computadora de Dinámica hwle cular

(mí)

y Monte Carlo

(XC).

-

teorlas en base a l a solución de ecuaciones integrales, desarrollos

-

En

e l primer grupo se cuentan las teorias de Born-Green-Yvon

(BU),

de Percus-Yevick (PY)

,

de l a cadena hipertej ida VSC)

,

l a aproxima- ción e s f é r i c a promedio (>S.\), l a de

fase

aleatoria optimizada (O,W.4), l a ex

ponencia1 (E'YP) y alamas o t r a s ,

De

estas teorias pueden obtenerse a p o x i -

maciones px-a g p c , para l a presión, l a compresibilidad y l a energía interna del sistema, pero e s t e procedimie:ito no permite un czilculo directo de Fpc ,

-

Los resultados de est;is teorlas aplicadas a pozos son l o s s i -

E l cálculo de l o s 2 pr~imercs términos en un desarrollo de gp,en guientes:

Lhi para

detallado de l a

teorla

BGY (con l a aproximaci6n de Cupetpsici6q)

de

Á =

1 . 5 y 1.85 ( 3 1 - 3 4 ) .

~~ ~ ~~

Sus resultados para

2

= 1.85 fueron satisfactorios a i conparir-

los con dat.os expc-:hentales del argón. Los resultados para

A

= 1 . 5 cor -

cuer&n hastante bien con datos de simulación en computzidora de

D

l

( 35 ')

hasta

del punto c r i t i c o , en particular de l a compresibilidad.

A =

1 . 5 y T * >

T,

,

l a temperatura'crltica.

*

p

= 0.7, pero SUS predicciones son malas a a l t a &,sidad y p o ~ . z-rik

) una

BOi

modificada mejoran 10s resultados de l a compresibilidad para

Young

e t al. ( 36

En

las aplicaciones de l a teoría PY para pozos de

A =

1 . 5 (y en

algunos casos

A

= 1.85), se cuentan l o s trabajos de Levesque ( 37 ) , Verlet e t a i . ( jp, )

,

Tag0 (39,401 _y Smith e t a l . ( 41

1.

Sus resultados para

cuando

13"

2 1 . 5 y

p

= 0.8

,

su description de g p c (r<1.5) es mala.

Además, l a presi61i y l a compresibilidad que predice para

T*

baja y

p

*

a l t a son madecuadas, ya que en estas teorlas no se describe correctamente e l efec t o de las fuerzas atractivas a a l t a densidad,

I

i _{son s a t i s f a c t o r i o s a a l t a s temperaturas, pero cerca del punto tri.ple,}

*

PC

I

-

La

t e o r í a HNC incluye más diagramas que PY, pero esto no es nece

-

sariamente ventajoso. mostraron que supera

Sin embargo, para

A

= 1 . 5 Henderson e t a l . ( 42, 43

l a s predicciones de

PY,

especialmente a a l t a densidad.

De

l a aplicación de l a !.EA para pozos con

1

= 1 . 5 , Smith e t a l .

(

4 4

ve inexacta en e l límite

y*+-

O .

) encontraron que cuando

FE

= O , gpc(bSA) = g _{E 9}

(PY)

.y que se vue1

-

Anderson e t a l . ( 45) propusieron como forma modificada do l a S A , l a OW..\ y sus resultados para pozos de

A =

1 . 5 son mejores que 1 ~ s di: l o s K.1.

( 4 6 ) que es exacta en e l

lhp*-+

C _y que mejor?

a

l a ORPA en l a descriii ci6n de gpc (r 7 1 , 5 ) , aunque para r

<

1 . 5 es menos aciecuada que 1.a %A y 'la

0F.Pii.

Estos autores propusiercn posteriomente l a aproxin~ación EYP

manera de cerrar l a ecuación de Onistein-Zeri1icke

[o'!)

en

s a t i s f a c t o r i o s , excepto e l de l a energk. interna, l a cüa:L rr-

teorfas introduce bastante inexactitud, por i o que su.; re.;ult;idos

estas

no son

P

,duccn mujj bien.

Carley ( 4 7 ) propuso una ecuación de estado par?

rozas

inedia2

integral paramétrica, y sus resultados a

T*

a l t a y ,,O" b a j 3

-

te una

buenos, pero cerca d e l punto c r i t i c o f a l l a completamente.

kl segundo STJPO, correspondient, los desamollos perturba

_-

en base a ED, se tienen resultadas tanto para gpc Como para l a ener- libre de Helrnnoltz FPC

.

Smith et a l . ( - 4 8 ) calcularon por s b u l a

cion

de

)

I

C

e l termino a ler. orden en perturbaciones de gpc y sus resulta

dos son bastante buenos excepto a a l t a s densidades, pero e s t e conportanien t o fue corregido por Henderson e t a l . ( 4 9

1,

quienes estudiaron esa r e -

gion usando l a presión obtenida

por NC.

Calcularon también e l témino de

20.

orden en l a perturbación en potencias de

P E

-

-

-

.

En

un

desarrollo sme

_-

j;?ts,

$L&,

st ai..[ 5 :

>

t;i-l%;-cjn 1;s t&-minzs ~ o i y , = ~ i ) ~ ~ i ~ i ~ ~ ~ i r ; ~ e,,

z,í.

Por l o que toca a l a energfa l i b r e , este procedimiento propor- ciona l a información más valiosa ( 1 8 , 25, 35, 4 8

-

5 1 )

.

k

l

estudio

del termino

a

ler. orden Fpci calculado por Tpl o por bIC, Ponce y P.en6n

(PR) ( 52

T*

y

A

,

p

*

pcquefia.

) propusieron una aproximación a n a l í t i c a como f w c i ó n de

p*

Esta expresión predice resultados correctos para

A

=

1 . 5 y

Reiinhart ( 5 3 ) propuso una eupresión Dara F

pi

_{basada en} resi1it.i i,,.; de Barker v ilenderson ( 5 ) , E l conocimiento de

F

pernit!: íociular una representación para F

%imxhcinnes de cmnresibilidad local

o

aacroscópica

.

vc h

usando cialq<iier:+ de 1x5 P C 2

-

k n t r o del tercer grapo, e l conocimiento de l o s pozos

por

r e -

sultados directos de sinulaci6n en computadora puede separarse en 2 etapas:

la PrjJWa, en l a que se estudiaron pozos cor.

2

= 1 . 5 y 1.85 para algunos

, , ~ , ,, , , , ,, ,

,.

, , < _ -. , ,,

..

,.* ,.*--,... I.*-c-,.,,-"-^c.~^.. , ." ... " . ..~. ,,,,- I ., , , , ~ , . ,... -

__._

i ' "

25.

. . .

1976,

en

la

que se empezaron a estudiar pozos con nuevas

Als.

f

Motivados por las necesidades del presente trabajo, llenderson

et al.

(

58

con

A

=

1.125, 2.00 (0.125) para

p *

=

0.4,

0.6 y

0.8

y

algunas tempera

turas reducidas entre 0.5

y

4.0.

1

calcularon por el método de

>IC

las prapiedadec de

los

pozos

-

S I

El

trabajo de Collings

( 5 9 )

en

ill,

proporcionó informaciór.

adicional para

A

= 1.3,

1.4, 1.5

,

1.6

,

1 . 7 5

y

2.00

y

estados tenodiná

micüs p%i-ti~xJeies.

A

esta informaci6n de hIC dr llenderson

y

de

D4

de

callings,

se

le^

identificará

q u i

como

l o s

"dairis de g

pc

euactos"

(LGE)

,

-

Rosenfield et al.

[60,61)

han calculado algunas propiedades

de pozos con

A

=

1.2042

y

1.3675.

En

las secciones siguientes se discute la manera como se esco

gi6 la representación de g

pc

y

FPC

a

partir de la información anterior.

-

La

función de distribución radial

_gpt

_(r)

En

esta sección se presentan formas alternativas de representa

_-

ción de

g p c

,

partiendo del caso especial más simple, en orden creciente

de complejidad

y

generalidad.

a)

Limite de baja'densidad.

Pt

d<r<

R

r >

R

La

aproximación

y p c

=

1, i.e.

para cualquier densidad, ignora las correlaciones entre las partí'zulas

del

sistem

y

su

variación con la densidad. Evidentemente,

gpc (d

+

) = g p c

(R-1

+

(R

3

=

1 (ver Fig. 3a).

y

g p c

= e

PE

Los

parámetros efectivos

db,y

R b o @ 4

a,b]

que se o5tje-

nen usando esta aproximaci6n en la teoría

b l i p ,

son independientes

Zr

la

I .,,. .. .. . . .~ . ,... . , ,, . , , , , , , ., ,,, , ,. ~ ,_..,.,,.,,._ *,& ..<,.. <., “ . ~ _ , . - U . . ” ~ X , < - _ _ _ . , , , , . , . ,“,,...____I--

PC _?C

y en esta aproximación predice

L

Pt .. !-

+ p *

B 2

(TI,

con

B Z

(T) exacto, dado por

de orden superior.

2 7 1

,

pero que carece de l o s coeficientes v i r i a l e s -

b)

Límite de alta,densidad.

Como a densidad a l t a l a estructura del fluido está determinada

principah-nte por las fuerzas repulsivas, proponer

YPC = )’ED

,

a liitilquiei- Üeiisiiaci,

introduce una dependencia aproximada con

P * ,

que es consistente con e l l í m i t e de baja densidad. Azemás, como yEp= para r

>

d, se tiene

g~~

¿ < r < R

7

r > R

gpc

-

que en e l l í m i t e de a l t a temperatura, cual es exacta a cualquier densidad.

aproximación es despreciable a

T*

a l t a independientemeitz de l a densidad.

P-P

O, resu1t.n en g p c = g E p , l a

En

otras palabras, e l error de esta

este caso l a p ~ e s i 6 n del

PC

e s t a dada

por

desarrollo de g E D m potencias de l a densidad contribuye,

por

e l término de orden c e r 0 , a l

;U.

Coeficiente v i r i a l exacts del ~ O Z O ,

y

corno

yidependiente de l a temperatura, l a s potencias superiores de

p

*

contribyen con coeficientes v i r i a l e s que exhiben l a misma dependencia con l a temperatu

1-2 que Eiz

(TJ,

l o cual es

es "€U

-

rrccto (29, 62-65).

?C

I

c)

Caso general

La

aproximación anterior desprecia e l efecto dependiente de l a densidad, de las correlaciones en e l interior del pozo y en l a vecindad de él. Estas se manifiestan en valores del cociente gPC/gEDdistintos de

.

e

,

para r =

d

,

R-

y de 1 para r =

K+,

l o

cual

puede expresarse como

!

t

+

La

función C i

,

cuya dependencia con

p*

,

T*

y

A

se omite por simplici-

dad,

debe escogerse de t a l forma que

y p c

sea contínua y que contenga

co-

rrectamente

los

limites de

los

casos a) y

b),

por i o cual es necesario con

sidzrar 3 regiones

(Fig.

4): l a región

i

= 1 corresponde a r 5 d y en

(r) es una fun e l l a gpc (r) = O, en l a región i = 2 , con d 5 rC.

R-, gp,

ción suave y uniforme de r , y en l a región i = 3 para r 2, R

,

g p , (r)

una función conthua de amplitud decreciente qi'e oscila alrededor del valor

l

-

+

-

+

<

es

g p c = 1.

(i)

terpolación l i n e a l (IL) eii r , del \alar de g!,c

/gEn

er.tre r = d y r =

R-

(ver Fig. 3c), i.e.

E l comportamiento 1 ~ 5 s simple que pus'e piopor?er;e Consiste en LIM i n

_-

r

3 4 4

Y

-

Para representar correctamente a g en l a región 1 , s e usa PC

la

condici6n de continuidad de ypc en x = 1 , y para l a región 3 se prop0

_-

ne l a dependencia exponencial.

-

con e i parjmetro

X,

obtenido de l a condición asintótica gpc(x) = gED (x) para x

> > l .

continuidad de yPC en x

=i\

,

resultando

E l coeficiente

a

e s t á deteirninado por l a condición de con-

In

este caso, l a dependencia con l a terrperatura de los coeficientes viria

l e s 3 3 , , . . , se modifica con respecto a 1; 6ei llmite de a l t a densidad, por 13 dep ~ ' ~ r i c i a de C,(x) con

T.

siendo

I

1 3 9 1

con

líh'<h

y n 2

,

n

y h funciones de ,o*,

T*

y

_,

La

deteriiinaciór. de 18.5 f~~.!?cicccs ,b t e y h E 3 4 a,c] y [3G] t respectivamente, requiere e l conocimiento de l o s valores de

-

[I*,

,

'

A

>('

1,

con 1

<

X'Ch.

En estas condiciones, l a minima infoma

xc -

-

ción requerida para caracterizar l a IL

,

son l o s valores g p c ( s )

3

=

ti',

)

'

1

,

y para l a I C , l o s valores g p c (xc ) . En l a siguiente sec ción s e discute l a obtención de estos valores a p a r t i r de l o s valores gpc

(xc

) para l o s valores

,

,

,

A

po*

y

To*

contenidos en l o s E E .

g p c ( x ) en

con

-

Los valores ,ope (xc

1.

E l problema planteado por e l

manejo

del sistema de referencia en l a teorla de pei-turbaciones referida a l PC (TPPC), surge de que, Como se men cion6, g'p,

(x,"

) contiene datos solamente para ciertos valores de

p"?

T" y

A ,

por l o que se hizo necesario desarrollar un proceso de interpolaCi6n en estas variables en l a fonna siguiente:

1) Iiiterpolación en T*.

De los datos gpc(xc ) como función de j3C- a l mmrener l o s 13

-

lores de

h,

y

Po

constantes, se interpol6 g r g f i < ar.er:tc para l o s valores

de

T"

que se deseaban. Se evitó l a extrapolaci6n p:.ra

T"

Srande t o n c i i ~ o ea cuenta e l 1Dnite

fue inevitable extrapolar dada 13 f a l t a de datos de gk,ís, particularmente para

>

1.5.

-

O

-

-+ O , esto es g p c = g E D

.

S i l . embarzo, para

T"<

1

O

C m e l comportamiento de gpc(f)

con

¡a temperatura es tinifor

me

y Suave, e l conocimiento de SUS valores e i

varios

puntos dzntro de

ciertc intervalo de te.erütUr3, gelmite usa; UT ajüste bajado en un c r i t e r i o de mínimos cuadrados en polinomios de Chebsliev para predecir

los

\ralo res correspondientes a cualquier

T

en ese interviilo.

-

-

-

A

los

resuitadas de

P <

proceso '¿e interpolación en

T"

se l e s identificará como 3 _{T'j.,

2) Interpolacibn en

p*.

-

l a iiiterpolacibn en

p *

a cada cuadrados.

p

*

-c O , en el. rual gpL = P': y4ro t1-P.v cil-!? extrapolarse en l a región

de a l t a densidad.

p *

= 0.0, 0.8 (0.1) están contenidos en gPcQ">.

Con l o s _{datos ya interpolados} en temperatura g p c

(T*)

se hizo

Aqu€ s e evitó evtra,.::,l.ar a

p"

pequeña, tomando e l límite de interés mediante un ajuste de mínimos

Los resultados de e s t a interpolación en

p*,

para

I 3) intenpoiación en

1.

Finalmente, como l a

TPPC

introduce una dependencia con

_h

,

_es

np.-o.c3

.._.."--.

_',?

...

,-nrpcrr _6.2 los _{> r - T - ~ . ~ - - r u L u i G a}

22

_{g p c}

(3;

_CúiTtG Tuiici6ii de esta _nueva varia-

ble, l o que condujo a l proceso de interpolación en

A

segriida. .

que se describe en-

Como los datos i n i c i a l e s de sirnulacion g pc

(xt

) contienen in- formación para

l o =

1.125; 1.75 (0,125), _y é s t e es un intervalo suficiente mente q l . i o , l a dependencia con

A

se ob.wvo meciimte m a inteiyolacjin

de Aitken-Lagrange conesospmtos, nanteniendo

p*

y

T*

constantes, gene- r h d o s e a s í gPt(X}.

-

Lo

anterior puede resuinirse

en

e l expiema de interpolaci6n en

Se

estima

que l a s incertidumbres debidas

a

l a s manipulacianes gráficas y numéricas en e s t e esquema, ttngan su valor máximo entre 2 y 3 veces l o s errores estirriados de

lis

N E

originales excepto en las res:ior,es

extrapoladas. Debido a que g pc (X

1

contenía muy pocos valores de g pc (

2')

para A

_#

_{1 . 5 y estados arbitrarios} (

p

*,

T*), el mismo esquema de interpolación usñdo para los valores de

s T c

en

3

pr-?r.j:. r . ~ s n i + i & c p ~ z : sistemáticos y en ocasiones claramento no f í s i c o s , Para corregir e s t a s i

tuación, se supuso que g pc ( 3')

z

1/2

[

g pc (i'j + g pc ( 2-1

)

y

se

asigno una desviación fracciona1 dependiente de

p*,

pero f i j a en

T*

y

2

,

basada en e l comportamiento sistemático observado en g pc (

2:)

a l variar l a densidad.

De

esta manera se c o q l e t ó l a base de datos de

(

1')

necesaria en e l esquema

ITDA.

A continuacion se discuten l o s g PC

resultados obtenidos con dicho esquema..

-

Resultados del Esquena ITD.4 de F~~ (s

Interpelación en

T*.

de g pc (X c ) para

g pc

T*

1.

Las t r e s curvas exhibcn JrI c.)q>oitamiento Semejante: para

0.5 f T" 5 2.0, l o s valores en

5

y ea -1 punto medio decrecen rápidamente

con

T*

y a a l t a s temperaturas e s t e dezrocrnierito se vuelve más lento y

1

-

--

--

En l a Fig. 5 s e muestra €1 :o-pirtaniento con l a temperatlira

. . ..

*

,31ación

cn

9

InteL IJ

la

intomaci6n 1.ontenida en g _{( y * )} se _{obtuvo :'a Fig. 6 ,}

PC

ue se observa l a viaria( i6n de g pc

( 5

) con

y

*,

para

:i

= 1,625 Para

T*

= 1 , gp, (1') decrece suavemente con l a d a s i la q

T~

= 1, 2

y

3. Y

u3d b s r a

p

"=0.55, valor a prtir del

cual

empieza

a

aumentar y er,.

R 0.65 su crecimiento s e acelera grandenente. Aumentando l a t«!ipera

?

-

tura

(T*

2 2 )

valo de dens:J.i:id, y a densidades a l t a s como e l efecto de l a s fusrzas r e -

P

._.

8 pc (1') Se vuelve Una función creciente en todo e l inter-

ulsivas es mas importante, es independiente de

T*.

Por 10 que toca a g

, , , ( 2 - ) ,

es

una

función decreciente de

p

*

cuya razdn de decrecimiento a a l t a densidad es menos importante cuando e l

está más f r i o

.

btos en g pc

i

3

f

Las Figs. 7 y 8 son ejemplos de l a infomacion contenida en

pc (1)

.

Frr

l a Fig. 7 s e muestra e l comportamiento de g pc (1') con Wd

para

T*

= 1 y

y

*

.= 0.2, 0.8 (0.2). Todas l a s Curvas presentan caracte-

rlsticas semejantes: disminuyen con

2

hasta W. ";,,,A

,

cuyo valor de- pende de l a densidad y

a

p a r t i r de l a cual empiezan a crecer. A l a den-

sidad

más

baja,

9

'*

= 0 . 2 , e l decrecimieito no es muy marcado y l a

A ,

. _z 1.63; a l aumentar l a densidad l a razón de decrecímiento va aumen-

L x d o y

2

.:'J razón de crecimiento para A

.; :::3 :~lqidad mayor

( p *

= 0.3) l a posición del mínino para ";,,,A 1 1.38

\' . : . r ? n t e definida p0r.p" :1 comportamiento general es mucho nás zar

i 3 h . . L k i s , las i n t c r s e x i o i e j ,le las cunas en e l intervalo de deiisi-

"I,? (0.2

-

o.

61, indican qae g (, (:+:

y * )

; K ';(l

p*

,+

A ?

*) dependi:n.lo d31 pozo considerado.

se va desplazandu ;lacia valores

m5s

pequeños, mientras que

I,.,;" y

p

*

= 0.6 se reduce bastante.

/. . - 1

-

puede ser mayor o menor que

l a Fig. 8 s e s x ~ i )e el cowportmiento de g pc (

2-1

en

los

33.

disminuye

con

'x

hasta U M

cierta

2

E

1.5, a p a r t i r de l a cual

aumenta

Suavemente.

rier3 que, mieixras para 2 = 1 , 1 2 5 gp,(

1-

;

p

*

+

A?*)

7

q pc (

a-;

y*),

para ; i > l . 3 e l comportamiento se invierte,

E l decrecimiento es nás intenso

11

aumentar l a densidad, de ma

-

Resultados de l a F.enresentnción con

~-

l a

IL

v l a I C ,

Se presentar ahora l o s resultados de l a representacion 48s

(r) usando ambas interpolaciones: l a lineal v l a cuadrática. i e consi

g PC

__

&ran situaciunes en l a s que se "?r,ta con i n f o m c i 6 n de l o s Dc;E y en las

que

es

necesario aplicar e l es. ,.::::a ITD.1 para l a determinacj6n de l o s valo- res g pr

(xc

1

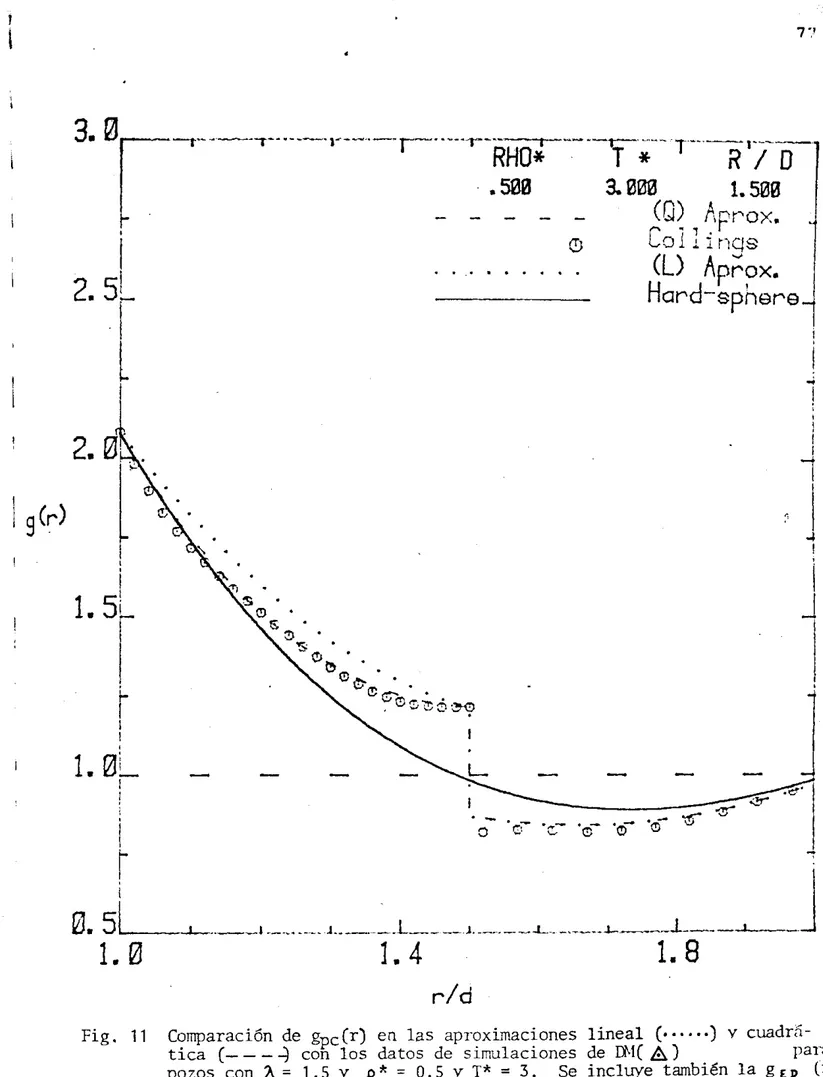
I

Las Figs. (9-15) permiten juzgar l a bondad de los c r i t e r i o s con

10s cuales se hizo e s t a representaci6n, a l comarar sus resultados con da- t o s conocidos de

EM

y >IC a c i e r t o s valores de

todos estos casos se us6 el valor de g pc (A'= 1.25) obtenido d.e l a s simula -

cienes

.

.. ~

*

y

T"

con '2 = 1 . 5 , En

Comportamiznto con l a temperatura.

Las Figs. (9-11) mUestran l a deDendencia con l a temueratura de

(r) para

p

*

= 0.5 = c t e . Es f á c i l notar que e l límite de M i a den- g PC

sidad es una mala aproximaci6n para o; pc (r)

a

esta densidad, ya que predice

un valor constante dentro del pozo igual a

T* = 1, 2 y 3 , resaectivamente, y fuera de é l un valor de 1 ,

e p c = 2.72, 1 , 6 5 y 1 . 4 0 para

Similamente deficlente es l a represataci6n de qp, en e l limi -.

t e

de

a l t a densidad, \;a que sus \ralores

ePC

g ED s3hrecstinm considera -

blaw!;te l o s valores de gp, dentro del MZO -: &u!: fuera de él.

Los resultados de l a renresenta:i in cc\n l a interpolaci6n lineal superan notablemente los resultados de las .ip.-o:.:i:.uc iones anteriores, nar-

ticu1arnient.e a a l t a temperatura.

sentacióri con l a interpelación cuadrsrica es %xce!.erite cuando se l e propor

-

ciona correctanente e l valor

2

.

Satur3lmcn.':e a d u s representaciones

coinciden fuera del pozo.

mortami.ento con l : ~ densidad.

De

l a s Fli:: I (9, 12-14) puede observarse e l comportamiento de g, con l a densidad, ya que en e l l a s se mantiene f i j a

T*

= 1

Y

p

*

cambia de iina d uti-a a i :,O

,

w~ipe¿aiL;u en y * = 0.5 (Fig. 9) y terminan do en

9

*

= 0.8

(Fig.

1 4 ) .

-

La

comparación de los resultados de l a

IL

con l o s de DI y hjC, muestra que en todos 10s casos l a I L sobreestha e l valor de g pc

(x)

para

i

c x c l , y que, como era de esperarse, l a s diferencias son menos impor

cantes ai aumentar i a densidad por l a importancia de l a s fuerzas repulsi vas

en

esa región.

a l t a s den'sidades l a diferencia entre l a ,,g y l a q G D es notable a tern peraturas bajas y moderadas. Debe notarse que l o s _{datos de >IC que apare}

ten en e s t a figura corresponden a una temperatura

T* =

0.666, l o que expli

ca en parte SUS G i e r e n c i a s con l o s valores de D f en

3

, .41 aumentar

l a temperatura l a diferencia entre y p c v q E D disminuye, Der0 como mues t r a l a F i g . 15, a

T* =

3 e s t a diferencia es

aun

aoreciable, esnecialmeri- t e

en

l a región alrededor de

-

- Sin embargo, como s e muestra en l a F i g , 14 aun

a

-

-

-

-

x =

1

,

Por i o que respecta a ?i .eirr,sentación de IC, Duede concluir

-

se que e l conocimiento "eYacto" d -

:

r'

racterización de u

i n t e q o i a c i ó n esponencid 35

3

re?r ~U-ici: Faastante bien e l comportamien-

to de g p c fuera del mismv.

:i'j garantiza una excelente ca- (-U) dentro 2.1 p >:'I. E:n arribas representaciones l a

0 PC

35.

en

el caso general que requiere e> USO del esquema ITiA para detemi.nar

los d o r e s g pL (x

1.

dos

es

necesario cornparer

con

d: tos de

DE.r

y de

MC

en estados cercanos.

Pari poder estimar lo correcto de estos resulta

l a s diferencias deben pode] explicarse en función de l a s teiidencias

-

I

I

de g pL (X ) descrita? en l a s Figs, (5-8).

I

La

Fig. 16 muestr::. 1,- comparación de e s t e e s t i l o para e l caso

en que

2

es prácticamente l a misma

y

exhihe e l efecto de internolación

a

temperatura y densidad para Tx = I. , 3 5 y

p

*

= 0.4,

nota que e l v d ; , j r ' de g pc

(1

J e5 inenor que los valores de íP.f (a l a mis-

ma

p

*

y

T"

= ].,O L 1.35) y de ?IC

9

*

= 0,s

>

0.4 y

T* =

1,333). Esta disminución en e l valor en contacto es cowletamente cofisistente con

SU comportamiento: l a F i g . 5 muestra que ,g pc (1') s i e T r e disminuíe a l

aumentar

T*

y de l a F i g . 6 se ve que para

y*

= 0.5, también disminuye a l disminuir l a densidad.

De

esta figura se +,

(para

I

Por l o que toca a g pc ( 1-1

,

é s t a tiene

un

valor considerahle- ~3?',7';1- 2 Ir tezpey;tcr= &; b ~ j x )7

l

i

2

~

?;,-;y

~

~

q.2-

~

e1

~

$ 3

~

t

~

l a densidad

más

a l t a ,

presentado en l a s Figs, 5 y 6 ,

Ambos efectos concuerdan

con

e l comportamiento r e -

I

En l a Fig. 16 s e observa también que para esa densidad y tem- peratura, e l valor elegido de g pc ( 2'

1

hace que l a representación con

l a I C coincida con l a I L .

l e un valor en

2'

concordante con l o s datos de simulación, que por l o

aquí obserxrado debe s e r menor quc e l obtenido con l a IL.

representación de g pc fuera del pozo presenta una desviación más impor-

tante con respecto a l o s &tos de siinulacióri que en

los

casos de l a s F i g s .

(9-14)-

1 La representación de I C puede mejorarse dando

-

En e s t e caso l a

Esta desviación m&>-ctr st ?rho en parte a que se compaan estados :+ temdin5mmicos diferentes,

Falta discutir 1:is c : r z c t e r í s t i c a s generales de l a g pc

(XI

obtenida usando l a I L y l a I C n l vúriar l a dwisidad y l a temperatcira.

l a Fig. 1 7 , para

y

*

= 0 . 3 , :;e o1 s c n a qu: tlnnlcamente a l a temperatura n í s b a j a ,

T*

= 0.75 l a

IC

disminuye ,igera.;iente con respecto a l a i L dentro del

i

36. . ,

aumentar

l a

densidad

a

j

_*

= 0.5,

como se

muestra en l a r i g . 4 ,

pozo

1

ta disminución es apra:iable para

T*

= 0.75 y

se

hace menos importante a l

es

coinciden, y

a

T* = 1.74, el valor de o l a

IL.

de

s

PL

l a temperatfira, de modo que para T* = 1.35 amhas practicamente

(X c A ) de l a I C es nayor queel de

PC

Como s e vió antes, l a representacibn con l a

'[L

predice r d 1 v r . s en esa regiSn myores _que lcs obtenidos por 21 Estodo (36:

G

,#: ';I:,,

así que 19s _{casos en l o s que l a I C esta por arriba de l a I L son i n c o r r e c x s .}

Este coinprtamiento de l a aproximación de I C r e f l e j a e l hecho de que l a s e -

lsció,-: de i o s vaiores de g pc en e l punto medio del pozo, que componen l a

base de datos del esquema ITn4, f u e - a r b i t r a r i a ,

En l a F i g , 18 se muestra como, a a l t a densidad (

p

*

= 0.8) y

T*

= 0.75 l a I C presenta e l comportamiento correcto, t a l vez exagerándolo ~1 POCO como puede verse de l a F i g . 1 4 , pero para

T" =

1.15 ya es idéntico a l a

IL,

aumentando su valor dentro del pozo

a

temperaturas mayores.

Es-

t e aumento de g pc ocasiona UM dismin~ición en e l alcance efectivo; i o

c:;ul riplejayz 2x1 125 pi-qi&&=j 621 sist%,a pep>ui-?&",

.En

cada UM de las F i g s , 4, 17 y 18 se puede apreciar también

el comportamiento con l a temperatura de gp(. (x) obtenido de l a

IL

y de l a

IC,

Se observa que

a

baja densidad (

p

*

= 0.3), g pc es un escalón cuya

altura disminuye a l aumentar l a temperatura;

a

UM densidad intermedia

( f

*

= 0.5) ,. g pC (1') disminuye con

T*

hasta una c i e r t a

T

,

*

2

1 , 1 5 a

partir de l a cual empieza a c r e c e r , de manera qus para T* Z 1 . 3 5 coincide

con e l valor en

T*

= 1.15, y e l valor de g pc [

x )

disminuye continuamente

con un aumento en l a . tr'nperatura; y a l a densidad más a l t a (

p *

= 0.81,

n

a PC (1 \ ) aL1:;:enta y gw,( A-) iisminuye a a l t a te:?eratura desde

T*

= 9.75.

t

De l o anterior pu'de concluirse qiir s i bien l a representación

de interpelación cuadr5tjci e; ~ o r e ~ ~ i a l n c n t e l a mejor aproximaci6n a l a

Sp, (X) mando se t:icne infornasión precisa y confiable de l a zcna central

lativamente arbitrarios en e l pxnlo medio del pozo, produjo que esta repre

37.

satación

tuviera l a s desviaciones respecte a l comportamiento correcto I antes mencionadas, y LUI tanto imprede:ibles. Estas limitaciones deben

iorai'se eii ciierita eri ios i-es:ii;tados de l a

TPPC

obteiiidos con esta i n - terpolación,

I

PEira completar e l a n á l i s i s de l o s resultados para 1 i fiyl.v:,ín

dc dist;ibuciSn rcdial del pozo cuadrak, en l a s Figs, 19 y 20 k!: -~::i!.,c

e l comportamiento con l a densidad de su representación con l a

IL,

mmte niendo

T*

=. c t e . ' Como se ve en l a F i g , 1 9 para

T*

= 0,75, g pc (r) tielie l a forma de un escal6n c~uya huella s e curva y cuyo peralte disminuye a l aumentar l a densidad, de manera que para

p

*

>

0,6 el valor en

r

= d+ empieza a a'.men:rr ~c;üjjc:itr, z i ~ t r z ; q ~ r 1; UItura en r =

R -

sigue disminuyendo. Se puede observar también que l a posición e intensidad del segundo msimo se conporta adecuadamente con

p

*,

-

~l aumentar i a temperetura, como se muestra en

iá

Fig. 20 para

T*

= 2.74, l a huella del escalón para

p *

= 0.1 se deforma barrien

<io wia c i e r t a área airecieáor. at, un punto aeiitro á e i pozo, aumenranño su

curvatura y ángulo de barrido con e l aumento en l a densidad.

peratura, . l a altura del escalón

en

r = R s e reduce en proporción a l fac t o r e P g

,

-

A esta tem-

-

I

Finalmente, en l a Fig. 21 se presenta l a función y pc (r) co-

Se observa claramente que y p c es

rrecpondisnte a l a gpc de l a F i g , 2 0 ,

una función continua de r que en e l 15niite

T*

-

00 tiende a l valor

Y ,

Ir)

= g,

(rl

= g Ep(r),

De

los resultados anteriores ciede ccncluirse que e l esqiima

de representación para ,,g (r) aquí ?TI?':C ;to, sintetiza e l conociniento

actual de l a estructura de l o s

pozos

C ~ ~ ! ~ . I & I S

y

que l a flexibilidad de