Inferencia en modelos econométricos
condicionales no lineales
Noriko Amano
∗e Ignacio N. Lobato
∗∗Resumen
Los modelos paramétricos (sobre la distribución condicional de las variables económicas) tienen la ventaja de resumir en algunos pará-metros fácilmente interpretables la dependencia entre estas variables, facilitando su uso. La metodología actual usual para hacer inferencia sobre este tipo de modelos es elMétodo Generalizado de Momentos que se basa en emplear algunos momentos incondicionales derivados de estos momentos condicionales. Sin embargo, en modelos definidos por momentos condicionales no lineales, esta metodología puede llevar a estimadores inconsistentes. Domínguez y Lobato (2004) propusieron una metodología alternativa que genera procedimientos consistentes.
Clasificación JEL: C13, C18.
1.
Introducción
Generalmente en econometría, la relación entre variables económicas apare-ce reflejada en modelos paramétricos de algunos aspectos de la distribución condicional de estas variables. Por ejemplo, el modelo de regresión esta-blece una restricción paramétrica sobre la media condicional; el modelo de regresión cuantílica establece una restricción paramétrica sobre cuantiles condicionales; por otra parte, los modelos ARCH establecen restricciones sobre varianzas condicionales.
Estos modelos paramétricos (sobre la distribución condicional de las va-riables económicas) tienen la ventaja de resumir en algunos parámetros fácilmente interpretables la dependencia entre estas variables, facilitando su uso. Ejemplos de ellos son modelos con variable dependiente transforma-da, modelos de expectativas racionales, modelos de sistemas de ecuaciones no lineales y modelos con variables medidas con error. Abordamos estos ejemplos en la sección 2.
La metodología actual usual para hacer inferencia sobre este tipo de mo-delos es elMétodo Generalizado de Momentos (que denotamos por GMM)
que se basa en emplear algunos momentos incondicionales derivados de estos momentos condicionales. Describimos dicha metodología en la sección 3.
Sin embargo, en modelos definidos por momentos condicionales no li-neales, esta metodología puede llevar a estimadores inconsistentes como se ilustra en la sección 4.
Domínguez y Lobato (2004) propusieron una metodología alternativa que genera procedimientos consistentes. Veremos dicho método en la sec-ción 5, lo llamaremosMétodo Consistente de Momentos (siguiendo la no-menclatura de Domínguez y Lobato (2010)) y lo abreviaremos CMM. En esta metodología se sustituyen las restricciones de momentos condicionales impuestas por el modelo, por una infinidad de restricciones de momentos no condicionales que caracterizan por completo las restricciones que definen el modelo y por tanto la metodología genera estimadores consistentes. Ade-más, tiene la ventaja de proveer de un test de especificación “natural”que permite contrastar la idoneidad del modelo. Por último, en la sección 6 se expone brevemente un sencillo procedimiento de Bootstrap desarrollado por Domínguez y Lobato (2010) para estimar valores críticos y llevar a cabo en la práctica el test de especificación mencionado.
2.
Modelos condicionales no lineales
En diversas áreas de la econometría (como macroeconometría y finanzas) y en muchos problemas econométricos de estimación, por ejemplo usando da-tos longitudinales o de elección discreta, hay modelos definidos en términos de restricciones de momentos condicionales, es decir, modelos que se definen naturalmente mediante restricciones de la forma
E[h(wt, θ0)|xt] = 0 a.s. (1)
para un únicoθ0∈Θ, dondewtes un vector de variables aleatorias tal que
xt⊆wt, conΘ⊆Rm. Este tipo de modelos son llamadosmodelos de
varia-bles instrumentalesy las variablesxtson llamadas instrumentos o variables
explicativas exógenas dependiendo del contexto. Es decir, consideramos un vector de parámetros θ0 identificados por la restricción de momentos con-dicionales (1), donde interpretamos h(wt, θ0) como un error, por ejemplo
un error de predicción realizado por los agentes económicos. En resumen, el objeto de interés es un vector de parámetros definido mediante momentos condicionales.
Ejemplos de este tipo de modelos son los siguientes.
Ejemplo 1. (Modelo de regresión en media)
En el modelo de regresión (no lineal), se tiene una variable aleatoriayt
Usualmente se denota porm(x, θ) a un modelo paramétrico para E[yt|xt],
es decir,
E[yt|xt] =m(xt, θ0).
De modo que definiendoh(wt, θ0) =yt−m(xt, θ0), podemos expresar este
modelo como
E[h(wt, θ0)|xt] = 0 a.s..
Ejemplo 2. (Modelo con variable dependiente transformada)
Cuando hay heterocedasticidad y asimetría en los residuos de la regre-sión, un posible camino para eliminarlas o atenuarlas, es estimar un modelo en el que la variable dependiente ha sido sujeta a una transformación no lineal. Hay muchas maneras de realizar esta tranformación, pero la trans-formación de Box-Cox es la transtrans-formación no lineal comúnmente usada en econometría y estadística. La transformación de Box-Cox está dada por
y(λ0)
t =
( yλ0
t −1
λ0 siλ06= 0 ln(yt) siλ0= 0
de manera que el modelo de regresión lineal para la variable dependiente transformada establece que
E[yt(λ0)|xt] =α+βxt.
En este caso,h(wt, θ0) =y (λ0)
t −α−βxt.
Notemos que éste no es un modelo de regresión convencional porque la variable dependiente ha sido transformada y, por tanto, el método de mínimos cuadrados no lineales produce estimadores inconsistentes
Ejemplo 3. (Modelo de expectativas racionales)
Este tipo de modelos son un caso particular de los modelos derivados de optimización por parte de los agentes. Consideremos por ejemplo el modelo usado por Hansen y Singleton (1982) para la composición de portafolio, donde la condición de equilibrio es
βE
"
(1 +ri,t+1) c t+1 ct −α −1 xt # = 0
con ct el consumo del agente representativo en el periodo t, β el factor
de descuento, xt la información disponible en el periodo t, (1 +ri,t+1) el
rendimiento bruto deli-ésimo bien financiero y αel coeficiente de aversión al riesgo. Para este ejemplo,
h(wt, θ0) =β "
Ejemplo 4. (Modelo de sistemas de ecuaciones no lineales)
Sih(wt, θ0)es un vector, entonces el modelo
E[h(wt, θ0)|xt] = 0 a.s.
representa un sistema de ecuaciones simultáneas. En particular, sih(wt, θ0)
es un vector de funciones no lineales (o tales que algunas variables endóge-nas han sido transformadas de forma no lineal; por ejemplo, transformadas mediante logaritmos), el modelo representa un sistema de ecuaciones no li-neales. Sin embargo, en este artículo nos centraremos en funcionesh(wt, θ0)
escalares.
Ejemplo 5. (Modelo no lineal con variables medidas con error)
Un caso particular de este tipo de modelos son los modelos de regresión en media con algunas variables explicativas no observables. Consideremos por ejemplo, el modelo paramétrico
E[yt|x∗1t] =m(α0+β0x
∗
1t)
dondex∗1t no es observable pero x1t =x∗1t+et sí lo es. Cuando existe un
vector x2t tal que los parámetros (α0, β0) están identificados por E[yt−
m(α0+β0x1t)|x2t] = 0, entonces para h(wt, θ0) =yt−m(α0+β0x1t),
E[h(wt, θ0)|x2t] = 0
es un modelo no lineal con variables medidas con error.
Ejemplo 6. (Modelo de regresión cuantílica)
Seam(xt, θ0)elα-ésimo cuantil1deytcondicional enxt. Entonces
E[Iyt≤m(xt,θ0)−α|xt] = 0 (Véase Koenker (2005)).
Todos los modelos de los ejemplos anteriores estan definidos por restric-ciones de algunos aspectos de la distribución condicional de estas variables y son bastante comunes en econometría.
El problema central que intenta abordar este artículo es el de identifi-cación en modelos paramétricos condicionales. La identifiidentifi-cación en modelos paramétricos es esencial para que, teniendo datos, se puedan construir esti-madores consistentes de estos parámetros como se comentará más adelante.
1Elα-ésimo cuantilQ(α) de una cdfF es el mínimo de un conjunto de valoresy tal
Antes de considerar este concepto para modelos condicionales como los vis-tos anteriormente, resulta conveniente repasar la definición de identificación para modelos incondicionales. Intuitivamente, Un modelo paramétrico in-condicional está identificado si establece que existe un único valor de los parámetros que satisfacen las restricciones incondicionales que lo definen. Formalmente la definición está dada como sigue.
Definición 7. Identificación para modelos incondicionales Sea Θel conjunto de valores que pueden tomar los parámetros. Dado un modelo paramétrico incondicional con parámetros enΘ, decimos que el modelo estaidentificado si existe un vector de funciones g :Rp×Θ→Rr tal queθ0∈Θ⊆Rr es el único valor enΘtal que E[g(w, θ0)] = 0.
Nótese que esto nos permite definir una función objetivo, por ejemplo, (E[g(w, θ)])2 cuyo único mínimo global es el verdaderoθ0.
El problema central que intenta abordar este artículo es el de identifica-ción en modelos paramétricos condicionales. Estos modelos establecen que existe un único valor de los parámetros que satisface ciertas restricciones de momentos condicionales. Notemos que, por tanto, este único valor de los parámetros tiene que satisfacer una infinidad de restricciones de momentos incondicionales. El problema de identificación en este caso, reside en cons-truir una función objetivo con un único mínimo global que incluya todas estas restricciones.
3.
Método de estimación generalizado de
mo-mentos.
Consideremos primero un modelo definido por las restricciones de momentos incondicionales
E[g(wt, θ0)] = 0
donde wt = (yt,xt), xt y θ son vectores de dimensión py g es un vector
de funciones dewtde dimensiónq. Para una muestra aleatoria de tamaño
n, definimos el valor esperado empírico de una función genérica m como En[m(w)] = n1Pnt=1m(wt). Haciendo uso de esta notación, sea
gn(θ) =En[g(w, θ)].
Entonces, sip=q,gn(θ) = 0es un sistema depecuaciones en p
incóg-nitas y por tanto, bajo ciertas condiciones, tiene una única solución. Dicha solución nos provee de un estimador consistente deθ0(conocido como el
es-timador por el método de momentos deθ0). Sin embargo, siq > p,gn(θ) = 0
El Método Generalizado de Momentos da solución a este problema eli-giendo como estimador al parámetro más cercano a la solución deg(wt, θ) =
0, que llamaremosθˆGM M
n , donde la medida de distancia está dada por
Qn(Wn, θ) =gn(θ)0 Wngn(θ),
con Wn una matriz positiva semidefinida de dimensión (q×q) y tal que
Wn=W+op(1), W positiva definida.
El estimador de GMM para θ0 basado en la condición de momentos E[g(wt, θ0)] = 0, está dado por
ˆ
θnGM M(Wn) = arg m´ın
θ∈ΘQn(Wn, θ).
La definición anterior deja claro que el estimador de GMM es un caso particular de unEstimador de Mínima Distancia(véase Newey y McFadden (1994)).
El siguiente ejemplo puede resultar ilustrativo.
Ejemplo 8. Consideremos el modelo lineal y = x0β +u, donde x y β son vectores de dimensión py sea zun vector de instrumentos para x de dimensiónq≥p. En este caso, las restricciones de momentos incondicionales que definen el modelo están dadas por las condiciones de ortogonalidad, es decirg(w, β) =z(y−x0β), de modo que gn(β) =En[z(y−x0β)]. Entonces
el estimador GMM deβ está dado por ˆ
βnGM M(Wn) = arg m´ın
β∈BQn(Wn, β)
Donde de las condiciones de primer orden obtenemos ˆ
βnGM M(Wn) = [En(xz0)WnEn(zx0)]−1En(xz0)WnEn(zy).
De esta manera, para el casoq =p, βˆGM Mn coincide con el estimador por variables instrumentales dado por
ˆ
βnIV = [En(zx0)]−1En(zy).
3.1.
Tests de especificación para estimadores de
míni-ma distancia
Recordemos que para definir el estimador de GMM supusimos que el modelo estaba bien especificado en el sentido de queE[g(wt, θ0)] = 0para un único θ0, es decir, no hay otros parámetrosθ∈Θque verifiquen la restricción in-condicional. Si este supuesto es falso, entoncesθˆGM M
n no es consistente. Así,
no este supuesto. Sip=q entonces θˆnGM M es tal que todos los momentos
muestralesgn(ˆθnGM M)son cero y la distanciaQn(Wn, θ) =gn(θ)0 Wngn(θ)
es cero. Pero para el casoq > p, el estimador no hace todos los momentos muestrales cero. Recordemos que θˆGM M
n es el parámetro más cercano a la
solución de g(wt, θ) = 0, con Qn(Wn, θ) como una medida de distancia.
Como lasprestricciones que identifican al parámetro de interés,θ0, repre-sentan la información usada en la estimación, sus análogos muestrales se satisfacen enθˆnGM M por construcción. Llamemos a estasprestricciones
res-tricciones de identificacióny a las(q−p)restricciones restantesrestricciones de sobreidentificación. En contraste con las restricciones de identificación, las restricciones de sobreidentificación son ignoradas en la estimación y por lo tanto sus análogos muestrales no se satisfacen. Sin embargo, esto resulta útil ya que de esta manera,Qn(Wn, θ)puede interpretarse como una medida
de qué tan lejos está la muestra de satisfacer las restricciones de sobreiden-tificación. En el caso de muestreo aleatorio, resulta que si la matrizWn se
elige de manera óptima, es decir, siplimWn=E[gn(θ0)gn(θ0)0]−1, entonces
n veces la distancia minimizada Qn(Wn, θ), se distribuye asintóticamente
χ2.
Sea cW un estimador consistente de E[gn(θ0)gn(θ0)0]y consideremos el
caso en que la distancia es evaluada en el verdadero valor del parámetroθ0, entonces
n Qn(cW , θ0) =n gn(θ0)W gc n(θ0) =
√
n gn(θ0) 0
c
W √n gn(θ0)
.
Usando que√n gn(θ0) d
−→ N(0,E[gn(θ0)gn(θ0)0])ycW p
−→E[gn(θ0)gn(θ0)0],
la distribución asintótica den Qn(cW , θ0)esχ2(q). Por otra parte, se puede demostrar que, evaluandoQnenθˆnGM Men lugar deθ0, los grados de libertad
cambian deqa (q−p).
Fue Hansen (1982) quien propuso el uso del estadísticoJn(ˆθGM Mn ,cW) =
n Qn(cW ,θˆnGM M) para probar si las restricciones de sobreidentificación se
satisfacen.
Podemos ver este estadístico como la función objetivo de GMM mi-nimizada. La figura a continuación ilustra gráficamente al estadístico Jn.
4.
Inconsistencia de GMM en modelos
condi-cionales
4.1.
GMM para modelos condicionales
El modelo que consideramos a lo largo de este artículo está dado por la ecuación (1), es decir, se define por un conjunto de restricciones de momentos condicionales
E[h(wt, θ0)|xt] = 0, a.s..
Sabemos que si se satisface dicha ecuación, entonces para cualquier función f tal que
E(|h(wt, θ0)f(xt)|)<∞,
se tiene que
E[h(wt, θ0)f(xt)] = 0.
un vector de instrumentosv(xt)q-dimensional (que puede depender deθ0),
se tiene que
E[v(xt)h(wt, θ0)] = 0. (2) Entonces el estimadorθˆnGM M se define como el parámetro más cercano
a la solución de En[v(xt)h(wt, θ0)] = 0, donde el concepto de cercanía es
análogo al mencionado para el caso incondicional. Es decir, si Wn es una
matriz que satisface las condiciones antes mencionadas, el estimadorθˆGM M n
está dado por ˆ
θnGM M = arg m´ın
θ∈ΘEn[v(x)h(w, θ)]
0W
nEn[v(x)h(w, θ)].
El supuesto crítico en la estimación incondicional GMM es que el con-junto identificado por las restricciones de momentos no condicionalesΘI =
{θ∈Θ :E[v(xt)h(wt, θ)] = 0}, tiene como único elemento aθ0, y por tanto
queE[v(xt)h(wt, θ)] = 0 implica queθ=θ0.
Éste es el llamado “supuesto de identificación global de GMM”y fue el supuesto cuestionado por Domínguez y Lobato (a partir de ahora nos refe-riremos a ellos por DL). Ellos dieron algunos ejemplos donde tal supuesto no se satisface. Veremos estos ejemplos a continuación. El segundo de ellos con base en la generalización hecha por Bravo, Escanciano y Otsu (2009).
4.2.
Ejemplos de inconsistencia de GMM
Ejemplo 9. Sea Y una variable aleatoria que satisface E(Y|X) = Xθ0 donde θ0 = 4 yX es una variable aleatoria con distribución N(0,15) (ob-servemos que entonces es simétrica alrededor del cero, con cuarto y sex-to momensex-tos iguales). Supongamos que el investigador especifica el mo-delo correctoE(Y|X) =Xθ con θ ∈ Θ = [2,∞). El modelo implica que E(Y −Xθ0)g(X)= 0para cualquier funcióngtal que
E(Y −Xθ0)g(X)<
∞. Supongamos que el investigador usa las funciones (instrumentos)1yX. Dichos instrumentos no identificanθ0= 4puesto que el sistema
E[(Y −Xθ)] = 0 E[(Y −Xθ)X] = 0 también se satisface paraθ= 6. En efecto,
E[(Y −X6)] = E[E(Y −X6|X)] =E[E(Y|X)−X6] =E[X4−X6] = 0 y
Ejemplo 10. Supongamos ahora queY satisface el modelo simple no lineal E(Y|X) =θ20X+θ0X2. Supongamos queθ0= 54y queV(Y|X)es constante. Supongamos también que el investigador especifica el modelo adecuadamen-te, pero en lugar de elegir un instrumento arbitrario, elige el óptimo2dado
porZ∗= 2θ0X+X2. En este caso, el parámetroθ0no está identificado en el sentido de que el valorθ=−5
4 también satisface la condición E[(Y −θ2−θX2)Z∗] = 0
cuando X sigue una normal N(−1,1). De hecho, se tiene más aún, si Z es un instrumento de X, para la restricción incondicional de momentos E[Z(Y −θ2−θX2)] = 0, se observa que
E[Z(Y −θ2X−θX2)] = 0 ⇔ E[ZY]−θ2E[XZ]−θE[ZX2] = 0
⇔ E[Z(θ02X+θ0X
2+U)] =θ2
E[XZ] +θE[ZX2]
⇔ θ20E[ZX] +θ0E[ZX2] =θ2E[XZ] +θE[ZX2]
⇔ (θ2−θ02)E[ZX] =−(θ−θ0)E[ZX2]
⇔ (θ+θ0)E[ZX] =−E[ZX2]
⇔ θ=−E[X
2Z]
E[XZ]
−θ0.
Por lo tanto, el conjunto identificado por las restricciones de momentos no condicionales está dado por ΘI = {θ0, θ1}, con θ1 = −E
[X2Z]
E[XZ] −θ0. Entonces la identificación global de θ0 se satisface si y sólo si θ0 = θ1, o equivalentemente
−E[X
2Z]
E[XZ]
−2θ0= 0 ⇔ E[X2Z] + 2θ0E[XZ] = 0
⇔ E[(X2+ 2θ0X)Z] = 0
⇔E[Z∗Z] = 0, (3)
por lo tanto, por un lado, dado queE[Z∗]>0, Z∗ no puede indentificar a θ0. Por otro lado, para poder identificar θ0 hay que elegir un instrumento que verifique 3.
GMM típicamente introduce el supuesto adicional de que las restriccio-nes no condicionales seleccionadas identifican globalmente los parámetros de interés. Sin embargo, como ilustran los ejemplos anteriores, éste supues-to adicional depende de los instrumensupues-tos seleccionados y de las variables
2Chamberlain (1987) probó que si W
condicionantes; de hecho, restringe la distribución marginal de las variables condicionantes. Así, la introducción de este supuesto adicional nos lleva a la siguiente paradoja: La distribución de las variables condicionantes debería de ser irrelevante para la estimación consistente de modelos condicionales y sin embargo, es crucial para estimadores GMM porque garantiza la iden-tificación global de los parámetros de interés.
Ejemplo 11. (Modelo básico de fijación de precios para activos de consumo)
El siguiente ejemplo proveniente de DL (2010) es una versión simplificada del modelo de fijación de precios para activos de consumo (Consumption-based asset pricing model) que ilustra el problema de inconsistencia de GMM.
Consideramos un agente representativo que maximiza
Et "∞
X
s=0 βsc
1−α t+s
1−α
#
sujeto a la restricción presupuestaria
ct+PtQt≤PtQt−1
dondeEt denota el valor esperado condicional a la información disponible
en el periodo t, ct el consumo representativo del agente en el instante t,
Pt es el valor del activo en el periodot, (1 +rt)es el rendimiento nominal
bruto de bonos en el instantet(i.e.rt=−1 + Pt+1
Pt ), Qt es la cantidad del activo que posee el individuo al final del periodot, yWt es el ingreso real
al trabajo en el periodot. De sus condiciones de primer orden se obtiene la siguiente ecuación de Euler.
β0E
"
ct+1 ct
−α0
(1 +rt+1) Ωt
#
= 1, (4)
dondeβ0es el factor de descuento yΩtdenota la información pública
dispo-nible en el instantet. El parámetro de mayor interés esα0, que corresponde al coeficiente de aversión relativo al riesgo del agente.
Simplificaremos (4) para que sea claro el problema de identificación. Sea xt una variable aleatoria dada por xt+1 = ct+1c
t que toma valores positivos yα0 yK0 los valores reales de los parámetros dados por
(1 +rt) = r¯
K0 = 1 ¯ rβ0.
Ex−t+1α0|Ωt
=K0.
Nos enfocaremos en la inferencia del parámetro de aversión al riesgoα0, así que supondremos queK0es conocido. Estamos interesados en hacer infe-rencia estadística sobreα0y sobre la idoneidad del modelo. Por el momento, supongamos quext toma únicamente tres valores(x1, x2, x3) = (0.8,1,1.2)
(de modo que el nivel de consumo puede decrecer, permanecer igual o au-mentar) y evoluciona de acuerdo con una cadena de Markov, de manera que el efecto del pasado infinito en el presente quede completamente descrito en el periodo anterior. Denotemos por{pij :i, j= 1,2,3} a la probabilidad de
transición de pasar del estado ial estadoj. La distribución estacionaria y ergódica es el valor propio normalizado asociado al valor propio unitario, llamémosle(p1, p2, p3).
Nótese que a pesar de que este ejemplo es de apariencia sencilla, es muy general y permite estructura de dependencia complicada; por ejemplo heterocedasticidad condicional, que es una característica común en las series financieras.
El procedimiento estándar para hacer inferencia sobreα0es usar el mé-todo de GMM, que como mencionamos se basa en la selección de uno o más restricciones de momentos no condicionales, como
E(x−tα) =K0. (5)
Es decir, GMM supone que hay un único valor para el parámetro α que satisface (5). A pesar de que este supuesto sea generalmente cierto en una vecindad deα0, esta condición no es globalmente cierta. En efecto, la condición (5) sólo impone
p10.8−α+p2+p31.2−α=K0 (6) La gráfica deE(x−tα) =K0para(p1, p2, p3) = (
1 3,
1 3,
1
3)está dada por la Figura 1.
Figura 1: función p10.8−α+p2+p31.2−α=K0
Por otra parte, sixtuviera una distribución continua, el problema tam-bién permanecería. Notemos que escribiendo la esperanza no condicional como
E(x−tα) =E[x
−α
t |xt>1]P(xt>1) +E[xt−α|xt<1]P(xt<1)
se tiene que como E[x−tα|xt > 1] es decreciente en α y E[x−tα|xt < 1] es
creciente enα, la funciónE(x−tα)sigue teniendo forma deU asimétrica.
Hemos considerado entonces el caso más simple en el que el instrumen-to seleccionado es el constante, y visinstrumen-to que GMM genera estimación in-consistente. Podría pensarse que el problema de identificación puede ser resuelto seleccionando el instrumento óptimo o usando más instrumentos, pero el instrumento óptimo no cambia la naturaleza del problema. Las tres restricciones condicionales que definen el modelo junto con la restricción incondicional definen un sistema de ecuaciones con 9 incógnitas y sólo 4 restricciones, de modo que hay muchas soluciones.
La restricción incondicional asociada al instrumento óptimo puede escri-birse como
w10.8−α+w2+w31.2−α=C0, (7) dondewi=pizi, C0 es una constante yzi denota el valor del instrumento
óptimo para eli-ésimo estado. En el caso del instrumento óptimo no factible, zies conocido y el argumento geométrico de la figura 1 también es aplicable
instrumento óptimo factible donde los valores parazitambién dependen del
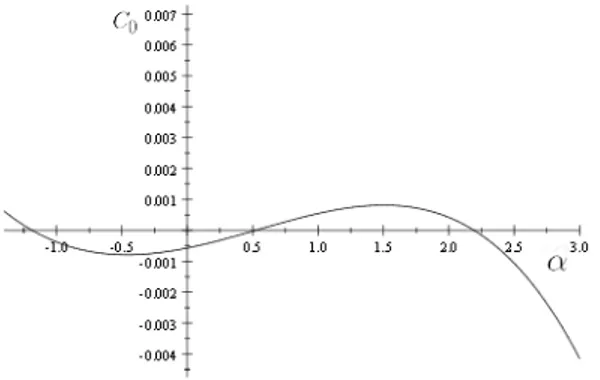
parámetroα, la ecuación (7) puede tener más de dos soluciones. Como ilustra la siguiente figura (véase DL(2010) para más detalles).
Figura 2: función funciónp10.8−α+p2+p31.2−α=K0
El ejemplo anterior no tiene nada de especial. La estructura Markovia-na fue impuesta por simplicidad, y para estructuras de dependencia más complicadas la falta de identificación global también aparece.
4.3.
Discusión de GMM en modelos condicionales
Estos ejemplos ilustran que el supuesto adicional que necesita GMM para garantizar identificación; es decir, queθ0 es el único que satisface (2), no necesariamente se cumple. En particular, para las funciones v(x) elegidas en los ejemplos, la ecuación (2) no se cumple.
Notemos que en este último ejemplo, como el dominio de la variable con-dicionante tiene únicamente tres puntos, podemos identificar el parámetro seleccionando de manera apropiada tres restricciones incondicionales. Simi-larmente, si el dominio de la variable condicionante tuvierak puntos, uno podría identificar los parámetros seleccionando apropiadamente k restric-ciones no condicionales. Por extensión, para variables condicionantes conti-nuas, se necesitaría un continuo de restricciones incondicionales para lograr identificación. Por tanto,“la identificación no es la regla sino la excepción en modelos no lineales definidos por momentos condicionales que se estiman usando un número finito de restricciones incondicionales”(DL (2010)).
cualquier3 funciónf, pero usualmente sólo se revisan algunas funciones f, y pueden haber muchos más parámetros que también verifiquen estas res-tricciones incondicionales en particular. Por ejemplo, consideremos un valor paramétrico distintoθ1 y seaDθ1(xt) =E[h(wt, θ1)f(xt)|xt]. Por la Ley de esperanzas iteradasE[h(wt, θ1)f(xt)] = 0 es equivalente aE[Dθ1(xt)] = 0. Por lo tanto, en cuanto la variableDθ1(xt)tome valores positivos y negati-vos, surgirá el problema de falta de identificación.
5.
El estimador CMM
En esta sección abordamos el problema central de este artículo: el de identi-ficación en modelos paramétricos condicionales, que reside en construir una función objetivo con un único mínimo global que incluya todas las restric-ciones incondicionales implicadas por el modelo paramétrico.
Consideremos el modelo de restricciones de momentos condicionales no lineal de (1) dado por E[h(wt, θ0)|xt] = 0, a.s. donde wt denota todas
las variables en el modelo y xt a las variables exógenas. Estamos
interesa-dos en estimar el vector de parámetrosθ0, y sabemos que la restricción de momentos condicionales de (1) es equivalente a la restricción de momentos incondicionales
E[h(wt, θ0)f(xt)] = 0 (8)
para cualquier función mediblef (respecto a la medida de probabilidad).4
La estimación basada en elegir todas las funciones medibles dexten la
prác-tica, no es factible. Lo usual es seleccionar un número finito de momentos incondicionales en (8) y estimarθ0usando el método de GMM. Sin embargo, en los ejemplos previos vimos que si éstas restricciones no se eligen adecua-damente no hay garantía de queθ0pueda ser identificado globalmente. Este problema de identificación produce un estimador de GMM inconsistente.
La idea de DL (2004) es elegir la función indicadora para generar un con-tinuo de instrumentos en (8) Formalmente, su construcción es la siguiente. SeaI(xt≤v)la función indicadora del ortante definido porx. Consideremos
el conjunto de restricciones de momentos no condicionales
H(v, θ) =E[h(wt, θ)I(xt< v)] 5
Entonces, existe un únicoθ0 tal que H(v, θ0) = 0 para toda v (véase Bi-llingsley (1995, Teorema 16.10, (iii))).
Por tanto, existe un únicoθ0 tal que EH(v, θ0)2= 0.
3Véase sección 3.
4Cadafpuede interpretarse como un instrumento que ayuda a identificarθ
0
Sea
Q(θ) =E
H(v, θ0)2
. (9)
Observemos que comoH(v, θ)2es no negativa, para todaθ6=θ0,Q(θ)>0, de modo queθ0 puede identificarse así
θ0= arg m´ın
Θ E[H(v, θ) 2].
Consideremos la siguiente notación
Hn(v, θ) = En[h(w, θ)I(x≤v)], (10)
˙
Hn(v, θ0) = En[ ˙h(w, θ)I(x≤v)], y (11)
Qn(θ) =En[Hn(v, θ)2].
El estimador de CMM deθ0 se define como
ˆ
θ= arg m´ın
θ∈ΘQn(θ)
Para este modelo, DL (2004) probaron que θˆes consistente y asintóti-camente normal. Por un lado probaron que bajo supuestos estándar en la literatura de GMM,θˆ−→p θ0a.s. Por otra parte, bajo supuestos que permiten datos de series de tiempo, probaron que este estimador es asintóticamente normal. En particular probaron que
√
n(ˆθ−θ0)−→d N(0,Ω),
(véase DL(2004) para ver detalles respecto a la varianza asintóticaΩ; en particular, nótese queΩes distinta a la cota de Chamberlain (1987)).
Por lo tanto el estimador θˆes ineficiente, sin embargo puede ser utili-zado como un estimador preeliminar en un procedimiento de dos etapas. Denotemos por θ˜ al estimador eficiente de GMM y sea Qn(θ) la función
objetivo que converge aQ(θ). Supongamos queθ0 está localmente identifi-cado porQ(θ)y seaV0una vecindad deθ0 tal queQ(θ)> Q(θ0)para toda θ∈V0\{θ0}. La consistencia deθˆnos asegura queθˆ∈V0 con probabilidad 1 paransuficientemente grande. Más aún, nos asegura queθ˜es consistente y asintóticamente eficiente cuando restringimosΘaV0. Así, es posible cons-truir un estimador asintóticamente eficiente deθˆaplicando un único paso iterativo del proceso de Newton-Raphson en dirección deθ.˜
simplificado de “Modelo básico de fijación de precios para activos de con-sumo” mencionado en el ejemplo de la sección 11, en el que la razón del consumo sigue una cadena de Markov con 4 estados y hay un único acti-vo libre de riesgo en la economía. Calibraron la cadena de Markov usando datos de consumo en bienes no durables y servicios en E.U. desde enero de 1959 hasta diciembre de 2007 y encontraron que las varianzas asintóticas para los estimadores CMM y los GMM eficientes difieren en menos de 1 %.
5.1.
Acerca de la metodología
A continuación damos una breve intuición del método CMM siguiendo DL (2010) para el caso no lineal. Para escribirθˆen términos familiares, usaremos aproximaciones lineales locales y notación matricial.
Definamos H(θ) como el vector de errores generalizados integrados, es decir, el vectorn-dimensional cuyat-ésima entrada esHn(xt, θ). La función
objetivo en este caso en notación matricial puede escribirse como la suma de cuadrados de los residuos,
Qn(θ) =
1 n H(θ)
0
H(θ) (12)
dondeH(θ)es el vector de dimensiónncuya t-ésima entrada esHn(xt, θ),
es decir, los errores integrados generalizados.
SeaH˙(θ)la matriz den×kcuyot-ésimo renglón es el vectork-dimensional ˙
H(xt, θ0). Entonces,
√
n(ˆθ−θ0) =√n H˙(θ0)0H(θ0)
−1
H(θ0)0H(θ0) +op(1) (13)
La expresión (13) es similar a la linealización del estimador por mínimos cuadrados no lineales (NLS). Entonces en nuestro caso, los estimadores de los parámetros pueden ser interpretados como los valores que definen la proyección ortogonal de los “errores integrados” (H(θ0)) en el subespacio generado por las “ derivadas integradas ”(H˙(θ0)). La diferencia con NLS es que en nuestro caso tanto los regresores como los errores son procesos escalados integrados (véanse (10) y (11)).
5.2.
Test de especificación
Una vez que los parámetros de interés han sido consistentemente estimados, la metodología CMM se completa usando el valor mínimo de la función objetivo de CMM,Qn(ˆθ), para contrastar si el modelo está bien especificado,
es decir, que el modelo considerado es correcto. Formalmente, consideramos la hipótesis nula
para contrastarla contra la hipótesis alternativa dada por H1: para todoθ, P(E[h(wt, θ)|xt] = 0)<1.
Por lo comentado en la sección 3.1, el estadístico natural para contrastar la especificación del modelo está dado por
Tn =n Qn(ˆθ).
Sin embargo, DL (2010) prueba que los valores críticos de dicho estadís-tico dependen del proceso de generación de datos, entonces los resultados teóricos para el test de especificación no pueden ser aplicados automática-mente porque no hay valores críticos fácilautomática-mente disponibles. Retomaremos este problema en la sección 6. Veamos primero un poco más respecto a la intuición del estadísticoTn. Primero notemos que de (12)
Tn =n Qn(ˆθ) =H(ˆθ)0H(ˆθ).
Entonces mediante la expansión asintótica de la función objetivo y definien-do
P(θ0) = H˙(θ0)
˙
H(ˆθ0)0H˙(ˆθ0)
−1
˙ H(θ0)0
M(θ0) = I−P(θ0), tenemos que
Tn=H(θ0)0M(θ0)H(θ0) + 0p(1), (15)
que es la suma de cuadrados de la proyección de errores integrados(H(θ0)) en el espacio ortogonal generado por las derivadas integradas (H˙(θ0)).
6.
Test de especificación en la práctica
El boostrap es una técnica no paramétrica para hacer inferencia que em-plea técnicas de remuestreo para estimar la distribución muestral de un estadístico. Es un método para hacer inferencias respecto a los parámetros poblacionales que se basa en una analogía entre la muestra y la población de la que se obtiene la muestra. La idea central es que a veces puede ser mejor sacar conclusiones de las características de una población a partir de la muestra que se tiene, que hacer supuestos, quizá poco realistas, respecto a dicha población. El bootstrap usa remuestreo de los datos con reemplaza-miento (muchas veces) para generar un estimador empírico de la distribución muestral completa de un estadístico.
Recordemos que de la sección 5.2, los valores críticos del estadísticoTn
antes, los resultados teóricos para el test de especificación no pueden ser aplicados automáticamente.
DL (2010) usa bootstrap para estimar la distribución deTn. En
particu-lar, de la expresión (15) proponen estimar consistentemente la distribución deTn con la distribución de Tn∗, donde
Tn∗=H∗(ˆθ)0M(ˆθ)H∗(ˆθ),
conH∗n(xt,θ)ˆ como elt-ésimo elemento del vectorn-dimensionalH∗(ˆθ)dado por
H∗n(xt,θ) =ˆ
1 n
n X
t=1
h(wt,θ)I(xˆ t≤x)zt (16)
y{zt} una secuencia de variables aleatorias independientes con media cero
y varianza unitaria.
En detalle, la hipótesis nula (14) se contrastaría de la siguiente manera:
Paso 1:Minimizar la función objetivo (9) y calcular el estadísticoTn=
n Qn(ˆθ).
Paso 2: Obtener los errores integrados Hn(xt,θ)ˆ de la ecuación (10),
las derivadas integradasH˙n(xt,θ)ˆ de la expresión (11) y construir la matriz
(n×k), H˙(ˆθ).
Paso 3: Generar una sucesión de n variables independientes {zt} con
media cero y varianza unitaria. Calcular el vector(n×1) de errores inte-grados mediante bootstrap,H∗(ˆθ), donde la t-ésima coordenada del vector esHn∗(xt,θ)ˆ dado por (16).
Paso 4:Correr una regresión lineal del vector n-dimensional H∗(ˆθ) en la matriz den×k H˙(ˆθ), cuyo t-ésimo renglón es el vector k-dimensional
˙
H(xt, θ0). SeaTn∗ la suma residual de los cuadrados de la regresión. Paso 5: Repetir los pasos 3 y 4 B veces, donde en el paso 3 cada
se-cuencia{zt} es independiente una de otra. Esto produce un conjunto deB
valores independientes (condicionalmente en la muestra) deTn∗que compar-ten la distribución asintótica deTn.
Paso 6:Sea T[1∗−α] el(1−α)-cuantil de la distribución empírica de los B valores de Tn∗. El estadístico propuesto de nivel nominal α rechaza la hipótesis nula siTn> T[1∗−α].
La distribución del procedimiento de Bootstrap descrito es consisten-te puesto que dados los datos,√n Hn(x, θ0) y
√
7.
Conclusión
En econometría, los modelos definidos por restricciones de momentos con-dicionales son muy comunes. En este tipo de modelos, los parámetros deben satisfacer una infinidad de restricciones. Sin embargo, el enfoque usual para estimar este tipo de modelos (GMM) únicamente emplea una cantidad fini-ta de ésfini-tas, de manera que no necesariamente identifica a los parámetros y por tanto puede llevar a estimadores inconsistentes.
En este artículo se describe la metodología desarrollada por DL para ha-cer inferencia estadística consistente para modelos definidos por momentos condicionales. La construcción del estimador por CMM consiste en consi-derar un continuo de restricciones de momentos incondicionales que son equivalentes a las restricciones condicionales impuestas por el modelo, don-de los momentos incondicionales don-dependon-den don-de “instrumentos” generados por funciones indicadoras y caracterizan por completo dichas restricciones con-dicionales. Es por esta razón que el estimador propuesto por DL resulta consistente. Cabe destacar que la construcción de éste estimador es sencilla de llevar a cabo, y además, una vez obtenido el estimador por CMM, la me-todología tiene la ventaja de que provee de un contraste de especificación “natural” que permite contrastar si el modelo es adecuado.
Es posible usar otras clases de funciones para generar el continuo de restricciones incondicionales que caracterizan el modelo en lugar de la de funciones indicadoras, por ejemplo, la clase de funciones exponenciales (véa-se Bierens (1990) y Carrasco y Florens (2000)).
Finalmente, recordamos la facilidad para implementar la metodología CMM, que adicionalmente permite la realización de un procedimiento de Bootstrap sencillo para estimar los valores críticos del test de especificación, que únicamente requiere de calcular dos series integradas y correr regresiones lineales.
8.
Referencias
Billingsley, P. (1995).Probability and Measure, Wiley and Sons, New York. Bravo, Francesco. Escanciano, Juan Carlos. Otsu, Taisuke.(2011).A Simple Test for Identification in GMM under Conditional Moment Restrictions
(March 28, 2011). Cowles Foundation Discussion Paper No. 1790. Avai-lable at SSRN: http://ssrn.com/abstract=1797689
Chamberlain, G. (1987).Asymptotic Efficiency in Estimation with Condi-tional Moment restrictions. Journal of Econometrics, 34, 305-334. Domínguez, Manuel A., Lobato, Ignacio N. (2004). Consistent Estimation
72, No. 5, 1601-1615.
Domínguez, Manuel A., Lobato, Ignacio N. (2010).Consistent Inference in Models defined by Conditional Moment Restrictions: An alternative to GMM. Discussion Paper Series, CIE, Discussion Paper 10-05.
Hall, Alastair R. (2001).Generalized Method of Moments. A companion to Theoretical Econometrics, Blackwell Publishers.
Hayashi, Fumio. (2001).Econometrics. Princeton University Press.
Koenker, Roger. (2005).Quantile Regression. Cambridge Books, Cambridge University Press.
Newey, Whitney K., McFadden Daniel. (1994). Large Sample Estimation and Hypothesis Testing. Handbook of Econometrics, Volume IV, Else-vier Science B.V., 2114-2119.