tema3 cdcs ex pdf

(EXEMPLES)

Exemple 1. Calculeu la integral

I = Z Z

D

ycos(xy) dxdy,

on D´es el domini definit per:

D={(x, y)∈_R2: 1≤y ≤4,1≤xy ≤4};

usant el canvi de variables T :x= u

v, y=v (⇔T

−1 _{:u=xy, v=y).}

/Soluci´o. Com que 1 ≤y ≤4, es segueix, de la segona condici´o: 1≤xy ≤4 que 1

x ≤y ≤

4

x. ´Es a

dir, D´es el domini limitat per les rectesy = 1, y = 4 i les hip`erbolesy = 1

x, y =

4

x, tallant-se en els

punts: (1,1),(1/4,4),(4,1) i (1,4) —veure figura1—. Tanmateix: 1≤u=xy ≤4, 1≤v=y≤4

i llavors el domini d’integraci´o, en les noves variables (u, v) ve donat pel rectangle:

D∗ =T−1(D) ={(u, v)∈R2: 1≤u≤4,1≤v≤4} = [1,4]×[1,4].

D’altra banda, si calculem el jacobi`a de la transformaci´o, obtenim:

JT(u, v) = det

∂(x, y)

∂(u, v)(u, v)

=

∂x ∂u(u, v)

∂x ∂v(u, v) ∂y

∂u(u, v) ∂y ∂v(u, v)

=

1

v − u v2

0 1

= 1

v.

(observem que el canvi est`a ben definit per v6= 0). Aix´ı:

I = Z Z

D∗

vcosu

1

v

| {z } Jacobi`a

dudv=

Z 4

1

cosudu

×

Z 4

1 1 dv

= 3×[sinu]u_u=4₌₁ = 3(sin 4−sin 1). .

Exemple 2. Calculeu l’`area del cercle de radi R: D={(x, y)∈_R2_:x2_+y2 _≤R}

/Soluci´o.

`

Area(D) = Z Z

D

dxdy= Z Z

D∗

rdrdθ,

on D∗ =T−1(D) = [0, R]×[2, π]; de manera que, en coordenades polars, podem aplicar directament el teorema de Fubini sobre rectangles:

`

Area(D) =

Z R

0

rdrd

×

Z 2π

0 dθ

=

r2

2 r=R

r=0

×[θ]θ_θ=2₌₀π =πR2. .

Date: 4 maig 2012.

Figura 1. El dominiDve limitat per les

rec-tes y = 1, y = 4 i les hip`erboles xy = 1 i

xy = 4. 0

1 2 3 4

0 1 2 3 4 5 6

xy=4 xy=1

y=4

y=1 D

x

Exemple 3. C`alcul de la integral RR

Df(x, y) dxdy, on f(x, y) ´es la funci´o: f(x, y) = e−(x2+y2)

iD el domini definit per:

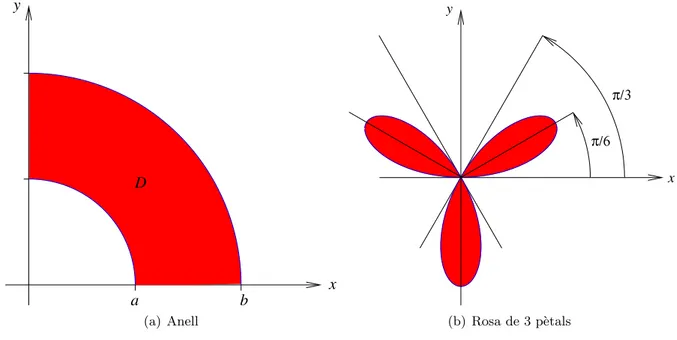
D={(x, y)∈R2:a2 ≤x2+y2 ≤b2, x≥0, y≥0} (veure figura 2(a)).

/ Soluci´o. En coordenades polar el domini D es transforma en un rectangle, i. e., D∗ =T−1(D) = [a, b]×[0,π₂]. Aleshores:

Z Z

D

e−(x2+y2)dxdy = Z Z

D∗

e−r2rdrdθ

=

Z b

a

e−r2rdr

×

Z π

2

0 dθ

!

= π 2

−1

2e

−r2r=b r=a

= π 4

e−a2 −e−b2

. .

Remarca 1. Si us´essim integrals iterades en coordenades cartesianes, caldria calcular: Z Z

D

e−(x2+y2)dxdy= Z a

0 Z

√ b2_−x2 √

a2_−x2

e−(x2+y2)dy

!

dx+ Z b

a

Z

√ b2_−x2

0

e−(x2+y2)dy

!

dx.

Exemple 4 (rosa de tres p`etals). Quan en domini on volem integrar est`a definit en coordenades polars, l’us d’aquestes esdev´e imprescindible. A tall d’exemple, considerem el cas la rosa de tres p`etals, que ve donada per l’equaci´o:

r=asin(3θ),

amb a >0 (veure, per ex., l’article sobre la “rosa polar” en la Wikipedia: http://es.wikipedia.org/wi-ki/Rosa polar; tamb´e teniu un applet Java en http://www25.brinkster.com/denshade/que us permet generar algunes corbes planes notables). Es vol calcular l’`area d’un dels p`etals∗(veure figura 2(b)).

/Soluci´o. Observem primer de tot que, si l’angleθpren valors entre 0 i 2π, aleshoresr=asin(3θ)≥0 sii:

θ∈h0,π

3 i

∪

2π

3 , π

∪

4π

3 , 5π

3

.

∗

x

a b

y

D

(a) Anell

x π/6

π/3 y

(b) Rosa de 3 p`etals

Figura 2. Figures dels exemples 3i4.

En variar θ sobre cadascun d’aquests intervals, la corba recorre la vora del p`etal corresponent (com es pot deduir de la figura 2(b)). Aix´ı, si prenem 0≤θ ≤ π

3, queda clar que l’`area que busquem, A, s’obt´e mitjan¸cant la integral:

A= Z Z

D

dxdy= Z Z

D∗

rdrdθ,

on D∗ ´es el domini donat per:

D∗ =n(r, θ)∈[0,+∞)×h0,π

3 i

: 0≤r ≤asin(3θ)o,

i finalment, fent els c`alculs:

A= Z π

3

0

Z asin(3θ) 0

rdr

!

dθ= Z π

3

0

r2

2

r=asin(3θ)

r=0

dθ= a 2 2

Z π

3

0

1−cos(2θ)

2 dθ=

πa2

12 . .

Exemple 5. C`alcul del volum del dominiD de R3 compr´es entre el con z2 =x2+y2 i el paraboloide

z=x2+y2, per z≥0.

/ Soluci´o. La intersecci´o de les superf´ıciesz2 =x2+y2 iz =x2+y2 amb el pla z = constant≥0 s´on dos cercles de radis z i√z respectivament. Aquest dos cercles s´on el mateix si z = 0 (col.lapsen en un punt) i z= 1 (circumfer`encia de radi 1).

La figura 3(a) mostra una secci´o amb el semipl`a x = 0, y ≥ 0. Aquesta secci´o ´es la mateixa si tallem per qualsevol pla que contingui l’eixz. Llavors el domini D´es el volum de revoluci´o entorn de l’eix z de la part ombrejada. Per tant D ´es un domini amb simetria cil´ındrica, que en coordenades polars s’expressa, siD=T(D∗):

D∗={(r, θ, z)∈R3 : 0≤θ≤2π, z≤r ≤

√

0 0.5 1 1.5

0 0.5 1 1.5 2

2

y z=y

(a)

x z

r =

r =z

(b)

Figura 3. Figures de l’exemple5.

Llavors avaluem el volum integrant en coordenades cil´ındriques:

Volum(D) = Z Z Z

D

dxdydz= Z Z Z

D∗

rdrdθdz= Z 2π

0 Z 1

0 Z

√ z z

rdr

!

dz

!

dθ

= Z 2π

0 Z 1

0

r2

2 r=

√ z r=z

dz

!

dθ= Z 2π

0

Z 1

0

z

2 −

z2

2

dz

dθ

= Z 2π

0 dθ

×

Z 1

0 1 2

z−z2 dz

= 2π

1 2

z2

2 −

z3

3 z=1

z=0 = 2π

1 2 −

1 3

= π

6. Alternativament, usant el principi de Cavalieri: si fem seccions pel pla z = constant ≥ 0, amb

z∈[0,1], obtenim que D∩ {z= constant}´es una corona circular (veure figura3(b)), que t´e `area:

A(z) =π√z2−z2=π(z−z2).

Llavors,

Volum(D) = Z 1

0

A(z) dz= Z 1

0

π(z−z2) dz=π

z2

2 −

z3

3 1

0 =π

1 2 −

1 3

= π

6. .

Exemple 6. Calculeu la integral:

I = Z Z Z

D

(x2+y2) dxdydz,

on D´es el domini definit per:

D={(x, y, z)∈R3: 1≤x2+y2 ≤4,0≤z≤2}.

/Soluci´o. D´es el domini compr´es entre dos cilindres de radis 1 i 2 i els plansz= 0 iz= 2. La secci´o verticalz = constant ´es doncs l’anell de radis que es mostra a la figura4. Aleshores, en coordenades cil´ındriques, el dominiD s’expressa com:

y

x r =2

r =1

Figura 4. Secci´o del domini de l’exemple6

pel pla z= constant. Correspon a un anell de radis 1 i 2.

que ´es un paral.lep´ıped. Integrant en aquestes coordenades, obtenim:

I = Z Z Z

D∗

r2rdrdθdz

=

Z 2

1

r3dr

×

Z 2π

0 dθ

×

Z 2

0 dz

=

r4

4 r=2

r=1

×2π×2 = 4π

16

4 − 1 4

= 15π. .

Exemple 7. Calculeu el volum de l’esfera D de radiR: x2+y2+z2 =R2.

/Soluci´o. En coordenades esf`eriques, el dominiD´es es transforma en el paral.lep´ıped:

D∗=T−1(D) =n(r, θ, ϕ)∈R3: 0≤r ≤R,0≤θ≤2π,−π

2 ≤ϕ≤

π

2 o

.

I el volum s’obt´e f`acilment integrant en aquestes coordenades:

Volum(D) = Z Z Z

D∗

r2cosϕdrdθdϕ= Z 2π

0

Z π

2

−π

2

Z R

0

r2cosϕdr

dϕ

!

dθ

=

Z R

0

r2dr

×

Z π₂

−π

2

cosϕdϕ

!

×

Z 2π

0 dθ

= 4π

r3

3 r=R

r=0 = 4

3πR 3_{. .}

Exemple 8. Calculeu la integral:

I = Z Z Z

D

p

x2_+y2_+z2_dxdydz,

on D´es el domini donat per les desigualtats:

z2 ≤x2+y2 ≤3z2, 1≤x2+y2+z2≤4, (1) amb x≥0, y ≥0, z≥0.

/Soluci´o. De (1) tenim que el dominiDest`a limitat per dos cons i dues esferes (veure figura5). En coordenades esf`eriques:

x=rcosθcosϕ, y =rsinθcosϕ, z=rsinϕ,

les desigualtats de (1) s’escriuen com:

0

0.5

1

1.5

2 0 0.5

1 1.5

2 0

0.5 1 1.5 2

z

x

y z

(a)

0 0.2

0.4 0.6

0.8 1

1.2 1.4

1.6 1.8 0 0.2

0.4 0.6 0.8 1

1.2 1.4 1.6

1.8 0.4

0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5

z

x

y z

(b)

Figura 5. Figures de l’exemple8. La intersecci´o de les esferes i els cons es representa

a la figura (a) El dominiD est`a limitat pels cons: 3z2 =x2+y2 (en verd a la figura),

z2 _=x2_+y2_{(en rosa) i les esferes: x}2_+y2_+z2 _{= 4, de radi 2 (en vermell) ix}2_+y2_+z2₌ 1, de radi 1 (en blau), ambx≥0, y≥0, z≥0 (1er“octant”). Aix´ı, finalment, el domini

D’altra banda, com que x≥0, y ≥0 i z≥0, llavors: 0≤θ≤ π

2, 0≤ϕ≤

π

2. (3)

Amb aix`o, (2) ´es equivalent a:

π

6 ≤ϕ≤

π

4, 1≤r≤2 i afegint la primera desigualtat en (3) queda, tot plegat:

(x, y, z)∈D⇐⇒1≤r≤2, 0≤θ≤ π

2,

π

6 ≤ϕ≤

π

4.

Amb la qual cosa tenim queD—el domini “complicat” de la figura5(b)— correspon, en coordenades esf`eriques, al paral.lep´ıped:

D∗ =T−1(D) = n

(r, θ, ϕ)∈[0,+∞]×[0,2π]×h−π

2,

π

2 i

: 1≤r≤2,0≤θ≤ π

2,

π

6 ≤ϕ≤

π

4 o

= [1,2]×h0,π

2 i

×hπ

6,

π

4 i

.

Finalment, tenint en compte quer =px2_+y2_+z2_{, la integral buscada ara es calcula com:}

I = Z Z Z

D

p

x2_+y2_+z2_dxdydz= Z Z Z

D∗

rr2cosϕdrdθdϕ

=

Z 2

1

r3dr

×

Z π₂

0 dθ

!

×

Z π₄

π

6

cosϕdϕ

!

=

16 4 −

1 4

×π

2 ×

√

2 2 −

1 2

!

= 15π 16

√ 2−1