Análisis de regresión y correlación

(1)

Cap. VII Regresión y correlación 90

Capítulo

VII

Análisis de regresión y correlación

...

Objetivo del

Capítulo

Establecer la relación

entre

dos

o

más

variables: análisis de

correlación. Establecer

un modelo matemático

para estimar el valor

de

una

variable

(2)

7.1 Introducción

El Análisis de Regresión y correlación es una metodología estadística que se utiliza para predecir hechos o eventos y también para pronosticarlos. Con respecto al análisis de regresión lo que se hace es evaluar la contribución de una o más variables con respecto de otra, es decir éste análisis permite evaluar que tan bien una o más variables (independientes) ayudan a explicar a otra (dependiente). El análisis de correlación mide la asociación lineal que presentan las variables sin tomar en cuenta cual es la variable dependiente y cual(es) es (son) las variable(s) independiente(s). Para realizar un análisis de regresión y correlación es recomendable seguir los siguientes pasos: 1. Recopilar los datos a través de fuentes como cuestionarios, formatos, formularios o bases de datos, textos,

folletos, revistas, internet, mediciones directas, etc.

2. Dibujar el diagrama de dispersión, el cual le sugiere que modelo se podría utilizar, sólo hasta planos de tres dimensiones se pueden observar mejor los modelos sugeridos, cuando se trabaja con 4 o más variables los gráficos son áreas de superficies.

3. Calcular los valores del Coeficiente de Correlación y del Coeficiente de Determinación (Nota: el Coeficiente de Correlación mide el porcentaje de asociación lineal entre las variables y el Coeficientes de Determinación mide el porcentaje de variabilidad de la variable dependiente explicada por la variable independiente)

4. Establecer el modelo que sugiere el diagrama de dispersión o los sugeridos por la experiencia del investigador. 5. Estimar la línea de Regresión usando un programa procesador con aplicaciones estadísticas (Excel, SPSS,

Statgraphics,Minitab, Stattif, SAS, Stadistics, entre otros)

6. Hacer pronósticos siempre y cuando la muestra sea suficientemente grande o cuando el periodo de tiempo sea suficientemente confiable para que las predicciones no estén desfasadas de la realidad.

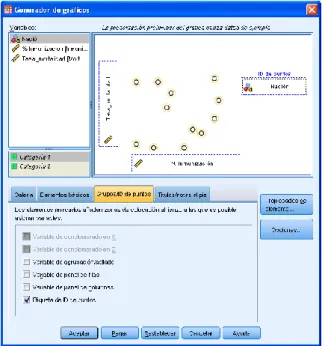
7.2 Diagrama de dispersión o nube de puntos

La distribución conjunta de dos variables puede expresarse gráficamente mediante diagrama de dispersión: en un plano cartesiano se representa cada elemento observado haciendo que sus coordenadas sobre los ejes cartesianos sean los valores que toman las dos variables para esa observación. Es costumbre representar la variable dependiente en el eje vertical (ordenadas) y la independiente en el eje horizontal (abscisas). Cuando se estudia la relación entre dos variables, una puede considerarse causa y la otra resultado o efecto de la primera. Llamaremos variable exógena, o variable independiente a la que causa el efecto y variable endógena, o variable dependiente a la que lo recibe.

Por ejemplo, se está interesado en demostrar la relación que existe entre la tasa de mortalidad y el porcentaje de inmunización que tienen los países en estudio

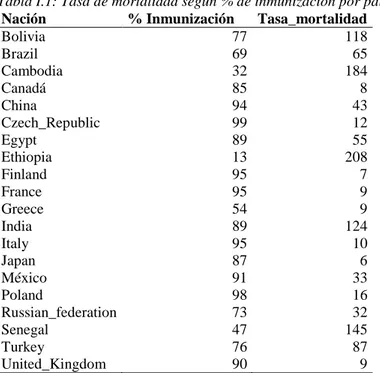
Tabla I.1: Tasa de mortalidad según % de inmunización por países

Nación % Inmunización Tasa_mortalidad

Bolivia 77 118

Brazil 69 65

Cambodia 32 184

Canadá 85 8

China 94 43

Czech_Republic 99 12

Egypt 89 55

Ethiopia 13 208

Finland 95 7

France 95 9

Greece 54 9

India 89 124

Italy 95 10

Japan 87 6

México 91 33

Poland 98 16

Russian_federation 73 32

Senegal 47 145

Turkey 76 87

United_Kingdom 90 9

(3)

Figura I: 1 Diagrama de dispersión de la tasa de mortalidad según % de inmunización en países del mundo

En el diagrama de dispersión de la figura I.1 observamos un indicio del tipo de relación que existe entre las variables. Estando claro a partir de la observación de los puntos que existe una tendencia general que a mayor cantidad de % de inmunización se obtendrá una menor tasa de mortalidad. A este tipo de relación se le conoce como inversa o negativa. Si se observase un proceso contrario, la correlación sería directa o positiva.

Características del diagrama de dispersión

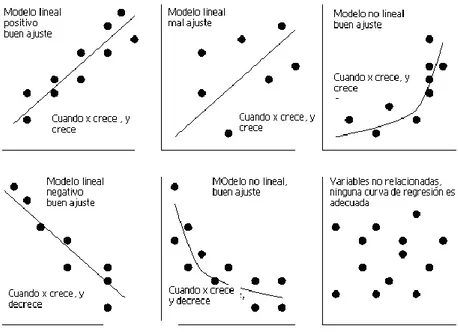
Según la forma de la nube de puntos podemos obtener la siguiente información: Conocer si existe una relación directa o inversa entre las variables Saber si esa relación es fuerte o débil.

Determinar si la relación se ajusta a un modelo lineal o bien a otro modelo matemático (Ej.: modelo curvilíneo).

La producción de este tipo de diagramas es el paso más importante a la hora de estudiar la correlación entre dos variables. Así también la inspección del diagrama es esencial para detectar problemas como son las puntuaciones "outliers", que pueden deberse desde una mala introducción de la información, a la mezcla de datos correspondientes a distribuciones distintas.

(4)

Figura I. 2: Diferentes diagramas de dispersión y sus respectivos modelos de regresión para ellas

7.3 Análisis de correlación

El análisis de correlación o de la covariabilidad puede verse como una propiedad conjunta de dos o más variables, donde se intenta averiguar si las propiedades medidas se relacionan entre sí. Por ejemplo cuando nosotros intentamos averiguar si las personas más adultas sufren más o menos depresión que las personas más jóvenes, o cuando nosotros deseamos saber si las personas más inteligentes tienen mejor rendimiento académico. En su formulación clásica, y de forma general, el estudio de la covariación o correlación entre dos variables exige que ambas variables se expresen en el mismo tipo de escala de medida. Cumplido esto, los datos pueden describirse en forma de matriz rectangular; en el siguiente ejemplo:

Sujeto Edad Inteligencia

S1 15 140

S2 16 93

S3 21 105

S4 22 109

En este ejemplo, puede observarse como tendencia general que la inteligencia aumenta con la edad (caso cierto si comparamos los sujetos S2, S3 y S4). No obstante, existe un sujeto (el primero) que rompe esta regla general (es el más

joven y el que tiene más inteligencia).

Ejemplo: A continuación veremos un ejemplo, donde la figura representada refleja la covariación entre la inteligencia

(CI) y el rendimiento (Nota) de los sujetos estudiados.

Tabla I.2: Nota según CI de un grupo de alumnos de Psicología de la UPeU, 2010

CI NOTA CI NOTA CI NOTA

70 10 85 12 96 13

70 10 75 12 110 13

70 9 73 11 105 13

80 10 79 10 106 14

80 11 72 11 107 15

90 14 80 14 125 15

90 12 85 12 124 14

100 14 84 14 128 15

100 15 81 14 129 14

(5)

X

6 5 4 3 2 1 0

Y

7

6

5

4

3

2

1

110 12 90 10 131 18

120 15 94 12 135 19

120 16 97 15 137 18

140 19 93 13 140 17

Figura I.3: Diagrama de dispersión de las notas según CI

Coeficiente de correlación lineal r de Pearson

Para investigar la correlación entre variables es que se han creado los coeficientes de correlación que permiten expresar el grado de relación que existe entre dos variables (si es lineal simple).

La naturaleza de las distribuciones que se correlacionan, sus escalas de medidas, y sus características, son los factores determinantes para el uso de la técnica y del coeficiente de correlación que se aplicará. La formula es la siguiente:

r =

2 2 2 2

) ( )

(

) ( ) (

y y n x x n

y x xy

n _{, o también}

Donde se resuelve utilizando la covarianza y las desviaciones típicas de las dos variables (en su forma insesgada).

Interpretación: Este estadístico, refleja el grado de correlación lineal que existe entre dos variables. El resultado numérico fluctúa entre los rangos de < -1 a +1>, encontrándose en medio el valor “0” que indica que no existe asociación lineal entre las dos variables a estudio. Un coeficiente de valor reducido no indica necesariamente que no exista correlación ya que las variables pueden presentar una relación no lineal como puede ser el peso del recién nacido y el tiempo de gestación. En este caso el r infraestima la asociación al medirse linealmente. Los métodos no paramétrico estarían mejor utilizados en este caso para mostrar si las variables tienden a elevarse conjuntamente o a moverse en direcciones diferentes.

Una correlación de +1 significa que existe una relación lineal directa perfecta (positiva) entre las dos variables. Es decir, las puntuaciones bajas de la primera variable (X) se asocian con las puntuaciones bajas de la segunda variable (Y), mientras las puntuaciones altas de X se asocian con los valores altos de la variable Y.

r

y x

xy xy

s

(6)

X

6 5 4 3 2 1 0

Y

7

6

5

4

3

2

1

X

6 5 4 3 2 1 0

Y

6

5

4

3

2

1

0

X

12 10 8 6 4 2

Y

12

10

8

6

4

2

CRITERIOS:

Resulta difícil precisar a partir de qué valor de “r” podemos considerar que existe una correlación lineal entre las variables. Siempre debemos tener en cuenta para la interpretación el tipo de variables a las que se aplica así como del tamaño de la muestra.

Sin embargo, para tener un referente, y siendo concientes de que estos coeficientes no son aplicables a todas las situaciones, tomamos los determinados por Bisquerra

Una correlación (r<0) significa que existe una relación lineal inversa o negativa entre las dos variables. Lo que significa que las puntuaciones bajas en X se asocian con los valores altos en Y, mientras las puntuaciones altas en X se asocian con los valores bajos en Y.

Una correlación de (r 0) es decir cercana a cero, se interpreta como la no existencia de una relación lineal entre las dos variables estudiadas

Outliers

Una puntuación "outlier" es una o varias puntuaciones extremas dentro de una variable (por ejemplo si en un variable los sujetos puntúan normalmente entre 20 y 35 puntos, el valor 80 debería ser considerado como "sospechoso" en principio).

Este tipo de valores afecta gravemente a la correlación, sobre todo si trabajamos con muestras pequeñas. La distorsión producida normalmente es aumentar de forma "espuria" el grado de relación lineal.

Un ejemplo de "outlier" puede ser observado en la siguiente gráfica:

(7)

Ejemplo: para el ejemplo de la tabla I.1: tasa de mortalidad según % de inmunización por países tenemos:

En el SPSS para pedir el coeficiente de correlación:

Analizar<correlaciones<bivariadas<pasar las variables<Pearson

Ho: No hay correlación entre la tasa de mortalidad dado el % de inmunización por países

Ha: Si hay algún grado de asociación entre la tasa de mortalidad dado el % de inmunización por países

%

Inmunización Tasa_mortalidad %

Inmunización

Correlación de

Pearson 1

-.791(**)

Sig. (bilateral) .000

N 20 20

Tasa_mortalida d

Correlación de

Pearson -.791(**) 1

N 20 20

** La correlación es significativa al nivel 0,01 (bilateral).

Interpretación

R = - .791** Existe una alta correlación inversa entre la tasa de mortalidad y él % de inmunización; es decir a mayor % de inmunización la tasa de mortalidad disminuye significativamente (Sig = .000)

Rechazamos la Ho dado una significancia de .000

Ejemplo: para el ejemplo de la tabla I.2: la inteligencia (CI) y el rendimiento (Nota) de los sujetos estudiados tenemos:

Ho: No hay correlación entre el rendimiento dado la inteligencia

Ha: Si hay algún grado de asociación entre el rendimiento dado la inteligencia

CI NOTA

CI Correlación de Pearson 1 .849(**)

N 42 42

NOTA Correlación de Pearson .849(**) 1

N 42 42

** La correlación es significativa al nivel 0,01 (bilateral).

Interpretación

R = .849** Existe una alta correlación directa o positiva entre la inteligencia y el rendimiento medido a través de las notas; es decir a mayor CI las notas se incrementan significativamente (Sig = .000)

7.4 Coeficiente de determinación

Nos indica el porcentaje del ajuste que se ha conseguido con el modelo lineal, es decir el porcentaje de la variación de Y(rendimiento) que se explica a través del modelo lineal que se ha estimado, es decir a través del comportamiento de X(inteligencia). Para los ajustes de tipo lineal se tiene que los coeficientes de determinación son iguales a r2, y por tanto representan además la proporción de varianza explicada por la regresión lineal; es decir la proporción de las variaciones totales en la variable dependiente Y que es explicada (no causada) o atribuida a las variaciones en la variable independiente X, también se le denomina bondad del ajuste.

El coeficiente de determinación es el cuadrado del coeficiente de correlación, y varía de 0 a 1. .000

(8)

2 / 2 2

/y y x

x

r

R

Para el ejemplo de la tabla I.1: tasa de mortalidad según % de inmunización por países tenemos:

R2 = (-.791)2 % = 62.6%; es decir se ha eliminado un 62.6% de los errores con la regresión; la tasa de mortalidad está siendo explicado en un 62.6% por la variabilidad del % de inmunización y un 37.4% se debe a la intervención de otras variables.

Para el ejemplo de la tabla I.2: la inteligencia (CI) y el rendimiento (Nota) de los sujetos estudiados tenemos:

R2 = (. 849)2 % = 72.1%; es decir se ha eliminado un 72.1% de los errores con la regresión; el rendimiento está siendo explicado en un 72.1% por la variabilidad de la inteligencia medida a través del CI y un 27.9% se debe a la intervención de otras variables.

7.5 Análisis de regresión

El objetivo del análisis de la regresión lineal es analizar un modelo que pretende explicar el comportamiento de una variable (Variable endógena, explicada o dependiente), que denotaremos por Y, utilizando la información proporcionada por los valores tomados por un conjunto de variables (explicativas, exógenas o independientes), que denotaremos por X1, X2 , ..., X n

Las variables del modelo de regresión deben ser cuantitativas. Pero dada la robustez de la regresión es frecuente encontrar incluidas en el modelo como variables independientes a variables ordinales e incluso nominales transformadas en variables ficticias. Pero la variable dependiente debe ser cuantitativa. Para una variable dependiente binaria de emplea la regresión logística.

Las técnicas de regresión permiten hacer predicciones sobre los valores de cierta variable Y (dependiente), a partir de los de otra X (independiente), entre las que intuimos que existe una relación. Ejemplo, si sobre un grupo de personas observamos los valores que toman las variables

X = altura en centímetros, Y = peso medido en kilogramos

La razón no es por cierto que conocida la altura xi de un individuo, podamos determinar de modo exacto su peso yi

(dos personas que miden 1,70 cm pueden tener pesos de 60 y 65 kilos). Sin embargo, alguna relación entre ellas debe existir, pues parece mucho más probable que un individuo de 2,0 cm pese más que otro que mida 1,20 cm.

A la deducción, a partir de una serie de datos, de este tipo de relaciones entre variables, es lo que denominamos regresión.

Mediante las técnicas de regresión inventamos una variable

Y

como función de otra variable X (o viceversa),

Y

= f(x) , esto es lo que denominamos relación funcional. El criterio para construir

Y

, tal como citamos

anteriormente, es que la diferencia entre Y e

Y

sea pequeña.

Y

= f(x), Y-

Y

= error

El término que hemos denominado error debe ser tan pequeño como sea posible. El objetivo será buscar la función (también denominada modelo de regresión) que lo minimice.

Modelos de regresión (variable dependiente cuantitativa).

 Lineal

 Logarítmico

 Inverso

 Cuadrático

 Cúbico

 Potencia

 Compuesto

X

Y

₀ ₁

)

ln(

1

0

X

Y

)

/

(

₁

0

X

Y

2 2 1

0

X

Y

3 3 2 2 1

0

X

Y

1

0

X

(9)

 Logístico

 Exponencial

 Lineal Múltiple

Modelo de regresión lineal simple

Es un modelo de regresión lineal entre dos variables:

Y

0 1

x

, a la variable Y se la denomina variable dependiente y a X independiente.

Ecuación de regresión:

E

(

Y

)

₀ ₁

x

Condiciones para usar el modelo de regresión lineal:

i) Para cada valor xi de X existe una v.a. Y|xi cuya media está dada por el modelo

ii) todas las variables Y|xi son normales, independientes y con igual varianza.

Ejemplo: Se quiere estudiar la relación entre consumo de sal y tensión arterial. A una serie de voluntarios se les administra distintas dosis de sal en su dieta y se mide su tensión arterial un tiempo después.

Variable X: gr. de sal diarios (no aleatoria) Variable Y: presión arterial en mm. de Hg.

Asumimos que para cada valor de X, Y no está determinada, sino que sigue una distribución normal cuya media está

dada por el modelo:

Y

₀ ₁

X

0: Presión arterial media de los que no toman nada de sal

1: Cambio de la media de presión arterial por aumentar 1 gr. el consumo de sal, asumiendo que es constante.

Si fuera 0, quiere decir que la presión no cambia con el consumo de sal, por tanto ambas variables son independientes, un valor distinto de cero indica que están correlacionadas y su magnitud mide la fuerza de la asociación.

A partir de una muestra aleatoria, la teoría estadística permite:

i) estimar los coeficientes _i del modelo (hay dos procedimientos mínimos cuadrados y máxima verosimilitud que dan el mismo resultado).

ii) estimar las varianzas de las variables Y/x_i llamada cuadrados medios del error y representada por

s

2 o MSE. a su raíz cuadrada se le llama error estándar de la estimación.

iii) conocer la distribución muestral de los coeficientes estimados, tanto su forma (t) como su error estándar, que permite hacer estimación por intervalos como contrastes de hipótesis sobre ellos.

Modelo:

Y

0 1

X

A través del método de los mínimos cuadrados (MMC) se debe obtener: Y

a

bx

X

u

Y

1 0

1

X

e

Y

1

0

n

X

Y

₀ ₁ ₁ ₂ ₂ ₃ ₃



Función lineal

Se llama función lineal de una variable, a una función de la forma:

1 0 1

0

X

,

y

Y

Constantes

0: ordenada en el origen (valor de Y

cuando X = 0)

1: Pendiente (cambio de Y al aumentar X

(10)

Cap. VII Regresión y correlación 99 El método de los Mínimos Cuadrados consiste en definir la función que tenga menos rango o desviación respecto a los valores observados: f(x,y), se trata de un problema de minimización del área o (desviación), estimación entre los valores observados o reales Yi son los valores calculados o estimados a partir de una función o línea de regresión.

0 y 1 son parámetros que se determinan al aplicar el MMC la cual significa minorizar.

2 2

2 0

) ( x x

n

xy x y x

2 2

1

)

(

x

n

y

x

xy

n

Ejemplo: de la relación entre consumo de sal y tensión arterial, una muestra produce los siguientes datos:

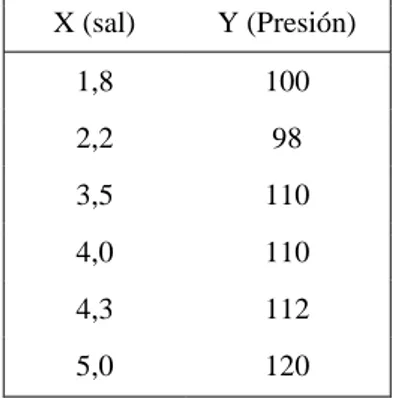
Tabla I.3: consumo de sal y tensión arterial X (sal) Y (Presión)

1,8 100

2,2 98

3,5 110

4,0 110

4,3 112

5,0 120

En el SPSS para pedir el análisis de regresión:

Analizar<regresión lineal<pasar la variable “y” a dependiente y la variable “x” a independientes<aceptar La "salida" del SPSS es:

1º. Resumen del modelo

Resumen del modelo

Modelo R R cuadrado

R cuadrado corregida

Error típ. de la estimación

1 .967(a) .934 .918 2.33162

a Variables predictoras: (Constante), sal

Reporta r=.967 (alta correlación positiva)

2

r

=.934 (93.4% del porcentaje de varianza explicada)

2º. Reporta el análisis de varianza para la regresión, que separa la variabilidad explicada por la regresión y la variabilidad no explicada o residual, y calcula el estadístico F y su significancia estadística.

Esta es una primera aproximación inferencial al modelo de regresión lineal, que evalúa globalmente el modelo. En nuestro ejemplo es estadísticamente significativo (Sig=p=.002) y se concluye rechazando la Ho, es decir existe asociación entre las dos variables mediante una regresión lineal); en otras palabras el modelo que daremos a continuación es bueno.

ANOVA(b)

Modelo

Suma de

cuadrados gl

Media

cuadrática F Sig.

1 Regresión 309.587 1 309.587 56.946 .002(a)

Residual _21.746 ₄ _5.436

Total 331.333 5

a Variables predictoras: (Constante), sal b Variable dependiente: presión

(11)

Coeficientesa

86.371 3.062 28.206 .000

6.335 .840 .967 7.546 .002

(Constante) Sal (x) Modelo

1

B Error típ.

Coeficientes no estandarizados

Beta Coeficientes estandarizad

os

t Sig.

Variable dependiente: Presión (y) a.

Donde:

86.371 presión arterial media sin nada de sal. (constante en el origen)

6.335 aumento de presión por cada gr. de sal; como es distinto de cero indica correlación (pendiente de la recta) En términos de contrastes de hipótesis.

H0: ₁ = 0

H1: 1

0

según iii) ₂

1 1

)

(

t

n

error

t

₇_.₅₄

840 . 0

335 . 6

t , aquí t = 7,546 con un valor p = 0,002 (sig < 0.05)

Se rechaza H0. Esto es, existe relación significativa entre el consumo de sal y tensión arterial.

Predicción: Tomando como base la data de los 6 pacientes de los cuales se midió su tensión arterial y su consumo de

sal, ¿Qué valor de tensión arterial se esperaría si un paciente consume en su dieta 3.2 gr.de sal?

Presión= 86.371+(6.335*3.2 gr.)=106.643

Con estos resultados concluimos:

1º. Que las variables están asociadas o relacionadas linealmente en la población de la que proviene la muestra (con una muy pequeña probabilidad de que la relación encontrada sea explicada por el azar, menos del uno por mil

2º. Que la relación encontrada es muy fuerte (r=.967), de hecho que la variable independiente (consumo de sal) explica en un 93.4% ( 2 .934)

r la variabilidad de la variable dependiente (presión)

3º. Que la relación es directa, aumentando en promedio 6.335 de presión por cada aumento de 1 gr de sal. Con estos coeficientes se puede construir la recta de regresión:

Presión= 86.371+(6.335*consumo de sal gr.)

Nota: En todo análisis de regresión debe realizarse la evaluación de los residuales (el supuesto de la normalidad, que exista linealidad y que se cumpla el requisito de la homocedasticidad). En nuestro curso de estadística descriptiva no lo llevaremos, dejándolo para la estadística inferencial)

Ejemplo: En un grupo de 8 pacientes se miden las cantidades antropométricas peso y edad, obteniéndose los

siguientes resultados: Tabla I: 4

Resultado de las mediciones

X = edad 12 8 10 11 7 7 10 14

Y = peso 58 42 51 54 40 39 49 56

¿Existe una relación lineal importante entre ambas variables? Calcular la recta de regresión del peso en función de la edad. ¿Qué peso se podría predecir para un paciente que tiene una edad de 8 años de edad?. ¿En cuánto aumenta la edad por cada kilo de peso?. Calcular la bondad del ajuste ¿En qué medida, por término medio, varía el peso cada año? ¿En cuánto aumenta la edad por cada kilo de peso?.

Solución:

Para saber si existe una relación lineal entre ambas variables se calcula el coeficiente de correlación lineal:

(12)

años

x 9.875 ;

y

= 48.625 Kg ; 8

1

3963

i i

iy

x ; x 2.315 ; y 6.963

Método 1:

año Kg x

S_xy 9.875 48.625 15.2031 . 8 3963 9431 . 0 9631 . 6 3150 . 2 2031 . 15 x S r y x

xy _{, donde}

Método. De acuerdo a la formula de mínimos cuadrados:

943 . 0 66322 . 1031 973 ) 389 ( 19303 * 8 ) 79 ( 823 * 8 389 * 79 ) 3963 ( 8 ) ( ) ( ) ( ) ( 2 2 2 2 2

2 _x _n _y _y r

x n y x xy n r

Siendo r=0.943 se considera una correlación alta positiva o directa, por tanto el ajuste lineal es muy bueno.

El diagrama de dispersión lo confirma:

edad 14 12 10 8 pes o 60 55 50 45 40 35

Sq r lineal = 0,89

La recta de regresión del peso en función de la edad es:

año

Kg

S

Kg

x

y

X

x

Y

x xy

/

837 .

2

612 .

20

837 .

2

612 .

20

2 1 1 0 1 0

Por el método de los mínimos cuadrados:

612 . 20 ) 79 ( 823 * 8 3963 * 79 389 * 823 )

( 2 2

2 2 0 x x n xy x y x 837 . 2 343 973 ) 79 ( 823 * 8 389 * 79 3963 * 8 )

( 2 2

2 1 x x n y x xy n

Reporte en el SPSS

Coeficientesa

Modelo

Coeficientes no estandarizados

Coeficientes tipificados

t Sig.

B Error típ. Beta

1 (Constante) 20,612 4,140 4,979 ,003

edad 2,837 ,408 ,943 6,950 ,000

a. Variable dependiente: peso

(13)

Estimación:

Peso=20.612+2.837 * 8 años= 43.308 Kg

La bondad del ajuste o coeficiente de determinación es:

8894

.

0 )

9431

.

0 (

2

2 2

/ 2

/

R

r

R

_x _y _y _x

Por tanto podemos decir que el 88.94 % de la variabilidad del peso en función de la edad es explicada mediante la recta de regresión correspondiente. Lo mismo podemos decir en cuanto a la variabilidad de la edad en función del peso. Del mismo modo puede decirse que hay un 100 – 88.94 % = 11.06 % de varianza que no es explicada por la recta de regresión. Por tanto la varianza residual de la regresión del peso en función de la edad es:

años

K

x

r

S

E y

2 2

33 .

5

484 .

48 1106

.

0 .

1

Por último la cantidad en que varía el peso de un paciente cada año es, según la recta de regresión del peso en función de la edad, la pendiente de esta recta, es decir, b1 = 2,837 Kg./año.

Pasos en Excel y SPSS para el ejemplo anterior

x y xy x2 y2

12 58 696 144 3364

8 42 336 64 1764

10 51 510 100 2601

11 54 594 121 2916

7 40 280 49 1600

7 39 273 49 1521

10 49 490 100 2401

14 56 784 196 3136

(sumatoria)

79.00 389 3963 823 19303

X(edad) Y(peso)

Media 9.875 Media 48.625

Varianza 5.359 Varianza 48.484

Desviación 2.315 Desviación 6.963

Reporte del SPSS

Correlaciones

edad peso

Edad Correlación de Pearson

1 ,943**

Peso Sig.

(bilateral)

,000

Suma de

cuadrados y productos cruzados

42,875 121,625

Covarianza 6,125 17,375

N 8 8

(14)

PROBLEMAS DE REPASO DEL CAPÍTULO

En cada uno de los siguientes ejercicios (de la pregunta 1 a la pregunta 8), (a) Dibujar un diagrama de dispersión, (b) calcular el coeficiente de correlación muestral e intérprete, (c) ¿existe evidencia de que hay una asociación entre las dos variables?, verificar Ho: = 0, (d) Determinar la ecuación de regresión que mejor ajuste los datos, (e) ¿existe

evidencia de que hay una relación lineal entre las dos variables? Verificar Ho: 1 = 0. (g) al nivel de significación de

0.05 (f) Calcule el coeficiente de determinación r2 e intérprete su significado en cada problema.

1. Supóngase que a 10 personas se les aplica una prueba que mida la actitud que tienen hacia el éxito (o bien, el número de prejuicios o actitudes negativas hacia el). Al mismo tiempo se les pregunta el número de años de estudio que hasta la fecha han realizado. Se pide encontrar la relación que existe entre ambas variables. Los resultados de esta encuesta son los siguientes:

Personas Años de estudio: X N° de prejuicios: y A B C D E F G H I J 10 3 12 11 6 8 14 9 10 2 1 7 2 3 5 4 1 2 3 10

Realizar el análisis respectivo. Tomando como base las 10 personas de la muestra, ¿Qué número de prejuicios podría predecir para una persona que tiene 15 años de estudio?.

2. A 25 individuos se les miden las pulsaciones por minuto del corazón antes de someterlos a una entrevista de tipo laboral, obteniéndose los siguientes datos:

Pulsaciones por minuto

Puntajes en la entrevista Pulsaciones por minuto Puntajes en la entrevista 72 77 85 99 107 110 82 73 92 92 104 74 80 5.0 8.0 7.5 8.9 7.3 5.3 8.0 5.2 8.3 8.6 6.5 6.0 8.4 95 98 70 105 88 78 103 95 70 83 94 115 7.8 7.7 5.0 6.1 8.1 7.4 6.7 7.9 5.1 7.4 8.8 5.2

3. En la Facultad de Ciencia Humanas y Educación de la Universidad Peruana Unión, se quiere entender los factores de aprendizaje de los alumnos que cursan la asignatura de Estadística inferencial aplicada a la psicología, para lo cual se escoge al azar una muestra de 15 alumnos y ellos registran notas promedios en la asignaturas de Psicometría, y Estadística inferencial aplicada a la psicología como se muestran en el siguiente cuadro.

Alumno

Estadística inferencial

aplicada a la psicología Psicometría Alumno

Estadística inferencial

aplicada a la psicología Psicometría

1 13 15 9 13 15

2 13 14 10 13 14

3 13 16 11 11 12

4 15 20 12 14 16

5 16 18 13 15 17

6 15 16 14 15 19

7 12 13 15 15 13

(15)

Cap. VII Regresión y correlación 104 4. En un estudio de la relación entre el metabolismo de la anfetamina y una psicosis de anfetamina, a seis usuarios

crónicos de este compuesto se les asignó una calificación de intensidad de psicosis. Los niveles de anfetamina en el plasma (mg./ml) se dan en la siguiente tabla:

Nº de pacientes

Calificación de intensidad de psicosis

Anfetamina en el plasma (mg./ml)

1 15 150

2 40 100

3 45 200

4 30 250

5 55 250

6 30 500

5. A 10 enfermos esquizofrénicos en un hospital psiquiátrico se les hacen dos evaluaciones, una para medir la percepción de la profundidad de distancia ante un estimulo visual, y la otra para medir la percepción auditiva ante un estimulo, obteniéndose los siguientes datos:

Paciente A B C D E F G H I J Visual m 4 6 4 8 10 10 12 6 12 8 Auditiva m 25 22 26 17 16 21 13 18 19 22

6. Un equipo de investigaciones de un hospital psiquiátrico realizó un experimento para estudiar la relación que existe en pacientes esquizofrénicos entre el tiempo de reacción a un estímulo particular y el nivel de la dosis de una droga. Específicamente, los investigadores deseaban hacer el experimento con dosis de 0.5, 1.0, 1.5, 2.0, 2.5 y 3.0 mg. Seleccionaron una muestra aleatoria de 18 pacientes en una población hospitalaria de esquizofrénicos y asignaron al azar a cada paciente una de las dosis.

Paciente

Dosificación

X Tiempo de reacción Y

(mseg) Paciente

Dosificación X (mg)

Tiempo de reacción Y (mseg) (mg)

1 0.5 12 10 2 40

2 0.5 22 11 2 44

3 0.5 30 12 2 50

4 1 18 13 2.5 44

5 1 32 14 2.5 44

6 1 36 15 2.5 60

7 1.5 40 16 3 64

8 1.5 34 17 3 68

9 1.5 46 18 3 76

7. Supongamos que los siguientes datos corresponden a pacientes de enfisema: el número de años que el paciente ha fumado (x) y la evaluación subjetiva del médico en relación al daño sufrido por los pulmones (y). La última variable se mide en una escala de 0 a 100. Las observaciones correspondientes a 10 pacientes son las siguientes:

Paciente Años que ha fumado Daño en los pulmones

1 25 55

2 36 60

3 22 50

4 15 30

5 48 75

6 39 70

7 42 70

8 31 55

9 28 30

10 33 35

(16)

Cap. VII Regresión y correlación 105 8. La mortalidad infantil es un hecho que depende de varios factores. En el siguiente cuadro están indicadas tres

variables o hechos que pudieran explicar los niveles de mortalidad infantil. Considerando a la mortalidad infantil (y) como una variable dependiente se pide calcular los coeficientes de correlación e indicar cuál o cuáles son las variables que mejor explican el comportamiento de la mortalidad infantil.

PERÚ: CONJUNTO DE INDICADORES SOCIO-DEMOGRÁFICOS PARA UNA MUESTRA DE 13 DEPARTAMENTOS PARA EXPLICAR LA MORTALIDAD INFANTIL, 2003.

Departamentos Mortalidad infantil x 1000 Y Madres analfabetas (%) X1 Desnutrición crónica en niños

X2

Viviendas sin instalación de agua

X3 Amazonas Apurimac Ayacucho Callao Huancavelica Ica La Libertad Lima

Madre de Dios Pasco Puno Tacna Ucayali 68 85 85 23 107 39 46 26 63 66 90 40 69 29 52 46 5 48 8 18 6 13 23 33 11 13 64 69 64 20 72 29 48 24 54 57 52 18 52 81 82 73 28 88 41 50 29 78 74 84 34 80

Se puede afirmar que los niveles de mortalidad infantil tienen una obvia relación directa con el nivel educativo (analfabetismo) y los estados de nutrición infantil. Determine el mejor modelo de predicción.

9. Un investigador cree que la inteligencia de los niños, medida a través del coeficiente intelectual (CI en puntos), depende del número de hermanos. Toma una muestra aleatoria de 15 niños y ajusta una regresión lineal simple. Los resultados aparecen en la tabla adjunta:

Nº CI Nº hermanos Nº CI Nº hermanos

1 110 0 9 98 3

2 115 1 10 99 4

3 120 1 11 98 4

4 118 1 12 100 5

5 110 2 13 90 5

6 108 2 14 93 5

7 105 2 15 90 6

8 104 3

a) Dibuje el diagrama de dispersión e interprete el reporte, b) determine e interprete el coeficiente de correlación (r=-.929), c) determine e interprete el coeficiente de determinación o bondad de ajuste, d) de la ecuación de la recta de regresión. Interprete los estimadores en el contexto de la pregunta (constante=119.295), Nº hermanos=-.5143), e) ¿existe una relación lineal significativa entre el número de hermanos y el coeficiente intelectual?

10. La tabla siguiente muestra las notas obtenidas por 8 alumnos en un examen, las horas de estudio dedicadas a su preparación y las horas que vieron la televisión los días previos al examen.

Nota 5 6 7 3 5 8 4 9

Horas de estudio 7 10 9 4 8 10 5 14

Horas de TV 7 6 2 11 9 3 9 5

a) Representa gráficamente los diagramas correspondientes a nota-estudio y nota-TV., b) ¿Se observa correlación entre las variables estudiadas? ¿De qué tipo? ¿En qué caso estimas que es más fuerte?, c) determina el coeficiente de correlación de nota-estudio y nota-TV. ¿Qué puede deducirse con más precisión conociendo la nota que obtuvo una persona en el examen: el tiempo que dedicó al estudio o el que dedicó a ver la televisión?, d) halla las rectas de regresión correspondientes y estima para un alumno que sacó un 2 en el examen: