Desarrollo e implementación de un brazo robótico en un auto explorador de lazo abierto

Texto completo

(1)INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA. ¨DESARROLLO E IMPLEMENTACIÓN DE UN BRAZO ROBÓTICO EN UN AUTO EXPLORADOR DE LAZO ABIERTO¨. QUE PARA OBTENER EL TITULO DE: INGENIERO EN COMUNICACIONES Y ELECTRÓNICA. PRESENTAN: MONTEMAYOR VELARDE MA. DOLORES PÉREZ RAMÍREZ ARTURO. ASESORES: LÓPEZ CÁRDENAS RODRIGO TRUJILLO VALVERDE ERASMO. MÉXICO D.F., JUNIO 2012.

(2)

(3) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. CONTENIDO OBJETIVO GENERAL .................................................................................................................................................................. 2 OBJETIVOS PARTICULARES .................................................................................................................................................... 2 JUSTIFICACION ............................................................................................................................................................................ 3 PLANTEAMIENTO DEL PROBLEMA ........................................................................................................................................ 4 CAPÍTULO 1 .................................................................................................................................................................................. 5 INTRODUCCION ....................................................................................................................................................................... 5 CAPÍTULO 2 .................................................................................................................................................................................. 7 MARCO TEÓRICO .................................................................................................................................................................... 7 1.1 TELEMETRÍA .................................................................................................................................................................... 7. 1.1.1.. Definición .............................................................................................................................................................. 7. 1.1.2.. Aplicaciones .......................................................................................................................................................... 8. 1.2. INTRODUCCIÓN A LA ROBÓTICA .................................................................................................................................. 8. 1.2.1. Clasificación de los robots manipuladores .................................................................................................................. 9 1.3. ROBÓTICA Industrial ..................................................................................................................................................... 10 1.4. SISTEMA Común De Cinemática De Manipuladores .................................................................................................... 11. 1.4.1. Manipulador Articulado (RRR) .................................................................................................................................... 11 1.5. CINEMATICA DE ROBOTS MANIPULADORES ............................................................................................................ 13 1.6. DESCRIPCIONES ESPACIALES Y TRANSFORMACIONES ...................................................................................... 14. 1.6.1. Formulación Matricial De Las Transformaciones ..................................................................................................... 14 1.6.1.1 Matriz de traslación................................................................................................................................................. 14.

(4) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. 1.6.1.2 Matriz de rotación ................................................................................................................................................... 16 1.7.Cinematica Directa ................................................................................................................................................................ 17. 1.7.1. Resolución De Cinemática Directa A Través De Matrices De Transformación Homogéneas. …………………18. 1.8.Cinematica Inversa ............................................................................................................................................................... 21 1.9.Introducción Al Control ..................................................................................................................................................... 22. 1.9.1. Definiciones ................................................................................................................................................................. 212 1.9.1.1. Procesos ................................................................................................................................................................. 22 1.9.1.2. Plantas..................................................................................................................................................................... 22 1.9.1.4. Control Retroalimentado ....................................................................................................................................... 22 1.9.1.5 Sistemas De Control Realimentado ..................................................................................................................... 23 1.9.2. Control De Lazo Cerrado Y Lazo Abierto .............................................................................................................. 23 1.9.2.1 Sistemas De Control De Lazo Cerrado ............................................................................................................... 23 1.9.2.2. Sistemas De Control En Lazo Abierto ................................................................................................................ 23 1.10.Modelos Matemáticos De Sistemas Físicos ................................................................................................................... 24. 1.10.1.Modelos Matemáticos ................................................................................................................................................. 24 1.11. ESTRUCTURA DE UN BRAZO ROBOT INDUSTRIAL ............................................................................................... 25 1.12.Caracteristicas Del Brazo Robot ....................................................................................................................................... 25. 1.12.1. Eslabones Y Articulaciones .................................................................................................................................... 25 1.12.2. Reductores................................................................................................................................................................... 26 1.12.3. Actuadores ................................................................................................................................................................... 26 1.12.3.1. Motores De CD .................................................................................................................................................... 27.

(5) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. 1.12.3.2. Servomotor ........................................................................................................................................................... 27. 1.12.3.2.1. Diagrama de un servomotor típico ................................................................................................................ 28 1.12.3.2.2. Motor De Corriente Continúa ......................................................................................................................... 28 1.12.3.2.3. Funcionamiento ................................................................................................................................................ 30 1.12.3.2.4. Caracteristicas Generales Y Funcionamiento ............................................................................................. 30 1.13.D ISPOSITIVO DE ADQUISICION DE DATOS (DAQ) ............................................................................................................ 32. 1.13.1 Caracteristicas Principales ......................................................................................................................................... 33 1.14.1. Componentes Del Controlador ................................................................................................................................. 34 1.15.Camara DE RED (IP) ......................................................................................................................................................... 35 1.16.Joystick ................................................................................................................................................................................. 36 CAPÍTULO 3 ................................................................................................................................................................................ 37 DESARROLLO Y DISEÑO ........................................................................................................................................................ 37 3.0. DISEÑO Y CONSTRUCION DEL AUTO EXPLORADOR ............................................................................................. 37 3.1.DISEÑO Y CONSTRUCCIÓN DEL BRAZO ROBOTICO ..................................................................................... 38. 3.1.1. Diseño ............................................................................................................................................................................. 38 3.1.1.1. Dimensiones del diseño ........................................................................................................................................ 38 3.1.1.2 Diseño de la Base................................................................................................................................................... 38 3.1.1.3 Diseño del Hombro. ................................................................................................................................................ 39 3.1.1.4 Diseño del Eslabón 0. ............................................................................................................................................. 40 3.1.1.5 Diseño del Eslabón 1. ............................................................................................................................................. 40 3.1.1.6 Diseño de la Pinza. ................................................................................................................................................. 41.

(6) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. 3.2. Construcción...................................................................................................................................................................... 41 3.2.1. Materiales necesarios para la construcción .......................................................................................................... 41 3.2.2 Herramienta necesaria para la construcción. ......................................................................................................... 42 3.2.3 Construcción de la Base............................................................................................................................................ 42 3.2.4 Construcción del Hombro ......................................................................................................................................... 43 3.2.5 Construcción del Eslabón 0 ...................................................................................................................................... 44 3.2.6 Construcción del Eslabón 1 ....................................................................................................................................... 45 3.2.7 Construcción de la Pinza ........................................................................................................................................... 46 3.3 Ensamble ............................................................................................................................................................................ 47 3.3.1 Base – Hombro ........................................................................................................................................................... 47 3.3.2 Hombro – Eslabón 0 ................................................................................................................................................... 48 3.3.3 Eslabón 0 – Eslabón 1................................................................................................................................................ 49 3.3.4 Eslabón 1 – Pinza ....................................................................................................................................................... 50 3.4 Presentación Del Brazo Robóttico ................................................................................................................................... 51 CAPÍTULO 4 ................................................................................................................................................................................ 52 MODELO CINEMATICO DEL MANIPULADOR ROBOTICO ............................................................................................... 52. 4.1 Herramienta De MATLAB/ SIMULINK “HEMERO” .................................................................................................... 52 4.2 Planteamiento Del Problema ........................................................................................................................................... 52 4.3 Obtención De La Cinemática De Directa ........................................................................................................................ 54 4.5 Comunicación ..................................................................................................................................................................... 70 CAPÍTULO 5 ................................................................................................................................................................................ 71 SIMULACION Y PRUEBAS ....................................................................................................................................................... 71.

(7) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA.

(8) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. OBJETIVO GENERAL. Desarrollo de una herramienta que facilite el mantenimiento e inspección de áreas de trabajo donde la vida del trabajador se ve comprometida, para esta labor diseñaremos un prototipo electrónico que será un móvil que lleve consigo un brazo mecánico para que realice dicha acción, esto se controlara a través de una comunicación inalámbrica.. OBJETIVOS PARTICULARES. Obtener un diseño mecánico, electrónico y de software que nos permita explorar el área de trabajo y así mismo poder manipular el prototipo. Lograr una comunicación inalámbrica para controlar el mismo desde una computadora a distancia, así como la transferencia de datos para ala manipulación del mismo. Así mismo se adaptara el controlador polulo mini maestro, para el buen manejo del brazo mecánico.. 1.

(9) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. JUSTIFICACIÓN. Este trabajo se hará desarrollando un prototipo como base para una gran variedad de aplicaciones, estas aplicaciones pueden estar en las áreas de exploración, seguridad e incluso militar, etc. En la Industria puede haber áreas nocivas para el personal que labora ahí, si este es el caso con este prototipo, haciéndole las adecuaciones necesarias, se podría monitorear la atmósfera esto implicaría la instalación de sensores y la información de los sensores se enviaría por medio de la comunicación inalámbrica ya existente e incluso tomar muestras con su brazo mecánico. Para el caso de desastres con el móvil con dimensiones adecuadas podría explorar áreas de riesgo, como puede ser derrumbes, posibles explosiones e incendios y también se le pueden implementar diferentes tipos de sensores dependiendo del interés en ese momento, que también esa información puede enviarse por medio de su transmisión inalámbrica.. 2.

(10) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. PLANTEAMIENTO DEL PROBLEMA. El ser humano en muchas ocasiones se encuentra limitado para realizar tareas, operaciones, aplicaciones o procesos en los que se ve comprometida su seguridad; por ello se necesita crear dispositivos robóticos que puedan realizar dichas tareas. El desarrollo de este proyecto tiene como fin mostrar las bases para la solución de un problema planteado anteriormente. Problema común, pero al que siempre se han encontrado soluciones más sencillas y menos cómodas. Cuando un médico no puede llegar a una cirugía, lo que se hace es reprogramarla o que alguien más la lleve a cabo. Lo que aquí se plantea, es que se puede llevar a cabo esa actividad sin la necesidad de causar más problemas, es decir realizar la actividad vía remota. Para lograr este objetivo se necesitaron de muchos conocimientos en diferentes áreas, como lo es el buen manejo y conocimiento de un software, la electrónica (hardware); la manipulación de una computadora para que se lograran los fines, la operación adecuada de circuitos y elementos electrónicos necesarios para el desarrollo y también, por qué no decirlo, un aprendizaje en la aplicación de algunos de los dispositivos ocupados.. 3.

(11) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. CAPÍTULO. 1. INTRODUCCIÓN El desarrollo de este proyecto es un esfuerzo por obtener la solución a problemas en los que personas de importancia o que llevan a cabo actividades de prioridad no puedan realizar su trabajo por el problema distancia. Para poder desarrollar esto, se tuvo que contar con una gran cantidad de conocimientos tanto teóricos como prácticos en el área de la electrónica y la computación, pues la mayor parte de las herramientas empleadas fueron dispositivos programables que al mismo tiempo debían ser parte de un circuito eléctrico. Aun cuando los circuitos diseñados no fueron de gran dificultad, se necesitaron bastantes conocimientos, tanto en micro controlador, transistores y relevadores. En este trabajo pretendemos hacer la relación de las distintas áreas de la electrónica, por esta razón se decidió hacer un móvil que relacionara e interactuara con los conceptos de electrónica analógica, digital, comunicaciones, computación y por supuesto control, por lo tanto se decidió que hay que implementarlo con un móvil que tenga tracción trasera y se pudiera controlar su desplazamiento y posición, para hacer esto es necesario controlar su trayectoria a distancia y la única forma es mediante comunicación inalámbrica, también se piensa saber donde está ubicado o por donde se desplaza y para esto se decidió implementar una cámara web que transmitiera la imagen para saber por dónde se desplaza, estas imágenes serian enviadas 4.

(12) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. por el mismo protocolo de comunicación, se desea también utilizar un brazo mecánico, para que al localizar un objeto con la cámara, si es de las dimensiones adecuadas pudiera ser tomado por el brazo. Para poder desarrollarlo debemos hacer un análisis de lo necesario para llevar a cabo su funcionamiento, lo primero es como hacer para mover el móvil, necesitamos motores y que estos motores tengan movimiento en el sentido de las manecillas del reloj y en sentido contrario a las manecillas del reloj, elegimos por motores de corriente continua y la mejor forma de controlarlo será usando la técnica de control de motores en función de lo que conocemos como puente H. En el brazo mecánico también necesitamos motores, pero aquí el movimiento debe ser más preciso y controlado en su desplazamiento, la opción es utilizar servomotores, pero estos necesitan ser manipulados con una técnica conocida como control de ancho de pulso que nos permite tener un buen control de desplazamiento de cada una de las partes del brazo mecánico. Se utilizara una computadora como terminal remota mediante esta se enviara la información hacia el prototipo, había dos opciones de desarrollar el programa para generar las pantallas y desde ahí manipularlo o utilizar un software comercial; la decisión fue un software comercial y utilizaremos MatLab que es para instrumentación virtual, en donde de manera sencilla y rápida se pueden implementar los instrumentos virtuales necesarios para el control de motores ya que su programación es grafica se implementara un ventana y se programara también el teclado para que funcionen los comandos para cada uno de los motores, con respecto a la comunicación inalámbrica se utilizara un acces point y se le dará una IP fija para que se pueda controlar por internet la pc. Es por eso, que en capitulo 1, se plantearán los conocimientos teóricos que fueron necesarios para poder llevar a cabo éste trabajo. Se abordarán temas desde definiciones y conceptos básicos de control, robótica y comunicaciones. Así como características generales de los dispositivos empleados para el desarrollo del prototipo y su buen funcionamiento. En los capítulos posteriores se profundizará en lo desarrollado físicamente, en la solución que nosotros planteamos al problema y la forma en que éste funcionó ante nuestra lógica y pruebas realizadas. En el capítulo 2, dedicado al desarrollo del prototipo, se encontraran todas las especificaciones y generalidades físicas y eléctricas de los dispositivos utilizados durante el proyecto, que son el brazo mecánico, el móvil empleado, el joystick seleccionado, la cámara utilizada, el controlador polulo mini maestro, DAQ. Con respecto al brazo se hablará sobre los servomotores empleados que maneja y la manera de cómo estos se comportan. Sobre el móvil se hablará un poco de los motores de DC que este utiliza. Para el caso del joystick y la cámara se tocaran sus características generales. Del controlador Pololu mini maestro hablaremos de sus. 5.

(13) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. características tanto de hardware y software. Por último hablaremos un poco del software que utilizaremos para el control de posición y así mismo la velocidad del auto que será MATLAB.. CAPÍTULO. 2. MARCO TEÓRICO 1.1 TELEMETRÍA La necesidad de conocer parámetros y mediciones de un proceso el cual se encuentra a una gran distancia, y la prioridad de administrar y controlar dicho proceso fue la razón por la que ha avanzado la tecnología y se ha desarrollado tanto con respecto a la Telemetría. La Telemetría se utiliza en infinidad de campos, tales como la exploración científica con naves tripuladas o no (submarinos, aviones de reconocimiento y satélites), diversos tipos de competición (por ejemplo, Fórmula 1 y MotoGP), o la operación de modelos matemáticos destinados a dar sustento a la operación de embalses.. 6.

(14) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. 1.1.1. Definición. La telemetría es una tecnología que permite la medición remota de magnitudes físicas y el posterior envío de la información hacia el operador del sistema (figura 1.1). Fue desarrollada en 1915, a mediados de la primera guerra mundial, por el alemán Khris Osterhein y el italiano Francesco Di Buonanno para medir a qué distancia se encontraban objetivos de artillería.. Figura2 2.1. Descripción gráfica de la telemetría. La palabra telemetría procede de las palabras griegas τῆλε (tele), que quiere decir a distancia, y la palabra μετρον (metrón), que quiere decir medida. El envío de información hacia el operador en un sistema de telemetría se realiza típicamente mediante comunicación inalámbrica, aunque también se puede realizar por otros medios (teléfono, redes de ordenadores, enlace de fibra óptica, etcétera). Los sistemas de telemetría reciben las instrucciones y los datos necesarios para operar mediante desde el Centro de Control.. 1.1.2. Aplicaciones La telemetría se utiliza en grandes sistemas, tales como naves espaciales, plantas químicas, redes de suministro eléctrico, redes de suministro de gas entre otras empresas de provisión de servicios públicos, debido a que facilita la monitorización automática y el registro de las mediciones, así como el envío de alertas o alarmas al centro de control, con el fin de que el funcionamiento sea seguro y eficiente. Por ejemplo, las agencias espaciales como la NASA, la. 7.

(15) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Q.K, la ESA y otras, utilizan sistemas de telemetría y de telecontrol para operar con naves espaciales y satélites.. 1.2. INTRODUCCIÓN A LA ROBÓTICA El termino robótica, el cual se refiere a una ciencia relacionada con la inteligencia artificial y con la ingeniería mecánica; fue utilizado por primera vez en 1942 por el bioquímico, escritor y divulgador científico norteamericano de origen ruso Isaac Asimov en su novela “Runaround”. La capacidad de las máquinas para comunicar y controlar procesos, dirigir operaciones y cumplir las órdenes, e incluso aprender, llevó al desarrollo de una nueva ciencia: a la cual se le denomino Cibernética, esta palabra fue fundada en la década de 1940 por el matemático norteamericano Norbert Wiener, y la define como la ciencia que estudia la comunicación entre el hombre y la máquina, y entre las propias máquinas. De la mano de la Cibernética se desarrolló la Biónica, que es la ciencia que estudia todos los aspectos relativos a la simulación de actividades humanas y animales por medio de máquinas. Básicamente el área de conocimiento en la que se enmarca la Robótica es la Automática. En la Automática se pueden diferenciar dos componentes claros que son: -Unidad de Control: Dirige las acciones a realizar, debe cumplir ciertos criterios u objetivos del control como la estabilización ante perturbaciones, o la evolución temporal y el comportamiento dinámico óptimo respecto a determinados parámetros de calidad. -Actuador: Este realiza las acciones programadas bajo la supervisión de la unidad de control. Estos dispositivos pueden ir desde los casos más elementales, como accionadores hidráulicos, neumáticos o electromecánicos hasta máquinas más complejas como manipuladores. La coordinación entre ambos componentes mediante el intercambio de información es lo que permite conseguir la realización correcta de las tareas a realizar.. 1.2.1. CLASIFICACIÓN DE LOS ROBOTS MANIPULADORES La potencia del software en el controlador determina la utilidad y flexibilidad del robot dentro de las limitantes del diseño mecánico y la capacidad de los sensores. Los robots han sido clasificados de acuerdo a su generación, a su nivel de inteligencia, a su nivel de control, y por su. 8.

(16) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. nivel de lenguaje de programación. La generación de un robot se determina por el orden histórico de desarrollos en la robótica. Algunas clasificaciones que podemos tener son: 1.- Robots Play-back: Regeneran una secuencia de instrucciones grabadas, como un robot utilizado en recubrimiento por spray o soldadura por arco, comúnmente tienen un control de lazo abierto. 2.- Robots controlados por sensores: Tienen un control en lazo cerrado de movimientos manipulados, y trabajan mediante decisiones basadas en datos obtenidos por sensores. 3.- Robots controlados por visión: Manipulan un objeto, al utilizar información desde un sistema de visión. 4.- Robots controlados adaptablemente: Automáticamente reprogramar sus acciones sobre la base de los datos obtenidos por los sensores. 5.- Robots con inteligencia artificial: Utilizan técnicas de inteligencia artificial para hacer sus propias decisiones y así resolver problemas. De acuerdo a la Asociación Francesa de Robótica Industrial (AFRI) tenemos la siguiente clasificación: Tipo a: Manipulador con control manual o telemando. Tipo b: Manipulador automático con ciclos pre ajustados. Tipo c: Robot programable con trayectoria continúa punto a punto. Tipo d: Robot de adquisición de datos. También pueden ser clasificados mediante los programas en el controlador del robot, y por ello pueden ser agrupados de acuerdo al nivel de control que estos realizan como lo son: 1.-Nivel de inteligencia artificial: donde el programa aceptará un comando el cual lo descompone dentro de una secuencia de comandos de bajo nivel basados en un modelo estratégico de las tareas. 2.- Nivel de modo de control: Aquí los movimientos del sistema son modelados, para lo que se incluye la interacción dinámica entre los diferentes mecanismos, trayectorias planeadas, y los puntos de asignación seleccionados. 3.- Niveles de servosistemas: Los actuadores controlan los parámetros de los mecanismos mediante una retroalimentación interna de los datos obtenidos por los sensores. 9.

(17) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. 4.- Niveles de lenguaje de programación: Al desarrollarse lenguajes de alto nivel, habrá una aplicación más efectiva de los robots para una amplia variedad de tareas. Existen muchos sistemas de programación de robots, y caen dentro de tres clases: 1.- Sistemas guiados: El usuario conduce el robot a través de los movimientos a ser realizados. 2.- Sistemas de programación de nivel-robot: El usuario escribe un programa de computadora al especificar el movimiento y el censado. 3.- Sistemas de programación de nivel-tarea: El usuario especifica la operación por sus acciones sobre los objetos que el robot manipula.. 1.3. ROBÓTICA INDUSTRIAL Un robot industrial es un dispositivo de maniobra destinado a ser utilizado en la industria y dotado de uno o varios brazos, fácilmente programable para cumplir operaciones diversas con varios grados de libertad, la ejecución de trabajos diversos en las diferentes etapas de la producción industrial, ya sea en una posición fija o en movimiento. Básicamente está destinado a sustituir la actividad física del hombre en las tareas repetitivas, monótonas o peligrosas. De igual forma parte del progresivo desarrollo de la automatización industrial, favorecido notablemente por el avance de las técnicas de control por computadora, y contribuye de manera decisiva a la automatización en los procesos de fabricación de series de mediana y pequeña escala.. Algunos tipos de automatización industrial son: Automatización fija: Se utiliza cuando el volumen de producción es bastante, por lo cual se adecua para diseñar equipos especializados para procesar productosos componentes de éstos con alto rendimiento y elevadas tasas de producción. Automatización Programable: Empleada cuando el volumen de producción es relativamente bajo y hay una diversidad de productos a obtener. En este caso, la producción se obtiene por lotes.. 10.

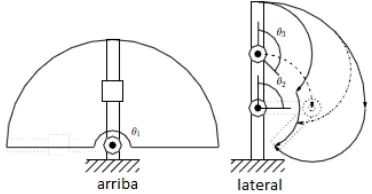
(18) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Automatización Flexible: Es una categoría situada entre las dos anteriores. Es más adecuada para el rango medio de producción. Con este tipo de automatización pueden obtenerse simultáneamente varios tipos de producto, en el mismo sistema de fabricación. La definición anterior es un ejemplo de las muchas definiciones que podemos encontrar provenientes de diversas fuentes, básicamente todas las definiciones de robot industrial son parecidas, a continuación se verán un par de definiciones un poco más formales.. 1.4. SISTEMA COMÚN DE CINEMÁTICA DE MANIPULADORES Existen diversas maneras de usar las articulaciones prismáticas y de revolución en la construcción de las cadenas cinemáticas, en la práctica solo unos pocos son de uso común. A continuación se describen brevemente algunos arreglos los cuales son los más típicos.. 1.4.1. MANIPULADOR A RTICULADO (RRR) El manipulador articulado también llamado de revolución, o manipulador de antropomorfas. El brazo articulado IRB1400 ABB se muestra en la Figura 1.2. y un conjunto de diseño de revolución común es la vinculación paralelogramo.. Figura 2.2.Robot IRB1400 ABB. En este tipo el eje de articulación z2 es paralela a z1 y estos ambos son perpendiculares a z0.Este tipo de manipulador que se conoce como un manipulador de codo. La estructura y terminología asociadas con el manipulador del codo se muestran en la Figura 1.3 y Su área de trabajo se muestra en la Figura 1.4.. 11.

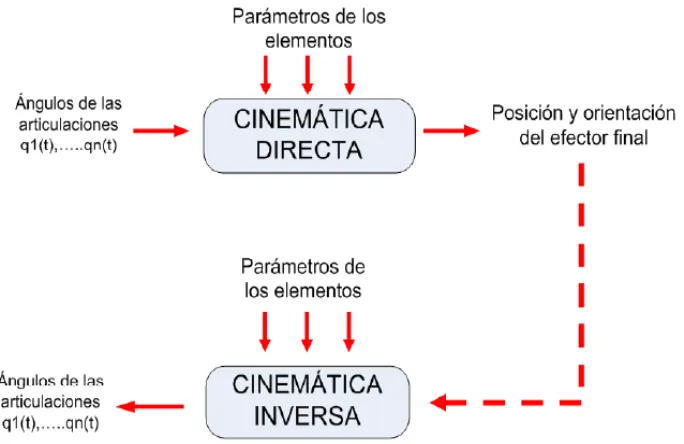
(19) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Figura 2.3 Estructura del Manipulador Codo. Figura 2.4 Área de trabajo del Manipulador Codo. El manipulador de revolución establece la libertad de movimiento relativamente grande en un espacio compacto. La vinculación paralelogramo, tiene varias ventajas que lo convierten en un diseño atractivo y popular. La característica más notable del manipulador de vinculación paralelogramo, es que el actuador para tres conjuntos se encuentra en un solo link. También su dinámica es más simple que la del manipulador de codo, por lo que es más fácil de controlar.. 1.5. CINEMÁTICA DE ROBOTS MANIPULADORES La cinemática del robot estudia el movimiento con respecto a un sistema de referencia sin considerar las fuerzas que intervienen en él. Así, la cinemática se interesa por la descripción analítica del movimiento espacial del robot como una función de tiempo, y en particular de las relaciones entre la posición y la orientación del extremo final de robot con los vectores que toman sus coordenadas articulares. Existen dos problemas fundamentales a resolver en la cinemática del robot; el primero se conoce como el problema cinemática directo o cinemática 12.

(20) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. directa, y consiste en determinar cuál es la posición y orientación del extremo final del robot, con respecto a un sistema de coordenadas que se toma como referencia, conocidos los valores de las articulaciones y los parámetros geométricos e los elementos del robot; el segundo, denominado el problema cinemática inverso o cinemática inversa, resuelve la configuración angular que debe adoptar el robot para una posición y orientación del extremo conocidas. Denavit-Hatenberg propusieron un método sistemático para describir y representar la geometría espacial de los elementos de una cadena cinemática, y en particular de un robot, con respecto a un sistema de referencia fijo. Este método utiliza una matriz de transformación homogénea para describir la relación espacial entre dos elementos rígidos adyacentes, reduciéndose el problema cinemática directo a encontrar una matriz de transformación homogénea 4x4 que relacione la localización espacial del extremo del robot con respecto al sistema de coordenadas de su base. Por otra parte, la cinemática trata de también encontrar las relaciones entre las velocidades del movimiento de articulaciones y las del extremo. Esta relación viene dada por el método diferencial expresado mediante la matriz jacobiana.. Figura 2.5 cinemática directa y cinemática inversa. 13.

(21) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. 1.6. DESCRIPCIONES ESPACIALES Y TRANSFORMACIONES 1.6.1. FORMULACIÓN MATRICIAL DE LAS TRANSFORMACIONES Un robot está diseñado para manipular piezas y realizar operaciones diversas, dentro de una determinada región de trabajo. Esta manipulación se reduce a giros y traslaciones realizados en el espacio tridimensional; además, el robot puede estar dotado de una visión, en cuyo caso debe de ser capaz de reconocer una misma pieza a diferentes distancias y en distintas posiciones. El enfoque matricial de estos problemas presenta grandes ventajas, puesto que las transformaciones de giro, traslación, cambio de ejes, etc., se plantean mediante el producto matriz y un vector, con lo que se obtiene una formulación muy sencilla. Además, es muy importante que estas transformaciones vengan definidas por un producto, ya que de este modo, se pueden aplicar transformaciones sucesivas sobre un mismo objeto, de forma que el conjunto de todas ellas pueda considerarse, a su vez, como una nueva transformación.. 1.6.1.1 MATRIZ DE TRASLACIÓN Sea un sólido rígido en un espacio tridimensional; un punto P del mismo vendrá definido por tres coordenadas (x,y,z), que agrupamos en un vector X1, tal que: EC. 2.1. Una traslación vendrá definida por un vector D, de modo que, si se aplica a un sólido, el punto de posición X1 pasara a ocupar una nueva X2 definida por: EC. 2.2 O de forma desarrollada: EC. 2.3 De esta forma, la matriz de transformación de traslación se representa, de forma muy sencilla, como suma de dos vectores; sin embargo, no es posible encontrar una matriz de orden 3x3 que represente las traslación pero existe una matriz 4x4, de forma que:. 14.

(22) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. EC. 2.4. La figura 1.17 muestra la traslación de un cuerpo rígido que representa la ecuación 2.4.. Figura 1.17 Ejes que representan un sólido rígido que se traslada de una posición a otra O en notación compacta: EC. 2.5. Donde [Td] es la “matriz de transformación”. En la expresión anterior se ha añadido un cuarto elemento al vector de coordenadas X. Este modo de representar un vector se denomina de “coordenadas homogéneas”. EC. 2.6. 1.6.1.2 MATRIZ DE ROTACIÓN Las ecuaciones de rotación en dos dimensiones se describen a continuación:. EC. 2.7 Que, en forma matricial utilizando coordenadas homogéneas es: EC. 2.8. 15.

(23) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Que en notación compacta es representada por: EC. 2.9 En el caso de tres dimensiones, el problema es más complejo; el procedimiento a seguir depende de la forma en que la rotación venga definida. Cuando esta está determinada por tres rotaciones θ, φ, alrededor de los ejes z,y,x respectivamente, cada una de ellas representadas por matrices: EC. 2.10. EC. 2.11. EC. 2.12 La rotación total se calcula mediante el producto matricial: EC. 2.13 Es preciso observar que el producto de las tres matrices no tiene la propiedad conmutativa. Por tanto esta última ecuación permite encontrar la matriz rotación en tres dimensiones calculables. Un ejemplo de la rotación tridimensional de un cuerpo rígido o eslabón se muestra en la figura 1.6.. 16.

(24) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Figura 2.6 Rotación de un sólido rígido en un espacio tridimensional. 1.7.CINEMATICA DIRECTA La resolución de la cinemática directa permite conocer cuál es la posición y orientación que adopta el extremo del robot cuando cada una de las variables, que fijan la posición u orientación de sus articulaciones, toma valores determinados. El modelo cinemática directo es el problema geométrico que calcula la posición y orientación del efector final del robot dados una serie de ángulos entre las articulaciones con respecto al marco referencial de la base del manipulador. Para esto es necesario conocer los valores de las articulaciones y los parámetros geométricos de los elementos del robot. Dado que son las variables articulares las que pueden ser leídas directamente de los correspondientes sensores por la unidad de control del robot, el modelo cinemática directo será utilizado para representar al investigador información relativa a la localización del extremo del robot.. 1.7.1. RESOLUCIÓN DE CINEMÁTICA DIRECTA A TRAVÉS DE MATRICES DE TRANSFORMACIÓN HOMOGÉNEAS Utiliza fundamentalmente el algebra vectorial y matricial para representar y describir la localización de un objeto en el espacio tridimensional con respecto a un sistema de referencia fijo. Dado que un robot es considerado como una cadena cinemática formada por eslabones unidos entre sí por articulaciones, se puede establecer un sistema de referencia fijo situado en la base del robot y describir la localización de cada uno de los eslabones con respecto a dicho sistema de referencia. De esta forma, el problema cinemática directo se reduce a encontrar una matriz de transformación homogénea T que relacione la posición y la orientación del extremo del robot respecto del sistema de referencia fijo situado en la base del mismo. La matriz de transformación homogénea que representa la posición y orientación relativa entre los sistemas asociados a dos eslabones consecutivos del robot se suele denominar matriz i1 Ai, así pues, 0A1 describe la posición y orientación del sistema de referencia solidario a la base, 1 ª2 describe la posición y orientación del segundo eslabón respecto al primero, etc. Del mismo modo, denominando 0Ak a las matrices resultantes del producto de las matrices i-1ª1 con i desde 1 hasta k, se puede representa de forma total o parcial la cadena cinemática que forma el robot. 17.

(25) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Así, por ejemplo, la posición y orientación del sistema solidario con el segundo eslabón del robot con respecto al sistema de coordenadas de la base se puede expresar mediante la matriz 0 A2: 0. A2=0A11A2. EC. 2.14. La ecuación 3.14 describe la posición y orientación del sistema solidario con el segundo eslabón. De manera analógica, la matriz 0A3 representa la localización del sistema del tercer eslabón. 0. A3= 0A11A 22A3. EC. 2.15. La matriz de transformación homogénea resultante corresponde a la localización en la que se desea posicionar al robot. De esta igualdad se obtiene la solución al problema cinemática directo.. 1.7.2. Algoritmo De Denavit-Hatenberg Para La Obtención Del Modelo Cinemático Directo En 1955 Denavit-Haterbeg proponen un método matricial que establece la localización que debe toma cada sistema de coordenadas {Si} ligado a cada eslabón i de una cadena articulada, para poder sistematizar la obtención de las ecuaciones cinemáticas de la cadena completa. Aplicando esta metodología será posible pasar de un eslabón al siguiente mediante cuatro transformaciones básicas que depende exclusivamente de las características geométricas del eslabón. Las cuatro transformaciones básicas consisten en una sucesión de rotaciones y traslaciones que permiten relacionar el sistema de referencia del elemento i-1 con el sistema del elemento i. Es importante recordar que el paso del sistema {Si-1} al {Si} mediante estas 4 transformaciones está garantizado solo si los sistemas han sido definidos de a cuerdo a las siguientes normas: 1. El eje X es perpendicular al eje Z0 2. El eje X1 interseca al eje Z0 Las transformaciones en cuestión son las siguientes: 1. Rotación alrededor del eje Zi-1un ángulo θi. 2. Traslación a lo largo de Zi-1 una distancia di; vector di(0,0, di). 3. Traslación a lo largo de Xi una distancia ai; vector ai (ai, 0, 0). 18.

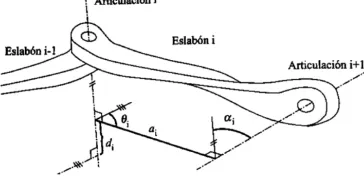
(26) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. 4. Rotación alrededor del eje Xi un ángulo αi. Estas 4 transformaciones se refieren al sistema móvil del robot y están expresadas en la figura 1.19. Ya que el producto de matrices no es conmutativo, las transformaciones se deben realizar en el orden indicado, como una norma general:. i-1. EC. 2.16. La ecuación 2.16 muestra la Transformación de matrices para los algoritmos de DH, y como resultado de producto de matrices se obtiene que: i-1. i-1. EC 2.17. La ecuación 2.17 muestra el resultado del producto de matrices en el algoritmo de D-H, donde θi, di, ai, αi son los parámetros D-H del eslabón i. De este modo, basta con identificar los parámetros θi, di, ai, αi para poder obtener las matrices i-1 y relacionar así todos y cada uno de los eslabone del robot.. 1.7.2.1. Parámetros de DENAVIT-HATENBEG Los cuatro parámetros de D-H (θi, di, ai, αi) dependen únicamente de las características geométricas de cada eslabón y de las articulaciones que le unen con el anterior y el siguiente. Parámetros relativos al tamaño y forma del eslabón: ai: Es la distancia entre los ejes i e i+1 de las articulaciones a lo largo de la normal común. Este parámetro define la longitud del eslabónαi: Es el ángulo que existiría entre los ejes i e i+1 de las articulaciones si estos se cortasen en los puntos de corte de la línea normal común. Este parámetro en cierto modo mide la. 19.

(27) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. forma del eslabón a través del ángulo que sobre el mismo se encuentra girado, por lo que se le conoce ángulo de torsión del eslabón. Parámetros relativos a un eslabón y su predecesor di: Es la distancia entre las intersecciones de las normales comunes al eje de la articulación i, medida a lo largo de dicho eje. Esta medida expresa en cierto modo de la distancia entre los dos eslabones, marcados por el tamaño y forma de la articulación, por lo que se denomina longitud articular.. Figura 2.7 Parámetros Denavit-Haterbeg para una articulación prismática θi: Es el ángulo que existiría entre las intersecciones de las normales comunes al eje de la articulación i si s cortasen en el mismo punto del eje de la articulación. De alguna forma expresa el ángulo que forman dos eslabones, marcado nuevamente por la forma de la articulación, por lo que se denomina ángulo articular.. Figura 2.8 Parámetros Denavit-Haterbeg para una articulación rotatoria. 1.8.CINEMATICA INVERSA. 20.

(28) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. El objetivo de la solución de la cinemática inversa consiste en encontrar los valores que deben adoptar las coordenadas articulares del robot q=[q1,q2,…,qn]T para que su extremo se posicione y oriente según determinada localización espacial (p,[n,o,a]). Dada la posición y orientación del efector final del robot, el problema cinemática consiste en calcular todos los posibles conjuntos de ángulos entre las articulaciones que podrían usarse para obtener la posición y orientación deseada. La obtención de las ecuaciones que rigen la cinemática inversa son fuertemente dependientes de la configuración del robot. El problema cinemática inverso es más complicado que la cinemática directa ya que las ecuaciones no son lineales, sus soluciones no son siempre fáciles e incluso posibles en una forma cerrada. También surge la existencia de una o diversas soluciones. La existencia o no de la solución define el espacio de trabajo de un robot dado. La ausencia de una solución significa que el robot no puede alcanzar la posición y orientación deseada porque se encuentra fuera del espacio de trabajo del robot o fuera de los rangos permisibles de cada una de las articulaciones. A la hora de resolver el problema cinemática inverso es mucho más adecuado encontrar una solución cerrada. Esto es, encontrar una relación matemática explícita de la forma: EC. 2.18. 1.9.INTRODUCCIÓN AL CONTROL. El control automático es la rama de la ingeniería que juega un papel fundamental en los procesos de manufactura e industriales modernos. El control se ha vuelto esencial en operaciones dentro de las industrias de procesos, esto debido a que el control automático brinda un medio para lograr el funcionamiento óptimo de sistemas dinámicos, mejorar la calidad y hacer más baratos los costos de producción, expandir el ritmo de producción, liberar la complejidad de algunas rutinas y tareas manuales repetitivas.. 1.9.1. DEFINICIONES 1.9.1.1. PROCESOS. 21.

(29) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Se define como una operación o desarrollo natural, progresivamente continuo, caracterizado por una serie de cambios graduales que llegan a determinado resultado final; o una operación artificial o voluntaria, progresivamente continua que consiste en una serie de acciones controladas o movimientos dirigidos sistemáticamente hacia determinado resultado.. 1.9.1.2. PLANTAS Una planta es un proceso que se va a modelar y posteriormente a controlar, cuyo objetivo es realizar una operación determinada. Se le denomina planta a cualquier objeto físico que ha de ser controlado.. 1.9.1.3. Sistemas Un sistema es una combinación de componentes que actúan juntos y realizan un objetivo determinado. Un sistema no necesariamente es físico. El concepto de sistema se aplica a fenómenos abstractos y dinámicos, por ejemplo en la rama de economía. Por lo tanto, la palabra sistema debe interpretarse como una implicación de sistemas físicos, biológicos, económicos y similares.. 1.9.1.4. CONTROL RETROALIMENTADO Se refiere a una operación que, en presencia de perturbaciones, tiende a reducir la diferencia entre la salida de un sistema y alguna entrada de referencia y lo continúa haciendo con base en esta diferencia. Lo anterior solo tiene que ver con las perturbaciones impredecibles, ya que las perturbaciones predecibles o conocidas siempre pueden compensarse dentro del sistema.. 1.9.1.5 SISTEMAS DE CONTROL RETROALIMENTADO Es aquel que tiende a tener una relación preestablecida entre la salida y la entrada de referencia, comparando ambas y utilizando la diferencia como parámetro de control. Es de notar que los sistemas de control realimentado no están limitados al campo de ingeniería, sino que se pueden encontrar en campos ajenos a la misma, por ejemplo la biología y economía.. 1.9.2. CONTROL DE LAZO CERRADO Y LAZO A BIERTO 22.

(30) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. A continuación se definirán ambos tipos de control para analizarlos a detalle y comprarlos entre sí.. 1.9.2.1 SISTEMAS DE CONTROL DE LAZO CERRADO Un sistema de control de lazo cerrado es en el cual la señal de salida tiene efecto directo sobre la acción de control como indica la figura 1.9.. Figura 2.9 Diagrama de bloques de un sistema de control retroalimentado La señal de error actuante, que es la diferencia entre la señal de entrada y la señal retroalimentada, entra al detector o control a manera de reducir el error y llevar la salida del sistema al valor deseado. En otras palabras, el término “lazo cerrado” implica el uso de acción de retroalimentación para reducir el error del sistema.. 1.9.2.2. SISTEMAS DE CONTROL EN LAZO ABIERTO Se les denomina sistemas de control en lazo abierto a aquellos sistemas en los cuales la salida no afecta la acción de control. En otras palabras, en un sistema de control en lazo abierto no se mide la salida ni se realimenta para compararla con la entrada.. Figura 2.10 Diagrama de bloques de un sistema de control en lazo abierto En cualquier sistema de control en lazo abierto, la salida no se compara con la entrada de referencia, por tanto, a cada entrada de referencia le corresponde una condición operativa fija, como resultado, la precisión del sistema depende de la calibración. Ante la presencia de perturbaciones, un sistema de control en lazo abierto no realiza la tarea deseada. En la práctica, el control, el control en lazo abierto solo se usa si se conoce la relación entre la entrada y la. 23.

(31) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. salida y si no hay perturbaciones internas ni externas. Es evidente que estos sistemas no son de control realimentado.. 1.10.MODELOS MATEMÁTICOS DE SISTEMAS FÍSICOS Una herramienta indispensable para poder controlar un sistema es la representación que el mismo tiene en forma matemática, siendo específicos, podemos decir que muchos sistemas ya sean mecánicos, eléctricos, hidráulicos, etc. Pueden ser caracterizados por ecuaciones diferenciales. Se puede obtener la respuesta de un sistema dinámico a una entrada, si se resuelven estas ecuaciones diferenciales. Para obtener las ecuaciones se utilizan las leyes físicas que gobiernan un sistema en particular, por ejemplo las leyes de Newton para sistemas mecánicos, las leyes de Kirchhoff para sistemas eléctricos, etc.. 1.10.1.MODELOS MATEMÁTICOS La descripción matemática de las características dinámicas de un sistema se denomina modelo matemático. El primer paso en el análisis de un sistema dinámico, es elaborar su modelo. Hay que tener presente siempre que desarrollar un modelo matemático es la parte más importante de todo el análisis. Los modelos pueden tener muchas formas distintas. Según el sistema particular que se trate y las circunstancias, una representación matemática puede ser más adecuada que otras representaciones. Una vez obtenido el modelo matemático de un sistema se puede usar diversas herramientas analíticas y computacionales con el objeto de su adecuado análisis y síntesis.. 1.11. ESTRUCTURA DE UN BRAZO ROBOT INDUSTRIAL Eslabones y articulaciones. 24.

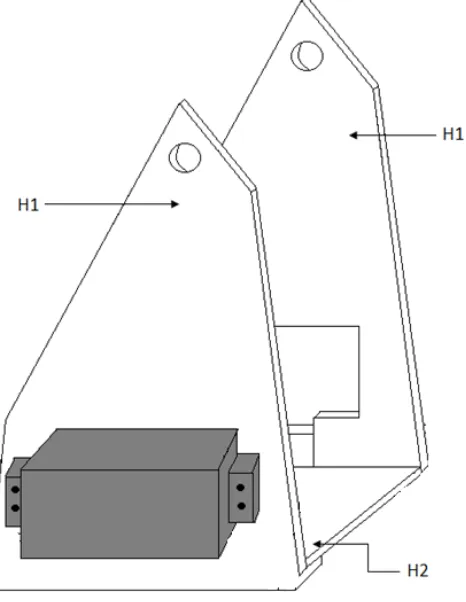
(32) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Reductores Actuadores Sistema sensorial Sistema de control Elementos terminales. Figura 2.11 Estructura del robot. 1.12.CARACTERISTICAS DEL BRAZO ROBOT. 1.12.1. ESLABONES Y ARTICULACIONES Mecánicamente, el robot está formado por una serie de elementos o eslabones unidos mediante articulaciones que permiten un movimiento relativo entre cada dos eslabones consecutivos. En la figura 1.12 se muestran los distintos tipos de articulaciones que disponen los sistemas brazo-robot.. 25.

(33) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Figura 2.12 Distintos tipos de articulaciones para robot El movimiento de cada articulación puede ser de desplazamiento, de giro, o una combinación de ambos. De este modo son posibles seis tipos diferentes de articulaciones, aunque en la práctica, en los robots solo se emplean la de rotación y la prismática.. 1.12.2. REDUCTORES La misión de los reductores es adaptar par y velocidad de salida del actuador para el movimiento de los eslabones del robot y de esta forma dar altas prestaciones a las aplicaciones especificas de los robots. Las características principales de los reductores son: Bajo peso, tamaño y rozamiento Capacidad de reducción elevada en un solo paso Mínimo momento de inercia Mínimo juego de Backslash Alta rigidez torsional. 1.12.3. ACTUADORES Los actuadores son dispositivos inherentemente mecánicos cuya función es proporcionar fuerza para mover o “actuar” otro dispositivo mecánico. La fuerza que provoca el actuador proviene de tres fuentes posibles: Presión neumática, presión hidráulica, y fuerza motriz eléctrica (motor eléctrico o solenoide). Dependiendo de el origen de la fuerza el actuador se denomina “neumático”, “hidráulico” o “eléctrico”.. 26.

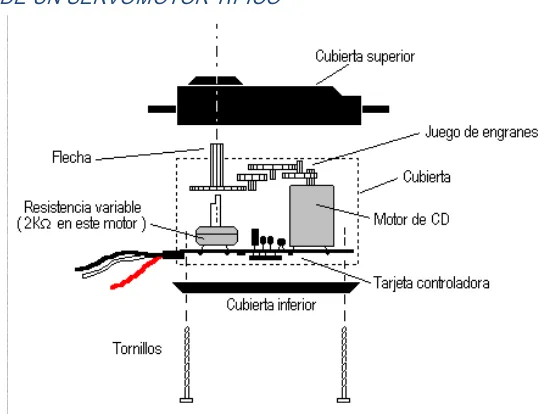
(34) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Los actuadores mas importantes dentro de los robots industriales son los motores, ya que son parte fundamental para el movimiento de estos, a continuación se muestran algunos tipos de motores más utilizados dentro de la robótica.. 1.12.3.1. MOTORES DE CD Un motor de corriente directa es una maquina que convierte energía eléctrica en energía mecánica, esto se logra haciendo pasar corriente a través de los devanados, tanto del rotor como del estator, la cual crea un campo magnético en las caras polares produciendo un par de fuerzas, las cuales por medio de su flecha se convertirá en trabajo mecánico. Las partes principales de un motor son: 1) Rotor: La parte giratoria de un motor 2) Estator: La parte fija del motor 3) Flecha: Éste está unida al rotor y a su vez es el que mueve la carga proporcionalmente a la velocidad del rotor. 4) Escobillas: Son piezas de grafito en contacto al rotor, las cuales sirven para hacer circular corriente eléctrica en los devanados del rotor. En principio hay dos tipos de motores: imán permanente y reluctancia variable, en el primero el movimiento es creado por la interacción de dos campos magneticos uno es producido por un imán se dice que es permanente ya que la corriente aplicada a este es constante y el campo magnético lo podemos considerar fijo y el otro es debido a la corriente que fluye a través de las bobinas del rotor, estos dos campos crean un torque el cual moverá al rotor. Cuando éste este girando la corriente en las bobinas debe ser conmutada para producir una salida de torque. Los motores de reluctancia variable siguen teniendo un rotor y un estator, con la diferencia de que ahora el rotor no es un imán permanente, sino simplemente de material magnético como hierro dulce, además de que es dentado, cuando pasa corriente a través de la bobinas este es atraído, hasta que logra alinearse con los polos del estator minimizando así la reluctancia entre el rotor y el estator, de este tipo son los motores a pasos.. 1.12.3.2. SERVOMOTOR También llamado (Servo) es un dispositivo similar a un motor de corriente continua, que tiene la capacidad de ubicarse en cualquier posición dentro de su rango de operación, y mantenerse gradualmente estable en dicha posición. Está conformado por un motor, una caja reductora y un circuito de control. Los servos se utilizan frecuentemente en sistemas de radio control y en robótica, pero su uso no está limitado a estos. Es posible modificar un servomotor 27.

(35) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. para obtener un motor de corriente continua que, si bien ya no tiene la capacidad de control del servo, conserva la fuerza, velocidad y baja inercia que caracteriza a estos dispositivos. Un servo normal o Standard tiene 3kg por cm. de torque que es bastante fuerte para su tamaño. También potencia proporcional para cargas mecánicas. Un servo, por consiguiente, no consume mucha energía. La corriente que requiere depende del tamaño del servo. Normalmente el fabricante indica cual es la corriente que consume. Eso no significa mucho si todos los servos van a estar moviéndose todo el tiempo. La corriente depende principalmente del par, y puede exceder un amperio si el servo está enclavado. Hay tres tipos de servomotores: -Servomotores de CC -Servomotores de AC -Servomotores de imanes permanentes o Brushless.. 1.12.3.2.1. DIAGRAMA DE UN SERVOMOTOR TÍPICO. Figura 2.13 Estructura del servomotor. 1.12.3.2.2. MOTOR DE CORRIENTE CONTINÚA Es el elemento que le brinda movilidad al servo. Cuando se aplica un potencial a sus dos terminales, este motor gira en un sentido a su velocidad máxima. Si el voltaje aplicado sus dos terminales es inverso, el sentido de giro también se invierte. 28.

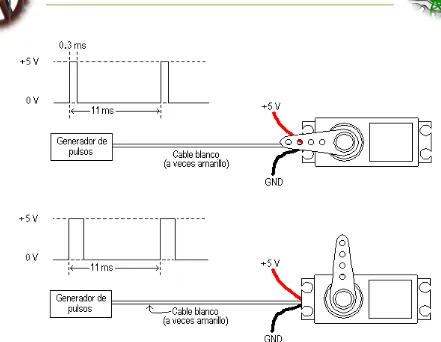
(36) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. -Engranajes reductores Se encargan de convertir gran parte de la velocidad de giro del motor de corriente continua en torque. -Circuito de control Este circuito es el encargado del control de la posición del motor. Recibe los pulsos de entrada y ubica al motor en su nueva posición dependiendo de los pulsos recibidos.. Figura 2.14 Circuito de control del servomotor Tiene además de los circuitos de control un potenciómetro conectado al eje central del motor. Este potenciómetro permite a la circuitería de control, supervisar el ángulo actual del servo motor. Si el eje está en el ángulo correcto, entonces el motor está apagado. Si el circuito checa que el ángulo no es correcto, el motor volverá a la dirección correcta, hasta llegar al ángulo que es correcto. El eje del servo es capaz de llegar alrededor de los 180 grados. Normalmente, en algunos llega a los 210 grados, pero varía según el fabricante. Un servo normal se usa para controlar un movimiento angular de entre 0 y 180 grados. Un servo normal no es mecánicamente capaz de retornar a su lugar, si hay un mayor peso que el sugerido por las especificaciones del fabricante. Los servomotores tienen 3 terminales: . Terminal positivo: Recibe la alimentación del motor (4 a 8 volts) Terminal negativo: Referencia tierra del motor (0 volts) Entrada de señal: Recibe la señal de control del motor. Los colores del cable de cada terminal varían con cada fabricante: el cable del terminal positivo siempre es rojo; el del terminal negativo puede ser marrón o negro; y el del terminal de entrada de señal suele ser de color blanco, naranja o amarillo.. 29.

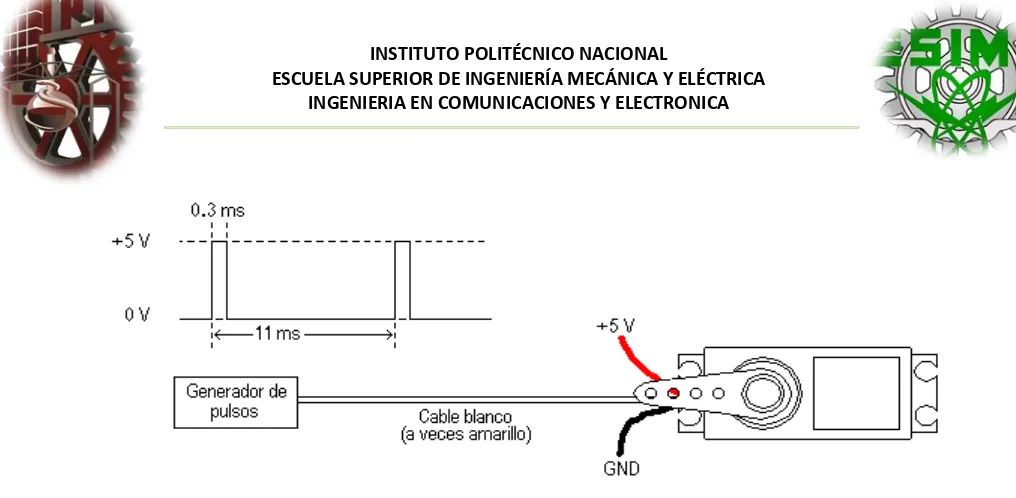
(37) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Figura 2.15 Conexión externa del servomotor. 1.12.3.2.3. FUNCIONAMIENTO El motor del servo tiene algunos circuitos de control y un potenciómetro (una resistencia variable) esta es conectada al eje central del servo motor. Este potenciómetro permite a la circuitería de control, supervisar el ángulo actual del servo motor. Si el eje está en el ángulo correcto, entonces el motor está apagado. Si el circuito chequea que el ángulo no es el correcto, el motor girará en la dirección adecuada hasta llegar al ángulo correcto. El eje del servo es capaz de llegar alrededor de los 180 grados. Normalmente, en algunos llega a los 210 grados, pero varía según el fabricante. Un servo normal se usa para controlar un movimiento angular de entre 0 y 180.. 1.12.3.2.4. CARACTERÍSTICAS GENERALES Y FUNCIONAMIENTO Estos servos tienen un amplificador mecanico, servo motor, piñonearía de reducción y un potenciómetro de realimentación; todo incorporado en el mismo conjunto. Esto es un servo de posición (lo cual significa que uno le indica a qué posición debe ir), con un rango de aproximadamente 180 grados. Ellos tienen tres cables de conexión eléctrica; Vcc, GND, y entrada de control. Para controlar un servo, usted le ordena un cierto ángulo, medido desde 0 grados. Usted le envía una serie de pulsos. En un tiempo ON de pulso indica el ángulo al que debe posicionarse; 1ms = 0 grados, 2.0ms = máx. Grado (cerca de 120) y algún valor entre ellos da un ángulo de salida proporcional. Generalmente se considera que en 1.5ms está el "centro." Entre límites de 1 ~ 2ms son las recomendaciones de los fabricantes, usted normalmente puede usar un rango mayor de 1.5ms para obtener un ángulo mayor e incluso de 2ms para un ángulo de rendimiento de 180 grados o más. El factor limitante es el tope del potenciómetro y los límites mecánicos construidos en el servo.. 30.

(38) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. El tiempo de OFF en el servo no es crítico; puede estar alrededor de los 20ms. Hemos usado entre 10ms y 30 ms. Esto No tiene que ser de ésta manera, puede variar de un pulso a otro. Los pulsos que ocurren frecuentemente en el tiempo de OFF pueden interferir con el sincronismo interno del servo y podría escucharse un sonido de zumbido o alguna vibración en el eje. Si el espacio del pulso es mayor de 50ms (depende del fabricante), entonces el servo podría estar en modo SLEEP entre los pulsos. Entraría a funcionar en pasos pequeños y el rendimiento no sería el óptimo. Figura 2.16 Ejemplo de una señal que debe tener el servo Como se observa en la figura 2.8, la duración del pulso indica o dictamina el ángulo del eje (mostrado como un círculo verde con flecha). Nótese que las ilustraciones y los tiempos reales dependen del fabricante de motor. El principio, sin embargo, es el mismo El cable de control se usa para comunicar el ángulo. El ángulo está determinado por la duración de un pulso que se aplica al alambre de control. A esto se le llama PCM Modulación codificada de Pulsos. El servo espera ver un pulso cada 20 milisegundos (.02 segundos). La longitud del pulso determinará los giros de motor. Un pulso de 1.5 ms., por ejemplo, hará que el motor se torne a la posición de 90 grados (llamado la posición neutra). Si el pulso es menor de 1.5 ms., entonces el motor se acercará a los 0 grados. Si el pulso es mayor de 1.5ms, el eje se acercará a los 180 grados.. Figura 2.17 Duración del pulso que dictamina el ángulo del eje La señal de pulsos controla al servo de la siguiente forma (figura 1.19):. 31.

(39) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. Figura 2.18 señal de pulso que controla al servo. 1.13.DISPOSITIVO DE ADQUISICIÓN DE DATOS (DAQ) NI USB-6008, DAQ Multifunción De Bajo Costo De 12 Bits, 10 kS/s MATLAB ® es una técnica de alto nivel de lenguaje de computación y de entorno interactivo para desarrollo de algoritmos, visualización de datos, análisis de datos y cálculo numérico. El uso del producto MATLAB, puede resolver problemas de computación técnica más rápida que con los lenguajes de programación tradicionales, tales como C, C + + y Fortran. Puede utilizar MATLAB en una amplia gama de aplicaciones, incluyendo señales y procesamiento de imágenes, comunicaciones, diseño de control, de prueba y medición, modelado y análisis financiero, y la biología computacional. Add-on de herramientas (colecciones de funciones 32.

(40) INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA INGENIERIA EN COMUNICACIONES Y ELECTRONICA. especiales de fin de MATLAB, disponible por separado) ampliar el entorno de MATLAB para resolver determinadas clases de problemas en estas áreas de aplicación. MATLAB proporciona una serie de características para documentar y compartir su trabajo. Puede integrar su código de MATLAB con otros lenguajes y aplicaciones, y distribuir sus algoritmos de MATLAB y sus aplicaciones.. 1.13.1 CARACTERÍSTICAS PRINCIPALES Lenguaje de alto nivel para la computación técnica. Entorno de desarrollo para la gestión de código, archivos y datos. Herramientas interactivas para la exploración iterativa, el diseño y la resolución de problemas. Funciones matemáticas para álgebra lineal, estadísticas, análisis de Fourier, filtrado, optimización e integración numérica. 2-D y gráficos 3-D las funciones de visualización de datos. Herramientas para la creación de interfaces personalizadas gráfica de usuario. Funciones para integrar los algoritmos basados en MATLAB con aplicaciones externas, e idiomas, tales como C, C + +, Fortran, Java, COM y Microsoft Excel. El USB-6008 de National Instruments brinda funcionalidad de adquisición de datos básica para aplicaciones como registro de datos simple, medidas portátiles y experimentos académicos de laboratorio. Es accesible para uso de estudiantes, pero lo suficientemente poderoso para aplicaciones de medidas más sofisticadas. Utilice el NI USB-6008 que incluye el software registrador de datos para empezar a tomar medidas básicas en minutos o prográmelo usando LabVIEW o C y el software de servicios de medida NI-DAQmx Base para un sistema de medida personalizado. .. 1.14.CONTROLADOR (POLOLU MINIMAESTRO ) Para controlar todo el proceso que llevara a cabo el explorador, se utilizo el controlador pololu mini maestro, este dispositivo es un pequeño controlador de servomotores, el cual nos da la facilidad también de configurar sus canales como entradas o salidas analógicas o digitales, lo cual nos permitió programar directamente desde este mismo dispositivo los motores de tracción y los diferentes sensores utilizados. Como controlador de servomotores, el minimaestro proporciona una salida de pwm de 2.93 MHz hasta 12 MHz. Este rango de salida de pulso servirá para indicar el ángulo de rotación necesario que realizara el servomotor. 33.