PROCEDIMIENTO DE MUESTREO Y RECONSTRUCCION DE PROCESOS ALEATORIOS DE RAYLEIGH

(1)

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA SECCIÓN DE ESTUDIOS DE POSTGRADO E INVESTIGACIÓN

MAESTRÍA EN CIENCIAS EN INGENIERÍA DE TELECOMUNICACIONES

T E S I S

PROCEDIMIENTO DE MUESTREO Y

RECONSTRUCCIÓN DE PROCESOS

ALEATORIOS DE RAYLEIGH

QUE PARA OBTENER EL GRADO DE MAESTRO EN CIENCIAS EN INGENIERÍA DE TELECOMUNICACIONES

PRESENTA

ING. JAZZIEL OSORIO GARCIA

DIRECTOR DE TESIS

DR. VLADIMIR A. KAZAKOV ERASOVA

MÉXICO,D.F. OCTUBRE 2006

INSTITUTO POLITÉCNICO

(2)

(3)

(4)

Para aquellas personas, cuyo constante soporte y apoyo hacen una

realidad el término de este trabajo:

En primer lugar a mis padres que han sabido crear y mantener mi

inquietud mi ambición y mis sueños.

A mis hermanos, Francisco, Abisai y Mario, quienes me han

apoyado siempre y con quienes he vivido experiencias agradables y un

crecimiento compartido.

A mis compañeros de la Maestría y a todos mis amigos, por

compartir conmigo su tiempo, sus conocimientos y su amistad, ya que son

parte importante que valoro y deseo conservar.

A mis profesores, por compartir sus conocimientos y experiencias, y

de manera especial al Dr. Kazakov por su apoyo y recomendaciones para

este presente trabajo.

(5)

JUSTIFICACIÓN iv

RESUMEN v

ABSTRACT v

CAPÍTULO 1 INTRODUCCIÓN 1.1 ANTECEDENTES 1

1.2 TEOREMA DE BALAKRISHNAN 3

1.3 OBSERVACIONES ACERCA DEL TEOREMA DE BALAKRISHNAN 4

1.4 CASO GENERAL 5

1.4.1 DESCRIPCIÓN DE LOS PROCESOS ALEATORIOS 5

1.4.2 FUNCION DE COVARIANZA 7

1.4.3 DENSIDAD ESPECTRAL DE POTENCIA 9

1.4.4 FUNCIONES QUE CARACTERIZAN A UN SISTEMA LINEAL 9

1.4.5 RESPUESTA DE UN SISTEMA LINEAL A PROCESOS ALEATORIOS 10

CAPÍTULO 2 REGLA DE LA ESPERANZA MATEMÁTICA CONDICIONAL Y SU APLICACIÓN PARA EL PROCEDIMIENTO Y RECONSTRUCCIÓN DE LOS PROCESOS GAUSSIANOS. 2.1 CASO GAUSSIANO 14

2.2 REGLA DE LA ESPERANZA MATEMATICA CONDICIONAL 14

2.2.1 EJEMPLOS GAUSSIANOS MARKOVIANOS UTILIZANDO LA FUNCIÓN DE COVARIANZA R_x

( )

τ

=e−ατ 16

2.2.2 EJEMPLOS GAUSSIANOS NO MARKOVIANOS UTILIZANDO LA FUNCIÓN DE COVARIANZA R_x

( )

τ =

(

1+ατ

)

e−ατ 26

2.2.3 EJEMPLOS GAUSSIANOS NO MARKOVIANOS UTILIZANDO LA FUNCIÓN DE COVARIANZA

( )

τ ατ

( )

ατ _⎟⎟ −ατ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = e R_x 3 1 2 36

2.2.4 EJEMPLOS PARA EL CASO PARTICULAR DE LA FUNCIÓN SENO 46

2.2.5 COMPARACIÓN ENTRE LOS DIFERENTES RESULTADOS DE LAS DIFERENTES FUNCIONES 58

CAPÍTULO 3 LA REGLA DE LA ESPERANZA MATEMÁTICA CONDICIONAL Y SU APLICACIÓN PARA EL PROCEDIMIENTO Y RECONSTRUCCIÓN DE LOS PROCESOS NO GAUSSIANOS. (SIN PROMEDIO Y CON PROMEDIO DE LA MULTITUD DE LOS MUESTREOS) 3.1 INTRODUCCIÓN 62

3.2.1 EXPRESIONES GENERALES PARA EL PMR DEL PROCESO MARKOVIANO DE RAYLEIGH 64

3.2.2 PMR DEL PROCESO MARKOVIANO DE RAYLEIGH EN EL RÉGIMEN DE EXTRAPOLACIÓN. 73

(6)

3.3.1 RECONSTRUCCIÓN DEL PROCESO DE RAYLEIGH NO MARKOVIANO 88

3.3.2 RECONSTRUCCIÓN DEL PROCESO DE RAYLEIGH NO MARKOVIANO CON LA FUNCIÓN Q= +

(

1 ε τ₀

) (

exp −ε τ₀

)

89

3.3.2.2 PMR DEL PROCESO NO MARKOVIANO DE RAYLEIGH EN EL RÉGIMEN DE EXTRAPOLACIÓN. 89

3.3.2.3 PMR DEL PROCESO NO MARKOVIANO DE RAYLEIGH EN EL RÉGIMEN DE INTERPOLACIÓN. 94

3.4 RECONSTRUCCIÓN DEL PROCESO DE RAYLEIGH NO MARKOVIANO CON LA FUNCIÓN.

( )

0 2 0 0 1 3 Q=⎛⎜ +ε τ + ε τ ⎞⎟e−ε τ ⎜ ⎟ ⎝ ⎠ 101

3.4.1 RÉGIMEN DE EXTRAPOLACIÓN 102

3.4.2 RÉGIMEN DE INTERPOLACIÓN 106

CAPíTULO 4 MUESTREO Y RECONSTRUCCIÓN CON JITTER DE LOS PROCESOS DE RAYLEIGH. 4.1 INTRODUCCIÓN 114

4.1.1 POR QUÉ EL ESTUDIO DEL JITTER 114

4.1.2 DEFINICIÓN DE JITTER 114

4.2 EL PMR DEL PROCESO DE RAYLEIGH EN PRESENCIA DE JITTER 115

4.2.1 EL PMR DEL PROCESO MARKOVIANO DE RAYLEIGH EN PRESENCIA DE JITTER PARA EL CASO DE EXTRAPOLACIÓN. 117

4.2.2 EL PMR DEL PROCESO MARKOVIANO DE RAYLEIGH EN PRESENCIA DE JITTER PARA EL CASO DE INTERPOLACIÓN 121

4.2.3 EL PMR DEL PROCESO DE RAYLEIGH CUADO EXISTE LA PRESENCIA DE JITTER EN LAS DOS MUESTRAS 130

CAPÍTULO 5 CONCLUSIONES 136

RECOMENDACIONES 138

ANEXOS A. PROGRAMAS DE SIMULACIÓN 139

B. ARTÍCULOS PRESENTADOS EN CONGRESOS 160

(7)

ij

a

Inverso de la matriz de covarianza

( )

j

B t

Función básica

T

∆

Periodo de muestreo

( )

m

f ⎡_⎣x t ⎤_⎦

Función de densidad de probabilidad de orden m

( )

F t

Función de distribución acumulativa

( )

h t

Respuesta al impulso

( )

H jω

Transformada de fourier del impulso

( )

x

K τ

Función de covarianza

x

K

Matriz de covarianza

( )

m t

Función de esperanza matemática

( )

~

m t

Función de esperanza matemática condicional

N Entero que indica el número total de muestras

Q Función auxiliar empleada como función de covarianza

( )

x

R τ

Función de covarianza normalizada

( )

2

t

σ

Función de varianza matemática

( )

~

t

σ

Función de varianza matemática condicional

t

Tiempo

i

T

Instante de muestreo de la i-enésima muestra

~

T

Función aleatoria de tiempo

τ

Intervalo de tiempo

(

tj −ti

)

, o instante de tiempo donde ocurre una

transición

c

τ

Tiempo de covarianza

( )

u t

Proceso aleatorio de entrada

( )

m t

ω ⎡ ⎤_{⎣ ⎦}

Función de densidad de probabilidad de orden m de un

proceso aleatorio

( )

x t

Proceso aleatorio

( )

~

x t

Proceso aleatorio condicional

( )

i

x T

Valor de una muestra de un proceso aleatorio en un instante de tiempo T_i

Operador del promedio estadístico

i,j,k,m,n Variables enteras

ψi

Distribución del Jitter

(8)

El objetivo de este trabajo es aplicar la teoría estadística de las comunicaciones para describir el Procedimiento de Muestreo – Reconstrucción de Procesos de Rayleigh, con base en la regla de la esperanza matemática condicional.

Llevar acabo el análisis de reconstrucción tomando en cuenta diferentes funciones de covarianza de determinados sistemas para:

• Calcular la función de reconstrucción y la función de error de reconstrucción de los procesos.

• Describir el análisis para el cálculo del error promedio de reconstrucción para los casos de extrapolación e interpolación sin Jitter.

• Describir el análisis para el cálculo del promedio estadístico del error de reconstrucción para los casos de extrapolación e interpolación con Jitter.

Aplicar la programación para calcular y verificar la obtención de los resultados.

JUSTIFICACIÓN

En el teorema de Balakrishnan como generalización del teorema clásico de muestreo para la reconstrucción de los procesos aleatorios, se observa que existen algunas cuestiones al considerar su descripción estadística en el Procedimiento de Muestreo-Reconstrucción, por ejemplo, se detecta que este teorema no utiliza alguna característica estadística importante de algún proceso estocástico, tal como su función de densidad de probabilidad o su función característica (ya sea unidimensional o multidimensional), el teorema es valido sólo para procesos Gaussianos, ya que su comprobación solo está basada en el espectro de potencia.

(9)

teorema clásico de muestreo asociado con los nombres de Whittaker, Kotel’nikov y Shannon (WKS), ha sido demostrado para funciones determinísticas con espectro limitado y la generalización es válida sólo para procesos Gaussianos, ya que las características de los procesos no Gaussianos no son tomadas en cuenta.

En el presente trabajo se ilustran resultados sobre algunos procesos no Gaussianos con el apropiado fundamento estadístico, se utilizan diferentes tipos de funciones de covarianza para poder realizar una comparación y así lograr establecer algunas conclusiones.

Primeramente se estudiará la regla de la esperanza matemática condicional para procesos Gaussianos, enseguida se aplicara regla de la esperanza matemática condicional para procesos no Gaussianos (sin promedio y con promedio), posteriormente se aborda el caso de los procesos no Gaussianos no Markovianos con las mismas distribuciones del capítulo II, y finalmente se estudia el proceso de Rayleigh en presencia de Jitter.

Las funciones de reconstrucción, error de reconstrucción, error promedio de reconstrucción y el promedio estadístico son obtenidos tanto para el caso de extrapolación como para interpolación.

ABSTRACT

In the theory of the communications, a fundamental problem is the reconstruction of stochastic processes with a given set of samples. The classical theorem of sampling associated with the names of Whittaker, Kotel’nikov and Shannon (WKS), that has been demonstrated for deterministic functions with a limited spectrum and the generalization is valid for Gaussian processes only because the principal characteristics of non Gaussian processes are not considered.

In this work is illustrated the results on some non Gaussian processes with suitable statistic fundamentation, is used several types of covariance functions for comparison and establish some conclusions.

First we shall study the conditional mean rule for Gaussian Processes, after that cases it is applied the conditional mean rule for non Gaussian Processes (without mean and with mean), immediately we study the case of the non Gaussian non Markovian processes with the same distributions of the chapter II and finally we consider study the Rayleigh processes in presence of Jitter.

(10)

Un problema fundamental en el campo de la teoría de las comunicaciones es la reconstrucción de los procesos aleatorios a partir de un conjunto de valores de muestreo dados. El presente trabajo se lleva acabo utilizando las propiedades estadísticas de los procesos aleatorios, el cual estará enfocado para Procesos Aleatorios Gaussianos y no Gaussianos, haciendo uso de diferentes tipos de función de covarianza, para posteriormente poder realizar una comparación de los resultados obtenidos. Así mismo cabe mencionar que el estudio de Procesos Aleatorios de Rayleigh es muy importante dado que es usado en modelos de canales con multitrayectoria.

El presente trabajo esta desarrollado de la siguiente manera:

En la primera parte se presenta un bosquejo de como es que se realizaba la reconstrucción de los procesos aleatorios, posteriormente se estudia el teorema clásico y se hace mención de las características estadísticas importantes de los procesos aleatorios que deben ser consideradas en los procesos de reconstrucción.

La segunda parte esta dedicada al estudio de Procedimiento de Muestreo y Reconstrucción de los Procesos aleatorios Gaussianos aplicando la regla de la esperanza matemática condicional, la cual se aplicara para caso Gaussiano Markoviano y caso Gaussiano no Markoviano.

La tercera parte contiene el estudio de los procesos aleatorios de Rayleigh, en la cual se consideran los casos de extrapolación e interpolación, así mismo el cálculo del error promedio de reconstrucción considerando distintas funciones de covarianza.

En la última sección se realiza el estudio de los procesos aleatorios de Rayleigh con presencia de Jitter.

1.1 ANTECEDENTES

La reconstrucción de una señal o de una función que pasa a través de determinados puntos conocidos como muestras, tiene largos antecedentes, en el siglo XVIII Newton comenzó a trabajar en este tema. En un principio se utilizó la propiedad básica que tienen los polinomios algebraicos para determinar un polinomio adecuado P_n

( )

t que nos lleve a los valores y₀,y₁,...,y_n de una función asociados con todas las n+1 abscisas diferentes t₀,t₁,...,t_n.

Este problema fue primeramente respondido por la fórmula de interpolación de Lagrange:

( )

_∑

( )

=

= n

k k k

n t y l t

p

0

(1.1)

donde, k=0,1,2,….,n,

( )

₍

_{) ( )}

( )

k n k

n k

t g t t

t g t

l _'

1 1

+ +

−

(11)

polinomio P_n

( )

t directamente en términos de las muestras.

E.T Whittaker analizó la interpolación entre puntos en su articulo publicado en 1915 [2]. El planteo el problema para encontrar los valores de una función f(t) que pasa a través de ciertos puntos (t_k,f_k), donde t_k =a+kω, f_k = f

( )

t_k , a, ω son complejos y k

∈

Z. donde llamó al conjunto de todas las funciones como conjunto cotabular Z asociado con la secuencia

{ }

f_k de valores conocidos y destacó a una función especial:

( )

(

)

(

)

(

)

∑

∞ −∞

= ₋ ₋

− − +

=

k _t _a _k

k a t sen k a f t

C

ω ω

π

ω ω

π

ω , (1.3)

A la cual él llamó la función cardinal del conjunto cotabular, donde C(t) = f(t).

En 1933 en la Unión Soviética el teorema de muestreo fue presentado por Kotel’nikov [3], y Shannon en 1948 [4,5] utilizó el teorema de muestreo para demostrar que una señal analógica limitada en banda es equivalente a la secuencia de sus muestras tomadas a un intervalo determinado y conocido como el intervalo de Nyquist [6]. El teorema de muestreo de Whittaker – Kotel’nikov- Shannon (WKS) dice:

Toda la función de una señal f(t) definida en RR que está limitada en banda dentro de un _R intervalo [-ω,ω] (donde ω > 0) puede ser completamente reconstruida con respecto a toda t∈RR partiendo de sus valores muestreados f(kR π / ω) que son tomados en los puntos kπ / ω (donde k ∈ZZ igualmente espaciados sobre el eje real _Z RR en términos de: R

∑

(

)

∞

−∞

= −

− ⎟

⎠ ⎞ ⎜ ⎝ ⎛ =

k wt k

k t sen k f t

f

π π ω ω

π

)

( . (1.4)

Cronológicamente en 1947 A.V Balakrishnan generaliza el teorema de muestreo para procesos aleatorios estacionarios [7], en 1960 A. Linden y N. M. Abramson [8] proporcionan una generalización mediante la expansión de las M – derivadas de una función limitada en banda, aproximándola a una serie de Taylor caracterizada con una densidad Gaussiana sobre cada muestra. En 1962 Petersen y D. Middlenton [9] extienden el teorema de muestreo para dimensiones espaciales de mayor orden.

(12)

1.2 TEOREMA DE BALAKRISHNAN

El teorema clásico de muestreo usualmente asociado con los nombres de Whitattaker, Kotel´nikov y Shannon (o teorema WKS) ha sido establecido para funciones determinísticas con espectro limitado. La mayoría de sus generalizaciones están también conectadas con la descripción del Procedimiento de Muestreo – Reconstrucción (PMR) de funciones determinísticas. El teorema de Balakrishnan transfiere el significado del teorema clásico WKS utilizado para funciones determinísticas sobre todos los procesos estocásticos estacionarios con el espectro finito. Esta el la razón, por la que este teorema es llamado a veces el teorema WKS para los procesos estocásticos.

El teorema de Balakrishnan durante algunas décadas y hasta la actualidad ha sido citado muy frecuentemente. Estos hechos ilustran que el teorema de Balakrishnan es ejercido a gran escala. Dada la popularidad de este teorema para la teoría estadística de comunicación, es necesario incluir el texto del mismo [7] para su posterior mención y discusión.

A continuación la formulación del teorema de Balakrishnan:

Sea x(t) -∞ <t<∞ un proceso estocástico evaluado real o complejo, estacionario en el ¨ sentido amplio* ¨ y que posee una densidad espectral, la cual desaparece fuera del intervalo de la frecuencia angular [-2πW,2πW]. Entonces se tiene la representación:

( )

∑

₍

(

₎

)

∞ ∞ − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = n Wt n Wt sen W n x t x 2 2 2 lim π π (1.5)

para cada t, donde lim simboliza el límite en el sentido cuadrático medio.

Más explícitamente, esto significa

( )

₍

(

₎

)

0 2 2 2 lim 2 = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

∑

− ∞ → N N

N _Wt _n

n Wt sen W n x t x E π π (1.6)

Se asume que todos los procesos tienen sus varianzas y sus promedios finitos.

(13)

( )

∑

( )

∞

−∞ =

=

i

i t

T x t

x ( ).

~

ψ (1.7)

donde ( ) ~

t

x es la función de reconstrucción;

ψ_i

( )

t es la función básica determinada por la expresión:

( )

(

)

(

t i T

)

T i t sen t

b b

i ₋ _∆

∆ − =

ω ω

ψ (1.8)

Pero la descripción estadística del Procedimiento de Muestreo-Reconstrucción de los procesos estocásticos basado en el teorema de Balakrishnan deja algunas dudas.

Esto no significa que el teorema de Balakrishnan sea incorrecto, sino que es necesario hacerlo más especifico en cuanto a su formulación, y especificar que es un caso particular del procedimiento general de la descripción estadística del Procedimiento de Muestreo – Reconstrucción de los procesos estocásticos.

Nuestra propuesta es utilizar la regla de la esperanza matemática condicional, demostrando con algunos resultados, que tiene ventajas con respecto a la descripción estadística del PMR de los procesos estocásticos en comparación con la descripción del PMR en base al teorema de Balakrishnan.

1.3 OBSERVACIONES ACERCA DEL TEOREMA DE BALAKRISHNAN

En esta parte se mencionan cuestiones y observaciones sobre el planteamiento del teorema de Balakrishnan, que como se mencionó anteriormente, esto no significa que el teorema de Balakrishnan esté incorrecto, sino que, una de nuestras metas es precisar la formulación de este teorema y especificar su rango de aplicación:

Este teorema no utiliza la principal característica estadística de algún proceso aleatorio – su función de densidad de probabilidad o sus funciones características unidimensional o multidimensional.

¿Por qué la función

x senx

es usada para todo tipo de proceso aleatorio?

Este teorema no contiene alguna característica estadística importante en el tiempo de algún proceso estocástico – sus diferentes momentos, quasi_momentos o funciones cumulantes (en particular una función de covarianza).

No se habla en ningún caso de algún procedimiento de extrapolación, dado que se trabaja con un número infinito de muestras.

Este teorema menciona que la función del error de reconstrucción es igual a cero para todos los procesos estocásticos. Los procesos estocásticos reales no tienen tales características.

(14)

información que nos proporcionan las muestras, las cuales se hacen pasar a través de ciertos filtros lineales con diferentes características. Primero definiremos las propiedades estadísticas de los procesos aleatorios, enseguida definir las características de los procesos aleatorios al pasar por sistemas lineales, ya que para los procesos aleatorios no hay una función explícita como en el caso determinístico, por lo que se debe hacer una descripción de la salida que incluya la función de covarianza y la función de densidad espectral.

El análisis se llevará acabo con filtros pasa bajas, del tipo RC con una, dos y tres etapas. Esto se realizará a cabo tomando en cuenta la influencia que proporciona tanto el número de muestras que se toma en cuenta, como su magnitud o valor, además del intervalo de tiempo que se pone entre muestras, además de cuantificar el error que implica cada reconstrucción.

1.4.1 DESCRIPCIÓN DE LOS PROCESOS ALEATORIOS

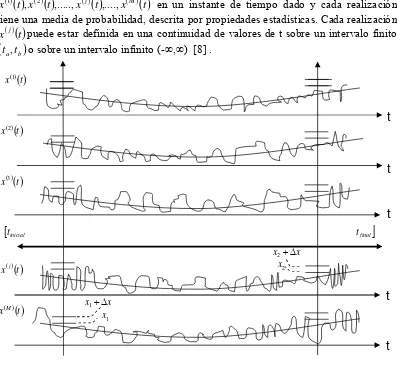
Sabemos que un proceso aleatorio continuo x(t) tiene muchas realizaciones

( )

_{( )}

_t _x( )

_{( )}

_t _x( )

_{( )}

_t _x( )

_{( )}

_t

x1 , 2 ,..., j ,...., M en un instante de tiempo dado y cada realización tiene una media de probabilidad, descrita por propiedades estadísticas. Cada realización

( )

_{( )}

_t

[image:14.612.83.480.318.686.2]

x j _{puede estar definida en una continuidad de valores de t sobre un intervalo finito}

(

ta,tb

)

o sobre un intervalo infinito (-∞,∞) [8] .

Fig. 1.1 Conjunto de posibles realizaciones x( )1

( )

t ,x( )2

( )

t,...,x( )j

( )

t ,....,x( )M

( )

t que puede tener un proceso aleatorio continuo.

( )

_{( )}

_t

x1

( )

_{( )}

_t

x2

( )

_{( )}

_t

x3

( )

_{( )}

_t

xj

( )

_{( )}

_t

xM x1+∆x 1 x

x x₂+∆

2 x

t

(15)

seleccionamos un intervalo

(

x₁,x₁+∆x

)

y posteriormente medimos la probabilidad de x en este intervalo, contando el número de realizaciones correspondientes:

P

(

x₁< x<x₁+∆x;t₁

)

, (1.9) Si tomamos los límites M→∞ y ∆x→dx, obtenemos la probabilidad de x,t está en el intervalo

(

x₁,x₁+∆x

)

P

(

x₁ <x< x₁+∆x;t₁

)

→ω_|₁

[

x₁,t₁

]

dx₁ (1.10) Repitiendo esta operación para cada unidad podemos encontrar la función de densidad de probabilidad deseada en cada intervalo, y también se puede encontrar la densidad de probabilidad que existe en cada instante de tiempo t₁,t₂,...,t_mdentro del intervalo

(

tinicial,tfinal

)

del procesos aleatorio y hallar su función de distribución de probabilidad

(fdp) ω₁

[ ]

x

( )

t . De manera similar podemos continuar con la función de probabilidad de segundo orden ω₂

[

x₁

( ) ( )

t₁ ,x₂ t₂

]

y con las densidades de probabilidad de mayor orden

( ) ( )

( )

[

₁ , ₂ ₂ ,..., _m

]

.

m xt x t xt

ω Es importante tomar en cuenta los tiempos ( t₁,t₂,....,t_n) en que estas probabilidades son calculadas, ya que la estructura actual de las densidades puede ser muy diferente para tiempos distintos, como se muestra en la fig. 1.2

Fig. 1.2 Funciones de densidad de probabilidad de primer orden de un proceso aleatorio en dos instantes de tiempo diferentes.

Conociendo las fdp’s unidimensionales

(

ω₁

[

x

( )

t₁

]

,ω₁

[

x

( )

t₂

]

,...,ω₁

[

x

( )

t_m

]

)

de cada tiempo t₁,t₂,...,t_m es posible obtener alguna información estadística acerca del proceso, tal como la función de la esperanza matemática m

( )

t = x

( )

t en cada instante

m t t

t₁, ₂,..., , así como la función de la varianza matemática 2

( )

(

( ) ( )

)

2

t m t x

t = −

σ y

las funciones de sus momentos iniciales y momentos centrales de orden n, las expresiones en forma continua son las siguientes:

1

t

1

t t2

t

)] [(₁ 1 t

ω

( )

t x

( )

t

m =

)] [(₂ 1 t

(16)

2) Función varianza matemática:

( )

(

( ) ( )

)

∫

(

( ) ( )

)

[ ]

( )

∞

∞ −

− =

−

= xt mt xt mt xt dx

t ω

σ2 2 2 _(1.12)

3) Función momento inicial de orden n:

( )

∫

( ) ( )

[ ]

∞

∞ −

= x t xt dx t

xn n ω (1.13) 4) Función momento central de orden n:

( )

(

( ) ( )

)

∫

(

( ) ( )

)

[ ]

( )

∞

∞ − •

− =

−

= xt mt xt mt xt dx

t

x n nω (1.14)

1.4.2 FUNCION DE COVARIANZA

Es indispensable considerar otra característica de suma importancia estadística que refleja las diferencias de la estructura en el tiempo de los diferentes procesos aleatorios conocida como función de covarianza K_x

( )

t₁,t₂ .que es una función determinística con dos argumentos del tiempo t₁ y t₂, que demuestran cómo el momento de covarianza cambia cuando la distancia entre estas dos secciones cambia también.

( )

( ) ( )

∞

_∫

(

( ) ( )

) ( ) ( )

(

)

[

]

( ) ( )

∞ − •

•

− −

− =

= 1 2 1 1 2 2 2 2 1 1 2

2

1,t xt xt xt mt xt m t x;t t dxt dxt

t

K_x ω (1.15)

donde m(t) es la función de esperanza matemática, ω es la función de densidad de probabilidad.

Fig. 1.3 Función de covarianza K_x

( )

τ que podría tener a) un proceso aleatorio suave o b) un proceso aleatorio caótico.

( )

x t x t

( )

( ) ( )

x x

K τ =K −τ

( )

x x

K τ =K −τ

( )

0

x

K K_x

( )

0

2 1

t t

τ = −

2 1

t t

τ = −

(17)

de covarianza tiende a ser independiente cuando t₁ se aleja de t₂. Si la función de covarianza tiende a cero lentamente es un proceso suave, en cambio cuando la función de covarianza tiende a cero rápidamente, se dice que es un proceso caótico.

Si el proceso es estacionario de segundo orden, la función de covarianza es solo una función de la diferencia del tiempo τ =t₂ −t₁, por lo tanto, la función de covarianza

( )

t1,t2

K_x será representada de la siguiente forma K

( )

τ = K

( )

t₁,t₂ . Algunas propiedades que tiene esta función de covarianza son las siguientes [9]:

a) Tiene valor máximo cuando t₁ = t₂, en donde τ =t₂ −t₁=0: K_x

( )

0 = x

( ) (

t xt+τ

)

= x

( )

t 2 =σ2

( )

t =σ_x2

• •

•

(1.16) b) Es una función par:

K_x

( )

τ =K_x

( )

−τ (1.17) c) Tiende a cero cuando τ →∞:

K_x

( )

∞ =0 (1.18)

d) Existe una función de covarianza normalizada R_x

( )

τ donde:

( )

₀

( )

2

x x

x x x

K K

K R

σ τ τ

τ = = (1.19)

e) Existe una función de covarianza para procesos estacionarios:

K_x

( )

τ =

[

x

( )

t −m_x

]

⋅

[

x

(

t+τ

)

−m_x

]

(1.20)

f) Su rango de valores está contenido en:

K_x

( )

τ ≤K_x

( )

0 por lo tanto: 0≤ R_x

( )

τ ≤1 (1.21)

g) Tiene relación con un parámetro llamado tiempo de covarianza τ_c en función de R_x

( )

τ

∫

( )

∞

=

0

τ τ

τ_c R_x d (1.22)

(18)

Existe otro parámetro muy importante que sugiere caracterizar las propiedades espectrales de los procesos aleatorios con la distribución de potencia de cada armónico en función de la frecuencia. Es claro que esta función espectral debe caracterizar las propiedades espectrales de todas las realizaciones del proceso aleatorio dado. El Teorema de Wiener- Khintchine sugiere que la función de covarianza K_x

( )

τ está relacionada con la función de densidad espectral de potencia S

( )

ω mediante la transformada de Fourier [8, 10]. Para este caso tomamos la función de covarianza como función de autocovarianza.

Teorema de Wiener- Khintchine:

( )

_∫

∞

( )

∞ −

−

= ω ω

π

τ _S _e ω_d

K_x _x j

2 1

, (1.23)

( )

_∫

∞

( )

∞ −

−

= τ τ

ω _K _e ωτ_d

S j

x

x . (1.24)

Se puede escribir que para un proceso suave la densidad espectral de potencia es más estrecha y para un proceso caótico la densidad espectral de potencia es más ancha. Debido a los atributos espectrales de la función de covarianza K_x

( )

τ su transformada de Fourier S_x

( )

ω tiene las siguientes propiedades:

9 Sx

( )

ω siempre es real.

9 S_x

( )

ω ≥0

9 Es una función simétrica S_x

( )

ω =S_x

( )

−ω

1.4.4 FUNCIONES QUE CARACTERIZAN A UN SISTEMA LINEAL

Suponga que u(t) y x(t), como se muestra en la fig. 1.4, son la entrada y la salida, respectivamente, de un sistema lineal con parámetros fijos. Por parámetros fijos entendemos que si u(t) produce la salida x(t), entonces la entrada u

(

t+τ

)

produce la salida x

(

t+τ

)

. Y por lineal entendemos que si u₁

( )

t produce la salida x₁

( )

t , entonces la entrada u

( )

t =a₁u₁

( )

t +a₂u₂

( )

t produce la salida x

( )

t =a₁x₁

( )

t +a₂x₂

( )

t .

Fig. 1.4 Relación entrada salida en un sistema lineal

Sistema Lineal

h(t)

u(t)

U(j

ω

)

H(j

ω

)

x(t)

(19)

( )

jω

U

Por lo tanto, si deseamos encontrar la salida del sistema conociendo como dato la señal de entrada, tenemos:

( )

( ) ( )

( )

( ) ( )

ω ω ω

π ω

ω

ω _U _j _H _j _x_t _U _j _H _j _e ω_d

j

X

∫

j t

∞

∞ −

⋅ =

⇔ =

2 1

(1.26) donde X

( )

jω y U

( )

jω , son las respectivas transformadas de Fourier de la señal de salida y de entrada del sistema. Una entrada de especial interés es el impulso unitario, que tiene una transformada de Fourier igual a la unidad para toda ω

u

( ) ( )

t =δ t ⇔ X

( )

jω =1 (1.27)

En este caso y considerando la expresión (1.26), la transformada de Fourier de la correspondiente salida es:

( )

ω ω

π ω

ω

ω _H _j _H _j _h_t _H _j _e ω_d

j

X j t

∫

∞

∞ −

= ⇔ =

⋅ =

2 1

1 , (1.28)

donde h(t) es conocida como la respuesta al impulso unitario del sistema lineal. La respuesta de un sistema lineal a una entrada transitoria puede ser expresada en términos de la respuesta al impulso unitario del sistema, en lugar de la función de transferencia. Asi tenemos:

( )

∞

_∫

( ) (

)

∞ −

− = hτ u t τ dτ

t

x . (1.29)

O alternativamente se puede expresar, cambiando las variables de la integral de convolución

( )

∞

_∫

( ) (

)

∞ −

− = uτ ht τ dτ

t

x . (1.30)

1.4.5 RESPUESTA DE UN SISTEMA LINEAL A PROCESOS ALEATORIOS Suponga ahora, que en la entrada tenemos un procesos aleatorio del tipo Gaussiano “u(t)”, del que conocemos algunas propiedades; por ejemplo, las funciones de esperanza matemática, varianza y de covarianza son conocidas [11]. Deseamos determinar las propiedades del proceso aleatorio a la salida del sistema lineal. La función de covarianza en la salida está dada por, por definición

( )

( ) ( )

∫

( ) (

)

∫

( ) (

)

∞

∞ −

• ∞

∞ −

• •

•

− −

=

= 1 2 1 1 1 1 2 2 2 2

2

1,t xt xt hτ u t τ dτ hτ u t τ dτ

t

(20)

( )

τ₁ τ₁

( )

τ₂ τ₂

(

₁−τ₁, ₂−τ₂

)

.

=

∫

∞ − ∞

−

t t K d h d

h _u

Si el proceso aleatorio en la entrada es estacionario en el sentido amplio, tenemos K_u

(

t₁−τ₁,t₂ −τ₂

)

=K_u

(

τ −τ₁+τ₂

)

(1.32) donde τ =t₁−t₂. En este caso, la función de covarianza en la salida llega a ser:

( )

∫

( )

∫

( ) (

) ( )

∞

∞ − ∞

∞ −

+ −

= τ1 τ1 τ2 τ τ1 τ2 τ2

τ h d h K d

K_x _u (1.33) El resultado muestra que si el proceso aleatorio en la entrada de un sistema lineal es estacionario en el sentido amplio, entonces el proceso en la salida también lo será.

Ahora la densidad espectral S_x

( )

ω de la salida del sistema será

( )

ω _K

( )

τ _e ωτ_dτ

S j

x

∫

∞

∞ −

−

= (1.34)

donde ω=2πW. Así de la ecuación (1.34), se obtiene:

S

( )

ω h

( )

τ dτ h

( ) ( )

τ dτ K

(

τ τ τ

)

e jωτdτ u

x

− ∞

∞ −

∞

∞ − ∞

∞

−

∫

+ −

= 1 1 2 2 1 2 (1.35)

Introduciendo una nueva variable, donde z=τ −τ₁+τ₂, y al despejar τ =z+τ₁−τ₂. Al sustituir τ en la ecuación (1.35), obtenemos finalmente:

S_x

( )

ω =H

( ) ( )

jω H* jω S_u(jω)= H

( ) ( )

jω 2S_u jω . (1.36)

Es claro en (1.36) que la densidad espectral de potencia en la salida de un sistema lineal, en respuesta a un proceso aleatorio estacionario en el sentido amplio en la entrada, es por consiguiente igual al cuadrado de la magnitud de la función del sistema multiplicado por la densidad espectral de potencia de la entrada del sistema.

Se considerara un ejemplo para determinar la función de densidad espectral S_x

( )

ω y la función de covarianza R_x

( )

τ en la salida de un filtro RC de primer orden cuando éste es alimentado por ruido blanco unitario. Como se muestra en la figura 1.5.

Figura 1.5 Un filtro RC pasa _ bajas de primer orden alimentado con ruido blanco.

R

C

i(t

Filtro RC

u(t)

Ruido

x(t)

H(j

ω

)

( )

1

u

(21)

C j RC j Z ω ω +

=1 ;

( ) ( )

( )

j C RC j t u Z t u t i ω ω + = =

1 ;

( )

C j t u C j t i v ω ω = + ⋅ = 1 1 0 ,

Por lo tanto tenemos

( ) ( )

_{( )}

ω α α ω ω j RC j t u t x j H + = + = = 1 1

donde α =1RC. De aquí que la función espectral de salida según la expresión (1.36) es:

( )

₂ ₂ 2 1 ω α α ω α α ω α α ω + = ⋅ − ⋅ + = j j

S_x (1.37)

Ahora vamos a calcular la función de covarianza normalizada, ya que la mayoría de nuestros posteriores resultados los vamos a obtener con este tipo de funciones. Y además la función de densidad espectral de nuestra función de covarianza normalizada no es la expresión (1.37). Para hacer esto, es necesario considerar la expresión (1.23) multiplicada por un factor C denominado factor de normalización

( )

2 2 2 1 2 j x

R τ C α e ωτdω

π α ω ∞ − −∞ = +

∫

. (1.38)

De la expresión anterior vamos a calcular primeramente a C, igualando a uno la expresión (1.38), ya que es su magnitud máxima cuando τ =0.

(

0

)

1 ₂ ₂ 1

2 = + = =

_∫

∞ ∞ − ω ω α α π

τ C d

R_x

despejando a C tenemos

α α π α π α ω α α π ω ω α α π 2 2 1 2 0 2 0 2 2 2 = ⎥⎦ ⎤ ⎢⎣ ⎡ = ⎥⎦ ⎤ ⎢⎣ ⎡ = + = _∞ _∞

∫

d arctg

C (1.39)

Sustituyendo el valor de C en (1.38) y resolviendo la integral obtenemos finalmente

( )

ωτ ω ατ ω α α π τ ∞ − ∞ − = +

=

_∫

e d e

R_x ₂2 ₂ j

2 1

(1.40)

donde la función de densidad espectral de nuestra función de covarianza es

( )

₂2 ₂

ω α α ω + = x

(22)

Figura 1.6 a) La función de covarianza normalizada R_x

( )

τ y b) la función de densidad espectral S_x

( )

ω en la salida de un filtro RC.

De manera similar podemos calcular la función de covarianza normalizada R_x

( )

τ y la función de densidad espectral S_x

( )

ω de un filtro RC de dos etapas, de un filtro RC de tres etapas y de un filtro ideal para analizar con ellas posteriormente la reconstrucción de un proceso aleatorio al pasar por diferentes tipos de sistemas lineales.

( )

ω

x S

ω

τ

2/α

1 ( )

τ

x R

(23)

APLICACIÓN PARA EL PROCEDIMIENTO Y RECONSTRUCCIÓN DE LOS PROCESOS GAUSSIANOS.

2.1 CASO GAUSSIANO

Para el caso gaussiano: si un proceso aleatorio del tipo Gaussiano u(t) es aplicado a un filtro lineal estable, la salida en el filtro será Gaussiano también; si se considera un conjunto de variables aleatorias o muestras x

( ) ( )

T₁ ,xT₂ ,...,x

( )

T_n , obtenidas al observar un proceso aleatorio x(t) en cada instante de tiempo T₁,T₂,....,T_n. Y si este proceso x(t) es Gaussiano, entonces, este conjunto de variables aleatorias son conjuntamente Gaussianas para cada n, y son descritas completamente por su matriz de covarianza

( )

i j

x T T

K , de orden n. Donde cada elemento de la matriz es:

K_x

( )

T_i,T_j =

(

x

( )

T_i −m_x

( )

T_i

)

(

x

( )

T_j −m_x

( )

T_j

)

i,j,=1,2,3,…,n. (2.1) Si la matriz de covarianza K_x

(

T_i,T_j

)

se llegara a transformar en una matriz diagonal, se tiene que las variables aleatorias son no correlacionadas y por lo tanto, se concluye que las variables aleatorias Gaussianas son independientes. La función de densidad de probabilidad de n dimensiones queda especificada por completo por los momentos de primer y segundo orden ( es decir, por la media, la varianza y covarianza)

[ ]

( )

[

DetK

]

[

(

x m

)

k

(

x m

)

]

t

x T _x

x n

n = ⋅ − − −

−1 2

1 2

1

2 exp(

2 1

π

ω (2.2)

Y, finalmente, si un proceso Gaussiano es estacionario en el sentido amplio, también lo es en el sentido estricto.

2.2 REGLA DE LA ESPERANZA MATEMÁTICA CONDICIONAL

Suponga que se tiene un proceso estocástico x(t) caracterizado por sus funciones de distribución de probabilidad multidimensionales ω_m

[

x

( ) ( )

t₁ ,xt₂ ,....,x

( )

t_m

]

. Y que una realización de este proceso es discretizado en los instantes de tiempo

{

T T TN

}

T = ₁, ₂,...., . Entonces tenemos un conjunto de muestras

{ ( ) ( )

xT xT x

( ) }

TN

T

X, = ₁ , ₂ ,..., , donde el número de muestras N y sus tiempos de ocurrencia T =

{

T₁,T₂,....,T_N

}

son arbitrarios, entonces las funciones momento inicial, central y densidad de probabilidad se ven modificadas. Tales nuevas densidades de probabilidad y funciones son condicionales ó a posteriori.

(24)

( )

( ) ( )

∫

( ) ( )

[

( )

]

∞ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋

= xt mt X T xt mt xt X T dx

t , ω ,

σ (2.5)

La reconstrucción que se obtiene dependerá de las muestras x

( ) ( )

T₁ ,xT₂ ,...,x

( )

T_N y de conocer su función de distribución de probabilidad fdp ω_m

[

x

( ) ( )

t₁ ,xt₂ ,....,x

( )

t_m

]

, donde N<m. Las posibles realizaciones del proceso aleatorio condicional x

( ) ( )

t xt X,T

~

=

pasan a través de las muestras como se observa en la figura 2.1 Cada realización es una entre un número infinito de otras realizaciones del proceso estocástico condicional

( )

t x

~

. No podemos conocer exactamente, pero uno puede estimar esta reconstrucción estadísticamente en un momento de tiempo t. Para hacer esto, es necesario seleccionar la regla estadística apropiada para la función de reconstrucción, después calcular una función de reconstrucción y luego determinar una función de error de esta reconstrucción. En la mayoría de los casos este error no tiene que ser igual a cero.

Figura 2.1 Posibles realizaciones de un proceso aleatorio condicional, dado un conjunto de muestras X,T.

Existe un criterio estadístico conocido para la estimación de una variable aleatoria: la regla de la esperanza matemática condicional, aplicando esta regla podemos usar la función de la esperanza matemática condicional, como función de reconstrucción, y el error de reconstrucción será evaluado por la función de covarianza condicional como función de error de reconstrucción, también podemos incorporar otra característica del Procedimiento de Muestreo- Reconstrucción que es la función de covarianza del proceso reconstruido.

Considerando el caso general de un proceso Gaussiano no estacionario x(t) con la esperanza matemática m(t), la varianza σ2

( )

t y la función de covarianza k_x

( )

τ . Esta es la información completa acerca del proceso dado, debido a que uno puede escribir la expresión exacta de la fdp multidimensional de orden m arbitraria:

( ) ( )

( )

[

]

( )

[

( )

]

( ) ( )

[

]

[

( )

]

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − ⋅ ⋅ − − • =

∑∑

= = − − Tj m T x aij T m t x t t DetK t x t x t x j m i m j i j i x m m m 1 1 1 2 1 2 2 1 2 1 exp , 2 ,..., , π ω

, (2.6) 1

T T₂ T3 T4 TN

( )

t m

~

( )

T1

x x

( )

T2

( )

T3

x

( )

TN x

(25)

( )

(

, 1

)

(

, 2

)

(

,

)

x i j

x n x n x n n

K t t K t t K t t

y a_i_,_j es la inversa de la matriz de covarianza,

a_i_,_j = K_x

( )

t_i,t_j −1 (2.8) Si fijamos el conjunto de muestras X,T =

{ ( ) ( )

xT₁ ,xT₂ ,...,x

( ) }

T_N , entonces la función de distribución de probabilidad condicional será Gaussiana también. Las principales características de este proceso condicional están descritas en las siguientes expresiones y el proceso Gaussiano condicional queda totalmente expresado:

( )

∑∑

( )

[

( ) ( )

]

= = − ⋅ + = N i j j ij N j i x

x t mt K tT a xt mT

m

1 1 ~

, (2.9)

( )

t

( )

t K

( )

t T a K_x

( )

T_j t N i ij N j i

x , ,

1 1 2 2 ~ ⋅ ⋅ − =

∑∑

= = σ

σ (2.10)

(

)

(

)

( )

(

₂

)

1 1 2 1 2 1 ~ , , ,

,t K t t K t T a K T t

t

K _x _j

N i ij N j i x x

x = −

∑∑

⋅ ⋅

= =

(2.11)

Todas las fórmulas de esta sección son válidas para el caso no estacionario y para el conjunto arbitrario de muestras X,T.

2.2.1 EJEMPLOS GAUSSIANOS MARKOVIANOS UTILIZANDO LA FUNCIÓN DE COVARIANZA

R_x

( )

τ

=e−ατ (2.12)

A continuación se muestran algunos ejemplos aplicando la regla de la esperanza matemática en el caso gaussiano, igual al que se obtiene en la salida de un filtro RC integrador lineal cuando la entrada es alimentada con ruido blanco. La respuesta de tal filtro RC está dada por una función de covarianza normalizada del tipo exponencial. Se mostrarán algunos gráficos con un número limitado de muestras, diversos intervalos de muestreo y diversas funciones de correlación normalizadas R_x

( )

τ .

Primero se ilustra el caso para R_x

( )

τ

=e−ατ , esto para llegar a una comparación de resultados se trabajará con funciones normalizadas, con un τ_c =1, que es una característica de la respuesta de un filtro que determina el tiempo de influencia entre los mismos valores de un proceso. Entonces si α =1:

∫

( )

∫

∞ ∞ − ₌ = = 0 0 1 α τ τ τ τ ατ d e d R_x

(26)

Las expresiones de la regla de la esperanza matemática condicional quedan de la siguiente forma:

( )

∑

( )

∑

( )

= =

−

− _⋅

=

= N

j

N

i

ij T t

j e a

T x t

m t

x i

1 1

~

~ _α

, (2.14)

( )

∑∑

( ) ( )

= =

− − −

− _⋅ _⋅

−

= N

i N

j

t T ij T

t i j

e a e

t

1 1 2

~

1 α α

σ . (2.15)

Se Realizaran algunos ejemplos empleando función de covarianza normalizada en el régimen de interpolación; dado que en otros trabajos se ha considerado el caso Gaussiano, solo se tomarán ejemplos de este tipo no tomando en cuenta el régimen de extrapolación ya que el área de interés es el caso no Gaussiano:

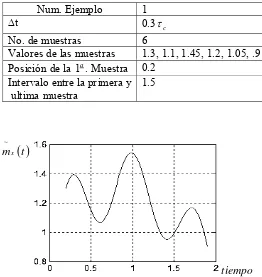
Num. Ejemplo 1

∆t 0.3τ_c

No. de muestras 6

Valores de las muestras 1.3, 1.1, 1.45, 1.2, 1.05, .9 Posición de la 1a. Muestra 0.2

Intervalo entre la primera y ultima muestra

1.5

(27)

Fig. 2.2 Función de error de reconstrucción para el proceso Gaussiano Markoviano con 6 muestras y una función de covarianza R_x

( )

τ

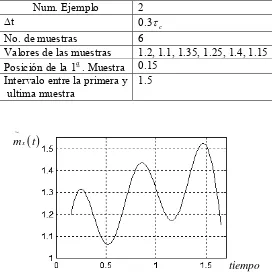
=e−ατ .

Num. Ejemplo 2

∆t 0.3τ_c

No. de muestras 6

Valores de las muestras 1.2, 1.1, 1.35, 1.25, 1.4, 1.15 Posición de la 1a. Muestra 0.15

1.5

(28)

( )

τ

=e−ατ .

Num. Ejemplo 3

∆t 0.3τ_c

No. de muestras 6

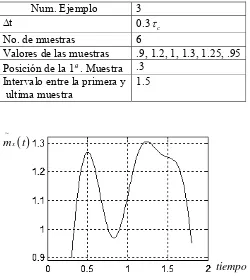
Valores de las muestras .9, 1.2, 1, 1.3, 1.25, .95 Posición de la 1a. Muestra .3

1.5

Fig. 2.5 Función de reconstrucción para el proceso Gaussiano

(29)

( )

τ

=e−ατ .

Num. Ejemplo 4

∆t 0.3τ_c

No. de muestras 6

Valores de las muestras .7, 1, 1.3, .9, .8, 1.1 Posición de la 1a. Muestra .1

1.5

(30)

( )

τ

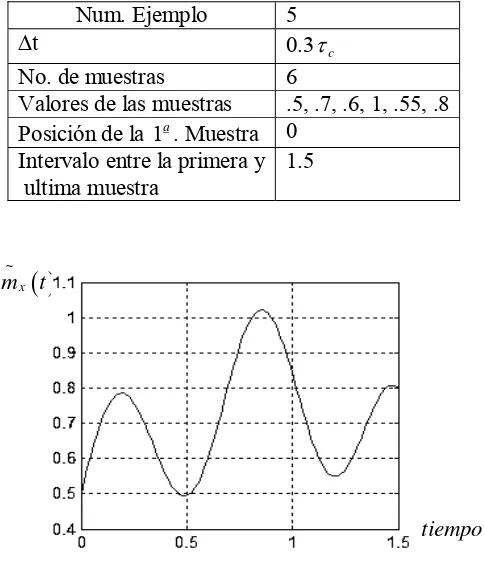
=e−ατ .

Num. Ejemplo 5

∆t 0.3τ_c

No. de muestras 6

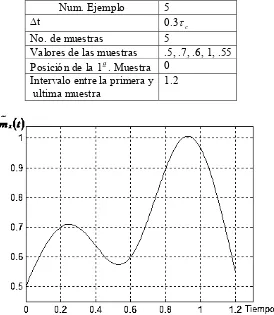
Valores de las muestras .5, .7, .6, 1, .55, .8 Posición de la 1a. Muestra 0

1.5

(31)

( )

τ

=e−ατ .

Num. Ejemplo 6

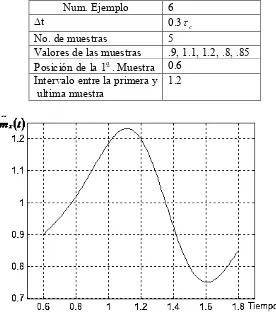
∆t 0.3τ_c

No. de muestras 6

Valores de las muestras .9, 1.1, 1.2, .8, .85, 1 Posición de la 1a. Muestra 0.6

1.5

(32)

( )

τ

=e−ατ .

Num. Ejemplo 7

∆t 0.3τ_c

No. de muestras 6

Valores de las muestras 1, .8, 1.1, 1.3, .9, .6 Posición de la 1a. Muestra 0

1.5

(33)

( )

τ

=e−ατ .

Num. Ejemplo 8

∆t 0.3τ_c

No. de muestras 6

Valores de las muestras .5, .7, .9, 1.1, .8, .45 Posición de la 1a. Muestra 0

1.5

(34)

( )

τ

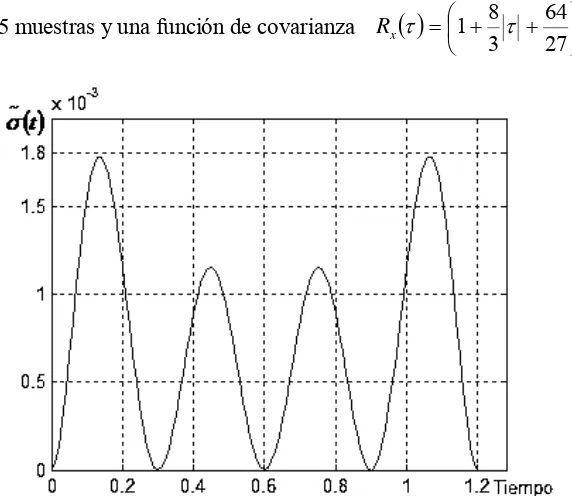
=e−ατ .

Num. Ejemplo 9

∆t 0.3τ_c

No. de muestras 6

Valores de las muestras .9, .6, .3, .8, 1, .9 Posición de la 1a. Muestra .2

1.5

(35)

( )

τ

=e−ατ .

2.2.2 EJEMPLOS GAUSSIANOS NO MARKOVIANOS UTILIZANDO LA FUNCIÓN DE COVARIANZA

( )

_τ ₌

(

₊_α_τ

)

−ατ

e

R_x 1 (2.16)

Ahora se utilizara la función de covarianza (2.16), para lograr una comparación correcta de resultados, las funciones deberán estar normalizadas y por tanto tener un tiempo de covarianza unitario, si tomamos σ =1:

∫

( )

∫

(

)

∞ ∞ − ₌ + = = 0 0 2 1 α τ τ α τ τ τ ατ d e d R_x

c , (2.17)

Donde se desea un tiempo de covarianza unitario, entonces α = 2. Las

expresiones para la función de reconstrucción y de error de reconstrucción quedan de la siguiente manera:

( )

(

)

( t T ) _ij

N

i

i N

j

j t T e a

T x t

m t

x − − i

= =

∑

+ − ⋅ = = _α α 1 1 ~ ~

1 (2.18)

( )

∑∑

(

)

( )

(

)

( ) = − − − − = ⋅ − + ⋅ − + − = N i t T j ij T y N j i j

i _a _T _t _e

e T t t 1 1 ~ 1 1

1 α α α α

σ (2.19)

(36)

Valores de las muestras 1.3, 1.1, 1.45, 1.2, 1.05 Posición de la 1a. Muestra 0.2

1.2

Fig. 2.19 Función de reconstrucción para el proceso Gaussiano no Markoviano con 5 muestras y una función de covarianza R_x

( )

τ =

(

1+ατ

)

e−ατ .

(37)

1.2

Fig. 2.21 Función de reconstrucción para el proceso Gaussiano no Markoviano con 5 muestras y una función de covarianza

( )

_τ ₌

(

₊_α_τ

)

−ατ

e

R_x 1 .

(38)

Valores de las muestras .9, 1.2, 1, 1.3, 1.25 Posición de la 1a. Muestra .3

1.2

( )

τ =

(

1+ατ

)

e−ατ .

(39)

No. de muestras 5

Valores de las muestras .7, 1, 1.3, .9, .8 Posición de la 1a. Muestra .1

1.2

( )

τ =

(

1+ατ

)

e−ατ .

(40)

Valores de las muestras .5, .7, .6, 1, .55 Posición de la 1a. Muestra 0

1.2

( )

τ =

(

1+ατ

)

e−ατ .

(41)

Valores de las muestras .9, 1.1, 1.2, .8, .85 Posición de la 1a. Muestra 0.6

1.2

( )

τ =

(

1+ατ

)

e−ατ .

(42)

Valores de las muestras 1, .8, 1.1, 1.3, .9 Posición de la 1a. Muestra 0

1.2

( )

τ =

(

1+ατ

)

e−ατ .

(43)

Valores de las muestras .5, .7, .9, 1.1, .8 Posición de la 1a. Muestra 0

1.2

( )

τ =

(

1+ατ

)

e−ατ .

(44)

Valores de las muestras .9, .6, .3, .8, 1 Posición de la 1a. Muestra .2

1.2

( )

τ =

(

1+ατ

)

e−ατ .

(45)

( )

_τ _α_τ

( )

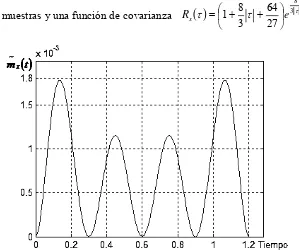
ατ −ατ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = e R_x 3

1 (2.20)

Se continua trabajando con resultados normalizados y un tiempo de covarianza unitario, esto implica que:

( )

α τ ατ τ α τ τ τ ατ 3 8 3 1 0 0 2 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = =

_∫

∞

_∫

∞ − d e d R_x

c , (2.21)

por lo que 3 8 =

α , por lo tanto la función de covarianza normalizada es:

( )

τ τ 3τ 8 27 64 3 8 1 e

R_x ⎟

⎠ ⎞ ⎜

⎝

⎛ ₊ ₊

= . (2.22)

Utilizando la expresión (2.22) se obtendrá la función de reconstrucción y la función de error de reconstrucción de la siguiente manera:

( )

(

)

_ij

N j N i T t i i

j e a

T t T t T x t m t

x i ⋅

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₊ ₋ ₊ − = =

∑

= = − − 1 1 2 2 ~ ~ 3

1 α α α (2.23)

( )

_∑∑

(

)

(

)

= = − − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ + − + ⋅ ⋅ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ + − + − = N i N j t T j j ij T t i i j

i _a _T _t T t _e

e T t T t t 1 1 2 2 2 2 2 ~ 3 1 3 1

1 α α α α α α

σ

(2.24)

(46)

1.2

( )

τ τ 3τ

8

27 64 3

8

1 e

R_x ⎟

⎠ ⎞ ⎜

⎝

⎛ ₊ ₊

= .

Fig. 2.38 Función de error de reconstrucción para el proceso Gaussiano no Markoviano con 5 muestras y una función de covarianza

( )

τ τ 3τ

8

27 64 3

8

1 e

R_x ⎟

⎠ ⎞ ⎜

⎝

⎛ ₊ ₊

(47)

1.2

Fig. 2.39 Función de reconstrucción para el proceso Gaussiano no Markoviano con 5

muestras y una función de covarianza

( )

τ τ 3τ 8

27 64 3

8

1 e

R_x ⎟

⎠ ⎞ ⎜

⎝

⎛ ₊ ₊

= .

Fig. 2.40 Función de error de reconstrucción para el proceso Gaussiano no Markoviano

con 5 muestras y una función de covarianza

( )

τ τ 3τ 8

27 64 3

8

1 e

R_x ⎟

⎠ ⎞ ⎜

⎝

⎛ ₊ ₊

(48)

Valores de las muestras .9, 1.2, 1, 1.3, 1.25 Posición de la 1a. Muestra .3

1.2

( )

τ τ 3τ

8

27 64 3

8

1 e

R_x ⎟

⎠ ⎞ ⎜

⎝

⎛ ₊ ₊

= .

Fig. 2.42 Función de error de reconstrucción para el proceso Gaussiano no Markoviano con 5 muestras y una función de covarianza

( )

τ τ 3τ

8

27 64 3

8

1 e

R_x ⎟

⎠ ⎞ ⎜

⎝

⎛ ₊ ₊