Análisis fractal de yacimientos naturales fracturados

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA

SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN UNIDAD PROFESIONAL ADOLFO LÓPEZ MATEOS

ANÁLISIS FRACTAL DE YACIMIENTOS

NATURALES FRACTURADOS

T E S I S

MAESTRO EN CIENCIAS

P R E S E N T A

ING. JOSÉ RAFAEL GARCÍA PAREDES

DIRECTOR: DR. ORLANDO SUSARREY HUERTA

CONTENIDO

Resumen iii

Abstract iv

Lista de símbolos v

Lista de figuras viii

Lista de tablas ix

CAPÍTULO 1. INTRODUCCIÓN

1.1 Presentación 2

1.2 Objetivo 3

1.3 Justificación 3

1.4 Estado del arte 3

1.5 Referencias 7

CAPÍTULO 2. FRACTALES

2.1 Dimensión topológica 10

2.2 Historia 12

2.3 Concepto de auto-similitud 14

2.4 Concepto de auto-afinidad 16

2.5 Dimensión fractal 19

2.5.1 Primeras formas de la dimensión fractal 19

2.6 Movimiento browniano 20

2.7 Referencias 23

CAPÍTULO 3. PERCOLACIÓN

3.1 Generalidades 25

3.2 Modelo de percolación 26

3.3 Sitio de percolación en una red cuadrada 29

3.4 Percolación auto-similar de cluster 32

3.5 Cluster finito de percolación 36

3.6 Distribución del tamaño del cluster en pc 38

3.7 Correlación de longitud 41

3.8 Cluster de percolación del espinazo 44

3.9 Invasión por percolación 49

3.10 Referencias 51

CAPÍTULO 4. MEDIOS POROSOS

4.1 Estructura y clasificación 54

4.2 Estructura y propiedades 55

4.3 Porosidad 56

4.4 Medición de porosidad 56

4.4.1 Método directo 56

4.4.2 Método de expansión de gas 56

4.4.3 Método de inyección de mercurio 57

4.4.5 Método de imbibición 58

4.4.6 Método estadístico 58

4.5 Permeabilidad 59

4.6 Saturación de fluido, presión capilar y ángulo de contacto 60

4.7 Distribución de tamaños de poros 63

4.8 Propiedades fractales de los medios porosos 64

4.8.1 Método de absorción 64

4.8.2 Método de la función de correlación 65

4.8.3 Método espectral 67

4.8.4 Método de conteo de cajas 68

4.9 Porosidad y distribución de tamaños de poros de medios porosos fractales 70

4.10 El papel como medio poroso 70

4.11 Referencias 73

CAPÍTULO 5. METODOLOGÍA EXPERIMENTAL Y ANÁLISIS DE RESULTADOS

5.1 Introducción 75

5.2 Selección del material 76

5.3 Desarrollo experimental 79

5.4 Determinación del exponente de rugosidad H 83

5.5 Resultados experimentales 83

5.6 Discusiones 88

5.9 Referencias 95

CONCLUSIONES 97

TRABAJOS A FUTURO 98

ANEXO A: Determinación del exponente de rugosidad mediante el software BENOIT 1.2

A1 Método de análisis R/S 100

A2 Espectro de potencia 101

A3 Longitud de rugosidad 102

A4 Variograma 103

A5 Ondoletas 104

RESUMEN.

En el presente trabajo se encontró que el exponente de rugosidad local del frente húmedo varía continuamente con el tiempo y se encontraron tres exponentes de rugosidad que fueron caracterizados en inicial, transitorio y de saturación; dentro de la etapa inicial (t < τ1) el movimiento del frente húmedo muestra anti-persistencia caracterizada por el exponente de rugosidad local ζ < 0.5, el cual se incrementa desde ζ = 0.2 hasta ζ = 0.5, por ejemplo, para el tiempo t = τ1 el frente húmedo llega ser aleatorio. En régimen transitorio(τ₁<t<τS) las

configuraciones del frente húmedo poseen persistencia y el exponente de rugosidad local también se incrementa con el tiempo y logra un máximo ζmax = 0.76 en el tiempo de saturación τS. En la

etapa de saturación ( t > τS ) el exponente de rugosidad local decrece logaritmicamente para el

ABSTRAC.

In the following work, we have found that the local roughness exponent of a moving wet front changes continuously with time, we have found three different regime behaviour during the imbibitions, and we have characterized them as: initial, transient and saturation imbibition. In the initial stage (t < τ1) the moving wet front displays anti-persistence, which is characterized by the

local roughness exponent ζ < 0.5, them it increases from ζ = 0.2 until ζ = 0.5, for example: for the time t = τ1 the wet front becomes random. During the transient regimen (τ1 < t < τS) the wet front configurations possess persistence and the local roughness exponent is also increased with time, achieving a maximum of ζmax = 0.76 at the saturation time τS. On the saturation stage the local roughness exponent decreases logarithmically to the value ζ = 0.70, which is determined by the long-range correlations in the pore network. This behaviour is related to the complex dynamics of avalanches, which criticality leads to the self-organized interface of movement.

LISTA DE SÍMBOLOS.

α Exponente de rugosidad global, exponente para percolación en redes.

β Exponente de crecimiento, exponente para percolación en redes.

δ Exponente de escalamiento dinámico, radio de esferas, exponente de movimiento del frente.

γ Exponente para percolación en redes.

φ Porosidad.

λ,λi Parámetro de escalamiento.

µ Viscosidad de fluido.

ρ Densidad.

ρ Densidad promedio.

ρB Densidad bruta de la muestra.

ρg Densidad de material granulado.

ρw Densidad de agua, densidad de fluido mojable.

ρnw Densidad de fluido no mojable.

σ Desviación estándar

σo Sección transversal de molécula.

σos Tensión superficial entre aceite y superficie.

σs Enlace superficial por sitio.

σws Tensión superficial entre agua y superficie.

τ Intervalos de tiempo, exponente para percolación en redes,

τs Tiempo de saturación.

τF Tiempo final.

υ() Velocidad de frente húmedo.

ω Velocidad angular.

ξ Longitud de correlación.

ζ Exponente de rugosidad local.

∆P Diferencia de presión.

Ξ Área superficial especifica.

A Área.

A Amplitud efectiva estimada desde un tamaño finito. c constante de orden unitario.

cs Probabilidad normalizada por sitio.

c() Función de auto correlación.

C punto critico.

υ

C Coeficiente de correlación. d Dimensión global.

df Dimensión fractal local.

dH Diámetro hidráulico.

P T

d Dimensión topológica de punto.

C T

d Dimensión topológica de curva.

S T

V T

d Dimensión topológica de volumen. D,Df Dimensión fractal.

DA Dimensión fractal de avalancha.

De Dimensión euclidiana.

DP Dimensión fractal de poro.

Ds Dimensión fractal obtenida.

E Dimensión euclidiana, dimensión espacial. h Altura.

H Exponente de rugosidad de Hurst. K Permeabilidad.

l1 Límite superior

l2 Límite inferior.

L Longitud. M Masa.

ns Distribución del tamaño de cluster.

N Número de poros, número de abogrado, número de esferas para cubrir un sistema. n Exponente de distribución, enlace molecular, exponente de escalamiento.

p, q Probabilidad de sitios ocupados. p’ Concentración de sitios ocupados. pc Umbral de percolación.

P Presión.

Pc Presión de capilaridad.

Po Presión de aceite.

Pw Presión de agua.

P1 Presión inicial.

P2 Presión final.

∞

P Probabilidad de un enlace a un cluster infinito. q Rapidez de flujo.

r1,r2 Radios principales de la curvatura de la interfase.

Rg Radio de giro.

Rp Tamaño de partícula euclidiana.

R1 Presión de capilaridad en el radio interior de rotación.

R2 Radio de rotación de la muestra.

s Distribución del tamaño de cluster por enlace, número de sitios del cluster. SA Tamaño de avalancha, número de poros llenos.

Sp Superficie de poros.

Sw Saturación del agua.

S(ω) Densidad espectral. t Tiempo inicial. T Temperatura. Tc Temperatura critica

VP Volumen de poros.

VB Volumen total.

VS Volumen de sólido.

Va Volumen donde se introduce la muestra.

W Ancho.

LISTA DE FIGURAS.

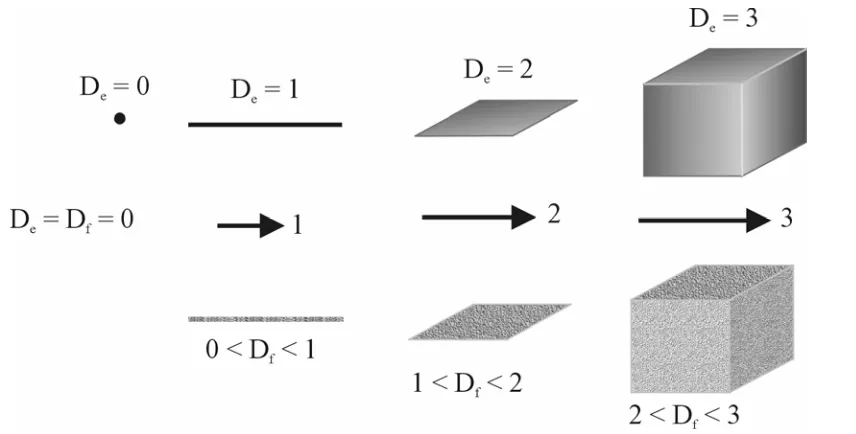
Figura 2.1.- La división del objeto que se estudia se realiza mediante otro objeto el cual tiene dimensión menor, donde dimensión topológica de un punto, es dimensión topológica de curva, dimensión topológica de superficie, dimensión topológica de volumen.

P T

d d_TC

S T

d d_TV

Figura. 2.2.- Primeras dos iteraciones en la regla de agregación para construir el fractal triángulo de Sierpinski.

Figura 2.3.- Fractal de Sierpinski después de cuatro iteraciones.

Figura 2.4.- Dos superficies rugosas, observadas en escalas diferentes. (a) superficie de cobre pulida en arena[15], cuando las rugosidades son observadas en una escala alrededor de 50 µm, (b) fatiga de cobre policristalina[16], cuando las rugosidades se encuentra a una escala de unos cientos de ángstrom.

Figura 2.5- Fractal auto-afín.

Figura 2.6.- Esquema simplificado entre dimensión euclidiana (De) y dimensión fractal (Df).

Figura 2.7.- Conjunto de Mandelbrot.

Figura 3.1.- El bosquejo para un gas real. El punto “C” es el punto crítico.

Figura 3.2.- La densidad de un cluster infinito, P∞, como una función de probabilidad de un

enlace que está presente, p. P∞ es un ejemplo de un parámetro de orden, y p es un ejemplo de parámetro de control.

Figura 3.3.- Una red cuadrada con un medio de nodos ocupados por poros, como se muestra a la izquierda de la figura. En la figura del lado derecho se muestra regiones conectadas o clusters. Los clusters grandes se distinguen por usar diferentes símbolos para los poros. La red consiste de L x L con nodos de L = 20.

Figura 3.4.- El efecto probabilístico de crecimiento ocupacional de una red cuadrada de 160x160 de la cima al fondo se tiene p=0.58, 0.6 y 0.62 en cada una de las tres figuras el cluster más grande del color más suave. El cluster más pequeño es el color más oscuro. Los sitios vacíos son negros.

Figura 3.5.- La probabilidad, PN(p), el sitio que pertenece al cluster más grande como una función de probabilidad p un sitio es un poro abierto en L x L en una red cuadrada. La curva llena es obtenida para L = 450, y las líneas fracturadas con L = 200 y 50. La línea vertical es en p = pc

= 0.59275.

Figura 3.7.- (a) en una red triangular con cluster en pc. Un veteado en una red triangular con un

factor b= 3. Los sitios ocupados se muestran como círculos llenos y sitios abiertos como círculos abiertos. Los sitios de los grupos bloqueados indicados con triángulos obscuros. Si la mayoría de los sitios pertenecen a un triángulo acopado entonces forman el triángulo oscuro. (c) La percolación del veteado en una red donde los sitios son llenos y corresponden a los triángulos oscuros.

Figura 3.8.- El cambio en la concentración de sitios ocupados, P’ – p, como una función de la concentración de sitos ocupados, p, en la red triangular antes del reescalamiento de la red para un factor de b= 3.

Figura 3.9.- La auto-similaridad y el efecto de la granulación áspera en la red triangular del umbral de percolación. El cambio de escala por un factor b = 3, usando el procedimiento de la renormalización ilustrado en la figura 3.7. (a) La percolación del cluster en el umbral sobre la red original 180 x 180. (b) Los sitios obtenidos después de un escalamiento de la red original en (a) para un factor b = 3. (c) La percolación del cluster de la red escalada (b). (d) la red escalada es insertada dentro de la red original en la región marcada por el marco. Las figuras muestran el resultado del cluster de percolación.

Figura 3.10.- Un cluster finito sobre una red cuadrada en pc. El radio del círculo de giro,

Rg(s)=51, de un cluster conteniendo 6700 sitios. La caja en la figura tiene un lado L=60. El lado

de la caja más pequeña que contiene el cluster es Ls=150.

Figura 3.11.- La dependencia de la masa de los clusters s (número de sitios ) en su tamaño de su línea Ls, para una red cuadrada en pc = 0.5927. El error en las barras indica una desviación

estándar acerca del promedio. La inserción muestra la exploración de la inclinación local para s → ∞, donde

s

eff s L

D =∂ln /∂ln D=1.89±0.01

Figura 3.12.- La densidad de los sitios en el cluster más grande de una red cuadrada en (círculos llenos) y

35 . 0 = −p_c

p p− p_c =0.022(círculos vacíos) con un tamaño de caja L alrededor de un sito ocupado. La inclinación para L<ξ es D – 2 con D ≅ 1.9, y la parte recta para L > ξ es P∞(p).

Figura 3.13.- El espinazo (círculos llenos) y el cluster de percolación a partir de una simulación sobre una red cuadrática de 147 x 147 en p_c =0.593.

Figura 3.15.- Los espinazos de los cluster de percolación en la red cuadrática pc mostrada en la

figura 3.4b. (a) El espinazo que conecta a un sitio simple en el borde izquierdo a un sitio simple en el borde derecho de la red de 160 x 160. (b) El espinazo que conecta todos los sitos sobre el borde izquierdo con todos los sitos del borde derecho.

Figura 3.16.- Invasión de percolación sobre una red cuadrada de 5 x 5 (a) en el tiempo inicial y (b) después de 15 intervalos de tiempo.

Figura 4.1.- Ejemplos de materiales porosos naturales (X10): (a) arena de playa, (b) arena de piedra, (c) pan de centeno, (d) madera, (f) pulmón humano.

Figura 4.2.- Angulo de contacto formado entre un par de líquidos y la roca.

Figura 4.3.- Curvas típicas de presión de capilaridad.

Figura 4.4.- Construcción de la curva de Koch.

Figura 4.5.- Red aleatoria de 2000 fibras uniformes, representando aproximadamente 1 cm2 de una capa de fibras.

Figura 5.1.- (a) En la ilustración esquemática de un arreglo experimental se examina el movimiento de la interfase en medios aleatorios. Los parámetros como tipo de papel, temperatura, humedad, dirección de crecimiento y concentración de tinta pueden ser variados sistemáticamente. Estos cambios afectan el área, la velocidad de mojar y el ancho global de la superficie rugosa. Pero no afecta las propiedades de escalamiento de la superficie. (b) la interfase experimental digitalizada; el tamaño horizontal del papel fue de 20 cm. (c) el resultado típico discreto que imita el movimiento de la interfase en medios desordenados.

Figura 5.2.- Configuración de las probetas de papel para los ensayos de imbibición.

Figura 5.3.- Marco de madera.

Figura 5.4.- Fotografías en formato BMP de una probeta: (a) exposición a 10 segundos de iniciado el ensayo de la primera serie de 10 segundos, (b) exposición a 255 segundos de la segunda serie de 15 segundos, (c) exposición a 1800 segundos de la tercera serie.

Figura 5.5.- (a) Configuraciones de la interfase de movimiento en intervalos de tiempo: ∆t = 10 segundos cuando t = 300 segundos y ∆t = 60 segundos cuando la interfase es detenida; (b) Configuraciones de la velocidad del frente húmedo en tiempos diferentes; observar que la distribución (1) corresponde o la etapa inicial, la distribución (2) corresponde a el régimen transitorio y las distribuciones (3) y (4) corresponden al etapa-fija (régimen saturado).

Figura 5.7.- (a) Gráfica de la distribución fractal de velocidad del frente húmedo para t = 10 segundos (1), t = τ1 (2), y t = τS (3); (b) Gráfica de velocidad del frente húmedo del exponente de

distribución contra el tiempo; (c) distribución estadística de n. (d) El promedio de velocidad del frente húmedo contra el tiempo; (e) Correlación de la velocidad del frente húmedo contra el tiempo. (f) Correlaciones temporales de la velocidad del frente húmedo en posiciones x y a + 1 durante el tiempo experimental.

Figura 5.8.- (a) Graficas de configuraciones fractales del frente húmedo en t = 10 segundos (1), t = τ1 (2), t = τS (3), y t = 2000 segundos (4); (b, c) Distribuciones estadísticas del exponente de

rugosidad local y la diferencia ∆ζ = ζ (τS) - ζ(τF).

Figura 5.9.- Correlaciones temporales de la velocidad del frente húmedo en posiciones x y x + 1 durante: (1) la etapa inicial, (2) el régimen transitorio, y (3) la etapa de saturación. Observe que las gráficas fueron movidas por claridad.

Figura 5.10.- Distribuciones de tamaño de avalancha en las etapas de imbibición transitoria (a) y la saturada (b).

Figura 5.11.- Correlaciones espaciales entre configuraciones del movimiento del frente húmedo contra el tiempo.

LISTA DE TABLAS.

Tabla. 3.1.- El sitio y enlace del umbral de percolación para diferentes tipos de red. Se incluye los valores del campo medio del umbral de percolación para unos tipos de red.

Tabla 3.2.- Algunos exponentes críticos para percolación en redes de 2 y 3 dimensiones.

CAPÍTULO 1

1.1 PRESENTACIÓN.

En la actualidad, el petróleo representa una de las principales fuentes primarias de energía, para obtenerlo, se explotan las grandes acumulaciones del mismo que se encuentran en el subsuelo y son llamados yacimientos.

Sin embargo, las características tanto de los yacimientos como de las rocas almacenantes, como son los fluidos almacenados, entre los cuales se incluye al petróleo, exigen estudios cada vez más representativos de dichas propiedades para la mejor extracción de los hidrocarburos del subsuelo.

Estudios de evaluación de formaciones en yacimientos naturalmente fracturados, requieren del conocimiento previo de ciertos factores, tales como área del yacimiento, factor volumétrico del aceite, porosidades de las fracturas y saturaciones de agua en la matriz y en las fracturas. Establecer valores exactos de los parámetros mencionados, resulta bastante difícil dada la complejidad de este tipo de yacimientos; sin embargo, técnicas desarrolladas recientemente permiten determinar dichos valores que pueden considerarse como representativos.

1.2 OBJETIVO.

Analizar el comportamiento del petróleo en los yacimientos naturalmente fracturados (YNF) utilizando herramientas como la geometría fractal para obtener parámetros que nos permitan desarrollar modelos físicos que describan mejor el complejo comportamiento de flujos en medios porosos.

1.3 JUSTIFICACIÓN.

México es uno de los principales productores de petróleo, en el cual está basada su economía nacional, lo que implica que se deban invertir una gran cantidad de recursos económicos, tecnológicos, materiales y de mano de obra calificada. Por otro lado, la gran mayoría de la riqueza petrolera se encuentra en el sureste de México ya que en esta región se encuentra el mayor número de yacimientos petroleros.

Sin embargo, estos yacimientos tienen una característica que los distingue de la mayoría de los yacimientos petroleros que se encuentran en el mundo, tienen la característica de ser yacimientos naturalmente fracturados (YNF) y su explotación requiere de técnicas de explotación especiales con el fin de no alterar sus propiedades fisicoquímicas.

1.4 ESTADO DEL ARTE.

Uno de los graves problemas contemporáneos del mundo es el desperdicio de recursos naturales, y la consigna de esta época bien podría ser su aprovechamiento máximo.

Los yacimientos del país se encuentran en una etapa avanzada de explotación, más sin embargo hay una tremenda incertidumbre en cuanto a su modelado, lo cual no permite la implementación de programas adecuados para su explotación. A la industria petrolera por ejemplo, le afectan las pérdidas que ocurren con las técnicas de extracción, al petróleo se le extrae de dos formas:

Extracción primaria: El petróleo fluye porque se encuentra a presiones muy altas en el subsuelo.

Extracción secundaria: Una vez que ha finalizado la extracción primaria gran parte del crudo permanece atrapado en los poros de las rocas. Por ello, es necesario efectuar la extracción secundaria que se realiza; generalmente, por la inyección de agua, aire o nitrógeno en el casquete de gas o en el acuífero del yacimiento.

Sin embargo, ambos procesos no bastan para recuperar al crudo en su totalidad y aunque su desperdicio parece despreciable cuando se habla de millones de barriles la suma ya no resulta tan insignificante.

Un procedimiento para la evaluación y detección de yacimientos naturalmente fracturados fue desarrollado por R. Aguilera [1.10-1.13] para determinar la distribución de fluidos. Existen una gran diversidad de registros de pozos; sin embargo, los parámetros físicos necesarios para evaluar un yacimiento son: porosidad, saturación de hidrocarburos y espesor de la capa de permeabilidad. Esta técnica tiene la ventaja de no requerir el conocimiento previo de la resistividad del agua y porosidad, valores que pueden ser representativos, los cuales pudieron haberse determinado en una forma experimental. Dada su naturaleza estadística, el método proporciona resultados más representativos en yacimientos de espesores considerables.

Estudios llevados a cabo en yacimientos fracturados indican que la permeabilidad debida a la porosidad primaria es generalmente baja y que son las fracturas las que incrementan la permeabilidad en una forma considerable. En este modelo, desarrollado para el estudio de yacimientos fracturados, el sistema está formado por doble porosidad, uniformemente distribuida a través de todo el yacimiento. El concepto de medio de doble porosidad fue introducido por Barenblatt y Zheltov [1.14], resultado del estudio del comportamiento de un acuífero fracturado. Hay variantes de este modelo que han sido investigados por gran número de autores [1.15], obteniéndose soluciones analíticas para el comportamiento transitorio de presión en el yacimiento.

Se posee un bajo conocimiento acerca del origen, evolución y geometrías de los sistemas que caracterizan las rocas almacenadoras de los campos productores de hidrocarburos; además, no se han realizado estudios tectónicos a nivel de campo para comprender el origen del problema y no se cuenta con una metodología ni con herramientas adecuadas para manejar en forma precisa la información obtenida, ya sea directamente o indirectamente, útil para obtener mayor conocimiento de fluidos en medios porosos, ya que se han efectuado estudios en los yacimientos naturalmente fracturados sin el conocimiento adecuado de los mismos, lo que ha dado como consecuencia recuperaciones limitadas de hidrocarburos y malos resultados económicos.

Dentro del Instituto Mexicano del Petróleo se llevan a cabo varios estudios de caracterización de este tipo de yacimiento, para explorarlos de manera adecuada es preciso identificar y modelar los sistemas de fracturas, cavidades de disolución y bloques de matriz. Se llevan a cabo cuatro tipos de estudios:

• CARACTERIZACIÓN DINÁMICA: Se desarrollan y adecuan metodologías que expliquen la interacción del sistema roca-fluido del yacimiento, cómo se desplazan los fluidos a través de las rocas. Los parámetros que se obtienen son utilizados para los modelos de simulación numérica de yacimientos.

• SIMULACIÓN NUMÉRICA DE YACIMIENTOS: El objetivo es desarrollar herramientas de simulación propias no incluidas en simuladores comerciales. Se busca el comportamiento de producción de aceite, gas y agua de las formaciones, se realizan pronósticos a diferentes años y con diversos escenarios de producción. Es necesario contar con las herramientas que permitan considerar todos los procesos del yacimiento, la geometría de las formaciones productoras y la dinámica de los fluidos contenidos en las mismas.

• EXPLOTACIÓN AVANZADA DE YACIMIENTOS: Cuando un yacimiento termina su etapa de recuperación primaria de aceite y gas, y la presión decrece significativamente, es necesario aumentar o mantener ésta estimulación al yacimiento con la inyección de fluidos o gases externos. Por tal razón, es preciso desarrollar tecnologías que contribuyan a hacer más eficiente la recuperación de hidrocarburos.

Una novedosa técnica de comportamiento y recuperación de fluidos en yacimientos es la reducción dinámica de la capa de mojado; cuando se tiene un fluido viscoelástico en un tubo pequeño o en un poro y se quiere desplazar como un líquido o gas, al empujarlo siempre queda una capa delgada pegada a la pared del tubo. A ésta se le llama capa de mojado, la cual impide la recuperación del fluido viscoelástico.

Se encontró un sistema de extracción, el cual considera la frecuencia con que se bombea aire para empujar un fluido, y permite aprovechar un porcentaje mucho mayor de la sustancia, lo que es una metodología para conseguir que lo que queda adherido a las paredes de los tubos o poros sea menor, utilizando las características de los fluidos viscoelásticos. Ya que muchos de los fluidos no manifiestan dichas propiedades cuando se transportan por ductos muy grandes, este procedimiento funciona mejor cuanto más pequeños son los tubos o poros por donde pasan. Ya en la recuperación del petróleo, este método es muy valioso, ya que con sólo modificar la manera de inyectar el nitrógeno se rescatará más al extraerlo, incluso en yacimientos aparentemente extintos, pues podría adelgazarse la capa que se quedó pegada a los poros de las rocas para maximizar su aprovechamiento.

Coli y Bacillus Subtilis, Vicsek et al. [1.31] obtuvieron un exponente de rugosidad α = 0.78, un valor mucho más alto que aquel predicho por el modelo de Eden de α = 0.5 [1.34]. Por otro lado, en experimentos de imbibición en papel Barabási et al [1.24] obtuvieron α = 0.63, Family et al [1.32], encontraron un exponente de rugosidad 0.62 ≤ α ≤ 0.78, y Kwon et al [1.33] encontraron un exponente de rugosidad de α =0.67. Por otro lado, en experimentos de quemado de papel Zhang et al [1.37] reportaron un exponente de rugosidad de 0.71. Para el caso de experimentos de fractura en papel Kertész et al [1.30] reportaron un exponente de 0.63 ≤ α ≤ 0.72. Todos estos valores observados experimentalmente son mucho más altos que el valor de α = 0.5 predicho por la mayoría de los modelos teóricos convencionales [1.20-1.28]. Para explicar esta rugosidad anormal, indicada por los valores altos de α, los investigadores han tomado en cuenta el ruido inherente generado por el desorden del medio.

Hasta donde se sabe, se han reportado pocos estudios experimentales sobre el comportamiento de escalamiento dinámico de interfases fractales auto-afines en crecimiento [1.32-1.35]. Horvath et al [1.35] midieron el exponente de crecimiento β =0.65en un experimento de desplazamiento de un fluido por otro. Horvath y Stanley [1.34] obtuvieron β = 0.56 en experimentos de imbibición. Ambos valores son mucho más altos que aquellos predichos por los modelos teóricos, 0.25 – 0.50. Por otro lado, Family et al [1.32] obtuvieron un exponente de crecimiento 0.29 ≤ β ≤ 0.40 en experimentos de imbibición en papel, sus valores concuerdan con el valor teórico de 1/3 predicho por el modelo de Eden [1.38].

Dentro de los experimentos de imbibición realizados en papel secante en la dirección longitudinal con respecto a la orientación de las fibras del papel [1.39]. Se encontraron los siguientes resultados, en la etapa inicial de la región húmeda forma la llamada escalera del diablo; posteriormente alcanza un máximo y el ancho de la interfase se satura, conforme aumenta el ancho de la probeta aumenta la saturación donde aumenta el tiempo de saturación donde β es el exponente de crecimiento y α es exponente de rugosidad global [1.40].

1.5 REFERENCIAS:

[1.1] VIEIRA, L. P. “Fractured Reservoirs ” 7th World Petroleum Congress Proc. (1967) vol. 3

[1.2] SMCKHOV, E. M.: “Fractured Oil and Gas Reservoirs and Present Status of Their Study”, 2nd _{U. N. Develop Resources, Asia and Far East Smp. (Teheran, Iran.}

1962).

[1.3] ANDRZESEN, K. H. BAKEN, R. I., and RAOOFI, J.: “Development of Methods for Analysis of Iranion Asmari Reservoirs”, paper 14, Proc. 6th World Petroleum Congress (1963) II.

[1.4] GIBSO, H.S.: “The Production of Oil From the Fields of South Western Iran”, J. Inst. Petroleum. Vol. 34 (1948).

[1.5] FREEMAN H. A.: “Techniques in the Kirkuf Oildfield”, Proc. of 3rd World Petroleum Congress: Section II (1951).

[1.6] BASSÓ, A. S.: “Estudio del Campo Artesa. Evaluación de la formación” (Segundo Reporte), División de Evaluación de Formaciones, Subdirección de tecnología de la Explotación . I. M. P. 1979.

[1.7] MANRIQUEZ, G. RAFAEL, ABREU, N. T. LEÓN V. R. “Estudio del Campo Artesa.- Evaluación de Formaciones, subdirección de Tecnología de la Explotación. I. M. P. 1979.

[1.8] GUTIÉRREZ, M. M.: “Justificación para Suspender la Inyección de Agua al campo Artesa”. Departamento de Ingeniería de Yacimientos, Sección de Recuperación Secundaria, Villahermosa, Tab. 1979.

[1.9] BASSÓ, A. S.: “Estudio del Campo Artesa.- Evaluación de la Formación”, (Cuarto Reporte) Determinación del Volumen en el sistema de Fracturas, División de Evaluación de Formaciones Subdirección de Tecnología de la Explotación, I. M. P. 1980.

[1.10] AGUILERA, ROBERTO: “Analysis of Naturally Fractured Reservoins From Sonic and Resistivity Logs”, J. Pet. Tech. 1974.

[1.11] AGULERA, ROBERTO: “Analysis of Naturally Fractured Reservoins From Conventional Well Logs” J. Pet. Tech 1976.

[1.12] AGUILERA, ROBERTO. “The Uncertainly of Evaluating Original Oil-in-Place in Naturally Fractured Resevoirs”, Trans, SPWLA, El paso, Tex. 1978.

[1.13] AGUILERA, ROBERTO. “Evaluation of Fine-Groined Laminated Systems From Well Logs, Wasatch Formations, Utah” Ph. D. Thesis 1959, Colorado School of Mines, Golden, Colo. (1973).

[1.14] BARENBLATT, G. E., In P. ZHELTOV and I. I. KOCHINA, 1960. Basic

Concepts in the Theory of Seepage of Homegeneous Liquids in Fissured Rocks. J. Appl. Math. Mcch., 24 (5).

[1.15] GRINGARTEN, A. L.: “Flow Test Evaluation of Fractured Reservoirs”. Present at the Symposium on “Recent Treds in Hydrology”. Berkeley California 1979. [1.16] F. FAMILY, T. VICSEK, J. Phys. A 18, L 75 (1985).

[1.17] F. FAMILY, Physca A 168, pp. 561 (1990).

[1.18] F. FAMILY, “Rough Surfaces: Scaling Theory and Universality” en Universalities in Condensed Matter Physics, eds. R. Jullien, L. Pslitu, R. Rammal y N. Boccara, Springer Soc. Phys., Berlin (1988).

[1.20] P. MEAKIN, P RAMMANLAL, L. M. SANDER, R. C. BALL, Phys. Rev. A 34, 5091 (1986).

[1.21] S. F. EDWARDS, D. R. WILKINSON, Proc. Roy. Soc. A 381, pp. 17. London (1982).

[1.22] D. FOSTER, D. R. NELSON, M. J. STEPHEN, Phys. Rev. A 16, pp. 732 (1977). [1.23] S. V. BULDYREY, A. L. BARABÁSI, F. CASERTA, S. HAVLIN, H. E.

STANLEY, T. VICSEK, Phys. Rev. A 45, R 8313 (1992).

[1.24] A. L. BARABÁSI, S. V. BULDYREV, S. HAVLIN, G. HUBER, H. E. STANLEY, T. VICSEK, “Imbibition in Porous Media: Experiment and Theory” en Surface Desordering: Growth, Roughening and Phase Transitions, eds. R. Julien, J. Kertesz, P. Meakin, D. E. Wolf (Nova Science, Cammack, N. Y., 1992), pp. 193.

[1.25] L. A. N. AMARAL, A. L. BARABÁSI, S. V. BULDYREV, S. HAVLIN, H. E. STANLEY, Fractals 1, pp. 818 (1993).

[1.26] L. A. N. AMARAL, A. L. BARABÁSI, S. V. BULDYREV, S. HAVLIN, H. E. STANLEY, Phys. Rev. Lett 72, pp. 641 (1994).

[1.27] L. A. N. AMARAL, A. L. BARABÁSI, H. A. MAKSE, H. E. STANLEY, Phys. Rev. E, 52 pp. 4087 (1995).

[1.28] H. LESCHHORN, Physica A, 195, pp. 324 (1993).

[1.29] M. A. RUBBIO, C. A. EDWARDS, A. DOUGHERTY, J. P. GOLLUB, Phys. Rev. Lett 63, 1685 (1989).

[1.30] J. KERTÉSZ, V. K. HORVÁTH, F. WEBER, Fractals 1, 67 (1993).

[1.31] T. VICSEK, M. CSERZO, V. K. HOROVÁNTH, Physica A 167, 315 (1990). [1.32] F. FAMILY, K. C. B. CHAN, J. G. AMAR, Surface Desordering: Growth

Roughnening and Phase Transitions, eds. R. Julien, J. Kertesz, P. Meakin, D. E. Wolf, Nova Science, Commack, N. Y. (1992), pp. 205.

[1.33] T. H. KWON, A. E. HOPKINS, S. E. O´DONNELL, Phys. Rev. E 54, 685 (1996). [1.34] V. K. HOROVATH, H. E. STANLEY Phys. Rev. E 52 5166 (1995).

[1.35] V. K. HOROVATH, F. FAMILY, T. VICSEK, J. Phys. A 24, L 25 (1991). [1.36] S. HE, G. L. M. K. S. KAHANDA, P. Z. WONG Phys. Rev Lett 69, pp. 3731

(1992).

[1.37] J. ZHANG, Y. C. ZHANG, P. ALSTROM, M. T. LEVINSEN, Physica A 189, 383 (1992).

[1.38] M. EDEN, “A Two Dimensional Growth Process” en Proccedinds of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, ed. J. Neyman, University of California Press, Berkeley (1961), pp. 223.

[1.39] ALEXANDER S. BALANKIN, ARMANDO BRABO-ORTEGA and DANIEL MORALES MATAMOROS. Some new features of interface roughening dynamics in paper-wetting experiments. Philosophical Magazine Letters, 2000, Vol. 80, No. 7, 503-509.

CAPÍTULO 2

2. FRACTALES.

2.1. DIMENSIÓN TOPOLÓGICA.

El concepto de dimensión no tiene grandes dificultades mientras se trata de figuras sencillas, tales como puntos, rectas, triángulos y poliedros. Un punto único o conjunto finito de puntos tiene dimensión cero, un segmento rectilíneo es unidimensional y la superficie de un triángulo es bidimensional, el conjunto de puntos de un cubo sólido es tridimensional. Pero cuando se trata de extender este concepto a conjuntos más generales de puntos, surge la necesidad de dar una definición precisa.

En 1912, H. Poincaré llamó la atención acerca de la necesidad de analizar más profundamente y de dar una definición precisa del concepto de dimensión. Poincaré observó que la recta es unidimensional, debido a que podemos esperar dos puntos cualquiera de ella, cortándola en un sólo punto (conjunto de dimensión cero), mientras que el plano es bidimensional, porque para separar dos puntos cualquiera debemos cortarlo a lo largo de una curva cerrada (conjunto de dimensión 1). Esto nos sugiere la naturaleza inductiva de la dimensión topológica: un espacio es (n –1) dimensiones, mientras no siempre es posible obtener el mismo resultado suprimiendo un conjunto de menos dimensiones. En los elementos de Euclides aparece una definición inductiva del concepto de dimensión, donde se dice que un figura unidimensional es aquella cuya frontera está formada por puntos; bidimensional si su frontera está formada por curvas y tridimensional, aquella figura cuya frontera se compone de superficies [2.1].

La dimensión topológica nos sirve para saber el número de coordenadas que se necesitan conocer para definir un punto. La dimensión topológica debe ser un número natural entero y positivo. Con excepción de la dimensión cero, la dimensión de cualquier objeto se puede obtener dividiéndolo en dos partes iguales, la dimensión que nos permita dividir en dos partes iguales + 1, será la dimensión topológica del objeto. Figura. 2.1.

Figura 2.1.- La división del objeto que se estudia se realiza mediante otro objeto el cual tiene dimensión menor, donde

dimensión topológica de un punto, es dimensión topológica de curva, dimensión topológica de superficie, dimensión topológica de volumen.

P T

d

C T

d d_TS dV_T

En topología, una línea recta puede ser deformada y convertirse en una curva cerrada. Una línea recta, un triangulo, un círculo y la frontera de la curva de Von Koch, topológicamente son equivalentes.

El número de huecos en un objeto es también topológiacamente invariante, esto significa que una esfera puede transformarse en la superficie de una herradura, pero nunca en un toroide. A este tipo de transformaciones las llamamos homomorfismos cuando no deben de cambiar las propiedades invariantes de los objetos.

Una línea recta tiene dimensión uno. Así desde el punto de vista topológico debemos esperar que la curva de Von Koch tenga dimensión uno. La historia de las distintas nociones del concepto de dimensión, involucra grandes matemáticos de aquel tiempo como H. Lebesgue, L. E. J. Brouwer, G. Cantor, K. Menger, Huerewiez, P. Alexandroff, L. Pontrjagin, G. Peano. P. Urysohn, E Cech y D Hilbert [2.2].

Existen diferentes nociones del concepto de dimensión, todas ellas son de naturaleza topológica. La más importante es la dimensión de Hausdorff y de aquí Mandelbrot se basa para su concepto de dimensión fractal. La dimensión de Hausdorff para una línea recta es uno y para la curva de Von Koch es de log 4/log 3. En otras palabras, la dimensión de Hausdorff sí logra cuantificar el cambio de una línea recta de dimensión uno a la curva de Von Koch. Sin embargo; log 4/log 3 = 1.2619.... no es número entero, la dimensión fraccionaria es típica de los objetos fractales.

2.2. HISTORIA:

Para describir en forma completa ciertas irregularidades y patrones fragmentados de las formas que aparece en la naturaleza tales como líneas costeras, nubes, montañas, etc, en 1977 B.B. Mandelbrot [2.3] generó una nueva geometría. Introdujo el término fractal para identificar la familia de formas descritas por esta geometría. Fenómenos físicos como difusión, movimiento browniano, etc; también muestran un comportamiento fractal. Un aspecto relevante es que mediante algoritmos matemáticos pueden generarse distintas formas geométricas con estructura fractal ideal.

La teoría de los fractales no se desarrolló independiente de otras disciplinas, ésta nace de consecuencias matemáticas que datan de finales del siglo pasado. El problema de dimensión era crucial para la caracterización de conjuntos de puntos, curvas, superficies y volúmenes. A medida que se definía este importante concepto, se creaban por los mismos matemáticos, conjuntos de puntos o curvas que contradecían dichas definiciones. Hombres como G. Cantor, W. Sierpinski, H. Von Koch, G. Peano y D. Hilbert contribuyeron notablemente a elucidar el concepto de dimensión y al nacimiento de una nueva herramienta de investigación: la teoría de fractales, aunque ellos nunca lo supieron. [2.2].

Los orígenes de la teoría de fractales se remonta al siglo XIX, con las ideas de Henri Poincaré, quien inició el estudio formal de los sistemas dinámicos. Posteriormente diversos científicos y matemáticos trabajaron con distintos aspectos de esta teoría.

El desarrollo cronológico de los conceptos y técnicas que constituyen la teoría de los fractales ocurrió desde diferentes vertientes. En el recorrido histórico que se presenta enseguida se puede constatar el carácter tan variado de esta teoría. Por lo antes dicho, el desarrollo histórico dado a continuación no presenta una estructura estrictamente lineal. Se verá cómo la teoría de fractales se ha nutrido de la matemática, la física y otras disciplinas tan diversas que quedan contenidas en los trabajos de B.B. Mandelbrot [2.3].

JEAN BAPTISTE PERRIN.

Uno de los científicos que observaron y publicaron con respecto a objetos familiares de forma irregular fue el físico Jean B. Perrin (1870 – 1942). El prólogo de su célebre obra, Les Atomes (Perrin 1913) [2.3] expresa:

tangente son la recta, y las curvas regulares, tales como el círculo, son casos interesantes, pero particulares. Y como ocurre la mayoría de las veces, aquellas personas que se las habla de curvas sin tangente o funciones sin derivada piensan que la naturaleza no presenta tales complicaciones y que no nos sugiere esas ideas.

En la realidad experimental si se mira a través de un microscopio, se observa el movimiento browniano que agita cualquier pequeña partícula en suspensión en un fluido y se quiere una tangente a su trayectoria, se tendría que encontrar un límite, por lo menos aproximado, a la dirección de la recta que une las posiciones de dicha partícula en dos instantes sucesivos muy próximos. Ahora bien, hasta donde permita llegar la experiencia, esta dirección varía localmente cuando se disminuye el tiempo transcurrido entre ambos instantes...>>

NORBERT WIENER.

Hacia 1920, las ideas de Perrin las retomó el joven Norbert Wierner (1894 – 1964) y lo estimularían en la construcción de su modelo probabilístico del movimiento browniano. Wiener tenía afición para denominar una forma extrema del desorden natural. Él lo llamaba con la palabra “caos”, y nos permite apreciar que Perrin hizo dos observaciones distintas. Por una parte, que la geometría de la naturaleza es caótica y está mal representada por el orden perfecto de las formas usuales de Euclides o del cálculo newtoniano. Por otra parte, que dicha geometría evoca la complicación de las matemáticas creadas hacia 1900. Fue la obra de Wiener la principal fuente de inspiración para la creación de los objetos fractales. El dominio fractal había emergido (sin nombre) cuando se estudiaron fenómenos reales (tales como la longitud de una costa) por medio de teoría matemática avanzada, que surgieron en estudios donde el azar estaba involucrado.

Fue hasta mucho más tarde (1967) que estos acontecimientos se fundieron en una nueva disciplina: la geometría fractal. Esta se caracteriza por dos aspectos importantes: la existencia de problemas en el caos de la naturaleza y la aplicación de la herramienta matemática para su caracterización.

Con su maduración progresiva, esas dos características han creado algo nuevo: entre el dominio del caos y el orden excesivo de Euclides, así hay a partir de ahora una nueva zona fractal.

LEWIS FRY RICHARDSON.

La variación de la longitud aproximada de las fronteras entre dos países o las costas de algún país en particular fue estudiada empíricamente por el matemático inglés Lewis Fry Richardson (1881 – 1953), aunque su originalidad se tomara por excentricidad, y no haya alcanzado la celebridad que merecía. Rehuía los formalismos sin vacilar, empleaba conceptos finos y precisos allí donde él los creía útiles.

criterio de seguridad del cálculo. Al no conocerse aún la necesidad de tales normas, el error apenas evitable, pero debido a ello, la validez del principio del método de Richardson tuvo que esperar veinte años para ser reconocida.

Siguió con el estudio de la turbulencia, y sus trabajos le valieron ser elegido miembro de la Royal Society. Su obra muestra cómo se puede estudiar la difusión por el viento sin tener que hablar de su velocidad. Alude a la función continua sin derivada de Weierstrass. Así, Richardson no disponía del elemento fractal, pero su razonamiento es fácilmente traducible en términos de la visión “fractal” de la turbulencia. Aparecieron dos volúmenes después de su muerte, así como artículos, uno de los cuales salvó del olvido sus trabajos acerca de la longitud de las costas.

BENOIT B. MANDELBROT.

Mandelbrot es considerado como el padre de la geometría fractal. Sin embargo, se piensa que varios de los fractales y su descripción viene de las matemáticas clásicas; de hecho, como se verá varios matemáticos del siglo XIX y XX inventaron algoritmos especiales para su creación, tales como G. Cantor (1872), G. Peano (1890), D. Hilbert (1891), H. Von Koch (1904), W. Sierpinski (1916), y F. Hausdorff (1919), sólo por nombrar unos pocos. Es verdad que aquella matemática jugó un papel importante en los conceptos de Mandelbrot para la creación de la nueva geometría. Pero es verdad que aquellos matemáticos no pensaron, que de dichos algoritmos se pudiese generar conceptos para una nueva geometría de la naturaleza. Dichos algoritmos que generaban objetos matemáticos “raros” fueron relegados como objetos excepcionales o “monstruos matemáticos”.

En la obra de B. B. Mandelbrot, The Fractal Geometry of Nature 1982, se citan 48 referencias debidas a él mismo que de una o de otra forma influyeron para desarrollar el concepto fractal [2.3]. Dichas publicaciones datan de 1951 a 1986. Mandelbrot es un experto en la aplicación de la probabilidad y estadística a problemas concretos y reales en áreas tan diversas como termodinámica, sistemas de comunicación, teoría de la información, economía, climatología, cosmografía, mecánica de fluidos e ingeniería de materiales.

El concepto más importante para la teoría de fractales es el de auto-similitud, dicho concepto no aparece instantáneamente en los trabajos de Mandelbrot, va evolucionando a medida que aplica la herramienta matemática a las diferentes áreas arriba mencionadas y es hasta la década de los sesentas donde habla por primera vez de auto-similitud [2.3]. Pero es hasta 1967 cuando ya había madurado bien el concepto y además pudo cuantificarlo [2.4].

2.3. CONCEPTO DE AUTO-SIMILITUD.

reproducido como rectángulo, un triángulo con ciertos ángulos es reproducido en un triángulo con los mismos ángulos, etc. Lo único que cambia es la escala de la imagen.

El conjunto de Cantor, el triángulo de Sierpinski, la curva de Von Koch, la curva de Peano, la curva de Hilbert y todas las geometrías que emanan de ellas, presentan características de auto-similitud.

El triángulo de Sierpinski se define operacionalmente como un “proceso de agregación” que se obtiene a partir de un simple proceso de iteraciones. Para construir este fractal simplemente se itera una regla de crecimiento, muy parecido al juego de un niño cuando edifica un castillo con piezas. La unidad básica es el triangulo equilátero, como el que se muestra en la figura 2.2, además considere que este triangulo tiene una masa unitaria (M=1) y una longitud unitaria (L=1). En la etapa uno se juntan tres triángulos de tal manera que se obtiene una estructura que se muestra en la figura 2.2-b, un objeto de masa M = 3, y una arista de L = 2. El efecto de la etapa uno es generar un objeto con una densidad menor. Si se define la densidad menor como:

_{( ) ( )/} 2 (2.1) L

L M L ≡

ρ

entonces la densidad disminuye de 1 a ¾ como resultado de la primera etapa.

Figura. 2.2. Primeras dos iteraciones en la regla de agregación para construir el fractal triángulo de Sierpinski.

Ahora simplemente se itera; es decir, se repite la regla una y otra vez. Así pues, en la segunda etapa se unen las estructuras de la figura 2.2-b, dando como resultado un objeto con ρ = (3/4)2_{. y}

Figura 2.3. Fractal de Sierpinski después de cuatro iteraciones.

2.4. CONCEPTO DE AUTO-AFINIDAD.

Figura 2.4. Dos superficies rugosas, observadas en escalas diferentes. (a) superficie de cobre pulida en arena[2.15], cuando las rugosidades son observadas en una escala alrededor de 50 µm, (b) fatiga de cobre policristalina[2.16], cuando las rugosidades se

encuentra a una escala de unos cientos de ángstrom.

Para algunas superficies rugosas esta función h(r) es caracterizada como un fractal auto-afín. Los fractales auto-afines han sido definidos por Mandelbrot [2.5] como objetos geométricos que son invariantes (estadísticamente) bajo una dilatación anisotrópica, esto significa en el caso presente que allí existe un exponente H menor que 1 tal que la transformación deja a la superficie estadísticamente invariante (figura. 2.5). En contraste con el caso auto-similar, para el caso auto-afín se deben distinguir dos diferentes dimensiones, una “global”y una “local” [2.6, 2.7]. La dimensión global, que es observada a partir de una cierta escala crítica, es simplemente d – 1. Esto significa que, a grandes distancias, los fractales auto-afines tienen una apariencia tersa. La dimensión fractal local d

h h

r

r →λ , →λH

f puede ser determinada por los métodos clásicos, como el conteo de cajas [2.5, 2.8] y está relacionada con el exponente H por:

d_f =d−H (d−1≤d_f ≤d). (2.2)

En el ejemplo de la figura 2.5, el cual es invariante ante la transformación y , y . En general, los cortes paralelos al sustrato tienen una dimensión y pueden ser usados para medir d

r

r →5 h→3h

68 . 0 5 log / 3

log ≅

=

H d_f ≅1.32

1 − f

d f. Estos cortes son auto-similares.

Figura 2.5 Fractal auto-afín.

A fin de discutir la diferencia entre fractales auto-similares y fractales auto-afines, considere un conjunto limitado F, el cual es un d-espacio euclidiano. La posición de cada punto en F se describe por un vector X = (x1, x2,....xd). Una transformación auto-afín de cocientes de escalas

reales λi (0<λi<1, i = 1, 2,...., d) toma cada elemento de F con posición X dentro de un elemento

del conjunto λ(F) con una posición R = (λ1x1, λ2x2,...., λdxd). El conjunto F es auto-afín si es la

unión de N subconjunto congruentes distintos a λ(F). El conjunto F es estadísticamente auto-afín si sus subconjuntos son estadísticamente congruentes a λ(F).

Por ejemplo, una superficie estadísticamente auto-afín es invariante bajo una transformación afín, x’→λxx, λ’→λyy, z’→λzz. Requiriendo que tales transformaciones se combinen, implican una

estructura de grupo. Como una consecuencia λy y λz tienen que ser funciones homogéneas de λx;

ambas escaladas como:

y Z (2.3)

x Z x y

ν ν _{λ λ}

λ

λ ∝ , ∝

pero los exponentes νy y νz son diferentes en general [2.9]. Si es así, entonces λz ∝ λyH donde el

y z H ν ν

= (2.4)

Esto significa que el exponente de Hurst, ecuación 2.4, es inútil cuando se discuten en el mismo contexto los fractales auto-afines y los fractales auto-similares. Para una superficie auto-similar el exponente de rugosidad se define como H = νy = νz [2.12]. En el caso especial de una superficie

isotrópica con plano medio paralelo al plano coordenado (x, y), se tiene que ν ≡ 1, así que H = νz.

La última relación también es válida para cualquier fractal auto-afín en un plano bidimensional. Como un ejemplo de una curva auto-afín en un plano, se puede referir a la gráfica de la función de Mandelbrot-Weierstrass [2.13, 2.14], la cual se puede representar en la siguiente forma particular:

∑

[

]

z λ λ , (2.5)

donde λ >1 y 0< H < 1.

La gráfica de la función dada en la ecuación 2.5 posee un escalado auto-afín, esto implica que toda la función z(x) se puede reconstruir (en un sentido estadístico) a partir de su valor en el intervalo .x₀ ≤ x<λx₀ Por ejemplo, z(x) en los intervalos de y son versiones aumentadas y disminuidas en amplificación, respectivamente de z(x) en el

intervalo .

0 2 0 x x

x λ

λ ≤ < 0 0

1

x x x ≤ <

−

λ

0 0 x x

x ≤ <

2.5. DIMENSIÓN FRACTAL.

2.5.1. PRIMERAS FORMAS DE LA DIMENSIÓN FRACTAL.

Cuando Mandelbrot en 1967 “exhumó” el trabajo de Richardson de una colección en la que hubiera podido permanecer perdido por siempre, consistió en interpretar el exponente 1 + α como una dimensión fractal. Por ejemplo, la definición que se basa en recubrir la costa por puntos gruesos de radio η es precisamente la utilizada por Pontrjagin y Schnirelman 1932 para definir la dimensión de recubrimiento; la idea de la definición basada en el recubrimiento por una banda de anchura 2η fue utilizada por Minkowski 1901; otras dimensiones están relacionadas con la épsilon-entropía de Kolmogorov y Tihomirov 1959 – 1961.

La dimensión fractal Df, que es una propiedad del objeto la cual nos indica qué tanto ocupa el

Figura 2.6. Esquema simplificado entre dimensión euclidiana (De) y dimensión fractal (Df).

En la figura 2.6 en la parte superior se presentan 4 objetos considerados por la geometría euclidiana en algunas de las tres dimensiones (dimensiones euclidianas “De”), o bien cero (el

punto). Si estos cuerpos fueran continuos en el espacio; ejemplo cubo sólido, su dimensión fractal coincidiría con la dimensión euclidiana (Df = De); sin embargo, al ir amplificando el cubo o las

representaciones de la línea y el plano, en determinada escala de amplificación nos encontraremos que estos objetos tienen espacios vacíos, están llenos de “poros”, por lo que de acuerdo a la geometría fractal, la línea tiene una dimensión fraccional o fractal mayor que 0 pero menor que 1, dependiendo qué tantos “poros” tiene el plano 1 < Df < 2 y el cubo 2 < Df < 3.

2.6 MOVIMIENTO BROWNIANO.

A principios del siglo XIX, el botánico escocés Robert Brown (1773-1858) descubrió una gota de agua de un trozo de cuarzo. El agua, pensó Brown, debía de haber permanecido inaccesible durante siglos al polen y las esporas transportadas por el viento o la lluvia. Al enfocar dicha gota en un microscopio, observó trazas de partículas suspendidas en la misma que oscilaban sin cesar con un movimiento completamente irregular. Este movimiento le resultaba familiar a Brown: había observado antes semejante tipo de oscilaciones en sus estudios de granos de polen en agua. Brown concluyó con razón que la agitación de las partículas atrapadas en el interior del cuarzo debía de ser fenómeno físico y no biológico, pero no pudo llegar a mayores precisiones.

las moléculas circundantes. Por otro lado, como el microscopio es esencialmente un filtro que sólo pone de manifiesto los efectos de fluctuaciones de cierta magnitud en el entorno molecular local, el movimiento observado sólo insinúa la complejidad de la trayectoria real. Si el poder de resolución del microscopio se incrementa en un factor de 10, 100 ó 1000, se detectarán los efectos del bombeo por grupos progresivamente menores de moléculas. A un mayor aumento, partes de la trayectoria de la partícula que inicialmente había aparecido como rectas se observarán ahora dotadas de una estructura quebrada e irregular. La trayectoria de una partícula en el movimiento browniano fue uno de los primeros fenómenos naturales en los que se reconoció una auto-similitud a cada grado de aumento, una propiedad clave de los objetos geométricos que Benoit B. Mandlebrot ha denominado fractales [2.3]. En la figura 2.7 se presenta el conjunto de Mandelbrot [2.17].

Desde el principio de siglo, el estudio del movimiento browniano ha ejercido una poderosa influencia en física, química y matemáticas. En manos de Albert Einstein se convirtió en un método de observación concluyente para la confirmación de la teoría atómica de la materia. Einstein demostró, que la medición de ciertas propiedades del movimiento browniano de las partículas determinaban diversas constantes físicas de importancia: las masas de los átomos, de las moléculas y el valor del número de Avogrado (unidad química estándar de cualquier sustancia). El movimiento browniano también ha contribuido a una compresión teórica más profunda de los principios de la termodinámica, formulado con anteoridad sobre lo que resultaron ser generalizaciones empíricas.

2.7 REFERENCIAS:

[2.1] COURANTR.Y ROBBINS H.; ¿Qué es la Matemática?, Editorial Aguilar, quinta edición, primera reimpresión 1971.

[2.2] PEITGEN, H. O.; JORGEN, H,; SAUPE, D.; Chaos and Fractals; Springer Verlag, (1992).

[2.3] MANDELBROT, B. B., The Fractal Geometry of Nature; W. H. Freeman and Company New York (1983).

[2.4] MANDELBROT, B. B.; How lolg is the coast of Britain?. Statistical self Similary and Fractional Dimension, Science. Mayo 1967.

[2.5] B. B. MANDELBROT: The Fractal Geometry of Nature (W. H. Freeman, New York 1982).

[2.6] B. B. MANDELBROT, IN: Fractals in Physics, ed. by L. Pietronero, E. Tossat, North-Holland, Amsterdam (1986), P. 3

[2.7] T. VICSEK: Fractal Growth Phenomena, 2nd ed. (Word Scientific, Singapore 1991). [2.8] JFEDER: Fractals (Plenum, New York 1988); J. F. Gouyet: Physics and Fractal

Structure (Springer, New York, 1995).

[2.9] MANDELBROT B. B., Self-affine fractal sets, II: length and surface dimensions, in fractals in Physics (Edited by L. Pietronero and E. Tosatti); Elsevier, New York, (1986) pp. 17-20.

[2.10] UNDERWOOD E. E. and BANERJI K., Fractals in fractography, Materials Sci. and Eng. 805, (1986) pp. 1-14.

[2.11] UNDERWOOD E. E. and BANERJI K. K., Fractal analysis of fracture surfaces, in Metals Handbook. V 12: Fractography, ASM, New York, (1992) pp. 211-215. [2.12] BALANKIN A. S., Fractal mathematics for physicists: 1. Basic concepts, Physical

notions, and mathematical tools, Rev. Phys. To be published.

[2.13] BERRY M. V. and LEWIS Z. V., On the Weierstrass-Mandelbrot fractal function, Proc. R. Soc. Lon. A370 (1980) pp. 459-484.

[2.14] AUSLOOS M. and BERMAN D. H., A multivariate Weierstrass-Mandelbrot function, Proc. R. Soc. Lond. A400, (1985) pp. 331-350.

[2.15] C. ROQUES-CARMES, Private communication.

[2.16] M. W. Mitchel, D. A. Bonnell: J. Mater. Res. 5, 2251 (1990).

[2.17] PETGEN, H. O., RITCHER, P. H.; The Beaty of Fractals; Spinger-Verlag, (1986). [2.18] JURGENS, H,; PETGEN, H., O.; SAUPE, D.; El lenguaje de los fractales;

CAPÍTULO 4

4. MEDIOS POROSOS.

4.1. ESTRUCTURA Y CLASIFICACIÓN.

En sentido general, un material poroso es un sólido que contiene hoyos. Sin embargo, un cilindro metálico hueco no es clasificado como un material poroso; por consiguiente, una mayor especificación del termino material poroso es requerido. Para el propósito de este estudio un sólido que contiene hoyos o vacíos conectados o no conectados, dispersos dentro de él de manera aleatoria, puede ser clasificado como un material poroso, dado que estos agujeros ocurren frecuentemente dentro del sólido.

Una gran variedad de materiales naturales y artificiales son porosos; un cubo de arena, una pieza de piedra caliza, un manojo de algodón, un bollo o pan son ejemplos de materiales porosos, en la figura 4.1 algunos ejemplos de materiales porosos son mostrados. De estos, es obvio que gran variedad en el tamaño y estructura de poros existen en tales materiales. Algunas clasificaciones de poros es posible; sin embargo, los poros pueden estar interconectados o no. Un fluido puede fluir por medio de un material poroso sólo si por lo menos algunos de los poros están interconectados; el espacio del poro interconectado es llamado el espacio del poro efectivo, mientras que la totalidad del espacio del poro es llamado espacio del poro total.

Los espacios dentro de un material poroso pueden además ser clasificados de acuerdo a su tamaño. Son posibles tres primeras clasificaciones basadas en el comportamiento de fluidos dentro del espacio vacío. En los espacios vacíos más pequeños, las fuerzas moleculares entre las moléculas del sólido y las del fluido son significativas. Estos espacios diminutos vacíos son llamados intersticio molecular. En el espacio vacío más grande, el movimiento de un fluido es parcialmente determinado por las paredes de la cavidad: Estos espacios más grandes son llamados cavernas. Los espacios que tienen un tamaño intermedio entre los intersticios y las cavernas son llamados poros. Algunas veces es realizada una clasificación adicional de estos poros, principalmente en las piedras calizas o rocas de dolomita. Las cavidades de tamaño más pequeño (vugs) y el espacio formado por estas es llamado espacio del poro vugular.

Una clasificación adicional de los materiales porosos divididos dentro de dos grupos, ordenados y aleatorios. El significado es obvio, un empaquetamiento regular de esferas es ordenado mientras un bollo o pan es aleatorio en su estructura porosa.

4.2. ESTRUCTURA Y PROPIEDADES.

La mayor parte de materiales porosos naturales y artificiales tienen una estructura hueca aleatoria; en realidad, la estructura de los materiales puede ser descrita solo en términos estadísticos. Aun así, es posible tratar el flujo de fluidos a través de dichos materiales sobre una base macroscópica en términos precisos, como la situación es mucho más parecida con la energía cinética de la teoría de los gases; en una escala microscópica las variables en cuestión deben, a su gran número y complejidad, ser tratadas como variables aleatorias pero a una escala macroscópica el sistema puede ser tratado en términos de unas pocas cantidades completamente determinables.

Muchas teorías se han inventado, como intentos para relacionar en una manera detallada las propiedades macroscópicas de los materiales porosos con las propiedades estadísticas de su estructura microscópica. Dichas teorías intentan relacionar “la distribución del tamaño de poro” con las propiedades macroscópicas del material [4.1]. Algunos intentos han relacionado “la distribución del tamaño del grano”[4.2] de materiales, con sus propiedades macroscópicas. Mientras que las teorías contribuyen grandemente para el entendimiento de los procesos físicos básicos dentro de medios porosos, en general no contribuyen a la solución de problemas a una escala macroscópica.

4.3. POROSIDAD.

La porosidad de un material poroso es la fracción del volumen total para el material ocupado por vacíos. El símbolo usado es φ aunque algunas veces también es usado f así:

total Volumen poros de Volumen = = φ B P V V (4.1)

por lo tanto es una cantidad adimensional.

Puesto que la porción de volumen total no ocupado por poros es ocupada por los granos del sólido o matriz del material. Como sigue:

total Volumen solido de Volumen 1−φ= =

B s

V V

(4.2)

Dos clases de porosidad pueden ser definidas; es decir, absoluta o total y porosidad efectiva. Porosidad absoluta es el espacio vacío fraccional con respecto al volumen total sin tener en cuenta las conexiones del poro. La porosidad efectiva es la fracción del volumen total constituido por la interconexión de poros. En rocas naturales, como lava y otras rocas ígneas, tienen una alta porosidad pero esencialmente no tienen porosidad efectiva. La porosidad efectiva es una indicación de la permeabilidad pero no una medida de ella.

4.4. MEDICIÓN DE POROSIDAD.

A partir de la definición de porosidad, es evidente que la porosidad de una muestra de un material poroso y puede ser determinada por la medición de dos de las tres cantidades: volumen total, volumen de poro o volumen de sólido.

4.4.1. MÉTODO DIRECTO.

El procedimiento más directo es medir el volumen total, triturar el espécimen, remover todos los poros, y entonces medir el volumen restante del sólido, esta técnica es a menudo usada para ladrillo y cerámica. Este método produce una medición de la porosidad total.

4.4.2. MÉTODO DE EXPANSIÓN DE GAS.

1 2 2 Poro de Volumen P P P V V V_{B a b}

− −

−

= (4.3)

donde

VB = Volumen total de la muestra.

Va = Volumen donde se introduce la muestra. Vb = Volumen de la segunda cámara (la evacuada). P1 = Presión inicial.

P2 = Presión final.

Una variedad de instrumentos de muchas formas diferentes han sido desarrollados usando este principio básico. Sin embargo el método de expansión de gas no es tan exacto como otras técnicas.

4.4.3. MÉTODO DE INYECCIÓN DE MERCURIO.

La medición de porosidad efectiva mediante el método de inyección de mercurio está basado en el hecho que, una muestra porosa puede ser sumergida en el mercurio sin que éste se introduzca en su interior a una presión atmosférica, esto es debido a las propiedades del mercurio tales como la tensión superficial y que no moja. Así, el volumen total de la muestra puede ser determinado mediante el desplazamiento del mercurio desde una cámara de volumen conocido.

Si la muestra es encerrada en una cámara y la presión hidrostática de mercurio en la cámara es incrementada a un gran valor, el mercurio entra en los poros comprimiendo el aire atrapado en ellos hasta un volumen despreciable. El volumen de mercurio inyectado es, por lo tanto, igual al volumen del poro.

Una ventaja de este método es que tanto el volumen total y el volumen del poro son determinados directamente. Este método no es muy preciso puesto que el volumen ocupado por el aire comprimido no es determinado. Es indeseable ya que la muestra invariablemente contiene mercurio contaminado aun después de intensivos procedimientos de limpieza y por lo tanto no es apropiado para otro ensayo.

4.4.4. MÉTODO DE DENSIDAD.

Ya que la masa de un material poroso recae completamente en los poros, o matriz, se sigue que:

M =ρ_gV_g =ρ_BV_B (4.4)

donde

M = Masa de la muestra.

ρg = Densidad del material granulado.

en vista de la ecuación 4.2 se sigue que:

g B

ρ ρ − =

φ 1 (4.5)

La densidad bruta puede ser fácilmente determinada pesando la muestra y midiendo el volumen total mediante una técnica de desplazamiento volumétrico. Se puede usar la inmersión en mercurio pero es mejor aplicar un recubrimiento impermeabilizante y sumergirlo en agua.

La densidad del material sólido puede ser determinada triturando una muestra del material, pesándolo y luego empleando una técnica para la determinación del volumen. Este método da la porosidad total.

4.4.5. MÉTODO DE IMBIBICIÓN.

Es un método muy directo para medir el volumen efectivo de poro, y por lo tanto ampliamente empleado en la industria petrolera. Ya que la mayoría de las rocas limpias preferencialmente mojables por agua, ellas imbiben agua fácilmente. Así, si una muestra de roca se sumerge en agua al vacío por una semana o algo así, el espacio poroso se satura completamente con agua. Entonces, la masa de la muestra saturada será:

M'= M +ρ_wV_P (4.6)

donde ρw es la densidad del agua (≈1) y M es la masa seca de la muestra. Por lo tanto:

w P

M M V

ρ −

= ' (4.7)

con la muestra completamente saturada con agua, una medición del desplazamiento volumétrico en agua da directamente el valor de VB sin ningún procedimiento de recubrimiento y de esta forma φ pueda ser calculada.

Excepto por la gran cantidad de tiempo para que ocurra completamente la saturación, este es por lo tanto uno de los mejores métodos para la medición de la porosidad que actualmente se usa.

4.4.6. MÉTODO ESTADÍSTICO.

Este principio a sido empleado por Chalkley, Corrfield y Park [4.3] para medir la porosidad. Una aguja se deja caer varias veces de manera aleatoria sobre una fotomicrografía ampliada de una sección del material poroso. Se puede demostrar que en el límite, cuando el número de lanzamiento de la aguja es grande, la relación del número de veces que el punto cae en un poro con respecto con el número total de lanzamientos se aproxima al valor de φ.

Observe que ya que los poros aislados como los conectados están expuestos este método da la porosidad total.

4.5. PERMEABILIDAD.

Es la propiedad de un material poroso que caracteriza la facilidad con la cual un fluido puede ser obligado a fluir a través del material por un gradiente de presión aplicado. La permeabilidad es la conductividad del fluido del material poroso. Dicho parámetro caracteriza la conductividad del fluido de un material poroso y fue demostrado por Darcy 1856 [4.4]. de hecho la ecuación que define la permeabilidad en términos de cantidades medibles es llamada la ley de Darcy.

Si un flujo lineal y horizontal de un fluido incompresible es establecido a través de una muestra de material poroso de longitud L en la dirección de flujo y una sección transversal de área A, entonces la permeabilidad, K, del material es definida como:

) / ( p L A

q K

∆ µ

= (4.8)

donde q es el gasto, la µ es la viscosidad del fluido y ∆P es la diferencia de presión del fluido a través de la sección del espécimen.

El valor de la permeabilidad, K, es determinado por la estructura del material poroso. A partir del análisis de la ecuación 4.8, se observa que K tiene dimensiones de longitud al cuadrado. K es aproximadamente una medición de la media cuadrática del diámetro del poro en el material. Muchos materiales porosos tienen una calidad direccional en su estructura, como consecuencia las permeabilidades medidas con un flujo perpendicular a cada cara de un cubo de dicho material no son iguales. Dichos materiales son conocidos como medios porosos anisotrópicos.

La unidad más ampliamente utilizada para la permeabilidad es el Darcy (d). Esta es definida como: Para un material cuya permeabilidad sea un darcy y una diferencia de presión de una atmósfera producirá un gasto de 1 cm3/s de un fluido que tenga una viscosidad de 1centipoise a través de un cubo cuyos lados tienen una longitud de 1 cm. Así:

) / ( 1 ) ( 1 ) ( 1 ) / ( 1 darcy

1 ₂3

cm atm cm cp seg cm ⋅ ⋅