Curvas y Superficies (Integrales)

CAPITULO 1. CURVAS Y SUPERFICIES

1.1. Curvas en el plano

Definición 1 .Definimos curva en el plano

 

 

t



x

   

t ,y t



α t

R R b , a : α

C 2

 

  

que nos lleva a la ecuación paramétrica de la curva C : t[a,b] ,curva que une el punto A con el punto B del plano

En este punto definimos las características más importantes de las curvas o caminos.

• Una curva C es continua si x (t), y (t) son continúas.

• Una curva C es cerrada si A = B, es decir, si empieza y termina en el mismo punto.

• Una curva C es simple si no pasa dos veces por el mismo punto.

• Una curva C es regular si existen x'(t) y’(t) y son continuas. Cuando ocurre esto salvo en un número finito de puntos se dice que la curva es regular a trozos. Salvo que se indique lo contrario trabajaremos con curvas regulares a trozos.

• Una curva C es rectificable si tiene longitud finita.

• Una curva C es de Jordan si es cerrada y simple.

1.2. Superficies: primeros conceptos

El estudio de las superficies exige una representación analítica de ellas. Vamos a ver diversas representaciones comenzando por el caso de coordenadas cartesianas. Consideremos una referencia afín,



0

,

i

,

j

,

k



en R3 donde los vectores

 

i

,

j

,

k

forman base ortonormal.

Definición 2 .Una superficie es una aplicación r:DR2 R3 , es decir

  

u,v x(u,v),y(u,v),z(u,v)



La expresión r

 

u,v x(u,v)iy(u,v)jz(u,v)k recibe el nombre de ecuación vectorial de la

superficie. Descomponiendo dicha expresión en sus funciones componentes se obtiene

D ) v , u ( v) , z(u z

v) , y(u y

v) , x(u x

 

   

  

Denominadas ecuaciones paramétricas de la superficie. Los parámetros u y v reciben el nombre de coordenadas curvilíneas de la superficie. Se denomina ecuación explícita de la superficie aquella en que los parámetros son dos las variables por ejemplo (x, y) obteniéndose z = f (x, y) Una relación entre las variables x, y, z de la forma F(x, y, z) = 0 recibe el nombre de ecuación implícita de la superficie.

Una superficie se dice de clase C k _{si la función}

_r

_{(u, v) es de clase C} k _{, o lo que es lo mismo, si las}

funciones x (u, v), y (u, v), z (u, v) son de clase C k _{.Si no se dice otra cosa se supondrá que la superficie es}

de clase C k

1.3. Algunas superficies importantes

Describiremos aquí las superficies más importantes que aparecen en la práctica. Empezaremos con las principales cuádricas canónicas: Esfera, elipsoide, hiperboloides, paraboloides, y algunos casos de cilindros y conos. A continuación analizaremos las superficies de revolución y traslación para acabar con una pincelada sobre las superficies regladas, que serán analizadas con más detenimiento posteriormente. Esta clasificación que hemos realizado no es excluyente. Por ejemplo un cilindro circular es una superficie de revolución y reglada.

La esfera de ecuación implícita x 2 _+y2 _{+ z} 2 _{= a} 2_{, admite como ecuaciones paramétricas}































u

sen

a

z

π

2

v

0

v

sen

u

cos

a

y

2

π

u

2

π

v

cos

u

cos

a

x

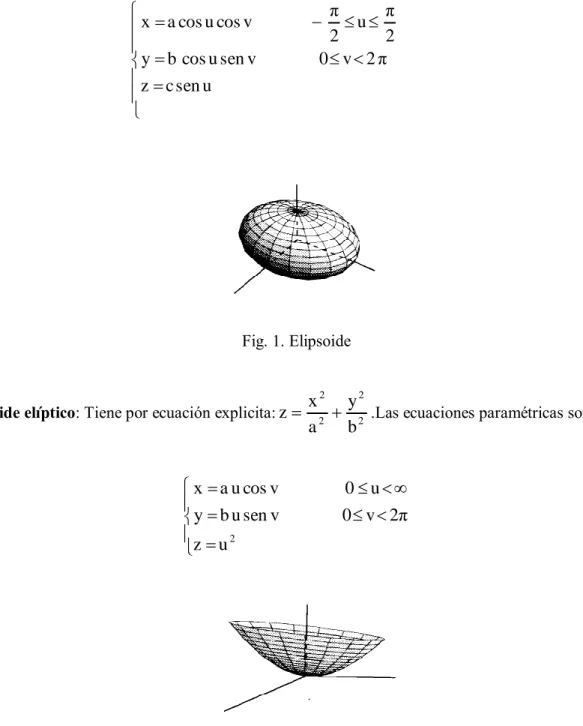
El elipsoide (Fig.1) de ecuación implícita

1

c

z

b

y

a

x

2 2

2 2

2 2



































u

sen

c

z

π

2

v

0

v

sen

u

cos

b

y

2

π

u

2

π

v

cos

u

cos

a

x

Fig. 1. Elipsoide

Paraboloide elíptico: Tiene por ecuación explicita: ₂ 2

2 2

b

y

a

x

z





.Las ecuaciones paramétricas son



























2

u

z

2π

v

0

v

sen

u

b

y

u

0

v

cos

u

a

x

Fig. 2. Paraboloide elíptico

Si a = b el paraboloide se denomina circular.

Paraboloide Hiperbólico: ₂ 2

2 2

b

y

a

x

z





es la ecuación del paraboloide hiperbólico (Fig.3). La

                   2 2 v u z v v b y u u a x Fig.3.Paraboloide hiperbólico

Hiperboloide de una hoja:

1

c

z

b

y

a

x

2 2 2 2 2 2







(Fig. 4). Unas posibles ecuaciones paramétricas son

               u h sen c z 2π v 0 v sen u h cos b y u v cos u cosh a x

Fig. 4. Hiperboloide de una hoja

Hiperboloide de dos hojas:

1

a

x

b

y

c

z

2 2 2 2 2 2







.Unas ecuaciones paramétricas de la primera hoja son

             u h cos c z 2π v 0 v sen u h sen b y u 0 v cos u h sen a x

    

 

  

   

u cos c . z

2π v 0 v

sen u h sen b y

u 0 v

cos u h sen a x

Cilindro circular con generatrices paralelas al eje OZ, tiene por ecuación implícita x 2 _{+ y}2 _{= a}2_{. Unas}

posibles ecuaciones paramétricas son

    



  

     

u z

2π v 0 v sen a y

u v

cos a x

Cono circular de vértice el origen puede expresarse en forma x 2 + y2 - a2z2 =0

Fig. 5: Cono circular

Unas posibles ecuaciones paramétricas son

    



  

     

u z

π 2 v 0 v sen u a y

u v

cos u a x

1.4. Primeros conceptos sobre superficies

Definición 3 .Sea la superficie S definida en forma implícita por F(x, y, z) = 0, donde la función F es al menos de clase Cl_{. Sea P}

0(x0, y0, z0) un punto de la superficie S, esto es, verifica F (x0, y0, z0) =0 .El punto P0

se dice punto singular de S sí

│F x (x0, y0, z0)│+ │F y (x0, y0, z0)│+ │F z (x0, y0, z0)│=0

En caso contrario el punto P0(x0, y0, z0) recibe el nombre de punto regular.

Sea la superficie S de ecuaciones paramétricas

 

    

   

v) , z(u z

v) , y(u y

v) , x(u x v , u r

donde r (u, v) es al menos de clase C l _{en un entorno de (u, v)}

_

_D.

El punto P0(x0, y0, z0) =(x (u0, v0),y(u0,v0),z(u0,v0)) es un punto regular de S si se verifica



r

u



r

v



_u₀,v_0



0

que es equivalente a decir que la matriz tiene rango dos.

Un punto de la superficie S es punto singular de S si no es regular.

El que un punto sea singular para una superficie expresada en forma implícita es algo inherente a la superficie. Así por ejemplo, el punto (0, 0, 0) es un punto singular para el cono de ecuación x2 _{+ y}2 _{- z}2 _{= 0,}

que corresponde a su vértice.

Sin embargo, ser punto singular para una superficie expresada en forma paramétrica puede depender de la parametrización elegida, pudiendo un punto ser singular para una parametrización y regular para otra.

Los dos ejemplos anteriores muestran que hay dos tipos de puntos singulares: Esenciales, que son debidos a la "geometría" de la superficie y que son independientes de la parametrización de la superficie y artificiales, que se deben a la parametrización elegida para la superficie.

En todo lo que sigue supondremos que todos los puntos de una superficie son regulares. En caso de existencia de puntos singulares se pondrá de manifiesto de forma explícita.

1.5. Vectores normales a una superficie. Plano tangente

Un vector normal a la superficie rr

 

u,v en un punto regular P, correspondiente a los valores (u0, v0) de

los parámetros, es cualquier vector que tenga la dirección del vector

 

v v v

u u u v

,

u _{x y z}

z y x

k j i

v r u r

0 o

 

  

 

    

Si la superficie viene expresada en la forma implícita, F(x, y, z) = 0, un vector normal a la superficie, en un punto regular P0(x0, y0, z0) de ella, viene dado por el vector (F x(x0, y0, z0), F y (x0, y0, z0), F z(x0,y0,z0) )

Un vector normal unitario será el vector _{ }





 





 0 0 0 0 0

0

v , u v u

v , u v u v

, u

r r

r r ν

  

El plano tangente a la superficie rr

 

u,v en un punto regular P de coordenadas (x0, y0, z0)

correspondiente a los valores (u0, v0) de los parámetros, es el plano que pasa por P y tiene como vector

característico un vector normal a la superficie en P. Siendo r_ (x,y,z) una ecuación del plano tangente

será







r





r

u

₀

,

v

₀



.





_{ }

0 0,v u v u

r

r



=0

que puede expresarse en la forma

0 z

y x

z y

x

z z y

y x

x

v v

v

u u

u

0 0

0

  



El plano tangente contiene a los vectores ru,r_v lo que nos permitirá deducir, en el apartado siguiente, que dicho plano contiene a todas las rectas tangentes a curvas que estén contenidas en la superficie y pasen por el punto r



u₀,v₀



Se denomina recta normal a la superficie en un punto regular P, correspondiente a los valores (u0, v0) de los

parámetros, a la recta que pasa por P y tiene como vector director un vector normal a la superficie en P. Una ecuación vectorial de la recta normal será



u0,v0



λr



u0,v0



r

R 

1.6. Expresiones de una curva sobre una superficie

Sea la superficie rr

 

u,v .Una curva sobre dicha superficie viene dada por una relación entre los

parámetros u y v. Esta relación puede adoptar diversas formas:

2. Forma explícita: u =  (v)

3. Forma paramétrica: u=u(λ) , v=v(λ)

4. Forma diferencial:

f

 

u

,

v

u

d

v

d



La forma diferencial representa una familia de curvas, ya que su integración dará lugar a una expresión de la forma (u, v, k)=0, debiéndose fijar alguna condición para determinar la constante k.

5. Forma cuadrática diferencial: A(u,v)du2_{+2B(u,v)du dv+C(u,v)dv}2_{=0 . Vamos a suponer C ≠ 0.}

Resolviendo

A

0

du

dv

B

2

u

d

v

d

C

2



















se obtienen dos familias de curvas en forma diferencial que son:

 

f

 

u

,

v

du

dv

,

v

,

u

f

du

dv

2

1





para valores (u, v) tales que B2 _{- AC > 0.Representa pues dos familias de}

curvas sobre la superficie.

1.7. Curvas coordenadas sobre una superficie

Las relaciones u=C1 (Cte.), v=C2 determinan al variar v y u respectivamente, dos familias de curvas sobre

la superficie que reciben el nombre de curvas coordenadas o paramétricas

Fig. 8

Las curvas

u



C

₁

,

v



C

₂ fibran la superficie

Si queremos prever el futuro de la matemática, el camino adecuado para conseguirlo es el de estudiar la historia y el estado actual de esta ciencia.

Henri Poincaré

CAPITULO 2.INTEGRALES MULTIPLES

2.1. Integral doble

Sea D un dominio acotado del plano XOY, limitado por una curva cerrada C que se supondrá rectificable. Supongamos que dicho dominio D tiene un área A. Sea f(x,y) una función acotada en el dominio D . Dividamos de forma arbitraria D en n dominios parciales, 1, 2……n de áreas ω1,ω2…….ωn . Cualquiera que sea la forma en que se ha hecho la partición, se





 n 1 p

p

ω

A

(1)

Consideremos ahora en cada dominio parcial p un punto arbitrario de coordenadas ( ωp , p) y formemos la siguiente suma





p

n

1 p

p p ,η ω

ψ f

Ω





 (2)

Llamemos diámetro del dominio al extremo superior de la distancia entre dos cualesquiera de sus puntos.

Diremos que la función f(x ,y) es integrable en D si el límite de la expresión (2) tiende a un límite finito I cuando n -> ∞ de modo que el mayor de los diámetros de los dominios parciales tienda a cero.



ψ ,η



ω f

 

x,ydxdy

f lim I

D p n

1 p

p p

n









2.2. Clase de funciones integrables

1.Toda función continua en un dominio D es integrable en este dominio.

2.Si f(x,y) permanece acotada en D y tiene en dicho dominio un número finito o infinito de puntos de discontinuidad , estando estos puntos distribuidos sobre un número finito de arcos rectificables de curvas planas contenidas en D , la función es integrable en el citado dominio.

2.3. Propiedades de la integral doble

1.Si la función f(x,y) es acotada e integrable en los dominios D y E teniendo estos dominios una parte de frontera común , también es integrable en D+E

 

 

 









 

E

D D E

dxdy y x, f dxdy y x f dy dx y x f

2.Si las funciones f(x,y) y g(x,y) son acotadas e integrables en D , se verifica

   









 



 







D fx,y gx,y dxdy Dfx,y dxdy Dgx,y dxdy

3.Si f(x,y) es acotada e integrable en D y k es una constante, se verifica

 

x,y dxdy k f

 

x,y dxdy f

k

D D







4.Si f(x,y) es integrable en D , también lo es │f(x,y)│ verificándose

 

_

 





D

2.4. Teorema de la media

Si f(x,y) y g(x,y) son funciones acotadas e integrables en un dominio D y g(x,y) tiene signo constante en el citado dominio, se verifica







Df(x,y)g(x,y)dxdy μ Dg(x,y)dxdy (3)

 es un número comprendido entre los extremos m y M de f(x,y) en D

Casos particulares

1.Si f(x,y) es continua en el dominio D , tomara el valor  (ψ ,) del dominio y de la expresión ( 3 ) se obtiene







Df(x,y)g(x,y)dxdy f(ψ(η) Dg(x,y)dxdy (4)

Si f(x,y) es continua en el dominio D y g(x,y)=1 en las fórmulas (3) y (4), se verifica









  

D

Df(x,y)dxdy μA f(x,y)dxdy Afψ,η

f(ψ , ) es el valor medio de f(x,y) en el dominio D





D y)

,

medio(x _A1 f(x ,y )dxdy

f

2.5. Calculo de integrales dobles

Si D es un dominio de integración horizontalmente simple o verticalmente simple , la integral doble sobre D de una función continua es una integral iterada. Es decir, sea





 

 



x ,y / a x b ,f x y f x



Siendo f1(x) y f2(x) funciones continuas en [a,b].

Entonces





_

_

_{ } 







 b

a

x 2 f

x 1 f

D f x ,y dxdy dx f x ,y dy

(5)

Análogamente, sea





 

 



x ,y / c y d ,g y x g y



D   1   2

Siendo g1(y) y g2(y) funciones continuas en [c, d] . Se verifica









   

dx y , x f dy dxdy y , x

f d

c

y 2 g

y 1 g

D









Ejercicios de aplicación

1

. Calcular I 4x y dxdy D

2 2





 D es el dominio limitado por el triángulo de lados x =1, y = 0, y =x

dy y 4x dx

I x

0

2 2 1

0









Calculemos la integral 



x 

0

2 2

1 4x y dy

I

Cambio de variable: y =2 x sen t , t 0

6 π

t 

    

  

 









2 3 3 π x dt t cos x

4 dt cost cost x

4

I π/6 2

0 2 2

π/6 0 2 1

Por tanto.

18 π 2 3 3 dx x 2

3 3 π

I 1 2

0

  

   

  



2.

Calcular 



D xydxdy

I donde D es el área limitada por la recta y= x y la curva y= x2





24 1 dx x x 2 1 dy y dx x I 1

0

x 2 x

1 0

5 3









 



2.6. Suplicación del cálculo de integrales dobles

Sea f(x,y) integrable en un dominio D acotado

1. Si D es simétrico respecto al eje OX y f(x,-y)=-f(x,y) , entonces I=0

2. Si D es simétrico respecto al eje OX y f(x,-y) = f(x,y)



2 f(x,y)dxdy I

extendida a la mitad inferior o superior del dominio D

3. Si D es simétrico respecto al eje OY y f(-x , y)= -f(x ,y) , entonces I=0

4. Si D es simétrico respecto al eje OY y f(-x , y)=f(x,y)



2 f(x,y )dxdy I

extendida a la mitad izquierda o derecha del dominio D

5. Si D es simétrico respecto al origen de coordenadas y f(- x ,-y)=-f(x,y) , I=0

6. Si D es simétrico respecto al origen de coordenadas y f(- x ,-y)=f(x,y)



Ejercicios de aplicación

1. Calcular I



x y y x



dxdy

D 3



 

 donde D es el dominio x2_+y2

-1≤0 , x≥0

D es un dominio simétrico respecto al eje OX













D D D

3_{ydxdy ydxdy xdxdy}

x I

___I1 __ __I2 __ __I3__

Cálculo de I1: f(x,y)f(x,y)I10

Cálculo de I2

0 I y) f(x, y)

f(x,   ₂

Calculo de I3





  



 

  1

0

2 x 1 0

1 0

2 3 2 xdx dy 2 x 1 x ₃2

I

Luego 3

2 I

2.Calcular 









D

3 3 _{y dxdy} x

sen

I donde D es el dominio 1 9 y 4

x2 2

  .

D es un dominio simétrico respecto al origen de coordenadas, verificándose:

) y sen(x ]

y) ( x)

sen[( 3  3  3 3

2.7. Cambio de variables en integrales dobles

Sea la integral doble



 

Df x,y dxdy extendida a un dominio plano D limitado por la curva cerrada C.

Se quiere cambiar las variables (x, y) por otras (u ,v) mediante las ecuaciones







u ,v



(6)

y y

v , u x x

   



La nueva integral se extenderá a un dominio R limitado por una curva T imagen de C . La

correspondencia definida por las ecuaciones (6) es biunívoca cuando a cada punto del dominio D limitado

por C , le corresponde un único punto del dominio R limitado por T y recíprocamente. Para que la

correspondencia sea biunívoca es preciso que el determínate Jacobiano sea ≠0

Se denomina determinante Jacobiano (x,y) con respecto a u y v y se simboliza por

v) D(u,

y) D(x,

al determinante

v y u y

v x u x

v) D(u,

y) D(x,

   

   



Si f(x,y) es continua en D y las funciones x(u ,v) , y(u,v) son derivables con derivadas continuas en R y el Jacobiano anteriormente definido es ≠0 en R , entonces se tiene

 

_





 





_

 

_





Δ

D Du,v dudv (7)

y , x D v , u y , v , u x f dxdy y x, f

El elemento diferencial dx dy se ha tomado positivo . Si queremos considerar positivo du dv , será preciso tomar positivo el jacobiano , lo cual implica que la expresión (7) adopta la forma

   





Coordenadas Polares:x=ρ Cos θ , y =ρ Sin θ







u ,v



ρdρdθ

D y , x D





x ,y



dxdy f



ρcosθ ,ρsen θ



ρdρdθ f

Δ

D







Ejercicios de aplicación

1.

Calcular I



x y



dxdy D

2 2





 donde D es el área de la lemniscata ρ2 _2a2cos2θ

_.

Coordenadas polares

2 a π dθ 2θ cos a 4 dρ ρ θ

d 4 dθ dρ ρ ρ 4

I 4

D

4 π

0

2θ cos 2 a 0

4 π

0 2 4

3 2





 









2.8. Calculo de volúmenes

Se trata de calcular el volumen del cuerpo limitado por la superficie z=f(x,y) el plano XOY y una superficie cilíndrica de generatrices paralelas a O Z , cuya directriz es la curva C del dominio D , en el cual se supondrá f(x,y) positiva e integrable. Este volumen viene dado por la integral doble

 





D

dy dx y x, f V

El volumen comprendido entre dos superficies z1=f1(x,y) y z2=f2(x,y) siendo f2(x,y) > f1(x,y)

contenido en un cilindro de base D y generatrices paralelas a OZ viene dado por

   











D f2 x,y f1 x,y dxdy

V

1.

Calcular el volumen limitado por (x-c)2_{+ (y-d)}2_=R2 _{, z=0 y x y =a z}

Cambio de variables









 1

        

    

1 0

0 1 Y , X J

y , x J Y d y Y d y

X c x X c x

El plano z=0 se transforma en z=0 , la superficie x y = a z se ha transformado en (X+c) (Y + d)= a Z y el cilindro (x-c)2_+(y-d)2_=R2 _{se ha transformado en X}2 _+Y2 _=R2 _{. Por tanto, el volumen será}





D zdxdy , V

Siendo D=X2 _+Y2 _=R2









  



D D

D

D a XdY

c d dXdY Y a c dXdY X a d dXdY Y X a 1 V

Calculemos 



D

2 d_a XdXdY

I :

f(-X ,Y)=-f(X,Y) y el dominio es simétrico respecto del eje OY. Por tanto I2=0

De la misma forma







D

3 _ac YdXdY 0 I

f(X ,-Y)=- f(X,Y) y el dominio es simétrico respecto al eje OX . Igualmente







D

1 _a1 XYdXdY 0 I

El valor del volumen será

a c d R π dY X d a

c d

V 2

D







2. Calcular el volumen del sólido determinado por las superficies x=y2 , y=0 , z=0 y z + x=1









15 4 dy dx x 1 dy dx x 1 dy

dx z

V x

0 1

0

D  D    











3. Calcular el volumen común a la esfera y al cilindro de ecuaciones x2+y2+z2=R2 , x2+y2-R x= 0.

Coordenadas polares:

dθ dρ ρ ρ R 4 dxdy z 4 V

D D

2 2











D es el primer cuadrante del círculo de ecuación: ρ=R cos θ

       









3 4 π 3 R 2 dρ ρ ρ R dθ

4

V R cosθ 3

0

2 2 2

π

0

2.9.Integrales triples

Sea K un dominio acotado del espacio limitado por una superficie cerrada que constituye su contorno. Sea V el volumen de K y consideremos la función f(x,y,z) acotada en K . Descompongamos de forma arbitraria mediante superficies auxiliares el dominio K en n dominios parciales 1 , 2……n

de volúmenes v p y elijamos en cada dominio parcial p un punto de coordenadas (ψ p , p , θ p) .

Diremos que f(x, y, z) es integrable en K si la suma







  n

1 p

p p p p,η ,θ v ψ

tiene limite finito cuando n → ∞ de forma que el mayor de los diámetros de los dominios parciales tienda a cero , cualquiera que sea la forma de realizar la partición y elegir un punto (ψ p , p , θ p) en

cada uno de los dominios parciales. El valor I es





Vf(x,y,z)dxdydz

I

2.10. Cálculo de integrales triples

Vamos a suponer que el dominio K que se proyecta en el dominio D del plano XOY , está limitado superior e inferiormente por las superficies S1 y S2 de ecuaciones z=z1(x,y) , z=z2(x,y) , con

z2≥z1 , siendo ambas superficies continuas en D . El dominio D está limitado por una curva simple

cerrada C . K se supondrá limitado lateralmente por una superficie cilíndrica de generatrices paralelas a OZ

Supongamos que toda paralela a OZ trazada desde un punto (x ,y) interior a C corta al contorno C en dos puntos de cotas z1(x,y) y z2(x,y) siendo z1< z2 y suponiendo que toda paralela a OY que

corte al eje OX en un punto x comprendido entre a y b , corta a la curva C en sólo dos puntos de coordenadas f1(x) , f2(x) con f1(x) < f2(x) siendo estas funciones continuas. El cálculo de la integral se

reduce a tres integraciones reiteradas.





 









K

b a

(x) 2 f

(x) 1 f

y) (x, 2 z

y) (x, 1 z

y) (x, 2 z

y) (x, 1 z

Ddxdy f(x,y,z)dz z)dz

y, f(x, dy

dx z)dxdydz y,

f(x,

Ejercicios de aplicación

1

. Calcular la integral



D

3

2 _{yz dxdydz}

x extendida al volumen comprendido entre el plano X Z y

















  

  a

0 9 2 4 2 x a 4 0 a 0 2 x ax 0 4 2 3 2 21 a 2 dx x ax x 2a dy y dx x 4a dz z dxdy x 2 I

2.

Calcular



_

        D 2 2 2 dz dy dx z x z 1 y x

donde D es el paralelepípedo construido sobre los ejes de

longitudes 1, 2, 1.

3 1 6 π dz z x z 1 y x dy dx dz dy dx z x z 1 y x ₂ 2 2 1 o 2 0 1 0 D 2 2 2                       



 



3.Calcular



D zdxdydzdonde D es el primer octante positivo limitado por los planos y=0 , z=0 , x+

y=2 , 2y + x = 6 y el cilindro y2+z2=4

.

3 26 dz z dx dy dz dy dx z D 2 0 2y 6 y 2 2 y 4 0











  

2.11 .Cambio de variables en integrales triples

Sea la integral f



x,y,z



dxdydz K



extendida al dominio K. Se quieren cambiar las variables x, y, z

por otras u, v, w mediante las ecuaciones:











u, v,w



 

9

z z w v, u, y y w v, u, x x        

La nueva integral se extenderá a un dominio K’ imagen de K por las ecuaciones (9) . La correspondencia que definen las ecuaciones (9) es biunívoca cuando a cada punto de K le corresponde un único punto de K’. Recíprocamente, para que la correspondencia sea biunívoca es preciso que el jacobiano



x,y,z



dxdydz f



x



u,v,w

 

,y u,v,w

 

,z u,v,w





Jdudvdw f

K K,







Coordenadas Cilíndricas

z z senθ ρ y cosθo ρ

x   







ρ,θ,z



ρdρdθdz

J z y, x,

J _

Coordenadas Esféricas

  

sen ρ z

cos θ sen ρ y

cos cosθ ρ x

  

  

 ,ρ varíade0 a 2

π a 2 π de varía , 2π a 0 de varía

θ 

En estas condiciones se barre todo el espacio. Cálculo del jacobiano







ρ ,θ ,



ρ cos

J z y, , x

J _{ 2}

Ejercicios de aplicación

1. Calcular 



 

D

2 2 2

2_{sen x 4y 9z dxdydz}

x

I donde D es es el dominio limitado por la elipse

x2 _{+ 4y}2 _{+ 9z}2 ₌₁

Transformemos el elipsoide en una esfera mediante el cambio

Z 3 1 z , Y 2 1 y , X

El elipsoide se ha transformado en la esfera X2_+Y2_+Z2₌₁









6

1 Z , Y , X J

z , y , x

J _

Por tanto: X sen X Y Z dXdYdZ 6

1

I



2 2  2 2

Pasando a coordenadas esféricas

]

2 1 sen 2 1 [cos 9

π 2 dρ ρ sen ρ d cos dθ

θ cos 6 1

I 2

π

2 π

1 0

4 3

2π 0

2 _{  }









  

2.Calcular





D _x2 _y2 dz dy dx

D es el dominio limitado por la superficie esférica de ecuación x2 _{+ y}2 _+z2

– 2 R y =0

Pasando a coordenadas esféricas







D 2

cos ρ

dθ dρ d cos ρ I

  

Donde D’ es el dominio de ecuación: D'2Rsenθsen

2 2 2RsenθRse

0 π/2

π/2 2π

0dθ d ρdρ π R

I















2.12. Simplificación en el cálculo de integrales triples

1. f(-x,y,z)=-f(x,y,z) y dominio simétrico respecto al plano

x

= 0 I=0

2. f(x,-y, z)=-f(x, y, z) y dominio simétrico respecto al plano y = 0 I=0

3. f(x, y,-z)=-f(x, y, z) y dominio simétrico respecto al plano z=0 I=0

5.f(-x,y,-z)=-f(x,y,z) y dominio simétrico respecto al eje OY  I=0

6. f(x,-y,-z)=-f(x, y, z) y dominio simétrico respecto al eje OX I=0

7. f(-x,-y,-z)=-f(x,y,z) y dominio simétrico respecto al origen I=0

Ejercicios de aplicación

1. Calcular







  K

2 2

2_{y z 1dxdydz}

x cos z y, x, sen

x siendo K

:

9

3 z 2 y

x2_ 2 _ 2 _

f(x,-y ,z)=-f(x,y,z) y el dominio es simétrico respecto al plano y=0 .Por tanto I= 0

Ejercicios de aplicación

1.Calcular el volumen del elipsoide (x/a)2(y/b)2(z/c)21

Al ser el elipsoide simétrico respecto a los planos coordenados, podemos hallar la octava parte del volumen y el volumen total será



8 dxdydz V

Cambio de variables: _xau1/2_{, ybv}1/2_{, zcw}1/2

El nuevo dominio es el limitado por los planos: u=0 ,v=0 , w=0 , u+v+w=1









dw dv du w v u c b a 8 1 8 dz dy dx 8 I

w v u c b a 8 1 w v, u, J

z y, x, J

2 1 2 1 2 1 2 1 2 1 2

1

     









Por tanto:

 

c b a π 3 4

2 5 Γ

1 Γ 2 1 Γ 2 1 Γ 2 1 Γ c b a

I 

     

                 



2.13. Teoremas de Guldin

Primer Teorema El área engendrada por una línea plana al girar alrededor de un eje de su plano, es igual al producto de la longitud de la línea por la circunferencia descrita por su centro de gravedad.

El área engendrada por una curva regular al girar alrededor del eje OX viene dada por

L 2π yds 2π

A b

a  





Segundo Teorema El volumen engendrado por un recinto plano al girar alrededor de un eje de su plano es igual al producto del área de dicho recinto por la circunferencia descrita por su c. d. g

.

η A π 2 V

Ejercicios de aplicación

1.Hallar el centro de gravedad de un cuadrante de círculo.

Hay simetría respecto de la bisectriz y = x , con lo cual ξηApliquemos el teorema de Guldín

3π R 4

4 R π 2π

R π 3 2

A π 2

V η A η π 2

V ₂

3  

  

ya que al girar alrededor del eje OX , el cuadrante de círculo engendra media esfera de volumen

3 R π 3

2.Hallar el c. d. g del recinto formado por el eje OX, la parábola y=x2 y las rectas x = -1 , x=1

Por ser el eje OY de simetría ξ0 . Apliquemos el segundo teorema de Guldin:

10 3 dx x dx x 2 1 dx y π 2 dx y π A π 2 V η A η π 2 V ₁ 1 2 1 1 4 2      









 

Ejercicios de aplicación

1. Calcular

 

 

 

 dxdy y x 1 y x 1

I _{2 2}

2 2

extendida al primer cuadrante del círculo x2_y2 _1_.

Coordenadas polares dρ ρ ρ 1 ρ 1 dθ I 1 0 2 2 2 π 0





_ 

Calculemos la integral ρdρ

ρ 1 ρ 1 I 1 0 2 2 1



  

Cambio ρ2 _{= u}













           1 0 1 0 1 0 1 0 2 2 2 1 u 1 du u 2 1 u 1 du 2 1 u 1 du u 1 2 1 du u 1 u 1 2 1 I      _      _{ }  1 2 π 2 1 u 1 u sen arco 2 1 1 0 2     _      





1

2 π 4 π dθ 1 2 π 2 1

I 2

π

0

2. Calcular el volumen limitado por la superficie x y z3 1

La superficie es simétrica respecto a los tres ejes de coordenadas. 2 3 3 2 3 4 2

3 1 4

5 1           

 x y

z

z 1

5

3 2

1x 4 3_4y

2 3         3 2

Al realizar la integral sobre el octante positivo, adoptamos el signo positivo.





         

 1 x 4y dxdy

5 8 dy dx z 8 V 2 3 3 2 3 4 2 3

Transformemos la integral en una de Dirichlet mediante el cambio de variables

2 3 3 2 4 3 3 4 v 4 1 y v y 4 , u x u x              

Adoptaremos el signo (+) ya que en el primer octante x≥0 , y≥0 . Por otra parte la proyección de la superficie sobre el plano z=0 se transforma en el recinto u≥0 , v≥0 , u+v=1

 

 

2

1 4 1 v u 64 9 v u, J y x, J   5 1925 π 9 ) 4 19 Γ( ) 2 5 Γ( ) 2 3 Γ( ) 4 3 Γ( 8 dv du v) u (1 v u 5 320 72 V 2 3 5 2 3 2 1 4 1     





3. Hallar el volumen común al paraboloide z2x2 y2 y al cilindro z= 4-y2



 zdxdy V

2 2 2

2 2 e

paraboloid

cilindro z 4 y 2x y 4 2x 2y

z

z        

cono e paraboloid z

z 

Recinto proyección sobre el plano X Y: 2x2+2y2=4 . Pasando a coordenadas polares el nuevo dominio

es ρ2











  



 

4 4 2x 2y dxdy 4 4 2ρ ρdρdθ

V 2 2 2

=16 2 dθ ρdρ 8 dθ ρ dρ 4π

π

0

2 0

2 π

0

2 0

3 _ 









Segundo método



 zdxdy

V

4 2y 2x z

z

z 2 2

cilindro e

paraboloid    





 

















2x 2y 4dxdy 4



2ρ 4ρdρdθ

V 2 2 2

=4 22ρ dρ dθ 4 ρdρ dθ 4

0

2 π

0

2 π

0 2 0

3 _{ }









4. Calcular el volumen engendrado por la superficie x y z3 1

2 3 2 3 2

 

 y los planos x≥0 , y≥0 , z≥0 .



 dxdydz

Pongamos ahora la superficie en la forma siguiente 1                    

 2/3 2/3 2/3 a z a y a x

Cambio de variables

3/2 ,

3/2

3/2_{,y av z aw} au

x  









2

1 2 1 2 1 3_{u v w} a 8 27 w v, u, J z y, x, J 







 a u v w dudvdw 8 27 dz dy dx V 2 1 2 1 2 1

3 _{, donde el dominio es el limitado por los planos u=0}

, v=0 , w=0 , u+v+w=1 .

70 a π 2 11 Γ ) 1 ( Γ 2 3 Γ 2 3 Γ 2 3 Γ a 8 27

V 3  3

                        

5. CalcularI





x3y3z3



dxdydz extendida al interior de la curva x2+y2+z2-2 a(x+y+z)+2 a2=0

El recinto pertenece a la esfera: (x-a)2_+(y-a)2_+(z-a)2_=a2 ₍₁₀₎

Hagamos una transformación de ejes al punto (a ,a ,a)

Z a z Z a z Y a y Y a y X a x X a x               

La ecuación (10) se transforma en la esfera X2_+Y2_+Z2_=a2



 

 





a X a Y a Z



dXdYdZ

Por simetría, los términos de potencia de grado impar se anulan y, por tanto, el valor de la integral será







  

3 a aX aY aZ dXdYdZ

I 3 2 2 2 _{, extendida a la esfera X}2_+Y2_+Z2_=a2

Transformemos la esfera mediante el cambio









2

1 2 1 2 1 3 2 1 2 1 2 1 w v u a 8 1 w v, u, J Z Y, X, J w a Z , v a Y , u a X       

Podemos calcular la integral extendida al recinto limitado por los planos u=0 , v=0 w=0 , u+v+w=1 y multiplicar por 8



3 2 2 2



6

 

_4πa6

2 5 Γ 1 Γ 2 1 Γ 2 1 Γ 2 1 Γ a 3 dXdYdZ aZ aY aX a 24 I                              



15 a π 12 dw dv du w u v a 3 dYdZ dX X a 24

I 2 6

1 2 1 2 1 6 2

2 









 

De la misma forma se obtiene:

15 12π2 I , 15 12π2

I₃  6 ₄  6

Por tanto:

5 a π 32

I 6

6. Un sólido está limitado por los planos x=0 , y=0 , z=0 , x/ay/bz/c1. La densidad del sólido

en el punto (x,y,z) es ,

4 1 c z b y a x k         

 donde k es una constante. Calcular la masa del sólido.





_



           V 4

V c 1 dxdydz

Primer cambio de variables: x= a X , y= b Y , z= c Z







X,Y,Z



abc

J z , y , x

J _



X Y Z 1



dXdYdZ abc

k

m 4

D





  

 : D es el volumen limitado por los planos: X=0 , Y=0 , Z=0 ,

Z+X+Y+1=0

Segundo cambio de variables









    



 

 

W V U Z

W 1 V U Y

V 1 U X







U,V,W



U VdUdVdW

J

Z Y, X,

J _ 2











 

D

2

4 _{U VdUdVdW} 1

U abc k

m

D’ es el volumen limitado por los planos U=0 ,V=0 W=0 y por los planos U=1 ,V=1 ,W=1 . Por tanto





48

c b a k dW dV V dU 1 U

U abc k

m 1

0

1 0 1

0 4

2

 









Ejercicios propuestos

1. Calcular



Dxydxdy extendida a la parte del cuadrado 0x1 , 0y1 situada entre la diagonal y=x

y la curva y=x3

SOLUCION:

1

2. Calcular



D /y 2 x

- _dxdy

e

x extendida a la porción de plano limitada por x=0 , y= x2 _{, y =1, y=2}

SOLUCION:





4e

1 e 3 

3. Calcular a x dxdy

D

2 2



 a lo largo del primer cuadrante del círculo x2_+y2_=a2 _.

SOLUCION: 3 2a3

4. Calcular



Dxdxdy siendo D el recinto plano limitado por las líneas x =0, y =0, x

2_+y 2 _{=10 , x y=3.}

SOLUCION: 10008

3

5. Calcular



2x y 1



dxdy

D

2 2



  siendo D el cuadrante de vértices (1,0), (2,1), (1,2) y (0,1).

SOLUCION: 9

6. Calcular 4a ρ ρdρdθ

D

2 2



 extendida al círculo de centro (a,0) y radio a , ρ2acosθ

SOLUCION: 

     

3 2 2 π 3 16a3

7. Calcular dxdy

y 2ay y x D

2 2



  extendida al dominio D limitado por la semicircunferencia x2_+y2_{-2 a y=0,}

( 0ya) y por el diámetro y=a ( -a x a).

SOLUCION:



4 3π



9

a3

8. Calcular



D

2_cosθdυdθ

ρ siendo D el recinto plano limitado por la cardiode ρ1cosθ.

SOLUCION: 4 5π

9. Calcular



Dxydxdyextendida al recinto D limitado en el primer cuadrante por los círculos x

2_+y2_-2

x=0, x2_+y2_{-4 x=0 y el eje OX.}

SOLUCION:

10

10. Hallar las áreas de las figuras limitadas por las siguientes curvas:

a) x y =a2 _{, x+y = 5 a/2 , (a >0)}

b)



_xy



2_x2 _a2_{, (a0)}

SOLUCION: a) 2L2 a2 8

15 _

  

  _

b)πa2

11. Calcular



  

dy dx y

x

x y 2 )x y (x

2 2

2 2

2

donde D es el primer cuadrante del círculo de centro el origen y

radio 3.

SOLUCION: -3

12. Calcular el volumen comprendido entre x2y2 az , x2 y2 ax y el plano z=0

SOLUCION: 32 3ππ3

SOLUCION: 6 a3

14. Calcular 









D

2 2 _{y dxdy}

x cos arc

I extendida al dominio ρ cosθ

SOLUCION: π-2

15. Dado el cambio de variables: v=x+y , u=- x + y , calcular

y d dx e D

x y

x y







, siendo D el triángulo de vértices (0, 0) , (0, 1) , (1, 0).

SOLUCION: Sh1 2 1

16. Calcular el volumen común a los dos cilindros circulares x2+y2=a2 , x2+z2=a2

SOLUCION: 3 16a3

17. Calcular x



b x a y



2 dxdy

1

D

2 2 2 2 2



 donde D es el área encerrada por la elipse 1 b y a x

2 2 2 2

  .

SOLUCION: 5

b πa4 2

18. Calcular



y 2 y 2



dxdy

D 2



  donde D es el dominio que representa la elipse de ecuación 4 x2₊₉

y2_{-16 x+18 y+24=0 .}

SOLUCION:

181



216

19. Calcular el volumen limitado por el paraboloide

q 2 y p 2 x

SOLUCION: _   

  

 q b

1 p a

1 24ab

c

2 2 4

20. Calcular el volumen limitado por el conoide cz y a2x2 ,el plano XOY y los planos x=0 ,x=a , y=0 , y=b .

SOLUCION: 8c

b πa2 2

21. Calcular el volumen limitado por el plano XY, el cilindro x2+y2-2 a x =0 y el cono circular recto que tiene su vértice en O, siendo su eje OZ y su ángulo en el vértice de 90 grados

SOLUCION: 9 32a3

22. Hallar el volumen comprendido entre el paraboloide x2+y2=a(a-z) y el plano z=0 .

SOLUCION: 2 πa3

23. Hallar el área limitada por las parábolas de ecuaciones y2=x , y2=2 x , x2=y , x2=3 y .

SOLUCION

:

2/3

24. Calcular sen 4x 9 y dxdy

D

2 2



 siendo D es el dominio limitado por la elipse 4 x2_{+9 y}2_{=1 .}

SOLUCION:



sen1 cos1



3

π _

25. Calcular el volumen encerrado por la superficie de ecuación x2+y2=4 a z y el plano x+y+2z=4 a

SOLUCION: 25a

3

26 Calcular el volumen encerrado por las superficies z=0 y 

    _ 

_y2 _e x2 y2

z .

SOLUCION:



8

27. Calcular el volumen comprendido entre los planos x=0 , y=0 ,z=0 y los cilindros x2+z2=25 y2+z2=25

SOLUCION:

250

3

28. Calcular









D

2 2 _{y dxdy} x

siendo D el dominio limitado por la astroide de ecuación

3 2 3 2 3 2

a y

x   .

SOLUCION: ₈ 4

2 a π 21 I

29. Calcular









D x y dxdy

2

2 _{donde D es el área del triángulo limitado por los ejes y la recta}

1 b y a

x_{  .}

SOLUCION:



_a2 _b2



12

b a

I 

30. Calcular



 

D 2 2

3

dy dx y x

x

I donde D es el primer cuadrante del círculo de ecuación x2_+y2_{=9 .}

SOLUCION: I= 27 / 2

SOLUCION: 20 137a3

32. Calcular dxdy

y 1

x 2 y x

D 2

5



_ donde D es el dominio limitado por el cuadrilátero de vértices ( 0, 0),

(2 ,0), (2 ,1) y (0,1).

SOLUCION: L2 π 3

16

I  

33. Calcular I x y 1 x y dxdy

D

2 2 2

2



 

 donde D es el dominio definido por x≥0 , y≥0 , x2_+y2_{1 .}

SOLUCION: 210

π I

34. Calcular 









D

2 2 _{y dxdy} x

I donde D es el segmento parabólico de ecuación xa , y2_2

_{p x}

_.

SOLUCION: _

  

  _ 

15 p 2 7 a a p 2 a 4

I 2

35. Calcular I x y2 1 x2 y2 dxdy

D

2 _{ }





donde D es el área del triángulo limitado por las rectas

x=0 , y=0 , x+y=1 .

SOLUCION:

225 128 2 L 140

I 

36. Hallar el volumen comprendido entre la superficie



x



y



z



1

y los planos x≥0 , y≥0 x≥0 .

SOLUCION:

1

9 0

37. Calcular la integral



   

2 2 2 _{y z} x

1

dz dy dx

SOLUCION: 

2

8

38. Calcular







V _xyz3

dz dy

dx _{extendida al volumen V limitado por los planos x≥0 , y≥0 x≥0 , x+y+z1}

SOLUCION:  _  _

8 5 2 L 2 1 I

39. Calcular



V zdxdydz , extendida al octante positivo de la esfera de ecuación x

2_+y2_+z2₌₁

SOLUCION:



16

40. Calcular el centro de gravedad de la sección comprendida entre la semielipse de semiejes a y b y el semicírculo de radio b .

SOLUCION:





3π

b a 4 