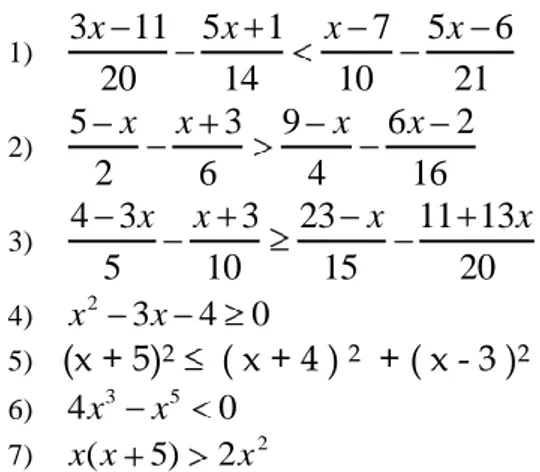CÁLCULO NUMÉRICO
1º Potencias y radicales
1.- Halla el valor de las siguientes expresiones:
3 2 4 2 2 2 4 3 15 3 2 3 5 2 1 3 2 1 2 1 3 8 1 4 2 3 ) 10 4 5 3 5 5 1 2 3 2 4 1 1 1 3 1 ) 2 3 3 4 5 3 5 3 5 3 ) c b a
2.-Simplifica y reduce las siguientes expresiones a potencias:
a)
3
x 1
x b)
3 1 10 2 1 3 2 2 3 3 2 3 2 c) 8 8 6 3 4 8 7 5 4 6 5 4 3 3 2 a a a a a a . a a . a a a a d) y x x3 e) c x b a c b a x 3 1 2 1 6 3 1 1 f) 2 4 3 6 3 2 0 4 2 3 5 2 2 3 2 3 2 3 2 y x x yx x x y x x x y x y y x g) 2
4 2 3 5 4 3
5 b a c b a c b a h) a a a a a a 9 3 8 6 4 : i) 2 3 5 4 3 2 3 2 2 : c b a c b a
j) 4 3 3 2 3 5 5
b a c b a abc
3.- Efectúa las siguientes sumas y restas y racionaliza en el caso que sea necesario: a) 2 2 2 2 2 ab ab b a a b b a
b) 3
3 4 2 2 4 2 6 4 d c b c d d b c a a d b cd a a cd c) 125 , 0 . 9 2 2 2 18 18 , 0 3 , 0 4 3 2 2 2 2 c a c c a c a b b a b a b
d) a2m a2n 4 (m n)2.b2 6 c6(m n)3
4.- Realizar los siguientes ejercicios como radicales a)
4 2 3
3 3 2 3 a b a ab b a b ab b)
6 2 3 4 2 3 2 3 y x xy y x y x c) 2 3 2
-3 2 4
4 2 2 3 ) (a a b b b a a b a d)
5.- Opera y simplifica a)
500 3
125 4 80 2 20 3
b) 2 2 2 2
) 2 .( ) 2 ( ) 2 .( ) 2
( x y x y x y x y
c)
3 2
3 3 2
1 3 1
3 2
d)
a a
a a a
a
1 1
1 e) 40
125 2 80 20
f)
6
56 4 150 24
g)
3 2
3 3
5
2 3 2
3
h)
3 1
3 1
1
3 1
3 1
1
2º Logaritmos
1.- Aplicando la definición de logaritmo resolver los siguientes ejercicios:
a) log264 = x g) log343 7 = x n) 3 x
5
1 625
log
b) log381 = x h)
3 5
125 1
log =x ñ) log2/381/16 = x
c) log101 10201 = x i)
9 3
log27 =x o) log5/3 27/125 = x
d) log16 0,5 = x j) log125 1/ 5 = x p) log84 2 = x
e) log10 0,00001 = x l)
128 1
log 2 =x q) x
343 1 log 7
f) 5 x
3
1 81
log m)log163 2 x r) x
32 1 log 2
2.- Hallar la base de los logaritmos en las siguientes igualdades: a) loga 4=2
b) loga 9=2
c) loga 0,125=3
d) loga 125 = 3/2
e) loga 1/3 = -1/2
f) loga 0,001=-3
3.- Halla el resultado de las siguientes expresiones utilizando las propiedades de los logaritmos y su definición:
a) log5 625 – log3 243 + log4 256 c) log2 4 + log3 81 – log6 216 + log4 64
b) log3 1 + log2 64 + log3 9 + log7 49 d) log3 1/9 – log5 0,2 + log6 1/36 – log2 0,5
4.- Considerando que log2 5 = 2,322 y que log2 6 = 2,585, calcule los valores de los
siguientes logaritmos sin usar calculadora:
a) log 2 10 ; b) log 2 40 ; c) log 2(5/4) ; d) log 2 30 ; e) log 2 125 ; f) log 2 (36/5)
5.- Utilizando las propiedades, exprese con un solo logaritmo:
a) log 6 + log 8 – log 3 ; b) log 9 + log 28 – ( log 7 – log 9 ) c) 3(1 – log a) ; d) ln (et ) – ln (e/t) ; e) 2log 3 + log 5 ; f) -1+
2 1
log 5
Considerando que log6 2 = 0,387 y que log6 3 = 0,613, calcule los valores de los
a) log 6 72 ; b) log 6 0,5 ; c) log6 2 24 ; d) log6 3
3 2 3
3 2
e)log6
5 12 2
1
3º Binomio de Newton
Desarrolla
1. 7
b a
2. 5
b a
3. 4
2n m
4. 8
1
a
5. x 2 5
6. x 2 5
7.
4 4 1 3 1
b a
8. 2 6
c b a
9. a b 7
10.
5 3 1 3 1
y x
11. 2 3 5 2 2a
12. 2 2 7 2x a
13.
5 5
2 1 2
1
a a
14.Halla el noveno término del desarrollo de 12
y x
15.Halla el quinto término del desarrollo de
15 2 1
a
16.Halla el sexto término del desarrollo de x y 8
17.Halla el término central del desarrollo de 8
y x
18.Halla el cociente que resulta de dividir el término noveno por el sexto del desarrollo de 14
2 1
a
19.Halla el término medio del desarrollo de
6 2 1
b a
20.Halla los dos términos medios del desarrollo de 7 1 , 0
x
21.Halla el término que ocupa el lugar 505 en el desarrollo de 3 2 506
c b a
22.Hallar el término que contenga la cuarta potencia de a en el desarrollo de 2 a10
23.Hallar el término medio en el desarrollo de 3 x 3 y 6
24.Justifica del modo más rápido la igualdad: 16 4 4
3 4
2 4
1 4
0 4
25.Encuentra una regla que generalice el cálculo anterior y que permita obtener el valor de
n n n
n
R-MATCNSI 4
CÁLCULO ALGEBRÁICO
1º Polinomios
1º FACTORIZACIÓN DE POLINOMIOS - MCM
Conceptos
Factorizar un polinomio: Descomponer un polinomio como producto de factores primos.
Factor primo: En el caso de los polinomios, son polinomios que no tienen mas raíces reales, por lo tanto aquellos que no se pueden descomponer en factores mas simples.
Mínimo común múltiplo: Una vez descompuestos en factores primos los polinomios, se eligen los factores que sean comunes a todos los polinomios elevados al mayor exponente y se multiplican por todos los factores que no sean comunes.
Procedimientos
1) Factorizar un polinomio
a) Si no tiene término independiente se saca x o xn factor común
b) Si tiene término independiente se buscan sus raíces
Ruffini por
dos que mayor grado
de es Si
grado 2º de ecuaciones las
en como procede se
dos grado de es Si
c) Se factoriza del siguiente modo P(x) = (x – raíz1)(x – raíz2)....
2) Calcular el MCM
a) Se factorizan todos los polinomios siguiendo el procedimiento anterior. b) Se toman todos los factores que sean comunes a todos los polinomios
elevados a la mayor potencia y los factores que no sean comunes y se multiplican
Ejemplo: Factorizar 2x5 – 6x3 + 4x2 ;
Sacamos 2x2 factor común a los tres sumandos 2x2(x3 – 3x + 2) El polinomio (x3 – 3x + 2) se factoriza como se explica a continuación
Ejemplo: x3 – 3x + 2 1 0 -3 2 x3 – 3x + 2 = (x – 1)(x2 +x – 2) Raíz = 1 1 1 -2
1 1 -2 0
x2 +x – 2 = 0; x =
2 3 1 2
9 1 2
) 2 .( 1 . 4 1 1
; de donde x = 1; x = -2 Por lo tanto x2 +x – 2 se factoriza del siguiente modo: x2 +x – 2 = (x –1)(x + 2) La factorización final de 2x5 – 6x3 + 4x2 será:
2x5 – 6x3 + 4x2 = 2x2(x3 – 3x + 2) = 2x2(x – 1)(x2 +x – 2) = 2x2(x – 1)(x –1)(x + 2) 2x5 – 6x3 + 4x2 = 2x2(x – 1)2(x + 2)
Ejemplo:
Halla el MCM de los siguientes polinomios: x5 – 4x3; 2x5 – 6x3 + 4x2; x2 + 4x +4. x5 – 4x3 = x3(x – 2)(x + 2)
2º IGUALDADES NOTABLES
a) (a + b)(a – b) = a2 – b2 Ej: (3x3 – 5xy) (3x3 + 5xy) = (9x6 – 25x2y2)
b) (a + b)2 = a2 + 2ab + b2 Ej: (5y2 + 3x)2 = 25y4 + 30y2x + 9x2
c) (a – b)2 = a2 – 2ab + b2 Ej: (6y2 – 2y)2 = 36y4 – 24y3 + 4y2
d) (a + b)3 = a3 + 3a2b + 3ab2 + b3 Ej: (2x + 3y)3 = 8x3 + 36x2y + 54xy2 + 27y3
e) (a - b)3 = a3 - 3a2b + 3ab2 - b3 Ej: (x2 – 2x)3 = x6 – 6x5 + 12x4 – 8x3
Ejercicios
1.- Aplica las fórmulas de las igualdades notables a las siguientes operaciones: a) (2x – 4)(2x + 4)
b) (3y2 + 2x)(3y2 – 2x)
c) (3y + 2x)2
d) (2x3 – 5y)2
e) (5 – 3x)3
f) (2y – 3)3
2.- Factorizar los siguientes trinomios en cuadrados perfectos 1. a2 − 2ab + b2
2. x2 + 4x + 4
3. b2 − 2b + 1
4. m2 − 2mn + n2
5. x2 − 10x + 25
6. a2 − 2a + 1
7. 1/25 + (1/3)x + (25/36)x2
8. 1 − (2/3)c + c2
9. (9/4)c2 − 6x + 1
10. 4a2 − 12ab + 9b2
11. a8 − 18a4 + 81
12. x6 − 2x3y3 + y6
13. m6/16− 2m3n2 + 16n4
14. 9c6 − 30c3 + 25
15. 1 − 2(x − y) + (x − y)2
16. 4 − 4(1 − x) + (1 − x)2
17. x2 + 2x(b + c) + (b + c)2
18. (x + y)2 − 2(x + y)(y + z) + (y + z)2
19. (a + b)2 + 2(a + b)(a − c) + (a − c)2
20. (a + b + c)2 + 2(a + b + c)(b + c − a) + (b + c − a)2
3.- Utiliza las fórmulas de las igualdades notables para factorizar los siguientes polinomios, cuando sea posible:
a) (9 – x2)
b) (4x2 – 9)
c) (x2 – 6x + 9)
d) (x2 + 2x + 1)
e) (2x2 – 20x +25)
f) (x3 + 6x2 + 12x + 8)
g) (x3 – 12x2 + 48x – 64)
h) (x 4- 5x3 - 2x2 + 24x)
i) (x4 – 4x3 – x2 +16x – 12)
j) (2x3 – x2 – 2x + 1)
k) 4 2 1
x
l) x2 10x 25 m) 2 10 25
x x
n) x2 9 o)
4 1 2
x x
p) 9x2 4
q) 2
4 20
25 x x
3º Fracciones algebraicas
1.- Opera y simplifica:
a) 2 1 + x 1 : x x 4 b) x 4 -x . ) 2 + (x 2 + x 2
2 c)
2 + x 1 : x 2 . 2 x2
d) . x
1 + x 1 x : 1 + x 1 + x 2
e) . 2x
2 -x 1 + x x 2 + x + x 3 2 2
2.- Haz las operaciones indicadas y simplifica:
a) x y y x . y + x y -x y -x y + x b) y + x 2xy . xy y + x + y 1 x 1 c) x 1 x . 1 + x x 1 -x 1 + x 3.- Simplifica: a) 2 -x 8 + 8x -x 2 : 2/8 + 3/4 4 -2x x + x 3 x -x 3 x -9 x + 6x + 9 2 3 2 3 2 2 2 · b) 4x -x 2x -x + 4 -x 2 -x 4 + 5x -x 5 + 6x + x 2 3 2 2 2 · c) 0x + x -x x : x 2 -x + x 2 x + 2x 1 x x -x 1 x 1 x x 2 3 2 2 2 5 20 2 5 5 2 50 0 14 4 4 · 2 2 3 2 d) 10 + 7x -x 4 -x 1 + x : 2 -x + x 2 + 2x 1 -x 10 -8x -x 2 1 + 2x + x 1 -x 2 3 2 2 2 2 · e) 2x 12 + 12x + x 3 _ 6 -3x + x 3 2x -x 2 4 + 4x + x 2 -x + x : 2 + 3x -x 3 -2x + x . 9 -x 6 -11x + x 6 -x 2 2 2 2 2 2 2 2 2 3 f) 1 3 -x 3 + x 3 3 + x x 3 + x _ 3x x -3 3 + x 3 -x + 1 g) x + x 6 + 5x -x : 9x + x 6 + x 9 x _ x + x 6x -x + x 2 2 2 3 2 2 2 3 h) y -xy y -x y x + 1 2 2
2 i)
b -a b + a 1 b -a b + a + 1 j) ) 1 -(a 1 + 2a -a _ a 1 + a : 1 -a 1 + a 1 + a 1 -a 1 -a 1 + a 1 + a 1 -a 2 2 2 2 2 2 2 k) 4 2 1 2 1 : 2 1 1 2 2 x x x x l) y y y x x y y x 1
1 m) n) x x
2º Ecuaciones
1º Ecuaciones bicuadradas y de grado superior
Resuelve las siguientes ecuaciones
1) x2 2x 1 0
2) x2 12x 2 0
3)
6 1 2 3
2 1x 1x x
4) 0 4 1 4 5 2 4 x x
5) x5 3x4 5x3 15x2 4x 12 0
6) (x-1)3-x3=0
7) x5+x4-8x3+14x2-8x=0 8) x3-x2-17x-15=0
9) x4 29x2 100 0
10)9x4 16 40x2
11)34 2 2252
x x
12)(x2 4)2 0
13) 0 9 28 4 32 2 2 x x 14) 0 72 16 9 2 2 2 x x 15) 3 3 3 2 3 2
2 x x x
x x x
16) 2 3
4 2 4 x x x x 17) 3 2 2 2 2 4
4 2 2
2 4 x x x x 18) 2 5 3 2 4 2 2 2
2 x x x x x x x x
19) 3 3 2 2 2 2 4 4 2 2 2 4 x x x x
20) 2x 1 2x 1 2x 12 2 2x 2
21) x2 4 2 5 x2 4 4 0
22) 2 3 1
1 3 2 3 2 1 1 4 3 2 1 x x x x x 23) 3 1 3 2 2 6 2 2 2 x x x
24) 3 2
4 4 0
x x x
25) x4 3x3 3x2 11x 6 0 26)
4 3 2
4 3
1 10 24
x x x
x x
27)
3 2
2 6 12
2
x x x
x x
28) x x( 2 5x 13) 77 60
x
29)x6 – 9x3 + 8 = 0 30) 4 11 44 9 3 22 4 3 11 6 2 2
2 x x x x
x 31) 3 4 1 x x
32) x8 x4 240 0
33) 2 1
110
1
x
x
34) 0 5 1 3 4 3 19 1 3 20 x x x35) x6 19x3 216
36) =(x-2)
2 3) -(x x + 2) -(x 3) -(x 2
37) =0
2 x + x 1) + (x x
38) =(x-2) - 4
2 2) + (x 2) -(x 3 2 + x x 2) -(x 2
2º Ecuaciones irracionales
Procedimiento:
Si la ecuación tiene sólo un término con raíz cuadrada: Ejemplo:
3 1 2 5
9 x x ;
Quitando denominadores 3 9 x 15 2x 1
1) Se deja la raíz sola a un lado del signo =. 3 9 x 2x 16
2) Se elevan los dos términos de la igualdad al cuadrado. 2 2 16 2 9
3 x x
9(9 + x) = 4x2 + 216 + 64x
3) Se termina resolviendo como una ecuación normal. 81 + 9x = 4x2 + 216 + 64x
4x2 + 55x –135 = 0; x =
8
2160 55
55 2
(terminar)
Si la ecuación tiene dos términos con raíz cuadrada: Ejemplo 2x 1 x 4 6 1) Se deja una raíz a cada lado del signo =. 2x 1 6 x 4
2) Se elevan los dos términos al cuadrado. 2x 1 2 6 x 4 2 2x 1 36 (x 4) 12 x 4 3) Se deja la raíz que queda sola un lado de la igualdad.
2x – 1 – 36 – (x + 4) = -12 x 4; x – 41 = -12 x 4 4) Se vuelve a elevar al cuadrado. 2 2
4 12
41 x
x ; x2 1681 82x 144(x 4)
5) Se termina resolviendo como una ecuación normal. x2 1681 82x 144x 576 0; x2 + 226x + 1105 = 0 (resolver)
Ejercicios:
Resuelve las siguientes ecuaciones irracionales
1. x 1 x 6 5
2.
3 3 6
3
x x
x
3. 4 1
1 1
1 1
1 1
1
1 2
2 2
2 2
2 2
2 2
x x
x
x x
x x
x x
4.
4 3 5
5 1 5
5 1
x x
x x
5.
x x
x
2 1 2
1 1
6. 3 3 x 2x 1 1
7. 3x 6 2x 6 9x 4
8. x 4 3 x 1
9.
4 1 4
4
x x x
x
10. 4 16x2 8x3 x4 2
11. 1
6 1 2 2 5 1
2 x x
12. 1 x 1 2x 4 7x2
13. 5 2x 5 2
14. 2x 14 x 7 x 5
15. 2
1 3
1 3
x x
16. a2 1 2x 2a a2 1 2x 17.
18. 2
1 2 3 2
1 3 2
9 3 1
3 x x x x
19.
2 5 2
6 6
2
x x x
x
20.
4 3 5
5 1 5
5 1
x x
x x
x x
x
2 1 2
3º Ecuaciones racionales
Procedimiento:
1) Descomponer los polinomios de los denominadores como producto de factores primos (factorizar los denominadores).
1 1 1 2 1 2 x x x x x ; ) 1 )( 1 ( 1 1 2
1 x x x
x x
x
2) Calcular el MCM de los denominadores. MCM de (x – 1); (x + 1); (x – 1)(x + 1) = (x – 1)(x + 1)
3) Multiplicar los dos lados de la ecuación por el MCM simplificando en cada término. (x – 1)(x + 1)
1 2 1 x x x x
= (x – 1)(x + 1)
) 1 )( 1 ( 1 x x ) 1 )( 1 ( ) 1 )( 1 ( 1 ) 1 )( 1 )( 2 ( 1 ) 1 )( 1 ( x x x x x x x x x x x x
; simplificando x(x +1) – (x – 2)(x – 1) = 1 4) Operar y proceder como en una ecuación normal hasta obtener el valor o valores de x. operando; x2 + x – x2 + x +2x –2 = 1; 4x = 3; x =
4 3
Ejercicios: Resolver :
1. 1 2
2 1 3 2 1 x x
2. 7 2
4 3 4
4 12
2 x x
x 3. 2 1 3 4 1 7 1 1 2 x x x x x x 4. x x x x x 2 1 2 1 1 1 1 5. 9 9 12 5 8 15 x x 6. 24 6 10 4 2 1 6 3 1 2 2 x x x x x x 7. 1 9 7 4 3 7 3 4 x x x x 8. 3 1 1 3 1 x x x 9. 0 9 28 4 32 2 2 x x 10. 12 1 2 1 1 1 x x
11. 1 6 1 6 24
x x x x
12. = 0
1 -x 2 1 -x 2 + 1 + x x - 2 2
13. = 0
1 + x 2 1 -x 2 1 + 2x -x 3 + x 2
14. =0
2 + x 5 + x 2 + x 1 + x + 1 + x 2 + x 15. 6 -x -x x 5 + 3x = 2 + x x 3 -x x + 1 2 2 16. 1 -x 1 + x = 1 + x 3 + 1 -x x 2
17. - 2
4º Ecuaciones logarítmicas y exponenciales
1.- Resuelve las siguientes ecuaciones logarítmicas:
1) 2log x – log (x –16) = 2 2) log x = 1 + log (22 – x)
3) log (3x – 1) – log (2x + 3) = 1 – log 25
4) log 8 + (x2 – 5x + 7)log 3 = log 24 5) log (5x + 4) – log 2 =
2
1log (x + 4) 6) (x2 – x – 3)log 4 = 3log
7) (x2 – 4x + 7) log 5 + log 16 = 4 8) lg(22-x)2+x+lg1250=4
9) 2
) 5 lg(
) 11 ( lg 2
lg 2
x x
10)2lgx =3 + lg(x/10) 11)3lgx -lg32 =lg(x/2) 12)
2 7 log
125 log log
5 5 5
x x
13)lg 2 x · lg x 2x · lg 2x y = lg x x2
14)
9 32 3
3 2 2
5lg x lg x lg x lg
15) lg 3x 1 lg 2x 3 1 lg5
16)log6 (2x - 3) = log6 12 - log6 3
17)log2 (9x-1 + 7) = 2 + log2 (3x-1 + 1)
18) logx log x
19)
x
log 5
1
+ 1
log 1
2
x
20)5log(x 3) log32
21) log 3x 5 log x 1
22)log (x - 5)- 1/2 log (3x - 20) = log 2
23) xlog x 10
24)log (x3)- 1/2log x = 5 25)xlogx 1=100
26) lg x x2 1 lg x x2 1 0; x 1
27)
2 3 log
logx 1 x 1
28) log12x log12(x 2) 1
29) log x 1 log(x 1) log x 4
30)2+log2x=log2(x+6)
31) 2
) 2 ( log
log 2
3 3
x x
32)logx 100 – Logx 25 =2
33) 5 2
5 7
7 Log
x Log
34)Log 2 +Log x 4=Log 2 3x 1
35) 2
) 3 (
2
x Log
Log Logx
2.- Resolver las siguientes ecuaciones exponenciales:
1) x 1 2 x
2 . 12
2) 25 x 124.5 x 125
3) 3x 1 1 x
3 3
4) 252x-1=
3 5
1 x
5) 22x+2 = 0,52x-1
6) 23x-1=
3 2
8 1
x
7) 52x-2=
3
125 1
x
8) 162x-1=
3 2 2
1 x
9) x 2
3 x
100 10
10
10) x 1 5 x x 1 2x 5 a a
11) ax ax ax a 12)2.3x-1+3x=5
13)2.9x+1-6=4.3x+1
14) 4
3 1 3x x 1
15)72x+3 –8.7x+1 +1=0
16)4x+1 +2x+3 –320 =0
17)52x- 6. 5x+1+125=0
18)2x-1+2x-2+2x-3+2x-4=960
19)4e -3x -5e -x+ex =0
20)5x -97·5x/2 +64 =0
21)32(x+1) -28·3x +3 =0
22)52x 1 5x 2 2500 23)e2x 5(ex e) ex 1 0 24)4x-3.2x+1+8=0
25)81+x+23x-1=17/16
26)71+2x-50.7x+7=0
27)9x-2.3x+2+81=0
3º Inecuaciones
Procedimientos
Grado 1: Se trabaja como en una ecuación normal, salvo que si tenemos un número negativo multiplicando a la variable y lo pasamos al otro lado de la desigualdad dividiendo (o viceversa), la desigualdad cambia de sentido. Se da como solución a la inecuación el intervalo de la recta real (- , a) o (a, ), según corresponda.
Ejemplo:
6 3 5 2 10 4 1 5 3
2 x
x x x
; se calcula el MCM para quitar los denominadores MCM = 12; 4(2x) – 15(1 - x) < 120x + 24 + 2(5x – 3); 8x – 15 + 15x < 120x + 24 +10x – 6 ; 23x – 15 < 130x + 18; - 107x < 33; x >
107 33
; Solución: ,
107 33
Grado 2 o mayor que 2: Se buscan las raíces de la ecuación y se hace una tabla de signos para la ecuación. Se dan como solución los intervalos que correspondan al signo de la
inecuación.
Ejemplo: x4 – 2x2 + x > 0, (se nos piden los valores de x tales que al sustituirlos en el polinomio
nos den valores mayores de 0 , es decir, valores positivos).
Calculamos las raíces de esta ecuación, para ello sacamos x factor común y al polinomio resultante le hacemos Ruffini por ser un polinomio de grado 3. x(x3 – 2x +1) = x(x – 1)2(x +
2), de donde se deduce que las raíces que hemos obtenido son x = 0; x = 1; x = -2.
Tabla de signos del polinomio: + - + +
-2 0 1
Los signos de la tabla se han obtenido sustituyendo la x por –3, -1, 0,5 y 2 en el polinomio.
Solución: (- , -2) U (0, 1) U (1, )
Inecuaciones racionales: Se procede como en el apartado anterior haciendo una tabla de signos con los valores que anulan el numerador y el denominador.
Ejemplo: 0
2 x
3 -2x
, Haciendo una tabla de signos tenemos:
2x – 3 = 0 x = 3/2 + + Solución = (- , -2) 3/2. )
x + 2 = 0 x = -2 -2 3/2 Ejercicios:
1.- Resuelve las siguientes inecuaciones:
1)
21 6 5 10
7 14
1 5 20
11
3x x x x
2)
16 2 6 4 9 6
3 2
5 x x x x
3)
20 13 11 15 23 10
3 5
3
4 x x x x
4) x2 3x 4 0
5) (x + 5)2 ( x + 4 ) 2 + ( x - 3 )2 6) 4x3 x5 0
7) x(x 5) 2x2
8)
2 1 4
1 1
3 1 2
3 x x x 2 x
2.- Resuelve las siguientes inecuaciones racionales:
1. 1 2
2 1 3 2 1 x x 2. 0 6 2 3 2 2 x x x x 3. 0 1 9 2 2 x x x 4. 0 5 4 3 1 2 x x x x x 5. 2 3 2 1 4 4 2 2 x x x x x
6. 7 2
4 3 4
4 12
2 x x
x 7. 2 1 3 4 1 7 1 1 2 x x x x x x 8. x x x x x 2 1 2 1 1 1 1 9. 9 9 12 5 8 15 x x 10. 24 6 10 4 2 1 6 3 1 2 2 x x x x x x 11. 2 2 9 ) 6 2 ( x x x 0 12. 2 2 9 ) 6 3 ( x x x 0 13. 0 ) 3 )( 6 )( 1 ( ) 7 )( 1 ( x x x x x 14. 1 1 1 1 x x x x 15. 0 4 15 8 2 2 x x x 16. 2 1 5 1 2 x x 17. 2 1 5 1 2 x x 0 2 3 x x
18. x 6 x2 1 0 19. 2x 1 3x 5 0 20.
21. 22.
4º Sistemas de tres ecuaciones. Método de Gauss
1. Una empresa desea disponer de dinero en efectivo en euros, dólares y libras esterlinas. El valor total entre las tres monedas ha de ser igual a 264.000 euros. Se quiere que el valor del dinero disponible en euros sea el doble del valor del dinero en dólares y que el valor del dinero en libras esterlinas sea la décima parte del valor del dinero en euros. (1 libra = 0,615 Euros; 1 dólar = 0,896 Euros)
2. La suma de las edades de tres personas es 73 años, en el momento actual. Dentro de diez años, la edad de la mayor de ellas será el doble de la edad de la más joven. Hace doce años, la persona con edad intermedia tenía el doble de años que la más joven. Halla las edades de las tres personas.
3. Una tienda tiene tres tipos de conservas cárnicas A,B y C . Un cliente compra el primer mes 30 unidades de tipo A, 20 de B y 10 de C , teniendo que abonar 840 € Al mes siguiente compra 20 unidades de A y 25 de C y abona 690€ Sabiendo que el precio medio de los tres productos es 15€ halla el precio de cada una de las unidades
0 2 3 x x 0 1 6 2 x x 0 5 3 1
4. Sea un triángulo de vértices A(1, a), B(5, b) y C(3, c). Se sabe que las ordenadas de sus tres vértices suman 9, que la ordenada b es la media aritmética de las otras dos, y que b y c son números naturales consecutivos, siendo c > b.
5. En un instituto, donde se imparten primero y segundo ciclo de enseñanza obligatoria y bachillerato hay en total 20 grupos de alumnos . Si se suman los grupos de bachillerato y de segundo ciclo de enseñanza obligatoria se tiene el triple del número de grupos del primer ciclo. Si hubiera un grupo más del segundo ciclo , su número igualaría al de bachillerato. ¿Cuántos grupos hay de cada uno?
6. Se dispone de tres cajas A, B y C con monedas de 1 euro . Se sabe que en total hay 36 euros. El número de monedas de A excede en dos a la suma de las monedas de las otras cajas . Si traslada una moneda de la caja B a al caja A , esta tendrá el doble de monedas que B averigua cuantas monedas hay en cada caja
7. Un grupo de personas se reúne para ir de excursión, juntándose un total de 20 entre hombres, mujeres y niños. Contando hombres y mujeres juntos, su número resulta ser el triple del número de niños. Además, si hubiera acudido una mujer más, su número igualaría al del hombres. Resolver el problema. Sol, habrán asistido 8 hombres, 7 mujeres y 5 niños a la excursión
8. Cierto estudiante obtuvo, en un control que constaba de 3 preguntas, una calificación de 8 puntos. En la segunda pregunta sacó dos puntos más que en la primera y un punto menos que en la tercera. Resolver el sistema. Sol 1 punto en la primera pregunta, 3 en la segunda y 4 en la tercera.
9. En una confitería envasan los bombones en cajas de 250 gr., 500 gr. Y 1 kg. Cierto día se envasaron 60 cajas en total, habiendo 5 cajas más de tamaño pequeño (250 gr.) que de tamaño mediano (500 gr.). Sabiendo que el precio del kg. de bombones es 4.000 ptas. y que el importe total de los bombones envasados asciende a 125.000 ptas: Sol se habrán envasado 25 cajas pequeñas, 20 medianas y 15 grandes.
10.- Una autoescuela tiene abiertas 3 sucursales en la ciudad. El número total de
matriculados es 352, pero los matriculados en la tercera son sólo una cuarta parte de los matriculados en la primera. Además, la diferencia entre los matriculados en la primera y los matriculados en la segunda es inferior en dos unidades al doble de los
matriculados en la tercera. Plantear y resolver el sistema de ecuaciones para averiguar el número de alumnos matriculados en cada sucursal. Sol: 200 alumnos matriculados en la primera sucursal, 102 en la segunda y 50 en la tercera
11.-Una persona disponía de 60.000 € y los repartió en tres fondos de inversión diferentes (A, B y C), obteniendo así 4.500€ de beneficios. Sabemos que en el fondo A invirtió el doble que en los fondos B y C juntos; sabemos también que el rendimiento de la inversión realizada en los fondos A, B y C fue del 5%, 10% y 20% respectivamente. Plantear y resolver un sistema para determinar las cantidades invertidas en cada uno de los fondos.
12.- Parte de los 63 huéspedes de un pequeño hotel se encuentra en el comedor; en el mismo momento otra parte se encuentra en la sala de estar y el resto en la biblioteca. Posteriormente, 4 se desplazan del comedor a la biblioteca, 1 de la sala de estar al comedor y 2 de la biblioteca a la sala de estar. Ahora, ha quedado el mismo número de personas en cada una de las tres estancias. Plantear y resolver un sistema para
13.- Una tienda de música ha obtenido unos ingresos de 12768 C= al vender 600 discos compactos de tres grupos musicales. Los discos se vendían a 24 C=; sin embargo, los del segundo y tercer grupo, al ser menos recientes, se vendieron con descuentos del 30% y del 40% respectivamente. Sabemos que el número de discos vendidos con descuento fue la mitad que el número de discos que se vendieron a su precio original. Plantear y resolver un sistema de ecuaciones para determinar cuantos discos de cada grupo se vendieron.
14.- Una empresa ha vendido 42000 artículos de papelería, bolígrafos, gomas y rotuladores, al precio de 1.2, 1.5 y 2 € respectivamente. El total de los ingresos producidos por esas ventas asciende a 64000 €. Se sabe, además, que el número de bolígrafos que se ha vendido es el 40% del número total del resto de artículos vendidos.
a) Plantear un sistema para determinar el número de cada tipo de artículos vendidos.
b) Resolverlo
15.- Una librería ha vendido 3900 libros de matemáticas, correspondientes a tres editoriales diferentes, A, B, y C. Sabemos que de la editorial B se han vendido el doble de ejemplares que de la editorial A. Sabemos, también, que la razón entre el número de ejemplares vendidos de las editoriales B y C es igual a 2/3 Plantear un sistema para determinar el número de libros vendidos de cada editorial. Resolverlo 16.-Una editorial va a lanzar al mercado tres libros de bolsillo L1, L2 y L3 . El importe total
de la edición es de 18750 €. Los costes, en euros, por unidad, son 7, 5 y 6, respectivamente. Se sabe que el número de ejemplares de L3 es igual a los dos séptimos de los del tipo L2 y que, si al triple del número de ejemplares de L1 se le suma el número de ejemplares de L3 , se obtiene el doble de ejemplares de L2.
a) Plantea un sistema de ecuaciones para averiguar cuántos libros de cada tipo se han editado.
b) Resuelve dicho sistema
23.- Un autobús urbano transporta en hora punta 90 viajeros de tres tipos: viajeros que pagan el billete entero, que vale 1 €; estudiantes que tienen un 25% de descuento al presentar el carnet; jubilados de la localidad que únicamente pagan el 50% del precio del billete. La recaudación del autobús en ese viaje fue de 64 €. Calcula el número de viajeros de cada clase sabiendo que el número de jubilados era el mismo que el número del resto de viajeros.
24.- Una empresa tenía, en el año 2001, cierto número de empleados, unos hombres y otros mujeres. En el año 2002 aumentaron en 5 los trabajadores de la empresa y en 6 el número de trabajadoras, quedando así doble número de mujeres que de hombres. En el año 2003 aumentaron en 2 las trabajadoras y se redujo en 4 el número de
trabajadores, resultando quedar el triple de mujeres que de hombres. Plantea un sistema para determinar el número de hombres y mujeres que trabajan en dicha empresa en el año 2003. Resuélvelo si es posible.
26.- Se juntan 30 personas entre hombres, mujeres y niños. Se sabe que entre los hombres y las mujeres duplican al número de niños. También se sabe que entre los hombres y el triple de las mujeres exceden en 20 al doble de niños. Plantear un sistema de ecuaciones que permita averiguar el número de hombres, mujeres y niños. Resolver el sistema de ecuaciones planteado
27.- Un estado compra 540 000 barriles de petróleo a tres suministradores diferentes que lo venden a 27, 28 y 31 $ el barril, respectivamente. La factura total asciende a 16 millones de $. Si del primer suministrador recibe el 30% del total del petróleo comprado, ¿cuál es la cantidad comprada a cada suministrador?.
5º PROGRAMACIÓN LINEAL
PROCEDIMIENTO:
1º) Se plantean las inecuaciones (restricciones) y la función Z objeto de la maximización o minimización.
2º) Se dibujan las rectas dadas en las restricciones haciendo tablas de valores y se ralla el recinto determinado por las inecuaciones.
3º) Se calculan los vértices de este recinto como puntos de corte de dos rectas, resolviendo el sistema de ecuaciones que forman las rectas.
4º) Se sustituyen las coordenadas de los vértices en la función Z
5º) Se da la solución al problema observando en qué vértice se maximiza o minimiza la función Z según se pida
Se recuerda que:
a) En recintos acotados (cerrados) siempre hay solución para máximo y mínimo. b) En recintos no acotados superiormente sólo hay solución para mínimo
c) En recintos no acotados inferiormente sólo hay solución para máximo
EJERCICIOS
1.- a) En un ejercicio de programación lineal con dos variables, ¿cómo ha de ser necesariamente la región factible para que se alcance, necesariamente, en algún punto determinado de la misma, el valor óptimo de la función objetivo?.
b) En la región determinada por: x + y 2; x y; x 0 e y 0, hallar las coordenadas de los puntos en los que la función f(x, y) = 3x + 4y alcanza su valor mínimo y máximo. (Jun. 1996, 3 ptos)
2.- Los alumnos de un instituto pretenden vender dos tipos de lotes A y B, para sufragarse los gastos de un viaje de estudios. Cada lote de tipo A consta de una caja de mantecados y cinco participaciones de lotería; cada lote del tipo B consta de dos cajas de mantecados y dos
participaciones de lotería. Por cada lote de tipo A vendido los alumnos obtienen un beneficio de 1225 ptas y por cada lote de tipo B de 1250 ptas.
Por razones de almacenamiento pueden disponer a lo sumo de 400 cajas de mantecados . Los alumnos sólo cuentas con 1200 participaciones de lotería y desean maximizar sus beneficios. a) Determínese la función objetivo y exprésense mediante inecuaciones las restricciones del
problema.
b) ¿Cuántas unidades de cada tipo de lote deben vender los alumnos para que el beneficio obtenido sea máximo?. Calcúlese dicho beneficio. (Jun. 1999, 3 ptos)
3.- En un depósito se almacenan bidones de petróleo y de gasolina. Para poder atender la demanda se han de tener almacenados un mínimo de 10 bidones de petróleo y 20 de gasolina. Siempre debe haber mas bidones de gasolina que de petróleo, siendo la capacidad del depósito de 2000 bidones. Por razones comerciales, deben mantenerse en el inventario al menos 50 bidones. El gasto de almacenaje de un bidón de petróleo es de 20 ptas y el de uno de gasolina de 30. Se desea saber cuántos bidones de cada clase han de almacenarse para que el gasto de almacenaje sea mínimo.
a) Exprésense la función objetivo y las restricciones del problema.
4.- Considerar el siguiente problema de programación lineal: Minimizar z = -3x – 2y
Sujeto a –2x + y 2 x – 2y 2 x 0; y 0
a) Mediante la resolución gráfica del problema discutir si existen soluciones factibles y si existe solución óptima.
b) Si se añade la restricción x + y 10, discutir si existe solución óptima y en caso afirmativo calcularla. (3 ptos)
5.- Un proyecto de asfaltado puede llevarse a cabo por dos grupos diferentes de una misma empresa: G1 y G2. Se trata de asfaltar tres zonas: A, B, y C. En una semana el grupo G1 es capaz de asfaltar 3 unidades en la zona A, 2 en la zona B y 2 en la C. El grupo G2 es capaz de asfaltar semanalmente 2 unidades en la zona A, 3 en la zona B y 2 en la C. El coste semanal se estima en 3300 € para G1 y 3500€ para G2. Se necesita asfaltar como mínimo 6 unidades en la zona A, 12 en la zona B, y 10 en la zona C. ¿Cuántas semanas deberá trabajar cada grupo para finalizar el proyecto con el mínimo coste?. (3 ptos) (Junio 2002)
6.- Determinar los valores máximo y mínimo de la función Z = 3x + 4y sujeta a las siguientes restricciones:
3x + y 3 x + y 5
x -2 (3 ptos) (Sep 2002) y 10
y 0
7.-Un centro dedicado a la enseñanza personalizada de idiomas tiene dos cursos, uno básico y otro avanzado, para los que dedica distintos recursos. Esta planificación hace que pueda atender entre 20 y 65 estudiantes del curso básico y entre 20 y 40 del curso avanzado. El número máximo de estudiantes que puede atender en total es de 100.
Los beneficios que obtiene por cada estudiante del curso básico es de 145 € y de 150 € para cada estudiante del curso avanzado. Halla el número de estudiantes que debe haber en cada curso para obtener el máximo beneficio. (Muestra 2003, 3 ptos)
8.- Determinar los valores máximo y mínimo de la función z = 5x + 3y, sujeta a las siguientes restricciones:
5 5 0
6 4 3
x y y x
y x
(3 ptos) (Sep 2003)
10.- Una compañía naviera dispone de dos barcos A y B para realizar un determinado crucero. El barco A debe hacer tantos viajes o más que el barco B, pero no puede sobrepasar 12 viajes. Entre los dos barcos deben hacer no menos de 6 viajes y no más de 20. La naviera obtiene un beneficio de 18000 € por cada viaje del barco A y 12000 € por cada viaje de B. Se desea que las ganancias sean máximas.
a) Expresar la función objetivo
b) Describir mediante inecuaciones las restricciones del problema y representar gráficamente el recinto definido.
c) Hallar el número de viajes que debe efectuar cada barco para obtener el máximo beneficio. Calcular dicho beneficio máximo. (Modelo 2005)
11.- Una empresa de alimentación dispone de 24 kg de harina de trigo y 15 de maíz, que se utilizan para obtener dos tipos de preparados A y B. La ración del preparado A contiene 200 g de harina de trigo y 300 g de maíz, con 600 cal de valor energético. La ración de B contiene 200 g de harina de trigo y 100 g de maíz, con 400 cal de valor energético. ¿Cuántas raciones de cada tipo hay que preparar para obtener el máximo rendimiento energético total. Obtener el rendimiento máximo. (Sep 2005)
12.- Una aerolínea quiere optimizar el número de filas de clase preferente y de clase turista en un avión. La longitud útil del avión para instalar las filas de asientos es de 104 m, necesitándose 2 m para instalar una fila de clase preferente y 1,5 m para las de clase turista. La aerolínea precisa instalar al menos 3 filas de clase preferente y que las filas de clase turista sean como mínimo el triple que las de clase preferente. Los beneficios por fila de clase turista son 152€ y de 206€ para la clase preferente.
¿Cuántas filas de clase preferente y de clase turista se deben instalar para obtener el beneficio máximo?. Calcular dicho beneficio. (Sep 2007, 3 ptos)
13.- a) representar la región del plano de finida por el siguiente sistema de inecuaciones.
40 3 11
40 60
y x
y x
y x
(Modelo 2008, 3 ptos)
b) Maximizar la función f(x, y) = 10x – y en la región obtenida. c) Minimizar la función g(x, y) = x – 10y
14.- Un distribuidor de aceite de oliva compra la materia prima a dos almazaras, A y B. Las almazaras A y B venden el aceite a 200 y 3000 € por tonelada, respectivamente. Cada
almazara le vende un mínimo de 2 toneladas y un máximo de 7 y para atender a su demanda, el distribuidor debe comprar en total un mínimo de 6 toneladas. El distribuidor debe comprar como máximo a la almazara A el doble de aceite que a la almazara B. ¿Qué cantidad de aceite debe comprar el distribuidor a cada una de las almazaras para obtener el mínimo coste?. Determinar dicho coste mínimo. (Jun. 2008, 3 ptos)
ANÁLISIS
1º Funciones
Dominio: Es el conjunto de números reales para los cuales existe imagen mediante la función f(x).
Dom f(x) = x R f(x)
Funciones polinómicas.- f(x) = P(x), Dom f(x) = R
Funciones racionales.- f(x) = Polinomio/Polinomio, Dom f(x) = R - x R tales que anulan el polinomio del denominador .
irracionales.- Funciones
x2 – 5x + 6 = 0, x= 2, x= 3, + + Dom f(x) = (- , 2 3, )
2 3 Ejemplo 2: f(x) =
2 x
3 -2x
, , Haciendo una tabla de signos tenemos:
2x – 3 = 0 x = 3/2 + + Dom f(x) = (- , -2) 3/2. ) x + 2 = 0 x = -2 -2 3/2
Funciones exponenciales.- f(x) = ag(x), Dom f(x) = R - Problemas de g(x) .
f(x) = ax, Dom f(x) = R
Ejemplo 1: f(x) = 2x3 3
e , Dom f(x) = R
Ejemplo 2: f(x) = 3/x 4
e , Dom f(x) = R - 4 .
Funciones logarítmicas.- f(x) = log(g(x)), Dom f(x) = x R / g(x) > 0
Ejemplo: f(x) = Ln(x2 – 4) x2 – 4 >0, hacemos x2 – 4 = 0 x = 2 y x = -2
Hacemos una tabla de signos para x2 – 4 + +
-2 2
Por lo tanto Dom f(x) = (- , -2) (2, ) Funciones trigonométricas.-
f(x) = sen(g(x)) Dom f(x) = R - Problemas de g(x) . f(x) = cos(g(x)) Dom f(x) = R - Problemas de g(x) . f(x) = tang (g(x)) Dom f(x) = R - x R / cos (g(x)) = 0 . f(x) = Cosec (g(x)) Dom f(x) = R - x R / sen (g(x)) = 0 . f(x) = Sec (g(x)) Dom f(x) = R - x R / cos (g(x)) = 0 . f(x) = Cotang (g(x)) Dom f(x) = R - x R / sen (g(x)) = 0 . Puntos de corte con los ejes:
Eje OX Si y = 0, despejando se obtienen los valores de x. Eje OY Si x = 0, sustituyendo se obtiene el valor de y.
0 2 x
3 -2x
0 g(x) / R x f(x) Dom , ) ( )
(x g x f
3 -R f(x) Dom , 9 x
3 -2x f(x) : Ejemplo
2
radicando el
para signos de Tabla 0,
6 5x x , 6 5x -x f(x) : 1
Simetrías:
Par Se tiene esta simetría cuando f(-x) = f(x). En este caso la función es simétrica respecto del eje OY.
Impar Se tienen esta simetría cuando f(-x) = -f(x). En este caso la función es simétrica respecto del origen de coordenadas, el punto (0, 0).
EJERCICIOS
1º Funciones dadas por tablas ( Interpolación)
1.- El gasto en fotocopias de una oficina viene dado por la tabla:
Meses Enero Febrero Marzo
Gasto 10 12 17
Obtener el polinomio interpolador de segundo grado y deducir el gasto de fotocopias para el mes de abril.
2.- El número de alumnos matriculados en miles en las pruebas de selectividad de la Universidad de Murcia en tres años fue el siguiente:
Años 1984 1988 1989
Alumnos 10 15 18
Obtener el polinomio interpolador de segundo grado para estimar el número de alumnos matriculados en 1986 y el número de alumnos que se matricularán en 1996.
3.- El número de funcionarios de una Comunidad Autónoma en tres años fue el siguiente:
Años 1989 1991 1995
Funcionarios 3000 3800 4100
Obtener el polinomio interpolador de segundo grado para estimar el número de
funcionarios en 1992 y el número en 1998. ¿Cuál de las dos estimaciones es más fiable?. 4.- El gasto en material de oficina en euros de una empresa viene dado por la tabla:
Meses Abril Mayo Junio
Gasto 110 150 155
Obtener el polinomio interpolador de segundo grado y deducir el gasto de fotocopias para el mes de julio.
5.- La temperatura en grados Fahrenheit (ºF) puede ser expresada como una función de primer grado de la temperatura x en grados Celsius (ºC). En la escala Fahrenheit el agua se congela a 32ºF y hierve a 212 ºF; en la escala Celsius, se congela a 0 ºC y hierve a 100 ºC. Expresar la temperatura Fahrenheit , y, como una función de la temperatura Celsius, x. Si la temperatura normal del cuerpo humano es de 98,6 ºF, ¿a qué
temperatura corresponde en la escala Celsius?.
6.- De una función f(x) se conocen los valores f(1) = 4, f(2) = 7 y f(4) = 31.
1) Calcular la función de interpolación cuadrática que toma dichos valores. 2) Calcular el valor de la función de interpolación para x = 3.
7.- Dada la tabla de la función f(x):
Calcular el error cometido cuando se calcula f(4) mediante la interpolación cuadrática utilizando los otros tres valores de la tabla.
x 1 2 3 4
2º Concepto de función
1.-Se quiere construir un pozo en forma cilíndrica de 2 m. de diámetro. Expresa el volumen del agua que cabe en el pozo en función de su profundidad x.
2.- El radio de un círculo mide 10 cm. Expresa el área de un rectángulo inscrito en el mismo en función de la medida x de la base. ¿Cuál es el dominio?
3.- En un bloque de viviendas las ventanas son rectangulares y deben tener 2 m2
de luz. Si x es la longitud del lado de la base, obtén el perímetro en función de x. ¿Cuál es el dominio?
4.- Se dispone de una cartulina de 100 x 40 cm y se quiere construir una caja con tapadera cortando un cuadrado en dos esquinas y dos rectángulos en las otras dos. Halla la expresión del volumen en función del lado x del cuadrado.
5.- El coste de la energía eléctrica se obtiene mediante un sumando fijo y otro proporcional a la cantidad de energía gastada. En dos meses distintos se ha pagado 35,70 € por 340 kwh y 31,14 € por 283 kwh. ¿Cuál es el sumando fijo?
6.- Feliciano quiere comprar un coche; tiene muy claro el modelo pero no sabe si comprarlo de gasolina o de gasóleo. El primero vale 18000 € y el segundo 20000 €. El precio de la
gasolina es de 1,08 €/l, y el del gasóleo 0,90 €/l. Supongamos que el consumo de un coche diesel es de 5 litros cada 100 km y el de un coche de gasolina de 6 litros cada 100 km.
a) Di la función que relaciona el coste (precio del coche más precio del combustible) con el número de kilómetros de cada coche.
b) Representa estas funciones. Observa el punto de corte. ¿Qué significa?
7.- Los piojos del cabello se reproducen duplicando su número cada 4 días. Si un niño tiene un piojo en su cabeza, y que todos viven:
a) ¿Cuántos piojos tendrá dentro de 12 días? b) Escribe la función y represéntala.
c) Si en el momento inicial un niño tenía 10 piojos, contesta a los apartados a) y b).
8.- La cantidad Q(t) que queda de una masa M mg de una sustancia radiactiva al cabo de t días viene expresada por la fórmula:
Q(t) = M . e-0,1 . t
1) Al cabo de cuanto tiempo la masa M se ha reducido a la mitad
2) Si la masa inicial M es de 27 mg, ¿cuánta sustancia quedará aproximadamente al cabo de 10 días?. Representar en este caso la masa aproximada de Q(t).
9.- Un lago está repoblado por una nueva especie de peces. Actualmente se estima una
población de 136.000 peces y tres años antes de 17.000 peces. Suponiendo que la población de peces crece de forma exponencial ( y = k.at ), calcular:
a) La función que expresa el número de peces en función del tiempo. b) ¿Cuándo habrá 1.000.000 de peces?
c) ¿Cuántos años hace que se introdujeron los 132 primeros ejemplares?
10.- Después de invertir en bolsa un individuo pasa de tener 1000 euros a tener 1300 euros en un mes. Si sabemos que la inversión que realiza sigue una ley exponencial ( y = k.at ),
calcular:
a) La función que expresa el dinero en función del tiempo b) Cuánto dinero tendrá al cabo de un año
c) En qué mes tendrá 66541 euros
1) Hallar la ecuación que relaciona y con t.
2) Hallar el nivel de contaminación a las 5 de la tarde.
13.- Para fomentar la utilización del transporte público entre dos puntos de una determinada ciudad, una compañía de transportes ofrece sus servicios en unas determinadas
condiciones:
1. Si el número de viajeros es menor o igual que 20 el billete costará 80€ por persona. 2. A partir de 20 viajeros el precio por billete se obtendrá restando de 80 € el número de
viajeros que excedan de 20.
14.-Teniendo en cuenta que en cada autobús caben como máximo60 viajeros y designando como x el número de personas por viaje, se pide:
a) La expresión algebraica y la representación gráfica de la función P(x) que proporciona el precio que ha de pagar cada viajero.
b) La expresión algebraica y la representación gráfica de la función I(x) que proporciona los ingresos por viaje de la compañía.
c)Obtener el número de viajeros que proporciona el máximo ingreso por viaje a la compañía, así como el valor de dicho ingreso.
15.- A las nueve de la mañana surge un rumor en una ciudad que se difunde a un ritmo de e2t
+ 1000 personas /hora. Sabiendo que t representa el número de horas transcurridas desde la aparición del rumor, calcular el número de personas que lo habrán oído entre las diez y las doce de la mañana.
16.- Se sabe que cuando comienza el invierno el número de moscas de una región decrece y dicho número viene dado por la función bt
e a t
N( ) . . , donde t es el tiempo en días y a y b son dos constantes no nulas.
a) Determinar el signo de las constantes a y b justificadamente
b) Sabiendo que al cabo de 64 días el número de moscas se ha reducido una 64ª parte de la población inicial, determinar el valor de b
c) Si en esta población se estima que el numero de moscas al comenzar el invierno es de 10,000 ¿Cuántas quedarán al cabo de 60 días?
d) en el supuesto anterior cuánto tiempo tiene que pasar para que queden la mitad de moscas
17.- Hace cuatro años que se repobló una zona con 100 ejemplares de una nueva especie de pinos. Actualmente hay 25.000 ejemplares. Se estima que el número N de pinos viene dado en función del tiempo, t, por la función N = AeBt, donde A y B son dos constantes. El
tiempo t se considera expresado en años desde el momento de la repoblación.
a) Determina la función que expresa el número de pinos en función del tiempo
b) ¿Cuánto tiempo se ha de esperar para que haya 200.000 ejemplares?
18.- El crecimiento de una colonia de mosquitos viene dado por la función A(t)=A0.ek.t
Donde A0 y k son constantes no negativas y t es el tiempo en días a) Razona el signo de A0 y k
b) Si inicialmente había 1000 mosquitos y al cabo de un día aumento a 1800, determina la función que expresa el número de mosquitos en función del tiempo en días
c) ¿ Cuánto tiempo tiene que pasar para que la colonia tenga 10000 mosquitos?
19.- El crecimiento de una colonia de abejas viene dada por la siguiente función
t
e
t
P
0,37..
5
,
56
1
230
)
(
a) ¿Cuántas abejas había inicialmente?
20.- La función
f
x
.X)
09
,
1
.(
499
1
1200
)
(
da la venta en x días después del lanzamiento de unvideo juego
a) ¿Cuántos video juegos se vendieron el primer día?
b) ¿Cuántos días tienen que pasar para que se vendan 6000 juegos?
21.- Se administran 50 mg. de anestesia aun paciente al principio de una operación. Se sabe que la concentración en la sangre humana disminuye exponencialmente con arreglo a la función
f(x) = k ⋅0'95x , donde K es la cantidad inicial y x el tiempo, en minutos, que ha transcurrido
desde su administración.
a) ¿Cuántos mg. de anestesia quedan en la sangre del paciente a la hora y media de su administración?
b) ¿Cuanto tiempo tiene que transcurrir para que le quede en sangre la mitad de la anestesia
22.- Una empresa tiene unos ingresos brutos a lo largo de los años que siguen una función del tipo i(t)=0’5t2, con unos gastos que se adaptan a una función del tipo g(t)=2t.
a) Representa gráficamente ambas funciones.
b) ¿Qué función nos da los beneficios de la empresa a lo largo del tiempo, b(t)?
c) ¿En cuánto tiempo empezará a tener beneficios?
d) ¿Qué función h(t) nos indica a lo largo de los años, cuántas veces son mayores los ingresos que los gastos?
3º Dominios
1º Dadas las siguientes funciones calcular su dominio, puntos de corte : 1) 4 6 5 ) ( 2 2 x x x x
f 2) f (x) x 4 3)
4 6 5 ) ( 2 2 x x x x f 4) 4 6 5 ) ( 2 2 x x x x f 5) 5 3 2 ) ( x x x f 6) 1 3 3 ) ( x x x f 7) 1 3 3 ) ( x x x f 8) 5 4 ) ( 2 x x x f 9) 5 3 2 ) ( x x x f 10) 9 5 ) ( x x x f 11) 3 1 ) ( 2 x x x
f 12)
4 9 ) ( 2 x x x f 13) 25 4 2 ) ( 2 x x x f 14) 25 4 2 ) ( 2 x x x f 15) 25 4 2 ) ( 2 x x x
f 16)
1 4 ) ( 2 2 x x x f
17) f(x) x3-4x 2 18) f(x) 8 2x
19) 2 1 ) ( 2 x x x
f 20) 1
1 2 ) ( 2 x x x f
21) f(x) x4 5x2 4 22)
4 3 ) ( 2 x x x f 23) 4 5 2 )
( 4 2
x x x x f 24) 6 6 2 ) ( 2 x x x x f 25) x x x y 5 4 2 2 26) 0 x si 5 o x si 1 7 ) ( 2 x x f
27) f(x) 3 x 1
28) 2 3 2 2 3 x x x x y 29) 1 2 x x y 30) -1 x si 5 -1 x si 1 ) (x x
f 31) 2 9
x x y 32) x x y 1
33)y log2(x4 5x2 4) 34) 2 2 ) ( x x Ln x f 35) 1 2 ) (x ex
4º Composición de funciones y función recíproca
1º Dadas las funciones f(x)= x2 + 1 y g(x)= x3 , halla: a) (f o g)(x) b) (g o f)(x)
2º Dadas las funciones f(x) = 2x + 1 y g(x) =x3 escribe:
a) (f o f)(x) b) (f o g)(x) c) (g o f)(x) d) (f o (f o f))(x) 3º Dadas las funciones
9 3
2 ) (
x x
f y g(x) x 2, calcular la expresión y el dominio de las funciones f+g, f-g, f·g y f/g
4º Dadas las funciones del apartado anterior, realizar g o f y f o g, indicando el dominio de cada una de ellas.
5º Sean las funciones f(x) 2x 1, g(x) x2 1 y
1 1 ) (
x x
h , comprobar con ellas la
propiedad asociativa de la composición, es decir, que se cumple . Calcular el dominio de la función resultante.
6º Calcula la función inversa de f(x) 5x 4 y comprueba el resultado. 7º Calcula la inversa de la función
4 3
1 2 ) (
x x x
f , compruébalo y calcula los dominios de
ambas.
8º Realizar las composiciones indicadas con las funciones propuestas: a) f x 2x 1, g x x2 3,
2 5 x x h
x g
f , hg x , f gh x
b)
2 x
3 x 3 x
f ,
1 x 2
1 x 2 x
g ,
x 1 x h
x f
f 1 , fh x , f hg x c) f x x,
2 x
1 x
g , h x x3
x h
f , hg x , gf x , hfg x
9º Calcular la función recíproca de las siguientes funciones, comprobando el resultado: a) f x 3x 4 b) f x 2x 5 c)
2 1 x x
f d)
3 2 x 5 x f
e)
6 7 x 2 x
f f)
5 x 2 1 x
f g)
7 9 x 2 x
f h)
9 2 x 7 x f
i)
1 x
2 x x
f j)
x 1
2 x 3 x
f k) f x 3x 2 l)
2 x
2º Continuidad y derivabilidad
Definición 1: Continuidad
Se dice que la función f(x) es continua en x = a sí se verifica: a)La función está definida en x = a, es decir, f(a). b)Existe f(x)
a x
Lim . Para ello es necesario que f(x) y f(x)
a x a
x
Lim
Lim y ambos sean
iguales.
c)El valor del límite coincide con el valor de la función en el punto, es decir, f(a)
f(x)
a x
Lim .
Por lo tanto, el valor de una función en un punto debe ser el que le asigna el límite en ese punto. De no ser así se dice que la función f(x) es discontinua en el punto x = a.
Una función f(x) es continua en el intervalo a, b cuando lo es en todos los puntos del intervalo.
Clasificación de las discontinuidades:
Discontinuidad evitable en x = a: Esta discontinuidad se tiene cuando f(x)
a x
Lim , pero
no existe f(a). Geométricamente corresponde a una gráfica que tiene un agujero en x = a.
Para hacer que la función sea continua en este punto basta con definir f(a) f(x)
a x
Lim .
Discontinuidad de 1ª especie en x = a: Esta discontinuidad se tiene cuando f(x)y
a x
Lim
f(a), Pero toman valores distintos. Gráficamente corresponde a una gráfica donde el punto (a, f(a)) está fuera de su lugar.
Discontinuidad de 2ª especie con salto finito en x = a: Esta discontinuidad se tiene cuando existen los límites laterales en x= a pero toman valores distintos. Geométricamente corresponde a una gráfica que en el punto
(a, f(a)) está rota y presenta una especie de escalón.
Discontinuidad de 2ª especie con salto infinito en x = a: Esta discontinuidad se tiene cuando alguno de los límites laterales en x = a tiende a ó a - . Geométricamente la función tiene una asíntota vertical en ese punto.
Definición 2: Derivabilidad
Se dice que la función f(x) es derivable en x = a si: a) Es continua en x = a.
b) Existe f ´(a), es decir, existe f+´(a) y existe f-´(a) y son iguales
Ejercicios
1º Dadas las siguientes funciones, estudiar su continuidad y derivabilidad
a)
x si x 2 f (x) 1 si 2 x 5
x 6 si x 5
b)
5x 2 si x 1 f (x) 2 si x 2
1
x si x 2 2
c)
2
x 4
si x 2 f (x) x 2
3 si x 2
d)
x 2 si x 3 f (x) x 2
si x 3 x 2
e)
1 si 8 x 4 f (x) x 2 si 4 x 2
8
si 2 x x
f)
2
x 4 si 4 x 4 f (x)
2x 1 si x 4
g) 2
2x si x 0 f (x) x 1 si 0 x 4
1
si x 4 x 4
h) 2
x
si 4 x 0 2
f (x) x si 0 x 2 x 6
si 2 x 4 2
i) 2
2
3 si x 2 3x 3 si 2 x 0 f (x)
x 2x 3 si 0 x 3 x 9x 18 si x 3
j) 2 x 4 -x 6 -3x 2 x 1 4x 1 x 2 2 ) ( x x f k) 2 x 9 x 2 x 1 4x 1 x 1 3 ) ( 2 x x f l) 0 x si 3 2 0 x si 1 ) ( 2 x x x f
2º Calcular los valores los parámetros para que la función sea continua en R. Estudiar la derivabilidad para esos valores
1) 2 x 3 3x 2 x 1 2 1 x 1 )
( x b
ax x f 2) 2 x 2 x 2 x 1 1 x 2 )
( x b