Estudi espectroscòpic de les transicions electròniques i dels modes de vibració del semiconductor ternari GaInP parcialment ordenat

ESTUDI ESPECTROSCOPIO DE LES

TRANSICIONS ELECTRONIQUES I DELS

MODES DE VIBRACIÓ DEL

SEMICONDUCTOR TERNARI GalnP

PARCIALMENT ORDENAT

TESI

per a l'obtenció del grau de

DOCTOR EN CIÈNCIES FÍSIQUES

presentada a

LA FACULTAD DE CIÈNCIES

de la

UNIVERSITAT AUTÒNOMA DE BARCELONA

per

En Francesc Alsina i Sureda

i dirigida pels doctors

Jordi Pascual i Gainza

i

Miquel Garriga i Bacardi

Capítol 8

Conclusions

Per estudiar l'ordenament espontani hem utilitzat un seguit de tècniques complementàries, com són: les de microscopía electrónica, fotoluminiscencia i reflectivitat, el·lipsometria i Raman. A partir de l'anàlisi de les mesures experimentals hem arribat a les següents conclusions:

1) La microscòpia electrònica ens ha permès evidenciar el creixement de la fase ordenada CuPt a les mostres a través de l'aparició de spots su-plementaris en els espectres de difracció. Si bé només qualitativament, la intensitat dels spots de la superxarxa dóna un indici de la gradualitat del creixement a les mostres. Les observacions en secció planar i vista planar, posen d'evidència la coexistència de l'ordenament a llarg abast amb ma-nifestacions pròpies d'una certa distribució a petita escala d'agregats. Es tractaria d'un mecanisme competitiu amb l'ordre, i de fet això s'observa, ja que el contrast que associem amb aquesta disgregació disminueix en aug-mentar l'ordenament de les mostres.

2) L'ordenament no és pefecte, els plans ordenats no són Ga pur o In pur sino que són plans amb una major o menor presència d'un dels cations. El paràmetre o grau d'ordre rj estableix la composició dels plans alterns. Mit-jançant mesures de les propietats òptiques del material és possible establir el valor de rj a la mostra. El grau d'ordre no és uniforme en tot el material, que consisteix de dominis amb graus d'ordre diferents. En aquests cas s'ha de parlar d'una funció de distribució F(rj) entorn d'un valor màxim T/P. Això

dóna lloc, entre altres coses, a que les estructures excitòniques siguin més suaus i amples, i a una diferència en el valor del gap fonamental segons si es mesura per reflectivitat o fotoluminiscencia.

3) Hem observat l'efecte de l'ordenament en la reducció del gap fona-mental i la relació amb els paràmetre de creixement (en concret l'orientació del substrat i la temperatura de creixement). El trencament de la banda

de valencia ha estat difícil de detectar en observar-se en els espectres de reflectivitat unes estructures excitòniques força amples. Només en el cas de les mostres crescudes al LEP, segurament amb una funció F(r)) més estreta que les altres mostres, s'han observat les dues transicions associades al tren-cament de la Bv, i s'ha evidenciat la dependència de les intensitats amb la polarització. Ens hem trobat amb la dificultat de interpretar els espec-tres polaritzats a partir de les regles de selecció calculades en funció del grau d'ordre. Considerant el cristall sotmès a una tensió biaxial, s'ha exemplificat l'efecte important que pot tenir una pertorbació superposada a l'ordenament, en les intensitats de les transicions. En el cas concret de l'efecte del petit desacord de xarxa amb el substrat, quantificable amb raigs X, no explica les desviacions de les intensitats trobades experimentalment.

4) L'estudi realitzat amb la tècnica d'el·lipsometria ha estat del tot no-vedós. La investigació dels efectes de la reducció de la simetria en els estats electrònics, tan experimental com teòrica, s'havia centrat fins ara en els estats propers al gap fonamental. Hem observat efectes similars a la tran-sició Ei que té lloc en direccions (111) de la zona de Brillouin (línia A) i els hem interpretat a partir del trencament de l'equivalència de les direccions (111) degut a l'ordenament. Es detecta la disminució i trencament de la tr-ansició i es relaciona amb el grau d'ordenament a la mostra. En els espectres obtinguts de les mostres d'una sola variant ordenada, observem una estruc-tura addicional que assignem a les transicions a la banda de conducció que prové del plegament de la línia A en la direcció en la direcció amb k paral·lel a la direcció d'ordenament. S'ha realitzat un estudi detallat de la modificació de les línies A i de les intensitats de les transicions en funció del paràmetre d'ordre. Finalment ressaltar les mesures realitzades a una mateixa energia i variant l'orientació de la mostra respecte el pla d'incidència. En aquestes mesures l'ordenament es manifesta en comportar-se la mostra com un ma-terial uniaxial, en el cas de les mostres d'una variant ordenada, o biaxial, les mostres amb la mateixa proporció de les dues variants. Això possibilita la distinció entre el creixement d'una o dues variants, i en el primer cas, saber quina de les dues es troba present.

5) Les vibracions de la xarxa tenen un fort caràcter local, de manera que en mostres parcialment ordenades són més sensibles al desordre existent en els plans de cations, que a la periodicitat dels propis plans. Així per exem-ple, si bé en el material ordenat es preveu el plegament del punt L, i per tant l'observació dels modes acústics, en el material desordenat s'observen estructures relacionades amb les bandes acústiques degut al trencament de la simetria de translació. Com a resultat els espectres Raman del material parcialment ordenat i del desordenat són molt semblants. Únicament en les mostres d'una sola variant ordenada hem trobat variacions remarcables.

Això posssiblement sigui degut a que aquestes mostres presenten dominis ordenats de gran extensió i, a més, no es té el desordre addicional que repre-senten les fronteres d'antifase. Hem observat l'aparició d'un pic a 352 c m- 1 no present en mostres desordenades. La relació de la intensitat d'aquest mode amb el grau d'ordenament i la peculiarietat de les regles de selecció que segueix sembla indicar que el seu origen cal buscar-lo en l'ordre. Per sobre de les estructures relacionades amb les bandes dels modes acústics activades pel desordre, es remarca una estructura més aguda (tant en els modes transversals com longitudinals) que sobresurt, a freqüències prope-res a on s'esperen els modes plegats als quals associem. Sembla doncs que s'estableix una competència entre els efectes d'ordre i de desordre que hauria de esultar, per mostres mé properes a l'ordenament perfecte, un successiu pas d'estructures amples activades pel desordre a pics més definits.

Apèndix A

A.l Teoria de Pelasticitat

L'aplicació d'una força mecànica en un cristall produeix la deformació de la xarxa cristal·lina caracteritzada per un camp de desplaçaments uXljX2iX3, on %i, %2i £3 són les coordenades d'un punt referides a un sistema de coordenades Cartesià. Es defineix el tensor de deformacions com [106, 46]

Dins del límit elàstic la relació entre la força aplicada al sòlid i la defor-mació d'aquest ve donada per la llei de Hooke generalitzada

ê = Sâ (A.2) o bé

£_{ij = Sijkl CTkl (A.3)}

on S és el tensor de les constants de deformació elàstiques. Equivalentment es poden definir les relacions inverses

ò =

Ce

va = Cijki eu (A.4) on C és el tensor de les constants de rigidesa.

Per simplificar és corrent utilitzar el següent canvi de notació

£11 £22 £33 £23 £31 £12

•I* •*• "T 4' 4* 4* £1 £2 £3 £4 £5 • £6

(A.5)

£11 £22 £33 £23 £31 £12

4? «J' 4* 4" 4 4*

£1 £2 £3 £4 £5 £6

de manera que tindrem les relacions

El no deracions té

mbre < i de si

/ £ i \ £2 £3 £4 £5 \ee) ie co metr

£¿ = SÍJ <Tj i,j = 1,2,..., ai = dj Sj i,j = 1 , 2 , . . . ,

6 6

nstants dj 0 SÍJ independents es pot reduir a del cristall. Així per un cristall cúbic (T<¿ / S'n S12 S12 0 0 0 \ / <rx \

Su S u S12 0 0 0 a2 S'12 S12 S u O 0 0 <T3

0 0 0 S44 0 0 CT4

0 0 0 0 S44 0 <75

\ 0 0 0 0 0 S44 ) \ a6 ) Les relacions entre SÍJ i dj són les següents

p _ Su + S'12

\S\\ — Si2j(Sii + 2S12)

c -

^

(Su — Si2)(Síi

C44 = TT -044

+ 2S12)

peí 0 (A.6) • consi-Oh) es (A.7) (A.8)

1. Pressió uniaxial aplicada al llarg d'una direcció G [a, ß,j]

a2 _{aß aj} <T = a\ aß ß2 ßj

a_{l ßl 7}2

(A.9)

ê = a S'12 + er

a2_{( 5 n - S i}

2) aß^~

aß^ ß2_(Su-S

l2)

Ä

-/?7T

aj^-ßl

72( S n - 5 i2)

(A.10)

1.1 Al llarg de la direcció [001]:

0 0 0

a = a | 0 0 0 0 0 1

(A.ll)

€xx — &yy — ^ 1 2 O"

ezz — Su &

Sxy r=z _Exz = _£yz = _{" yrí.íZ)}

1.2 Al llarg de la direcció [111]:

(A.13)

Exx — £yy — &zz — ~ÁS\l + 2S12) <T

£xy = £xz = eyz = - í ~SAi a \ (A.14)

2. Pressió biaxial aplicada en un pla perpendicular a G [a,ß,~f]

Una pressió biaxial en un pla (a,/3,7) es pot descomposar en una pressió hidrostàtica i una pressió uniaxial en la direcció normal al pla de manera que la força total en aquesta direcció sigui nul·la:

1 0 0 \ / a2 aß 07 \

0 = 0 ( 0 1 0 \ - a i aß ß2 _{ßj \ (A.15)} 0 0 1 / \ aj ß~i 72 /

. a2_(Sii-Si

2) aß^ äff

ê = a(Sii + Si2)-a{ aßf- ß2(Su - S12) ß l ^ « 7 T ß-T^ 72_{(5ii - S12)}

(A.16)

2.1 Pla (001)

(A.17)

£11 — £yy — (Sil + 'S'12) O"

ezz = 2Si2 er

£xy = £xz — Eyz = « (A.loJ

A.2 Simetria d'inversió temporal

L'operador d'inversió temporal, T, actua sobre un altre operador o funció d'ona canviant t —• — t i transformant l'operador o la funció d'ona en el seu complexe conjugat. Per a una partícula sense spin, l'efecte de T en el Hamiltonià H(f,p) i en la funció d'ona tp(f,t) és en un i altre cas

TH(r,p) = H{r,-p) (A.19) Tiß(r,t) = xl>*(r,-t) (A.20) Similarment per a una partícula de spin-una-meitat, es té

TH(r,p,ax,<Ty,crz) = H(r,-p,<Tx,-<ry,az) (A.21)

L'operador d'inversió temporal commuta amb el Hamiltonià d'un sistema quàntic isolat (sense camp magnètic extern). Considerem l'equació de va-lors propis

H^ = Exß (A.23) si el Hamiltonià és invariant sota simetria d'inversió temporal, llavors es té

HTiP = ETi> (A.24) La funció Tip és una funció pròpia de H com ip. Si les dues funcions són

linealment independents es produirà una degeneració addicional. Aquest és el cas per partícules amb spin-una-meitat, per les quals les funcions pròpies %f> i Ttß han de ser linealment independents i com a conseqüència es produeix almenys una doble degeneració. Aquesta degeneració essencial és coneguda com degeneració de Kramers.

Cas Cas a

Cas b Cas c

Relació entre D\D*

D i D* equivalents a la mateixa representació real irreduible

D i D* no equivalents D i D* equivalents

però no a una representació real

Test Frobenius-Shur

E*x(#) = *

EHXOT = O

EHXOT = -Ä

Partícula sense spin

No degeneració

extra Degeneració

doble Degeneració

doble

Partícula spin 1/2 Degeneració

doble

Degeneració doble

No degeneració

extra Taula A.l: Efectes de la simetria d'inversió temporal

D(k=o)

D(ky _ D(-k)

{E\r

}

1

0-ik-T„

0ik-f„

Taula A.2: Representacions irreduibles del grup de translació d'un cristall. Les representacions D^ i D^ (k ^ 0) estan degenerades per simetria d'inversió temporal.

Dl(k=0)

Dl{%=tí)

Dl(k)* _ £)/(-£)

{E|0} 1 1 1 {E|0} -1 -1 -1

{E\rn}

1

g-ti-íòtin

e«fc-íaii„

{E\7n}

-1

_g—ik-taun

_effc-iöu„

Taula A.3: Representacions irreduibles addicionals del grup de translació d'un cristall. Les representacions D'^ i D'W (k ^ 0) estan degenerades per simetria d'inversió temporal.

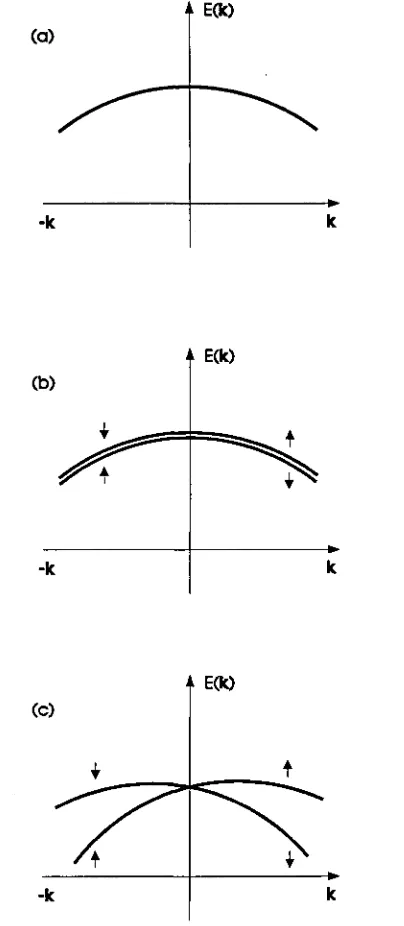
La introducció de degeneracions en un cristall degudes a inversió temporal es pot explicar a partir de la discusió anterior. Considerem en primer lloc el grup senzill de les translacions finites P, les representacions del qual es do-nen a la taula (A.2). Els efectes de la simetria d'inversió temporal es poden estudiar d'acord amb les regles de la taula (A.l). Per k / 0, es dona el cas (b) de la taula (A.l) perquè la representació irreduïble D^ no és equivalent a la seva representació complexa conjugada D^*. Com a conseqüència els valors propis corresponents a les representacions irreduibles k i — k estan degenerats, E(k) = E(—k). La representació irreduible amb k = 0 és real i pertany al cas (a), de manera que la inversió temporal no introdueix cap degeneració addicional. Això s'esquematitza a la Fig. (A.1(a)) on tots els estats per un k donat són de degeneració u, però hi ha una degeneració es-sencial entre els estats amb k i — k.

Considerem ara el grup doble T' amb les representacions irreduibles ad-dicionals de la taula (A.3). La representació amb k = 0 és real i pertany al

—*

cas (a), de manera que es té una doble degeneració. Per k ^ 0 les represen-tacions irreduibles no són equivalents a les seves complexes conjugades, cas (b), i de nou es té E(k) = E(-k).

Per simetria de translació hem mostrat que degut a la simetria d'inversió temporal E(k) = E(—k). Les altres operacions de simetria que hi puguin haver a més del grup de simetria de translació no lleven aquesta degeneració essencial x_{. L'efecte de l'operador d'inversió temporal sobre un estat k és el}

canvi a —k i si té spin una meitat en canvia la.direcció

2Vn,Éí = <-H (A-2 5)

x_{Una descripció dels efectes de la simetria temporal en general es té a les pàgines}

31-38, 43-45, 58-63 i 117 de la referència [45] i per cristalls zinc-blenda a la referència [107].

com es mostra a l'esquema de la Fig. (A.1(c)). Si el cristall a més posseeix simetria d'inversió espacial, que canvia la direcció de k però no la del spin

^ n , ï î = < - Í Í (A.26) l'estat ipn £ presenta una doble degeneració addicional corresponent als estats

amb spin up i spin down. En aquest cas la Fig. (A.1(c)) es redueix a la Fig. (A.l(b)).

En cristalls amb simetria d'inversió temporal, com per exemple l'estructura diamant, un estat general amb un vector k donat és almenys doblement degenerat. La situació és diferent a l'estructura zinc-blenda la qual no té centre d'inversió. En aquest cas, només els estats al llarg de línies A perma-neixen doblement degenerats. Al llarg de línies A, a diferència del cristall tipus diamant, els estats amb simetria A4 i A5 no es troben degenerats. En

canvi en els punts L persisteix la degeneració d'aquests dos estats en estar, els valors de k, separats dos a dos per un vector de la xarxa recíproca 2.

" E(k) (a)

-k k

A E(k)

—* —»

Apèndix B

Solucions aproximades de les

equacions d'ellipsometria en

mitjans anisotrops

Si bé el tractament de les dades experimentals obtingudes amb l'el·lipsòmetre s'ha realitzat a partir de les equacions exactes de la interacció de la llum amb materials anisotrops, sovint hem representat aquestes -sobretot quan s'ha mostrat l'espectre enter- en forma del que hem anomenat funció pseudo-dielèctrica aparent, que en un model isotrop de dues fases correspon a la funció dieléctrica del medi i es relaciona de forma directa amb la reflectància complexa. Anem a mostrar com, amb certes restriccions, la funció pseu-dodielèctrica està relacionada amb les components del tensor dielectric del material anisotrop i per tant no és merament una forma d'expressar els angles el·lipsomètrics.

Suposem que l'anisotropia del material es pot tractar com una correció a un valor isòtrop mitjà [108]. Les components principals del tensor dielectric al llarg de x, y, i z venen donades en primera aproximació per

ex = t + Aex ey = e + Aey

ez = e + Aez (B.l)

Expandim l'equació que ens relaciona la funció pseudodielèctrica amb la reflectància complexa

e = sin2 _9?

1 + tan

i - \ 2

2 I l_~P

fins a primer ordre amb p = p + Ap finalment La reflect< llavors es té mcia

e = e

e =

(e cos2 _ip

1

- s i n2y ? ) \ / e -sin2 _{ip cos ip}

complexa es defineix com

Ap = P

p=T

-™-fss

Arpp Aras

fpp fss sin2 _ipAp

P

(B.3)

(B.4)

(B.5)

(B.6) P ' pp ' ss

amb

ArPP)SS = rpp<ss(e + Aex, t + Aey, e + Aez) - rPP)SS(e) (B.7)

Considerem que el cristall es troba orientat de manera que la superfície és perpendicular a un dels eixos principals, per exemple ez, i el pla d'incidència en conté un altre. En aquest cas en l'equació (B.7) l'expressió dels coeficients complexes és la de l'eq. (5.56).

• Si el pla d'incidència és xz la funció pseudodielèctrica (eq. (B.4)) queda de la forma

t — sin2è A ecos2á — sin26 . 1 ,n . (e - l)sin2_{<p (t-l)sin}2_{<f> (e - 1 )} v _'

• Si el pla d'incidència és yz llavors es té la funció pseudodielèctrica e — sin2à> ecos2è — sin2¿ A 1 A _ .

*v* = e _{+ 7 n •}

2Aev - ~(—\\ • 2x Ae* - 7 TTA e- (B-9 (e — l)sin2_{(f> (e— l)sin}2_{(p (e — 1)}

Si l'eix principal x permaneix paral·lel a la superfície però l'eix principal y forma un angle a respecte aquesta (Secció (5.3.5) apartat B2) es pot veure com prenent nómes termes en primer ordre, a partir de l'eq. (B.4) es tornen a tenir les equacions (B.8) i (B.9) però amb la substitució de les components del tensor dielectric

Aey —* Aey cos2 a + Aez sin2 a

Aez -* Aey sin2 a + Aez cos2 a (B.10) Les solucions aproximades negligeixen l'acoblament entre modes s i p que es

de manera que no distingeixen entre els sentits +x i — x d'incidència.

Per valors de |e| corrents en materials semiconductors i per angles d'incidència típics d'entorn a </? ~ 70° es pot fer la següent aproximació de les equacions (B.8) i (B.9):

e*z ~ e + Aex = ex

£yz ~ e + Aey — Cy (B-ll)

En mostres poc anisotropes, la contribució dominat a la funció pseudo-dielèctrica mesurada en un pla d'incidència donat, prové de la projecció del tensor dielectric en la línia d'intersecció entre la superfície i el pla d'incidència.

Apèndix C

Caracterització òptica:

tècniques i equips

En aquest apèndix descriurem breument en una primera part els proces-sos de fotoluminiscencia i reflectí vit at. En una segona part descriurem les característiques més importants dels equips experimentals utilitzats.

C l Fotoluminiscencia i Reflectivitat

Reflectivitat

Hem emprat la reflectivitat com a mètode experimental alternatiu a l'absorció en les mesures del gap fonamental de l'aliatge GalnP. La dificultat que presenten les mesures d^absorció es deu al fet que les mostres de GalnP estan crescudes sobre substrats de GaAs, material que presenta un llindar d'absorció a més baixa energia que no pas el GalnP.

Considerem la reflexió de les ones electromagnètiques a la interfície entre dos medis restringint-nos al cas en què l'ona es propaga perpendicularment a la interfície. La reílectància R es defineix com la relació entre les intensitats de la llum incident i reflectida. Tenint en compte la continuïtat del camp electromagnètic paral·lel a la interfície i considerant que el primer medi, en el sentit de la propagació, és l'aire, es pot probar que

on e és la funció dieléctrica del segon medi. Les estructures de R(w) estan condicionades per les de e(uj).

Fotoluminiscencia

Quan en el procés d'una transició electrònica entre un estat donat i un estat de més baixa energia s'emet un foto, es diu que el procés és de recombinació radiativa. En el cas dels semiconductors, aquest es sol produir quan l'electró es troba fora de l'equilibri tèrmic amb un excés d'electrons a la banda de con-ducció i un excés de forats a la banda de valència. Per tal de portar l'electró fora del seu equilibri tèrmic és necessària algun tipus d'excitació. Així en el cas de la fotoluminiscencia es produeix l'excitació a través de fotons d'energia superior a la del gap. Per un procés de termalització els portadors es situen als extrems de les bandes de conducció (electrons) i de valència (forats). Les recombinacions seran radiatives només si la transició és directa -si no es tenen en compte els efectes de les imperfeccions i les vibracions de la xarxa-. L'espectre d'emissió de les transicions directes per recombinació dels elec-trons i forats està directament relacionat amb la probabilitat de transició entre les bandes de conducció i de valència (Eq. 3.3) i amb la probabilitat d'ocupació dels estats o funcions de distribució [109]

I(hu) oc / |e • Vcv(k)\2fe(k)fh(k) J S t (C.2)

Js \S/j¡[Ec(k)-Ev(k)]\

En el cas en què els extrems de les bandes de conducció i de valència coincideixin a k = 0 es pot utilitzar l'aproximació de la massa efectiva, de manera que l'expresió de la intensitat es redueix a

3

/ o c í y O \ë-Vcv(0)\2(hu-Eg)ifefh (C.3) on

m*ml m_ =

m*c + m*v

és la massa efectiva reduïda del parell electró-forat i m*, m* són les masses efectives de l'electró i del forat respectivament.

Si bé les funcions de distribució, fe o //,, són en general diferents de les distribucions a l'equilibri per les mateixes concentracions de portadors donat que hi ha una generació de portadors a través de processos no tèrmics, per simplificar s'agafaran com funcions de distribució tèrmiques. A més, si considerem aplicable una distribució clàssica (aproximació de Boltzmann),

tindrem E

IocCiE-E^e--^- (C.4) Introduirem l'efecte que t é en l'eixamplament de les línies de

de la convolució de / per una Gaussiana amb un FWHM de 8. En aquest cas el perfil és de la forma

f+_{°° , -41n2(E'-E)}

IA<xC I(E') e h dE' (C.5)

C.2 Equips emprats

Reflectivitat i fotoluminiscencia

a) Fonts excitadores.

Per a les mesures de reflectivitat, la font lluminosa ha estat una lampara de filament de tungstè, de 100 W de potencia, que emet dins d'una atmos-fera de iode. El seu espectre va de 0.8 a 2.2 ¡im. La llum es focalitza sobre la mostra per mitjà d'un mirall parabòlic, ajustant la intensitat incident amb l'ajuda d'un diafragma. Per millorar la relació senyal-soroll, la llum es modula amb un chopper mecànic de freqüència regulable.

Les mesures de fotoluminiscencia necessiten, en general, una font exci-tadora intensa, d'energia superior al gap i amb un punt d'impacte sobre la mostra el més petit possible. Hem utilitzat doncs un feix làser, en concret la ratlla blava 4880 Âd'un làsser d'Ar+_.

b) Criogènia.

Per a la realització de mesures a baixa temperatura hem utilitzat un criostat d'heli. Un buit secundari i una camisa de nitrogen n'asseguren l'isolament. Per evitar l'ebullició de l'heli, i per tant el pas de bombolles a través del feix lluminós, s'efectua un bombeig primari que baixa la temperatura de l'heli fins a 2 K: en el que s'anomena estat superfluid.

c) Espectroscopia.

La llum reflectida o emesa per la mostra es focalitza sobre l'escletxa d'entrada del monocromador. L'espectròmetre és del tipus THR 1500 d'alta resolució. La seva distància focal és de 1.70 m, i té una reresolució de AA/A ~ 6-10- 6

(mesurada resolguent la ratlla verda del mercuri).

El·lipsometria

S'ha utilitzat 1' el·lipsòmetre de polaritzador giratori ES4G fabricat per So-pra. Una lámpara de Xe d'alta pressió i de 75 W de potència, serveix de

Bibliografia

[1] T.Katsuyama, I. Yoshida, J. Hashimoto, Y. Taniguchi i H. Hayashi, J. Cryst. Growth 127, 697 (1992).

[2] H. Fujii, Y. Ueno, A. Gomyo, K. Endo i T. Suzuki, Appl. Phys. Lett. 65, 989 (1994).

[3] K.H. Huang, J.G. Yu, C.P. Kuo, R.M. Fletcher, T.D. Osentowski, L.J. Stinson, M.G. Craford i A.S.H. Liao, Appl. Phys. Lett.

[4] K.A. Bertness, S.R. Kurtz, D.J. Friedman, A.E. Kibbler, C. Kramer i J.M. Olson, Appl. Phys. Lett.

[5] G.B. Stringfellow, J. Cryst. Growth 27, 21 (1974). [6] D.M. Wood i A. Zunger, Phys. Rev. B 40, 4062 (1989).

[7] G.P.Srivasta, J.L.Martins i A.Zunger, Phys. Rev. B 31, 2561 (1985).

[8] J.E. Bernard, L.G. Ferreira, S.-H. Wei i A. Zunger, Phys. Rev. B 38, 6338 (1988).

[9] A. Zunger i S. Mahajan, Handbook of Semiconductors, Vol. 3, second edition, (Elsevier, Amsterdam, 1994).

[10] L.G. Ferreira, A.A. Mbaye i A. Zunger, Phys. Rev. B 37, 10547 (1988).

[11] S.-H. Wei, L.G. Ferreira i A. Zunger, Phys. Rev. B 41, 8240 (1990).

[12] R.G. Dandrea, J.E. Bernard, S.-H. Wei i A. Zunger, Phys. Rev. Lett. 64, 36 (1990).

[13] J.E. Bernard, R.G. Dandrea, L.G. Ferreira, S. Froyen, S.-H. Wei i and A. Zunger, Appl. Phys. Lett. 56, 731 (1990).

[14] G.B. Stringfellow, J. Appl. Phys. 54, 404 (1983).

[15] D.M. Wood i A. Zunger, Phys. Rev. Lett. 61, 1501 (1988).

[16] T.S. Kuan, T.F. Kuech, W.I. Wang i E.L. Wilkie, Phys. Rev. Lett. , 201 (1985).

[17] O. Ueda, M. Takikawa, J. Komeno i J. Umebu, Jpn. J. Appl. Phys. 26, 1824 (1987).

[18] A. Gomyo, T. Suzuki, K. Kobayashi, S. Kawata, I. Hiño i T. Yuasa, Appl. Phys. Lett. 50, 673 (1987).

[19] A. Gomyo, T. Suzuki i S. Iijima, Phys. Rev. Lett. 60, 2645 (1988).

[20] P. Bellon, J.P. Chevalier, E. Augarde, J.P. André i G.P. Martin, J. Appl. Phys. 66, 2388 (1989).

[21] S. Minagawa i M. Kondow, Elec. Letters, 25, 758 (1989).

[22] L.C. Su, LH. Ho, G.B. Stringfellow, Y. Leng i C.C. Williams, Mat. Res. Soc. Symp. Proc. 340, 123 (1994).

[23] S.R. Kurtz, J.M. Olson, D.J. Arent, M.H. Bode i K.A. Bertness, J. Appl. Phys. 75, 5110 (1994).

[24] G.S. Chen i G.B. Stringfellow, Appl. Phys. Lett. 59, 324 (1991).

[25] T. Suzuki, A. Gomyo, S. Iijima, K. Kobayashi, S. Kawata, I. Hiño i T. Yuasa, Jpn. J. Appl. Phys. 27, 2098 (1988).

[26] D. Cao, A. Kimball, G. Chen, K. Fry i G. Stringfellow, J. Appl. Phys. 66, 5384 (1989).

[27] S.R. Kurtz, J.M. Olson i A. Kibbler, Appl. Phys. Lett. 57, 1922 (1990).

[28] J.P. Goral, S.R. Kurtz, J.M. Olson i A. Kibbler, J. Electron. Mat. 19, 95 (1990).

[29] P. Gavrilovic, F.P. Dabkowski, K. Meehan, J.E. Williams, W. Stutius, K.C. Hsieh, N. Holonyak, M.A. Shahid i S. Mahajan, J. Cryst. Growth 93, 426 (1988).

[30] P. Bogulawski, Phys. Rev. B 42, 3737 (1990).

[31] S. Froyen i A. Zunger, Phys. Rev. Lett. 66, 2132 (1991).

[32] S. Froyen, J.E. Bernard, R. Osorio i A. Zunger, Physica Scripta. T45,

272 (1992).

[34] B.A. Philips, A.G. Norman, T.Y. Seong, S. Mahajan, G.R. Booker, M. Skowronski, J.P. Harbison i V.G. Keramidas, J. Crystal Growth 140,

249 (1994).

[35] A.G. Norman, NATO ASI Series Vol. B 203, 233, editat per D. Cherns (Plenum Press, NY & Londres, 1989).

[36] E. Morita, M. Ikeda, 0 . Kumagai i K. Kaneko, Appl. Phys. Lett. 53,

2164 (1988).

[37] T.L. McDevitt, S. Mahajan, D.E. Laughlin, W.A. Bonner i V.G. Kera-midas, Phys. Rev. B 45, 6614 (1992).

[38] F. Peiró, Tesi Doctoral, Universitat de Barcelona (1993). [39] M.A. Shahid i S. Mahajan, Phys. Rev. B 38, 1344 (1988).

[40] M.A. Shahid, S. Mahajan i D.E. Laughlin, Proceedings of the Royal Mi-croscopical Society Conference, editat per A.G. Cullis i J.L. Hutchison, Inst. Phys. Conf. Ser. 110, 143 (1989).

[41] P.N. Keating, Phys. Rev. 145, 637 (1966).

[42] T. Kanata, M. Nishimoto, H. Nakayama and T. Nishino, Phys. Rev. B

45, 6637 (1992).

[43] D.B. Laks, S.-H. Wei i A. Zunger, Phys. Rev. Lett. 69, 3766 (1992). [44] S.-H. Wei, D.B. Laks i A. Zunger, Appl. Phys. Lett. 62, 1937 (1993). [45] F. Bassani, Electronic States and Optical Transitions in Solids,

Perga-mon Press (1975).

[46] M.-F. Li, Modern Semiconductor Quantum Physics, World Scientific (1994).

[47] D.E. Aspnes, a Handbook on Semiconductors, editat per T.S. Moss i M. Balkanski, (North-Holland, Amsterdam, 1980) Vol. 2, Capítol 4A. [48] F.H. Pollak i M. Cardona, Phys. Rev. 172, 816 (1968).

[49] M. Garriga, Tesi Doctoral, Stuttgart (1990). [50] D.J. Chadi, Phys. Rev. B 16, 790 (1977).

[53] R. Román, Tesi Doctoral, Univ. Autònoma de Barcelona (1990).

[54] S.-H. Wei i A. Zunger, Phys. Rev. 39, 3279 (1988).

[55] S.-H. Wei i A. Zunger, Phys. Rev. 49, 14337 (1994).

[56] A. Mascarenhas, S. Kurtz, A. Kibbler i J.M. Olson, Phys. Rev. Lett. 63, 2108 (1989).

[57] R.G. Alonso, A. Mascarenhas, S. Froyen, G.S. Horner, K. Bertness i J.M. Olson, Solid State Comm. 85, 1021 (1993).

[58] T. Kanata, M. Nishimoto, H. Nakayama i T. Nishino, Appl. Pys. Lett. 63, 512 (1993).

[59] R.G. Alonso, A. Mascarenhas, G.S. Horner, S.R. Kurtz i J.M. Olson, Phys. Rev. 48, 11833 (1993).

[60] D.J. Mowbray, R.A. Hogg i M. S. Skolnick, M. C. De Long, S. R. Kurtz and J. M. Olson, Phys. Rev. B 46, 7232 (1992).

[61] G.S. Horner, A. Mascarenhas, S. Froyen, R.G. Alonso, K. Bertness i J.M. Olson, Phys. Rev. B 47, 4041 (1993).

[62] G.S. Horner, A. Mascarenhas, R.G. Alonso, S. Froyen, K. Bertness i J.M. Olson, Phys. Rev. B 49, 1727 (1994).

[63] B.T McDermott, K.G. Reid, N.A. El-Masry, S.M. Bedair, W.M. Dun-can, X. Yin i F.H. Pollak, Appl. Phys. Lett. 56, 1172 (1990).

[64] M.C. DeLong, P.C. Taylor i J.M. Olson, Appl. Phys. Lett. 57, 620 (1990).

[65] C.T.H.F. Liedenbaum, A. Valster, A.L.G.J. Severens and G.W. 't Hooft, Appl Phys. Lett. 57 (25), 2698 (1990).

[66] S.-H. Wei i A. Zunger, Appl. Phys. Lett. 56, 662 (1990).

[67] M. Moser, C. Geng, E. Lach, I. Queisser, F. Scholz, H. Schweizer i A. Dornen, J. Cryst. Growth 124, 333 (1992).

[68] H. Asai and K.Oe, J. Apl. Phys. 54, 2052 (1983).

[69] O.P. Kuo, S.K. Vong, R.M. Cohen, and G.B. Stringfellow, J. Apl. Phys. 57, 5428 (1985).

[70] H. Mathieu, Propriétés Optiques des Semiconducteurs, Cours DEA,

Université de Montpellier.

[71] P.T. Bailey, Phys. Rev. B 1, 588 (1970).

[72] R.M.A. Azzam i N.M. Bashara, Ellipsometry and Polarized Light, (North-Holland, Amsterdam, 1977).

[73] P. Yeh, Surf. Science 96, 41 (1980).

[74] D. E. Aspnes, J. Opt. Soc. Am. 64, 812 (1974).

[75] D. E. Aspnes i A. A. Studna, Phys. Rev. B 27, 985 (1983).

[76] A.G. Thompson, M. Cardona, K.L. Shaklee i J.C. Woolley, Phys. Rev.

146, 601 (1966).

[77] D.E. Aspnes, S.M. Kelso, R.A. Logan i R. Bhat, J. Appl. Phys. 60, 754 (1986).

[78] D. Brust, J.C. Philips i F. Bassani, Phys. Rev. Lett. 9, 94 (1962). [79] J.R. Chelikowsky i M.L. Cohen, Phys. Rev. B 14, 556 (1976).

[80] L. Viña, S. Logothetidis i M. Cardona, Phys. Rev. B 30, 1979 (1984). [81] P. Lautenschlager, M. Garriga, S. Logothetidis i M. Cardona, Phys.

Rev. B 35, 9174 (1987).

[82] P. Lautenschlager, M. Garriga i M. Cardona, Phys. Rev. B 36, 4813 (1987).

[83] S. Zollner, M. Garriga, J. Humlicek, S. Gopalan i M. Cardona, Phys. Rev. B 4 3 , 4349 (1991).

[84] S. Zollner, M. Garriga, J. Kircher, J. Humlicek i M. Cardona, Phys. Rev. B 48, 7915 (1993).

[85] S. Logothetidis, M. Alouani, M. Garriga i M. Cardona, Phys. Rev. B

41, 2959 (1989).

[86] C. Alibert, G. Bordure, A. Laugier i J. Chevalier, Phys. Rev. B 6, 1301 (1972).

[87] M. Kondow, H. Kakibayashi, Y. Inoue, T. Nishino i Y. Hamakawa, J. Cryst. Growth 9 3 , 412 (1988).

;88] S.-H. Wei, A. Franceschetti i A. Zunger, Phys. Rev. B (1995). 89] D. E. Aspnes, J. Opt. Soc. Am. 64, 639 (1974).

[91] T. Kato, T. Matsumoto i T. Ishida, Jpn. J. Appl. Phys. 27, 983 (1988).

[92] M. Kondow, H. Kakibayashi, S. Minagawa, Y. Inoue, T. Nishino i Y. Hamakawa, Appl. Phys. Lett. 53, 2053 (1988).

[93] M. Kondow i S. Minagawa, J. Appl. Phys. 64, 793 (1988).

[94] M. Kubo, M. Mannoh i T. Narusawa, J. Appl. Phys. 66, 3767 (1989).

[95] T.A. Gant, M. Dutta, N.A. El-Masry, S.M. Bedair i M.A. Stroscio, Phys. Rev. B 46, 3834 (1992).

[96] A. Krost, N. Esser, H. Selber, J. Christen, W. Richter, D. Bimberg, L.C. Su i G.B. Stringfellow, J. Cryst. Growth 145, 171 (1994).

[97] K. Shina, A. Mascarenhas, G.S. Horner, R.G. Alonso, K.A. Bertness i J.M. Olson, Phys. Rev. B 48, 17591 (1993).

[98] K. Uchida, P.Y. Yu, N. Noto, Z. Liliental-Weber i E.R. Weber, Phylo-sophical Magazine B 70, 453 (1994).

[99] J. Pujol, F. Alsina, J. Pascual i J. Camassel, Jpn. J. Appl. Phys. 32, suppl. 32-3, 739 (1993).

[100] R. Loudon, Advan. Phys. 13, 423 (1964).

[101] C.A. Arguello, D.L. Rousseau i S.P.S. Porto, Phys. Rev. 181, 1351 (1969).

[102] W. Hayes i R. Loudon, Scattering of Light by Crystals, editat per J. Wiley & Sons (NY, 1978).

[103] B.H. Bayramov, V.V. Toporov, Sh.B. Ubaydullaev, L. Hildisch i E. Janhe, Solid State Comm. 37, 963 (1981).

[104] E. Bedel, R. Carles, A. Zwick, M. A. Renucci i J.B. Renucci, Phys. Stat. Sol. (b) 130, 467 (1985).

[105] L. Artus, J. Pascual, J. Pujol, J. Camassel i R.S. Feigelson, Phys. Rev. Bbf43, 2088 (1991).

[106] J.F. Nye, Physical Properties of Crystals, Oxford University Press, 1957.

[107] M. Cardona, N.E. Christensen i G. Fásol, Phys. Rev. B 38, 1806

(1988).

[108] D.E. Aspnes, J. Opt. Soc. Am. 70, 1275 (1980).

[109] A. Mooradian i H.Y. Fan, Phys. Rev. 148, 873 (1966).

» uni

Departament de Física

Universitat Autònoma de Barcelona

ESTUDI ESPECTROSCOPIC DE LES

TRANSICIONS ELECTRONIQUES I DELS

MODES DE VIBRACIÓ DEL

SEMICONDUCTOR TERNARI GalnP

PARCIALMENT ORDENAT

ESTUDI ESPECTROSCOPIO DE LES

TRANSICIONS ELECTRONIQUES I DELS

MODES DE VIBRACIÓ DEL

SEMICONDUCTOR TERNARI GalnP

PARCIALMENT ORDENAT

TESI

per a l'obtenció del grau de

DOCTOR EN CIÈNCIES FÍSIQUES

presentada a

LA FACULTAD DE CIÈNCIES

de la

UNIVERSITAT AUTÒNOMA DE BARCELONA

per

En Francesc Alsina i Sureda

i dirigida pels doctors

Jordi Pascual i Gainza

i

Miquel Garriga i Bacardi

índex

1 Introducció 1

1.1 Models basats en l'equilibri termodinàmic d'estructures en

tres dimensions 4 1.1.1 Model clàssic 4 1.1.2 Model estructural 5 1.1.3 Ordenament a curt abast: clustering i anticlustering . 11

1.1.4 Efectes qualitatius del creixement epitaxial 12

1.1.5 Sumari 17 1.2 Observació d'ordenament espontani en compostos isovalents

III-V 17 1.3 Estabilitat superficial i dinàmica de l'ordenament 21

1.3.1 Energia a la superfície . . 21 1.3.2 Possibles mecanismes per fixar la fase ordenada . . . 24

2 Ordenament CuPt en aliatges GalnP 26

2.1 Característiques del creixement 26 2.2 Estudi per Microscopi Electrònic de Transmissió 28

2.3 Difracció de Raigs X 33 2.4 L'estructura CuPt 34 2.5 Aliatge parcialment ordenat amb acord de xarxa amb un

subs-trat (001) 42

3 Propietats òptiques i transicions interbanda 46

3.1 Teoria microscòpica de la funció dieléctrica 46 3.2 Punts crítics: expansions parabòliques locals 48 3.3 Canvis induïts per una pertorbació: efectes de la tensió sobre

l'estructura de bandes 51

3.3.1 Transició E0 53

3.3.2 Transició Ex 55

3.4 Model Tight-Binding de càlcul de bandes 58

4 Efectes de l'ordenament en el gap fonamental 60

4.2 : Resultats experimentals 63 4.3 Transició Eo: dependència amb l'ordre 69

4.4 Transició E0: dependència amb l'ordre i la tensió epitaxial . 80

4.5 Intensitats de les transicions 83

5 EHipsometria 93

5.1 Polarització de l'a llum 93 5.2 Principi de la mesura 95 5.3 Determinació de les propietats òptiques d'un material . . . . 97

5.3.1 Introducció 97 5.3.2 Propagació d'una ona plana en medis anisòtrops

ho-mogenis 98 5.3.3 Modes propis de propagació 101

5.3.4 Coeficients complexes de reflexió 102 5.3.5 Solucions de casos especials 103 5.4 EHipsometria amb element giratori 109

5.4.1 EHipsòmetre amb analitzador giratori 110 5.4.2 EHipsòmetre amb polaritzador giratori 112

5.5 Obtenció de la funció dieléctrica 113

6 Anisotropia òptica per sobre del gap fonamental 115

6.1 A propòsit de la mesura 115 6.2 Aliatge GalnP desordenat 115

6.2.1 Espectre en un model isotrop de dues fases 117

6.2.2 Transicions interbanda 117 6.3 Mesures en mostres amb dues variants ordenades 125

6.4 Mesures en mostres amb una sola variant ordenada 131 6.5 Estudi de la transició Ei en l'estructura CuPt 135

6.6 Intensitat de les transicions 146

6.7 Mesures amb ß variable 152

7 Modes polars en el compost ordenat 158

7.1 Vibracions de la xarxa en el centre de zona del GaInP2 . . . 159

7.2 Resultats experimentals 160 7.3 Tensors Raman en el grup C3,, 167

7.4 Dispersió Raman en un cristall uniaxial (C3,,) 171 7.4.1 Eficiència de la dispersió Raman 175

7.5 Discussió 178

A A.l A.2

Teoria de l'elasticitat . . . . Simetria d'inversió temporal

184 184 187 B Solucions aproximades de les equacions d'eHipsometria en

mitjans anisotrops 192 C Caracterització òptica: tècniques i equips 195

C l Fotoluminiscencia i Reflectivitat 195

C.2 Equips emprats 197

Capítol 1 .

Introducció

Els compostos semiconductors ternaris i quaternaris III-V s'han mostrat im-portants per a una àmplia serie d'aplicacions en l'optoelectrònica, com ara emissors de llum (làsers i diodes), detectors, cèl·lules fotovoltàiques ... En l'elecció dels materials constituents d'un determinat dispositiu a més de les condicions determinades pel propi dispositiu (per exemple la longitud d'ona d'emissió i l'índex de refracció en un emissor de llum) hi ha la limitació de la complexitat del creixement d'estructures multicapes. El creixement de les diferents capes s'ha de realitzar de manera de limitar les distorsions que poguessin donar lloc a defectes que degradessin el funcionament opti o elèctric del dispositiu. El creixement epitaxial de materials amb constant de xarxa pràcticament idèntica compleix aquesta exigència. Cal dir però, que les actuals tècniques de creixement han obert tot un camp d'estudi centrat en les heterostructures amb desacord de xarxa.

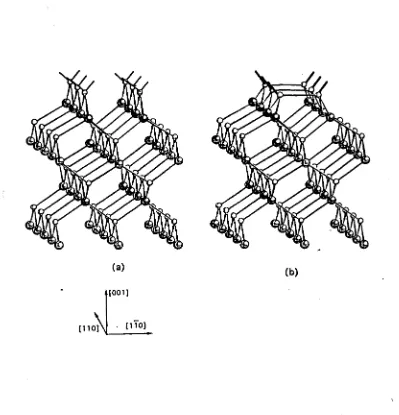
La majoria d'aquests compostos cristal·litza en una estructura zinc-blenda (veure la Fig. 1.1) formada per dues subxarxes f.c.c, una composta d'ions del grup III i l'altra composta d'ions del grup V, desplaçades una respecte de l'altra per aoVÏÏ/4 al llarg de la direcció (111) on ao és el paràmetre de xarxa. En un principi es pensava que aquests aliatges ternaris o quaternaris forma-ven exclusivament fases desordenades, o sigui, amb els ions corresponents als grups III i V disposats aleatòriament en les seves respectives subxarxes. A mitjans de la dècada dels anys vuitanta es suggerí teòricament i s'evidencià experimentalment la possibilitat d'obtenir desviacions respecte aquest des-ordre perfecte en forma de, o bé, ordenament a curt abast, en el qual es produeix un agrupament d'ions a petita escala, o bé, ordenament a llarg abast amb la repetició periòdica a gran escala d'una de les possibles unitats tetraèdriques (veure la Fig. 1.1).

aliat-I

TL

a

& _s il

3

Oi

>¿

e

S

ges ordenats formen compostos tipus ABC2 en una o més de les estructu-res CuPt, CuAu i/o calcopirita, alguns s'ordenen de la forma A3BC4 en l'estructura famatita o luzonita. L'ordenament afecta les propietats físiques del compost, com ara les propietats òptiques degut al canvi de les energies dels estats electrònics, les elèctriques i les de transport per la influència que té el desordre en un aliatge en la mobilitat dels portadors en el semiconduc-tor. Aquests efectes de l'ordenament tenen implicacions tecnològiques com ara: la varició del llindar d'emissió dels lasers, o l'aplicació en dispositius d'alta velocitat.

L'aliatge Gao.sIno.sPque és un material que creix amb acord de malla en substrats GaAs és de gran interès pel seu gap directe força gran (entorn de 2 eV) que el fa aplicable en lasers [1, 2], diodes emetent en el visible [3] i cèl·lules solars d'alta eficiència [4]. Com veurem en els successius capítols, l'aliatge GalnP s'ordena espontàniament en una estructura CuPt, donant lloc a efectes observables a l'estructura de bandes electrònica i també en els estats de vibració de la xarxa.

En aquest primer capítol donarem una visió general del fenomen de l'ordenament espontani i els intents que s'han realitzat per explicar-ne la seva presència. El segon capítol l'hem dedicat a la descripció de les carac-terístiques de creixement de les mostres que s'analitzen en aquest treball, i en l'estudi estructural i morfològic d'aquestes mitjançant tècniques de raigs X i de microscòpia electrònica. Per finalitzar aquests capítol es descriu-rà l'estructura CuPt, la disposició que s'assumeix que tenen els ions a la xarxa i finalment, introduirem l'anomenat paràmetre d'ordre que descriu l'ordenament parcial.

El tercer capítol és introductori a l'estudi de les propietats òptiques del material i la relació d'aquestes amb l'estructura electrònica de bandes. Expo-sem breument les variacions que introdueix una pertorbació en el Hamiltonià dels electrons de la banda de valència i de la banda de conducció, en reduir la simetria d'aquest. El capítol quart està dedicat als canvis que l'ordenament provoca en el gap fonamental. Amb fotoluminiscencia i reflectivitat estu-diem els efectes de reducció del gap fonamental i de trencament dels estats del màxim de la banda de valència i els correlacionem quantitativament amb l'ordenament present a la mostra. Per acabar, es mostra l'anisotropia de les transicions i es realitza un estudi de les intensitats.

la Hum en medis anisòtrops. Seguidament, ens centrem en les mesures d'el-lipsometria que ens permeten seguir l'evolució de la transició Ei amb l'ordre (capítol 6).

Per acabar, es mostra com l'espectroscòpia Raman permet observar efec-tes de la reducció de simetria en les vibracions de la xarxa (capítol 7).

1.1 Models basats en l'equilibri termodinàmic

d'estructures en tres dimensions

Històricament, pel fet que inicialment l'obtenció de compostos III-V, a partir de combinacions binàries, es realitzés amb tècniques que mantenen situacions properes a l'equilibri termodinàmic, tan per materials massius (tècniques de "melt") com per materials epitaxials (LPE o VPE), els criteris d'estabilització d'aquests materials es desenvoluparen en termes de l'estabilitat d'estructures tridimensionals.

1.1.1 Model clàssic

• Els models termodinàmics clàssics pels aliatges caracteritzen la seva energia per un sol paràmetre d'interacció [5]. L'entalpia de formació dels aliatges III-V, definida respecte els constituents binaris purs com

AH

(x) = HiAsB^C)

-

x H(AC) -(1-x) H(BC)

(1.1)

es pot escriure de la forma fi x(l—x), on fi és el "paràmetre d'interacció".

• En tots els casos examinats es troba una entalpia Aífm,r positiva (fi > 0). Així s'assumí que la interacció entre els constituents que formen l'aliatge és repulsiu. L'origen d'aquesta repulsió s'identifica amb l'energia elàstica associada amb l'empaquetament d'una xarxa amb àtoms de grandàries diferents i es demostra que fi depèn expo-nencialment del desacord de xarxa entre els constituents binaris:

n AS* — fins

fi OAC — «BC

<a>

En aquest model els diagrames de fase estan caracteritzats per un gap de miscibilitat dins del qual el sistema no és estable. La línia de separació que marca el límit d'estabilitat de l'aliatge i la separació de fases, depèn de la temperatura i es denomina límit spinodal.

Objeccions al model clàssic

Un tractament fenomenològic amb absència de graus de llibertat de confi-guració microscòpica (2^ arranjaments diferents dels àtoms A i B en les N posicions de la xarxa) no distingeix, energèticament, dues fases diferents a la mateixa composició i a la mateixa temperatura. Ara bé, les configuracions microscòpiques dels àtoms A i B poden ser "químicament" molt diferents — compartint les mateixes propietats elàstiques— i presentar diferents valors per l'entalpia. Els graus de llibertat deguts a les possibles configuracions constitueixen camins addicionals per assolir l'equilibri termodinàmic i afec-tar els límits d'una fase, per exemple la temperatura de la transició

ordre-desordre. Així, la reacció de desordre per a un compost ordenat ABC,

ABC —• A0.5B0.5C pot aconseguir-se a través d'una varietat d'entorns lo-cals tots consistents amb la composició macroscópica de l'aliatge x = 0.5, per exemple amb un 100 % de A2B2, o proporcions iguals de (A3B -f AB3)

—clustering— o (A4+Ä1) — anticlustering— entorn de C. El model continu falla, doncs, en reconèixer el rol central que té la temperatura en el control de la població de clusters (anticlusters) malgrat que l'energia macroscópica de l'aliatge depèn de manera important de les proporcions relatives en què es troben aquests.

1.1.2 Model estructural

En realitat l'entalpia de formació reflecteix "una competició" entre forces atractives i repulsives, el balanç de les quals és diferent entre fases ordenades i desordenades d'un mateix sistema, d'aquí que A(H) > 0 pot ser consistent amb ordenament i anticlustering (per exemple).

Considerem les 2^ configuracions possibles dels àtoms A i B en una xarxa de N punts. Podem caracteritzar cada configuració a pel seu excés d'entalpia Ai/(er, <¡>), referit a un nombre equivalent d'àtoms A i B e n els seus respectius equilibris (sòlids AC ï BC purs). Aquí <f> és el paràmetre de xarxa per a un bulk. Un aliatge amb una composició x fixa i a temperatura T

a la fase 7 és

4

AH^x, T) =< AH(a, <f>) >7= £ Pn(7, x, T)AH(n, <f>) (1.2)

n=0

on P„ és la probabilitat efectiva de trobar el cluster n.

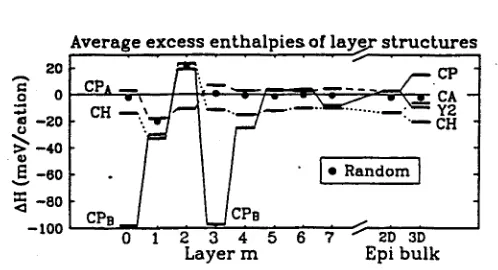
A. Compostos ordenats

Una estructura ordenada consta d'un sol arranjament local dels àtoms A i

B, A4-nBnC4, repetit translacionalment al llarg de tota la xarxa.

• Per n = 0 i n = 4 s'obté l'estructura convencional zinc-blenda (F43m).

• Per n = 2 tenim:

1. La xarxa tetragonal senzilla (P4m2 amb una xarxa catiònica

CuAu), (CA).

2. L'estructura tipus CuFeS2 calcopirita (I42d), (CH).

3. La xarxa trigonal (i?3m, amb subxarxa catiònica CuPt), (CP).

• Per n = 1 i 3 tenim:

1. L'estructura tipus CU3ASS4 luzonita (P43m).

2. L'estructura tipus Cu3SbS4 famatita ( J4rn amb subxarxa catiònica Al3Ti).

Per a cada fase ordenada n, es defineix l'excés d'entalpia respecte els com-postos binaris constituents en equilibri com

AHf = EAi_nBnCi - (^EAC + JEBC) (1.3)

El procés

(4-n)AC + nBC^A4-nBnC4 (1.4)

es pot dividir en tres [7]:

Primer, la compressió o dilatació dels compostos purs AC i BC des dels seus respectius volums en equilibri VA i VB (O si es vol, des dels respectius paràmetres de xarxa d'equilibri aAC i a°BC) al volum en equilibri Vf del

compost ordenat (oeg):

AC; VAC + BC; VBC A- ^ AC; V} + BC; Vf (1.5)

invertint una energia (que denominarem de deformació del volum)

Aquesta energia és nul·la quan els constituents estan en acord de xarxa

(VAC — VBC — V¡) i és positiva (afavoreix la separació de fases) en el cas contrari. Donat que els volums de les cel·les cúbiques en equilibri per a les diferents estructures són força similars [8], AEpv gairebé no depèn de l'estructura.

Segon, combinar AC i BC al volum final V¡ per formar l'estructura ordenada en la seva forma ideal no relaxada

AC; V} + BC; Vf A-^ A4.nBnC4 {ordenat, no relaxat); V¡ (1.7)

En aquesta "reacció" es forma una estructura que és combinació d'àtoms di-ferents de manera que és d'esperar que hi hagi una transferència de càrrega, hibriditzacions i d'altres efectes d'estructura de bandes, que poden bé dis-minuir, bé augmentar l'energia del compost respecte dels binaris. L'energia emprada AE-rc (energia de transferència de càrrega) és més aviat petita i independent del volum [8].

Tercer, relaxament de les posicions atòmiques internes per tal de mini-mitzar la tensió

A4-nBnC4 (ordenat, no relaxat); Vf —™L A4-nBnC4 (ordenat, relaxat); Vj

(1.8) Com en el cas de l'energia de deformació del volum, AREL també tendeix a

un valor nul per sistemes en acord de xarxa (ja que la longitud dels enllaços serà pràcticament idèntica) pero a diferència de AEpv, els relaxaments de-penen de la configuració n, pel fet que unes estructures relaxaran millor els esforços que d'altres. En qualsevol cas, sempre disminueix l'energia total afavorint, per tant, la formació del compost.

B. Compost aleatori

L'excés d'entalpia d'un aliatge on les posicions atòmiques estan ocupades aleatòriament, Eq. (1.1) es pot modelitzar assumint que les unitats A4-nBnC4 •

existeixen, a cada composició ar, amb una probabilitat aleatòria [7]

PR = (An) *n(i - * )4 _ n (1-9)

La reacció que descriu la formació de l'aliatge aleatori

(l-x)AC + xBCA^x AX-XBXC (1.10)

Així, les eiitalpies de formació dels compostos ordenat i desordenat que-den desglosáis en els passos bàsics descrits de la següent manera [9]:

AH](x) = AEDV{x) + AE%c(ord) + AE^EL(ord) (1.11) AHmix(x) = AEDV(x) + AETc(aleat) + AEREL(aleat) (1.12)

la seva diferència depèn de factors independents del volum

SHori = [AE$c{ord) - AETC(aleat)} + [AEREL{ard) - AEREL{aleat))

(1.13)

Representació e — G

La discussió feta a la secció anterior suggereix [10] de separar rigorosament l'energia de formació (d'un aliatge ordenat o no) en un terme depenent del volum —efectes "elàstics" (G(V(x)) = AEDV(X))—, i en un terme que depèn de l'estat d'ordenament n però no del volum —energia "substitu-cional" (gM = AETC + AEREL)—• L'excés d'entalpia de formació es pot escriure com una superposició

AH

(x, T)

=

G(x) + J2 P

e

(1-14)

per a l'aliatge desordenat, i

AH}(xn,T) = G(xn) + eW (1.15)

per a l'estructura ordenada n.

El fet que la teoria clàssica [5] no prevegi la fase ordenada és degut a què només considera el grau de llibertat estructural extern, o sigui, la part elàstica de l'energia total que comparteixen les fases ordenada i desordenada (Eq.1.11 i 1.12); l'expressió analítica ííx(l — x) és apropiada per G(x) [11]., El que diferencia aquestes són els graus de llibertat interns, sobretot la rela-xació dels àtoms a les seves posicions d'equilibri, generalment diferents per a cada arranjament atòmic. Aquest factor no tingut en compte per les teories estàndards, deixa oberta la possibilitat de la coexistència entre l'ordenament i la separació de fases.

Càlcul de AH i trets bàsics

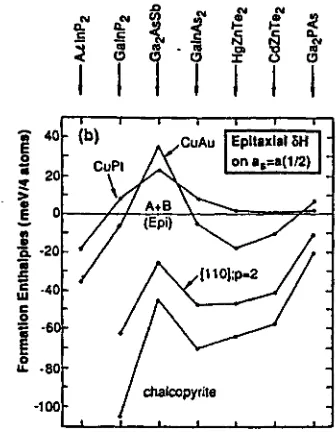
Sense entrar en els detalls dels càlculs efectuats pels autors citats [7, 8,11] en les seccions precedents fem una ullada a les anàlisi dels resultats obtinguts per aquests autors.

• Per les estructures en acord de xaxxa, es troba el següent ordre en les entalpies de formació:

AH(CA) > AH(CH) > AH(CP) > AHmix (1.16)

• Per contra pels sistemes en desacord de xarxa, es troba

AH(CP) > AH(CA) > AHmix > AH(CH) (1.17)

L'ordre de la primera seqüència * ha estat explicat [8] en termes d'energia de transferència de càrrega, donat que els sistemes en acord de xarxa exhi-beixen poca relaxació estructural. Pel contrari els sistemes en desacord de xarxa mostren una relaxació significant, donant lloc a enllaços A — CiB — C

dissimilare, reflectint l'ordre de la segona seqüència l'habilitat de les diverses xarxes a reduir la tensió associada a la diferència de grandàries atòmiques. S.-H. Wei et al [11], troben AHj > 0 per a vuit aliatges estudiats en sis estructures ordenades. El sistema amb fases separades, AC + BC, és menor en energia que qualsevol de les estructures ordenades; amb l'excepció de l'aliatge AlInP2 en l'estructura calcopirita, degut a un efecte d'estabilització per transferència de càrrega [12].

Els trets bàsics dels resultats obtinguts per S.-H. Wei et al són:

(i) L'ordre de les entalpies de formació per les diferents estructures a les equacions (1.16) i (1.17) reflecteix l'ordre de les energies de substitució (Fig. 1.2), ja que per a un sistema donat qui varia amb l'estructura és e, l'energia substitucional, mentre que G(x) no depèn de l'estructura en què s'ordeni el sistema.

(ii) Pels aliatges en acord de xarxa, G(x) ~ 0 i e > ~ 0 (veure Fig. 1.2). L'excés d'energia de formació és lleugerament positiva degut a, únicament, les interaccions químiques desfavorables (AETC > ~ 0) ja que pel fet que els'

tamanys atòmics són gairebé iguals tenim que AEDV = AEp.ei = 0. L'aliatge

desordenat té una entalpia més baixa que qualsevol de les estructures orde-nades; no es d'esperar, doncs, ordenament en aliatges semiconductors en acord de xarxa.

(iv) Pels sistemes en desacord de xarxa es troba G(x) > 0 i e < 0 però el ba-lanç global és positiu. La raó és que l'energia de deformació del volum, posi-tiva, excedeix en magnitud l'energia, favorable, de relaxament. L'estructura calcopirita presenta menor entalpia que l'aliatge desordenat, donat que "aco-moda" les diferències de tamany atòmic millor que l'estructura desordenada,

AEREL(CH) < AEREL{desordenat). Així doncs 6Hord(CH) < 0. Es pot

produir ordenament a llarg abast (calcopirita) metaestable donat que l'estat de mínima energia correspon a la separació de fases.

Figura 1.2: Separado de les entalpies de formació per a diversos compostos semiconductors ordenats en diferents estructures s en la part elàstica G(x =

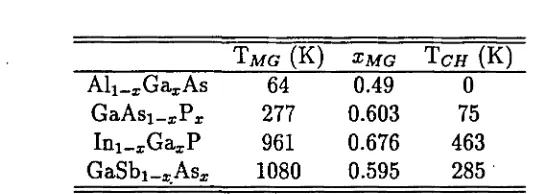
TMG (K) XMG T Ç H (K)

Alx-jjGaxAs GaAsi_xPx Ini-rGaxP

GaSbi-jjAsj;

64 277 961 1080

0.49 0.603 0.676 0.595

0 75 463 285

Taula 1.1: Temperatura del gap de miscibilitat, composició XMG = X(TMG) i

temperatura spinodal de la fase calcopirita TCH- S.-H. Wei, L.G. Ferreira, and A. Zunger, Phys. Rev. B 41, 8240 (1990).

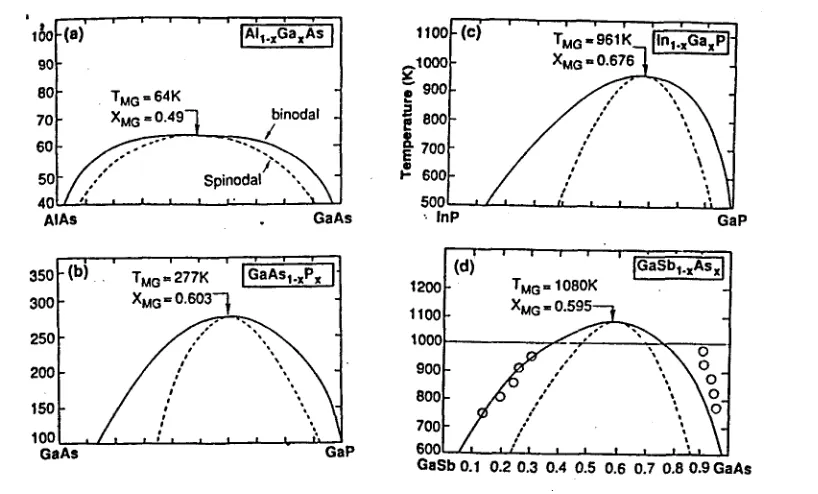
Diagrames de fase

A la Fig. 1.3 hi trobem els diagrames de fase calculats per alguns dels aliatges estudiats a la referència [11] en la part d'alta temperatura on l'aliat ge desordenat existeix. En tots els casos l'estat de mínima energia correspon a la separació de fases. A la Taula 1.1 es dona la temperatura màxima del gap de miscibilitat, TMG, calculada i la corresponent composició XMG- En equilibri termodinàmic, un sistema A^Bi-^C donat, es disgrega, per sota de

TA/GÍ en regions riques en AC o riques en BC; mentre que per sobre de TMG

es troba l'aliatge homogeni. Malgrat això, el fet que per certes configuracions ordenades l'entalpia de formació sigui menor que la de l'aliatge desordenat, possibilitaria en cas d'inhibir-se la separació de fases l'ordenament metaes-table per sota d'una certa temperatura Te (Taula 1.1).

1.1.3 Ordenament a curt abast: clustering i

anticlu-stering

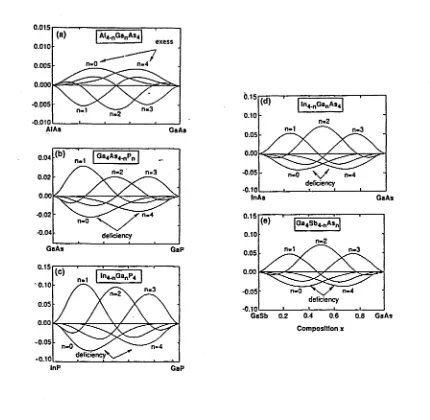
Pn(x,T) (Eq. 1.2), en mesurar la probabilitat de trobar el cluster A4_nß„ a (x,T), reflecteix l'ordre a curt abast a l'aliatge. L'excés de probabilitat [11] respecte un aliatge totalment aleatori a la mateixa composició (Eq. 1.9),

APn{x, T) = Pn( i , T)-P% (1.18)

s'anul·la per T —• co quan l'aliatge esdevé completament aleatori. A pesar que tant pels aliatges en acord com en desacord de xarxa es té que AHm{x > 0

i AHj > 0, i per tant s'esperaria la separació de fases per sota de la temperatura de miscibilitat, es troba el següent [11]:

(i) Per aliatges en acord de xarxa, APn(x,T) mostra un increment dels

100 90 80 70 60 50 iffl

r — I 1 1 ' ' ' 1 r

-(a)

TMG«64K

XM G = 0.49"J

/"T^*"'

/ *

1A . i i i

| A ' i . x G Ms

-binodal .

/

Spinodal \ \ "

•• , • \ \ AlAs GaAs GaAs 350 300 250 200 150 100 -(b) • /

TMG = 277K

XM G=0.603-|

/ t / 1 / 1 / t

1 1 ' 1 * 1

-'1 1 '"1

|GaAs,.xPx

-\ -\

\ \ \

\-__l L ¿

GaP 1100 ^1000 ^ 900 | 800 | 700 £ 600 500 (c) ' -» ' '

TMG-961K

XMQ = 0.676

/ *

f 1 1 t 1 (I ., L... 1

[ln1.xGaJtP

\ \

• ._ i i*

InP _GaP

— ' 1 — ' 1 — ' • . »

(d) [GaSb^As" TMG = 1080K

XM G. 0.595

1200 1100 1000 900 800 700 600

GaSbO.I 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 GaAs

Figura 1.3: Diagrames de fase deis aliatges: (a) AlGaAs, (b) GaAsP, (c) GalnP, i (d) GaSbAs. La línia contínua correspon al límit de miscibilitat (línia binodal), mentre que la discontínua descriu el límit de metaestabilitat (línia espinodal). S.-H. Wei, L.G. Ferreira, and A. Zunger, Phys. Rev. B

41, 8240 (1990).

i A3B són deficitaris respecte l'aliatge aleatori.

(ii) Per aliatges en desacord de xarxa es troba l'oposat: els clusters A4 i

B4 són deficitaris, mentre que els clusters formats per una barreja dels dos components es troba generalment en excés (anticlustering) (veure la Fig.

I.?)-(iii) La populació relativa de clusters n, APn(x,T), a una composició fixa

x no es veu afectada per G(x), la qual és comuna a tots els clusters a la mateixa composició x. LLavors, sistemes amb e > 0 (AlAs-GaAs i CdTe-HgTe a la Fig. 1.2) exhibeixen clustering (Fig. 1.4); mentre que sistemes amb e < 0 (GaAs-InAs, GaP-InP i GaSb-GaAs a la Fig. 1.2) exhibeixen

anticlustering (Fig. 1.4). Això mostra el fet que el coneixement de AEf

sol és insuficient i que la separació en termes depenents o independents del volum es fa necessària per a una millor comprensió i anàlisi profunda dels resultats.

1.1.4 Efectes qualitatius del creixement epitaxial

0.015 -0.010 AlAs GaAs GaAs 0.04 0.02 000 •0.02 •0.04 (b) • •

n-1 G M W n •v n-2

.. n-3

n-0 V /

deficiency GaP U.13 • 0.10 0.05 0 00 •0.05 -0.10 (c) n-1

/ " * \

• i i

ln4.n<3anP4

v/£2\ J ^

/ / \ / \ \

/ / \ / \ \

n - 0 N ^ _ _ _ ^ / "n-4 delicie n c y \ ^ ^ * ^

• i • .

•0.05 •0.10 InAs 0.15 0.10 0.05 0.00 -0.05 -0.10 (e)

ln4.„GanAs4

n-0 \ / n_"4

deficiency

Ga4Sb4.nAsn

n-2 n-1 n-3

n-0 N y / n_"4

deficiency

GaAs

GaSb 0.2 0.4 0.6 0.8 GaAs Composition x

InP GaP

Figura 1.4: Excés de probabilitat P^(x,T) a T=800 K dels clusters (a) Al4-„GaTlAs4, (b) Ga4As4_nPn, (c) Ga„ In4_nP4, (d) Ga„In4_nAs4, i (e) Ga^S^-n Asn per 0 < n < 4. S.-H. Wei, L.G. Ferreira, and A. Zunger,

troba suspesa. En el creixement epitaxial coherent, per altra part, la fase en creixement i els constituents estan constrets, per capes suficientment primes, a adoptar la constant de xarxa del substrat, a3, en el pla perpendicular a la

direcció de creixement â.

Considerem la reacció

x AC + (1 - x) BC ^ AXB^XC (1.19)

Si té lloc de forma epitaxial i totes les espècies són coherents amb el substrat, el canvi rellevant de l'entalpia és l'entalpia de formació epitaxial [6]

8Hep(as,x) = AHmix{x) + AEES(as,x) (1.20)

referida als constituents constrenyits epitaxialment, on l'energia de tensió deguda al substrat és [6]

AEEs{as,x,G) = KABc{as-aABc)2-x KAc{as-a,Acf-{^-x) KBc{as-aBc)2

(1.21) Per a una reacció on l'espècie resultant es troba en acord de xarxa amb el substrat, as = ÜABC] com que en aquest cas el primer terme de l'Eq.

(1.21) és nul, AEES(QS) < 0 i 8Hep(as) < AHmix, de manera que la

re-acció es produeix de forma més completa epitaxialment que no pas en bulk.

(1) SHep < 0

Si AHbk > 0 però —AEES > AH¡,k, aleshores SHep < 0; és a dir, es pot

produir la reacció de forma epitaxial (tot i que no es produeix en bulk). Això es mostra a la Fig. 4.23a on a la part esquerra es representen les energies de l'aliat ge i la corresponent als constituents, tan per a bulk com epilayer. Pel fet que ABC —aß a la figura— està en acord de xarxa amb el substrat la seva energia és la mateixa en bulk que en epilayer, i és menor en aquest últim cas que la suma d'energia dels constituents (separació de fases), altament tensionats degut al desacord de xarxa amb el substrat (a l'esquema s'observa l'increment, en AEES, de l'energia de la fase AC + BC

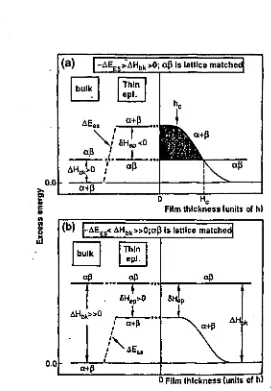
—a -f ß a la figura— en passar del bulk a l'epilayer). Es pot produir l'estabilització d'estructures inusuals com poden ser algunes estructures or-denades, respecte de la descomposició en els seus constituents (coherents amb el substrat). Aquest és el cas de l'estructura calcopirita, que com es pot veure a la Fig. 1.6 és estable per a tots els compostos en el cas de créixer epitaxialment. La part dreta de la Fig. 4.23a mostra la dependència de les energies de la fase ABC i dels constituents AC + BC amb l'espessor de l'epilayer h. Es pot veure com a partir d'un cert espessor crític, hc, la

0 Film thickness (units of h

ííHíl!

4 I • i i • .

Figura 1.6: Entalpies de formació calculades per a creixement coherent amb substrat. J.E. Bernard, R.G. Dandrea, L.G. Ferreira, S. Froyen, S.-H. Wei, and A. Zunger, Appl. Phys. Lett. 56, 731 (1990).

Hc. A partir d'aquest punt l'estabilització epitaxial deixa de produir-se.

(2) 6Hep > 0

Si AHmix > 0 és suficientment gran com per a que AHmix + AEES resti

positiu, la separació de fases és l'estat fonamental per a qualsevol espessor a pesar que 0 < 8Hep < AHmix (Fig.4.23b). Aquest és el cas dels compostos

ordenats ABC2 en l'estructura CuPt (Fig. 1.6) i dels aliatges desordenáis Ai-aBjC. Per a aquests últims una reducció de l'entalpia implica una re-ducció de la temperatura del gap de miscibilitat. El creixement epitaxial afavoreix la miscibilitat dels aliatges [14, 15].

L'exemple anterior mostra que l'estabilització per epitàxia no ve induïda per la tensió entre el substrat i l'epilayer ABC (ja que hem assumit que el-substrat està en acord de xarxa amb l'aliatge), sinó per la desestabilització deguda a l'epitàxia dels constituents (aquests estan en desacord de xarxa amb el substrat). Per tant, l'origen d'aquest efecte es troba en el desacord de xarxa Aa entre els constituents AC i BC i no en la tensió entre epilayer

ABC i substrat. Això esdevé obvi [6] introduint la llei de Vegard

o-ABC = x aAC + (1 - x) aBc (1.22)

a l'Eq.(1.21) i posant a, = ÜABC es té

AEES(X, a.) = -(Aa)2x(l - x)[(l - x)KAC + xKBc (1.23)

Així doncs, només si els constituents estan en desacord de xarxa

1.1.5 Sumari

Resumim els trets característics del comportament esperat en semiconduc-tors III-V en equilibri termodinàmic tridimensional.

• Aliatges en acord de xarxa:

1. L'efecte estabilitzador del creixement epitaxial és inexistent: do-nat que els tamanys dels constituents són pràcticament iguals, si l'aliatge es troba en acord de xarxa amb el substrat també s'hi trobaran els constituents.

2. AEf > 0, AEmix > 0 i SEord > 0. Exhibeixen separació de fases a

temperatures força baixes. Per sobre de TMG els sistemes mostren un dèbil ordenament de curt abast (clustering). No s'espera cap tipus d'ordenament a llarg abast.

• Aliatges en desacord de xarxa:

1. En creixement bulk presenten: separació de fases com a estat de mínima energia. Per sobre de TMG, que sol ser alta, l'aliatge desordenat exhibeix anticlustering.

2. AEf > 0, AEmix > 0 i 8Eord{CH) < 0. Ordenament metaestable

(amb l'excepció del compost AlInP2 que presenta AEmix(CH) <

0.

3. Si s'inhibeix la separació de fases, mitjançant l'epitàxia, l'ordena-ment en l'estructura calcopirita és estable.

1.2 Observació d'ordenament espontani en

compostos isovalents III-V

La constatació experimental del creixement espontani de fases ordenades en compostos isovalents III-V, quasi exclusivament amb tècniques de creixement en fase vapor (MBE, MOVPE,...,etc), va anar paral·lela amb els treballs teòrics d'estudi de l'estabilitat termodinámica.

La primera referència que es té del fenomen 2 és l'article de Kuan et al

[16] en aliatges Al^Gai-sAs crescuts per MOCVD sobre substrats (110) i (001) de GaAs. Els diagrames de difracció d'electrons (TED) mostren refle-xions prohibides (001,110,112,110,130,..., etc) per l'estructura desordenada però assolibles per una estructura tipus CuAu-I de la subxarxa catiònica.